5
Comparative Studies
It is deceptively simple to imagine that a curriculum’s effectiveness could be easily determined by a single well-designed study. Such a study would randomly assign students to two treatment groups, one using the experimental materials and the other using a widely established comparative program. The students would be taught the entire curriculum, and a test administered at the end of instruction would provide unequivocal results that would permit one to identify the more effective treatment.
The truth is that conducting definitive comparative studies is not simple, and many factors make such an approach difficult. Student placement and curricular choice are decisions that involve multiple groups of decision makers, accrue over time, and are subject to day-to-day conditions of instability, including student mobility, parent preference, teacher assignment, administrator and school board decisions, and the impact of standardized testing. This complex set of institutional policies, school contexts, and individual personalities makes comparative studies, even quasi-experimental approaches, challenging, and thus demands an honest and feasible assessment of what can be expected of evaluation studies (Usiskin, 1997; Kilpatrick, 2002; Schoenfeld, 2002; Shafer, in press).
Comparative evaluation study is an evolving methodology, and our purpose in conducting this review was to evaluate and learn from the efforts undertaken so far and advise on future efforts. We stipulated the use of comparative studies as follows:
A comparative study was defined as a study in which two (or more) curricular treatments were investigated over a substantial period of time (at least one semester, and more typically an entire school year) and a comparison of various curricular outcomes was examined using statistical tests. A statistical test was required to ensure the robustness of the results relative to the study’s design.
We read and reviewed a set of 95 comparative studies. In this report we describe that database, analyze its results, and draw conclusions about the quality of the evaluation database both as a whole and separated into evaluations supported by the National Science Foundation and commercially generated evaluations. In addition to describing and analyzing this database, we also provide advice to those who might wish to fund or conduct future comparative evaluations of mathematics curricular effectiveness. We have concluded that the process of conducting such evaluations is in its adolescence and could benefit from careful synthesis and advice in order to increase its rigor, feasibility, and credibility. In addition, we took an interdisciplinary approach to the task, noting that various committee members brought different expertise and priorities to the consideration of what constitutes the most essential qualities of rigorous and valid experimental or quasi-experimental design in evaluation. This interdisciplinary approach has led to some interesting observations and innovations in our methodology of evaluation study review.
This chapter is organized as follows:
-
Study counts disaggregated by program and program type.
-
Seven critical decision points and identification of at least minimally methodologically adequate studies.
-
Definition and illustration of each decision point.
-
A summary of results by student achievement in relation to program types (NSF-supported, University of Chicago School Mathematics Project (UCSMP), and commercially generated) in relation to their reported outcome measures.
-
A list of alternative hypotheses on effectiveness.
-
Filters based on the critical decision points.
-
An analysis of results by subpopulations.
-
An analysis of results by content strand.
-
An analysis of interactions among content, equity, and grade levels.
-
Discussion and summary statements.
In this report, we describe our methodology for review and synthesis so that others might scrutinize our approach and offer criticism on the basis of
our methodology and its connection to the results stated and conclusions drawn. In the spirit of scientific, fair, and open investigation, we welcome others to undertake similar or contrasting approaches and compare and discuss the results. Our work was limited by the short timeline set by the funding agencies resulting from the urgency of the task. Although we made multiple efforts to collect comparative studies, we apologize to any curriculum evaluators if comparative studies were unintentionally omitted from our database.
Of these 95 comparative studies, 65 were studies of NSF-supported curricula, 27 were studies of commercially generated materials, and 3 included two curricula each from one of these two categories. To avoid the problem of double coding, two studies, White et al. (1995) and Zahrt (2001), were coded within studies of NSF-supported curricula because more of the classes studied used the NSF-supported curriculum. These studies were not used in later analyses because they did not meet the requirements for the at least minimally methodologically adequate studies, as described below. The other, Peters (1992), compared two commercially generated curricula, and was coded in that category under the primary program of focus. Therefore, of the 95 comparative studies, 67 studies were coded as NSF-supported curricula and 28 were coded as commercially generated materials.
The 11 evaluation studies of the UCSMP secondary program that we reviewed, not including White et al. and Zahrt as previously mentioned, benefit from the maturity of the program, while demonstrating an orientation to both establishing effectiveness and improving a product line. For these reasons, at times we will present the summary of UCSMP’s data separately.
The Saxon materials also present a somewhat different profile from the other commercially generated materials because many of the evaluations of these materials were conducted in the 1980s and the materials were originally developed with a rather atypical program theory. Saxon (1981) designed its algebra materials to combine distributed practice with incremental development. We selected the Saxon materials as a middle grades commercially generated program, and limited its review to middle school studies from 1989 onward when the first National Council of Teachers of Mathematics (NCTM) Standards (NCTM, 1989) were released. This eliminated concerns that the materials or the conditions of educational practice have been altered during the intervening time period. The Saxon materials explicitly do not draw from the NCTM Standards nor did they receive support from the NSF; thus they truly represent a commercial venture. As a result, we categorized the Saxon studies within the group of studies of commercial materials.
At times in this report, we describe characteristics of the database by
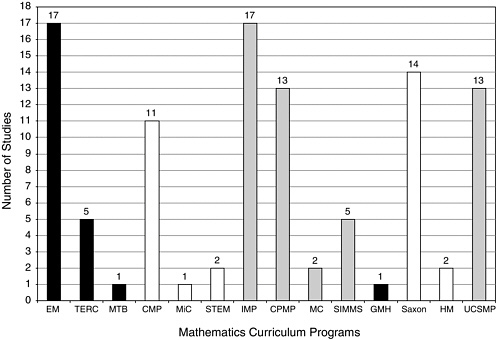
FIGURE 5-1 The distribution of comparative studies across programs. Programs are coded by grade band: black bars = elementary, white bars = middle grades, and gray bars = secondary. In this figure, there are six studies that involved two programs and one study that involved three programs.
NOTE: Five programs (MathScape, MMAP, MMOW/ARISE, Addison-Wesley, and Harcourt) are not shown above since no comparative studies were reviewed.
particular curricular program evaluations, in which case all 19 programs are listed separately. At other times, when we seek to inform ourselves on policy-related issues of funding and evaluating curricular materials, we use the NSF-supported, commercially generated, and UCSMP distinctions. We remind the reader of the artificial aspects of this distinction because at the present time, 18 of the 19 curricula are published commercially. In order to track the question of historical inception and policy implications, a distinction is drawn between the three categories. Figure 5-1 shows the distribution of comparative studies across the 14 programs.
The first result the committee wishes to report is the uneven distribution of studies across the curricula programs. There were 67 coded studies of the NSF curricula, 11 studies of UCSMP, and 17 studies of the commercial publishers. The 14 evaluation studies conducted on the Saxon materials compose the bulk of these 17-non-UCSMP and non-NSF-supported curricular evaluation studies. As these results suggest, we know more about the
evaluations of the NSF-supported curricula and UCSMP than about the evaluations of the commercial programs. We suggest that three factors account for this uneven distribution of studies. First, evaluations have been funded by the NSF both as a part of the original call, and as follow-up to the work in the case of three supplemental awards to two of the curricula programs. Second, most NSF-supported programs and UCSMP were developed at university sites where there is access to the resources of graduate students and research staff. Finally, there was some reported reluctance on the part of commercial companies to release studies that could affect perceptions of competitive advantage. As Figure 5-1 shows, there were quite a few comparative studies of Everyday Mathematics (EM), Connected Mathematics Project (CMP), Contemporary Mathematics in Context (Core-Plus Mathematics Project [CPMP]), Interactive Mathematics Program (IMP), UCSMP, and Saxon.
In the programs with many studies, we note that a significant number of studies were generated by a core set of authors. In some cases, the evaluation reports follow a relatively uniform structure applied to single schools, generating multiple studies or following cohorts over years. Others use a standardized evaluation approach to evaluate sequential courses. Any reports duplicating exactly the same sample, outcome measures, or forms of analysis were eliminated. For example, one study of Mathematics Trailblazers (Carter et al., 2002) reanalyzed the data from the larger ARC Implementation Center study (Sconiers et al., 2002), so it was not included separately. Synthesis studies referencing a variety of evaluation reports are summarized in Chapter 6, but relevant individual studies that were referenced in them were sought out and included in this comparative review.
Other less formal comparative studies are conducted regularly at the school or district level, but such studies were not included in this review unless we could obtain formal reports of their results, and the studies met the criteria outlined for inclusion in our database. In our conclusions, we address the issue of how to collect such data more systematically at the district or state level in order to subject the data to the standards of scholarly peer review and make it more systematically and fairly a part of the national database on curricular effectiveness.
A standard for evaluation of any social program requires that an impact assessment is warranted only if two conditions are met: (1) the curricular program is clearly specified, and (2) the intervention is well implemented. Absent this assurance, one must have a means of ensuring or measuring treatment integrity in order to make causal inferences. Rossi et al. (1999, p. 238) warned that:
two prerequisites [must exist] for assessing the impact of an intervention. First, the program’s objectives must be sufficiently well articulated to make
it possible to specify credible measures of the expected outcomes, or the evaluator must be able to establish such a set of measurable outcomes. Second, the intervention should be sufficiently well implemented that there is no question that its critical elements have been delivered to appropriate targets. It would be a waste of time, effort, and resources to attempt to estimate the impact of a program that lacks measurable outcomes or that has not been properly implemented. An important implication of this last consideration is that interventions should be evaluated for impact only when they have been in place long enough to have ironed out implementation problems.
These same conditions apply to evaluation of mathematics curricula. The comparative studies in this report varied in the quality of documentation of these two conditions; however, all addressed them to some degree or another. Initially by reviewing the studies, we were able to identify one general design template, which consisted of seven critical decision points and determined that it could be used to develop a framework for conducting our meta-analysis. The seven critical decision points we identified initially were:
-
Choice of type of design: experimental or quasi-experimental;
-
For those studies that do not use random assignment: what methods of establishing comparability of groups were built into the design—this includes student characteristics, teacher characteristics, and the extent to which professional development was involved as part of the definition of a curriculum;
-
Definition of the appropriate unit of analysis (students, classes, teachers, schools, or districts);
-
Inclusion of an examination of implementation components;
-
Definition of the outcome measures and disaggregated results by program;
-
The choice of statistical tests, including statistical significance levels and effect size; and
-
Recognition of limitations to generalizability resulting from design choices.
These are critical decisions that affect the quality of an evaluation. We further identified a subset of these evaluation studies that met a set of minimum conditions that we termed at least minimally methodologically adequate studies. Such studies are those with the greatest likelihood of shedding light on the effectiveness of these programs. To be classified as at least minimally methodologically adequate, and therefore to be considered for further analysis, each evaluation study was required to:
-
Include quantifiably measurable outcomes such as test scores, responses to specified cognitive tasks of mathematical reasoning, performance evaluations, grades, and subsequent course taking; and
-
Provide adequate information to judge the comparability of samples. In addition, a study must have included at least one of the following additional design elements:
-
A report of implementation fidelity or professional development activity;
-
Results disaggregated by content strands or by performance by student subgroups; and/or
-
Multiple outcome measures or precise theoretical analysis of a measured construct, such as number sense, proof, or proportional reasoning.
Using this rubric, the committee identified a subset of 63 comparative studies to classify as at least minimally methodologically adequate and to analyze in depth to inform the conduct of future evaluations. There are those who would argue that any threat to the validity of a study discredits the findings, thus claiming that until we know everything, we know nothing. Others would claim that from the myriad of studies, examining patterns of effects and patterns of variation, one can learn a great deal, perhaps tentatively, about programs and their possible effects. More importantly, we can learn about methodologies and how to concentrate and focus to increase the likelihood of learning more quickly. As Lipsey (1997, p. 22) wrote:
In the long run, our most useful and informative contribution to program managers and policy makers and even to the evaluation profession itself may be the consolidation of our piecemeal knowledge into broader pictures of the program and policy spaces at issue, rather than individual studies of particular programs.
We do not wish to imply that we devalue studies of student affect or conceptions of mathematics, but decided that unless these indicators were connected to direct indicators of student learning, we would eliminate them from further study. As a result of this sorting, we eliminated 19 studies of NSF-supported curricula and 13 studies of commercially generated curricula. Of these, 4 were eliminated for their sole focus on affect or conceptions, 3 were eliminated for their comparative focus on outcomes other than achievement, such as teacher-related variables, and 19 were eliminated for their failure to meet the minimum additional characteristics specified in the criteria above. In addition, six others were excluded from the studies of commercial materials because they were not conducted within the grade-
level band specified by the committee for the selection of that program. From this point onward, all references can be assumed to refer to at least minimally methodologically adequate unless a study is referenced for illustration, in which case we label it with “EX” to indicate that it is excluded in the summary analyses. Studies labeled “EX” are occasionally referenced because they can provide useful information on certain aspects of curricular evaluation, but not on the overall effectiveness.
The at least minimally methodologically adequate studies reported on a variety of grade levels. Figure 5-2 shows the different grade levels of the studies. At times, the choice of grade levels was dictated by the years in which high-stakes tests were given. Most of the studies reported on multiple grade levels, as shown in Figure 5-2.
Using the seven critical design elements of at least minimally methodologically adequate studies as a design template, we describe the overall database and discuss the array of choices on critical decision points with examples. Following that, we report on the results on the at least minimally methodologically adequate studies by program type. To do so, the results of each study were coded as either statistically significant or not. Those studies
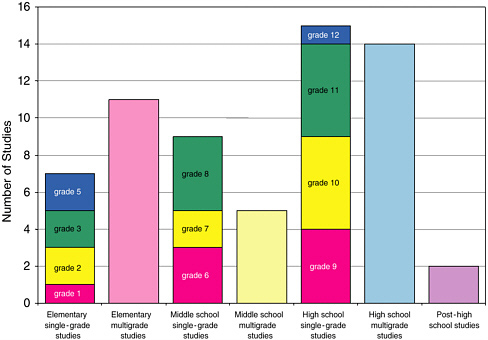
FIGURE 5-2 Single-grade studies by grade and multigrade studies by grade band.
that contained statistically significant results were assigned a percentage of outcomes that are positive (in favor of the treatment curriculum) based on the number of statistically significant comparisons reported relative to the total number of comparisons reported, and a percentage of outcomes that are negative (in favor of the comparative curriculum). The remaining were coded as the percentage of outcomes that are non significant. Then, using seven critical decision points as filters, we identified and examined more closely sets of studies that exhibited the strongest designs, and would therefore be most likely to increase our confidence in the validity of the evaluation. In this last section, we consider alternative hypotheses that could explain the results.
The committee emphasizes that we did not directly evaluate the materials. We present no analysis of results aggregated across studies by naming individual curricular programs because we did not consider the magnitude or rigor of the database for individual programs substantial enough to do so. Nevertheless, there are studies that provide compelling data concerning the effectiveness of the program in a particular context. Furthermore, we do report on individual studies and their results to highlight issues of approach and methodology and to remain within our primary charge, which was to evaluate the evaluations, we do not summarize results of the individual programs.
DESCRIPTION OF COMPARATIVE STUDIES DATABASE ON CRITICAL DECISION POINTS
An Experimental or Quasi-Experimental Design
We separated the studies into experimental and quasiexperimental, and found that 100 percent of the studies were quasiexperimental (Campbell and Stanley, 1966; Cook and Campbell, 1979; and Rossi et al., 1999).1 Within the quasi-experimental studies, we identified three subcategories of comparative study. In the first case, we identified a study as cross-curricular comparative if it compared the results of curriculum A with curriculum B. A few studies in this category also compared two samples within the curriculum to each other and specified different conditions such as high and low implementation quality.
A second category of a quasi-experimental study involved comparisons that could shed light on effectiveness involving time series studies. These studies compared the performance of a sample of students in a curriculum
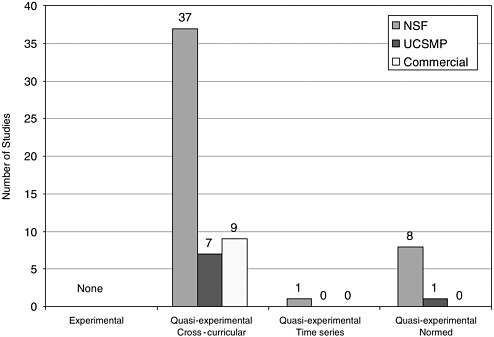
FIGURE 5-3 The number of comparative studies in each category.
under investigation across time, such as in a longitudinal study of the same students over time. A third category of comparative study involved a comparison to some form of externally normed results, such as populations taking state, national, or international tests or prior research assessment from a published study or studies. We categorized these studies and divided them into NSF, UCSMP, and commercial and labeled them by the categories above (Figure 5-3).
In nearly all studies in the comparative group, the titles of experimental curricula were explicitly identified. The only exception to this was the ARC Implementation Center study (Sconiers et al., 2002), where three NSF-supported elementary curricula were examined, but in the results, their effects were pooled. In contrast, in the majority of the cases, the comparison curriculum is referred to simply as “traditional.” In only 22 cases were comparisons made between two identified curricula. Many others surveyed the array of curricula at comparison schools and reported on the most frequently used, but did not identify a single curriculum. This design strategy is used often because other factors were used in selecting comparison groups, and the additional requirement of a single identified curriculum in
these sites would often make it difficult to match. Studies were categorized into specified (including a single or multiple identified curricula) and nonspecified curricula. In the 63 studies, the central group was compared to an NSF-supported curriculum (1), an unnamed traditional curriculum (41), a named traditional curriculum (19), and one of the six commercial curricula (2). To our knowledge, any systematic impact of such a decision on results has not been studied, but we express concern that when a specified curriculum is compared to an unspecified content which is a set of many informal curriculum, the comparison may favor the coherency and consistency of the single curricula, and we consider this possibility subsequently under alternative hypotheses. We believe that a quality study should at least report the array of curricula that comprise the comparative group and include a measure of the frequency of use of each, but a well-defined alternative is more desirable.
If a study was both longitudinal and comparative, then it was coded as comparative. When studies only examined performances of a group over time, such as in some longitudinal studies, it was coded as quasi-experimental normed. In longitudinal studies, the problems created by student mobility were evident. In one study, Carroll (2001), a five-year longitudinal study of Everyday Mathematics, the sample size began with 500 students, 24 classrooms, and 11 schools. By 2nd grade, the longitudinal sample was 343. By 3rd grade, the number of classes increased to 29 while the number of original students decreased to 236 students. At the completion of the study, approximately 170 of the original students were still in the sample. This high rate of attrition from the study suggests that mobility is a major challenge in curricular evaluation, and that the effects of curricular change on mobile students needs to be studied as a potential threat to the validity of the comparison. It is also a challenge in curriculum implementation because students coming into a program do not experience its cumulative, developmental effect.
Longitudinal studies also have unique challenges associated with outcome measures, a study by Romberg et al. (in press) (EX) discussed one approach to this problem. In this study, an external assessment system and a problem-solving assessment system were used. In the External Assessment System, items from the National Assessment of Educational Progress (NAEP) and Third International Mathematics and Science Survey (TIMSS) were balanced across four strands (number, geometry, algebra, probability and statistics), and 20 items of moderate difficulty, called anchor items, were repeated on each grade-specific assessment (p. 8). Because the analyses of the results are currently under way, the evaluators could not provide us with final results of this study, so it is coded as EX.
However, such longitudinal studies can provide substantial evidence of the effects of a curricular program because they may be more sensitive to an
TABLE 5-1 Scores in Percentage Correct by Everyday Mathematics Students and Various Comparison Groups Over a Five-Year Longitudinal Study
accumulation of modest effects and/or can reveal whether the rates of learning change over time within curricular change.
The longitudinal study by Carroll (2001) showed that the effects of curricula may often accrue over time, but measurements of achievement present challenges to drawing such conclusions as the content and grade level change. A variety of measures were used over time to demonstrate growth in relation to comparison groups. The author chose a set of measures used previously in studies involving two Asian samples and an American sample to provide a contrast to the students in EM over time. For 3rd and 4th grades, where the data from the comparison group were not available, the authors selected items from the NAEP to bridge the gap. Table 5-1 summarizes the scores of the different comparative groups over five years. Scores are reported as the mean percentage correct for a series of tests on number computation, number concepts and applications, geometry, measurement, and data analysis.
It is difficult to compare performances on different tests over different groups over time against a single longitudinal group from EM, and it is not possible to determine whether the students’ performance is increasing or whether the changes in the tests at each grade level are producing the results; thus the results from longitudinal studies lacking a control group or use of sophisticated methodological analysis may be suspect and should be interpreted with caution.
In the Hirsch and Schoen (2002) study, based on a sample of 1,457 students, scores on Ability to Do Quantitative Thinking (ITED-Q) a subset of the Iowa Tests of Education Development, students in Core-Plus showed increasing performance over national norms over the three-year time period. The authors describe the content of the ITED-Q test and point out
that “although very little symbolic algebra is required, the ITED-Q is quite demanding for the full range of high school students” (p. 3). They further point out that “[t]his 3-year pattern is consistent, on average, in rural, urban, and suburban schools, for males and females, for various minority groups, and for students for whom English was not their first language” (p. 4). In this case, one sees that studies over time are important as results over shorter periods may mask cumulative effects of consistent and coherent treatments and such studies could also show increases that do not persist when subject to longer trajectories. One approach to longitudinal studies was used by Webb and Dowling in their studies of the Interactive Mathematics Program (Webb and Dowling, 1995a, 1995b, 1995c). These researchers conducted transcript analyses as a means to examine student persistence and success in subsequent course taking.
The third category of quasi-experimental comparative studies measured student outcomes on a particular curricular program and simply compared them to performance on national tests or international tests. When these tests were of good quality and were representative of a genuine sample of a relevant population, such as NAEP reports or TIMSS results, the reports often provided one a reasonable indicator of the effects of the program if combined with a careful description of the sample. Also, sometimes the national tests or state tests used were norm-referenced tests producing national percentiles or grade-level equivalents. The normed studies were considered of weaker quality in establishing effectiveness, but were still considered valid as examples of comparing samples to populations.
For Studies That Do Not Use Random Assignment: What Methods of Establishing Comparability Across Groups Were Built into the Design
The most fundamental question in an evaluation study is whether the treatment has had an effect on the chosen criterion variable. In our context, the treatment is the curriculum materials, and in some cases, related professional development, and the outcome of interest is academic learning. To establish if there is a treatment effect, one must logically rule out as many other explanations as possible for the differences in the outcome variable. There is a long tradition on how this is best done, and the principle from a design point of view is to assure that there are no differences between the treatment conditions (especially in these evaluations, often there are only the new curriculum materials to be evaluated and a control group) either at the outset of the study or during the conduct of the study.
To ensure the first condition, the ideal procedure is the random assignment of the appropriate units to the treatment conditions. The second condition requires that the treatment is administered reliably during the length of the study, and is assured through the careful observation and
control of the situation. Without randomization, there are a host of possible confounding variables that could differ among the treatment conditions and that are related themselves to the outcome variables. Put another way, the treatment effect is a parameter that the study is set up to estimate. Statistically, an estimate that is unbiased is desired. The goal is that its expected value over repeated samplings is equal to the true value of the parameter. Without randomization at the onset of a study, there is no way to assure this property of unbiasness. The variables that differ across treatment conditions and are related to the outcomes are confounding variables, which bias the estimation process.
Only one study we reviewed, Peters (1992), used randomization in the assignment of students to treatments, but that occurred because the study was limited to one teacher teaching two sections and included substantial qualitative methods, so we coded it as quasi-experimental. Others report partially assigning teachers randomly to treatment conditions (Thompson, et al., 2001; Thompson et al., 2003). Two primary reasons seem to account for a lack of use of pure experimental design. To justify the conduct and expense of a randomized field trial, the program must be described adequately and there must be relative assurance that its implementation has occurred over the duration of the experiment (Peterson et al., 1999). Additionally, one must be sure that the outcome measures are appropriate for the range of performances in the groups and valid relative to the curricula under investigation. Seldom can such conditions be assured for all students and teachers and over the duration of a year or more.
A second reason is that random assignment of classrooms to curricular treatment groups typically is not permitted or encouraged under normal school conditions. As one evaluator wrote, “Building or district administrators typically identified teachers who would be in the study and in only a few cases was random assignment of teachers to UCSMP Algebra or comparison classes possible. School scheduling and teacher preference were more important factors to administrators and at the risk of losing potential sites, we did not insist on randomization” (Mathison et al., 1989, p. 11).
The Joint Committee on Standards for Educational Evaluation (1994, p. 165) committee of evaluations recognized the likelihood of limitations on randomization, writing:
The groups being compared are seldom formed by random assignment. Rather, they tend to be natural groupings that are likely to differ in various ways. Analytical methods may be used to adjust for these initial differences, but these methods are based upon a number of assumptions. As it is often difficult to check such assumptions, it is advisable, when time and resources permit, to use several different methods of analysis to determine whether a replicable pattern of results is obtained.
Does the dearth of pure experimentation render the results of the studies reviewed worthless? Bias is not an “either-or” proposition, but it is a quantity of varying degrees. Through careful measurement of the most salient potential confounding variables, precise theoretical description of constructs, and use of these methods of statistical analysis, it is possible to reduce the amount of bias in the estimated treatment effect. Identification of the most likely confounding variables and their measurement and subsequent adjustments can greatly reduce bias and help estimate an effect that is likely to be more reflective of the true value. The theoretical fully specified model is an alternative to randomization by including relevant variables and thus allowing the unbiased estimation of the parameter. The only problem is realizing when the model is fully specified.
We recognized that we can never have enough knowledge to assure a fully specified model, especially in the complex and unstable conditions of schools. However, a key issue in determining the degree of confidence we have in these evaluations is to examine how they have identified, measured, or controlled for such confounding variables. In the next sections, we report on the methods of the evaluators in identifying and adjusting for such potential confounding variables.
One method to eliminate confounding variables is to examine the extent to which the samples investigated are equated either by sample selection or by methods of statistical adjustments. For individual students, there is a large literature suggesting the importance of social class to achievement. In addition, prior achievement of students must be considered. In the comparative studies, investigators first identified participation of districts, schools, or classes that could provide sufficient duration of use of curricular materials (typically two years or more), availability of target classes, or adequate levels of use of program materials. Establishing comparability was a secondary concern.
These two major factors were generally used in establishing the comparability of the sample:
-
Student population characteristics, such as demographic characteristics of students in terms of race/ethnicity, economic levels, or location type (urban, suburban, or rural).
-
Performance-level characteristics such as performance on prior tests, pretest performance, percentage passing standardized tests, or related measures (e.g., problem solving, reading).
In general, four methods of comparing groups were used in the studies we examined, and they permit different degrees of confidence in their results. In the first type, a matching class, school, or district was identified.
Studies were coded as this type if specified characteristics were used to select the schools systematically. In some of these studies, the methodology was relatively complex as correlates of performance on the outcome measures were found empirically and matches were created on that basis (Schneider, 2000; Riordan and Noyce, 2001; and Sconiers et al., 2002). For example, in the Sconiers et al. study, where the total sample of more than 100,000 students was drawn from five states and three elementary curricula are reviewed (Everyday Mathematics, Math Trailblazers [MT], and Investigations [IN], a highly systematic method was developed. After defining eligibility as a “reform school,” evaluators conducted separate regression analyses for the five states at each tested grade level to identify the strongest predictors of average school mathematics score. They reported, “reading score and low-income variables … consistently accounted for the greatest percentage of total variance. These variables were given the greatest weight in the matching process. Other variables—such as percent white, school mobility rate, and percent with limited English proficiency (LEP)—accounted for little of the total variance but were typically significant. These variables were given less weight in the matching process” (Sconiers et al., 2002, p. 10). To further provide a fair and complete comparison, adjustments were made based on regression analysis of the scores to minimize bias prior to calculating the difference in scores and reporting effect sizes. In their results the evaluators report, “The combined state-grade effect sizes for math and total are virtually identical and correspond to a percentile change of about 4 percent favoring the reform students” (p. 12).
A second type of matching procedure was used in the UCSMP evaluations. For example, in an evaluation centered on geometry learning, evaluators advertised in NCTM and UCSMP publications, and set conditions for participation from schools using their program in terms of length of use and grade level. After selecting schools with heterogeneous grouping and no tracking, the researchers used a match-pair design where they selected classes from the same school on the basis of mathematics ability. They used a pretest to determine this, and because the pretest consisted of two parts, they adjusted their significance level using the Bonferroni method.2 Pairs were discarded if the differences in means and variance were significant for all students or for those students completing all measures, or if class sizes became too variable. In the algebra study, there were 20 pairs as a result of the matching, and because they were comparing three experimental conditions—first edition, second edition, and comparison classes—in the com-
parison study relevant to this review, their matching procedure identified 8 pairs. When possible, teachers were assigned randomly to treatment conditions. Most results are presented with the eight identified pairs and an accumulated set of means. The outcomes of this particular study are described below in a discussion of outcome measures (Thompson et al., 2003).
A third method was to measure factors such as prior performance or socio-economic status (SES) based on pretesting, and then to use analysis of covariance or multiple regression in the subsequent analysis to factor in the variance associated with these factors. These studies were coded as “control.” A number of studies of the Saxon curricula used this method. For example, Rentschler (1995) conducted a study of Saxon 76 compared to Silver Burdett with 7th graders in West Virginia. He reported that the groups differed significantly in that the control classes had 65 percent of the students on free and reduced-price lunch programs compared to 55 percent in the experimental conditions. He used scores on California Test of Basic Skills mathematics computation and mathematics concepts and applications as his pretest scores and found significant differences in favor of the experimental group. His posttest scores showed the Saxon experimental group outperformed the control group on both computation and concepts and applications. Using analysis of covariance, the computation difference in favor of the experimental group was statistically significant; however, the difference in concepts and applications was adjusted to show no significant difference at the p < .05 level.
A fourth method was noted in studies that used less rigorous methods of selection of sample and comparison of prior achievement or similar demographics. These studies were coded as “compare.” Typically, there was no explicit procedure to decide if the comparison was good enough. In some of the studies, it appeared that the comparison was not used as a means of selection, but rather as a more informal device to convince the reader of the plausibility of the equivalence of the groups. Clearly, the studies that used a more precise method of selection were more likely to produce results on which one’s confidence in the conclusions is greater.
Definition of Unit of Analysis
A major decision in forming an evaluation design is the unit of analysis. The unit of selection or randomization used to assign elements to treatment and control groups is closely linked to the unit of analysis. As noted in the National Research Council (NRC) report (1992, p. 21):
If one carries out the assignment of treatments at the level of schools, then that is the level that can be justified for causal analysis. To analyze the results at the student level is to introduce a new, nonrandomized level into
the study, and it raises the same issues as does the nonrandomized observational study…. The implications … are twofold. First, it is advisable to use randomization at the level at which units are most naturally manipulated. Second, when the unit of observation is at a “lower” level of aggregation than the unit of randomization, then for many purposes the data need to be aggregated in some appropriate fashion to provide a measure that can be analyzed at the level of assignment. Such aggregation may be as simple as a summary statistic or as complex as a context-specific model for association among lower-level observations.
In many studies, inadequate attention was paid to the fact that the unit of selection would later become the unit of analysis. The unit of analysis, for most curriculum evaluators, needs to be at least the classroom, if not the school or even the district. The units must be independently responding units because instruction is a group process. Students are not independent, the classroom—even if the teachers work together in a school on instruction—is not entirely independent, so the school is the unit. Care needed to be taken to ensure that an adequate numbers of units would be available to have sufficient statistical power to detect important differences.
A curriculum is experienced by students in a group, and this implies that individual student responses and what they learn are correlated. As a result, the appropriate unit of assignment and analysis must at least be defined at the classroom or teacher level. Other researchers (Bryk et al., 1993) suggest that the unit might be better selected at an even higher level of aggregation. The school itself provides a culture in which the curriculum is enacted as it is influenced by the policies and assignments of the principal, by the professional interactions and governance exhibited by the teachers as a group, and by the community in which the school resides. This would imply that the school might be the appropriate unit of analysis. Even further, to the extent that such decisions about curriculum are made at the district level and supported through resources and professional development at that level, the appropriate unit could arguably be the district. On a more practical level, we found that arguments can be made for a variety of decisions on the selection of units, and what is most essential is to make a clear argument for one’s choice, to use the same unit in the analysis as in the sample selection process, and to recognize the potential limits to generalization that result from one’s decisions.
We would argue in all cases that reports of how sites are selected must be explicit in the evaluation report. For example, one set of evaluation studies selected sites by advertisements in a journal distributed by the program and in NCTM journals (UCSMP) (Thompson et al., 2001; Thompson et al., 2003). The samples in their studies tended to be affluent suburban populations and predominantly white populations. Other conditions of inclusion, such as frequency of use also might have influenced this outcome,
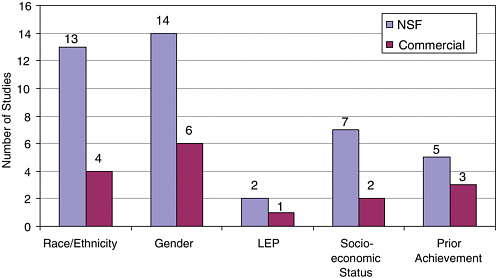
but it is important that over a set of studies on effectiveness, all populations of students be adequately sampled. When a study is not randomized, adjustments for these confounding variables should be included. In our analysis of equity, we report on the concerns about representativeness of the overall samples and their impact on the generalizability of the results.
Implementation Components
The complexity of doing research on curricular materials introduces a number of possible confounding variables. Due to the documented complexity of curricular implementation, most comparative study evaluators attempt to monitor implementation in some fashion. A valuable outcome of a well-conducted evaluation is to determine not only if the experimental curriculum could ideally have a positive impact on learning, but whether it can survive or thrive in the conditions of schooling that are so variable across sites. It is essential to know what the treatment was, whether it occurred, and if so, to what degree of intensity, fidelity, duration, and quality. In our model in Chapter 3, these factors were referred to as “implementation components.” Measuring implementation can be costly for large-scale comparative studies; however, many researchers have shown that variation in implementation is a key factor in determining effectiveness. In coding the comparative studies, we identified three types of components that help to document the character of the treatment: implementation fidelity, professional development treatments, and attention to teacher effects.
Implementation Fidelity
Implementation fidelity is a measure of the basic extent of use of the curricular materials. It does not address issues of instructional quality. In some studies, implementation fidelity is synonymous with “opportunity to learn.” In examining implementation fidelity, a variety of data were reported, including, most frequently, the extent of coverage of the curricular material, the consistency of the instructional approach to content in relation to the program’s theory, reports of pedagogical techniques, and the length of use of the curricula at the sample sites. Other less frequently used approaches documented the calendar of curricular coverage, requested teacher feedback by textbook chapter, conducted student surveys, and gauged homework policies, use of technology, and other particular program elements. Interviews with teachers and students, classroom surveys, and observations were the most frequently used data-gathering techniques. Classroom observations were conducted infrequently in these studies, except in cases when comparative studies were combined with case studies, typically with small numbers of schools and classes where observations
were conducted for long or frequent time periods. In our analysis, we coded only the presence or absence of one or more of these methods.
If the extent of implementation was used in interpreting the results, then we classified the study as having adjusted for implementation differences. Across all 63 at least minimally methodologically adequate studies, 44 percent reported some type of implementation fidelity measure, 3 percent reported and adjusted for it in interpreting their outcome measures, and 53 percent recorded no information on this issue. Differences among studies, by study type (NSF, UCSMP, and commercially generated), showed variation on this issue, with 46 percent of NSF reporting or adjusting for implementation, 75 percent of UCSMP, and only 11 percent of the other studies of commercial materials doing so. Of the commercial, non-UCSMP studies included, only one reported on implementation. Possibly, the evaluators for the NSF and UCSMP Secondary programs recognized more clearly that their programs demanded significant changes in practice that could affect their outcomes and could pose challenges to the teachers assigned to them.
A study by Abrams (1989) (EX)3 on the use of Saxon algebra by ninth graders showed that concerns for implementation fidelity extend to all curricula, even those like Saxon whose methods may seem more likely to be consistent with common practice. Abrams wrote, “It was not the intent of this study to determine the effectiveness of the Saxon text when used as Saxon suggests, but rather to determine the effect of the text as it is being used in the classroom situations. However, one aspect of the research was to identify how the text is being taught, and how closely teachers adhere to its content and the recommended presentation” (p. 7). Her findings showed that for the 9 teachers and 300 students, treatment effects favoring the traditional group (using Dolciani’s Algebra I textbook, Houghton Mifflin, 1980) were found on the algebra test, the algebra knowledge/skills subtest, and the problem-solving test for this population of teachers (fixed effect). No differences were found between the groups on an algebra understanding/applications subtest, overall attitude toward mathematics, mathematical self-confidence, anxiety about mathematics, or enjoyment of mathematics. She suggests that the lack of differences might be due to the ways in which teachers supplement materials, change test conditions, emphasize
and deemphasize topics, use their own tests, vary the proportion of time spent on development and practice, use calculators and group work, and basically adapt the materials to their own interpretation and method. Many of these practices conflict directly with the recommendations of the authors of the materials.
A study by Briars and Resnick (2000) (EX) in Pittsburgh schools directly confronted issues relevant to professional development and implementation. Evaluators contrasted the performance of students of teachers with high and low implementation quality, and showed the results on two contrasting outcome measures, Iowa Test of Basic Skills (ITBS) and Balanced Assessment. Strong implementers were defined as those who used all of the EM components and provided student-centered instruction by giving students opportunities to explore mathematical ideas, solve problems, and explain their reasoning. Weak implementers were either not using EM or using it so little that the overall instruction in the classrooms was “hardly distinguishable from traditional mathematics instruction” (p. 8). Assignment was based on observations of student behavior in classes, the presence or absence of manipulatives, teacher questionnaires about the programs, and students’ knowledge of classroom routines associated with the program.
From the identification of strong- and weak-implementing teachers, strong- and weak-implementation schools were identified as those with strong- or weak-implementing teachers in 3rd and 4th grades over two consecutive years. The performance of students with 2 years of EM experience in these settings composed the comparative samples. Three pairs of strong- and weak-implementation schools with similar demographics in terms of free and reduced-price lunch (range 76 to 93 percent), student living with only one parent (range 57 to 82 percent), mobility (range 8 to 16 percent), and ethnicity (range 43 to 98 percent African American) were identified. These students’ 1st-grade ITBS scores indicated similarity in prior performance levels. Finally, evaluators predicted that if the effects were due to the curricular implementation and accompanying professional development, the effects on scores should be seen in 1998, after full implementation. Figure 5-4 shows that on the 1998 New Standards exams, placement in strong- and weak-implementation schools strongly affected students’ scores. Over three years, performance in the district on skills, concepts, and problem solving rose, confirming the evaluator’s predictions.
An article by McCaffrey et al. (2001) examining the interactions among instructional practices, curriculum, and student achievement illustrates the point that distinctions are often inadequately linked to measurement tools in their treatment of the terms traditional and reform teaching. In this study, researchers conducted an exploratory factor analysis that led them to create two scales for instructional practice: Reform Practices and Tradi-
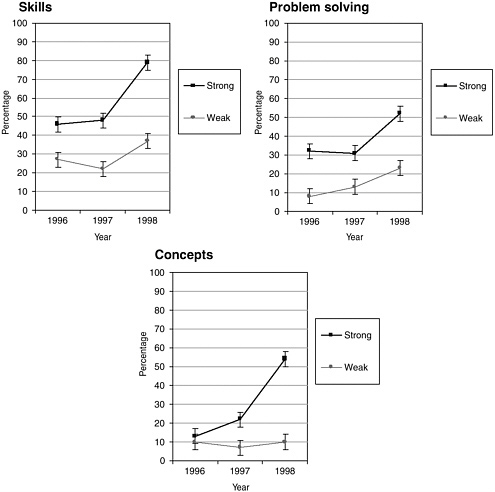
FIGURE 5-4 Percentage of students who met or exceeded the standard. Districtwide grade 4 New Standards Mathematics Reference Examination (NSMRE) performance for 1996, 1997, and 1998 by level of Everyday Mathematics implementation. Percentage of students who achieved the standard. Error bars denote the 99 percent confidence interval for each data point.
SOURCE: Re-created from Briars and Resnick (2000, pp. 19-20).
tional Practices. The reform scale measured the frequency, by means of teacher report, of teacher and student behaviors associated with reform instruction and assessment practices, such as using small-group work, explaining reasoning, representing and using data, writing reflections, or performing tasks in groups. The traditional scale focused on explanations to whole classes, the use of worksheets, practice, and short-answer assessments. There was a –0.32 correlation between scores for integrated curriculum teachers. There was a 0.27 correlation between scores for traditional
curriculum teachers. This shows that it is overly simplistic to think that reform and traditional practices are oppositional. The relationship among a variety of instructional practices is rather more complex as they interact with curriculum and various student populations.
Professional Development
Professional development and teacher effects were separated in our analysis from implementation fidelity. We recognized that professional development could be viewed by the readers of this report in two ways. As indicated in our model, professional development can be considered a program element or component or it can be viewed as part of the implementation process. When viewed as a program element, professional development resources are considered mandatory along with program materials. In relation to evaluation, proponents of considering professional development as a mandatory program element argue that curricular innovations, which involve the introduction of new topics, new types of assessment, or new ways of teaching, must make provision for adequate training, just as with the introduction of any new technology.
For others, the inclusion of professional development in the program elements without a concomitant inclusion of equal amounts of professional development relevant to a comparative treatment interjects a priori disproportionate treatments and biases the results. We hoped for an array of evaluation studies that might shed some empirical light on this dispute, and hence separated professional development from treatment fidelity, coding whether or not studies reported on the amount of professional development provided for the treatment and/or comparison groups. A study was coded as positive if it either reported on the professional development provided on the experimental group or reported the data on both treatments. Across all 63 at least minimally methodologically adequate studies, 27 percent reported some type of professional development measure, 1.5 percent reported and adjusted for it in interpreting their outcome measures, and 71.5 percent recorded no information on the issue.
A study by Collins (2002) (EX)4 illustrates the critical and controversial role of professional development in evaluation. Collins studied the use of Connected Math over three years, in three middle schools in threat of being classified as low performing in the Massachusetts accountability system. A comparison was made between one school (School A) that engaged
substantively in professional development opportunities accompanying the program and two that did not (Schools B and C). In the CMP school reports (School A) totals between 100 and 136 hours of professional development were recorded for all seven teachers in grades 6 through 8. In School B, 66 hours were reported for two teachers and in School C, 150 hours were reported for eight teachers over three years. Results showed significant differences in the subsequent performance by students at the school with higher participation in professional development (School A) and it became a districtwide top performer; the other two schools remained at risk for low performance. No controls for teacher effects were possible, but the results do suggest the centrality of professional development for successful implementation or possibly suggest that the results were due to professional development rather than curriculum materials. The fact that these two interpretations cannot be separated is a problem when professional development is given to one and not the other. The effect could be due to textbook or professional development or an interaction between the two. Research designs should be adjusted to consider these issues when different conditions of professional development are provided.
Teacher Effects
These studies make it obvious that there are potential confounding factors of teacher effects. Many evaluation studies devoted inadequate attention to the variable of teacher quality. A few studies (Goodrow, 1998; Riordan and Noyce, 2001; Thompson et al., 2001; and Thompson et al., 2003) reported on teacher characteristics such as certification, length of service, experience with curricula, or degrees completed. Those studies that matched classrooms and reported by matched results rather than aggregated results sought ways to acknowledge the large variations among teacher performance and its impact on student outcomes. We coded any effort to report on possible teacher effects as one indicator of quality. Across all 63 at least minimally methodologically adequate studies, 16 percent reported some type of teacher effect measure, 3 percent reported and adjusted for it in interpreting their outcome measures, and 81 percent recorded no information on this issue.
One can see that the potential confounding factors of teacher effects, in terms of the provision of professional development or the measure of teacher effects, are not adequately considered in most evaluation designs. Some studies mention and give a subjective judgment as to the nature of the problem, but this is descriptive at the most. Hardly any of the studies actually do anything analytical, and because these are such important potential confounding variables, this presents a serious challenge to the efficacy of these studies. Figure 5-5 shows how attention to these factors varies
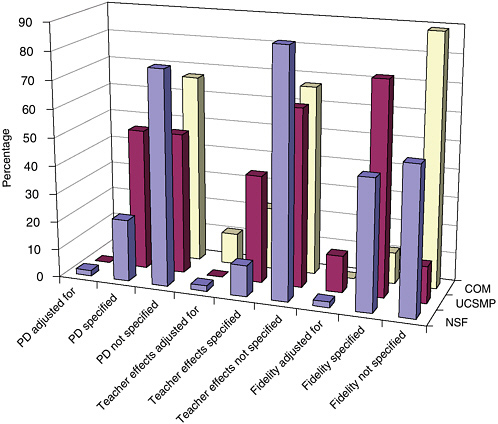
FIGURE 5-5 Treatment of implementation components by program type.
NOTE: PD = professional development.
across program categories among NSF-supported, UCSMP, and studies of commercial materials. In general, evaluations of NSF-supported studies were the most likely to measure these variables; UCSMP had the most standardized use of methods to do so across studies; and commercial material evaluators seldom reported on issues of implementation fidelity.
Identification of a Set of Outcome Measures and Forms of Disaggregation
Using the selected student outcomes identified in the program theory, one must conduct an impact assessment that refers to the design and measurement of student outcomes. In addition to selecting what outcomes should be measured within one’s program theory, one must determine how these outcomes are measured, when those measures are collected, and what
purpose they serve from the perspective of the participants. In the case of curricular evaluation, there are significant issues involved in how these measures are reported. To provide insight into the level of curricular validity, many evaluators prefer to report results by topic, content strand, or item cluster. These reports often present the level of specificity of outcome needed to inform curriculum designers, especially when efforts are made to document patterns of errors, distribution of results across multiple choices, or analyses of student methods. In these cases, whole test scores may mask essential differences in impact among curricula at the level of content topics, reporting only average performance.
On the other hand, many large-scale assessments depend on methods of test equating that rely on whole test scores and make comparative interpretations of different test administrations by content strands of questionable reliability. Furthermore, there are questions such as whether to present only gain scores effect sizes, how to link pretests and posttests, and how to determine the relative curricular sensitivity of various outcome measures.
The findings of comparative studies are reported in terms of the outcome measure(s) collected. To describe the nature of the database with regard to outcome measures and to facilitate our analyses of the studies, we classified each of the included studies on four outcome measure dimensions:
-
Total score reported;
-
Disaggregation of content strands, subtest, performance level, SES, or gender;
-
Outcome measure that was specific to curriculum; and
-
Use of multiple outcome measures.
Most studies reported a total score, but we did find studies that reported only subtest scores or only scores on an item-by-item basis. For example, in the Ben-Chaim et al. (1998) evaluation study of Connected Math, the authors were interested in students’ proportional reasoning proficiency as a result of use of this curriculum. They asked students from eight seventh-grade classes of CMP and six seventh-grade classes from the control group to solve a variety of tasks categorized as rate and density problems. The authors provide precise descriptions of the cognitive challenges in the items; however, they do not explain if the problems written up were representative of performance on a larger set of items. A special rating form was developed to code responses in three major categories (correct answer, incorrect answer, and no response), with subcategories indicating the quality of the work that accompanied the response. No reports on reliability of coding were given. Performance on standardized tests indicated that control students’ scores were slightly higher than CMP at the beginning of the
year and lower at the end. Twenty-five percent of the experimental group members were interviewed about their approaches to the problems. The CMP students outperformed the control students (53 percent versus 28 percent) overall in providing the correct answers and support work, and 27 percent of the control group gave an incorrect answer or showed incorrect thinking compared to 13 percent of the CMP group. An item-level analysis permitted the researchers to evaluate the actual strategies used by the students. They reported, for example, that 82 percent of CMP students used a “strategy focused on package price, unit price, or a combination of the two; those effective strategies were used by only 56 of 91 control students (62 percent)” (p. 264).
The use of item or content strand-level comparative reports had the advantage that they permitted the evaluators to assess student learning strategies specific to a curriculum’s program theory. For example, at times, evaluators wanted to gauge the effectiveness of using problems different from those on typical standardized tests. In this case, problems were drawn from familiar circumstances but carefully designed to create significant cognitive challenges, and assess how well the informal strategies approach in CMP works in comparison to traditional instruction. The disadvantages of such an approach include the use of only a small number of items and the concerns for reliability in scoring. These studies seem to represent a method of creating hybrid research models that build on the detailed analyses possible using case studies, but still reporting on samples that provide comparative data. It possibly reflects the concerns of some mathematicians and mathematics educators that the effectiveness of materials needs to be evaluated relative to very specific, research-based issues on learning and that these are often inadequately measured by multiple-choice tests. However, a decision not to report total scores led to a trade-off in the reliability and representativeness of the reported data, which must be addressed to increase the objectivity of the reports.
Second, we coded whether outcome data were disaggregated in some way. Disaggregation involved reporting data on dimensions such as content strand, subtest, test item, ethnic group, performance level, SES, and gender. We found disaggregated results particularly helpful in understanding the findings of studies that found main effects, and also in examining patterns across studies. We report the results of the studies’ disaggregation by content strand in our reports of effects. We report the results of the studies’ disaggregation by subgroup in our discussions of generalizability.
Third, we coded whether a study used an outcome measure that the evaluator reported as being sensitive to a particular treatment—this is a subcategory of what was defined in our framework as “curricular validity of measures.” In such studies, the rationale was that readily available measures such as state-mandated tests, norm-referenced standardized tests, and
college entrance examinations do not measure some of the aims of the program under study. A frequently cited instance of this was that “off the shelf” instruments do not measure well students’ ability to apply their mathematical knowledge to problems embedded in complex settings. Thus, some studies constructed a collection of tasks that assessed this ability and collected data on it (Ben-Chaim et al., 1998; Huntley et al., 2000).
Finally, we recorded whether a study used multiple outcome measures. Some studies used a variety of achievement measures and other studies reported on achievement accompanied by measures such as subsequent course taking or various types of affective measures. For example, Carroll (2001, p. 47) reported results on a norm-referenced standardized achievement test as well as a collection of tasks developed in other studies.
A study by Huntley et al. (2000) illustrates how a variety of these techniques were combined in their outcome measures. They developed three assessments. The first emphasized contextualized problem solving based on items from the American Mathematical Association of Two-Year Colleges and others; the second assessment was on context-free symbolic manipulation and a third part requiring collaborative problem solving. To link these measures to the overall evaluation, they articulated an explicit model of cognition based on how one links an applied situation to mathematical activity through processes of formulation and interpretation. Their assessment strategy permitted them to investigate algebraic reasoning as an ability to use algebraic ideas and techniques to (1) mathematize quantitative problem situations, (2) use algebraic principles and procedures to solve equations, and (3) interpret results of reasoning and calculations.
In presenting their data comparing performance on Core-Plus and traditional curriculum, they presented both main effects and comparisons on subscales. Their design of outcome measures permitted them to examine differences in performance with and without context and to conclude with statements such as “This result illustrates that CPMP students perform better than control students when setting up models and solving algebraic problems presented in meaningful contexts while having access to calculators, but CPMP students do not perform as well on formal symbol-manipulation tasks without access to context cues or calculators” (p. 349). The authors go on to present data on the relationship between knowing how to plan or interpret solutions and knowing how to carry them out. The correlations between these variables were weak but significantly different (0.26 for control groups and 0.35 for Core-Plus). The advantage of using multiple measures carefully tied to program theory is that they can permit one to test fine content distinctions that are likely to be the level of adjustments necessary to fine tune and improve curricular programs.
Another interesting approach to the use of outcome measures is found in the UCSMP studies. In many of these studies, evaluators collected infor-
TABLE 5-2 Mean Percentage Correct on the Subject Tests
|
Treatment Group |
Geometry—Standard |
Geometry—UCSMP |
Advanced Algebra—UCSMP |
|
UCSMP |
43.1, 44.7, 50.5a |
51.2, 54.5b |
56.1, 58.8, 56.1 |
|
Comparison |
42.7, 45.5, 51.5 |
36.6, 40.8b |
42.0, 50.1, 50.0 |
|
a“43.1, 44.7, 50.5” means students were correct on 43.1 percent of the total items, 44.7 percent of the fair items for UCSMP, and 50.5 percent of the items that were taught in both treatments. bToo few items to report data. SOURCES: Adapted from Thompson et al. (2001); Thompson et al. (2003). |
|||
mation from teachers’ reports and chapter reviews as to whether topics for items on the posttests were taught, calling this an “opportunity to learn” measure. The authors reported results from three types of analyses: (1) total test scores, (2) fair test scores (scores reported by program but only on items on topics taught), and (3) conservative test scores (scores on common items taught in both). Table 5-2 reports on the variations across the multiple- choice test scores for the Geometry study (Thompson et al., 2003) on a standardized test, High School Subject Tests-Geometry Form B, and the UCSMP-constructed Geometry test, and for the Advanced Algebra Study on the UCSMP-constructed Advanced Algebra test (Thompson et al., 2001). The table shows the mean scores for UCSMP classes and comparison classes. In each cell, mean percentage correct is reported first by whole test, then by fair test, and then by conservative test.
The authors explicitly compare the items from the standard Geometry test with the items from the UCSMP test and indicate overlap and difference. They constructed their own test because, in their view, the standard test was not adequately balanced among skills, properties, and real-world uses. The UCSMP test included items on transformations, representations, and applications that were lacking in the national test. Only five items were taught by all teachers; hence in the case of the UCSMP geometry test, there is no report on a conservative test. In the Advanced Algebra evaluation, only a UCSMP-constructed test was viewed as appropriate to cover the treatment of the prior material and alignment to the goals of the new course. These data sets demonstrate the challenge of selecting appropriate outcome measures, the sensitivity of the results to those decisions, and the importance of full disclosure of decision-making processes in order to permit readers to assess the implications of the choices. The methodology utilized sought to ensure that the material in the course was covered adequately by treatment teachers while finding ways to make comparisons that reflected content coverage.
Only one study reported on its outcomes using embedded assessment items employed over the course of the year. In a study of Saxon and UCSMP, Peters (1992) (EX) studied the use of these materials with two classrooms taught by the same teacher. In this small study, he randomly assigned students to treatment groups and then measured their performance on four unit tests composed of items common to both curricula and their progress on the Orleans-Hanna Algebraic Prognosis Test.
Peters’ study showed no significant difference in placement scores between Saxon and UCSMP on the posttest, but did show differences on the embedded assessment. Figure 5-6 (Peters, 1992, p. 75) shows an interesting display of the differences on a “continuum” that shows both the direction and magnitude of the differences and provides a level of concept specificity missing in many reports. This figure and a display (Figure 5-7) in a study by Senk (1991, p. 18) of students’ mean scores on Curriculum A versus Curriculum B with a 10 percent range of differences marked represent two excellent means to communicate the kinds of detailed content outcome information that promises to be informative to curriculum writers, publishers, and school decision makers. In Figure 5-7, 16 items listed by number were taken from the Second International Mathematics Study. The Functions, Statistics, and Trigonometry sample averaged 41 percent correct on these items whereas the U.S. precalculus sample averaged 38 percent. As shown in the figure, differences of 10 percent or less fall inside the banded area and greater than 10 percent fall outside, producing a display that makes it easy for readers and designers to identify the relative curricular strengths and weaknesses of topics.
While we value detailed outcome measure information, we also recognize the importance of examining curricular impact on students’ standardized test performance. Many developers, but not all, are explicit in rejecting standardized tests as adequate measures of the outcomes of their programs, claiming that these tests focus on skills and manipulations, that they are overly reliant on multiple-choice questions, and that they are often poorly aligned to new content emphases such as probability and statistics, transformations, use of contextual problems and functions, and process skills, such as problem solving, representation, or use of calculators. However, national and state tests are being revised to include more content on these topics and to draw on more advanced reasoning. Furthermore, these high-stakes tests are of major importance in school systems, determining graduation, passing standards, school ratings, and so forth. For this reason, if a curricular program demonstrated positive impact on such measures, we referred to that in Chapter 3 as establishing “curricular alignment with systemic factors.” Adequate performance on these measures is of paramount importance to the survival of reform (to large groups of parents and

FIGURE 5-6 Continuum of criterion score averages for studied programs.
SOURCE: Peters (1992, p. 75).
school administrators). These examples demonstrate how careful attention to outcomes measures is an essential element of valid evaluation.
In Table 5-3, we document the number of studies using a variety of types of outcome measures that we used to code the data, and also report on the types of tests used across the studies.
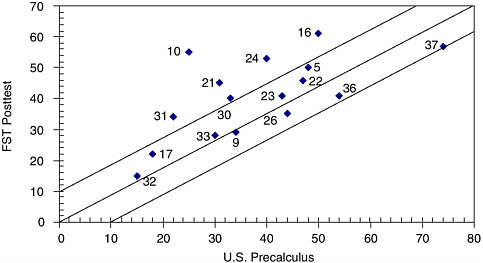
FIGURE 5-7 Achievement (percentage correct) on Second International Mathematics Study (SIMS) items by U.S. precalculus students and functions, statistics, and trigonometry (FST) students.
SOURCE: Re-created from Senk (1991, p. 18).
TABLE 5-3 Number of Studies Using a Variety of Outcome Measures by Program Type
|
|
Total Test |
Content Strands |
Test Match to Program |
Multiple Test |
||||
|
|
Yes |
No |
Yes |
No |
Yes |
No |
Yes |
No |
|
NSF |
43 |
3 |
28 |
18 |
26 |
20 |
21 |
25 |
|
Commercial |
8 |
1 |
4 |
5 |
2 |
7 |
2 |
7 |
|
UCSMP |
7 |
1 |
7 |
1 |
7 |
1 |
7 |
1 |
A Choice of Statistical Tests, Including Statistical Significance and Effect Size
In our first review of the studies, we coded what methods of statistical evaluation were used by different evaluators. Most common were t-tests; less frequently one found Analysis of Variance (ANOVA), Analysis of Co-
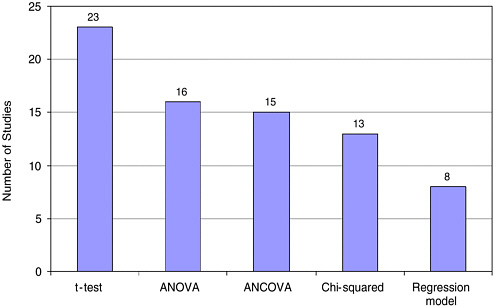
FIGURE 5-8 Statistical tests most frequently used.
variance (ANCOVA), and chi-square tests. In a few cases, results were reported using multiple regression or hierarchical linear modeling. Some used multiple tests; hence the total exceeds 63 (Figure 5-8).
One of the difficult aspects of doing curriculum evaluations concerns using the appropriate unit both in terms of the unit to be randomly assigned in an experimental study and the unit to be used in statistical analysis in either an experimental or quasi-experimental study.
For our purposes, we made the decision that unless the study concerned an intact student population such as the freshman at a single university, where a student comparison was the correct unit, we believed that for statistical tests, the unit should be at least at the classroom level. Judgments were made for each study as to whether the appropriate unit was utilized. This question is an important one because statistical significance is related to sample size, and as a result, studies that inappropriately use the student as the unit of analysis could be concluding significant differences where they are not present. For example, if achievement differences between two curricula are tested in 16 classrooms with 400 students, it will always be easier to show significant differences using scores from those 400 students than using 16 classroom means.
Fifty-seven studies used students as the unit of analysis in at least one test of significance. Three of these were coded as correct because they involved whole populations. In all, 10 studies were coded as using the
TABLE 5-4 Performance on Applied Algebra Problems with Use of Calculators, Part 1
|
Treatment |
n |
M (0-100) |
SD |
|
Control |
273 |
34.1 |
14.8 |
|
CPMP |
320 |
42.6 |
21.3 |
|
NOTE: t570= -5.69, p < .001. All sites combined. SOURCE: Huntley et al. (2000). Reprinted with permission. |
|||
TABLE 5-5 Reanalysis of Algebra Performance Data
|
|
Site Mean |
Independent Samples Dependent |
Difference Sample Difference |
|
|
Site |
Control |
CPMP |
||
|
1 |
31.7 |
35.5 |
|
3.8 |
|
2 |
26.0 |
49.4 |
|
23.4 |
|
3 |
36.7 |
25.2 |
|
-11.5 |
|
4 |
41.9 |
47.7 |
|
5.8 |
|
5 |
29.4 |
38.3 |
|
8.9 |
|
6 |
30.5 |
45.6 |
|
15.1 |
|
Average |
32.7 |
40.3 |
7.58 |
7.58 |
|
Standard deviation |
5.70 |
9.17 |
7.64 |
11.75 |
|
Standard error |
|
|
4.41 |
4.80 |
|
|
|
t |
1.7 |
1.6 |
|
|
|
p |
0.116 |
0.175 |
|
SOURCE: Huntley et al. (2000). |
||||
correct unit of analysis; hence, 7 studies used teachers or classes, or schools. For some studies where multiple tests were conducted, a judgment was made as to whether the primary conclusions drawn treated the unit of analysis adequately. For example, Huntley et al. (2000) compared the performance of CPMP students with students in a traditional course on a measure of ability to formulate and use algebraic models to answer various questions about relationships among variables. The analysis used students as the unit of analysis and showed a significant difference, as shown in Table 5-4.
To examine the robustness of this result, we reanalyzed the data using an independent sample t-test and a matched pairs t-test with class means as the unit of analysis in both tests (Table 5-5). As can be seen from the analyses, in neither statistical test was the difference between groups found to be significantly different (p < .05), thus emphasizing the importance of using the correct unit in analyzing the data.
Reanalysis of student-level data using class means will not always result
TABLE 5-6 Mean Percentage Correct on Entire Multiple-Choice Posttest: Second Edition and Non-UCSMP
in a change in finding. Furthermore, using class means as the unit of analysis does not suggest that significant differences will not be found. For example, a study by Thompson et al. (2001) compared the performance of UCSMP students with the performance of students in a more traditional program across several measures of achievement. They found significant differences between UCSMP students and the non-UCSMP students on several measures. Table 5-6 shows results of an analysis of a multiple-choice algebraic posttest using class means as the unit of analysis. Significant differences were found in five of eight separate classroom comparisons, as shown in the table. They also found a significant difference using a matched-pairs t-test on class means.
The lesson to be learned from these reanalyses is that the choice of unit of analysis and the way the data are aggregated can impact study findings in important ways including the extent to which these findings can be generalized. Thus it is imperative that evaluators pay close attention to such considerations as the unit of analysis and the way data are aggregated in the design, implementation, and analysis of their studies.
|
Non-UCSMPa |
|||||||
|
n |
Mean |
SD |
OTL |
SE |
t |
df |
p |
|
14 |
55.2 |
10.2 |
69 |
3.40 |
1.65 |
30 |
0.110 |
|
15 |
53.7 |
11.0 |
69 |
4.81 |
1.06 |
24 |
0.299 |
|
24 |
45.9 |
10.0 |
72 |
3.41 |
5.22 |
44 |
0.000 |
|
23 |
43.0 |
11.9 |
72 |
4.16 |
5.23 |
37 |
0.000 |
|
20 |
38.8 |
9.1 |
75 |
4.32 |
4.36 |
37 |
0.000 |
|
15 |
38.3 |
11.0 |
75 |
4.20 |
1.52 |
26 |
0.140 |
|
22 |
37.8 |
13.8 |
47 |
3.72 |
5.56 |
49 |
0.000 |
|
23 |
30.8 |
9.9 |
47 |
3.52 |
2.51 |
43 |
0.016 |
|
156 |
42.0 |
13.1 |
|
|
|
|
|
|
aA matched-pairs t-test indicates that the differences between the two curricula are significant.
SOURCE: Thompson et al. (2001). Reprinted with permission. |
|||||||
Second, effect size has become a relatively common and standard way of gauging the practical significance of the findings. Statistical significance only indicates whether the main-level differences between two curricula are large enough to not be due to chance, assuming they come from the same population. When statistical differences are found, the question remains as to whether such differences are large enough to consider. Because any innovation has its costs, the question becomes one of cost-effectiveness: Are the differences in student achievement large enough to warrant the costs of change? Quantifying the practical effect once statistical significance is established is one way to address this issue. There is a statistical literature for doing this, and for the purposes of this review, the committee simply noted whether these studies have estimated such an effect. However, the committee further noted that in conducting meta-analyses across these studies, effect size was likely to be of little value. These studies used an enormous variety of outcome measures, and even using effect size as a means to standardize units across studies is not sensible when the measures in each
study address such a variety of topics, forms of reasoning, content levels, and assessment strategies.
We note very few studies drew upon the advances in methodologies employed in modeling, which include causal modeling, hierarchical linear modeling (Bryk and Raudenbush, 1992; Bryk et al., 1993), and selection bias modeling (Heckman and Hotz, 1989). Although developing detailed specifications for these approaches is beyond the scope of this review, we wish to emphasize that these methodological advances should be considered within future evaluation designs.
Results and Limitations to Generalizability Resulting from Design Constraints
One also must consider what generalizations can be drawn from the results (Campbell and Stanley, 1966; Caporaso and Roos, 1973; and Boruch, 1997). Generalization is a matter of external validity in that it determines to what populations the study results are likely to apply. In designing an evaluation study, one must carefully consider, in the selection of units of analysis, how various characteristics of those units will affect the generalizability of the study. It is common for evaluators to conflate issues of representativeness for the purpose of generalizability (external validity) and comparativeness (the selection of or adjustment for comparative groups [internal validity]). Not all studies must be representative of the population served by mathematics curricula to be internally valid. But, to be generalizable beyond restricted communities, representativeness must be obtained by the random selection of the basic units. Clearly specifying such limitations to generalizability is critical. Furthermore, on the basis of equity considerations, one must be sure that if overall effectiveness is claimed, that the studies have been conducted and analyzed with reference of all relevant subgroups.
Thus, depending on the design of a study, its results may be limited in generalizability to other populations and circumstances. We identified four typical kinds of limitations on the generalizability of studies and coded them to determine, on the whole, how generalizable the results across studies might be.
First, there were studies whose designs were limited by the ability or performance level of the students in the samples. It was not unusual to find that when new curricula were implemented at the secondary level, schools kept in place systems of tracking that assigned the top students to traditional college-bound curriculum sequences. As a result, studies either used comparative groups who were matched demographically but less skilled than the population as a whole, in relation to prior learning, or their results compared samples of less well-prepared students to samples of students
with stronger preparations. Alternatively, some studies reported on the effects of curricula reform on gifted and talented students or on college-attending students. In these cases, the study results would also limit the generalizability of the results to similar populations. Reports using limited samples of students’ ability and prior performance levels were coded as a limitation to the generalizability of the study.
For example, Wasman (2000) conducted a study of one school (six teachers) and examined the students’ development of algebraic reasoning after one (n=100) and two years (n=73) in CMP. In this school, the top 25 percent of the students are counseled to take a more traditional algebra course, so her experimental sample, which was 61 percent white, 35 percent African American, 3 percent Asian, and 1 percent Hispanic, consisted of the lower 75 percent of the students. She reported on the student performance on the Iowa Algebraic Aptitude Test (IAAT) (1992), in the subcategories of interpreting information, translating symbols, finding relationships, and using symbols. Results for Forms 1 and 2 of the test, for the experimental and norm group, are shown in Table 5-7 for 8th graders.
In our coding of outcomes, this study was coded as showing no significant differences, although arguably its results demonstrate a positive set of
TABLE 5-7 Comparing Iowa Algebraic Aptitude Test (IAAT) Mean Scores of the Connected Mathematics Project Forms 1 and 2 to the Normative Group (8th Graders)
outcomes as the treatment group was weaker than the control group. Had the researcher used a prior achievement measure and a different statistical technique, significance might have been demonstrated, although potential teacher effects confound interpretations of results.
A second limitation to generalizability was when comparative studies resided entirely at curriculum pilot site locations, where such sites were developed as a means to conduct formative evaluations of the materials with close contact and advice from teachers. Typically, pilot sites have unusual levels of teacher support, whether it is in the form of daily technical support in the use of materials or technology or increased quantities of professional development. These sites are often selected for study because they have established cooperative agreements with the program developers and other sources of data, such as classroom observations, are already available. We coded whether the study was conducted at a pilot site to signal potential limitations in generalizability of the findings.
Third, studies were also coded as being of limited generalizability if they failed to disaggregate their data by socioeconomic class, race, gender, or some other potentially significant sources of restriction on the claims. We recorded the categories in which disaggregation occurred and compiled their frequency across the studies. Because of the need to open the pipeline to advanced study in mathematics by members of underrepresented groups, we were particularly concerned about gauging the extent to which evaluators factored such variables into their analysis of results and not just in terms of the selection of the sample.
Of the 46 included studies of NSF-supported curricula, 19 disaggregated their data by student subgroup. Nine of 17 studies of commercial materials disaggregated their data. Figure 5-9 shows the number of studies that disaggregated outcomes by race or ethnicity, SES, gender, LEP, special education status, or prior achievement. Studies using multiple categories of disaggregation were counted multiple times by program category.
The last category of restricted generalization occurred in studies of limited sample size. Although such studies may have provided more indepth observations of implementation and reports on professional development factors, the smaller numbers of classrooms and students in the study would limit the extent of generalization that could be drawn from it. Figure 5-10 shows the distribution of sizes of the samples in terms of numbers of students by study type.
Summary of Results by Student Achievement Among Program Types
We present the results of the studies as a means to further investigate their methodological implications. To this end, for each study, we counted across outcome measures the number of findings that were positive, nega-
tive, or indeterminate (no significant difference) and then calculated the proportion of each. We represented the calculation of each study as a triplet (a, b, c) where a indicates the proportion of the results that were positive and statistically significantly stronger than the comparison program, b indicates the proportion that were negative and statistically significantly weaker than the comparison program, and c indicates the proportion that showed no significant difference between the treatment and the comparative group. For studies with a single outcome measure, without disaggregation by content strand, the triplet is always composed of two zeros and a single one. For studies with multiple measures or disaggregation by content strand, the triplet is typically a set of three decimal values that sum to one. For example, a study with one outcome measure in favor of the experimental treatment would be coded (1, 0, 0), while one with multiple measures and mixed results more strongly in favor of the comparative curriculum might be listed as (.20, .50, .30). This triplet would mean that for 20 percent of the comparisons examined, the evaluators reported statistically significant positive results, for 50 percent of the comparisons the results were statistically significant in favor of the comparison group, and for 30 percent of the comparisons no significant difference were found. Overall, the mean score on these distributions was (.54, .07, .40), indicating that across all the studies, 54 percent of the comparisons favored the treatment, 7 percent favored the comparison group, and 40 percent showed no significant difference. Table 5-8 shows the comparison by curricular program types. We present the results by individual program types, because each program type relies on a similar program theory and hence could lead to patterns of results that would be lost in combining the data. If the studies of commercial materials are all grouped together to include UCSMP, their pattern of results is (.38, .11, .51). Again we emphasize that due to our call for increased methodological rigor and the use of multiple methods, this result is not sufficient to establish the curricular effectiveness of these programs as a whole with adequate certainty.
We caution readers that these results are summaries of the results presented across a set of evaluations that meet only the standard of at least
TABLE 5-8 Comparison by Curricular Program Types
|
Proportion of Results That Are: |
NSF-Supported n=46 |
UCSMP n=8 |
Commercially Generated n=9 |
|
In favor of treatment |
.591 |
.491 |
.285 |
|
In favor of comparison |
.055 |
.087 |
.130 |
|
Show no significant difference |
.354 |
.422 |
.585 |
minimally methodologically adequate. Calculations of statistical significance of each program’s results were reported by the evaluators; we have made no adjustments for weaknesses in the evaluations such as inappropriate use of units of analysis in calculating statistical significance. Evaluations that consistently used the correct unit of analysis, such as UCSMP, could have fewer reports of significant results as a consequence. Furthermore, these results are not weighted by study size. Within any study, the results pay no attention to comparative effect size or to the established credibility of an outcome measure. Similarly, these results do not take into account differences in the populations sampled, an important consideration in generalizing the results. For example, using the same set of studies as an example, UCSMP studies used volunteer samples who responded to advertisements in their newsletters, resulting in samples with disproportionately Caucasian subjects from wealthier schools compared to national samples. As a result, we would suggest that these results are useful only as baseline data for future evaluation efforts. Our purpose in calculating these results is to permit us to create filters from the critical decision points and test how the results change as one applies more rigorous standards.
Given that none of the studies adequately addressed all of the critical criteria, we do not offer these results as definitive, only suggestive—a hypothesis for further study. In effect, given the limitations of time and support, and the urgency of providing advice related to policy, we offer this filtering approach as an informal meta-analytic technique sufficient to permit us to address our primary task, namely, evaluating the quality of the evaluation studies.
This approach reflects the committee’s view that to deeply understand and improve methodology, it is necessary to scrutinize the results and to determine what inferences they provide about the conduct of future evaluations. Analogous to debates on consequential validity in testing, we argue that to strengthen methodology, one must consider what current methodologies are able (or not able) to produce across an entire series of studies. The remainder of the chapter is focused on considering in detail what claims are made by these studies, and how robust those claims are when subjected to challenge by alternative hypothesis, filtering by tests of increasing rigor, and examining results and patterns across the studies.
Alternative Hypotheses on Effectiveness
In the spirit of scientific rigor, the committee sought to consider rival hypotheses that could explain the data. Given the weaknesses in the designs generally, often these alternative hypotheses cannot be dismissed. However, we believed that only after examining the configuration of results and
alternative hypotheses can the next generation of evaluations be better informed and better designed. We began by generating alternative hypotheses to explain the positive directionality of the results in favor of experimental groups. Alternative hypotheses included the following:
-
The teachers in the experimental groups tended to be self-selecting early adopters, and thus able to achieve effects not likely in regular populations.
-
Changes in student outcomes reflect the effects of professional development instruction, or level of classroom support (in pilot sites), and thus inflate the predictions of effectiveness of curricular programs.
-
Hawthorne effect (Franke and Kaul, 1978) occurs when treatments are compared to everyday practices, due to motivational factors that influence experimental participants.
-
The consistent difference is due to the coherence and consistency of a single curricular program when compared to multiple programs.
-
The significance level is only achieved by the use of the wrong unit of analysis to test for significance.
-
Supplemental materials or new teaching techniques produce the results and not the experimental curricula.
-
Significant results reflect inadequate outcome measures that focus on a restricted set of activities.
-
The results are due to evaluator bias because too few evaluators are independent of the program developers.
At the same time, one could argue that the results actually underestimate the performance of these materials and are conservative measures, and their alternative hypotheses also deserve consideration:
-
Many standardized tests are not sensitive to these curricular approaches, and by eliminating studies focusing on affect, we eliminated a key indicator of the appeal of these curricula to students.
-
Poor implementation or increased demands on teachers’ knowledge dampens the effects.
-
Often in the experimental treatment, top-performing students are missing as they are advised to take traditional sequences, rendering the samples unequal.
-
Materials are not well aligned with universities and colleges because tests for placement and success in early courses focus extensively on algebraic manipulation.
-
Program implementation has been undercut by negative publicity and the fears of parents concerning change.
There are also a number of possible hypotheses that may be affecting the results in either direction, and we list a few of these:
-
Examining the role of the teacher in curricular decision making is an important element in effective implementation, and design mandates of evaluation design make this impossible (and the positives and negatives or single- versus dual-track curriculum as in Lundin, 2001).
-
Local tests that are sensitive to the curricular effects typically are not mandatory and hence may lead to unpredictable performance by students.
-
Different types and extent of professional development may affect outcomes differentially.
-
Persistence or attrition may affect the mean scores and are often not considered in the comparative analyses.
One could also generate reasons why the curricular programs produced results showing no significance when one program or the other is actually more effective. This could include high degrees of variability in the results, samples that used the correct unit of analysis but did not obtain consistent participation across enough cases, implementation that did not show enough fidelity to the measures, or outcome measures insensitive to the results. Again, subsequent designs should be better informed by these findings to improve the likelihood that they will produce less ambiguous results and replication of studies could also give more confidence in the findings.
It is beyond the scope of this report to consider each of these alternative hypotheses separately and to seek confirmation or refutation of them. However, in the next section, we describe a set of analyses carried out by the committee that permits us to examine and consider the impact of various critical evaluation design decisions on the patterns of outcomes across sets of studies. A number of analyses shed some light on various alternative hypotheses and may inform the conduct of future evaluations.
Filtering Studies by Critical Decision Points to Increase Rigor
In examining the comparative studies, we identified seven critical decision points that we believed would directly affect the rigor and efficacy of the study design. These decision points were used to create a set of 16 filters. These are listed as the following questions:
-
Was there a report on comparability relative to SES?
-
Was there a report on comparability of samples relative to prior knowledge?
-
Was there a report on treatment fidelity?
-
Was professional development reported on?
-
Was the comparative curriculum specified?
-
Was there any attempt to report on teacher effects?
-
Was a total test score reported?
-
Was total test score(s) disaggregated by content strand?
-
Did the outcome measures match the curriculum?
-
Were multiple tests used?
-
Was the appropriate unit of analysis used in their statistical tests?
-
Did they estimate effect size for the study?
-
Was the generalizability of their findings limited by use of a restricted range of ability levels?
-
Was the generalizability of their findings limited by use of pilot sites for their study?
-
Was the generalizability of their findings limited by not disaggregating their results by subgroup?
-
Was the generalizability of their findings limited by use of small sample size?
The studies were coded to indicate if they reported having addressed these considerations. In some cases, the decision points were coded dichotomously as present or absent in the studies, and in other cases, the decision points were coded trichotomously, as description presented, absent, or statistically adjusted for in the results. For example, a study may or may not report on the comparability of the samples in terms of race, ethnicity, or socioeconomic status. If a report on SES was given, the study was coded as “present” on this decision; if a report was missing, it was coded as “absent”; and if SES status or ethnicity was used in the analysis to actually adjust outcomes, it was coded as “adjusted for.” For each coding, the table that follows reports the number of studies that met that condition, and then reports on the mean percentage of statistically significant results, and results showing no significant difference for that set of studies. A significance test is run to see if the application of the filter produces changes in the probability that are significantly different.5
In the cases in which studies are coded into three distinct categories—present, absent, and adjusted for—a second set of filters is applied. First, the studies coded as present or adjusted for are combined and compared to those coded as absent; this is what we refer to as a weak test of the rigor of the study. Second, the studies coded as present or absent are combined and compared to those coded as adjusted for. This is what we refer to as a strong test. For dichotomous codings, there can be as few as three compari-
sons, and for trichotomous codings, there can be nine comparisons with accompanying tests of significance. Trichotomous codes were used for adjustments for SES and prior knowledge, examining treatment fidelity, professional development, teacher effects, and reports on effect sizes. All others were dichotomous.
NSF Studies and the Filters
For example, there were 11 studies of NSF-supported curricula that simply reported on the issues of SES in creating equivalent samples for comparison, and for this subset the mean probabilities of getting positive, negative, or results showing no significant difference were (.47, .10, .43). If no report of SES was supplied (n= 21), those probabilities become (.57, .07, .37), indicating an increase in positive results and a decrease in results showing no significant difference. When an adjustment is made in outcomes based on differences in SES (n=14), the probabilities change to (.72, .00, .28), showing a higher likelihood of positive outcomes. The probabilities that result from filtering should always be compared back to the overall results of (.59, .06, .35) (see Table 5-8) so as to permit one to judge the effects of more rigorous methodological constraints. This suggests that a simple report on SES without adjustment is least likely to produce positive outcomes; that is, no report produces the outcomes next most likely to be positive and studies that adjusted for SES tend to have a higher proportion of their comparisons producing positive results.
The second method of applying the filter (the weak test for rigor) for the treatment of the adjustment of SES groups compares the probabilities when a report is either given or adjusted for compared to when no report is offered. The combined percentage of a positive outcome of a study in which SES is reported or adjusted for is (.61, .05, .34), while the percentage for no report remains as reported previously at (.57, .07, .37). A final filter compares the probabilities of the studies in which SES is adjusted for with those that either report it only or do not report it at all. Here we compare the percentage of (.72, .00, .28) to (.53, .08, .37) in what we call a strong test. In each case we compared the probability produced by the whole group to those of the filtered studies and conducted a test of the differences to determine if they were significant. These differences were not significant. These findings indicate that to date, with this set of studies, there is no statistically significant difference in results when one reports or adjusts for changes in SES. It appears that by adjusting for SES, one sees increases in the positive results, and this result deserves a closer examination for its implications should it prove to hold up over larger sets of studies.
We ran tests that report the impact of the filters on the number of studies, the percentage of studies, and the effects described as probabilities
for each of the three study categories, NSF-supported and commercially generated with UCSMP included. We claim that when a pattern of probabilities of results does not change after filtering, one can have more confidence in that pattern. When the pattern of results changes, there is a need for an explanatory hypothesis, and that hypothesis can shed light on experimental design. We propose that this “filtering process” constitutes a test of the robustness of the outcome measures subjected to increasing degrees of rigor by using filtering.
Results of Filtering on Evaluations of NSF-Supported Curricula
For the NSF-supported curricular programs, out of 15 filters, 5 produced a probability that differed significantly at the p<.1 level. The five filters were for treatment fidelity, specification of control group, choosing the appropriate statistical unit, generalizability for ability, and generalizability based on disaggregation by subgroup. For each filter, there were from three to nine comparisons, as we examined how the probabilities of outcomes change as tests were more stringent and across the categories of positive results, negative results, and results with no significant differences. Out of a total of 72 possible tests, only 11 produced a probability that differed significantly at the p < .1 level. With 85 percent of the comparisons showing no significant difference after filtering, we suggest the results of the studies were relatively robust in relation to these tests. At the same time, when rigor is increased for the five filters just listed, the results become generally more ambiguous and signal the need for further research with more careful designs.
Studies of Commercial Materials and the Filters
To ensure enough studies to conduct the analysis (n=17), our filtering analysis of the commercially generated studies included UCSMP (n=8). In this case, there were six filters that produced a probability that differed significantly at the p < .1 level. These were treatment fidelity, disaggregation by content, use of multiple tests, use of effect size, generalizability by ability, and generalizability by sample size. In this case, because there were no studies in some possible categories, there were a total of 57 comparisons, and 9 displayed significant differences in the probabilities after filtering at the p < .1 level. With 84 percent of the comparisons showing no significant difference after filtering, we suggest the results of the studies were relatively robust in relation to these tests. Table 5-9 shows the cases in which significant differences were recorded.
Impact of Treatment Fidelity on Probabilities
A few of these differences are worthy of comment. In the cases of both the NSF-supported and commercially generated curricula evaluation studies, studies that reported treatment fidelity differed significantly from those that did not. In the case of the studies of NSF-supported curricula, it appeared that a report or adjustment on treatment fidelity led to proportions with less positive effects and more results showing no significant differences. We hypothesize that this is partly because larger studies often do not examine actual classroom practices, but can obtain significance more easily due to large sample sizes.
In the studies of commercial materials, the presence or absence of measures of treatment fidelity worked differently. Studies reporting on or adjusting for treatment fidelity tended to have significantly higher probabilities in favor of experimental treatment, less positive effects in fewer of the comparative treatments, and more likelihood of results with no significant differences. We hypothesize, and confirm with a separate analysis, that this is because UCSMP frequently reported on treatment fidelity in their designs while study of Saxon typically did not, and the change represents the preponderance of these different curricular treatments in the studies of commercially generated materials.
Impact of Identification of Curricular Program on Probabilities
The significant differences reported under specificity of curricular comparison also merit discussion for studies of NSF-supported curricula. When the comparison group is not specified, a higher percentage of mean scores in favor of the experimental curricula is reported. In the studies of commercial materials, a failure to name specific curricular comparisons also produced a higher percentage of positive outcomes for the treatment, but the difference was not statistically significant. This suggests the possibility that when a specified curriculum is compared to an unspecified curriculum, reports of impact may be inflated. This finding may suggest that in studies of effectiveness, specifying comparative treatments would provide more rigorous tests of experimental approaches.
When studies of commercial materials disaggregate their results of content strands or use multiple measures, their reports of positive outcomes increase, the negative outcomes decrease, and in one case, the results show no significant differences. Percentage of significant difference was only recorded in one comparison within each one of these filters.
TABLE 5-9 Cases of Significant Differences
|
Test |
Type of Comparison |
Category Code |
N= |
Probabilities Before Filter |
p= |
|
NSF STUDIES |
|||||
|
Treatment fidelity |
Simple compare |
Specified |
21 |
.51, .02, .47* |
*p =.049 |
|
|
Not specified |
|
24 |
.68, .09, .23* |
|
|
|
Adjusted for |
|
1 |
.25, .00, .75 |
|
|
Treatment fidelity |
Strong test |
Adjusted for |
22 |
.49*, .02, .49** |
*p=.098 |
|
|
Reported or not specified |
|
24 |
.68*, .09, .23** |
**p=.019 |
|
Control group specified |
Simple compare |
Specified |
8 |
.33*, .00, .66** |
*p=.033 |
|
|
|
Not specified |
38 |
.65*, .07, .29** |
**p=.008 |
|
Appropriate unit of analysis |
Simple compare |
Correct |
5 |
.30*, .40**, .30 |
*p=.069 |
|
|
|
Incorrect |
41 |
.63*, .01**, .36 |
**p=.000 |
|
Generalizability by ability |
Simple compare |
Limited |
5 |
.22*, .41**, .37 |
*p=.019 |
|
|
|
Not limited |
41 |
.64*, .01**, .35 |
**p=.000 |
|
Generalizability by disaggregated subgroup |
Simple compare |
Limited |
28 |
.48*, .09, .43** |
*p=.013 |
|
|
Not limited |
18 |
.76*, .00, .24** |
**p=.085 |
|
Impact of Units of Analysis on Probabilities6
For the evaluations of the NSF-supported materials, a significant difference was reported on the outcomes for the studies that used the correct unit of analysis compared to those that did not. The percentage for those with the correct unit were (.30, .40, .30) compared to (.63, .01, .36) for those that used the incorrect result. These results suggest that our prediction that using the correct unit of analysis would decrease the percentage of positive outcomes is likely to be correct. It also suggests that the most serious threat to the apparent conclusions of these studies comes from selecting an incorrect unit of analysis. It causes a decrease in favorable results, making the results more ambiguous, but never reverses the direction of the effect. This is a concern that merits major attention in the conduct of further studies.
For the commercially generated studies, most of the ones coded with the correct unit of analysis were UCSMP studies. Because of the small number of studies involved, we could not break out from the overall filtering of studies of commercial materials, but report this issue to assist readers in interpreting the relative patterns of results.
Impact of Generalizability on Probabilities
Both types of studies yielded significant differences for some of the comparisons coded as restrictions to generalizability. Investigating these is important in order to understand the effects of these curricular programs on different subpopulations of students. In the case of the studies of commercially generated materials, significantly different results occurred in the categories of ability and sample size. In the studies of NSF-supported materials, the significant differences occurred in ability and disaggregation by subgroups.
In relation to generalizability, the studies of NSF-supported curricula reported significantly more positive results in favor of the treatment when they included all students. Because studies coded as “limited by ability” were restricted either by focusing only on higher achieving students or on lower achieving students, we sorted these two groups. For higher performing students (n=3), the probabilities of effects were (.11, .67, .22). For lower
performing students (n=2), the probabilities were (.39, .025, .59). The first two comparisons are significantly different at p < .05. These findings are based on only a total of five studies, but they suggest that these programs may be serving the weaker ability students more effectively than the stronger ability students, serving both less well than they serve whole heterogeneous groups. For the studies of commercial materials, there were only three studies that were restricted to limited populations. The results for those three studies were (.23, .41, .32) and for all students (n=14) were (.42, .53, .09). These studies were significantly different at p = .004. All three studies included UCSMP and one also included Saxon and was limited by serving primarily high-performing students. This means both categories of programs are showing weaker results when used with high-ability students.
Finally, the studies on NSF-supported materials were disaggregated by subgroups for 28 studies. A complete analysis of this set follows, but the studies that did not report results disaggregated by subgroup generated probabilities of results of (.48, .09, .43) whereas those that did disaggregate their results reported (.76, 0, .24). These gains in positive effects came from significant losses in reporting no significant differences. Studies of commercial materials also reported a small decrease in likelihood of negative effects for the comparison program when disaggregation by subgroup is reported offset by increases in positive results and results with no significant differences, although these comparisons were not significantly different. A further analysis of this topic follows.
Overall, these results suggest that increased rigor seems to lead in general to less strong outcomes, but never reports of completely contrary results. These results also suggest that in recommending design considerations to evaluators, there should be careful attention to having evaluators include measures of treatment fidelity, considering the impact on all students as well as one particular subgroup; using the correct unit of analysis; and using multiple tests that are also disaggregated by content strand.
Further Analyses
We conducted four further analyses: (1) an analysis of the outcome probabilities by test type; (2) content strands analysis; (3) equity analysis; and (4) an analysis of the interactions of content and equity by grade band. Careful attention to the issues of content strand, equity, and interaction is essential for the advancement of curricular evaluation. Content strand analysis provides the detail that is often lost by reporting overall scores; equity analysis can provide essential information on what subgroups are adequately served by the innovations, and analysis by content and grade level can shed light on the controversies that evolve over time.
Analysis by Test Type
Different studies used varied combinations of outcome measures. Because of the importance of outcome measures on test results, we chose to examine whether the probabilities for the studies changed significantly across different types of outcome measures (national test, local test). The most frequent use of tests across all studies was a combination of national and local tests (n=18 studies), a local test (n=16), and national tests (n=17). Other uses of test combinations were used by three studies or less. The percentages of various outcomes by test type in comparison to all studies are described in Table 5-10.
These data (Table 5-11) suggest that national tests tend to produce less positive results, and with the resulting gains falling into results showing no significant differences, suggesting that national tests demonstrate less curricular sensitivity and specificity.
TABLE 5-10 Percentage of Outcomes by Test Type
TABLE 5-11 Percentage of Outcomes by Test Type and Program Type
TABLE 5-12 Number of Studies That Disaggregated by Content Strand
|
Program Type |
Elementary |
Middle |
High School |
Total |
|
NSF-supported |
14 |
6 |
9 |
29 |
|
Commercially generated |
0 |
4 |
5 |
9 |
Content Strand
Curricular effectiveness is not an all-or-nothing proposition. A curriculum may be effective in some topics and less effective in others. For this reason, it is useful for evaluators to include an analysis of curricular strands and to report on the performance of students on those strands. To examine this issue, we conducted an analysis of the studies that reported their results by content strand. Thirty-eight studies did this; the breakdown is shown in Table 5-12 by type of curricular program and grade band.
To examine the evaluations of these content strands, we began by listing all of the content strands reported across studies as well as the frequency of report by the number of studies at each grade band. These results are shown in Figure 5-11, which is broken down by content strand, grade level, and program type.
Although there are numerous content strands, some of them were reported on infrequently. To allow the analysis to focus on the key results from these studies, we separated out the most frequently reported on strands, which we call the “major content strands.” We defined these as strands that were examined in at least 10 percent of the studies. The major content strands are marked with an asterisk in the Figure 5-11. When we conduct analyses across curricular program types or grade levels, we use these to facilitate comparisons.
A second phase of our analysis was to examine the performance of students by content strand in the treatment group in comparison to the control groups. Our analysis was conducted across the major content strands at the level of NSF-supported versus commercially generated, initially by all studies and then by grade band. It appeared that such analysis permitted some patterns to emerge that might prove helpful to future evaluators in considering the overall effectiveness of each approach. To do this, we then coded the number of times any particular strand was measured across all studies that disaggregated by content strand. Then, we coded the proportion of times that this strand was reported as favoring the experimental treatment, favoring the comparative curricula, or showing no significant difference. These data are presented across the major content strands for the NSF-supported curricula (Figure 5-12) and the commercially generated curricula, (Figure 5-13) (except in the case of the elemen-
FIGURE 5-11 Study counts for all content strands.
tary curricula where no data were available) in the forms of percentages, with the frequencies listed in the bars.
The presentation of results by strands must be accompanied by the same restrictions as stated previously. These results are based on studies identified as at least minimally methodologically adequate. The quality of the outcome measures in measuring the content strands has not been examined. Their results are coded in relation to the comparison group in the study and are indicated as statistically in favor of the program, as in favor of the comparative program, or as showing no significant differences. The results are combined across studies with no weighting by study size. Their results should be viewed as a means for the identification of topics for potential future study. It is completely possible that a refinement of methodologies may affect the future patterns of results, so the results are to be viewed as tentative and suggestive.
FIGURE 5-12 Major content strand result: All NSF (n=27).
According to these tentative results, future evaluations should examine whether the NSF-supported programs produce sufficient competency among students in the areas of algebraic manipulation and computation. In computation, approximately 40 percent of the results were in favor of the treatment group, no significant differences were reported in approximately 50 percent of the results, and results in favor of the comparison were revealed 10 percent of the time. Interpreting that final proportion of no significant difference is essential. Some would argue that because computation has not been emphasized, findings of no significant differences are acceptable. Others would suggest that such findings indicate weakness, because the development of the materials and accompanying professional development yielded no significant difference in key areas.
FIGURE 5-13 Major content strand result: All commercial (n=8).
From Figure 5-13 of findings from studies of commercially generated curricula, it appears that mixed results are commonly reported. Thus, in evaluations of commercial materials, lack of significant differences in computations/operations, word problems, and probability and statistics suggest that careful attention should be given to measuring these outcomes in future evaluations.
Overall, the grade band results for the NSF-supported programs—while consistent with the aggregated results—provide more detail. At the elementary level, evaluations of NSF-supported curricula (n=12) report better performance in mathematics concepts, geometry, and reasoning and problem solving, and some weaknesses in computation. No content strand analysis for commercially generated materials was possible. Evaluations
(n=6) at middle grades of NSF-supported curricula showed strength in measurement, geometry, and probability and statistics and some weaknesses in computation. In the studies of commercial materials, evaluations (n=4) reported favorable results in reasoning and problem solving and some unfavorable results in algebraic procedures, contextual problems, and mathematics concepts. Finally, at the high school level, the evaluations (n=9) by content strand for the NSF-supported curricula showed strong favorable results in algebra concepts, reasoning/problem solving, word problems, probability and statistics, and measurement. Results in favor of the control were reported in 25 percent of the algebra procedures and 33 percent of computation measures.
For the studies of commercial materials (n=4), only the geometry results favor the control group 25 percent of the time, with 50 percent having favorable results. Algebra concepts, reasoning, and probability and statistics also produced favorable results.
Equity Analysis of Comparative Studies
When the goal of providing a standards-based curriculum to all students was proposed, most people could recognize its merits: the replacement of dull, repetitive, largely dead-end courses with courses that would lead all students to be able, if desired and earned, to pursue careers in mathematics-reliant fields. It was clear that the NSF-supported projects, a stated goal of which was to provide standards-based courses to all students, called for curricula that would address the problem of too few students persisting in the study of mathematics. For example, as stated in the NSF Request for Proposals (RFP):
Rather than prematurely tracking students by curricular objectives, secondary school mathematics should provide for all students a common core of mainstream mathematics differentiated instructionally by level of abstraction and formalism, depth of treatment and pace (National Science Foundation, 1991, p. 1). In the elementary level solicitation, a similar statement on causes for all students was made (National Science Foundation, 1988, pp. 4-5).
Some, but not enough attention has been paid to the education of students who fall below the average of the class. On the other hand, because the above average students sometimes do not receive a demanding education, it may be incorrectly assumed they are easy to teach (National Science Foundation, 1989, p. 2).
Likewise, with increasing numbers of students in urban schools, and increased demographic diversity, the challenges of equity are equally significant for commercial publishers, who feel increasing pressures to demonstrate the effectiveness of their products in various contexts.
The problem was clearly identified: poorer performance by certain subgroups of students (minorities—non-Asian, LEP students, sometimes females) and a resulting lack of representation of such groups in mathematics-reliant fields. In addition, a secondary problem was acknowledged: Highly talented American students were not being provided adequate challenge and stimulation in comparison with their international counterparts. We relied on the concept of equity in examining the evaluation. Equity was contrasted to equality, where one assumed all students should be treated exactly the same (Secada et al., 1995). Equity was defined as providing opportunities and eliminating barriers so that the membership in a subgroup does not subject one to undue and systematically diminished possibility of success in pursuing mathematical study. Appropriate treatment therefore varies according to the needs of and obstacles facing any subgroup.
Applying the principles of equity to evaluate the progress of curricular programs is a conceptually thorny challenge. What is challenging is how to evaluate curricular programs on their progress toward equity in meeting the needs of a diverse student body. Consider how the following questions provide one with a variety of perspectives on the effectiveness of curricular reform regarding equity:
-
Does one expect all students to improve performance, thus raising the bar, but possibly not to decrease the gap between traditionally well-served and under-served students?
-
Does one focus on reducing the gap and devote less attention to overall gains, thus closing the gap but possibly not raising the bar?
-
Or, does one seek evidence that progress is made on both challenges—seeking progress for all students and arguably faster progress for those most at risk?
Evaluating each of the first two questions independently seems relatively straightforward. When one opts for a combination of these two, the potential for tensions between the two becomes more evident. For example, how can one differentiate between the case in which the gap is closed because talented students are being underchallenged from the case in which the gap is closed because the low-performing students improved their progress at an increased rate? Many believe that nearly all mathematics curricula in this country are insufficiently challenging and rigorous. Therefore achieving modest gains across all ability levels with evidence of accelerated progress by at-risk students may still be criticized for failure to stimulate the top performing student group adequately. Evaluating curricula with regard to this aspect therefore requires judgment and careful methodological attention.
Depending on one’s view of equity, different implications for the collection of data follow. These considerations made examination of the quality of the evaluations as they treated questions of equity challenging for the committee members. Hence we spell out our assumptions as precisely as possible:
-
Evaluation studies should include representative samples of student demographics, which may require particular attention to the inclusion of underrepresented minority students from lower socioeconomic groups, females, and special needs populations (LEP, learning disabled, gifted and talented students) in the samples. This may require one to solicit participation by particular schools or districts, rather than to follow the patterns of commercial implementation, which may lead to an unrepresentative sample in aggregate.
-
Analysis of results should always consider the impact of the program on the entire spectrum of the sample to determine whether the overall gains are distributed fairly among differing student groups, and not achieved as improvements in the mean(s) of an identifiable subpopulation(s) alone.
-
Analysis should examine whether any group of students is systematically less well served by curricular implementation, causing losses or weakening the rate of gains. For example, this could occur if one neglected the continued development of programs for gifted and talented students in mathematics in order to implement programs focused on improving access for underserved youth, or if one improved programs solely for one group of language learners, ignoring the needs of others, or if one’s study systematically failed to report high attrition affecting rates of participation of success or failure.
-
Analyses should examine whether gaps in scores between significantly disadvantaged or underperforming subgroups and advantaged subgroups are decreasing both in relation to eliminating the development of gaps in the first place and in relation to accelerating improvement for underserved youth relative to their advantaged peers at the upper grades.
In reviewing the outcomes of the studies, the committee reports first on what kinds of attention to these issues were apparent in the database, and second on what kinds of results were produced. Some of the studies used multiple methods to provide readers with information on these issues. In our report on the evaluations, we both provide descriptive information on the approaches used and summarize the results of those studies. Developing more effective methods to monitor the achievement of these objectives may need to go beyond what is reported in this study.
Among the 63 at least minimally methodologically adequate studies, 26 reported on the effects of their programs on subgroups of students. The
TABLE 5-13 Most Common Subgroups Used in the Analyses and the Number of Studies That Reported on That Variable
|
Identified Subgroup |
Number of Studies of NSF-Supported |
Number of Studies of Commercially Generated |
Total |
|
Gender |
14 |
5 |
19 |
|
Race and ethnicity |
14 |
2 |
16 |
|
Socioeconomic status |
8 |
2 |
10 |
|
Achievement levelsa |
5 |
3 |
8 |
|
English as a second language (ESL) |
2 |
1 |
3 |
|
Total |
43 |
13 |
56 |
|
aAchievement levels: Outcome data are reported in relation to categorizations by quartiles or by achievement level based on independent test. |
|||
other 37 reported on the effects of the curricular intervention on means of whole groups and their standard deviations, but did not report on their data in terms of the impact on subpopulations. Of those 26 evaluations, 19 studies were on NSF-supported programs and 7 were on commercially generated materials. Table 5-13 reports the most common subgroups used in the analyses and the number of studies that reported on that variable. Because many studies used multiple categories for disaggregation (ethnicity, SES, and gender), the number of reports is more than double the number of studies. For this reason, we report the study results in terms of the “frequency of reports on a particular subgroup” and distinguish this from what we refer to as “study counts.” The advantage of this approach is that it permits reporting on studies that investigated multiple ways to disaggregate their data. The disadvantage is that in a sense, studies undertaking multiple disaggregations become overrepresented in the data set as a result. A similar distinction and approach were used in our treatment of disaggregation by content strands.
It is apparent from these data that the evaluators of NSF-supported curricula documented more equity-based outcomes, as they reported 43 of the 56 comparisons. However, the same percentage of the NSF-supported evaluations disaggregated their results by subgroup, as did commercially generated evaluations (41 percent in both cases). This is an area where evaluations of curricula could benefit greatly from standardization of ex-
pectation and methodology. Given the importance of the topic of equity, it should be standard practice to include such analyses in evaluation studies.
In summarizing these 26 studies, the first consideration was whether representative samples of students were evaluated. As we have learned from medical studies, if conclusions on effectiveness are drawn without careful attention to representativeness of the sample relative to the whole population, then the generalizations drawn from the results can be seriously flawed. In Chapter 2 we reported that across the studies, approximately 81 percent of the comparative studies and 73 percent of the case studies reported data on school location (urban, suburban, rural, or state/region), with suburban students being the largest percentage in both study types. The proportions of students studied indicated a tendency to undersample urban and rural populations and oversample suburban schools. With a high concentration of minorities and lower SES students in these areas, there are some concerns about the representativeness of the work.
A second consideration was to see whether the achievement effects of curricular interventions were achieved evenly among the various subgroups. Studies answered this question in different ways. Most commonly, evaluators reported on the performance of various subgroups in the treatment conditions as compared to those same subgroups in the comparative condition. They reported outcome scores or gains from pretest to posttest. We refer to these as “between” comparisons.
Other studies reported on the differences among subgroups within an experimental treatment, describing how well one group does in comparison with another group. Again, these reports were done in relation either to outcome measures or to gains from pretest to posttest. Often these reports contained a time element, reporting on how the internal achievement patterns changed over time as a curricular program was used. We refer to these as “within” comparisons.
Some studies reported both between and within comparisons. Others did not report findings by comparing mean scores or gains, but rather created regression equations that predicted the outcomes and examined whether demographic characteristics are related to performance. Six studies (all on NSF-supported curricula) used this approach with variables related to subpopulations. Twelve studies used ANCOVA or Multiple Analysis of Variance (MANOVA) to study disaggregation by subgroup, and two reported on comparative effect sizes. In the studies using statistical tests other than t-tests or Chi-squares, two were evaluations of commercially generated materials and the rest were of NSF-supported materials.
Of the studies that reported on gender (n=19), the NSF-supported ones (n=13) reported five cases in which the females outperformed their counterparts in the controls and one case in which the female-male gap decreased within the experimental treatments across grades. In most cases, the studies
present a mixed picture with some bright spots, with the majority showing no significant difference. One study reported significant improvements for African-American females.
In relation to race, 15 of 16 reports on African Americans showed positive effects in favor of the treatment group for NSF-supported curricula. Two studies reported decreases in the gaps between African Americans and whites or Asians. One of the two evaluations of African Americans, performance reported for the commercially generated materials, showed significant positive results, as mentioned previously.
For Hispanic students, 12 of 15 reports of the NSF-supported materials were significantly positive, with the other 3 showing no significant difference. One study reported a decrease in the gaps in favor of the experimental group. No evaluations of commercially generated materials were reported on Hispanic populations. Other reports on ethnic groups occurred too seldom to generalize.
Students from lower socioeconomic groups fared well, according to reported evaluations of NSF-supported materials (n=8), in that experimental groups outperformed control groups in all but one case. The one study of commercially generated materials that included SES as a variable reported no significant difference. For students with limited English proficiency, of the two evaluations of NSF-supported materials, one reported significantly more positive results for the experimental treatment. Likewise, one study of commercially generated materials yielded a positive result at the elementary level.
We also examined the data for ability differences and found reports by quartiles for a few evaluation studies. In these cases, the evaluations showed results across quartiles in favor of the NSF-supported materials. In one case using the same program, the lower quartiles showed the most improvement, and in the other, the gains were in the middle and upper groups for the Iowa Test of Basic Skills and evenly distributed for the informal assessment.
Summary Statements
After reviewing these studies, the committee observed that examining differences by gender, race, SES, and performance levels should be examined as a regular part of any review of effectiveness. We would recommend that all comparative studies report on both “between” and “within” comparisons so that the audience of an evaluation can simply and easily consider the level of improvement, its distribution across subgroups, and the impact of curricular implementation on any gaps in performance. Each of the major categories—gender, race/ethnicity, SES, and achievement level—contributes a significant and contrasting view of curricular impact. Further-
more, more sophisticated accounts would begin to permit, across studies, finer distinctions to emerge, such as the effect of a program on young African-American women or on first generation Asian students.
In addition, the committee encourages further study and deliberation on the use of more complex approaches to the examination of equity issues. This is particularly important due to the overlaps among these categories, where poverty can show itself as its own variable but also may be highly correlated to prior performance. Hence, the use of one variable can mask differences that should be more directly attributable to another. The committee recommends that a group of measurement and equity specialists confer on the most effective design to advance on these questions.
Finally, it is imperative that evaluation studies systematically include demographically representative student populations and distinguish evaluations that follow the commercial patterns of use from those that seek to establish effectiveness with a diverse student population. Along these lines, it is also important that studies report on the impact data on all substantial ethnic groups, including whites. Many studies, perhaps because whites were the majority population, failed to report on this ethnic group in their analyses. As we saw in one study, where Asian students were from poor homes and first generation, any subgroup can be an at-risk population in some setting, and because gains in means may not necessarily be assumed to translate to gains for all subgroups or necessarily for the majority subgroup. More complete and thorough descriptions and configurations of characteristics of the subgroups being served at any location—with careful attention to interactions—is needed in evaluations.
Interactions Among Content and Equity, by Grade Band
By examining disaggregation by content strand by grade levels, along with disaggregation by diverse subpopulations, the committee began to discover grade band patterns of performance that should be useful in the conduct of future evaluations. Examining each of these issues in isolation can mask some of the overall effects of curricular use. Two examples of such analysis are provided. The first example examines all the evaluations of NSF-supported curricula from the elementary level. The second examines the set of evaluations of NSF-supported curricula at the high school level, and cannot be carried out on evaluations of commercially generated programs because they lack disaggregation by student subgroup.
Example One
At the elementary level, the findings of the review of evaluations of data on effectiveness of NSF-supported curricula report consistent patterns of
benefits to students. Across the studies, it appears that positive results are enhanced when accompanied by adequate professional development and the use of pedagogical methods consistent with those indicated by the curricula. The benefits are most consistently evidenced in the broadening topics of geometry, measurement, probability, and statistics, and in applied problem solving and reasoning. It is important to consider whether the outcome measures in these areas demonstrate a depth of understanding. In early understanding of fractions and algebra, there is some evidence of improvement. Weaknesses are sometimes reported in the areas of computational skills, especially in the routinization of multiplication and division. These assertions are tentative due to the possible flaws in designs but quite consistent across studies, and future evaluations should seek to replicate, modify, or discredit these results.
The way to most efficiently and effectively link informal reasoning and formal algorithms and procedures is an open question. Further research is needed to determine how to most effectively link the gains and flexibility associated with student-generated reasoning to the automaticity and generalizability often associated with mastery of standard algorithms.
The data from these evaluations at the elementary level generally present credible evidence of increased success in engaging minority students and students in poverty based on reported gains that are modestly higher for these students than for the comparative groups. What is less well documented in the studies is the extent to which the curricula counteract the tendencies to see gaps emerge and result in long-term persistence in performance by gender and minority group membership as they move up the grades. However, the evaluations do indicate that these curricula can help, and almost never do harm. Finally, on the question of adequate challenge for advanced and talented students, the data are equivocal. More attention to this issue is needed.
Example Two
The data at the high school level produced the most conflicting results, and in conducting future evaluations, evaluators will need to examine this level more closely. We identify the high school as the crucible for curricular change for three reasons: (1) the transition to postsecondary education puts considerable pressure on these curricula; (2) the criteria outlined in the NSF RFP specify significant changes from traditional practice; and (3) high school freshmen arrive from a myriad of middle school curricular experiences. For the NSF-supported curricula, the RFP required that the programs provide a core curriculum “drawn from statistics/probability, algebra/functions, geometry/trigonometry, and discrete mathematics” (NSF, 1991, p. 2) and use “a full range of tools, including graphing calculators
and computers” (NSF, 1991, p. 2). The NSF RFP also specified the inclusion of “situations from the natural and social sciences and from other parts of the school curriculum as contexts for developing and using mathematics” (NSF, 1991, p. 1). It was during the fourth year that “course options should focus on special mathematical needs of individual students, accommodating not only the curricular demands of the college-bound but also specialized applications supportive of the workplace aspirations of employment-bound students” (NSF, 1991, p. 2). Because this set of requirements comprises a significant departure from conventional practice, the implementation of the high school curricula should be studied in particular detail.
We report on a Systemic Initiative for Montana Mathematics and Science (SIMMS) study by Souhrada (2001) and Brown et al. (1990), in which students were permitted to select traditional, reform, and mixed tracks. It became apparent that the students were quite aware of the choices they faced, as illustrated in the following quote:
The advantage of the traditional courses is that you learn—just math. It’s not applied. You get a lot of math. You may not know where to use it, but you learn a lot…. An advantage in SIMMS is that the kids in SIMMS tell me that they really understand the math. They understand where it comes from and where it is used.
This quote succinctly captures the tensions reported as experienced by students. It suggests that student perceptions are an important source of evidence in conducting evaluations. As we examined these curricular evaluations across the grades, we paid particular attention to the specificity of the outcome measures in relation to curricular objectives. Overall, a review of these studies would lead one to draw the following tentative summary conclusions:
-
There is some evidence of discontinuity in the articulation between high school and college, resulting from the organization and emphasis of the new curricula. This discontinuity can emerge in scores on college admission tests, placement tests, and first semester grades where nonreform students have shown some advantage on typical college achievement measures.
-
The most significant areas of disadvantage seem to be in students’ facility with algebraic manipulation, and with formalization, mathematical structure, and proof when isolated from context and denied technological supports. There is some evidence of weakness in computation and numeration, perhaps due to reliance on calculators and varied policies regarding their use at colleges (Kahan, 1999; Huntley et al., 2000).
-
There is also consistent evidence that the new curricula present
-
strengths in areas of solving applied problems, the use of technology, new areas of content development such as probability and statistics and functions-based reasoning in the use of graphs, using data in tables, and producing equations to describe situations (Huntley et al., 2000; Hirsch and Schoen, 2002).
-
Despite early performance on standard outcome measures at the high school level showing equivalent or better performance by reform students (Austin et al., 1997; Merlino and Wolff, 2001), the common standardized outcome measures (Preliminary Scholastic Assessment Test [PSAT] scores or national tests) are too imprecise to determine with more specificity the comparisons between the NSF-supported and comparison approaches, while program-generated measures lack evidence of external validity and objectivity. There is an urgent need for a set of measures that would provide detailed information on specific concepts and conceptual development over time and may require use as embedded as well as summative assessment tools to provide precise enough data on curricular effectiveness.
-
The data also report some progress in strengthening the performance of underrepresented groups in mathematics relative to their counterparts in the comparative programs (Schoen et al., 1998; Hirsch and Schoen, 2002).
This reported pattern of results should be viewed as very tentative, as there are only a few studies in each of these areas, and most do not adequately control for competing factors, such as the nature of the course received in college. Difficulties in the transition may also be the result of a lack of alignment of measures, especially as placement exams often emphasize algebraic proficiencies. These results are presented only for the purpose of stimulating further evaluation efforts. They further emphasize the need to be certain that such designs examine the level of mathematical reasoning of students, particularly in relation to their knowledge of understanding of the role of proofs and definitions and their facility with algebraic manipulation as we as carefully document the competencies taught in the curricular materials. In our framework, gauging the ease of transition to college study is an issue of examining curricular alignment with systemic factors, and needs to be considered along with those tests that demonstrate a curricular validity of measures. Furthermore, the results raising concerns about college success need replication before secure conclusions are drawn.
Also, it is important that subsequent evaluations also examine curricular effects on students’ interest in mathematics and willingness to persist in its study. Walker (1999) reported that there may be some systematic differences in these behaviors among different curricula and that interest and persistence may help students across a variety of subgroups to survive entry-level hurdles, especially if technical facility with symbol manipulation
can be improved. In the context of declines in advanced study in mathematics by American students (Hawkins, 2003), evaluation of curricular impact on students’ interest, beliefs, persistence, and success are needed.
The committee takes the position that ultimately the question of the impact of different curricula on performance at the collegiate level should be resolved by whether students are adequately prepared to pursue careers in mathematical sciences, broadly defined, and to reason quantitatively about societal and technological issues. It would be a mistake to focus evaluation efforts solely or primarily on performance on entry-level courses, which can clearly function as filters and may overly emphasize procedural competence, but do not necessarily represent what concepts and skills lead to excellence and success in the field.
These tentative patterns of findings indicate that at the high school level, it is necessary to conduct individual evaluations that examine the transition to college carefully in order to gauge the level of success in preparing students for college entry and the successful negotiation of majors. Equally, it is imperative to examine the impact of high school curricula on other possible student trajectories, such as obtaining high school diplomas, moving into worlds of work or through transitional programs leading to technical training, two-year colleges, and so on.
These two analyses of programs by grade-level band, content strand, and equity represent a methodological innovation that could strengthen the empirical database on curricula significantly and provide the level of detail really needed by curriculum designers to improve their programs. In addition, it appears that one could characterize the NSF programs (and not the commercial programs as a group) as representing a particular approach to curriculum, as discussed in Chapter 3. It is an approach that integrates content strands; relies heavily on the use of situations, applications, and modeling; encourages the use of technology; and has a significant dose of mathematical inquiry. One could ask the question of whether this approach as a whole is “effective.” It is beyond the charge and scope of this report, but is a worthy target of investigation if one uses proper care in design, execution, and analysis. Likewise other approaches to curricular change should be investigated at the aggregate level, using careful and rigorous design.
The committee believes that a diversity of curricular approaches is a strength in an educational system that maintains local and state control of curricular decision making. While “scientifically established as effective” should be an increasingly important consideration in curricular choice, local cultural differences, needs, values, and goals will also properly influence curricular choice. A diverse set of effective curricula would be ideal. Finally, the committee emphasizes once again the importance of basing the studies on measures with established curricular validity and avoiding cor-
ruption of indicators as a result of inappropriate amounts of teaching to the test, so as to be certain that the outcomes are the product of genuine student learning.
CONCLUSIONS FROM THE COMPARATIVE STUDIES
In summary, the committee reviewed a total of 95 comparative studies. There were more NSF-supported program evaluations than commercial ones, and the commercial ones were primarily on Saxon or UCSMP materials. Of the 19 curricular programs reviewed, 23 percent of the NSF-supported and 33 percent of the commercially generated materials selected had programs with no comparative reviews. This finding is particularly disturbing in light of the legislative mandate in No Child Left Behind (U.S. Department of Education, 2001) for scientifically based curricular programs and materials to be used in the schools. It suggests that more explicit protocols for the conduct of evaluation of programs that include comparative studies need to be required and utilized.
Sixty-nine percent of NSF-supported and 61 percent of commercially generated program evaluations met basic conditions to be classified as at least minimally methodologically adequate studies for the evaluation of effectiveness. These studies were ones that met the criteria of including measures of student outcomes on mathematical achievement, reporting a method of establishing comparability among samples and reporting on implementation elements, disaggregating by content strand, or using precise, theoretical analyses of the construct or multiple measures.
Most of these studies had both strengths and weaknesses in their quasi-experimental designs. The committee reviewed the studies and found that evaluators had developed a number of features that merit inclusions in future work. At the same time, many had internal threats to validity that suggest a need for clearer guidelines for the conduct of comparative evaluations.
Many of the strengths and innovations came from the evaluators’ understanding of the program theories behind the curricula, their knowledge of the complexity of practice, and their commitment to measuring valid and significant mathematical ideas. Many of the weaknesses came from inadequate attention to experimental design, insufficient evidence of the independence of evaluators in some studies, and instability and lack of cooperation in interfacing with the conditions of everyday practice.
The committee identified 10 elements of comparative studies needed to establish a basis for determining the effectiveness of a curriculum. We recognize that not all studies will be able to implement successfully all elements, and those experimental design variations will be based largely on study size and location. The list of elements begins with the seven elements
corresponding to the seven critical decisions and adds three additional elements that emerged as a result of our review:
-
A better balance needs to be achieved between experimental and quasi-experimental studies. The virtual absence of large-scale experimental studies does not provide a way to determine whether the use of quasi-experimental approaches is being systematically biased in unseen ways.
-
If a quasi-experimental design is selected, it is necessary to establish comparability. When quasi-experimentation is used, it “pertains to studies in which the model to describe effects of secondary variables is not known but assumed” (NRC, 1992, p. 18). This will lead to weaker and potentially suspect causal claims, which should be acknowledged in the evaluation report, but may be necessary in relation to feasibility (Joint Committee on Standards for Educational Evaluation, 1994). In general, to date, studies have assumed prior achievement measures, ethnicity, gender, and SES, are acceptable variables on which to match samples or on which to make statistical adjustments. But there are often other variables in need of such control in such evaluations including opportunity to learn, teacher effectiveness, and implementation (see #4 below).
-
The selection of a unit of analysis is of critical importance to the design. To the extent possible, it is useful to randomly assign the unit for the different curricula. The number of units of analysis necessary for the study to establish statistical significance depends not on the number of students, but on this unit of analysis. It appears that classrooms and schools are the most likely units of analysis. In addition, the development of increasingly sophisticated means of conducting studies that recognize that the level of the educational system in which experimentation occurs affects research designs.
-
It is essential to examine the implementation components through a set of variables that include the extent to which the materials are implemented, teaching methods, the use of supplemental materials, professional development resources, teacher background variables, and teacher effects. Gathering these data to gauge the level of implementation fidelity is essential for evaluators to ensure adequate implementation. Studies could also include nested designs to support analysis of variation by implementation components.
-
Outcome data should include a variety of measures of the highest quality. These measures should vary by question type (open ended, multiple choice), by type of test (international, national, local) and by relation of testing to everyday practice (formative, summative, high stakes), and ensure curricular validity of measures and assess curricular alignment with systemic factors. The use of comparisons among total tests, fair tests, and
-
conservative tests, as done in the evaluations of UCSMP, permits one to gain insight into teacher effects and to contrast test results by items included. Tests should also include content strands to aid disaggregation, at a level of major content strands (see Figure 5-11) and content-specific items relevant to the experimental curricula.
-
Statistical analysis should be conducted on the appropriate unit of analysis and should include more sophisticated methods of analysis such as ANOVA, ANCOVA, MACOVA, linear regression, and multiple regression analysis as appropriate.
-
Reports should include clear statements of the limitations to generalization of the study. These should include indications of limitations in populations sampled, sample size, unique population inclusions or exclusions, and levels of use or attrition. Data should also be disaggregated by gender, race/ethnicity, SES, and performance levels to permit readers to see comparative gains across subgroups both between and within studies.
-
It is useful to report effect sizes. It is also useful to present item-level data across treatment program and show when performances between the two groups are within the 10 percent confidence interval of each other. These two extremes document how crucial it is for curricula developers to garner both precise and generalizable information to inform their revisions.
-
Careful attention should also be given to the selection of samples of populations for participation. These samples should be representative of the populations to whom one wants to generalize the results. Studies should be clear if they are generalizing to groups who have already selected the materials (prior users) or to populations who might be interested in using the materials (demographically representative).
-
The control group should use an identified comparative curriculum or curricula to avoid comparisons to unstructured instruction.
In addition to these prototypical decisions to be made in the conduct of comparative studies, the committee suggests that it would be ideal for future studies to consider some of the overall effects of these curricula and to test more directly and rigorously some of the findings and alternative hypotheses. Toward this end, the committee reported the tentative findings of these studies by program type. Although these results are subject to revision, based on the potential weaknesses in design of many of the studies summarized, the form of analysis demonstrated in this chapter provides clear guidance about the kinds of knowledge claims and the level of detail that we need to be able to judge effectiveness. Until we are able to achieve an array of comparative studies that provide valid and reliable information on these issues, we will be vulnerable to decision making based excessively on opinion, limited experience, and preconceptions.