Complex Networks: Ubiquity, Importance, and Implications
ALESSANDRO VESPIGNANI
Indiana University
Bloomington, Indiana
Thanks to increasingly powerful computers and the informatics revolution, data sets on several large-scale networks can now be gathered and handled systematically. These data can then be used to reveal the structural and functional properties of these networks. Mapping projects of the World Wide Web (WWW) and the physical Internet offered researchers their first opportunity to study the topology and traffic of large-scale networks. Gradually, other studies followed describing networks of practical interest in social science, infrastructure analysis, and epidemiology. These studies, which involved researchers from many different disciplines, have led to a paradigm shift—the complexity of large-scale networks has become the central issue in our understanding, characterization, and modeling (Barabási, 2002; Dorogovstev and Mendes, 2003; Newman, 2003; Pastor-Satorras and Vespignani, 2004).
UBIQUITY
In general terms, a network system can be described as a graph with nodes (vertices) that identify the elements of the system; the connecting links (edges) represent the presence of a relation or interaction among these elements. From this very general vantage point, it is easy to perceive that a wide array of systems can be approached in the framework of network theory.
In the first instance, we can provide a rudimentary taxonomy of real-world networks. The two main classes of networks are infrastructure systems and natu-
ral or living systems. These classes can be further divided into subgroups. Networks belonging to the class of natural systems can be divided into biological networks, social-system networks, food webs, and ecosystems, just to mention a few. Biological networks can refer to complicated interactions among the genes, proteins, and molecular processes that regulate life. Social networks concern relations between individuals, such as family relationships, friendships, business relationships, and many others (Castells, 2000; Wasserman and Faust, 1994).
Infrastructure networks can readily be divided into two main subgroups, (1) virtual or cyber networks and (2) physical systems. Virtual or cyber networks exist and operate in the digital world of cyberspace. Physical systems include real-world networks, such as energy, transportation, and health care networks. Of course, this is just a rough classification because there are many interrelations and interdependencies among physical infrastructure networks, as well as between physical and digital networks.
The Internet, for instance, is a kind of hybrid network in which cyber features are mixed with physical features. The Internet is composed of physical objects, such as routers (the main computers that enable us to communicate) and transmission lines (the cables that connect computers). On top of this physical layer is a virtual world of software that defines networks, such as WWW, the e-mail network, and peer-to-peer networks.
These information-transfer media are used by hundreds of millions of people, and, similar to the physical Internet, virtual networks have become enormous and intricate as the result of a self-organized growing process. The dynamics of these virtual networks are the outcome of interactions among the individuals that form various communities within the network. In this sense, they include a mixture of complex socio-technical aspects. Other examples of socio-technical networks in which physical and technological constraints interact with social, demographic, and economic factors, include the worldwide airport and power-distribution networks.
COMPLEXITY
To understand complex networks, we must make a critical distinction between “complex networks” and “complicated networks.” The characteristic features and behavior of complex systems differ significantly from those of merely complicated systems. A minimal definition of complexity includes two main features: (1) complex systems exhibit complications and heterogeneities on all scales possible within the physical constraints of the system; (2) these complications and heterogeneities are spontaneous outcomes of interactions among the constituent units of the system; in other words, they are emergent phenomena.
It is easy to see that WWW, the Internet, and the airport network are systems that grow in time by following complicated dynamic rules without a blueprint or global supervision. The same can be said of many social and biological
networks. All of them are self-organizing systems that, at the end of their evolution, show an emergent architecture with unexpected properties and regularities.
If complexity is inherent in the emergence of complications on all scales, one might wonder what a signature of complexity would be in real-world networks. The first clue is the high level of heterogeneity in the degree of vertices, that is, the number of connections, k, to each vertex. This feature can easily be understood by visualizing airport networks and the “hub” policy that most air-lines have adopted. The same arrangement can be perceived in many other networks in which the presence of “hubs” is a natural consequence of different factors, such as popularity, strategies, and optimization. In the WWW, for instance, some pages become so popular they are pointed to by thousands of other pages; in general, however, most documents remain practically unknown.
The presence of hubs and connectivity ordering have a more dramatic manifestation than was initially thought (Albert and Barabási, 2002; Barabási and Albert, 1999). This can be observed by studying the degree distribution P(k), i.e., the probability that any given vertex has k connection to other vertices. For a large number of networks this distribution is very different from the one usually encountered in Poissonian random graphs and exhibits heavy-tail often approximated by power-law forms P(k) ~ k –γ. A peculiarity of distributions with heavy tails is that the average behavior of the system is not typical (Figure 1).
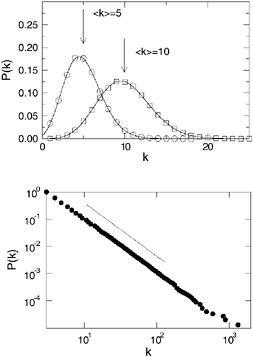
FIGURE 1 Poisson distributions (top) and a power-law distribution typical of scale-free graphs (bottom). Poisson distributions are peaked around the average value <k> and decay exponentially at large degree values. The power-law distribution P(k) ~ k –γ acquires a linear behavior on the double logarithmic scale. The slope identifies the value of the γ exponent. It is worth stressing the broad spectrum of the power-law distribution that extends up to very high values in k.
In mathematical terms, the heavy-tail property translates into a very high level of fluctuation, with the divergence of the standard deviation of the degree distribution limited only by the finite size of the system (Albert and Barabási, 2002; Amaral et al., 2000; Barabási and Albert, 1999). We are thus in the presence of structures with fluctuations and complications that extend over all possible scales allowed by the physical size of the system. In short, these are complex systems.
IMPORTANCE
Heavy tails and heterogeneity appear to be common characteristics of a large number of real-world networks, along with other complex topological features, such as the presence of communities, motifs, hierarchies, and modular ordering. The evidence that a complex topology is shared by many complex evolving networks cannot be considered incidental. Rather, it suggests a general principle that might explain the emergence of this architecture in very different contexts. From this perspective, it would be useful to have a theoretical understanding that might reveal the general principles that underlie the formation of a network.
When looking at networks from the point of view of complex systems, the focus is on the microscopic processes that govern the appearance and disappearance of vertices and links. Thus, attempts to model and understand the origin of observed topological properties of real-world networks require a radical change in perspective to predictions of the large-scale properties and behavior of the system on the basis of dynamic interactions among the constituent units. For this reason, recent activity has been focused on the development of dynamic models for networks. This intense activity has generated a vast field of research whose results and advances are providing new techniques for approaching conceptual and practical problems in the field of networked systems (Amaral et al., 2000; Barabási, 2002; Barabási and Albert, 1999; Dorogovstev and Mendes, 2003; Newman, 2003; Pastor-Satorras and Vespignani, 2004).
IMPLICATIONS
Advances in the understanding of large complex networks have also generated a great deal of interest in the potential implications of complex properties for the engineering, optimization, and protection of networks. These problems are emerging as fundamental issues that are relevant beyond the usual basic-science perspective. For instance, the complexity of networks has important consequences for the empirical analysis of the robustness of a network to failure or attack.
A natural question to ask in this context concerns the maximum amount of damage a network can withstand (i.e., the threshold value of the removal density
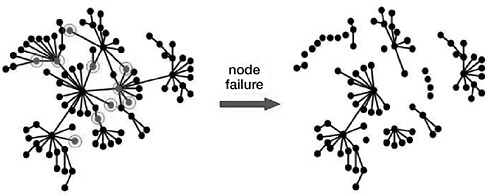
FIGURE 2 Analysis of topological resilience of a network to attacks and failures. If the circled nodes in the network (left) are removed as a result of malfunction or attack, the network is broken up into several fragmented components.
of vertices above which a network can be considered compromised). Contrary to non-complex networks, heavy-tailed networks have two levels of robustness in the face of component failures. First, they are extremely robust to the loss of a large number of randomly selected vertices. Second, they are extremely fragile in response to a targeted attack (Figure 2) (Albert et al., 2000; Cohen et al., 2000).
Studies of complex networks have also revealed important insights on the properties of disease-spreading in highly heterogeneous networks (Lijeros et al., 2001; Schneeberger et al., 2004). Indeed, the presence of heavy-tailed connectivity patterns changes the epidemic framework dramatically. In less complex networks, it is possible to show, on a general basis, that if the rate of spread during an epidemic—roughly speaking the disease transmission probability—is below a given threshold value, the epidemic will die out in a very short time. However, in scale-free networks, no matter the spreading rate, there is a finite probability that the infection will cause a major outbreak that pervades the system or will reach a long-lasting steady state. Thus, heavy-tailed networks lack epidemic thresholds (Pastor-Satorras and Vespignani, 2001a). Interestingly, the absence of an epidemic threshold corresponds to a general inadequacy of uniform immunization policies. Nevertheless, it is possible to take advantage of the connectivity pattern of heavy-tailed networks. One can show in mathematical terms that the protection of just a tiny fraction of the most connected individuals dramatically increases the tolerance level of the whole population to the disease (Cohen et al., 2003; Dezso and Barabási, 2001; Pastor-Satorras and Vespignani, 2001b).
Finally, complexity features also affect the dynamics of information or traffic flow on the network structure. The resilience, or robustness, of networks is a dynamic process that is affected by the time response of elements to different
damage configurations. For instance, when a router or connection fails, the Internet responds very quickly by updating the routing tables of other routers in the neighborhood of the failure point. In most cases, this adaptive response is able to circumscribe the damage, but in some cases failures may cascade through the network, causing far more disruption than one would expect from the initial cause (Lee et al., 2005; Moreno et al., 2003; Motter and Lai, 2002).
Cascading failure is typical of complex systems, in which emergent properties imply events and information flow over a wide range of length and time scales. In other words, small perturbations have a finite probability of triggering a system-wide response, so-called critical behavior. This happens through chains of events that eventually involve a large macroscopic part of the system and, in some cases, lead to global failure.
It is important to realize that in large networked systems this property is inherent in the system complexity and cannot be eliminated by local reinforcement or technological updates. We can vary the proportion of small and large events, but we must learn to live with appreciable probabilities of very large events. We must deal with the inherent complexity of the real world.
REFERENCES
Albert, R., and A.-L. Barabási. 2002. Statistical mechanics of complex networks. Reviews of Modern Physics 74(1): 47–97.
Albert, R., H. Jeong, and A.-L. Barabási. 2000. Error and attack tolerance of complex networks. Nature 406 (6794): 378–382.
Amaral, L.A.N., A. Scala, M. Barthélémy, and H.E. Stanley. 2000. Classes of small world networks. Proceedings of the National Academy of Sciences 97(21): 11149–11152.
Barabási, A.-L. 2002. Linked. Jackson, Tenn.: Perseus Books Group.
Barabási, A.-L., and R. Albert. 1999. Emergence of scaling in random networks. Science 286(5439): 509–512.
Castells, M. 2000. The Rise of the Network Society, vols. 1 and 2. Oxford, U.K.: Blackwell.
Cohen, R., K. Erez, D. ben-Avraham, and S. Havlin. 2000. Resilience of the Internet to random breakdowns. Physical Review Letters 85 (21): 4626–4629.
Cohen, R., S. Havlin, and D. ben-Avraham. 2003. Efficient immunization strategies for computer networks and populations. Physical Review Letters 91(24): 247201.
Dezso, Z., and A.-L. Barabási. 2001. Halting viruses in scale-free networks. Physical Review E 65(5): 055103.
Dorogovstev, S.N., and J.F.F. Mendes. 2003. Evolution of Networks. Oxford, U.K.: Oxford University Press.
Lee, E.J., K.-I. Goh, B. Kahng, and D. Kim. 2005. Robustness of the avalanche dynamics in data packet transport on scale-free networks. Physics Review E 71(5): 056108.
Lijeros, F., C.R. Edling, L.A.N. Amaral, H.E. Stanley, and Y. Åberg. 2001. The web of human sexual contacts. Nature 411(6840): 907–908.
Moreno, Y., R. Pastor-Satorras, A. Vázquez, and A. Vespignani. 2003. Critical load and congestion instabilities in scale-free networks. Europhysics Letters 62(2): 292–298.
Motter, A.E., and Y.C. Lai. 2002. Cascade-based attacks on complex networks. Physics Review E 66(6): 065102.
Newman, M.E.J. 2003. Structure and function of complex networks. SIAM Review 45(2): 167–256.
Pastor-Satorras, R., and A.Vespignani. 2001a. Epidemic spreading in scale-free networks. Physical Review Letters 86(14): 3200–3203.
Pastor-Satorras, R., and A. Vespignani. 2001b. Immunization of complex networks. Physical Review E 65(3): 036104.
Pastor-Satorras, R., and A. Vespignani. 2004. Evolution and Structure of the Internet. Cambridge, U.K.: Cambridge University Press.
Schneeberger. A., C.H. Mercer, S.A.J. Gregson, N.M. Ferguson, C.A. Nyamukapa, R.M. Anderson, A.M. Johnson, and G.P. Garnett. 2004. Scale-free networks and sexually transmitted diseases. Sexually Transmitted Diseases 31(6): 380–387.
Wasserman, S., and K. Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge, U.K.: Cambridge University Press.








