7
Methods for Analysis of Complex Surveys
The panel was asked to consider the appropriateness of the methods the Economic Research Service (ERS) is using to fit statistical models to data from the Agricultural Resource Management Survey (ARMS). The economists at ERS have been advised by the mathematical statisticians at the National Agricultural Statistics Service (NASS) that they should always take a design-based approach for making statistical inferences by using the survey weights. ERS has asked for more explanation on the appropriateness of such an approach. They would like to have a better understanding of the subtleties of this approach relative to a model-based approach, so they can better explain to the users of their analytic outputs, using sound statistical arguments, why they have adopted this approach. At the same time, ERS scientists are also interested in exploring alternative approaches to analyzing ARMS data, especially when fitting complicated econometric models. Finally, ERS is interested in obtaining specific advice on the suitability of statistical and econometric software programs for analyzing ARMS data.
Ideally, ERS would like to have a “Guide for Researchers” on these topics, which would address the various cases that arise in their work. As their analyses become more sophisticated, their questions are becoming more complex. Such a guide would be useful, but writing it is not a trivial task. The panel decided not to write even a short version of such a manual, as this could lead to inappropriate use of the methods if the details of such concepts as ignorability or how to handle analyses based on small sample sizes are not fully understood. Instead, in this chapter we discuss the gen-
eral principles of design-based and model-based inference, explain the main advantages and disadvantages of both, and provide some guidance on how such a guide could be written. The panel also did not address the software issue in detail, because this depends critically on the specific analyses being undertaken.
We begin with a short description of data analysis issues. We then discuss the conceptual and theoretical underpinnings for the different frameworks under which statistical modeling and analysis can be performed, as well as their implications for analytical inference. In the final section, we offer some guidance on how a Guide for Researchers for ARMS could be written.
DATA ANALYSIS ISSUES
The complex design of ARMS includes stratification, clustering, dual frames, and unequal probability sampling. Each year, NASS provides survey weights that account for these design features as well as for additional information available at the population level and various nonresponse adjustments (see Chapter 6). NASS has also developed and makes available sets of replication weights to facilitate computation of variance estimates, with the current method based on delete-a-group jackknife replication. The survey weights and the replication weights are provided with the ARMS datasets.
Recommendation 7.1: NASS should continue to provide survey weights with the ARMS data set, combined with replication weights for variance estimation.
An important use of data from surveys such as ARMS is for descriptive inference, in which population-level and domain-level quantities of interest are estimated from the survey data. An example of a population quantity of interest for ARMS is the average amount spent on fertilizer by all farms, while a domain quantity of interest is the average amount spent on fertilizer by all farms with annual sales over $50,000. Estimates for population and domain (i.e., a subset of the population) quantities are computed as weighted sums over the sample using the survey weights. The variance is estimated by computing jackknife replicates as the weighted sums for each set of replication weights and averaging the sum of the squared deviations from the mean over the full sample estimates (see Box 7-1). When targeting unknown simple or narrowly conditioned quantities of interest in a finite population and in medium-to-large domains within the populations, this randomization-based type of estimation, and the associated inference in terms of standard deviation and confidence intervals,
is generally accepted as being the most appropriate method for obtaining statistically valid estimates (Rao, 2005). NASS and ERS produce large numbers of estimates of this type each year.
Recommendation 7.2: NASS and ERS should continue to recommend the design-weighted approach as appropriate for many of the analyses for users of ARMS data and as the best approach for univariate or descriptive statistics.
In addition to descriptive inference, ERS staff and researchers in other organizations also use ARMS data in analytical inference, in which econometric models are fitted and inference is made about model parameters. In this situation, the goal of the inference is often not finite population quantities, but rather parameters or related quantities for the underlying postulated model, with the population representing a specific realization from that model. Because ARMS data are obtained under a complex design, the general consensus among statisticians is that analytical inference needs to account for the design (Little, 2004). Not accounting for the effects of the sampling design can cause estimators for parameters of the postulated model to be biased, their associated variance estimators to be biased, or both. As a simple example of the possible bias
|
BOX 7-1 Formula for the Delete-a-Group Jackknife Consider the linear prediction model, yk = xkβ+εk, where xk represents a 1 × p dimensional vector of predictors for case k, β represents a p × 1 dimensional vector of unknown regression coefficients, and εk represents an unknown error term. With the ultimate goal being to estimate Assume in the following that the sample was randomly divided into 15 mutually exclusive groups denoted by Sg, g =1, …, 15, and we let the complete sample with Sg removed be denoted as S−g. The only random quantity inyk is εk, and so if one could observe the εk directly, a delete-a-group jackknife estimator of the variance of 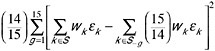 |
|
This can be justified as follows. Ignoring the outside term 14/15, inside the square we have the estimate of the total The only remaining complication is that we do not observe the εk—we can only observe residuals from the regression fit. This is a substantial complication, since the covariates xi can be unbalanced from one group to another. Without justifying this here, one method for dealing with this complication is to replace the εk with yk in the above expression, and replace the wk with the following: where the ci are terms in the regression computation that account for things like heterogeneous variances and correlations among the εj’s. The resulting delete-a-group jackknife can then be written: (Note that the 15/14 is already defined in the wk(g).) SOURCE: Kott, “Some Thoughts on the Delete-a-Group Jackknife with ARMS-III Data”, based on the presentation to the Panel to Review the Agricultural Resource Management Survey (ARMS), June 6, 2006. |
introduced by sampling, consider a population of size N where each element has an unobserved value of interest yi, and that has a true average equal to μy, which is unknown. Suppose that there is a second variable xi that is positively correlated with the yi, and the xi are observed for the whole population. Assume now that the sampling design is such that elements are sampled with higher probability for larger values of xi, which could be implemented through stratification or by using a probability-proportional-to-size design. Then, if one computes the average of the yi in a sample obtained following this sampling design, it is very likely that it will be larger than the population average of μy, that is, the sample mean will be a biased estimator for the population mean μy. Holt et al. (1980) and Pfeffermann (1993) give further examples to illustrate this potential bias due to sampling design, which
can occur not only for simple estimators as in this example but also in complex modeling situations.
While it is clear to many researchers that the effect of the sampling design needs to be addressed whenever models are fitted to ARMS data, it is less clear how this should be accomplished in practice. The statistical literature describes a number of alternative approaches for incorporating the sampling design in analytical inference for surveys (Little, 2004). One commonly recommended approach, which is also the one currently implemented by NASS and ERS, is to perform model analyses using the provided sampling weights and estimate the variability of parameter estimators under the sampling distribution. In the case of ARMS, the variance estimation can be done by repeating the analysis with the replication weights provided by NASS and computing the average sum of squared deviations over the full sample.
While this is a theoretically sound approach and has some important practical advantages, its current implementation suffers from a number of specific shortcomings, as outlined below.
EVALUATION OF CURRENT APPROACH
The survey weights and associated replicate weights provided by NASS make it possible for researchers to fit economic models using the large majority of statistical and econometric software programs that can handle weighted analyses, although assembling the replicate-based estimates to compute sampling error often requires more detailed programming. Performing statistical analyses using the combination of survey weights and replication weights provided by NASS is a theoretically valid approach that guards against potential bias caused by the unequal sampling of farms in the sample. The method is straightforward to implement, even if not completely automated in most software packages.
However, as currently implemented, this method also has some significant drawbacks, as identified by ERS researchers and some academic users of the ARMS data sets (Dubman, 2001). The small number of jackknife replicates (currently 15) means that the variance estimator has low degrees of freedom. This implies that the variance estimator can be highly variable in some situations, and, more problematically, that it is potentially inappropriate for complex models with large vectors of parameters. This puts a limit on the types of models that can be fitted and analyzed for the ARMS data. An additional problem is that the replicate weights contain negative values in years prior to 2005, causing many software programs to fail to run or to give erroneous answers. Recent changes in NASS procedures eliminated negative replicates for later years.
Two other issues are of concern regarding the jackknife methodology. First, the specific selection method of the 15 replicates is critical to ensuring
that the variance estimator is unbiased. The manner in which this needs to be done is well known and appears to be appropriately applied, but clear documentation of the specific implementation for ARMS is needed. Second, several “adjustments,” referred to in Dubman (2001) are made so that the jackknife variance reflects the estimation adjustments (calibration, regression, poststratification) made to the original weights. Again, the principles behind these adjustments are well known, but documentation of the specific implementation used for ARMS is needed.
More generally, there is a concern that the current one-size-fits-all approach for analytical inference for ARMS is somewhat restrictive and does not fully satisfy the diverse needs of researchers. Specifically, it would clearly be desirable to some researchers, both inside and outside ERS, if standard survey software (e.g., SAS “survey procs” such as Proc Surveymeans, Proc Surveyreg, and Proc Surveylogistic) could be used for conducting weighted analyses. Other users might be interested in conducting unweighted analyses that rely more heavily on modeling assumptions while remaining aware of the potential sensitivity of their models to the effects of the design and execution of the sample. For both of these types of users, the information currently provided as auxiliary data with the ARMS data file is likely to be insufficient, because these users need more specific information on the sampling design and on the nonresponse patterns and adjustments applied to the dataset to include in their procedures or models. All of these drawbacks of the current implementation of variance estimation can be overcome.
ESTIMATION STRATEGIES FOR COMPLEX SURVEYS
Concepts of Analytical Inference for Surveys
In survey statistics, the postulated model for the finite population from which the sample is drawn is often referred to as the superpopulation model, with the elements in the finite population treated as realizations from the superpopulation. In analytical studies, particularly economic studies, the superpopulation model is typically assumed to correspond to the model the researcher is interested in estimating. As an example, consider the following superpopulation model:
(1)
where Y and X = (X1, …,Xp) are random variables to be observed through a survey, the function f is assumed to be known, and ε is an unobserved zero-mean error random variable. The vector of parameters β = (β1, …,βp) is of analytical interest to the researchers. In many situations, the primary interest is not in the joint model for Y and X, but in the conditional model,
that is, the model for Y given values of X, in which case the marginal model for X is not explicitly considered in the analysis and X is treated as fixed. For example, Y and X could be dependent and independent variables in a regression model, respectively, and the vector β then denotes the regression parameters for the relationship between them. The regression model is often linear in practice, but the discussion below applies equally to more complicated regression contexts, such as nonlinear models or generalized models.
For now, we assume that the finite population is composed of N independent and identically distributed realizations from this superpopulation model. We use U =(1, … N) to denote the set of indices for the elements in the population. From this population, a sample is drawn according to a sampling design pN(s), which assigns a probability to each possible sample ![]() For a given sample s, the researcher wants to estimate the superpopulation parameters β based on the observations
For a given sample s, the researcher wants to estimate the superpopulation parameters β based on the observations ![]()
The critical issue in how to estimate β is whether the superpopulation model in (1) is a valid representation for the sampled observations ![]()
![]() In the regression model example, this would imply that the relationship between Y and X is unaffected by the manner in which the sample was selected, or equivalently, that the “unobservable” portion of the model, that is, the ε, does not depend on the sampling design. The situation in which the validity of the model of interest is unaffected by the design is referred to in the statistical literature as an ignorable design (see, e.g., Pfeffermann, 1993), based on the terminology introduced by Rubin (1976). It should be noted that ignorability depends on the relationship between the design and the model, so the sampling design for a survey can be ignorable for one model (e.g., the regression model between Y and X) but nonignorable for another (e.g., the joint distribution model for (Y, X)). When the sampling design is ignorable with respect to the model of interest, then it is in principle appropriate to proceed with statistical estimation and inference methods without using the survey weights.
In the regression model example, this would imply that the relationship between Y and X is unaffected by the manner in which the sample was selected, or equivalently, that the “unobservable” portion of the model, that is, the ε, does not depend on the sampling design. The situation in which the validity of the model of interest is unaffected by the design is referred to in the statistical literature as an ignorable design (see, e.g., Pfeffermann, 1993), based on the terminology introduced by Rubin (1976). It should be noted that ignorability depends on the relationship between the design and the model, so the sampling design for a survey can be ignorable for one model (e.g., the regression model between Y and X) but nonignorable for another (e.g., the joint distribution model for (Y, X)). When the sampling design is ignorable with respect to the model of interest, then it is in principle appropriate to proceed with statistical estimation and inference methods without using the survey weights.
When the sampling design is not ignorable for a specific model, the full model for the sampled observations is different from the original model for the population, or, in the regression context, the relationship between Y and X is different in the sample and in the population. Hence, the nonignorable design can cause estimators that are based on the original model to be biased. Also, ignoring the sample design information when it is nonignorable could lead to inappropriate estimated variances, confidence intervals, and incorrect p-values in a statistical hypothesis test. For an example of how a nonignorable design can induce bias on the relationship between dependent and independent variables in the linear regression context, see Nathan and Smith (1989). In economics, such selectivity issues are widely discussed, but generally they have been addressed with explicit modeling
assumptions about the nature of the selectivity, as in the classic paper by Heckman (1979).
When analyzing a data set, it is often impossible to know a priori whether the design is ignorable or not, so it is sound practice to guard against potential biases in estimation and inference. For specific modeling situations, it is possible to perform statistical tests for violations of the ignorability assumption, and variables related to the design can be added to the model as predictor variables. Although adding covariates clearly changes model (1), it makes it possible to create a new conditional model for which the design is now ignorable, so that model-based inference yields appropriate conclusions. An alternative approach, which is valid regardless of whether the design is ignorable or not, is to explicitly account for the sampling design in estimation and inference of model parameters through design-based (weighted) inference. We briefly describe that approach here.
The sampling weights are obtained from the sampling design, denoted by pN(s), which is used to draw random samples s from the population. Based on the sampling design, there is an associated inclusion probability πi for each element in the sample s, defined as
that is, the probability that element i is selected into the sample s under the design. For some multiphase designs, the πi are conditional probabilities that cannot, strictly speaking, be interpreted as inclusion probabilities, but they can be used as such in weight construction. For most commonly used designs, explicit formulas are available for obtaining πi (see, e.g., Sarndal et al., 1992; Lohr, 1999).
Fixed finite population quantities of interest, such as the population mean or total, can be estimated based on the sample observations, by using the design information captured by the inclusion probabilities. For any variable z, a sample estimator ![]() defined as
defined as
is design unbiased for the finite population total ![]() in the sense that over repeated random samples drawn from the population according to the design pN(·), the mean of the
in the sense that over repeated random samples drawn from the population according to the design pN(·), the mean of the ![]() is equal to tz. If the population mean is to be estimated, one can divide the estimator for the population total by N, the number of elements in the population.
is equal to tz. If the population mean is to be estimated, one can divide the estimator for the population total by N, the number of elements in the population.
For more complicated finite population quantities, it is often not possible to maintain design unbiasedness. However, the principle of using sampling weights wi = 1/ πi in the construction of sample-based estimators continues to apply. Under mild regularity conditions on the popu-
lation and the sample design, any finite population quantity of interest that can be expressed as a function of finite population totals, say θN = g(tz1, … ,tzq), can be estimated by a corresponding sample-based estimator ![]() with
with ![]() design consistent for θN (see, e.g., Sarndal et al., 1992). As a simple example of a function of population totals, consider a variable yi (e.g., total amount spent on fertilizers by farm i) and another variable xi (e.g., acreage planted by farm i). According to the above discussion, the ratio θN = ∑Uyi / ∑Uxi (i.e., the average fertilizer application per acre planted in the population) can be estimated consistently by the ratio of sample-weighted estimators
design consistent for θN (see, e.g., Sarndal et al., 1992). As a simple example of a function of population totals, consider a variable yi (e.g., total amount spent on fertilizers by farm i) and another variable xi (e.g., acreage planted by farm i). According to the above discussion, the ratio θN = ∑Uyi / ∑Uxi (i.e., the average fertilizer application per acre planted in the population) can be estimated consistently by the ratio of sample-weighted estimators
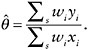
The function g(·) defining θN can be much more complicated than this simple ratio, and the sample-weighted estimation principle applies equally to both explicit population quantities of interest (e.g., coefficients for a population-level regression function) and implicit ones (e.g., solutions of population-level estimating equations).
The preceding discussion of design-based estimation did not refer to a superpopulation model, and indeed the design consistency of ![]() for θN does not depend on any model assumptions about the finite population (except for some mild regularity conditions, such as existence of limits). In analytical uses of survey data, it is possible to combine the above design-based estimation of finite population quantities with the estimation of (superpopulation) model parameters, by taking advantage of the fact that the finite population elements can be viewed as independent and identically distributed realizations from the superpopulation model. Unlike traditional design-based estimation, there are now two random processes determining the statistical properties of estimators: the sampling design and the superpopulation model. In what follows, we use the convention of using a subscript ξ to denote properties with respect to the model, p for properties with respect to the design, and ξp for joint properties.
for θN does not depend on any model assumptions about the finite population (except for some mild regularity conditions, such as existence of limits). In analytical uses of survey data, it is possible to combine the above design-based estimation of finite population quantities with the estimation of (superpopulation) model parameters, by taking advantage of the fact that the finite population elements can be viewed as independent and identically distributed realizations from the superpopulation model. Unlike traditional design-based estimation, there are now two random processes determining the statistical properties of estimators: the sampling design and the superpopulation model. In what follows, we use the convention of using a subscript ξ to denote properties with respect to the model, p for properties with respect to the design, and ξp for joint properties.
Considering again superpopulation model (1), suppose that it is possible to define a finite population estimator BN for the model parameter β, which could be computed if the complete population U were observed. If the components of the parameter vector BN can be expressed as functions of finite population totals similarly to θN above, it is again possible to estimate it by a sample-based estimator, say ![]() which is a function of design-weighted estimators, as previously done for
which is a function of design-weighted estimators, as previously done for ![]()
Figure 7-1 illustrates the traditional view of survey estimators. For the finite population, a parameter vector BN is defined (possibly but not necessarily based on a superpopulation model). A sampling process is used to randomly
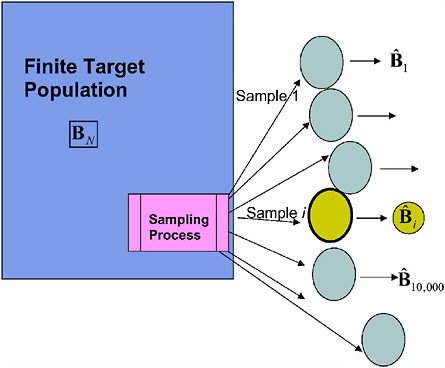
FIGURE 7-1 Diagram representing classical design-based inference.
generate samples, and for each sample an appropriately weighted estimator ![]() can be computed that targets BN. Under the distribution induced by repeated sampling from the fixed target population, the estimator
can be computed that targets BN. Under the distribution induced by repeated sampling from the fixed target population, the estimator ![]() will be consistent for BN, and it is possible to define properties such as
will be consistent for BN, and it is possible to define properties such as ![]() the design expectation of
the design expectation of ![]() and
and ![]() its design variance.
its design variance.
Figure 7-2 takes this idea one step further, by viewing the target population itself as a random realization from the superpopulation model. In this view, the finite population quantity BN is viewed as one particular realization of an estimator of the superpopulation model parameter β. From this particular realization, a sample is drawn according to the sampling design, and an estimator ![]() is constructed. By explicitly including the sampling weights in the construction of
is constructed. By explicitly including the sampling weights in the construction of ![]() we are guaranteed to have a valid (design consistent) estimator of BN, the finite population “estimator” of β. If the superpopulation model is correctly specified, then BN is itself (model) consistent for β. Combining both phases of this estimation process,
we are guaranteed to have a valid (design consistent) estimator of BN, the finite population “estimator” of β. If the superpopulation model is correctly specified, then BN is itself (model) consistent for β. Combining both phases of this estimation process, ![]() is a valid (design and model consistent) estimator of β under joint inference for the sampling design and the superpopulation model.
is a valid (design and model consistent) estimator of β under joint inference for the sampling design and the superpopulation model.
As noted above, when inference for a model is made jointly under a
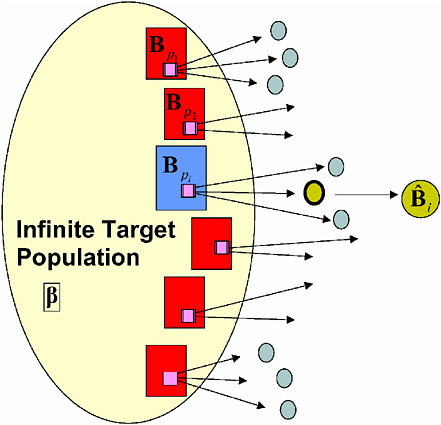
FIGURE 7-2 Diagram representing model design-based inference for superpopulation parameters.
superpopulation model and a sampling design, both of these components contribute uncertainty. Hence, formal inference (confidence intervals, variance, etc.) would need to explicitly incorporate both sources of uncertainty. For instance, using standard conditioning arguments, the joint model-design variance of ![]() for the parameter in model (1) can be written as
for the parameter in model (1) can be written as
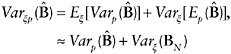
where the approximations assume that the model expectation of the design variance is close to the finite population design variance, and ![]() (both of these assumptions hold at least approximately in a broad range of modeling and sampling contexts, but not in all). The above expression implies that the total variance of the design-weighted estimator
(both of these assumptions hold at least approximately in a broad range of modeling and sampling contexts, but not in all). The above expression implies that the total variance of the design-weighted estimator ![]() is approxi-
is approxi-
mately equal to the sum of its design variance and the model variance of its finite population target BN. Both quantities can be estimated, the former based on the sampling distribution and the latter based on the superpopulation model. Typically, the former is inversely proportional to the number of primary sampling units, and the latter is inversely proportional to the population size. When the number of sampling units in the sample is much smaller than the population size, one can ignore the population variance component Varξ(BN), and the total variance ![]() is then estimated by using design-appropriate methods for estimating the design variance
is then estimated by using design-appropriate methods for estimating the design variance ![]() The above approach is quite general and has been described in the statistical literature for estimation of parameters in linear and nonlinear regression models, estimating equations, maximum likelihood, etc. The articles in Skinner et al. (1989) provide a good overview of design-based approaches for many of these models. Other cases not specifically covered by the above literature follow this same paradigm, as long as the concept of “equivalent finite population quantity associated with the model parameter” applies.
The above approach is quite general and has been described in the statistical literature for estimation of parameters in linear and nonlinear regression models, estimating equations, maximum likelihood, etc. The articles in Skinner et al. (1989) provide a good overview of design-based approaches for many of these models. Other cases not specifically covered by the above literature follow this same paradigm, as long as the concept of “equivalent finite population quantity associated with the model parameter” applies.
There are some important classes of statistical models for which design-based estimation will not provide valid estimators for the superpopulation model parameters. These include estimates of the variance components associated with random effects models, mixed effects models, structural equation models, and multilevel models. The fixed effects in these models can usually be estimated consistently, but not the variance components associated with the random effects, unless certain conditions on the sample sizes apply. If the random effects also need to be estimated, the design-based analysis becomes quite complex, and a model-based (unweighted) analysis might be preferable. Researchers working with ARMS data might also be interested in applying statistical methods that do not fall into the category of “model fitting,” for example principal components analysis, clustering, classification. In those cases, the concept of “equivalent finite population quantity” does not apply directly, and it is sometimes unclear how to interpret the results of a weighted analysis. We discuss model-based inference for survey data in a subsequent section in this chapter.
In the cases for which a weighted analysis is possible, the advantages of the design-based approach are that it fully accounts for the design, and that it is robust to model misspecification, in the sense that it does not require the design to be ignorable with respect to inference for the superpopulation model. The disadvantages of the design-based approach are the lesser availability of software programs that can accommodate the design-weighted analysis, as well as the loss of efficiency relative to unweighted estimators, in cases in which the design is ignorable. The loss of efficiency is due to the fact that if the superpopulation model is correct and the design ignorable, then an unweighted estimator will typically have smaller vari-
ance than a weighted estimator. However, for large sample sizes in which the proportion of observations with very small weights is not overly large, the increase in the variance resulting from using the weighted estimate will not have a serious impact on the analytic conclusions, whereas using an unweighted estimate that can have serious biases could lead to misleading and inappropriate conclusions. In the following two sections, we discuss some design-based and model-based inference options that might be useful for researchers working with ARMS data.
Applying Design-Based Inference
The design-based paradigm described in the previous section should continue to represent a default approach for analyzing ARMS data, because it ensures that the estimates are free of bias due to the sampling process. For most users, the survey weights and the associated replication variance estimation weights make it possible to perform statistically valid model fitting and inference, without having to gain in-depth knowledge of the ARMS design and weight generation procedures. In this section, we address some additional issues related to implementation of the design-based paradigm related to ARMS.
In ARMS and most other large-scale surveys, the survey weights wi that are included as part of the data set are not, strictly speaking, sampling weights, since that latter term is typically reserved for the inverses of the inclusion probabilities πi. Survey weights are based on the sampling weights but are often adjusted for nonresponse and calibrated for known population quantities, either through modeling or poststratification. The effect of these adjustments for analytical studies is important but not often explicitly addressed in the survey estimation literature. We briefly discuss the current consensus on the effect of these adjustments.
Nonresponse adjustments to the weights are important to ensure that, as for the sampling design itself, the effects of the response mechanism are properly accounted for in estimation. The effect of ignoring the response mechanism in model fitting has been extensively studied, although usually from a model-based standpoint (see, e.g., Little and Rubin, 2002), and the principle of weighting by the inverse of the response probability is one of the possible solutions usually recommended in that literature. While weighting to adjust for both the sampling design and the response mechanism is therefore a valid approach, there is a critical difference between the sampling design and the response mechanism. The former is known by the survey statisticians responsible for creating the weights, while the latter is not and needs to be modeled. Hence, inference under joint sampling and response mechanism is often referred to as pseudorandomization (Oh and Scheuren, 1983), to differentiate it from pure (design-based) randomization
inference. Sarndal and Swensson (1987) describe inference for finite population quantities under pseudorandomization, where the response mechanism is viewed as an additional phase of sampling.
For the purpose of estimating parameters of a superpopulation model, pseudorandomization would in principle need to be combined with the randomness of the model itself, using the same ideas as in the section on concepts for analytical inference for surveys. It is generally accepted that the survey weights represent the best available attempt by the statisticians responsible for a particular survey to account for both its design and the nonresponse. As long as the postulated response mechanism is correct, analyses performed using the joint sampling-nonresponse weights should result in consistent estimation of the finite population parameters, which are themselves model consistent for the superpopulation model parameters.
Calibration and the closely related model-assisted estimation approaches (Sarndal et al., 1992) are generally used to increase the efficiency of survey estimators and are also used for ARMS. While this increase in efficiency has been well documented for the case of estimating finite population quantities, the statistical literature on the effect of calibration on analytical inference for superpopulation model parameters is also very limited. Because properly applied calibration approaches create weights that remain “close to” the original inclusion probability weights and do not affect the design consistency of the weighted estimators, it is generally accepted that calibrated weights can be used in lieu of the original weights for the purpose of constructing design-consistent estimators for superpopulation model parameters. The recent monograph by Sarndal and Lundstrom (2005) describes estimation methods that account for both calibration and nonresponse, but it does not explicitly discuss analytical inference.
Variance estimators for survey-weighted estimators exist and are increasingly being implemented in a number of major statistical software programs. The most commonly used packages for design-based analysis are SUDAAN, STATA (survey module) and WesVar. Other packages incorporating some design-based methods are SAS, SPSS, and Mplus. However, for these latter programs, available procedures typically apply only to specific models and specific designs and currently almost completely ignore the effects of calibration and nonresponse adjustments. In situations in which the model and the design are covered by available software implementations, these offer a convenient way to perform design-based estimation and inference.
For these programs to correctly compute variances and perform statistical tests, using an analytic variance formula rather than using replication methods, it is necessary to specify detailed design characteristics, such as stratum identifiers and totals, cluster identifiers and weights. Hence, in order to be able to use this approach for ARMS, this information needs
to be provided to users, which might cause confidentiality and disclosure issues if some information becomes too specific to be released as part of a data set for outside researchers. Because it might in principle be possible for ERS researchers to obtain more detailed design information from NASS, analyses performed by staff within the agency could be performed using existing statistical programs that implement design-based analysis and model fitting. This might require more access to confidential data than ERS currently has and would require ERS researchers, possibly in collaboration with NASS statisticians, to gain sufficient expertise in design-based methods to be able to evaluate the appropriateness of these programs for their modeling needs.
In order to accommodate a wide range of modeling needs and to fully account for postsampling weighting adjustments without having to release detailed design information, replication methods offer a useful alternative. A number of such methods are available, including balanced repeated replication, jackknife, and bootstrap methods (Wolter, 1985; Rao et al., 1992; Rust and Rao, 1996). In all these methods, each set of replicate weights undergoes the same range of weight adjustments as the original weights, so that they incorporate the adjustments in the variance estimation. The delete-a-group jackknife, the method currently implemented for ARMS, falls in this category and represents a valid design-based variance estimation method. Jackknife variance estimators make it possible to construct confidence intervals for parameters and perform Wald-type hypothesis testing on them. Both inference tools rely on the asymptotic normality of the estimator, which is generally reasonable for large samples.
NASS has made available some general-purpose programs for implementing the delete-a-group jackknife for estimating design-based variances. Some commercial software is also available for similar estimates. In some cases, these may be easier to learn to use than the specialized software written by NASS. Although there are a growing number of options to perform design-based variance estimation, in order to ensure consistency of the results across researchers for similar analyses, we suggest that researchers use the NASS-developed delete-a-group jackknife software whenever they want to use replication methods for their variance estimation. Although not always easy to apply, the NASS software has the advantage of being extremely flexible to apply while the jackknife is somewhat less dependent on assumptions. This is not to say that the jackknife is optimal in all situations, but the various estimators are relatively comparable in a wide variety of applications, and the jackknife is relatively robust to the circumstances of use.
A number of improvements to the current implementation of the delete-a-group jackknife would be very beneficial. A larger number of replicates should help alleviate the problem of small degrees of freedom encountered when multiple parameter estimates need to be tested jointly. More careful
stabilization of the individual weights in the replicates is also advisable, to avoid either negative or unduly large weights that would result in unstable variance estimates. Alternative jackknife-based methods, such as the linearized jackknife (Yung and Rao, 1996; Binder et al., 2004), might provide a useful alternative methods for situations in which users are fitting models on small domains or for rare characteristics. Because of the importance of design-based estimation for many purposes, revision of the replicate generation process should be a high priority and implemented as soon as feasible as part of an overall strategy for improving data analysis.
Recommendation 7.3: NASS should investigate and implement improvements to the current jackknife replicates to make them more useful for the types of analyses performed by users in ERS and other organizations. In particular, NASS should increase the number of replicates and apply bounds to the magnitude of the weight adjustments.
Applying Model-Based Inference
As an alternative to the weighted, design-based analysis described above, it is also possible to consider a model-based analysis. This approach has a number of advantages, most importantly the fact that a wider range of statistical methods for analysis become available, many of which are already implemented in statistical software programs. The critical issue in this type of analysis is to ensure that the sampling design (and, as discussed above, the nonresponse mechanism) is ignorable with respect to the model of interest. As noted in Little (2004), “the major weakness of model-based inference is that if the model is seriously misspecified, it can yield inferences that are worse (and potentially much worse) than design-based inferences.” Therefore, unless the researcher has been able to determine that, to the best of his or her knowledge, the design and nonresponse are either a priori ignorable or sufficiently accounted for in the model, the results from a model-based statistical analysis will not be scientifically credible. Model building, model estimation, and model checking for survey data are difficult and time-consuming tasks that should be attempted only by experienced researchers with knowledge in both survey statistics and statistical methods in the subject-matter discipline.
As noted earlier, valid model-based analysis of survey data requires a model for which the design and nonresponse are ignorable. In the regression context, this is typically achieved by expanding the model by including so-called design variables as predictors, by themselves and in interaction with other predictors. In the more general modeling context, incorporating the design and the nonresponse mechanism requires explicitly modeling what is seen as the important dimensions of selectivity (see below). In the
case of multistage or clustered designs, it might also be necessary to specify a variance structure to account for design-induced correlation. Although the specific techniques for specifying the variance structure to account for design-induced correlation are not suggested here, they could include generalized estimating equation (GEE) methods, hierarchical modeling, or simply adding design variables to a regression model. In order to construct this expanded model, detailed information on the sampling design and the nonresponse characteristics of the survey is required, and each analysis may require different considerations for how to incorporate the informativeness of the sample in the model. It should be noted that the resulting model can be quite complex, both in terms of the mean structure and the variance structure.
The process of building a model for which the design and nonresponse are ignorable is often iterative. Once a suitable candidate model is specified, it is necessary to determine whether the design and the nonresponse are indeed ignorable. This can initially be done informally, through a comparison between the estimates obtained by traditional model-based methods and those obtained by a fully weighted analysis. If these estimates differ substantially, it is very likely that some aspect of the design is not yet fully incorporated into the model, so that further model expansion is required before proceeding with a model-based analysis. However, even when individual estimates are approximately similar, ignorability is not guaranteed and more formal statistical checks should be performed. In addition to general model diagnostics (e.g., residual plots, outlier detection) and goodness-of-fit tests on all aspects of the model, particular attention should be paid to possible effects related to the design variables, for example by plotting model residuals against survey weights. For a discussion of diagnostic plots for survey data, see Korn and Graubard (1999, Chapter 3.4).
A limited number of formal statistical tests are available to directly assess the effect of the design on regression model parameter estimates, based on the difference between the sample-weighted and the unweighted estimators (e.g., DuMouchel and Duncan, 1983; Fuller, 1984; Nordberg, 1989; and other references in Pfefferman, 1993, Sec. 4). The test procedure by DuMouchel and Duncan (1983) is particularly easy to implement, because it can often be performed as part of a fully model-based analysis.
Instead of incorporating the design variables as predictors in a regression, a more sophisticated approach involves modeling the sampling design and the nonresponse mechanism as part of the analytical model. This implies that the probability structure of the design becomes part of the model, and a full likelihood that includes the original model and the various selection mechanisms needs to be constructed. In situations involving complex stratification, clustering, and multiphase sampling, simply adding the design variables as predictors is often not sufficient, and this type of
explicit modeling is required. Some relevant work in this area includes Chambers (1986), Skinner (1994), Breckling et al. (1994), and Pfeffermann and Sverchkov (1999).
As an alternative to the fully model-based approaches described above, some researchers use the design-based (weighted) estimator but evaluate it from a model-based perspective. This has the advantage that the estimator itself will be design consistent and hence avoids the main risk of model misspecification due to selectivity issues. The other advantage is that many software programs that do not do proper survey inference are still able to include weights in their estimation routines. However, using standard software to compute the weighted estimates of the unknown parameters does not generally provide either correct design-based or correct model-based confidence intervals or statistical tests of significance. The reason for this is that in most statistical programs, the weights are used as adjustments for heteroskedasticity, with the sampling weight taken as the inverse of the variance of the observation. Hence, unless the model is truly heteroskedastic with observation variances related to their inclusion probabilities, the variance estimator of the weighted estimator is incorrect. This is true regardless of whether the weights have been normalized or not (normalized weights mean that they have been scaled so that they sum to the sample size).
However, the idea of considering the model properties of the design-weighted estimator does have merit in assessing the ignorability of the design. If weights are treated as fixed constants rather than heteroskedasticity variance adjustments in the model fitting, then the resulting estimated variance of the model estimators will target ![]() A few programs might have built-in options to treat the weights as constants, while for others, special macros or functions would have to written. In the specific case of a linear regression model with uncorrelated errors, some programs, including STATA, have implemented the Huber-White robust sandwich estimator, which is an appropriate estimator for
A few programs might have built-in options to treat the weights as constants, while for others, special macros or functions would have to written. In the specific case of a linear regression model with uncorrelated errors, some programs, including STATA, have implemented the Huber-White robust sandwich estimator, which is an appropriate estimator for ![]() The model-based variance
The model-based variance ![]() is generally not equal to
is generally not equal to ![]() which is the correct variance from a design-based perspective and an approximation to the full variance
which is the correct variance from a design-based perspective and an approximation to the full variance ![]() as explained in the section on concepts of analytical inference for surveys. However, when the design is ignorable with respect to the model being fitted, then it is usually the case that
as explained in the section on concepts of analytical inference for surveys. However, when the design is ignorable with respect to the model being fitted, then it is usually the case that ![]() This motivates an informal but useful way to assess the presence of a nonignorable design for the model-based analysis of a weighted estimator, by comparing the estimate of
This motivates an informal but useful way to assess the presence of a nonignorable design for the model-based analysis of a weighted estimator, by comparing the estimate of ![]() and the estimate of
and the estimate of ![]() obtained by a design-based method, for example the ARMS jackknife weights. If these two estimates are very different, then the design is likely to be nonignorable and the model-based inference is not reliable.
obtained by a design-based method, for example the ARMS jackknife weights. If these two estimates are very different, then the design is likely to be nonignorable and the model-based inference is not reliable.
While the model-based analysis of weighted estimators may seem at-
tractive because of its simplicity, it is not robust to model failure. Some ERS researchers have used the Huber-White robust sandwich estimator available in the STATA package. This estimator is used by STATA whenever a probability weight is specified for all procedures that allow the “robust” option. It is also used as the default variance estimator for all weighted analyses in NLOGIT, and in SAS the MIXED and GLIMMIX procedures can compute the Huber-White estimator by specifying the EMPIRICAL option. However, such model-based robust estimators of the variance are still using some (weaker) model assumptions that may not necessarily hold. If they do hold, the model-based robust estimators would be similar to the design-based estimator, such as would be obtained from a delete-a-group jackknife estimator.
If, however, the assumed model is indeed true, then the weighted estimators of the parameters of interest are less efficient under the model than the unweighted estimators. Hence, researchers who are interested in conducting a fully model-based (unweighted) analysis should consider incorporating the design into the model as described above.
Recommendation 7.4: NASS and ERS should investigate the feasibility of providing sufficient information on the design and nonresponse characteristics of ARMS, in order to perform design-based statistical analysis without using the replicate weights and to allow users to incorporate design and nonresponse information in model-based analyses.
ERS researchers in particular might be interested in investigating the appropriateness of these model-based approaches for some types of analyses. Access to the full set of microdata as well as the element-level design information could put ERS in a unique position with respect to the ability to evaluate alternative modeling approaches for ARMS, obtaining the most statistically rigorous and efficient estimators for their models of interest. Because of the importance of fully accounting for the design and nonresponse in the model, this might require ERS researchers to gain fuller access to potentially confidential portions of the ARMS design data and develop a more in-depth understanding of survey design issues and statistical survey expertise.
Recommendation 7.5: ERS should build an enhanced level of in-house survey statistics expertise, in cooperation with NASS. The specialized expertise in both econometrics and survey statistics needed to accomplish this is currently not present in ERS and is likely to require a significant effort in recruiting and training.
GUIDE FOR RESEARCHERS
When researchers first started using ARMS data, the focus of the analysis was primarily on descriptive quantities of the population, such as means, proportions, and totals for the complete population or for subpopulations. As the richness of the data for more in-depth analysis became apparent, the demands for taking fuller advantage of such a rich data source grew. However, questions on the appropriateness of certain methods also became more apparent. As a result, researchers at ERS and elsewhere would benefit greatly from guidance on how to approach certain commonly used analytical methods. This would ensure that analyses done using ARMS data are conducted appropriately, make it easier for new users to begin working with those data, and provide a clear indication to the user community that NASS and ERS are committed to ensuring that this survey meets a high standard. It would also help officials at ERS explain the rationale behind the approaches adopted in the production of analytical outputs.
In view of this need, the ERS staff has taken the initiative to develop materials to assist outside users, albeit on an ad hoc basis. One such publication is Robert Dubman’s ERS staff paper, “Variance Estimation With USDA’s Farm Costs and Returns Surveys and Agricultural Resource Management Study” (Dubman, 2000). This useful paper was published with caveats. It was “reproduced for limited distribution to the research community outside the U.S. Department of Agriculture and does not reflect an official position of the Department.” It serves a useful purpose in that it provides an overview of survey estimators, sample design, hypothesis testing, disclosure rules, and reliability measures for the two surveys and covers sums, ratios, means, multiple regression, binomial logit analysis, and order statistics. It is a beginning, in that it addresses one way to analyze the data, but the prescription does not cover all types of analysis and analysis at all scales, for example, small versus large samples.
In the panel’s view, the Dubman paper is a good primer on how to use the existing weights and replication method, but it does not cover the full range of possible applications of the ARMS data. The user’s guide should provide background on the issues associated with estimation for survey data (as we attempted to do, at a higher level of abstraction, in the current document) and also provide guidance for as close as possible to the full range of modeling and estimation problems encountered by users of the ARMS data. Because the range of estimation scenarios is so broad, it was not possible for us to recommend a single approach for all of them. Therefore, instead of attempting to recommend specific methods for all of them (or reverting to a one-size-fits-all approach), our goal was to provide a background on the issues and a set of recommendations on how NASS and ERS can broadly address the estimation needs of the ARMS data user community.
The panel recommends but has not developed a user’s guide. This is because of our view that the process of developing a guide should be managed by the USDA and conducted in a truly collaborative environment. The guide would best be designed jointly by experts at ERS and NASS working with key data analysts.
To help set the stage for the necessary user’s guide, this section builds on the previous discussion of the merits of adopting a design-based approach for many of the analyses. In this section, we now focus on some of the specific questions that arise from using the delete-a-group jackknife method to make inferences from the survey data.
To assist ERS in preparing the necessary user’s guide, we give a specific example of the type of issue that should be included. Suppose one is interested in estimating a production function such as
where Y is output, the X1,X2 are inputs, R is a measure of the farm’s environment or organization, and denotes residual stochastic noise. Initially, the researcher may specify a simple but restrictive functional form for a regression model:
This is a fairly standard representation of a production relationship. It is quite restrictive, and economic theory suggests that a more flexible form—allowing for a wider range of input substitution, scale relationships, and environmental interactions—might be called for, for example:
This new model includes 15 parameters. To decide which model is appropriate, design-based methods can be used to apply the Wald test to compare the full and reduced models (on 5 degrees of freedom) for the nested hypothesis or an appropriate design-based F-test that accounts for the degrees of freedom associated with the estimate of the variance-covariance matrix. A weighted likelihood-ratio test could also be computed, although the distributional properties of such a test are less well known. It has been suggested that a Rao-Scott adjustment to the likelihood ratio could be applied, but, for most purposes, we would suggest using the Wald test. The guide could make recommendations to allow users to choose between these different methods.
Several other common questions face researchers using ARMS data, for which the guide would be extremely valuable. For example, one important question to address is the most appropriate approach (design-based versus model-based) for analysis for different types of questions. The best method for analysis depends on the survey design, the sample size, and the type and reason for the analysis. Simple linear models may need a different treatment than hierarchical models, small domains may need different procedures than large ones, etc. When the sample size is small, a model-based approach may be preferred to a design-based approach, especially if the design-based approach leads to much higher variances (see Kalton, 1983).
When a particular method is known not to be appropriate, then this should be explicitly mentioned in the guide. For example, design-based estimation of random effect variances in hierarchical models is problematic. Caveats should also be added regarding the use of such methods as clustering and classification for data coming from a complex survey such as ARMS. The limitations of the delete-a-group jackknife should also be explicitly addressed in the guide, including the limit on the number of parameters that can be tested simultaneously.
It should be noted that when the sampling is ignorable, the model-based approach to inference could lead to better inferences than the design-based approach; however, this approach may not be as robust to departures from the model, especially with respect to the correlation structure of the model errors. A discussion of the pitfalls in modeling under nonignorable sampling, as well as guidelines on model construction and on testing for nonignorability of the design, would be very useful.
The guide should also discuss the issue of using weights in standard nonsurvey software, which provides the correct point estimates but potentially misleading inference. It might be possible to determine that certain programs provide inferences in this manner that are close to correct (possibly after weight normalization), in which case these could be recommended. For example, the Huber-White robust sandwich estimator for linear regression provides a way to estimate the model-based variance of the weighted estimator. For other programs, no automatic way is available to obtain valid variances for the weighted estimators, so that additional programming may be required. In general, the guide should stress that the model-based variance needs to be compared with the design-based variance, with any significant deviations between the two a cause for concern. The discussion in previous sections makes additional points that could be included on these topics.
Many analyses are based on domains (subpopulations) of the entire national population, so questions on the appropriateness of the delete-a-group jackknife come into play. Analysts notice that the sum of the domain weights for each jackknife replicate varies greatly among replicates, and
they wonder if the variance is unduly inflated as a result. A standard design-based method is still appropriate here, since the fact that the sum of the weights varies appreciably is a reflection of the randomness in the sample for estimating domains. For such quantities as domain means or regression coefficients, the effect of this variability may be less pronounced, compared with the estimation of domain totals. However, compared with a model-based analysis, the variances may appear to be large. This demonstrates more the deficiency in the model-based approach, which does not account for the randomness in the domain sample size, rather than reflecting badly on the design-based approach. This should be explained in the guide, so that researchers encountering this problem will understand the reason.
Another question of interest to researchers is how to integrate data from more than one survey. These questions are more complex, especially if there is a need to use a coordinated jackknife, so some guidelines to users would be very valuable. In this area ERS and NASS may not currently have the necessary expertise. In general, there are two choices for analyzing the data when it is thought that the parameters of interest are similar across surveys: (1) the separate approach, in which the estimates are produced for each survey separately and then combined using a composite weight, and (2) the combined approach, in which the files are combined and analyzed as one file with a possibly adjusted weight variable. Under the separate approach, it is possible to use meta-analytic methods to combine evidence from different surveys (e.g., Zieschang, 1990). If the combined approach is pursued, it is always recommended that the assumptions about equality of the parameters of interest across surveys be subjected to a statistical hypothesis test.
Finally, the guide should also include a list of relevant references for researchers dealing with survey data. Some possible references are Lohr (1999), Pfeffermann (1993), and Korn and Graubard (1999). A gentle introduction to the basic issues of design-based and model-based inference for survey data is provided by Carrington et al. (2000), which is available online at http://www.ces.census.gov/index.php/ces/1.00/cespapers.
Recommendation 7.6: ERS and NASS should collaborate on writing a Guide for Researchers for performing multivariable analyses using data from complex surveys, particularly data from ARMS. In areas in which expertise is not available for writing parts of such a guide, expertise should be sought from the statistics and economics community, especially those with experience in the analysis of survey data from complex survey designs.























