4
Drawing Inferences from Incomplete Data
In this chapter, we review and comment on several approaches for drawing inferences from incomplete data. A substantial literature on this topic has developed over the last 30 years, and the range of approaches to modeling and inference is extremely broad. We make no attempt here to summarize that entire literature; rather, we focus on those methods that are most directly relevant to the design and analysis of regulatory clinical trials. We begin by presenting a set of principles for drawing inference from incomplete data. A major theme that we reiterate throughout the chapter is that inference from incomplete data relies on subjective, untestable assumptions about the distribution of missing values. On its face, this statement seems obvious. However, for a number of commonly used methods, users are not always aware of the assumptions that underlie the methods and the results drawn from applying them. This lack of awareness is particularly true of single imputation methods—such as last or baseline observation carried forward (LOCF or BOCF) and random effects (mixed effects) regression models—that rely on strong parametric assumptions.
In the second section of the chapter, we introduce a set of notation that is used throughout (and in Chapter 5). The third section summarizes the assumptions that underlie inference from incomplete data (missing completely at random, missing at random, etc.). The remaining sections describe commonly-used methods of analysis and offer comments and recommendations about their use in practice. In some cases, we offer recommendations for further research and investigation.
For both this chapter and the next, it is important to note the role of software. None of the techniques for either the primary analysis of clini-
cal trial data or for the subsequent sensitivity analysis that are described in the next chapter can be widely used, either at the U.S. Food and Drug Administration (FDA) or by trial sponsors, unless they are made available in one or more of the standard statistical software packages. It is beyond the scope of this report to describe and review specific software packages or routines. Many of the commonly used commercial and open-source packages used in the analysis of trials for the regulatory setting (SAS, SPSS, Stata, and R) allow for the analysis of incomplete data, using methods such as direct likelihood, Bayesian analysis, generalized estimating equations, inverse probability weighting, and multiple imputation.
Statistical software is evolving at a rapid pace to keep up with new developments in methodology and to implement proven methods. However, although progress is being made, the current suite of available tools remain lacking regarding augmented inverse probability weighting (IPW), missing not at random (MNAR) models, and analysis of the sensitivity to assumptions concerning the mechanism for missing outcome data. Given the urgency of the greater application of MNAR models and sensitivity analysis, we encourage the development and release of software tools to address these deficiencies. We again emphasize the importance of understanding and communicating the assumptions underlying analyses that are implemented in whatever software package is being used to draw inference about treatment effects. In most cases, communication of this information will necessitate referring to technical documentation for a specific analysis routine or procedure.
PRINCIPLES
There is no universal method for handling incomplete data in a clinical trial. Each trial has its own set of design and measurement characteristics. There is, however, a set of six principles that can be applied in a wide variety of settings.
First, it needs to be determined whether missingness of a particular value hides a true underlying value that is meaningful for analysis. This may seem obvious but is not always the case. For example, consider a longitudinal analysis of CD4 counts in a clinical trial for AIDS. For subjects who leave the study because they move to a different location, it makes sense to consider the CD4 counts that would have been recorded if they had remained in the study. For subjects who die during the course of the study, it is less clear whether it is reasonable to consider CD4 counts after time of death as missing values.
Second, the analysis must be formulated to draw inference about an appropriate and well-defined causal estimand (see Chapter 2). The causal estimand should be defined in terms of the full data (i.e., the data that were
intended to be collected). It is important to distinguish between the estimand and the method of estimation, the latter of which may vary depending on assumptions.
Third, reasons for missing data must be documented as much as possible. This includes full and detailed documentation for each individual of the reasons for missing records or missing observations. Knowing the reason for missingness permits formulation of sensible assumptions about observations that are missing, including whether those observations are well defined.
Fourth, the trial designers should decide on a primary set of assumptions about the missing data mechanism. Those primary assumptions then serve as an anchor point for the sensitivity analyses. In many cases, the primary assumptions can be missing at random (MAR) (see Chapter 1). Assumptions about the missing data mechanism must be transparent and accessible to clinicians.
Fifth, the trial sponsors should conduct a statistically valid analysis under the primary missing data assumptions. If the assumptions hold, a statistically valid analysis yields consistent estimates, and standard errors and confidence intervals account for both sampling variability and for the added uncertainty associated with missing observations.
Sixth, the analysts should assess the robustness of the treatment effect inferences by conducting a sensitivity analysis. The sensitivity analysis should relate treatment effect inferences to one or more parameters that capture departures from the primary missing data assumption (e.g., MAR). Other departures from standard assumptions should also be examined, such as sensitivity to outliers.
NOTATION
Throughout this and the next chapter, we use the following conventions. Let X represent treatment indicators and baseline (i.e., pretreatment) covariates that are fully observed and conditioned on in the primary statistical analysis (such as study center and stratification variables). Another way to characterize X is as the design variables that would be adjusted for or conditioned on in the final analysis. Let Y denote the primary outcome variable, which may be a single outcome, a vector of repeated measurements, or a time to event. Auxiliary variables are denoted by V; these variables are distinct from design variables X and may represent individual-level characteristics (either pre- or posttreatment) that aid in drawing inference from incomplete response data. Information on compliance or side effects of treatments that may be useful for modeling the missing data but are not included in the primary analytic model may be included in V. (We note that the collection and use of all available covariate information that is predic-
tive of the outcome in the full data model, and the occurrence of missing outcome data in the missing data model, is important and can dramatically improve the associated inference.)
In the absence of missing data, let Z denote the values of (V,Y) for an individual participant. For simplicity, we assume throughout that observations on (V,Y) are independent within levels of X.
To distinguish between missing and observed data, let M denote the indicator of whether Y is missing. In repeated measures studies, we include a subscript for repeated measures. That is, if the intended outcome measures are Y = (Y1, Y2,…,YK), the corresponding missingness indicators are M = (M1,M2,…,MK), where Mj = 1 if Yj is missing, and Mj = 0 if it is observed. We generally will assume that Y and V have the same missing data pattern, though in practice this restriction can be relaxed.
In many situations, missing values can be denoted by a single value, such as M = 1; in other settings, it may be useful to allow more than one missing-value code to indicate different types of missing data, such as M = 1 for lack of efficacy, M = 2 for inability to tolerate a drug because of side effects, M = 3 for a missed clinic visit, and so on. This notation allows for different modeling assumptions for the different causes of missing data.
ASSUMPTIONS ABOUT MISSING DATA AND MISSING DATA MECHANISMS
The general missing data taxonomy described in this section is fully presented in Rubin (1976) and Little and Rubin (2002). Elaboration on the sequential versions of these for longitudinal data can be found in Robins et al. (1995) and Scharfstein et al. (1999). Discussion of the more general notion of coarsening can be found in Heitjan (1993) and Tsiatis (2006).
Missing Data Patterns and Missing Data Mechanisms
It is useful to distinguish the pattern of the missing data from the missing data mechanism. The pattern simply defines which values in the data set are observed and which are missing, as described for an individual by the vector of indicators M = (M1,…,MK). Some methods for handling missing data apply to any pattern of missing data; other methods assume a special pattern.
A simple example of a special pattern is univariate missing data, where missingness is confined to a single variable. Another special pattern is monotone missing data, where the variables can be arranged so that Yj+1 is missing for all cases where Yj is missing. This pattern commonly arises in longitudinal data, when the sole cause of missingness is attrition or dropouts, and there are no intermittently missing values.
The missing data mechanism relates to why values are missing and the connection of those reasons with treatment outcomes. The missing data mechanism can be represented in terms of the conditional distribution [M | X,V,Y]1 for the missing data indicators given the values of the study variables that were intended to be collected. To emphasize that this distribution may depend both on observed and missing values of V and Y, this is sometimes written as [M | X,Vobs,Vmis,Yobs,Ymis].
Missing Completely at Random
Missing data are missing completely at random (MCAR) if missingness does not depend on values of the covariates, auxiliary and outcome variables (X,V,Y). That is,
(1)
MCAR is generally a very strong assumption, unlikely to hold in many clinical trials. Situations in which MCAR might be plausible include administrative censoring, when outcomes are censored because a study is terminated at a planned date, and the outcome has not yet occurred for late accruals; and designed missing data, when expensive or onerous measurements are recorded only for a random subsample of participants. A closely related concept is conditional MCAR, which allows for the independence of the missing values, but is conditional on covariates X. Finally, it is useful to mention that MCAR is unique in that one can test whether the missing outcomes are MCAR if they are at least missing at random, which is discussed below.
Missing at Random
A more realistic condition than MCAR for many studies is MAR, which requires that missingness is independent of missing responses Ymis and Vmis, conditionally on observed responses (Yobs, Vobs) and covariates X. That is,
(2)
If Y and V are considered to be random variables with distributions based on a model, then one can show that condition (2) is equivalent to
(3)
which implies that the predictive distribution of the missing variables given the observed variables does not depend on the pattern of missing values. This version of MAR is relevant from an analysis perspective because it characterizes the predictive distribution of the missing values, which is the basis for principled methods of imputation.
As we describe below, many standard analysis methods for incomplete data operate under the MAR assumption. It is therefore imperative that both the MAR assumption and the assumptions underlying the full data model (e.g., multivariate normality) be thoroughly justified before results from these models can be considered valid for treatment comparisons. In general: (a) even under MAR, different assumptions about the full data model will lead to different predictive distributions; (b) with incomplete data, assumptions about both the missing data mechanism and the full data model are unverifiable from the data; and (c) nevertheless, inference and therefore decisions about treatment effect often crucially depend upon them.
MAR for Monotone Missing Data Patterns
With longitudinal repeated measures, and even for event time outcomes, the MAR assumption is not always intuitive for a general pattern of missing values.
However, it has a simple interpretation in the case of monotone missing data, such as that caused by dropouts. Suppose the data intended to be collected comprise repeated measures on an outcome Y, denoted by Y1,…,YK. Let Mj = 1 if Yj is missing, and let Mj = 0 if Yj is observed. Under monotone missingness, if observation j is missing (Mj = 1), then all subsequent observations also are missing (Mj+1 = … = MK = 1).
At any given time j, let ![]() denote the history of measurements up to but not including time j, and let
denote the history of measurements up to but not including time j, and let ![]() denote the future measurements scheduled, including and after time j. At time j, the predictive distribution of future values given the observed history is denoted by [
denote the future measurements scheduled, including and after time j. At time j, the predictive distribution of future values given the observed history is denoted by [![]() ]. The MAR condition holds if predictions of future measurements for those who drop out at time j are equivalent in distribution to predictions for those who have observed data at and after time j. Formally, MAR is equivalent to
]. The MAR condition holds if predictions of future measurements for those who drop out at time j are equivalent in distribution to predictions for those who have observed data at and after time j. Formally, MAR is equivalent to
(4)
Hence, under MAR, missing values at time j and beyond can be predicted sequentially from the histories of participants still in the study at time j.
MAR for monotone missing data patterns also can be written in terms of the probability of dropouts at each measurement occasion. At time j,
the dropout probability is P(Mj = 1 | Mj–1 = 0). In general, this probability can depend on any aspect of the observations intended to be collected. MAR states that the dropout probability can only depend on observed data history,
(5)
This representation shows that one can think of the MAR assumption as a sequentially random dropout process, where the decision to drop out at time j is like the flip of a coin, with probability of ‘heads’ (dropout) depending on the measurements recorded through time j – 1.
Both (4) and (5) can be generalized by allowing the past measurements to include auxiliary covariates. Specifically, let ![]() denote the observed history of both outcomes and auxiliaries. Then MAR can be restated by replacing
denote the observed history of both outcomes and auxiliaries. Then MAR can be restated by replacing ![]() with
with ![]() in (4) and (5). In fact, the MAR assumptions (4, 5) change depending on the set of auxiliary variables V included in the analysis. The validity of the MAR assumption can be improved by measuring and including auxiliary variables that are predictive of whether the outcome variables are missing and predictive of the values of the missing variables.
in (4) and (5). In fact, the MAR assumptions (4, 5) change depending on the set of auxiliary variables V included in the analysis. The validity of the MAR assumption can be improved by measuring and including auxiliary variables that are predictive of whether the outcome variables are missing and predictive of the values of the missing variables.
Missing Not at Random
MAR will fail to hold if missingness or dropout depends on the values of missing variables after conditioning on the observed variables. When MAR fails to hold, missing data are said to be MNAR.
For a monotone missing data pattern, missingness will be MNAR if there exists, for any j, at least one value of ![]() for which
for which
(6)
or equivalently, there exists, for any j, at least one value of ![]() , such that
, such that
(7)
For (6), the consequence of MNAR is that the prediction of future observations for those who drop out cannot be reliably predicted using data observed prior to dropping out; or, that the distribution [![]() ] differs between those who do and do not drop out at time j. Because these differences cannot be estimated from the observed data, they are entirely assumption driven. This is the central problem of missing data analysis in clinical trials.
] differs between those who do and do not drop out at time j. Because these differences cannot be estimated from the observed data, they are entirely assumption driven. This is the central problem of missing data analysis in clinical trials.
Example: Hypertension Trial with Planned and Unplanned Missing Data
Murray and Findlay (1988) describe data from a large multicenter trial of metopropol and ketanserin, two antihypertensive agents for patients with mild to moderate hypertension, with diastolic blood pressure as the outcome measure of interest. The double-blind treatment phase lasted 12 weeks, with clinic visits scheduled for weeks 0, 2, 4, 8, and 12. The protocol stated that patients with diastolic blood pressure exceeding 110 mmHg at either the 4- or 8-week visit should “jump” to an open follow-up phase—a form of planned dropout. In total, 39 of the 218 metopropol patients and 55 of the 211 ketanserin patients jumped to open follow-up.
In addition, 17 metopropol patients and 20 ketanserin patients had missing data for other reasons, including side effects. Analyses of the observed data clearly showed that those with missing blood pressure readings differed systematically from the patients who remained in the study, as would be predicted by the protocol for jumping to the open phase. This example provides an illustration of the importance of defining what is represented by a missing outcome. For the participants who were removed from protocol, it is possible to treat the missing values as values that would be observed had the individuals remained on treatment. The mechanism for those with missing values is MAR because missing outcomes resulted from the value of a recorded intermediate outcome variable for blood pressure, and are therefore a function of an observed value.
Summary
-
Inferences from incomplete data, whether model-based or not, rely on assumptions—known as missing data mechanisms—that cannot be tested from the observed data.
-
A formal taxonomy exists for classifying missing data mechanisms, including for longitudinal and event history data. The mechanisms can be classified as MCAR, MAR, and MNAR.
-
Missing data mechanisms describe the relationship between the missing data indicator(s) M, the full outcome data Y = (Yobs,Ymis), design variables X, and auxiliary covariates V. Traditionally, these assumptions characterize restrictions on the distribution of M given (Yobs,Ymis,X,V). Each has an equivalent representation in terms of the predictive distribution of missing responses, namely Ymis given (M,Yobs,X,V).
COMMONLY USED ANALYTIC METHODS UNDER MAR
Three common approaches to the analysis of missing data can be distinguished: (1) discarding incomplete cases and analyzing the remainder
(complete-case analysis); (2) imputing or filling in the missing values and then analyzing the filled-in data; and (3) analyzing the incomplete data by a method that does not require a complete (i.e., a rectangular) data set. Examples of (3) include likelihood-based methods, such as maximum likelihood (ML), restricted ML, and Bayesian methods; moment-based methods, such as generalized estimating equations and their variants; and semiparametric models for survival data, such as the Cox proportional hazards model. Multiple imputation (Rubin, 1987; Little and Rubin, 2002), an extension of single imputation that allows uncertainty in the imputations to be reflected appropriately in the analysis, is closely related to Bayesian methods (discussed later in this chapter).
Deletion of Cases with Missing Data
A simple approach to missing data is complete-case analysis, also known as listwise deletion, in which incomplete cases are discarded and standard analysis methods are applied to the complete cases. In many statistical packages, it is the default analysis.
Although it is possible to list conditions under which an analysis of complete cases provides a valid inference (essentially, conditional MCAR), this method is generally inappropriate for a regulatory setting. When missingness is in the outcome, the MAR assumption is generally weaker and can reduce bias from deviations from MCAR by making use of the information from incomplete data. Furthermore, when missingness is appreciable, rejection of incomplete cases will involve a substantial waste of information and increase the potential for significant bias.2
In addition, if data are not collected after withdrawal from treatment, then the MAR assumption relies only on information accumulated while subjects are on treatment. Hence, any method that relies on MAR is estimating the mean under the condition that everyone had remained on treatment. This generally will not provide a valid estimator of the intention-to-treat effect. On the other hand, if data are collected after withdrawal from treatment, this information can be used either within inverse probability weighting (IPW) or in an imputation context to estimate an intention-to-treat effect under MAR (Hogan and Liard, 1996). It is for this
reason that we emphatically recommend aggressive collection of outcome data after individuals withdraw from treatment.
Inverse Probability Weighting
Univariate Outcome
When data are MAR but not MCAR, a modification of complete-case analysis is to assign a sampling weight to the complete cases. This tends to reduce bias, to the extent that the probability of being observed is a function of the other measured variables. Consider the simple case in which the intended outcome is Y, the design variables are X, and some auxiliary variables V are available. As usual, M = 1 indicates that Y is missing. To describe IPW, it is useful to introduce a response indicator, R = 1 – M, such that R = 1 when Y is observed and R = 0 when it is missing.
An IPW estimator for the mean of Y can be computed as follows:
-
Specify and fit a model for π(X,V,θ) = Pθ(R = 1 | X,V), for example using logistic regression.
-
Estimate the mean of Y using the weighted average
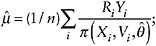
(8)
that is, the average of the observed Y weighted inversely by the probability of being observed.
-
Standard error estimators can be computed analytically or by bootstrap methods. (For details on the bootstrap estimator of variance, see Efron and Tibshirani, 1993.)
For large samples, this method properly adjusts for bias when the data are MAR, provided the model for π(X,V,θ) is correctly specified. In finite samples, the method can yield mean estimates that have high variance when some individual-specific weights are high (i.e., when π is close to zero). An alternative is to create strata based on the predicted probability of being complete and then weight respondents by the inverse of the response rate within these strata. Strata can be chosen to limit the size of the weights and hence control variance.
In addition to the MAR assumption, the IPW method requires two other key assumptions: (1) there are no covariate profiles (X,V) within which Y cannot be observed and (2) the support of the missing data distri-
bution is the same as that for the observed data distribution. Technically, (1) stipulates that P(R = 1 | X,V) > 0 for all possible realizations of (X,V). A potential restriction imposed by (2) is that individual missing values cannot be imputed outside the range of observed values.
IPW Regression for Repeated Measures
With repeated measures, a convenient way to estimate the treatment effect is through a regression model for the mean of the outcome vector conditional on the design variables X. With fully observed data, repeated measures regression models can be fit using generalized estimating equations (GEE) (Zeger and Liang, 1986).
With fully observed data, a desirable property of regression parameter estimates from GEE is that they retain such properties as consistency and asymptotic normality regardless of the assumed within-subject (longitudinal) correlation structure. When data are missing, this property no longer holds, and regression estimates may depend strongly on the assumed correlation structure (see Hogan et al., 2004, for an empirical example).
When missingness is MAR and follows a monotone pattern, the IPW method can be used to obtain consistent estimates of regression parameters using a specified procedure. Here, we emphasize that auxiliary information should be included in the observed-data history, Zj− = (Y1,…,Yj−1, V1,…,Vj−1) and the model for π(X,V,θ). The procedure is as follows:
-
Specify the regression model that would be used had all the intended data been collected.
-
Let
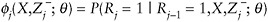 denote the probability that Yj is observed.
denote the probability that Yj is observed. -
Specify and fit a model for
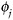 ; denote the estimated parameters by
; denote the estimated parameters by 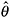 .
. -
Let
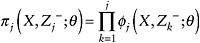 denote the probability that an individual has remained in the study to time j.
denote the probability that an individual has remained in the study to time j. -
Fit the regression specified in Step 1, and weight individual contributions to the model by
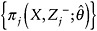 . Use the assumed independence correlation structure.
. Use the assumed independence correlation structure. -
Use the bootstrap technique for standard error estimation.
In large samples, the IPW GEE yields consistent estimators when the response probability model is correctly specified, but again may have high variance when individual weights are large. The augmented IPW GEE procedure (discussed below) can be used to partially remedy this weakness.
An example of this approach comes from Hogan et al.(2004): an analysis of repeated binary data from a smoking cessation study. The authors used inverse probability weighting to estimate the effect of a behavioral intervention involving supervised exercise on the rate of smoking cessation among 300 women. The primary outcome was smoking status, assessed weekly over 12 weeks. This example shows how to construct sequential weights for model fitting, and it illustrates how unweighted GEE estimators can vary under different choices for the assumed correlation when longitudinal data are incomplete. The authors include analyses using LOCF for comparison, and a critique is also included. The publication includes SAS code for fitting the model.
Augmented IPW Estimation Under MAR
The IPW GEE method does not make full use of the information in incomplete cases. The augmented IPW GEE procedure remedies this weakness. The procedure is best understood in the simple case in which only the values for the last time point are missing for some cases, and they are MAR. Suppose one wishes to estimate µ =E (YK ), the mean outcome in a particular treatment arm. As before, it will be convenient to introduce the variable RK =1 – MK, where now RK = 1 if YK is observed. Denote the observed history at time K as ![]() , and let
, and let ![]() , which can be modeled as described in the previous section.
, which can be modeled as described in the previous section.
The augmented IPW (AIPW) estimator of µ is
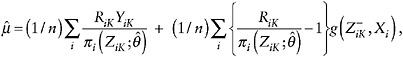
(9)
where ![]() is some function of the observed-data history up to K – 1.
is some function of the observed-data history up to K – 1.
The first term is just the IPW estimator of µ. The second (augmentation) term has mean zero, so that ![]() is still a consistent estimator. However, the variance of
is still a consistent estimator. However, the variance of ![]() will depend on the choice of g, where the optimal choice is
will depend on the choice of g, where the optimal choice is ![]() . The precise form of this expectation is unknown, but it can be estimated, for example, from a regression of YK on (
. The precise form of this expectation is unknown, but it can be estimated, for example, from a regression of YK on (![]() ) for those with observed YK. In that case,
) for those with observed YK. In that case, ![]() is replaced by the regression prediction
is replaced by the regression prediction ![]() . If this outcome regression model is approximately correct, then
. If this outcome regression model is approximately correct, then ![]() can be substantially more efficient than the standard IPW estimator. Since we can only estimate g, it is comforting that it appears to be the case that even if g is only approximately known, there is likely to be a substantial gain. However, more research is needed to fully justify this conjecture.
can be substantially more efficient than the standard IPW estimator. Since we can only estimate g, it is comforting that it appears to be the case that even if g is only approximately known, there is likely to be a substantial gain. However, more research is needed to fully justify this conjecture.
In summary, augmented IPW estimators are obtained by adding to the IPW estimating functions an augmentation term that depends on unknown functions of the observed data. Appropriate choices of these functions can lead to substantial efficiency improvements over standard IPW GEE.
Double Robustness Property of Augmented IPW Estimators
An important limitation of standard IPW estimation is that it yields biased estimates if the missingness model is incorrect. Remarkably, the augmented IPW estimator ![]() with the optimal choice for g offers not only efficiency improvements over IPW, but also bias protection against misspecification of the model for the missingness probabilities (for accessible accounts, see Tsiatis, 2006; Rotnitzky et al., 2009).
with the optimal choice for g offers not only efficiency improvements over IPW, but also bias protection against misspecification of the model for the missingness probabilities (for accessible accounts, see Tsiatis, 2006; Rotnitzky et al., 2009).
Methods that yield valid inferences when either one or the other of the outcome regression or the missingness model is correct are said to have a double-robustness property. Double robustness is a useful theoretical property, although it does not necessarily translate into good performance when neither model is correctly specified (Kang and Schafer, 2007). Empirical and theoretical studies of these estimators have begun to appear in the statistics and econometrics literature. With more published applications to real data and carefully designed simulation studies, the use of doubly robust estimators could become more commonly used in the near future. However, at present, the operating characteristics of this method in applied settings with finite samples need to become more completely understood.
Advantages and Disadvantages of IPW Methods
The IPW method is generally simple to implement when the missing values have a monotone pattern, and can be carried out in any software package that allows weighted analyses. A key advantage is that, under a correctly specified model for missingness, information on many auxiliary variables can be accommodated, including information on previously observed outcomes. IPW methods can be extended to estimation targets other than the mean, such as the median. Potential disadvantages include (a) the need to correctly specify the nonresponse model, and (b) potential instabilities associated with weights that are very large, leading to biased estimation and high variance in finite samples. Double robust estimators have the potential to alleviate both of these limitations.
Likelihood Methods
Likelihood approaches are dependent on a parametric model for the full-data distribution. Inference is based on the likelihood function of the
observed data. To describe these approaches, we define Y,V,X, and M as above. The objective is to draw inference about a parameter θ in a model p(y|x; θ) for the response data that were intended to be collected but that might not be fully observed.
Under MAR, methods such as ML and Bayesian posterior inference can be used to draw inference about θ without having to specify an explicit model that relates M to (Y,V,X). (To avoid distracting technicalities, we assume that V is not present.)
To understand this approach, first write the model for the joint distribution [Y, M | X] as
(10)
where p(y | x;θ) is the model for the full response data (i.e., the data that were intended to be collected), p(m | y,x;ψ) is the model for the missing data mechanism, and (θ, ψ) are unknown parameters.
Now let D = (Yobs,X,M) denote the observed data for an individual. The individual contribution to the likelihood function for (θ, ψ) given D is obtained by averaging (or integrating) over all possible realizations of the missing observations Ymis,
(11)
Under MAR, the second term under the integral simplifies as p(m | yobs, ymis, x;ψ) = p(m | yobs, x;ψ). If one further assumes that θ and ψ are functionally distinct (i.e., θ is not a function of ψ and vice versa), then the likelihood factors as
(12)
(13)
An immediate consequence is that inference about θ no longer depends on the functional form of the missing data mechanism because the likelihood for θ is directly proportional to p(yobs| x;θ). When missingness is MAR and when θ and ψ are functionally distinct, the missing data mechanism is said to be ignorable because it does not have to be modeled in order to draw inferences about θ. In practice, MAR is the key condition.
Maximum Likelihood Inference
Large-sample inferences about θ under the ignorability assumption follow from standard results in ML theory, which state that under some regularity conditions ![]() follows a normal distribution having mean θ and variance equal to the inverse information matrix I–1(θ). The variance can be estimated by I–1(
follows a normal distribution having mean θ and variance equal to the inverse information matrix I–1(θ). The variance can be estimated by I–1(![]() ) or by such other techniques as bootstrap or sandwich estimators. (For details on the sandwich estimator of variance, see Kauermann and Carroll, 2001.) Numerical methods for maximizing the likelihood include factored likelihood methods for monotone patterns and iterative methods like the EM algorithm and its extensions for general patterns; see Little and Rubin (2002) for details.
) or by such other techniques as bootstrap or sandwich estimators. (For details on the sandwich estimator of variance, see Kauermann and Carroll, 2001.) Numerical methods for maximizing the likelihood include factored likelihood methods for monotone patterns and iterative methods like the EM algorithm and its extensions for general patterns; see Little and Rubin (2002) for details.
Bayesian Inference and Data Augmentation
ML is most useful when sample sizes are large because the parameter estimates are consistent, and standard errors are well approximated by the large sample variance-covariance matrix. However, Bayesian inference offers a useful alternative in some settings. First, when sample sizes are small, a useful alternative approach is to add a prior distribution for the parameters and compute the posterior distribution of the parameters of interest. Second, when computation of the observed-data likelihood is difficult, data augmentation embedded in a posterior sampling algorithm can make computation of posterior modes much simpler. Although there are notable exceptions, for many standard models it is possible to specify priors that are diffuse enough so that inferences from ML and from a posterior are essentially equivalent.3
For ignorable models, this posterior distribution is
(14)
where p(θ) is the prior and L(θ | D) is the same likelihood as in (13)—the full-data likelihood averaged over all possible realizations of the missing data.
Because the posterior distribution rarely has a simple analytic form for incomplete-data problems, simulation methods are often used to generate draws of θ. Keeping in mind that the parameter θ indexes the distribution p(y | x;θ) of the full response data, generating from the posterior can be made easier by embedding a data augmentation step within the sampling algorithm; this approach effectively imputes the missing responses under
the model p(y | x;θ) specified for [Y | X] (see Tanner, 1996; Daniels and Hogan, 2008).
For monotone missing data patterns, when the parameters of the factored distributions are distinct, the factored likelihood methods yield simple direct simulation methods; for general patterns, iterative simulation methods like data augmentation and the Gibbs’ sampler play a prominent role (Little and Rubin, 2002). In particular, the Gibbs’ sampler starts with an initial draw θ(0) from an approximation to the posterior distribution of θ. Given a value θ(t) of θ, drawn at iteration t,
-
draw
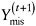 from the distribution
from the distribution 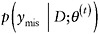 , and
, and -
draw θ(t+1) from the distribution
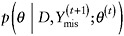 .
.
The iterative procedure can be shown in the limit to yield draws from the posterior distribution of θ given D, integrating over Ymis. This algorithm can be run independently L times to generate L independent, identically distributed draws from the approximate joint posterior distribution of (θ,Ymis).
Example: Multivariate Normal Regression For continuous outcomes and ignorable missing data, a common approach is to use a regression model based on a multivariate normal distribution. The general specification assumes that the vector Y = (Y1 ,…,YK)T follows a multivariate normal distribution, conditionally on design variables X. Hence, one assumes
(15)
where µ(x) is a K-dimensional mean vector, and Σ(x) is a K × K variance-covariance matrix. Especially if K is large or if X is high-dimensional, some choices must be made about the functional form and structure of both µ(x) and Σ(x) to ensure that the model can be fit to finite samples. For example, it is possible to assume µ(x) has a linear trend over time, separately by treatment group, or that Σ(x) has a simplified structure that can be described using a small number of parameters. As with the normality assumption itself, however, with incomplete data these choices will not lend themselves to empirical checking. The predicting distribution of the missing responses can differ substantially according to the specification.
In fact, with incomplete data, two models having the same mean specification but different specifications of Σ will yield different inferences about the mean.
In short, for a multivariate normal model (including random effects models), inference about the mean from incomplete data depends on specification of the variance-covariance matrix (Meng and Rubin, 1993; Daniels and Hogan, 2008).4 This dependence should be assessed, along with that for outlying or influential observations and most importantly for the missing data mechanism using sensitivity analyses, as described in Chapter 5.
Example: Random Effects Models (Mixed Models) For longitudinal data, random effects models provide a parsimonious way to specify a multivariate distribution. The simplest versions are specified on two levels. The first (top) level specifies the distribution of responses for an individual, conditional on individual-specific random effects. For example, if it is assumed that each individual’s repeated measures are governed by an underlying individual-specific mean, then variations in individual means can be represented through random effects u, and the top level model might be
(16)
where ui is the individual-specific random effect, eij is residual error, and both have mean zero. In most random effects models, u and e are assumed to be independent. In this simple model, the mean of Yij at time j is αj+ ui for those with xi = 0, and αj+ β + ui for those having xi = 1. The average treatment effect for an individual is β.
The second level specifies a distribution for the random effects; typically this is chosen to be the normal distribution, such as ui~ N(0,τ2). If one combines this with an assumption of normality for eij, the distribution of the responses is itself normal, with variance partitioned into its within- and between-individual components.
Importantly, regression coefficients in the random effects model are within-subject effects—or the average effect for a typical individual—because they are being estimated conditionally on the random effect u. By contrast, the treatment effect estimated in a multivariate normal regression or other model not having random effects is a between-subject effect—the average effect between the groups of individuals randomized to treatment and control.
When both the error and random effects distributions are normal, the random effects model coincides with a multivariate normal regression with a constrained parameterization of Σ. In this special case, the between- and
within-subject treatment effects are equivalent (though their standard errors will differ). However, in general nonlinear mixed models, the treatment effect estimated from a random effects model does not coincide with the standard between-subjects contrast that is typically of direct interest for regulatory decision making (see Diggle et al., 2002).
Likelihood-Based Models for Binary Data A substantial literature describing likelihood-based models for repeated binary data has developed over the last 10-15 years. Many of these models are based on a loglinear formulation and are parameterized directly in terms of between-subject treatment effects; see Fitzmaurice et al. (1993), Heagerty (1999, 2002).
Advantages and Disadvantages of Likelihood-Based Methods
If missingness is ignorable, ML and Bayesian approaches under ignorability provide valid inferences using models that are generally easy to fit using commercial software. Random effects models can be very useful for simplifying a highly multivariate distribution using a small number of parameters.
However, with incomplete data, there are several reasons that inference about a treatment effect should not be limited to a single likelihood-based model:
-
In addition to the ignorability assumption, inference relies on para metric assumptions about the model p(y | x;θ). These assumptions cannot be jointly checked from observed data, and it is difficult to ascertain the degree to which these different assumptions may be driving the inference.
-
When using Bayesian posterior inference, results can sometimes be dependent on prior specifications, such as variance components (see Gelman, 2006).
-
In the case of random effects models, parametric assumptions include those being made about the random effects. Frequently, these are made primarily for convenience of computation, as when the random effects are assumed to be normally distributed.
-
With random effects models, two estimands can be distinguished: a between-subject (population-averaged) and within-subject (or subject-specific) treatment effect. For models where the mean is a linear combination of treatment and covariates, these quantities are equal, but the standard errors will differ. For models where the mean is nonlinear in treatment and covariates (such as random effects logistic regression), the between- and within-subject treatment effects will differ. In either case, the estimand must be stated and justified in advance of conducting the analysis. For more discussion on this point, see Diggle et al. (2002).
For more information on specification and inference for likelihood-based models for repeated measures, see Verbeke and Molenberghs (2000), Diggle et al. (2002), Fitzmaurice et al. (2004), and Daniels and Hogan (2008). More information on Bayesian inference can be found in Carlin and Louis (2000) and Gelman et al. (2003).
Imputation-Based Approaches
Methods that impute or fill in the missing values have the advantage that, unlike complete-case analysis, the information from observed values in the incomplete cases is retained. Single imputation approaches include (a) regression imputation, which imputes the predictions from a regression of the missing variables on the observed variables; (b) hot deck imputation, which matches the case with missing values to a case with values observed that is similar with respect to observed variables and then imputes the observed values of the respondent; and (c) LOCF or BOCF methods for repeated measures, which impute the last observed value or the baseline value of the outcome variable. Two problems with single imputation are (1) inferences (tests and confidence intervals) based on the filled-in data can be distorted by bias if the assumptions underlying the imputation method are invalid, and (2) statistical precision is overstated because the imputed values are assumed to be true.
Example: LOCF Imputation
A common single imputation method is LOCF, which is based on the strong assumption that the outcome of a participant does not change after drop out. Even if this model is scientifically reasonable, attention needs to be paid to whether a single imputation by LOCF propagates imputation uncertainty in a way that yields valid tests and confidence intervals. For certain estimands, like the change from baseline to a fixed time after baseline, single LOCF imputation appropriately reflects uncertainty, since under the assumed model, the observation at time of dropout is essentially exchangeable with the observation at the end of the study, if observed. In general, however, this will not be the case. For instance, if imputed values are used to estimate a slope or area under the curve, statistical uncertainty from LOCF may be underestimated.
LOCF is sometimes mistakenly considered to be valid under MCAR or MAR, but in general it makes an MNAR assumption. Suppose for simplicity that there are K repeated measures, that missing data are confined to the last time point K, and that there are no auxiliary variables. The MAR assumption is
(17)
that is, that the predictive distribution of YK, based on design variables X and observed response data Yobs = (Y1 ,…,YK–1), is the same for those with missing and observed YK. By contrast, LOCF assumes that, for those with missing YK, the predicted value is YK–1 with probability one. Formally, it assumes5
(18)
Hence, p(yK| x,yobs, m = 1) ≠ p(yK | x,yobs, m = 0) in general, and LOCF is neither MCAR nor MAR. Moreover, the LOCF method attaches no uncertainty to the filled-in value of YK resulting in an artificial increase of sample size for some analyses. Similar comments apply to BOCF (Molenberghs and Kenward, 2007).
Although the utility of these methods does rest on the plausibility of the assumptions underpinning these estimators, the pragmatic justification often stems from the sometimes mistaken view that they provide a simple and conservative imputation that will help prevent approval of ineffective treatments. However, this is not necessarily the case, since, for example, LOCF is anticonservative in situations where participants off study treatment generally do worse over time. In such cases, if many participants discontinue study treatment due to problems with tolerability, the treatment can be made to look much better than the control by such an imputation strategy.
Multiple Imputation
Multiple imputation is designed to fill in missing data under one or more models and to properly reflect uncertainty associated with the “filling-in” process (Rubin, 1987). Instead of imputing a single value for each missing observation, a set of S (say S = 10) values for each missing observation is generated from its predictive distribution,6 resulting in S distinct filled-in
datasets. One then follows an analysis that would have been used on the full data for each of the S datasets and combines the results in a simple way. The multiple imputation estimate is the average of the estimates from the S datasets, and the variance of the estimate is the average of the variances from the S datasets plus the between-sample variance of the estimates over the S datasets.
The between-imputation variance estimates the contribution to the overall variance from imputation uncertainty, which is missed by single imputation methods. Another benefit of multiple imputation is that the averaging over datasets reduces sampling variance and therefore results in more efficient point estimates than does single random imputation. Usually, multiple imputation is not much more difficult than single imputation—the additional computing from repeating an analysis S times is not a major burden. Moreover, the methods for combining inferences are straightforward and implemented in many commercially available software packages. Most of the work is in generating good predictive distributions for the missing values. This aspect has been addressed in a variety of widely-available software packages. We emphasize here the need to fully understand and communicate the assumptions underlying any imputation procedures used for drawing inferences about treatment effects.
An important advantage of multiple imputation in the clinical trial setting is that auxiliary variables that are not included in the final analysis model can be used in the imputation model. For example, consider a longitudinal study of HIV, for which the primary outcome Y is longitudinal CD4 count and that some CD4 counts are missing. Further, assume the presence of auxiliary information V in the form of longitudinal viral load. If V is not included in the model, the MAR condition requires the analysis to assume that, conditional on observed CD4 history, missing outcome data are unrelated to the CD4 count that would have been measured; this assumption may be unrealistic. However, if the investigator can confidently specify the relationship between CD4 count and viral load (e.g., based on knowledge of disease progression dynamics) and if viral load values are observed for all cases, then MAR implies that the predictive distribution of missing CD4 counts given the observed CD4 counts and viral load values is the same for cases with CD4 missing as for cases with CD4 observed, which may be a much more acceptable assumption.
The missing values of CD4 can be multiply imputed using a model that includes the auxiliary variables, and the multiple imputation inference applied to an analysis model that does not condition on the auxiliary variables. Note that we assume here complete data on the auxiliary variables, so cases that have viral load measured but not historical CD4 levels are not useful. However, if the auxiliary variables are incomplete but measured in a substantial number of cases for which CD4 is missing, then multiple imputation can still be applied productively, multiply imputing the missing values of both CD4 and the missing auxiliary variable values in the imputation step.
The predictive distribution of the missing values can be based on a parametric model for the joint distribution of V and Y given X, using the Bayesian paradigm described in Section 4.3.2. Extension to more robust spline-based models are considered in Zhang and Little (2009). Implementation assuming MAR is as follows:
-
Specify an analysis model p(y x;θ) for [Y | X], the data that was intended to be collected. This is the model for the full response data.
-
Specify an imputation model
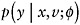 for [Y | X,V] that will be used to impute missing values of Y. Fit the model to {Y,V,X; R = 1}; that is, the data on observation times where Y is observed.
for [Y | X,V] that will be used to impute missing values of Y. Fit the model to {Y,V,X; R = 1}; that is, the data on observation times where Y is observed. -
For those with R = 0, generate S predicted values
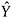 fsrom the predictive distribution of
fsrom the predictive distribution of 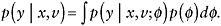 (Specific approaches to drawing from the predictive distribution, are give above.) This creates S completed datasets.
(Specific approaches to drawing from the predictive distribution, are give above.) This creates S completed datasets. -
Fit the model in step 1 to each of the S completed datasets, generating parameter estimates
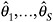 and associated standard errors.
and associated standard errors. -
Combine the estimates and standard errors into a summary inference about θ, using rules cited above.
Advantages and Disadvantages of Imputation-Based Procedures
Single-imputation methods such as LOCF and BOCF are simple to implement, but they generally do not conform to well-recognized statistical principles for drawing inference, especially in terms of reflecting all sources of uncertainty in an inference about treatment effect. Two popular misconceptions about LOCF and BOCF are (1) that they reflect an MAR or MCAR mechanism, and (2) that they result in estimates of treatment effect that tend to favor placebo or standard therapy over the experimental treatment. Claim (2) is generally not true because the methods do not always
yield conservative effect estimators, and standard errors and confidence interval widths can be underestimated when uncertainty about the imputation process is neglected.
Multiple imputation methods address concerns about (b), and enable the use of large amounts of auxiliary information. They can be relatively straightforward to implement, without special programming needs, and can handle arbitrary patterns of missing data. Moreover, the missing data assumptions are made explicit in the imputation model.
Although multiple imputation is a principled method, it does rely on parametric assumptions. Moreover, the data model p(y | x;θ) may be incompatible with the imputation model ![]() . Compatible models have the property that when auxiliary variables υ are integrated out of the imputation model, the result is the data model: that is,
. Compatible models have the property that when auxiliary variables υ are integrated out of the imputation model, the result is the data model: that is, ![]() . To verify compatibility, a model for [V | X] is needed (see Meng, 1994).
. To verify compatibility, a model for [V | X] is needed (see Meng, 1994).
As an example, with multivariate data, it is often possible to formulate a set of conditional distributions relating each variable to a set of the other variables, which are reasonable when taken one at a time, but incoherent in the sense that they cannot be derived from a single joint distribution. Such models, even when incoherent, may still be useful for creating multiple imputations (see, e.g., Baccini et al., 2010). Finally, robustness of multiple imputation inference to model form has also been investigated (see Zhang and Little, 2009), but more research would be valuable.
For key references, Rubin (1987, 1996) provides comprehensive reviews of multiple imputation. Discussions of the issues related to clinical trials are found in Glynn et al. (1993), Heitjan (1997), Liu et al. (2000), and Molenberghs and Kenward (2007).
MCAR-MAR Diagnostics As indicated above, while the observed data cannot be used to distinguish between MAR and MNAR missing data mechanisms, they can be used to distinguish between MCAR and MAR models and between competing MAR models. To this end, it is standard to assess the degree to which the treated and control groups differ in how the outcome variable Y relates to the various design variables X and auxiliary variables V. Therefore, various standard summary statistics and graphs should be used to assess the extent to which this is the case. Examples would include graphs for the treated and control groups of Y against X variables or V variables and means for the treated and control groups of Y for individuals with specific ranges of values of X and V in comparison with individuals with other ranges, and correlations of Y for the treated and control groups versus X or V.
Event Time Analyses
In event time analysis, missingness can take at least two important forms. First, with repeated event times, it is possible that some event times in a sequence are unobserved. This situation is entirely similar to the one described above. Second, it is common for event times to be unobserved because the event has not occurred when follow-up terminates. This situation is referred to as right censoring in the time-to-event (or survival) literature and has received considerable attention. It is a special case of coarsened data (Heitjan, 1993), which also includes left-censored and interval-censored data, heaped and grouped data.
The term “noninformative censoring” does not have a consistent definition, but it often refers to a censoring mechanism that is independent of the unobserved time to event, given an appropriate set of covariates (see Rotnitzky et al. [2009] for a discussion of this topic). Noninformative censoring implies that, among those still at risk at t, the hazard of death (or event) is equivalent between those who are censored at t and those who are not. Typically this assumption is made conditionally on an observed covariate history up to time t. A related and more general concept is “coarsened at random,” which extends the concept of MAR to coarsened data (Heitjan, 1993). Connections between missing data assumptions used in repeated measures and event time analyses are discussed in Scharfstein and Robins (2002).
ANALYTIC METHODS UNDER MNAR
MNAR models apply when missingness depends on the missing values after conditioning on observed information. For example, if a subject drops out of a longitudinal clinical trial when his blood pressure got too high and one did not observe that blood pressure, or if in an analgesic study measuring pain, the subject dropped out when the pain was high and one did not observe that pain value, missingness depends on the missing value.
Any analysis, whether based on likelihoods or moment assumptions, must be based on correct specification of the association between Y and M (given X and possibly V). Under MAR, the methods provided above will provide valid inferences. However, the MAR assumption cannot be verified from observed data, and even with modeling assumptions, the information to simultaneously estimate the parameters of the missing-data mechanism and the parameters of the complete-data model is very limited. Hence, model-based estimates tend to be very sensitive to misspecification of the model. In many if not most cases, a sensitivity analysis is needed to see how much the answers change for various alternative assumptions about the missing-data mechanism.
Definitions: Full Data, Full Response Data, and Observed Data
Analytic approaches for handling MNAR depend on making assumptions about the joint distribution [Y,M | X]. To describe analytic approaches for handling MNAR, it is necessary to carefully distinguish between full data, observed data, and their associated models. We describe both the full and observed data in terms of responses only, but these can be easily extended to include auxiliary variables V.
Full Data Full data refers to the sample that was intended to be collected. Importantly, the full data includes the missing data indicators. With univariate Y, the full data are (Y,X,M) for every individual.
Observed Data Observed data refers to the response, covariate, and missing data indicators that were actually observed. In a simple case in which Y is univariate and no covariates are missing, the observed data is (Y, X ,M = 1) for those with observed response, and it is (X, M = 0) for those with missing response.
With multivariate Y, it is useful to partition Y as (Yobs, Ymis). In particular, if K observations were intended to be taken on each individual, and the missing data pattern is monotone, then the observed data comprise Yobs = (Y1,…,Yj) for some j ≤ K, and M = (1,…,1,0,…,0) where the first j elements of M are 1’s and the remaining elements are 0’s. Notice that j will vary across individuals.
Full-Data Model The full-data model is the probability model that governs the joint distribution [Y,M | X]. Regardless of the form of this joint distribution, it can be written as p(y,m | x) = p(yobs,ymis,m | x), and factored as p(yobs,ymis,m | x) = p(yobs,m | x) × p(ymis | yobs,m,x).
This factorization makes clear which parts of the full-data model can be inferred from observed data and which cannot. Specifically, notice that the first factor on the right-hand side is a model for the distribution of variables that are observed. Generally speaking, the data analyst can estimate this distribution from the observed data, possibly by making modeling assumptions that can be evaluated using standard goodness-of-fit methods.
The second factor on the right-hand side is the model for the distribution of missing observations, and it cannot be inferred from observed data alone for the simple reason that no assumptions about the distribution can be checked from observed data. This factorization makes clear that inference from incomplete data requires the analyst to specify a model (or set of assumptions) for the observed-data distribution and to combine that with a set of untestable and unverifiable assumptions that describe how missing data are to be extrapolated from the observed data.
Target Distribution (or Parameter) Most often in clinical trials, primary interest centers on the distribution [Y | X] = [Yobs,Ymis | X], where X includes the treatment group and possibly other design variables. The target distribution is related to the full-data distribution through the identity:
(19)
Hence, inference about the target distribution relies critically on the untestable assumptions being made about p(ymis | yobs,m,x).
Selection and Pattern Mixture Models Two broad classes of models for the joint distribution of Y and M are selection models, which factor the full data distribution as
(20)
and pattern mixture models, which factor the full-data distribution as
(21)
Pattern mixture models can be factored to make the missing data extrapolation explicit within missing data pattern M, that is
(22)
Selection Models
Selection models can be divided into two types, (1) parametric and (2) semiparametric. Parametric selection models were first proposed by Rubin (1974) and Heckman (1976), based on parametric assumptions for the joint distribution of the full data (usually, a normal distribution for responses and a probit regression for the missing data indicators). For repeated measures, parametric selection models were described by Diggle and Kenward (1994), and semiparametric models were proposed by Robins et al. (1995) and Rotnitzky et al. (1998).
To illustrate a standard formulation, assume the full-response data comprise (Y1,Y2), and the objective is to capture the mean of Y2 in each treatment group. Further, assume Y2 is missing on some individuals. A parametric selection model might assume that the full-response data follows a bivariate normal distribution:
(23)
and the “selection mechanism” part of the model follows a logistic regression
(24)
Parametric selection models can be fit to observed data, even though there appears to be no empirical information about several of the model parameters. Specifically, there is no information about the association between M and Y2 because Y2 is missing. Likewise, there is no information about the mean, variance, and covariance parameters involving Y2.
The model can be fit because of the parametric and structural assumptions being imposed on the full-data distribution. This can be seen as both beneficial or as a reason to exercise extreme caution. Convenience is the primary benefit, especially if the model can be justified on scientific grounds. The reason for caution is that, again, none of the assumptions underlying this parametric model can be checked from the observed data. In parametric selection models fit under the MNAR assumption, identification of parameters and sensitivity to assumptions raises serious problems: see, for example, Kenward (1998), Little and Rubin (2002, Chapter 15), the discussion of Diggle and Kenward (1994), and Daniels and Hogan (2008, Chapter 9).
Semiparametric selection models do not assume a parametric model for the full-data response distribution, so they are therefore somewhat less sensitive to these assumptions. These models are discussed in greater detail in Chapter 5.
Pattern Mixture Models
Pattern mixture models were proposed for repeated measures data by Little (1993, 1994); a number of extensions and generalizations have followed. The connection between pattern mixture and selection models is described in Little and Wang (1996), in Molenberghs et al. (1998), and in Birmingham et al. (2003).
The models can be viewed from an imputation perspective, in which missing values Ymis are imputed from their predictive distribution given the observed data including M; that is,
(25)
Under MAR, this equals p(ymis | yobs,x). However, if data are not MAR, the predictive distribution (25) is a direct by-product of the pattern mixture formulation because it conditions on the missing data indicators. This more direct relationship between the pattern mixture formulation and the
predictive distribution for imputations yields gains in transparency and computational simplicity in some situations, as illustrated in Kenward and Carpenter (2008, Section 4.6).
Under MNAR, the selection model factorization requires full specification of the model for the missing data mechanism. Some pattern mixture models avoid specification of the model for the missing data mechanism in MNAR situations by using assumptions about the mechanism to yield restrictions on the model parameters (Little, 1994; Little and Wang, 1996; Hogan and Laird, 1997).
Many pattern mixture formulations are well suited to sensitivity analysis because they explicitly separate the observed data distribution from the predictive distribution of missing data given observed data. Sensitivity analyses can be formulated in terms of differences in mean (or other parameter) between those with observed and those with missing responses.
Advantages and Disadvantages of Selection and Pattern Mixture Models
Substantively, it seems more natural to assume a model for the fulldata response, as is done in selection models. For example, if the outcome is blood pressure, it may seem natural to assume the combined distribution of blood pressures over observed and missing cases follows a single distribution, such as the normal distribution. Moreover, if MAR is plausible, a likelihood-based selection formulation leads directly to inference based solely on the model for the full-data response, and inference can proceed by ML.
However, it may not be intuitive to specify the relationship between nonresponse probability and the outcome of interest, which typically has to be done in the logit or probit scale. Moreover, the predictive distribution of missing responses typically is intractable, so it can be difficult to understand in simple terms how the missing observations are being imputed under a given model. And, as indicated above, selection models are highly sensitive to parametric assumptions about the full data distribution. This concern can be alleviated to some degree by the use of semiparametric selection models.
Specification of pattern mixture models also appeals to intuition in the sense that it is natural to think of respondents and nonrespondents having different outcome distributions. The models are transparent with respect to how missing observations are being imputed because the within-pattern models specify the predictive distribution directly.
Pattern mixture models can present computational difficulties for estimating treatment effects because of the need to average over missing data patterns; this is particularly true of pattern mixture specifications involving regression models within each pattern.
Examples: Pattern Mixture Model for Continuous Outcomes
Daniels and Hogan (2008, Chapter 10) use pattern mixture models to analyze data from a randomized trial of recombinant human growth hormone (rHGH) on muscle strength in elderly people. More than 120 people were randomized to four different treatment arms. The primary outcome in this trial was quadriceps strength, assessed at baseline, 6 months, and 12 months. A pattern mixture model was fit under MAR and parameterized to represent departures from MAR. The example shows how to construct sensitivity plots to assess the effect of departures from MAR on the inferences about treatment effect. An important feature of the model is that the fit to the observed data is unchanged at different values of the sensitivity parameters. However, the model does rely on parametric assumptions, such as normality. These assumptions can be checked for the observed data, but have to be subjectively justified for the missing data.
Example: Pattern Mixture Model for Binary Outcomes
Daniels and Hogan (2008, Chapter 10) use pattern mixture models to analyze data from an intervention study for smoking cessation among substance abusers. The primary outcome was smoking status, assessed at baseline, 1 month, 6 months, and 1 year. A pattern mixture model was fit under MAR and expanded to allow for MNAR missingness. In addition to presenting sensitivity analysis, the example shows how to incorporate prior information about the smoking rate of dropouts to obtain a summary inference about treatment effect.
Sensitivity of Parametric Selection Models
The sensitivity of MNAR selection models to distributional assumptions is illustrated by Verbeke and Molenberghs (2000, Chapter 17), who show that, in the context of an onychomycosis study, excluding a small amount of measurement error drastically changes the likelihood ratio test statistics for the MAR null hypothesis. In a separate example, Kenward (1998) revisited the analysis of data from a study on milk yield performed by Diggle and Kenward (1994). In this study, the milk yields of 107 cows were to be recorded during 2 consecutive years. Data were complete in the first year, but 27 measurements were missing in year 2 because these cows developed mastitis, which seriously affected their milk yield and therefore deemed missing for the purposes of the study. Although in the initial paper there was some evidence for MNAR, Kenward (1998) showed that removing two anomalous profiles from the 107 completely eliminated this evidence. Kenward also showed that changing the conditional distribution
of the year 2 yield, given the year 1 yield, from a normal to a heavy-tailed t distribution led to a similar conclusion.
Several authors have advocated using local influence tools for purposes of sensitivity analysis (Thijs et al., 2000; Molenberghs et al., 2001; Van Steen et al., 2001; Verbeke et al., 2001; Jansen et al., 2006). In particular, Molenberghs et al. (2001) revisited the mastitis example. They were able to identify the same two cows also found by Kenward (1998), in addition to another one. However, it is noteworthy that all three are cows with complete information, even though local influence methods were originally intended to identify subjects with other than MAR mechanisms of missingness. Thus, an important question concerns the combined nature of the data and model that leads to apparent evidence for an MNAR process. Jansen et al. (2006) showed that a number of features or aspects, but not necessarily the (outlying) nature of the missingness mechanism in one or a few subjects, may be responsible for an apparent MNAR mechanism.
Selection and Pattern Mixture Models: Literature
The literature covering selection and pattern mixture models is extensive. Review papers that describe, compare, and critique these models include Little (1995), Hogan and Laird (1997, 2004), Kenward and Molenberghs (1999), Fitzmaurice (2003), and Ibrahim and Molenberghs (2009). The models are also discussed in some detail in Little and Rubin (2002), Diggle et al. (2002), Fitzmaurice et al. (2004), Molenberghs and Kenward (2007), and Daniels and Hogan (2008).
An extensive literature also exists on extensions of these models involving random effects, sometimes called shared-parameter or random-coefficient-dependent models. Reviews are given by Little (1995) and Molenberghs and Kenward (2007). Although these models can be enormously useful for complex data structures, they need to be used with extreme caution in a regulatory setting because of the many layers of assumptions needed to fit the models to data.
Recommendations
Recommendation 9: Statistical methods for handling missing data should be specified by clinical trial sponsors in study protocols, and their associated assumptions stated in a way that can be understood by clinicians.
Since one cannot assess whether the assumptions concerning missing data are or are not valid after the data are collected, one cannot assert that the choice of missing data model made prior to data collection needs to be
modified as a result of a lack of fit. Thus, one needs to carry out a sensitivity analysis. Of course, model fitting diagnostics can be used to demonstrate that the complete data model may need to be adjusted, but the missing data model raises no additional complexities.
Recommendation 10: Single imputation methods like last observation carried forward and baseline observation carried forward should not be used as the primary approach to the treatment of missing data unless the assumptions that underlie them are scientifically justified.
Single imputation methods do not account for uncertainty associated with filling in the missing responses. Further, LOCF and BOCF do not reflect MAR data mechanisms.
Single imputation methods are sometimes used not as a method for imputation but rather as a convenient method of sensitivity analysis when they provide a clearly conservative treatment of the missing data. This can obviously be accomplished by using a best possible outcome for the missing values in the control group and a worst possible outcome for the missing values in the treatment group. If the result of such a technique is to demonstrate that the results of the primary analysis do not depend on the treatment of the missing data, such an approach can be useful. However, techniques that are often viewed as being conservative and therefore useful in such an approach, are sometimes not conservative and so care is required.
Recommendation 11: Parametric models in general, and random effects models in particular, should be used with caution, with all their assumptions clearly spelled out and justified. Models relying on parametric assumptions should be accompanied by goodness-of-fit procedures.
We acknowledge that this is an area where the current toolkit is somewhat lacking, and therefore more research is needed. Some contributions to this area include Verbeke et al. (2001, 2008), Gelman et al. (2005), and He and Raghunathan (2009).
Recommendation 12: It is important that the primary analysis of the data from a clinical trial should account for the uncertainty attributable to missing data, so that under the stated missing data assumptions the associated significance tests have valid type I error rates and the confidence intervals have the nominal coverage properties. For inverse probability weighting and maximum likelihood methods, this can be accomplished by appropriate computation of standard errors, using either asymptotic results or the bootstrap. For imputation, it
is necessary to use appropriate rules for multiply imputing missing responses and combining results across imputed datasets because single imputation does not account for all sources of variability.
Recommendation 13: Weighted generalized estimating equations methods should be more widely used in settings when missing at random can be well justified and a stable weight model can be determined, as a possibly useful alternative to parametric modeling.
Recommendation 14: When substantial missing data are anticipated, auxiliary information should be collected that is believed to be associated with reasons for missing values and with the outcomes of interest. This could improve the primary analysis through use of a more appropriate missing at random model or help to carry out sensitivity analyses to assess the impact of missing data on estimates of treatment differences. In addition, investigators should seriously consider following up all or a random sample of trial dropouts, who have not withdrawn consent, to ask them to indicate why they dropped out of the study, and, if they are willing, to collect outcome measurements from them.
INSTRUMENTAL VARIABLE METHODS FOR ESTIMATING TREATMENT EFFECTS AMONG COMPLIERS
Estimates of treatment effects for all individuals randomized as in intention-to-treat analysis are protected against bias by the randomization. In this estimand, individuals who are assigned a treatment but never comply with it, perhaps because they cannot tolerate treatment side effects, are treated in the same way as individuals who comply with the treatment. Sometimes, particularly in secondary analyses, interest lies in the treatment effect in the subpopulation of individuals who would comply with a treatment if assigned to it. The average treatment effect in this population is called the complier-average causal effect (CACE) (Baer and Lindeman, 1994; Angrist et al., 1996; Imbens and Rubin, 1997a, 1997b; Little and Yau, 1998; White, 2005).
An alternative estimand to the CACE is the average treatment effect (ATE) (Robins, 1989; Robins and Greenland, 1996). It is defined as the difference in mean outcome if all individuals had been assigned and complied with the treatment (T = 1) and the mean if all individuals had been assigned and complied with the control treatment (T = 0). The ATE is defined for the whole target population, and it requires assumptions about the treatment outcome for noncompliers had they complied with the treatment. Whether this counterfactual event is meaningful typically depends on context. For example, noncompliance to a behavioral treatment, such as an exercise
regime, might plausibly be changed by increased motivation, as might occur if evidence of success of the treatment becomes widely known. In contrast, if noncompliance to a drug is the result of intolerable side effects, then compliance may require a reformulation of the drug to remove the side effects. Such reformulation may change the properties of the drug, and estimation of the ATE is consequently more speculative.
Simple approaches to estimating the CACE or the ATE include astreated analysis, in which participants are classified according to the treatment actually received, and per-protocol analysis, which restricts analysis to participants who comply with the assigned treatment. These analyses are subject to selection bias in that participants who comply with a treatment may be a biased sample of participants randomized to that treatment. The bias may be reduced by adjustment for covariates, but it remains a major concern.
Although this is often characterized as a problem of selection bias, recent approaches have suggested alternatives to as-treated and per-protocol analyses by applying a missing-data perspective. Consider a binary variable C(T) taking the value 1 if an individual would comply with a particular treatment T if assigned to it, and 0 otherwise. We call this variable principal compliance, to distinguish it from observed compliance, which depends on the treatment actually assigned. It is a special case of principal stratification (Frangakis and Rubin, 2002). Principal compliance C(T) is observed for participants who are assigned to treatment T, but it is not observed for participants assigned other treatments, T′, so for these individuals the values of C(T) can be regarded as missing.
In simple trials involving an active treatment and a control treatment, an alternative to as-treated and per-protocol estimates is based on the idea of treating the randomization as an instrumental variable (IV), in economic parlance. The IV estimator yields a direct estimate of the CACE, and it is protected from selection bias by the randomization. However, it requires certain assumptions to be valid, and it also yields estimators with potentially high variance, particularly if the treatment compliance rate is low. Model-based versions of the IV estimator based on treating C as missing for some participants have been proposed that are potentially more efficient, although they make stronger distributional assumptions. For a nontechnical article comparing this approach with as-treated and per-protocol estimates, see Little et al. (2009) for a discussion of extensions to two or more active treatments, see Long, Little, and Lin (in press).
An example illustrating the above discussion and a number of associated issues is provided by the evaluation of a trial to assess the effect of an influenza vaccine (Hirano et al., 2000). The trial randomly assigned physicians to encouragement (T1) or no encouragement (T2) to vaccinate their patients against influenza. The primary endpoint was hospitalization, and
the intention-to-treat estimates showed of those encouraged, 7.8 percent were hospitalized and of those not encouraged 9.2 percent were hospitalized. However, the trial had only a weak effect on the actual taking of the vaccine: of those encouraged, 31 percent of patients received the vaccine; of those not encouraged, 19 percent of patients received the vaccine.
Therefore, to better understand the trial results, at least a secondary estimand of interest was CACE, that is, in this case, the effect of encouragement on hospitalization for the patients who would have been vaccinated if their physician had been encouraged but not vaccinated if their physician had not been encouraged. Assuming the standard exclusion restrictions of IV, CACE was estimated as an 8.2 percent reduction in hospitalization. Yet, even this turned out to represent only part of a better understanding of the trial results.
In this study, there were a number of good baseline predictors of compliance under both arms, C(T1) and C(T2), and thus, the effect of compliers could be in part identified without the need of exclusion restrictions. When these restrictions were relaxed, the effect of encouragement on compliers was estimated at 3.7 percent, but there was at least as large of an estimated effect (5.3 percent) of encouragement on hospitalization for always-takers. Later commentaries on these results suggested that the latter effect is explainable by the earlier time in the season at which the always-takers likely receive the vaccine when encouraged, compared to when not encouraged. Since this effect is comparable to CACE, it suggested that the effect of vaccination lies more in its timing and not only on its receipt.
To further explicate this method, we offer an example of coprimary outcomes that induce missing data. For randomized controlled trials with two (or more) coprimary outcomes, say E and Y, values of E can determine whether Y has a meaning as a measurement. This effect presents a challenge in the very definition of the effect between the two interventions, say T1 and T2, on Y, because the existence of Y is determined after the intervention. This problem can be treated in principle in the context of missing information, not of Y (which is sometimes undefined) but of certain strata, called principal strata. Our example involves clinical trials for HIV.
The idea of cell-mediated immunity is to train the killer cells to recognize and attack a protein that human CD4 cells create when the CD4 cells are infected (as opposed to targeting the virus directly, whose identification is difficult due to mutations over time). For this reason, randomized trials for cell-mediated immunity vaccines should be designed to assess two coprimary outcomes: reducing primary infection (say, E), and, if a person is infected (E = 1), keeping low viral load (say Y). Work by Gilbert et al. (2003) and then by Mehrotra et al. (2006) showed how principal stratification (Frangakis and Rubin, 2002) can be used to formulate the target hypotheses with such coprimary outcomes. Specifically, the first coprimary
research hypothesis is that changing treatment T1 (placebo) to T2 (vaccine) changes the primary infection rate E. The second coprimary research hypothesis should capture that the vaccine can also affect viral load when infected. However, the viral load distributions between infectees under the placebo condition and those infected under the vaccine condition could be different simply because the immune system is inherently different between the two groups. (In fact, if the vaccine prevents some primary infections, infectees under vaccine are expected to have weaker baseline immune system than infectees under placebo.) One can disentangle baseline differences from vaccine effects if one focuses on the people who would have been infected regardless of receiving the vaccine or the placebo. This stratum is known as a principal stratum because membership to it does not change depending on assignment to different interventions. Thus, the second coprimary research hypothesis can be that changing treatment T1 (placebo) to T2 (vaccine) will change the viral load for those for whom changing T1 to T2 does not prevent primary infection.
For a person under placebo who gets infected (E(T1) = infected), one does not know if the person would have been also infected under vaccine (E(T2) = infected), so membership to the principal stratum—E(T1) = E(T2) = infected—is partly missing. (Estimation of the effect of vaccine on viral load Y for this stratum is discussed above.)
Additional examples of randomized controlled trials with coprimary outcomes using principal stratification include determining if the immune response to a vaccine is causing reduction in infection rates (Follmann, 2006); assessing more general surrogate outcomes in vaccine trials (Qin et al., 2008); and evaluating the effect of an intervention on severity of a disease (e.g., of prostate cancer) when a person does get the disease (Shepherd et al., 2008).
MISSING DATA IN AUXILIARY VARIABLES
The assumptions and models discussed above have been limited to outcome variables. Usually, there are many auxiliary variables collected at each visit that can be useful to incorporate into the analysis. Specifically, these variables are useful because they both help explain the reasons for future nonresponse as well as help predict the missing outcomes (and so help improve the efficiency with which the treatment effects are estimated). They can also serve to make the MAR assumption more tenable. We have assumed throughout that the collection of auxiliary variable data is complete, which is clearly not always the case. We do note that the above approaches can be modified to incorporate missing auxiliary data by augmenting the missing outcome variable with a missing V. Although including V along with the missing outcome variable will often address the problem,
the literature on missing data in longitudinal settings is fairly limited, and more research on dealing with missing auxiliary data would be useful. We do believe that many of the above approaches can be easily modified to incorporate auxiliaries by replacing ![]() in the conditional means and probabilities with
in the conditional means and probabilities with ![]() , which includes (Y1,…,Yk–1,V1,…,Vk–1). An excellent example of the use of this method is Liu et al. (2009).
, which includes (Y1,…,Yk–1,V1,…,Vk–1). An excellent example of the use of this method is Liu et al. (2009).




































