“Philosophy is written in this grand book—I mean the universe—which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures.”
So wrote Galileo Galilei in 1623, at the dawn of the scientific era. Nearly four centuries later, we can only marvel at his prescience, because what he wrote then is even more true today. The secrets of the universe are still written in geometric terms, although the figures Galileo wrote about have now been replaced by more exotic and abstract ones: manifolds, fiber bundles, and Calabi-Yau spaces.
In the early 1800s, it was shown that the familiar Euclidean geometry, which has been taught since the ancient Greeks and is still taught in high schools today, is only one of an infinite variety of possible geometries. Euclidean geometry is flat—it is the geometry of a tabletop, infinitely extended. By contrast, non-Euclidean geometries are curved. They may have the positive curvature of a sphere, or they may have negative curvature, which is harder to visualize but may be compared to the frilly surface of some leafy vegetables.
In the 1850s, Bernhard Riemann took another bold step forward, describing spaces in which the curvature could change from point to point within the space. Riemann’s geometry also allows space to take on any number of dimensions—two, three, or even more. He called these curved spaces “manifolds” (see Figure 22 on page 50).
For some time these new geometries remained just a mathematical curiosity. But in the early 1900s, Albert Einstein used Riemann’s mathematics as a language to express his theory of general relativity—a theory in which gravity results from the curvature of four-
A long list of profound discoveries followed from the equations that Einstein wrote down in 1915: black holes, the expanding universe, the big bang, and dark energy.

22 / Two-dimensional manifolds are also known as surfaces. A sphere (left) is positively curved, while the surface on the right, which resembles a six-connection pipe fitting, is negatively curved. Reprinted with permission from Gerard Westendorp. /
dimensional space-time. A long list of profound discoveries followed from the equations that Einstein wrote down in 1915: black holes, the expanding universe, the big bang, and dark energy. To understand any of these ideas fully, you have to learn Riemannian geometry. Somewhere, Galileo must be smiling.
But Einstein’s general relativity was only the beginning. Similar geometric constructions underlie the field theories that describe particle physics. The discovery of antimatter, in 1932, grew directly out of an attempt to reconcile relativity with the quantum-mechanical description of the electron. The equations predicted extra solutions that seemed like positively charged electrons. We now call them positrons. They are the key ingredients in positron emission tomography, or PET scans, which are used to study the workings of the human brain.
In the later 1930s and 1940s, physicists and mathematicians started losing touch with one another. Physicists started thinking about fields that permeate all of space, which they called “gauge fields.” (Examples include the electromagnetic field and the weak and strong nuclear forces.) Meanwhile mathematicians, for different reasons, became very interested in a new kind of geometric space, called a fiber bundle, which is roughly like a curved space with a quiver of arrows attached at every point (see Figure 23 for an example). It wasn’t until the 1970s that mathematicians and physicists realized that they were doing the same thing. The physicists’ gauge fields were like individual arrows in the mathematicians’ quiver of arrows.
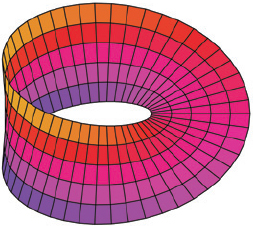
23 / The Mobius band is the simplest nontrivial example of a fiber bundle. The fibers are shown in red. The twist given to the fibers makes the Mobius band topologically different from an ordinary cylindrical band. /

24 / A cross-section of a quintic hypersurface. Reprinted with permission from Paul Nylander, http://bugman123.com. /
The cross-fertilization of ideas between the mathematical sciences and theoretical physics continues to this day. In the late 20th and early 21st centuries, string theory was formulated as an approach to unifying gravity and quantum physics into a theory of everything. Like all other theories in physics, it is highly mathematical—but the necessary mathematics has not yet been invented. There is still no rigorous context for the calculations that string theorists do, nor do mathematical scientists know the extent to which these techniques are valid.
However, the study of string theory has led to some important applications of the mathematical sciences. For example, since the 1800s, mathematicians have studied the solution sets of polynomial equations, such as a fifth degree polynomial in four variables. An example of such a polynomial is x5 + y5 + z5 + s5 + t5 = 0, which is known as a “quintic hypersurface” (see Figure 24.) These surfaces contain figures that Galileo would have recognized.
And why did string theorists care about quintic hypersurfaces? Because string theory postulates that the universe has six extra, unseen dimensions that are curled up into a tight ball. Except that “ball” is not really the correct word. They actually form a manifold—a type of space discovered by mathematical scientists.
The list of interactions between geometry and physics could go on and on. It is difficult to speculate where it will lead next, but it is virtually certain that unexpected ideas for both disciplines will continue to grow out of the interaction. Galileo’s words continue to hold true: Geometry is still the language spoken by the universe.




