From the Mathematical Sciences to … an IPO
In 1997, when Sergey Brin and Larry Page were graduate students at Stanford, they wrote a short paper about an experimental search engine that they called Google. Brin and Page’s idea—which was based on the research of many mathematical scientists—was to give each Web page a ranking, called PageRank, that indicates how authoritative it is. Your PageRank will improve if a lot of other Websites link to your Website. Intuitively, those other pages are casting a vote for your page. Also, Brin and Page assumed that a vote from a page that is itself quite authoritative should count for more. Thus your PageRank is a function of the PageRanks of all the pages that link to you.
The genius of Brin and Page’s PageRank was its ability to harness human judgments without explicitly asking for them. Every link to a Web page is an implicit vote for the relevance of that page. In an exploding Internet, its simplicity also turned out to be of paramount importance. The calculation could be done offline, and thus it could be applied to the entire Web. PageRank represented a major advance over approaches to Internet search that were based on matching words or strings on a page. These earlier search engines returned far too many results, even in a drastically smaller Internet than today.
The PageRank algorithm seems to pose a chicken-and-egg paradox: To compute one PageRank, you already need to know all of the other PageRanks. However, Brin and Page recognized that this challenge is a form of a well-known type of math problem, known as the eigenvector problem. A vector (in this case) is just a list of numbers, such as the list of the PageRanks of all pages on the Web. If you apply the PageRank algorithm to a collection of vectors, most will be changed, but the true PageRank vector persists: It is not changed by the algorithm.
This kind of “persistent” vector is known in mathematics as an eigenvector (eigen being the German word for “characteristic”). Eigenvectors have appeared in numerous contexts over the centuries. The concept (though not the terminology) first arose in the work of the 18th century mathematician Leonhard Euler on the rotation of solid bodies. Because any rotation in space must have an axis—a line that persists in the same direction throughout the rotation—Euler recognized that the axis and angle of rotation characterize the rotation (which justifies the term “characteristic,” at least in this context).
Fast forward a century or so, and you find eigenvectors used again in quantum physics. The motion of electrons is described by Schrödinger’s equation, formulated in 1926 by Austrian physicist Erwin Schrödinger. They do not orbit atomic nuclei in circles or ellipses in the way that planets orbit the Sun. Instead, their orbits form complicated three-dimensional shapes that are determined by the eigenvectors of Schrödinger’s equation. By counting the number of these solutions, you can tell how many electrons fit in each energy level or orbital of an atom, and in this way you can start to explain the patterns and periodicities of the periodic table.
Fast forward again to the present, and you can find the same concept used in genomics. Imagine that you have a large array of data; for example, the level of activity of 3,000 genes in a cell at 20 different times. Although the cell has thousands of genes, it does not have that many biologically meaningful processes. Some of the genes may work together to repel an invader. Other genes may be involved in cell division or metabolism. But the rest may not be doing much of anything, at least while you are watching them; their activity just amounts to random noise. The eigenvectors of the data set correspond to the most relevant patterns in the data, those which persist through the noise of chance variation. Figure 2 (on page 10) shows networks of genes found using eigenvectors. One eigenvector (the term “eigengene” has even been coined here) might correspond to genes that control metabolism. Another might consist of genes activated during cell division. The mathematics identifies the gene networks that appear most tied to biological activity, but it cannot tell what the networks do. That is up to the biologist.
Singular value decomposition (SVD) is a purely mathematical technique to pick out characteristic features in a giant array of data by finding eigenvectors. The idea is something like this: First you look for the one vector that most closely matches all of the rows of data in the array; that is the first eigenvector. Then you look for a second vector that most closely matches the residual variations after the first eigenvector has been subtracted out. This is the second eigenvector. The process can, of course, be repeated. For the PageRank example, only the first eigenvector is used. But in other applications, such as genomics, more than one eigenvector may be biologically significant.
Given the general applicability of eigenvector approaches, perhaps it is not too surprising that Google’s PageRank—an algorithm that involves no actual understanding of your search query—could rank Web sites better than algorithms that attempted to
analyze the semantic content of Web pages. However, the ability to use this eigenvector approach with real data that are random or contain much uncertainty is the key to PageRank. Within a few years, everybody was using Google, and “to google” had become a verb. When Brin and Page’s company went public in 2004, its initial public stock offering raised $27 billion.
In many other applications, finding eigenvectors through SVD has proved to be effective for aggregating the collective wisdom of humans. From 2006 to 2009, another hot Internet company ran a competition that led to a number of advances in this field.

Within a few years, everybody was using Google, and “to google” had become a verb.
Netflix, a company that rents videos and streams media over the Internet, had developed a proprietary algorithm called Cinematch, which could predict the number of stars (out of five) a user would give a movie, based on the user’s past ratings and the ratings of other users. However, its predictions were typically off by about 0.95 stars. Netflix wanted a better way to predict its customers’ tastes, so in 2006 it offered a million-dollar prize for the first person or team who could develop an algorithm that would be 10 percent better (i.e., its average error would be less than about 0.85 stars). The company publicly released an anonymized database of 100 million past ratings by nearly half a million users so that competitors could test their algorithms on real data.
Rather unexpectedly, the most effective single method in the competition turned out to be good old-fashioned SVD. The idea is roughly as follows: Each customer has a specific set of features that they like in a movie—for instance, whether it is a drama or a comedy, whether it is a “chick flick” or a “guy flick,” or who the lead actors are. A singular value decomposition of the database of past ratings can identify the features that matter most to Netflix customers. Just as in the genomics example, the mathematical sciences cannot say what the features are, but they can tell when two movies have the same constellation of factors. By combining a movie’s scores for each feature with the weight that a customer assigns to those features, it can predict the rating the customer will give to the movie.
The team that won the Netflix Prize combined SVD with other methods to reach an improvement of just over 10 percent. Not only that, the competition showed that computer recommendations were better than the judgment of any human critic. In other words, the computer can predict how much your best friend will like a movie better than you can.
The above examples attest to the remarkable ability of eigenvector methods (often in combination with other techniques) to extract information from vast amounts of noisy data. Nevertheless, plenty of work remains to be done. One area of opportunity
is to speed up the computation of eigenvectors. Recently mathematicians have found that “random projections” can compress the information in a large matrix into a smaller matrix while essentially preserving the same eigenvectors. The compressed matrix can be used as a proxy for the original matrix, and SVD can then proceed with less computational cost.
One of Google’s biggest challenges is to guard the integrity of PageRanks against spammers. By building up artificial networks of links, spammers undercut the underlying assumption that a Web link represents a human judgment about the value of a Web page. While Google has refined the PageRank algorithm many times over to ferret out fake links, keeping ahead of the spammers is an ongoing mathematical science challenge.
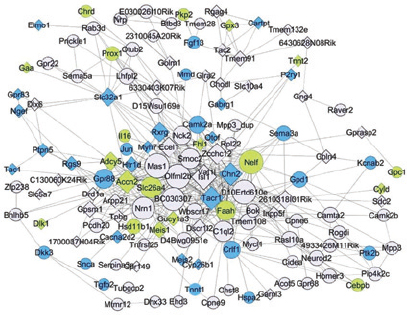
2 / When the gene expressions for the C57BL/6J and A/J strains of mice are compared, it is possible to find gene networks using eigenvectors that are specific for brain regions, independent of genetic background. Image from S. de Jong, T.F. Fuller, E. Janson, E. Strengman, S. Horvath, M.J.H. Kas, and R.A. Ophoff, 2010, Gene expression profiling in C57BL/6J and A/J mouse inbred strains reveals gene networks specific for brain regions independent of genetic background, BMC Genomics 11:20. /




