3
Evaluation of Risk Approach
and Calculations
The updated site-specific risk assessment (uSSRA) of the proposed National Bio- and Agro-Defense Facility (NBAF) uses a quantitative modeling framework. That is an important advance over the 2010 SSRA. The framework includes the identification of risk scenarios, calculation of event likelihoods as annual frequencies of occurrence, assessment of consequences of an infection event, calculation of annual expected consequences, total calculation of risk of all events, and uncertainty analysis.
APPLICATION OF RISK METHODS IN THE UPDATED SITE-SPECIFIC RISK ASSESSMENT
The modeling framework is a “scenario-based” approach that is well established for analyzing risk in complex systems. It is a solid method. However, the committee identified issues of concern in how the framework was implemented. Some of the concerns have broad implications for the adequacy and validity of the report. The uSSRA adopts the contemporary terminology of ISO 31000 in describing the modeling framework, which is to be commended; but inconsistencies in the presentation of the method and in the use of terminology make it at times difficult to understand how the methods were applied.
Risk Metric
Defining risk as an expected (probability weighted) consequence is consistent with current practice, but this metric masks the difference between high-probability/low-consequence events and low-probability/high-consequence events. That approach is not incorrect, but a preferred and more informative metric would be the probability–consequence “risk curve” in which various levels of consequence (Cevent) are plotted against corresponding probabilities (Pevent) (Cox, 2009). Although this is not a fundamental flaw in the chosen approach, presenting outcomes in the more informative way would have provided richer information to the reader.
The Logic Modeling Approach
The uSSRA uses a non-binary event tree modeling technique, which is appropriate and standard present practice. Whereas the technique seems to be correctly applied, it is difficult to understand the analysis and its results. The uSSRA uses fault tree symbols at branch points of the event trees, which is confusing and suggests a poor understanding of basic terminology. The uSSRA incorrectly refers to the event trees as fault trees in most cases but refers to them as event trees in others.
Typical risk scenarios in the report involve a temporal sequence of events; therefore, an event tree approach is effective for enumerating all possible chains of events in a scenario. In modeling failure of system components, however, a fault tree approach provides a better way of capturing system failure paths (e.g., minimal cut sets) than the event tree approach (Cox, 2009). For this reason, many industrial installations use risk analyses that are a hybrid of event trees and fault trees (Cox, 2009). The uSSRA should have followed suit by using a hybrid model, but it did not.
Mean Versus Median
The uSSRA lacks a consistent approach to calculating middle values or best estimates. Most of the risk calculations use the estimated 50th percentile (the median); some use the mean (for example, see discussion on Q values on p. 578 of the uSSRA). The median and mean can differ by orders of magnitude in highly skewed distributions, which appear to be the case for many parameters in the risk calculations. A consistent approach should have been used in the uSSRA, and it should have relied upon the mean rather than the median.
Implied and False Precision
The uSSRA provides estimates that do not appropriately consider significant figures; this was also a concern noted by the previous committee (NRC, 2010). As the present committee noted in its March 2012 public meeting, carrying more than one digit in calculations, where values of input parameters vary by many orders of magnitude, implies more precision than is possible. Rounding to one digit would have been appropriate.
The committee identified several issues in how the uSSRA carries out the risk assessment that would apply to the various event calculations and affect the overall estimates. The notable ones are related to rates of human error, sensitivity and uncertainty analysis, and probabilistic dependency.
Treatment of Human Error
Many scenarios identified in the uSSRA include human error. The uSSRA uses a generic probability of human error for most cases “based on human reliability assessments for highly reliable and trained workers such as those to be employed at the NBAF” (p. 139). It mostly adopts a value of 5 × 10–3 for failure per error opportunity, which is based on human error probabilities suggested for nuclear power industry applications (Spurgin, 2009). The uSSRA states that this failure probability is used for any mitigating systems or event nodes that are dependent upon a worker performing an action.
The committee finds the uSSRA’s treatment of human error inadequate. There is no evidence of a rigorous NBAF-specific human reliability analysis, which is a necessary component that is found in comprehensive risk analyses (U.S. NRC, 2005). Values for human error rates in work settings similar to the NBAF should be based on related empirical evidence. From the text provided in the uSSRA, the human error rate does not appear to be based on a rigorous and transparent analysis of the available data for similar operations. The human error rate of 1 in 200 and lower for “highly skilled workers” seems to have been arbitrarily selected and indiscriminately applied.
With the NBAF designs at only 65% completion, it may seem premature to develop human error probabilities that are site-specific and task-specific. Nevertheless, it is the responsibility of DHS and its contractors to provide such estimates for human error probabilities as part of the uSSRA. This could have been done given the available information about the site,
the general understanding of tasks involved, the experience of other laboratories, and the nature of a human role in the risk scenarios.
In at least one pathway, the uSSRA uses an unrealistically low value of 2 × 10–4 of failure per error opportunity for human error that is not justified in the report. The uSSRA claims that NBAF workers would be more highly skilled than “skilled workers” and provides an error rate of 5 × 10–3 of failure per error opportunity with no further substantive explanation.
It was critical for the uSSRA to have explored possible sources of data and operating experience related to human errors in research laboratory settings as the basis of generic or reference error probability. Rates of error in various types of tasks similar to those involved in a facility of the NBAF type are provided by Kletz (2001), and are all much higher than the values used in the uSSRA. Data from the U.S. Department of Agriculture and Centers for Disease Control and Prevention’s (CDC) annual Reports to Congress on Thefts, Losses, or Select Agents or Toxins may provide somewhat better information, but even such information would be based on mature operations that have been in practice for years at established facilities with experienced, integrated cores of workers, supervisors, and management. The NBAF’s large-animal capabilities will introduce unfamiliar operational risks. An analysis of the experience of the most similar operations—such as those at Pirbright, UK, Geelong, Australia, and Winnipeg, Canada, for comparable foreign laboratories, and the U.S. Army Medical Research Institute of Infectious Diseases, CDC, and University of Texas Medical Branch at Galveston for comparable U.S. laboratories—may provide more informative guidance than the apparently arbitrary assumption of human error rate used in the uSSRA.
The uSSRA does not account for the possibility that routine tasks can be associated with high failure rates even when carried out by highly trained workers. For example, in 2004, at least three researchers were exposed to and later developed tularemia when they handled a live rather than avirulent strain of the bacteria (Lawler, 2005). That event investigation revealed that researchers routinely failed to comply with safety and other protocols (Barry, 2005). In another case in early 2004, highly skilled workers shipped an anthrax sample that was supposed to be heat-killed but instead was alive and thereby exposed the recipients to anthrax (Enserink and Kaiser, 2004). Also in 2009, a military scientist who worked with cultures of tularemia bacteria was infected and developed symptoms of the disease; it took at least two weeks for the disease to be properly diagnosed (Eckstein, 2009).
The following are examples of the inappropriate treatment of human error in the uSSRA at several key events in mitigation pathways:
• System failure rates. Rates of system failure, such as failure of a cook tank to function properly to kill foot-and-mouth disease virus
(FMDv), are based generally on the notion that the system has been properly operated and maintained in accordance with a vendor’s claims (see additional discussion of cook tank failure later in this chapter). Inadequate operation or maintenance (human error) are not considered in the uSSRA.
• Disinfectant failure. The use of expired disinfectants or failure to apply disinfectant properly (human error) are not calculated in the event tree design.
• Efficiency of showering. Efficiency of showering to remove virus on the body is given as 81-98%, but the scenario tree does not include possible human errors in not following protocol for showering.
• Transference (contact, fomite). The event tree in Figure 4.5.1-8 (p. 160 of the uSSRA) assumes that employees will always submit rings, eyewear, etc. for disinfection. The uSSRA assumes that certain procedures would prevent such items from entering animal-handling rooms (AHRs). Human error in neglecting to acknowledge or disinfect these fomites is not included.
• Necropsy transference. An error consistently found in the event tree pathways involves omission of an acknowledgment or observation of an event, such as failing to notice a leaking glove, an inappropriately fitting respirator, or a spill or leak. Failure to include this type of human error, referred to as slip error, would in essence mean that the model assumes the slip error rate to be zero.
Sensitivity and Uncertainty Analysis
A critical part of risk analysis is characterizing the uncertainty in the results and the sensitivity of those results to changes in assumptions or parameter values. The importance of uncertainty analysis has been recognized since the early era of quantitative assessment of health, safety, and environmental risks in federal practice, and this has been expounded in a series of National Research Council reports on risk analysis (e.g., NRC, 1983, 1994, 2009).
Uncertainty in risk analyses is usually divided into two types: uncertainties due to natural randomness and uncertainties due to limited knowledge, which are referred to as aleatory and epistemic, respectively. Aleatory uncertainty refers to the inherent or natural variations in the physical world (NRC, 1996, 2000). Epistemic or knowledge uncertainty refers to scientific uncertainty due to lack of data or knowledge about real-world events (NRC, 1996, 2000). A model and its parameters may include aspects that have great scientific certainty and well-defined aleatory variability. The model and parameters may also include aspects with a high degree of scientific uncertainty and with a differing extent of variability.
The uSSRA mentions epistemic and aleatory sources of variability and
uncertainty in the risk assessment (p. 15). However, the statement that “modeling data included a thorough treatment of uncertainty, including both aleatory and epistemic, to provide a reasonable range of possible outbreak risks” is not supported in the text. In some sections of the uSSRA, some pieces are provided as a good start particularly for the sensitivity analysis, which covers mainly the aleatory variability but also some aspects of epistemic uncertainty (for example, see pp. 534-539). But even in that specific example, the sensitivity analysis examines the impact of a 0.5- to 2-fold change in parameter values that actually have far greater ranges between “low,” “median,” and “high”—at times 6–9 orders of magnitude.
It is unclear whether a consistent approach was used throughout the uSSRA for expressing uncertainty in input parameters. More specifically, the committee could not determine whether low, medium, and high values of some parameters represent corresponding percentiles of a continuous (or discrete) probability distribution. As previously mentioned, this is complicated by the fact that the middle value of the range is sometimes referred to in the report as the mean and in other occasions as the median. Both are meaningful only in the context of a probability distribution, and the distributional assumptions for the input parameters are unclear.
A major concern regarding the treatment of uncertainty is exemplified in how the point estimate and uncertainty distributions are calculated for Pi (the conditional probability of infection). The approach is described on p. 579:
Regardless of the pathway, for each event a separate estimate for Pi is computed for each Q value (QL, QM, and QH). The resulting conditional probabilities are listed as: PiL, PiM, and PiH. The value PiL is associated with QL, which represents the 5th percentile of possible Q values associated with a given loss-of-containment outcome. In other words, 5% of the time that a loss of containment occurs, the amount of FMDv involved in the release will be QL or less and the probability of an infection event is PiL. Similarly, 5% of the time that a loss of containment occurs, the amount of FMDv involved in the release will be QH or higher and the probability of an infection event is PiH. The remaining 90% of the time that a loss of containment occurs, the amount of FMDv involved in the release is assumed to be QM and the probability of an infection event is PiM. As a result, the estimate for Pi is obtained as follows: Pi=0.05PiL+0.90PiM+ 0.05PiH. The stochastic variability associated with Pi is based on a binomial distribution and is computed as ![]() .
.
The committee’s understanding is that the variable Pi is an event-dependent uncertain quantity subject to at least epistemic uncertainty. Once there is an uncertainty distribution for the variable Pi, there is an associated mean value, Pi. The distribution of the variable Pi is used in the uncertainty
propagation stage to calculate uncertainty bounds on the total risk. With that understanding, the committee offers the following observations:
• The quantity calculated in the first equation is denoted as Pi. It seems that through the second equation ![]() the uSSRA has attempted to develop a distribution for Pi presumably for use in uncertainty quantification. As previously stated, the correct quantity that is used in uncertainty quantification is the actual variable Pi and not its mean value Pi.
the uSSRA has attempted to develop a distribution for Pi presumably for use in uncertainty quantification. As previously stated, the correct quantity that is used in uncertainty quantification is the actual variable Pi and not its mean value Pi.
• One implication of assumptions behind the calculation of the (mean) Pi in the first equation is that the variable Pi is roughly distributed by a three point discrete distribution with 5th and 95th percentiles at PiL and PiH respectively. Based on the above discussions, the distribution developed based on ![]() not only is a conceptually wrong distribution to use for Pi but is numerically inconsistent with the range indicated by PiL and PiH.
not only is a conceptually wrong distribution to use for Pi but is numerically inconsistent with the range indicated by PiL and PiH.
The committee further questions the basis of using a binomial-based “stochastic variability” distribution to capture aleatory or epistemic uncertainty in Pi. Risk analysis methodology dictates that the assessment of uncertainty be based on the nature of the phenomena being considered and on the available information. The committee finds it disturbing that the above approach seems to be how many of the input uncertainty distributions were calculated in the uSSRA, which results in false and in some cases large ranges of uncertainty in the input and output of risk models.
Finally, the committee has concerns about the use of the median of a skewed distribution and its effect on the risk calculations. For instance, many of the Q values have multiple orders of magnitude between the 5th, 50th, and the 95th percentiles. Where the mean falls is difficult to determine without more information. Nevertheless, skewness of one order of magnitude from the median to the mean would alter—when properly using the mean rather than the median—the risk calculations upward by an order of magnitude or more for some factors. Whether or not specific Q determinations have sufficient information to determine the median and the mean, this issue deserves additional attention and resolution. The process of weighting the low, median, and high values continues to propagate the bias introduced in the uSSRA by not considering the possible skewness.
The uSSRA repeatedly mentions that Monte Carlo sampling was used for uncertainty propagation. Monte Carlo sampling is a well-established method, and the committee finds it appropriate for the application. However, the committee could not verify whether the approach was used consistently throughout the uSSRA. In some cases, the uncertainty measures of the output of models (or submodels) appear to have been obtained by
first using the low values of the input parameters to produce the low values of the output parameters, and the same approach was used to produce medium and high input values. Such an ad hoc method may be useful in performing sensitivity analysis to see the effects of compounding extremes but is entirely inappropriate for uncertainty analysis because it produces probabilistically incorrect bounds.
Treatment of Dependencies
It is of fundamental importance in probabilistic modeling to correctly characterize probabilistic dependencies among events and model variables and to account for such dependencies in calculating probabilities of the joint occurrence of those events and parameters. The committee finds that the uSSRA ignored potential dependencies in calculating probabilities for the risk scenarios and that this likely resulted in a serious underestimation of the total risk and in incorrect ranking of risk contributors.
A basic rule of the calculus of probability for the joint occurrence of two events E1 and E2 is
P(E1E2) = P(E2|E1)*P(E1)
where P(E1) is the probability of event E1 and P(E2|E1) is the conditional probability of event E2 given event E1.
When events E2 and E1 are independent, P(E2|E1) = P(E2), and consequently
P(E1E2) = P(E2)*P(E1).
Because in many cases P(E2|E1) > P(E2), ignoring potential dependencies can result in significant underestimation of the probability of the joint occurrence of E1 and E2. The problem is compounded when more events are involved.
An example of the uSSRA ignoring potential dependencies in risk scenario calculations is in the calculation of the probabilities of biosafety level 3 agriculture (BSL-3Ag) AHR events. In this case and for all other containment areas, the engineered mitigation solutions and expected protocols are designed to provide multiple layers of containment protection and redundancy. According to the uSSRA, all NBAF AHR exhaust systems provide filtration via double high-efficiency particulate air (double-HEPA) in series, multiple failure detection points, and built-in redundancies (p. 144). The filtration and discharge of large volumes of filtered air are provided by dedicated HEPA caissons that provide efficiency (by running in parallel
in nominal conditions) and that accommodate full room exhaust capacity even when one caisson is out of service. The smaller AHRs—Type A, A2 (large), A2 (small), A3, and B—provide full 2N redundancy (complete room air exhaust volume can be accommodated by either HEPA caisson), and the larger AHRs (Types C and D) provide N + 1 redundancy (complete room air exhaust volume can be accommodated with any three of the four caissons).
The uSSRA calculates the probability of Event AA10 as follows: Given the redundancies in filters, if a filter fails (at an estimated PFail rate of 1.5 × 10–4 failures/year), the redundant pressure alarms (each modeled with a failure probability of 10–3 per demand) will initiate the room exhaust redundancy. For one parallel caisson to exhaust unfiltered room air, there would have to be two filter failures, two primary alarm failures, and a redundant alarm failure. Therefore the uSSRA states that the probability of this event is given by
![]()
Clearly, in that and other similar calculations (such as probabilities of Events AA1 through AA9), the report assumes that failures of the identical filters and identical alarms are independent events.
To illustrate the potential numerical impact of the assumption of independence, the committee applied the beta (β) factor model, which is one of several popular approaches found in the literature (U.S. NRC, 1989a,b) for treating common causes of failures to the probability of Event AA10:
![]()
In this equation the likelihood of failure of system redundancies due to common cause failures is given by βP. Using a generic value of 0.1 for β factors (U.S. NRC, 1989a,b) and the same values of failure probabilities as before, then
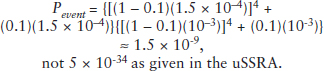
When properly calculated, that probability of 1.5 × 10–9 is 1025 times higher than the value calculated in the uSSRA. All other probabilities for Events AA1 through AA9 are also grossly underestimated in the report, and the same error exists for the other pathways.
In failing to address intrinsic and extrinsic dependencies, the uSSRA has grossly underestimated (perhaps by a factor of 1025) the risks of many scenarios for FMDv release from the NBAF that could lead to an outbreak.
INPUT DATA AND PARAMETER ESTIMATES
In several places in the uSSRA, the committee questions the input data and the resulting estimates of an event. Human error inputs are questionable, as previously discussed. Other data inputs that lack sufficient justification or rationale include the following:
1. Out-of-containment leaks. The event tree design omitted critical events that could lead to an FMD event by ignoring risk of out-of-containment leaks. These were identified by the previous National Research Council committee as a shortcoming (NRC, 2010). The uSSRA specifically states that only events from the Transshipping Facility and the laboratory will be considered. However, the location of the NBAF in a livestock-rich area necessitates consideration of the conveyance of packages from the Manhattan airport to the Transshipping Facility. Although all biological shipments to and from the NBAF must adhere to International Air Transport Association specifications, it is possible that a shipment destined for the NBAF could be inadequately packaged and result in a serious leak.
2. Power systems failure. No scenarios were indicated for power failures, either partial or complete, or for what systems and pathways would be affected and how. Presumably, there would be a correlation between systems events in such a way that a general or partial power failure would affect, at least temporarily, the efficiency of other systems and human error rates. For example, in 2005, the security system and freezers were disabled during a power loss and failure of the back-up electrical system at the CDC Division of Vector-Borne Infectious Diseases in Fort Collins, Colorado (Erickson, 2005), and in 2008, while back-up generators were out of service for upgrades, an electrical outage caused a loss of power to a containment laboratory at the CDC in Atlanta (Young, 2008).
3. Autoclave failure and incinerator failure. For both of these probability values, there were no references, and values given were termed “representative.”
4. Disinfectant efficiency. The uSSRA assumes that disinfectants will be 99.999% efficacious (when used as directed). On the bottom of p. 91 of the uSSRA, it states that a “representative” efficiency of 10–1 will be used in modeling assumptions for disinfectants, which seems reasonable given heavy organic load and dilution; but later (p. 102), it indicates that 10–5 was used, which is contradictory and confusing. The difference is a discrepancy of 10–4. No cited values were given for efficacy under these types of
laboratory conditions. This issue was cited as a shortcoming of the 2010 SSRA by the previous NRC committee.
5. Cook tank failure. No efficiency data were provided to support a reduction factor of 10–6 for the cook tank. The failure rate for both cook tanks was 10–5, but justification and data were not provided. The probability of partial failure, resulting in loss or partial loss of efficiency, was not indicated.
6. Glove failure rates and Tyvek suit reduction rates. No justification was given for the failure rate of unpunctured gloves (10–5) or for Tyvek suit reduction factor of 0.15.
7. Tissue autoclave and performance indicator failure. On p. 165 of the uSSRA, there are no references or validations for the values of 10–5 for the tissue autoclave and for the performance indicator of the tissue autoclave.
8. Estimate of FMDv MAR. Estimates for the amount of FMDv that is aerosolized consider only the amount of virus exhaled by infected animals and fail to consider virus shed in feces, saliva, nares, ruptured vesicles, etc. that is aerosolized by the room ventilation system, hosing and cleaning, and feeding and sampling procedures. The assumed material available for release (MAR) for special procedures, shipment spills, etc. was 3.46 × 104 plaque-forming units per milliliter (PFU/mL) (p. 130). For virus grown in cell culture, the figures mentioned in the uSSRA may be underestimates. Typical virus concentrations are 105–107 PFU/mL and sometimes 108 PFU/ mL for cell-adapted virus (Tam et al., 2009). The uSSRA even notes, in discussions of autoclave efficiency, that titers of virus tested were only 6.3 × 105 PFU/mL (p. 84).
CONCERNS ABOUT QUANTITATIVE ANALYSIS PRACTICES
A high-quality risk assessment consists of an integrated document that reports consistent information within and between sections. The methods and data need to have sufficient clarity for the results to be reproducible. In many instances, the committee could not verify the uSSRA results, because data and methods were unevenly or poorly presented throughout the document. The committee also struggled with interpretation of critical graphs and tables and was unable to duplicate or reconstruct important risk scenarios, given the information provided.
Use of Terminology
The uSSRA is inconsistent in its use of terminology, and it applies nonconventional graphic representations. For example, it uses the term “fault tree” when it had implemented an event tree throughout its analysis. It
initially uses the term Ploss to describe the conditional probability that a loss of containment will occur, given a specific opportunity; this interpretation is then inconsistently applied in other sections, where Ploss is used to represent the probability of a particular pathway conditional on the opportunity’s occurrence, including pathways where containment succeeds.
Inconsistencies in Figures, Tables, and Text
The uSSRA summarizes important concepts in figures and tables, and these figures and tables are intended to serve as an opportunity to graphically display technically sound and critical information. Some figures and tables are understandable, but others are difficult to interpret, and many captions and legends are unclear. Some examples follow.
Figures
The quantitative information presented in some of the figures in the uSSRA was not immediately obvious to the committee, often because the figures lacked sufficient annotative details. That is exemplified by, but not limited to, Figure 5.1.9-6 (p. 295) and Figures 5.1.10-1 through 5.1.10-6 (pp. 315–322). Furthermore, Figure 4.4.1-1 (p. 118) and Figure 4.4.1-2 (p. 120) may be confusing due to preparation or printing errors. Figures 5.1.8-6 through 5.1.8-11 also would have benefited from more explanation, as would Figures 5.1.10-1 and 5.1.10-2. Occasionally, a caption of a figure does not explain what the figure portrays; an example is Figure 8.2-1, “Frequency-Consequence Plot for All Event Trees,” on p. 607.
Another example where information is not clearly provided or misconstrued in the uSSRA is Figure 8.2-2, “Aggregate Risk by Event Tree.” The upper error bars are often 3–4 orders of magnitude above the median shown by the top of the colored bars. The uSSRA is deficient in not providing a further discussion, given the uncertainty of many model parameters and the wide range of results. The committee, although limited in the time it spent in tracking the parameters, has concerns that the emphasis on the median in this figure may lead readers to focus on risk that is orders of magnitude lower than is shown by the informative upper percentile results. Moreover, the “error” bars indicated on the graph and in Table 8.2-1 of the uSSRA are incorrectly given as the variance; the proper designation for comparing variation of the point estimates would have been the standard error of the mean.
Tables
Some tables in the uSSRA fail to clearly communicate critical information. Most notably, in Volume 1, Section 4 of the uSSRA (pp. 61–237), the base case (all controls in operation) was identified but can be confused with both the partial control failure and complete control failure pathways. The report would be more reader-friendly if the base case (no control failure) were differentiated and displayed more clearly. Many sections use incorrect or incomplete table headings. In one example, Table 7.4.1-1 of the uSSRA includes the heading “Economic Impacts Summary (Millions)” and subheadings “Producer Surplus” and “Consumer Surplus” (pp. 573–575). Those values could be interpreted as the level of producer and consumer surplus, whereas the text indicates that they are changes. The text and Table 7.3.1-9 of the uSSRA that follow immediately appear to provide conflicting information because of inaccurate table headings (p. 563).
Text
The uSSRA is often difficult to follow and verify because of inconsistencies within and between sections. The sections seem to have been composed independently, which is understandable, but the final assembly into one document failed to sufficiently merge the various parts. Referencing is not uniform throughout, and the writing style varies. The committee acknowledges the time constraints in assembling a document of this magnitude, but some lack of cross-referencing created critical holes. For example, the epidemiology section reports a detailed examination of vaccination and depopulation costs that are not incorporated into the economic analysis of the uSSRA (Section 7, pp. 541–576).
Barry, M.A. 2005. Report of Pneumonic Tularemia in Three Boston University Researchers. Boston Public Health Commission (March 28, 2005). Available online at http://www.bphc.org/programs/cib/environmentalhealth/biologicalsafety/forms%20%20documents/tularemia_report_2005.pdf (accessed April 27, 2012).
Cox, L.A., Jr. 2009. Risk Analysis of Complex and Uncertain Systems, New York: Springer.
Eckstein, M. 2009. Fort Detrick researcher may be sick from lab bacteria. Frederick News-Post, December 5, 2009. Available online at http://www.fredericknewspost.com/sections/news/display.htm?StoryID=98629 (accessed April 25, 2012).
Enserink, M., and J. Kaiser. 2004. Accidental Anthrax Shipment Spurs Debate Over Safety. Science 304(5678):1726-1727.
Erickson, J. 2005. Power Failure Hits CDC Germ Lab. Rocky Mountain News. Oct. 13. Available online at http://www.freerepublic.com/focus/f-news/1502425/posts (accessed April 27, 2012).
Kletz, T.A. 2001. An Engineer’s View of Human Error. 3rd Ed. Rugby, UK: Institution of Chemical Engineers.
Lawler, A. 2005. Boston University under fire for pathogen mishap. Science 307(5709):501.
NRC (National Research Council). 1983. Risk Assessment in the Federal Government: Managing the Process. Washington, DC: National Academy Press.
NRC. 1994. Science and Judgment in Risk Assessment. Washington, DC: National Academy Press.
NRC. 1996. Understanding Risk: Informing Decisions in a Democratic Society. P.S. Stern and H.V. Fineberg (eds.). Washington, DC: National Academy Press.
NRC. 2000. Risk Analysis and Uncertainty in Flood Damage Reduction Studies. Washington, DC: National Academy Press.
NRC. 2009. Science and Decisions: Advancing Risk Assessment. Washington, DC: The National Academies Press.
NRC. 2010. Evaluation of a Site-Specific Risk Assessment for the Department of Homeland Security’s Planned National Bio- and Agro-Defense Facility in Manhattan, Kansas. Washington, DC: The National Academies Press.
Spurgin, A.J. 2009. Human Reliability Assessment: Theory and Practice. Boca Raton, FL: CRC Press.
Tam, S., A. Clavijo, E. Englehard, and M. Thurmond. 2009. Fluorescence-based multiplex real-time RT-PCR arrays for the detection and serotype determination of foot-and-mouth disease virus. J Virol Methods 161(2):183-191.
U.S. NRC (Nuclear Regulatory Commission). 1989a. Procedures for Treating Common Cause Failures in Safety and Reliability Studies: Procedural Framework and Examples (NUREG CR-4780 V1). Available online at http://teams.epri.com/PRA/Big%20List%20of%20PRA%20Documents/NUREG%20CR-4780%20V1.pdf (accessed May 5, 2012).
U.S. NRC. 1989b. Procedures for Treating Common Cause Failures in Safety and Reliability Studies: Analytical Background and Techniques (NUREG CR-4780 V2). Available online at http://teams.epri.com/PRA/Big%20List%20of%20PRA%20Documents/NUREG%20CR-4780%20V2.pdf (accessed May 5, 2012).
U.S. NRC. 2005. Good Practices for Implementing Human Reliability Analysis (NUREG-1792). Available online at http://pbadupws.nrc.gov/docs/ML0511/ML051160213.pdf (accessed April 5, 2012).
Young, A. 2008. CDC: Offline generators caused germ lab outage. Atlanta Journal-Constitution. July 19 2008. Available online at http://www.ajc.com/ajccars/content/metro/atlanta/stories/2008/07/18/cdc_power_outage.html (accessed April 27, 2012).














