Statistical Methods for Assessing Probabilities of Extreme Events
Although it is difficult to predict individual extreme events on a decadal time-scale, there are nevertheless studies of how probabilities of extreme events have changed over the time period of the observed record as well as projections of possible future changes using climate models. To the best of our knowledge, such methods have not been used to project probabilities of extreme events over the decadal time-scale that is the specific focus of this report. We outline here some of the relevant concepts because in our view it would be fully feasible to obtain such projections.
METHODS BASED ON TIME SERIES ANALYSIS
In time series analysis, a sequence of observations (e.g., annual temperature means over a specified region) are analyzed statistically for changes in their means and variances. In most realistic settings, the observations are not statistically independent, so account must be taken of autocorrelation among consecutive observations. Standard methods for doing this have been presented in numerous texts, e.g., Brockwell and Davis (2002).
As an example, Hansen et al. (2012) provided empirical analyses of temperature means from numerous parts of the world and noted the increasing frequency of extreme events, which they defined as events that are more than three standard deviations from the 1951–1980 mean. An analysis of this nature is useful for documenting the increasing frequency of extreme events but does not lead to quantitative projections for the future.
A more statistically sophisticated approach is represented by Rahmsdorf and Coumou (2011). Treating observations as independent and Gaussian
distributed, but with changing means, they provided concrete formulas for calculating the probability that a specific threshold is exceeded over a given period of time. However, the restriction to independent observations limits the usefulness of their approach.
An alternative is to use Monte Carlo simulation. Based on any fitted time series model, such as an autoregressive moving average (ARMA) model with time-varying means, one could calculate future extreme event probabilities by simulating the time series many times and calculating the proportion of simulations for which the extreme event of interest occurs. The principal limitation of such methods lies not in the simulation itself, which is fast and accurate using modern computing techniques, but in the structure of the time series model; if this is misspecified, then the extreme value probabilities may be over- or under-estimated by orders of magnitude.
In particular, we question whether Gaussian probabilities are appropriate for extreme events. In the case of temperature series, simple plots of the data do show an approximately normal shape (Hansen et al., 2012, have several examples), but this does not preclude the possibility of some extreme events that are caused by natural variation in the weather. An example is given by Dole et al. (2011), where they dispute the assertion that the 2010 Russian heat wave was associated with anthropogenic climate change. A key point of their argument was the presence of a blocking event, which could be a natural occurrence, but one that is expected to lead to much more extreme temperatures than usual. In the presence of such phenomena, one would not expect the distributions of the most extreme events to be consistent with Gaussian probabilities. For other kinds of meteorological variables, such as precipitation and wind speed, it is not realistic to assume Gaussian probabilities at all.
METHODS BASED ON EXTREME VALUE THEORY
An alternative class of statistical methods, which do not assume Gaussian probabilities, is the class of methods based on the statistical theory of extreme values. One very readable book on this topic is by Coles (2001). According to classical extreme value theory, the distribution of maxima over a fixed time period (e.g., annual maximum temperatures) may be approximated by a family of probability distributions known as extreme value distributions. These may be summarized in the form of the Generalized Extreme Value (GEV) distribution, which is characterized by three parameters: a location parameter representing the center of the distribution, a scale parameter representing variability, and a third “shape” parameter, which is the key parameter in characterizing probabilities of very extreme events. Although in their original form such methods were developed for stationary (but not necessarily Gaussian) time series, they
are easily adapted to nonstationary time series by allowing the three GEV parameters to be time varying.
An extension of classical extreme value theory is to use threshold methods. Rather than characterize extreme events solely in terms of the distribution of annual maxima, threshold methods take account of all events beyond a given high threshold, also known as exceedances. A common probability distribution for events beyond a threshold is the Generalized Pareto distribution, which has properties very similar to those of the GEV distribution. In this case, also, one can take account of time dependence by allowing the parameters of the model to vary with time, thus creating a theoretical framework for calculating the probabilities of extreme events in the presence of a changing climate.
Kharin and Zwiers (2000) were possibly the first to use these methods to explore the effect of climate change on extremes. Recent contributions include assessing the role of anthropogenic influence on extremes of temperature (Zwiers et al., 2011) and precipitation (Min et al., 2011). Wehner et al. (2010) used the GEV distribution to compare observational and model-based calculations of precipitation extremes, showing that the agreement is highly dependent on the resolution of the climate model.
For all of these methods, the emphasis in most climate studies has been on relatively long time horizons (e.g., 40 years), but the same statistical models can be used (via simulation) to estimate probabilities over shorter time horizons, such as 10 years.
ATTRIBUTION OF INDIVIDUAL EXTREME EVENTS
As noted elsewhere in this report, our primary focus has not been on the question of attribution, that is, on whether observed climate change is due to anthropogenic factors as opposed to natural forcing or internal variability. Nevertheless, some of the analytic methods developed in that context are relevant to understanding how extreme event probabilities might change over a time span of 10 years or less.
In a paper motivated by the 2003 heat wave in Europe, Stott et al. (2004) calculated summer (June, July, August) annual temperature averages over a large area of western Europe and used climate models both with and without anthropogenic forcing to estimate the probability of an extreme event under either scenario. Their statistical methodology used a conventional detection and attribution approach to decompose the observational time series into components due to anthropogenic forcing, natural forcing, and internal variability, combined with the Generalized Pareto distribution, fitted to events beyond a high threshold, to estimate probabilities of extreme events. More recently, Pall et al. (2011) showed how to extend the methodology to much smaller temporal and spatial scales using large
numbers of climate model runs focused on the temporal/spatial scale of interest. Leaving aside the attribution question, these papers provide two specific examples of how observational and climate model data may be combined to estimate the probability of an observed extreme event under current climate conditions and, by extension, how those probabilities might change under scenarios of future climate change.
EXTREMES OF DEPENDENT EVENTS (EVENT CLUSTERS)
We are also concerned with the possibility of extreme events occurring simultaneously in different locations as a result of common meteorological features such as ENSO or Rossby waves. Statistical methods have been developed for this problem, primarily through the methods of multivariate extreme value theory. The bivariate case (where there are just two dependent events) has been particularly highly studied.
In its simplest form, the method used for bivariate analysis is first to perform an analysis of the two variables individually (either a GEV or Generalized Pareto analysis could be appropriate for this) and then to transform the distribution to unit Fréchet form [P(X<x)=e–1/x, x>0] using a probability integral transform. This transformation has the effect of exaggerating the most extreme events so that they stand out sharply on a plot. Traditional measures of dependence, such as correlation, are not readily interpretable in this context, but a number of alternative measures of dependence that are specifically adapted to extreme events have been proposed (Coles et al., 1999).
Going beyond simple characterizations of extremal dependence, there are a number of formal statistical models that have been used to calculate joint probabilities of extreme events. There has been limited practical application of these models to climate data, but we illustrate the possibilities by considering two examples related to earlier discussion.
Example 1. Herweijer and Seager (2008) argued that the persistence of drought patterns in various parts of the world may be explained in terms of sea surface temperature patterns. One of their examples (Figure 3 of their paper) demonstrated that precipitation patterns in the south-west United States are highly correlated with those of a region of South America including parts of Uruguay and Argentina. As an illustration of this, we have computed annual precipitation means corresponding to the same regions that they defined, and we show a scatterplot of the data in the left-hand panel of Figure D-1. The two variables are clearly correlated (r = 0.38; p <.0001). The correlation coefficient is lower than that found by Herweijer and Seager (r = 0.57), but this is explained by their use of a six-year moving average filter, which naturally increases the correlation. However, the feature of interest to us here is not the correlation in the middle of the
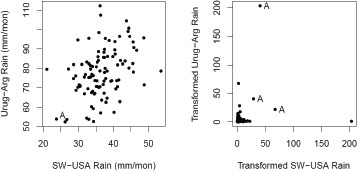
FIGURE D-1 Left: Plot of U.S. annual precipitation means over latitudes 25–35°N, longitudes 95–120°W, against Argentina annual precipitation means over latitudes 30–40°S, longitudes 50–65°W, 1901–2002. Right: Same data with empirical transformation to unit Fréchet distribution. Observations near the letter A in the left-hand plot and marked by A in the right-hand plot refer to simultaneous occurrences of extremely low precipitation in both locations. Data from gridded monthly precipitation means archived by the Climate Research Unit of the University of East Anglia (http://www.cru.uea.ac.uk/cru/data/hrg/timm/grid/CRU_TS_2_1.html [accessed November 15, 2012]).
distribution, but instead the dependence that exists in the lower tail (lower tail rather than upper tail, because our focus is drought). Therefore, the variables are transformed empirically to the unit Fréchet distribution (small values of precipitation corresponding to large values on Fréchet scale), with the results shown in the right-hand panel of Figure D-1. (Supplementary information on the methods and programs used in our analyses is available at http://sites.nationalacademies.org/DBASSE/BECS/DBASSE_073118 [accessed November 15, 2012].)
The effect of the Fréchet transformation is to highlight the most extreme observations in each variable. However, the most interesting observations are those that are not close to either of the axes, because these correspond to observations that are extreme in both variables. In particular, the triangle of observations near the letter A in the left-hand plot are transformed into the observations marked A in the right-hand plot, which are all far from either axis. This is empirical evidence that there is indeed dependence between the most extreme values in this example.
To go further, we have fitted one of the standard extremal dependence models—the logistic model, for which a detailed methodology based on
events exceeding a threshold was developed by Coles and Tawn (1991), although the model itself goes back to Gumbel and Mustafi (1967). We have used rather a low threshold (2.5 on the unit Fréchet scale) in order to illustrate the applicability of the method; ideally, we would like to use a longer series and a higher threshold. An intuitive way to understand the effect of this model is to show how the probability of a jointly extreme event in both variables is inflated compared with what it would be if the variables were independent. For example, if we consider the 10-year return level (the value of each variable that would be exceeded with a probability of 1/10 in a single year), if the variables were independent, the probability that both 10-year return values would be exceeded is (1/10)2 or 0.01. Under the logistic model fitted to this dataset, the joint probability is 0.027—an increase of 2.7 over the independent case. For more extreme events, the relative increase in joint probability compared with the independent case is larger—4.7 for the 20-year return level, and 10.8 for the 50-year return level. However, confidence intervals for these relative increases in joint probability are quite wide. For example, for the 50-year return level, a 90 percent confidence interval is (2.1, 18.8), obtained by bootstrapping.
The logistic model, although very widely used in bivariate extreme value modeling, has a couple of well-documented disadvantages: It assumes symmetry between the two variables, and it has also a property known as asymptotic dependence, which might not be satisfied in practice. Recent work by Ramos and Ledford (2009, 2011) has suggested an alternative, more complicated, model that does not make those assumptions. They called this model the ?-asymmetric logistic model, but for the present discussion we shall call it the Ramos–Ledford model. The estimation procedure used here follows Section 4.1 of Ramos and Ledford (2009). Under this model, the estimated probability ratios are very similar to those of the logistic model, although the confidence intervals are somewhat wider. A summary of all the estimates and confidence intervals is in Table D-1.
TABLE D-1 Estimates of the Increase in Probability of a Joint Extreme Event in Both Variables, Relative to the Probability Under Independence, for the United States/Uruguay–Argentina Precipitation Data
|
|
||||
| Logistic Model | Ramos-Ledford Model | |||
|
|
|
|||
| Estimate | 90% CI | Estimate | 90% CI | |
|
|
||||
| 10-year | 2.7 | (1.2, 4.2) | 2.9 | (1.2, 5.0) |
| 20-year | 4.7 | (1.4, 7.8) | 4.9 | (1.2, 9.6) |
| 50-year | 10.8 | (2.1, 18.8) | 9.9 | (1.4, 23.4) |
|
|
||||
NOTE: Shown are the point estimate and 90 percent confidence interval, under both the logistic model and the Ramos-Ledford model.
Example 2. Lau and Kim (2012) have provided evidence that the 2010 Russian heat wave and the 2010 Pakistan floods were derived from a common set of meteorological conditions, implying a physical dependence between these two very extreme events. Using the same data source as for Example 1, we have constructed summer temperature means over Russia and precipitation means over Pakistan corresponding to the spatial areas used by Lau and Kim. Figure D-2 shows a scatterplot; the left-hand plot is of the raw data, and the right-hand plot is of the data after transformation to the unit Fréchet distribution (with the largest values on the original plot corresponding to the largest value on Fréchet scale, because the right-hand tail is of interest here). Because the data source goes up only to 2002, we have approximated the 2010 values using a different data source (the National Centers for Environmental Prediction); this data point is shown in the left-hand panel of Figure D-2 but is not included in the subsequent analysis. The 2010 value is clearly an outlier for temperature but not for precipitation. It should be noted that, while the 2010 Pakistan flooding was severe, the overall rainfall over northern Pakistan was not unprecedented. This is because the heavy rain was concentrated in a very small area over the upper Indus river basin, over a few days (Dr. W.K. Lau, Chief of Atmospheres, National Aeronautics and Space Administration, 2012, personal communication).
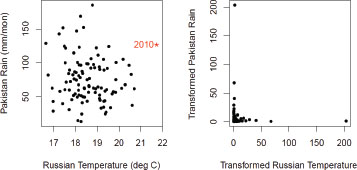
FIGURE D-2 Left: Plot of June, July, and August (JJA) Russian temperature means against Pakistan JJA precipitation means, 1901–2002. Right: Same data with empirical transformation to unit Fréchet distribution. Data from Climatic Research Unit, as in Figure D-1. The Russian data were averaged over 45–65°N, 30–60°E, while the Pakistan data were averaged over 32–35°N, 70–73°E, same as in Lau and Kim (2012).
TABLE D-2 Similar to Table D-1, but for the Russia-Pakistan Dataset
|
|
||||
| Logistic Model | Ramos-Ledford Model | |||
|
|
|
|||
| Estimate | 90% CI | Estimate | 90% CI | |
|
|
||||
| 10-year | 1.01 | (1.00, 1.01) | 0.33 | (0.04, 1.4) |
| 20-year | 1.02 | (1.00, 1.03) | 0.21 | (0.008, 1.8) |
| 50-year | 1.05 | (1.01, 1.07) | 0.17 | (0.001, 2.9) |
|
|
||||
NOTE: Shown are the point estimate and 90 percent confidence interval, under both the logistic model and the Ramos-Ledford model.
In contrast with Figure D-1, the right hand plot of Figure D-2 shows virtually no data point away from the axes, indicating that there is no evidence of dependence in the upper tail of the distribution. This is confirmed by repeating the same analyses as for Example 1, with results shown in Table D-2. For the logistic model, which is constrained to positive dependence between the two variables, the point estimates and confidence intervals (for the ratio of joint probability to the independent case) are all very close to 1. Under the Ramos-Ledford model, which does not have that constraint, the estimated probability ratios are <1 (indicating negative dependence), but the confidence intervals include 1. With either set of results, the net conclusion is that there is no evidence against the hypothesis of independence in the right hand tail of the distribution.
Conclusions. Example 1 confirms and extends the results of Herweijer and Seager (2008) by showing that the interdependence of drought conditions in the two given regions of the United States and South America extends to the tail of the distribution, although the confidence intervals for the probability ratios are still fairly wide as a result of the relatively small number of data points (102). However, Example 2 shows no evidence at all that there is any tendency for extreme high temperatures in Russia to be associated with extreme high precipitation in Pakistan; in other words, the 2010 event may have been truly an outlier without precedent in history. This should however be qualified by noting that the dataset used, consisting of monthly averages over half-degree grid cells, cannot be expected to reproduce extreme precipitation events over very short time and spatial scales, and it remains possible that an alternative data source, using finer-scale data, would produce a different conclusion.
FUTURE RESEARCH NEEDS
There is a substantial body of statistical literature on univariate and bivariate extremes and more limited research on extremes in higher dimensions. However, practical application of these methods in extreme value
statistics to the kinds of problems considered in the present report has been limited. For the univariate case, methods exist for determining trends in extreme event probabilities based on observational data and, by combining observations with climate models, for extrapolating these trends forward in time. However, we are not aware of published results that directly address the question of a 10-year time frame, which has been the main focus of the present report. There is no reason in principle that existing statistical methods could not be used to produce such estimates, and we recommend pursuing that.
For the bivariate case, the main question of interest is one of dependence: whether some underlying process creates a reliable association between the occurrence of an extreme event in one climate variable in one place and the probability of an extreme event in another variable or place. The relatively short length of most observational series limits the extent to which this question can be answered based on observational data. It would be valuable to conduct studies using longer series generated from climate models. Another question concerns the time-scale of dependence, e.g., if one extreme does indeed raise the probability of another, then for what period of time does this elevated probability of an extreme event remain valid?
More broadly, there is a need for research on clusters of extreme events. It is possible that an extreme value of one climate variable is systematically associated with extreme events in several related variables. Extensions of extreme value theory to multivariate data, to time series and spatial processes (see, e.g., Cooley et al., 2012), could in principle be used to answer such questions, but there is a need for more extensive practical development of these methods.
REFERENCES
Brockwell, P.J., and Davis, R.A. 2002. Introduction to time series and forecasting (2nd edition). New York: Springer Verlag.
Coles, S.G. 2001. An introduction to statistical modeling of extreme values. New York: Springer Verlag.
Coles, S.G., and J.A. Tawn. 1991. Modeling extreme multivariate events. Journal of the Royal Statistical Society, Series B 53:377–392.
Coles, S., J. Heffernan, and J. Tawn. 1999. Dependence measures for extreme value analysis. Extremes 2(4):339–365.
Cooley, D., J. Cisewski, R.J. Erhardt, S. Jeon, E. Mannshardt, B.O. Omolo, and Y. Sun. 2012. A survey of spatial extremes: Measuring spatial dependence and modeling spatial effects. Revstat 10:135–165.
Dole, R., M. Hoerling, J. Perlwitz, J. Eischeid, P. Pegion, T. Zhang, X.-W. Quan, T. Xu, and D. Murray. 2011. Was there a basis for anticipating the 2010 Russian heat wave? Geophysical Research Letters 38:L06702. doi:10.1029/2010GL046582.
Gumbel, E.J., and C.K. Mustafi. 1967. Some analytical properties of bivariate exponential distributions. Journal of the American Statistical Association 62:569–588.
Hansen, J., M. Sato, and R. Ruedy. 2012. Perception of climate change. Proceedings of the National Academy of Sciences 109(37):E2415–E2423. Available: http://www.pnas.org/cgi/doi/10.1073/pnas.1205276109 (accessed October 4, 2012).
Herweijer, C., and R. Seager. 2008. The global footprint of persistent extra-tropical drought in the instrumental era. International Journal of Climatology 28(13):1,761–1,774. DOI:10.1002/joc.1590. Available: http://www.ldeo.columbia.edu/res/div/ocp/pub/herweijer/Herweijer_Seager_IJC.pdf (accessed October 4, 2012).
Kharin, V.V., and F.W. Zwiers. 2000. Changes in the extremes in an ensemble of transient climate simulations with a coupled atmosphere-ocean GCM. Journal of Climate 13:3,760–3,788.
Lau, W.K.M., and K.-M. Kim. 2012. The 2010 Pakistan flood and Russian heat wave: Teleconnection of hydrometeorological extremes. Journal of Hydrometeorology 13:392–403.
Min, S.-K., X. Zhang, F.W. Zwiers, and G.C. Hegerl. 2011. Human contribution to more-intense precipitation extremes. Nature 470:378–381.
Pall, P., T. Aina, D.A. Stone, P.A. Stott, T. Nozawa, A.G.J. Hilberts, D. Lohmann, and M.R. Allen. 2011. Anthropogenic greenhouse gas contribution to flood risk in England and Wales in autumn 2000. Nature 470:302–306.
Rahmstorf, S., and D. Coumou. 2011. Increase of extreme events in a warming world. Proceedings of the National Academy of Sciences 108(44):17,905–17,909.
Ramos, A., and A. Ledford. 2009. A new class of models for bivariate joint tails. Journal of the Royal Statistical Society, Series B 71:219–241.
Ramos, A., and A. Ledford. 2011. An alternative point process framework for modeling multivariate extreme values. Communications in Statistics—Theory and Methods 40(12):2,205–2,224.
Stott, P.A., D.A. Stone, and M.R. Allen. 2004. Human contribution to the European heatwave of 2003. Nature 432:610–614.
Wehner, M.F., R.L. Smith, G. Bala, and P. Duffy. 2010. The effect of horizontal resolution on simulation of very extreme U.S. precipitation events in a global atmospheric model. Climate Dynamics 34:243–247.
Zwiers, F.W., X. Zhang, and Y. Feng, Y. 2011. Anthropogenic influence on long return period daily temperature extremes at regional scales. Journal of Climate 24:881–892.










