Page 708
Appendix C
Conservation Supply Curves for Buildings
Conservation supply curves relate energy savings achieved by implementing a given efficiency measure, to that measure's ''cost of conserved energy" (CCE).

(1)
The initial investment in an efficient technology or program is annualized by multiplying it by the "capital recovery rate" (CRR).

where d is the real discount rate and n is the number of years over which the investment is written off (i.e., amortized).
Conserved energy is liberated to be "supply" for other energy demands and therefore may be thought of as a resource and plotted on a supply curve. There are two different kinds of conservation supply curves. One shows technical potential, based on engineering and economic calculations without concern for the probability of successful implementation. The second type of curve shows achievable scenarios based on actual experience; typical utility conservation programs have captured only about 50 percent of the technical potential.
On a conservation supply curve, each measure or step (such as "efficiency improvements to residential refrigerators") is defined as follows:
|
Height = CCE (cents saved per kilowatt-hour), |
(2) |
|
Width = annual kilowatt-hours saved, |
(3) |
|
Area under the step = total annualized cost of investment. |
(4) |
Page 709
The steps are ranked in order of ascending CCE, with the cheapest options plotted first, causing the curve to be upward-sloping.
To decide whether a step is profitable (and how profitable), its CCE is compared to the "price" of the avoided kilowatt-hour. Table C.1 shows that "price" varies from different viewpoints. The average 1989 price of electricity in buildings (line 1) is 7.5 cents/kWh, whereas industry (line 2) pays only 4.7 cents/kWh. Because one cannot anticipate where a conserved kilowatt-hour will ultimately be used, the societal price is taken to be an all-sector average of 6.4 cents/kWh (line 3). One could then subtract the tax (1.1 cents/kWh), but tax would also have to be subtracted from the cost of conserved energy. However, both the competing utility and the conservation industries pay taxes, and only the difference (if any) in tax rates should be corrected for. To simplify, one will be assumed to cancel the other.
Line 4 addresses the fact that the short-run marginal cost of electricity may be lower than its average price. In some parts of the United States there is still a glut of electric generating capacity, so that the marginal cost of a kilowatt-hour is low. In such areas, the "rock bottom" price of generating a kilowatt-hour from coal and delivering it to the building meter is about 3.5 cents.
Line 5 addresses externalities, although they will not actually be used now. Today, many jurisdictions require a theoretical "environmental adder" of 1 to 3 cents/kWh; that is, they give efficiency an advantage of 1 to 3 cents/kWh over supply during resource planning. For example, New York has recently adopted a point system for evaluating competing resources in which the most environmentally disruptive resource (a new coal plant) under the most unfavorable circumstances is given. This point system provides an "environmental adder" of 1.4 cents/kWh. Desiring to be conventional and conservative in its claims for the profitability of efficiency investments,
TABLE C.1 "Prices" of Electricity at the Meter
|
Page 710
TABLE C.2 Unit Energy Consumption for a New Refrigerator
|
the Mitigation Panel has followed the standard sin of setting the adder tozero, but line 5 at least points out that if 1 to 3 cents/kWh is added to theall-sector average price, one arrives at a societal after-tax price of 7.4 to9.4cents/kWh, which brackets nicely the present 7.5-cent/kWh price to buildingsdrawn on all the supply curves in Part Three of this report.
Each of the energy prices above can be drawn as a horizontal line across a supply curve. All steps located below a selected price line are cost-effective, and the rational investor should take each of these steps, stopping where the staircase crosses the line. Of course, different price assumptions drastically alter estimates of dollar savings.
Having addressed the uncertainties in price (y-axis), the panel next addresses the uncertainties in savings (x-axis). To do this, in Table C.2 the unit energy consumption of an average new 1990 refrigerator (1000 kWh/yr) on line 1 is compared with the consumption of an optimal refrigerator (200 kWh/yr) on line 4. From an engineer's point of view, the potential savings from replacing line 1 with line 4 is obviously 800 kWh/yr. However, from the point of view of the utility forecaster or program manager, whose programs never achieve more than one-half to two-thirds of the potential savings, line 3 is more realistic and reflects a sales-weighted average of refrigerator efficiency that is below the optimum. The program manager would target an "achievable" savings of only 400 kWh/yr.
An additional complication should be noted. Many efficiency studies start with a year 2000 base case that has already been reduced by about 30 percent for anticipated efficiency gains, as a result of standards or occurring naturally (see Table C.2, line 2). They then subtract about 300 kWh/yr from their estimates of the savings. The problem with using this "estimated"
Page 711
TABLE C.3 Calculations of Conserved Electricity (using Table C.2 as an example)
|
||||||||||||||||||
base case is that estimates frequently change, thus muddying cleaner technical potential calculations.
Table C.3 shows how an energy savings of only one efficiency measure on a supply curve can be reported in four ways. In supply curve literature, each of these ways is used, often without explicit distinctions being drawn between types.
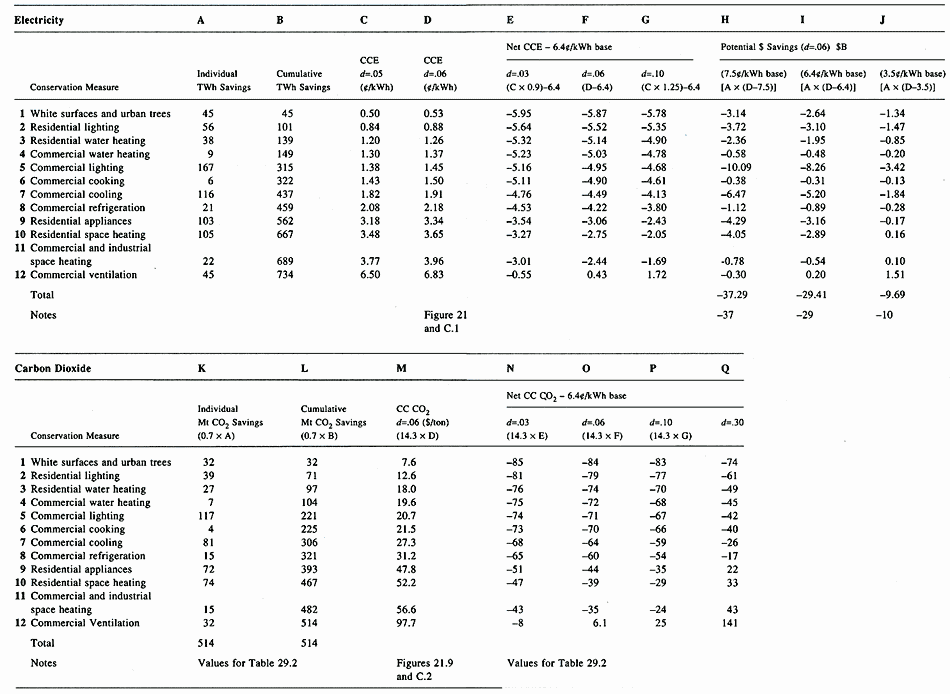
Figure C.1 displays the costs and technical potential of the 11-step EPRI conservation supply curve, with an additional first step for white surfaces/urban trees to save air conditioning. To transform these electrical savings into units of avoided CO2 as displayed in Figure C.2, two conversions must be made (see Table C.4).
First the x-axis is converted by using the CO2 produced from the mix of fuels burned by U.S. power plants—estimated to be 500 megatons (Mt) carbon (C) for 1990 electric sales of 2610 billion kilowatt-hours (BkWh) (Edmonds et al., 1989).1 To get tons of CO2, multiply by 3.666.
|
1 kWh = 0.7 g CO2, |
(5) |
|
1 TWh = 0.7 Mt CO2. |
Then the y-axis is divided by 5; so
|
1 cent/kWh = $14.3/Mt CO2. |
(5a) |
Figure C.1 has two y-axis scales: on the left, direct CCE for the investment in efficiency; on the right, net CCE, which accounts for the price of avoided electricity. By using equation (5a), net CCE can then be converted to net cost of conserved CO2 (CC CO2). The reason is that the ultimate goal is a "grand supply curve" of avoided CO2 from conserved electricity, oil, natural gas, and so forth. When these fuels are combined, it is no longer possible to track their individual prices; thus one can work only with net savings. Accordingly, Figure C.2 uses the all-sector electric price of 6.4 cents/kWh to create the net scale.
Page 712

FIGURE C.1 Cost of conserved electricity (CCE) for buildings.
Page 713

FIGURE C.2 Net cost of conserved carbon dioxide (CC CO2) for electric efficiency in the buildings sector.
Page 714
Table C.4 Worksheet for Conservation Supply Curves for Figures 21.8 and 21.9 (C.1 and C.2) and Table 29.2
Page 715
Table C.4 on page 714
Page 716
Note
1. Throughout this report, tons (t) are metric; 1 Mt = 1 megaton = 1 million tons.
Reference
Edmonds, J., W. Ashton, H. Cheng, and M. Steinberg. 1989. A Preliminary Analysis of U.S. CO2 Emissions Reduction Potential from Energy Conservation and the Substitution of Natural Gas for Coal in the Period to 2010. Report DOE/ NBB-0085. Washington, D.C.: Office of Energy Research, U.S. Department of Energy.









