Below is the uncorrected machine-read text of this chapter, intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text of each book. Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Movement of Contaminants in Groundwater: Groundwater r ~ ~ ~ ransport Advection and Dispersion 2 . INTROD UCTION MARY P. ANDERSON University of Wisconsin, Madison The relative success of attempts to model a process is a measure of how well it is understood. A first level of understanding produces a conceptual model and a higher level of understand- ing results in a quantitative model. Failure to understand dis- persion in porous media at a level necessary for constructing reliable mathematical models has impeded progress in studying contaminant transport in groundwater. However, within the past 5 years there have been many attempts at improving our understanding of the nature of dispersion in porous media. As a result there has been significant progress in refining contam- inant transport models. Some of this progress as well as back- ground information on dispersion in porous media is reviewed in this chapter. Dispersion in porous material refers to the spreading of a stream or discrete volume of contaminants as it flows through the subsurface. For example, if a spot of dye is injected into porous material through which groundwater is flowing, the spot will enlarge in size as it moves downgradient. More specifically, in a three-dimensional Cartesian coordinate system where the average groundwater velocity is parallel to the x axis, a sphere of dye moving horizontally along the x axis will undergo lon- gitudinal spreading or dispersion parallel to the x axis and transverse dispersion parallel to the y and ~ axes. Dispersion causes mixing with uncontaminated groundwa- ter, and hence dispersion is a mechanism for dilution. More- over, dispersion causes the contaminant to spread over a greater volume of aquifer than would be predicted solely from an analy- sis of groundwater velocity vectors. This spreading effect will be of particular concern when toxic or hazardous wastes are involved. Dispersion is chiefly of importance in predicting 37 transport away from point sources of contamination but is also influential in the spread of nonpoint-source contaminants, al- though of lesser importance. Contaminants introduced into the subsurface from nonpoint sources will be spread over a rela- tively large area because of the nature of the loading pattern. In this case, dispersion merely causes a relatively large zone of contaminated water to acquire some rough fringes. Disper- sion is of interest because it causes contaminants to arrive at a discharge point (e.g., a stream or a water well) prior to the arrival time calculated from the average groundwater velocity. The accelerated arrival of contaminants at a discharge point is a characteristic feature of dispersion that is due to the fact that some parts of the contaminant plume move faster than the average groundwater velocity. Dispersion is caused by both microscopic and macroscopic effects. Mechanical dispersion on a microscopic scale (Figure 2.1) is a result of deviations of velocity on a microscale from the average groundwater velocity. These velocity variations arise because water in the center of a pore space travels faster than the water near the wall and because diversion of flow paths around individual grains of porous material causes vari- ations in average velocity among different pore spaces. These two factors create mechanical dispersion on a microscopic scale. In addition, it is customary to include molecular diffusion as a component of microscopic dispersion. Molecular diffusion oc- curs as species move from higher to lower concentrations. Thus, microscopic dispersion includes the effects of mechanical dis- persion and molecular diffusion. One of the first field and laboratory investigations of dis- persion in porous media was performed by Slichter (1905~. He obtained S-shaped breakthrough curves (concentration versus time curves), which are characteristic of flow affected by dis-
38 FIGURE 2.1 Microscopic dispersion (adapted from Freeze and Cherry, 1979). persion, during field tracer tests that he performed for the purpose of estimating groundwater velocity. He correctly at- tributed the effect to dispersion: The writer formerly supposed that the gradual appearance of the elec- trolyte at the downstream well was largely due to the diffusion of the dissolved salt, but it is now evident that diffusion plays but a small part in the result. The principal cause of the phenomena [sic] is now known to be due to the fact that the central thread of water in each capillary pore of the soil moves faster than the water at the walls of the capillary pore, just as the water near the central line of a river channel usually flows faster than the water near the banks.... Owing to the repeated branching and subdivision of the capillary pores around the grains of the sand and gravel, the stream of electrolyte issuing from the well will gradually broaden as it passes downstream. The actual width of this charged water varies somewhat with the velocity of the ground water.... (Slichter, 1905, p. 23). In subsequent laboratory experiments Slichter (1905, p. 41) studied the phenomenon more carefully and concluded that "the spread of the electrolyte, as shown by these experiments, is not to be explained by the diffusion of the salt, but must be explained by the continued branching and subdivision of the capillary pores around the individual grains of the sand.,' In fact, some of the dispersion observed by Slichter in field studies was probably a result of macroscopic dispersion. On a macroscopic scale, dispersion is caused by the presence of large- scale heterogeneities within the subsurface. For example, Ski- bitzkie and Robinson (1963) demonstrated that lenses of high- permeability material within a matrix of lower permeability caused the spreading of streams of dye as water and dye moved through a tank filled with sand (see Figure 2.21. It is now generally recognized that the presence of heterogeneities in the subsurface, rather than microscopic dispersion alone, is responsible for the appreciable spreading of contaminants doc- umented in a number of field studies (e.g., Anderson, 1979~. FIGURE 2.2 Macroscopic dispersion (adapted from Skibitzkie and Robinson, 1963). MARY P. ANDERSON Pioneering theoretical work on dispersion was done by Tay- lor (1921, 1953), and serious efforts at applying modified forms of this theory to field studies involving the transport of con- taminants in groundwater have been under way since the early 1970s. However, there is still considerable uncertainty con- cerning methods for quantifying dispersion and for measuring dispersion in the field. To some extent this uncertainty has impeded progress in developing reliable contaminant-transport models. However, within the past 5 yr there has been much effort and some progress in quantifying macroscopic dispersion. These efforts are reviewed below. ADVECTIOI~-DISPERSION EQUATION Most attempts at quantifying contaminant transport have relied on a solution of some form of a well-known governing equation referred to as the advection-dispersion equation. Advection refers to the transport of contaminants at the same speed as the average linear velocity of groundwater (v), where v = Klln (2.1) and K is hydraulic conductivity, I is the head gradient, and n is effective porosity. The velocity defined by Eq. (2.1) has also been called the average pore velocity. The nomenclature used here (i.e., average linear velocity) was introduced by Freeze and Cherry (19791. Moreover, the term affection is used here in preference to the term convection because convection often carries the connotation of transport in response to temperature- induced density gradients. The advection-dispersion equation is derived by combining a mass-balance equation with an expression for the gradient of the mass flux (see Bear, 1972; Wang and Anderson, 19821. The in AVE RAG E FLOW - _ ~ A.' ..~. A I \COARSE LENS _
Contaminants in Groundwater: Transport difficulties in quantifying dispersion are related to the fact that field studies of flow through porous media are by necessity conducted at a macroscopic rather than a microscopic level. For example, Darcy's law, the fundamental equation for de- scribing flow through porous media, is a macroscopic equation. That is, K, I, and n in Eq. (2.1) are measured in some rep- resentative elementary volume (REV), and these values are assumed to represent an average of K, I, and n within the REV. Likewise, spatial averaging is routinely done when deriving the advection-dispersion equation. Fried (1975) noted that "The basis of dispersion theory is a measurement problem.... The- oretical macroscopic concentration, for instance, which appears in mathematical models, should correspond to the experimen- tal concentration; this is not simple...." The standard approach in analyzing dispersion, which is em- bodied in the advection-dispersion equation, is to use an av- erage linear velocity. A number of investigators maintain that this approach is reasonable because it will never be practical to define the velocity field in detail. The key assumption in deriving a term to represent disper- sion is that dispersion can be represented by an expression analogous to Fick's second law of diffusion: mass flux due to dispersion = ~ (D,* ~ ), (2.2) where c is concentration and D`*. is the coefficient of dispersion (the i, j indices refer to Cartesian coordinates). The coefficient of dispersion can be shown to be a second-rank tensor, where D,*. = Dij + D,`. (2.3) Then, Dij is the coefficient of mechanical dispersion and Dot is the coefficient of molecular diffusion (a scalar>. An effective diffusion coefficient is generally taken to be equal to the dif- fusion coefficient of the ion in water (D,') times a tortuosity factor. The tortuosity factor has a value less than 1 and is needed to correct for the obstructing effect of the porous medium. Effective diffusion coefficients are generally around 10-6 cm2/ see, although a range of 1O-5 to 10 7 cm2/sec is not incon- ceivable (Grisak and Pickens, 1981~. Except for systems in which groundwater velocities are very low, the coefficient of mechanical dispersion generally will be one or more orders of magnitude larger than D,'. Therefore, in many practical appli- cations the effects of molecular diffusion may be neglected (D,~ = 0~. The coefficient of mechanical dispersion is routinely taken to be the product of the magnitude of the velocity vector times a parameter known as dispersivity, which is commonly and somewhat vaguely referred to as a characteristic mixing length. The advection-dispersion equation in its most general form is written (Do*) -(cri)+ ~ Rk = dxi dXj Oxi n k= ~ at dispersion term advection sink/source chemical-reaction (2.4) term term term where c' is the concentration of solute in a source or sink fluid, and W is the volume flow rate of the sink or source fluid per unit volume of porous material. In the chemical-reaction term, Rk is the rate of production of the solute in reaction k of s 39 different reactions. The problems involved in quantifying the chemical-reaction term are discussed in Chapter 3 of this re- port. If the advection-dispersion equation is to be used to evaluate dispersion in groundwater systems, two questions must be ad- dressed: 1. Is it valid to assume that the dispersion component of Eq. (2.4) can be represented by a form of Fick's law tEq. (2.2~? 2. Can dispersivity be defined in terms of physically mea- surable parameters? IS DISPERSION A FICKIAN PROCESS ? Much ofthe theory on which the analysis of dispersion in porous material and in rivers is based stems from the pioneering work of Taylor (1921, 1953), who suggested that dispersion could be represented as a Fickian process. This assumption as applied to porous media has since been questioned by several re- searchers. Fried (1975, pp. 17-27) cites several examples of laboratory experiments in which the experimental results did not fit theoretical curves derived from solutions of the advec- tion-dispersion equation, and Dagan (1982) noted that"there is no a priori reason to believe that the diffusion type equation is valid at all" for contaminant transport through porous media. Taylor and others (e.g., Fischer, 1973) who continued the development of the theory of dispersion clearly recognized that the Fickian assumption is valid only after a certain length of time has elapsed in which the dispersion process develops. A procedure for predicting the length of this initial development period has not yet been perfected. Indeed, until recently it was not recognized that for the heterogeneous systems en- countered in the field this development process requires sub- stantial transport from the source. For example, some re- searchers believe that dispersion becomes Fickian only at distances on the order of lOs to lOOs of meters from the source in porous media (Matheron and DeMarsily, 1980; Gelhar and Axness, 1981; Dagan, 1982) and on the order of kilometers in rivers (Beltaos and Day, 19781. Furthermore, in certain hy- drogeologic settings dispersion may never become Fickian (Matheron and DeMarsily, 1980; Smith and Schwartz, 19801. After the initial development period, that is when dispersion has become Fickian, the concentration distribution and con- centration-time profiles should behave according to particular solutions of Eq. (2.41. Specifically, the solution for instanta- neous release of a contaminant from a point source predicts that concentration-distance curves will approximate a Gaussian distribution except for short times f Figure 2.3(a)~. However, concentration-time curves are typically skewed on the right except for long times or large distances from the source tFigure 2.3(b)1 The problems in applying Taylor dispersion theory to rivers are discussed in some detail by Beltaos and Day (1978~. Most concentration-time curves obtained from tracer studies in riv- ers are skewed on the right, and Gaussian curves are rare (Day and Wood, 1976~. Beltaos and Day (1978) noted that concen- tration-time curves in the Lesser Slave River deviated less from
40 SPRT I RL D I STR I BUT I ON .10 .08 .06 .04 .02 ~ .°Ot 1 2 4 6 IT= 1 ,IT= 1.5 it_ _ _ ~ ~ ,_ ~ ~ ~ 8 10 12 14 16 18 20 22 D I STRNCE {a) TEMPOROL D I STR I BUT I ON X10-9 20 . o 4. 6. 8. 10. 12. 14. ~10 / 1~.,.1.,.1.,.1.,. -b ~ TIME (b) FIGURE 2.3 (a) Concentration distribution in space; (b) concentra- tion-time curves. C/CO is a dimensionless concentration. The dimen- sions of distance and time and other variables and parameters are any consistent set of units (e.g., distance in meters, time in days, and velocity in meters/day). In this example, velocity and longitudinal dis- persivity were set equal to 1.0 and transverse dispersivities were 1/20. the Gaussian than did several mountain streams studied by Day (1915) and concluded that the Lesser Slave River is less "irregular" in that it deviates less from prismatic laboratory flumes where Gaussian curves are normally obtained relatively quickly. They also demonstrated that concentration-time curves for this river approximated Gaussian curves at a distance of about 14 km from the tracer release point. However, the growth of the variance of the concentration distribution during the non-Gaussian period did not follow a Fickian model. If dis- persion is a Fickian process, then the variance of the concen- tration distribution should increase linearly with time or dis- tance, and the longitudinal dispersion coefficient and the dispersivity will be a constant for constant velocity. However, the variance of the concentration distribution in the rivers con- sidered by Beltaos and Day (1978) increased with the square of the distance and the dispersion coefficient, and the disper- sivity also increased with distance for constant velocity. Based MARY P. ANDERSON on these analyses it appears that the initial development period of non-Fickian behavior may be long for many rivers. Similar behavior has been predicted for porous media on the basis of theoretical studies (Gelhar et al., 1979; Matheron and DeMarsily, 1980; Dagan, 1982~. Specifically, for long times or large travel distances, dispersion in some geologic settings can be accurately represented as a Fickian process. However, under certain conditions (e.g., flow parallel to bedding where lateral dispersion across bedding planes is negligible) theoretical stud- ies suggest that the Fickian limit (also known as the Taylor limit) may never be reached and dispersion may never become Fickian (Mercado, 1967; Gelhar et al., 1979; Matheron and DeMarsily, 1980~. Similarly, Smith and Schwartz (1980>, who conducted many numerical experiments of hypothetical aqui- fers, found that for most of the situations that they modeled the variance of the concentration distribution was highly ir- regular and did not approximate a Gaussian distribution within the lengths of the simulated flow paths. Field evidence to corroborate these theoretical findings for porous media is sparse. Results from a field tracer test de- scribed by Sudicky and Cherry (1979) suggested that the con- centration patterns were somewhat irregular near the source of the tracer but became approximately Gaussian farther down- gradient. An analysis of the variance of the concentration dis- tribution by Sudicky and Cherry (1979) indicated that the growth of the variance was nonlinear and the dispersivity increased with distance. Several other investigators (Molinari et al., 1977; Lee et al., 1980; Pickens and Grisak, 1981a, 1981b) also noted an increase in dispersivity with distance from the tracer source, which indicates that dispersion was not Fickian within the dis- tances in which the measurements were taken (see Figure 2.41. DEFINITION OF DISPERSIVITY Contaminant transport models usually have been applied to existing waste-disposal sites where a contaminant plume had been identified during a field monitoring program. The stan- dard modeling procedure has been to adjust values of disper- sivity until the model correctly reproduces the observed con- centration distribution. Anderson (1979), among others, noted that dispersivity values used in most applications of contami- nant transport models through 1979 were calibration (or fittings parameters. Values in the range of 3 to 200 m have been re- ported (see Anderson, 1979), but these values may not be physically meaningful. In order to obtain meaningful predic- tions of contaminant movement at existing sites and to apply advection-dispersion models to new or proposed sites, an ac- curate way of quantifying dispersivity needs to be developed. Results from theoretical studies suggest that dispersion is non-Fickian near the source of the contaminant but that dis- persion generally becomes Fickian at large times or travel dis- tances, when a constant dispersivity value is achieved. There- fore, for large times, it should be possible to use the standard form of the advection-dispersion equation fEq. (2.4~] if the dispersivity parameter in the coefficient of mechanical disper- sion can be evaluated in terms of parameters that can be mea- sured in the field.
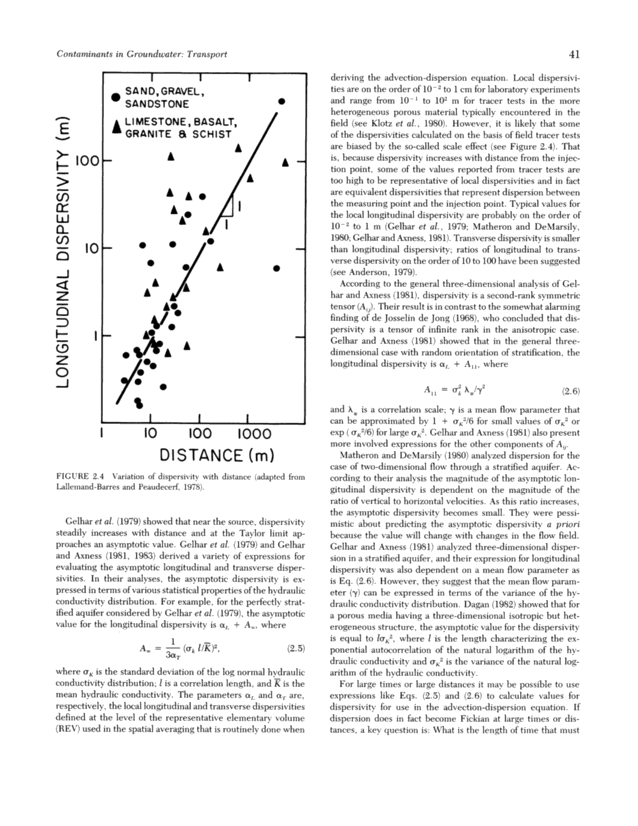
41 - 00 _ > in llJ ~ 10 J Cl Z 1 z o J Contaminants in Groundwater: Transport 1 ~ ~ SAND,GRaVEL, SaN DSTONE LIMESTONE, BaSALT, / GRANITE a SCHIST / . ~ _/ '1 ~ - 16. /11 · ~ · e/ 1-. · - _ /~, / y- - . I I I 1 10 100 1000 DISTANCE (m) FIGURE 2.4 Variation of dispersivity with distance (adapted from Lallemand-Barres and Peaudecerf, 1978). Gelhar et al. (1979) showed that near the source, dispersivity steadily increases with distance and at the Taylor limit ap- proaches an asymptotic value. Gelhar et al. (1979) and Gelhar and Axness (1981, 1983) derived a variety of expressions for evaluating the asymptotic longitudinal and transverse disper- sivities. In their analyses, the asymptotic dispersivity is ex- pressed in terms of various statistical properties of the hydraulic conductivity distribution. For example, for the perfectly strat- ified aquifer considered by Gelhar et al. (1979>, the asymptotic value for the longitudinal dispersivity is cx, + A=, where Ad =Irk I IK j2, (2. 5) 30`T where ELK iS the standard deviation of the log normal hydraulic conductivity distribution; l is a correlation length, and K is the mean hydraulic conductivity. The parameters cx, and a.,. are, respectively, the local longitudinal and transverse dispersivities defined at the level of the representative elementary volume (REV) used in the spatial averaging that is routinely done when deriving the advection-dispersion equation. Local dispersivi- ties are on the order of 10-2 to 1 cm for laboratory experiments and range from 10-i to 10- m for tracer tests in the more heterogeneous porous material typically encountered in the field (see Klotz et al., 1980~. However, it is likely that some of the dispersivities calculated on the basis of field tracer tests are biased by the so-called scale effect (see Figure 2.4~. That is, because dispersivity increases with distance from the injec- tion point, some of the values reported from tracer tests are too high to be representative of local dispersivities and in fact are equivalent dispersivities that represent dispersion between the measuring point and the injection point. Typical values for the local longitudinal dispersivity are probably on the order of 10-2 to 1 m (Gelhar et al., 1979; Matheron and DeMarsily, 1980; Gelhar and Axness, 1981~. Transverse dispersivity is smaller than longitudinal dispersivity; ratios of longitudinal to trans- verse dispersivity on the order of 10 to 100 have been suggested (see Anderson, 1979~. According to the general three-dimensional analysis of Gel- har and Axness (1981), dispersivity is a second-rank symmetric tensor (Aij). Their result is in contrast to the somewhat alarming finding of de Josselin de Jong (1968), who concluded that dis- persivity is a tensor of infinite rank in the anisotropic case. Gelhar and Axness (1981) showed that in the general three- dimensional case with random orientation of stratification, the longitudinal dispersivity is ax, + All, where Ail = ~` Alleys (2.6) and A* is a correlation scale; fly is a mean flow parameter that can be approximated by 1 + -/6 for small values of ~K- or exp ~ cr~2/6) for large ~K-. Gelhar and Axness (1981) also present more involved expressions for the other components of Aij. Matheron and DeMarsily (1980) analyzed dispersion for the case of two-dimensional flow through a stratified aquifer. Ac- cording to their analysis the magnitude of the asymptotic lon- gitudinal dispersivity is dependent on the magnitude of the ratio of vertical to horizontal velocities. As this ratio increases, the asymptotic dispersivity becomes small. They were pessi- mistic about predicting the asymptotic dispersivity a priori because the value will change with changes in the flow field. Gelhar and Axness (1981) analyzed three-dimensional disper- sion in a stratified aquifer, and their expression for longitudinal dispersivity was also dependent on a mean flow parameter as is Eq. (2.6~. However, they suggest that the mean flow param- eter (~y) can be expressed in terms of the variance of the hy- draulic conductivity distribution. Dagan (1982) showed that for a porous media having a three-dimensional isotropic but het- erogeneous structure, the asymptotic value for the dispersivity is equal to land, where l is the length characterizing the ex- ponential autocorrelation of the natural logarithm of the hy- draulic conductivity and (~,;2 is the variance of the natural log- arithm of the hydraulic conductivity. For large times or large distances it may be possible to use expressions like Eqs. (2.5) and (2.6) to calculate values for dispersivity for use in the advection-dispersion equation. If dispersion does in fact become Fickian at large times or dis- tances, a key question is: What is the length of time that must
42 elapse before the advection-dispersion equation is applicable and expressions such as Eqs. (2.5) and (2.6) are valid? Matheron and DeMarsily (1980) found that for a typical set of aquifer parameters, the Taylor limit would be reached after 140 days and 600 m of travel. Gelhar and Axness (1981) and Smith and Schwartz (1980) also suggested that the Taylor limit will not be reached until the contaminant has traveled on the order of tens or hundreds of meters from the source. According to a theoretical analysis by Dagan (1982), dispersion should be Fick- ian at a distance from the source approximately equal to SOL, where L is the integral scale of the natural logarithm of the hydraulic conductivity distribution. For two-dimensional flow fields, L may be hundreds to thousands of meters, but for three- dimensional analyses L is expected to be on the order of meters. While there has been much progress in defining dispersivity at large distances from the source, no clear consensus has emerged regarding the appropriate way to quantify dispersion near the source before the Taylor limit is reached. Gelhar et al. (1979) derived a revised form of the advection-dispersion equation, which includes several additional terms of higher order that are required to represent dispersion close to the source. They then analyzed the development of the dispersion process for early times and showed that the definition of the time-de- pendent dispersivity requires evaluation of an integral for which the small time limit for the case of one-dimensional flow through a stratified aquifer is a~ + A*, where A* = (~KIKj2x (2.7) and "x is the distance traveled (x = fit). The value of dispersivity given in Eq. (2.7) is equal to the value of dispersivity implied in an analysis of dispersion by Mercado (1967), where and then (rx= (V~K/K)t (2.8) A* = (d(J2/dt)/2v, (2.9) from which Eq. (2. 7) follows. Here, OK is the standard deviation of the hydraulic conductivity distribution and of is the standard deviation of the concentration distribution. According to Eq. (2.7), dispersivity should increase linearly with distance traveled. According to Mercado's result tEq. (2.8~], the standard deviation of the concentration distribution increases linearly with time or distance. If dispersion is Fickian, the standard deviation increases with the square root of the distance traveled. Thus, the dispersed zone grows more rapidly before the Taylor limit is reached. Pickens and Grisak (1981a) suggest using Eq. (2.7) or some similar equation in the standard advection-dispersion equation to describe the early portion of the dispersion process. Math- eron and DeMarsily (1980) consider a similar approach based on the concept of an equivalent dispersivity: (X' j = crxi2/2vt, (2. 10) where crX,2 is the variance of the concentration distribution at time i. Eq. (2.10) follows directly from Eq. (2.9) for a discrete time interval. The values of longitudinal dispersivity (~ ~) are defined such that Ax represents dispersion for the time from MARY P. ANDERSON t = 0 to t = t1 and CXL1 represents dispersion for the time from t = t1 to t = to, for example. However, Matheron and DeMarsily (1980) caution that because the use of Eq. (2.10) implies that dispersivity is really a constant and because the advection- dispersion equation is actually inapplicable for early times, the use of an equivalent dispersivity is not completely satisfactory. They conclude that, "A better mathematical formulation of the transport process in porous and fractured media, valid for all time, seems necessary." More specifically, according to Gill- ham and Cherry (1982~: "The present challenge is to develop a physically based transport model that incorporates spatially and/or temporally variable dispersion parameters that can be determined in a practical manner and with an acceptable de- gree of certainty." SUMMARY AND DISCUSSION The discussions of dispersion in the preceding sections focused on applications to continuous porous media; dispersion in frac- tured porous media will be considered in a later section of this chapter. The state of the art for quantifying dispersion in con- tinuous porous media is summarized below. Results from several studies suggest that dispersion is non- Fickian near the source of the contaminant and therefore the standard form of the advection-dispersion equation does not apply. A modified form could be derived for analyzing non- Fickian transport for small times. Gelhar et al. (1979) presented such an equation for one-dimensional flow in a perfectly strat- ified aquifer. However, they caution that the approach that they used to derive the equation requires certain restrictions that may not be valid at small times. Other approaches that rely on the standard form of the advection-dispersion equation call for use of time-dependent dispersivities (Gill and Sankar- asubramanian, 1972; Matheron and DeMarsily, 1980; Pickens and Grisak, 1981b). The standard approach in analyzing dispersion involves the use of an average linear velocity Em. (2.1~] and the use of a dispersion term tEqs. (2.2) and (2.3~] to represent deviations of velocity from the average. The rationale for this approach is based on the premise that a dispersion term is necessary be- cause it will never be practical to define the velocity field in detail. Moreover, according to Dagan (1982) it is inappropriate to assume that local dispersion does not influence advection. Hence, several investigators (Gelhar et al., 1979; Gelhar and Axness 1981, Dagan, 1982) maintain that the key to a rational application of the advection-dispersion equation is to define the dispersivity in terms of various statistical properties of hy- draulic conductivity. Another approach, used by Schwartz (1977) and Smith and Schwartz (1980, 1981a, 1981b) among others, is based on at- tempts to represent the velocity field in detail by defining the hydraulic conductivity in a stochastic manner and in this way to simulate the effects of macroscopic dispersion directly. Smith and Schwartz (1980) concluded that for their simulations local dispersion was negligible because most dispersion observed in their modeled systems occurred at a macroscopic scale. There- fore, in subsequent studies (Smith and Schwartz, 1981a, 1981b)
Contaminants in Groundwater: Transport they used an advective model to simulate contaminant trans- port in a number of hypothetical systems characterized by dif- ferent arrangements and shapes of heterogeneities. Results of their numerical experiments demonstrated that the solution of the contaminant transport model is quite sensitive to the struc- ture of the heterogeneities within the porous material. Con- sequently, detailed information on the arrangement and shapes of the heterogeneities, knowledge of the values of hydraulic conductivity for the various units, and information on head gradients (or direct measurements of velocities) are essential for accurate prediction. Although they demonstrated that it is theoretically possible to predict contaminant transport given sufficient hydrogeologic data, they remained pessimistic re- garding the practical limitations of obtaining the detailed in- formation needed (Smith and Schwartz, 1981b). In addition they concluded that ". . . large uncertainties can be associated with transport predictions in heterogeneous media. These un- certainties must be dealt with in order to develop confidence in the application of mathematical models of site-specific prob- lems. Unfortunately, the variety of possible sources of uncer- tainty and the difficulty in controlling their size suggest that progress will be slow." Similarly, Dagan (1982) concluded that "longitudinal dispersion can be represented asymptotically by a Fickian equation, with dispersivity much larger than pore- scale dispersivity," but given the uncertainties involved in de- fining the hydrogeologic system a stochastic approach is nec- essary and "the traditional approach of predicting solute con- centrations by solving deterministic partial differential equations is highly questionable in the case of heterogeneous formations." The conclusion drawn from these studies is that although there has been considerable progress within the past 5 years in understanding the nature of macroscopic dispersion in po- rous media, to date, a credible, practical, and reliable model for analyzing contaminant transport near the source has not been identified. However, theoretical studies by several re- searchers suggest that for large times (or large travel distances) the dispersion component of the advection-dispersion equation can be represented by an expression analogous to Fick's second law of diffusion Em. (2.2~], and therefore the classical advec- tion-dispersion equation will accurately simulate contaminant transport in porous media, provided that dispersivity can be quantified in a meaningful way. Gelhar et al. (1979), Gelhar and Axness (1981), and Dagan (1982) present formulas for defining dispersivity at large times in terms of statistical parameters. However, several investi- gators suggest that the length of time that must elapse before the advection-dispersion equation is applicable may be appre- ciable. Specifically, the travel distance of the contaminant must be on the order of 10s or 100s of meters from the source before the advection-dispersion equation is valid. Simulations of con- taminant transport by Pickens and Grisak (1981b) suggest that the scale dependence of dispersivity at early times may have little effect on results for large times or travel distances. Hence, the use of an asymptotic dispersivity may be adequate for these conditions provided that sufficient geologic data are available to characterize the statistical parameters of the hydraulic con- ductivity distribution (the variance and the correlation scales), as well as the orientation of the geologic units. More attention 43 is needed in characterizing geologic systems in terms of these statistical parameters (e.g., see Smith, 1981; Newman, 1982~. Moreover, field data needed to corroborate the theory itself are lacking. There is also a need for carefully designed field tracer tests to determine whether the theory is generally ap- plicable and to serve as a basis for estimating the length of time before the Taylor limit is reached and Eq. (2.4) is valid. Data from such tracer tests would allow an assessment of the reli- ability of recently derived expressions for dispersivity. DISPERSION IN FRACTURED ROCK The discussion in previous sections focused on dispersion in continuous porous media. Application of dispersion analysis to contaminant transport in fractured rock is in its infancy, yet it is of considerable importance. Certain types of fractured rock, such as shale, granite, and salt, are likely candidates for re- positories of high-level nuclear waste, and clay, which is also susceptible to fracturing, is currently used as a disposal medium for municipal, industrial, and low-level radioactive wastes. Recent work on flow through fractured rock has emphasized laboratory investigations and development and testing of ~nath- ematical models, most of which are based on the concept of a dual porosity medium (e.g., Grisak and Pickens, 1980; Ner- etnieks, 1980) as shown in Figure 2.5. In a few cases, models have been used in conjunction with results frown laboratory experiments (Grisak et al., 1980; Tang et al., 1981; Neretnieks et al., 1982) and field data (Bibby, 1981~. These results support the following conclusions: 1. Diffusion of contaminants from fractures to the rock ma- trix can serve as a significant retardation mechanism (see Grisak and Pickens, 1980; Neretnieks, 1980; Abelin et al., 1982; Bir- gersson and Neretnieks, 1982~. This phenomenon is illustrated schematically in Figure 2.5. 2. Dispersion in the fracture can significantly accelerate the arrival of contaminants at a discharge point when velocities in the fractures are relatively low. Experimental results suggest that velocity in fractures can be represented using the so-called cubic law (see Witherspoon _ _ FRACTURE FLOW I DIFFo5 POROU S ROCK MATRIX _ FIGURE 2.5 Schematic diagram representing flow through fractures and diffusion of contaminants from fractures into the rock matrix of a dual porosity medium.
44 et al., 1980), which is a form of Darcy's law in which the equivalent hydraulic conductivity of the fracture (Kf) is Kf = (pg/12~)b-, (2.11) where b is the aperture of the fracture, g is the constant of acceleration of gravity, p is the density of water, and ~ is the dynamic viscosity. The cubic law for the volumetric flow rate through the fracture is Q= (pg/121l)1Wb3, (~2.12) where I is the head gradient across the length of the fracture segment and W is the width of the fracture segment. A number of models (Grisak and Pickens, 1980; Tang et al., 1981; Neretnieks et al., 1982) consider dispersion in the frac- ture. Tang et al. (1981) derived an analytical solution of the advection-dispersion equation for one-dimensional contami- nant transport with longitudinal dispersion in the fracture, cou- pled to a solution of a model representing diffusion of solute frown the fracture into the rock matrix. Grisak and Pickens (1980) solved a similar problem using a finite-element model. Both concluded that while longitudinal dispersion in the frac- ture can be important, little is known regarding the magnitude of dispersivity in fractures except that it is a function of the roughness of the fracture. Experiments under way (see With- erspoon, 1981) may help in quantifying fracture roughness, which is a first step toward quantifying dispersivity in fractures. Analysis of flow of water through networks of fractures has been attempted (Bibby, 1981; Neuzil and Tracy, 1981; Sudicky and Frind, 1982~. But much additional work is needed to test and to modify these types of models. A major impediment to testing of fracture flow models is the difficulty of obtaining field data that describe the hydrogeologic characteristics of fractured rock. CONCLUSIONS 1. There has been significant progress in quantifying dis- persion in porous material since 1978. 2. The consensus is that dispersion in porous material is non- Fickian near the source of the contaminant, and therefore for small times or small distances from the source, the standard form of the advection-dispersion equation does not apply. 3. There is no consensus regarding the best way to quantify dispersion near the source of the contaminant. Some research- ers prefer to aim at attempting to describe the velocity field in sufficient detail so that contaminant transport can be sim- ulated by advection alone. Others prefer to rely on refining the advection-dispersion equation to handle non-Fickian dis- persion. 4. Theoretical studies suggest that for many hydrogeologic settings, dispersion should become Fickian for large times or large distances (on the order of 10s to 100s of meters). In this case it is possible to express the dispersion parameter known as dispersivity in terms of statistical properties of the hydraulic conductivity distribution. 5. Carefully designed field tracer tests are needed to eval- MARY P. ANDERSON uate the applicability of the theory for large times and to refine the theory for small tines. 6. Detailed hydrogeologic information is needed to predict dispersion for both small and large times. 7. The concept of a dual porosity media (Figure 2.5) is cur- rently used for modeling groundwater and contaminant flow through fractured rock. However, the difficulties involved in characterizing the geometry of a fractured-rock system in the field complicates the testing of the theory. As a result, none of the models developed to simulate dispersion and diffusion of contaminants in fractured rock have been verified by field experiment. REFERENCES Abelin, H., J. Gidlund, and I. Neretnieks (1982). Migration in a single fracture, in Scientific Basis for Nuclear Waste Management V, W. Lutze, ea., North-Holland, New York, pp. 529-538. Anderson, M. P. (1979). Using models to simulate the movement of contaminants through groundwater flow systems, Crit. Rev. Envi- ron. Controls 9(2), 97-156. Bear, J. (1972). Dyna?nics of Fluids in Porous Media, Elsevier, New York, 764 pp. Beltaos, S., and T. J. Day (1978). A field study of longitudinal disper- sion, Can. J. Civil Eng. 5, 572-585. Bibby, R. (1981). Mass transport in dual porosity media, Water Resour. Res. 17, 1075-1081. Birgersson, L., and I. Neretnieks (1982). Diffusion in the matrix of granitic rock. Field test in the Stripa nine, in Scientific Basis for Nuclear Waste Mana',e?nent V, W. Lutze, ea., North-Holland, New York, pp. 519-528. Dagan, G. (1982). Stochastic~nodelingofgrou~dwaterby unconditional and conditional probabilities, 2. The solute transport, WaterResour. Res. 18, 835-848. Day, T. J. (1975). Longitudinal dispersion in natural channels, Water Resour. Res. 11, 909-918. Day, T. J., and I. R. Wood (1976). Similarity of the mean motion of fluid particles dispersing in a natural channel, Water Resour. Res. 12, 655-666. de Josselin de Jong, G. (1968). The tensor character of the dispersions coefficient in anisotropic porous media, ill Fundamentals of the Transport Phenomenon in Porous Material, Elsevier, Amsterdam, pp. 259-267. Fischer, H. B. (1973). Longitudinal dispersion and turbulent mixing in open-channel flow, Ann. Rev. Fluid Mech. 5, 59-78. Freeze, R. A., and J. A. Cherry (1979). Groundwater, Prentice-Hall, Englewood Cliffs, N.J., 604 pp. Fried, J. J. (1975). Groundwater Pollution, Elsevier, Amsterdam, 330 PP Gelhar, L. W., and C. L. Axness (1981). Stochastic Analysis of Macro- Dispersion in Three-Dimensionally Heterogeneous Aquifers, Geo- physical Research Center, Hydrology Research Program, Rep. No. H8, New Mexico Inst. of Mining and Technology, Socorro, New Mexico, 140 pp. Gelhar, L. W., and C. L. Axness (1983). Three-dimensional stochastic analysis of macro-dispersion in aquifers, Water Resour. Res. l9. Gelhar, L. W., A. L. Gutjahr, and R. L. Naff(1979). Stochastic analysis of macrodispersion in a stratified aquifer, Water Resour. Res. 15, 1387-1397. Gill, W. N., and R. Sankarasubramanian (1972). Dispersion of non-
Contaminants in Groundwater: Transport uniformly distributed time-variable continuous sources in time-de- pendent flow, Proc. R. Soc. A327, 191-208. Gillham, R. W., and J. A. Cherry (1982). Contaminant transport in saturated unconsolidated geologic deposits, in Recent Trends in Hy- drogeolog,y, T. N. Narasimhan, ea., Geol. Soc. Am. Spec. Pap. 189, pp. 31-62. Grisak, G. E., and J. F. Pickens (1980). Solute transport through fractured media: 1. The effect of matrix diffusion, Water Resour. Res. 16, 719-730. Grisak, G. E., and J. F. Pickens (1981). An analytical solution for solute transport through fractured media with matrix diffusion, J. Hydrol. 52, 47-57. Grisak, G. E., J. F. Pickens, and J. A. Cherry (1980). Solute transport through fractured media: 2. Column study of fractured till, Water Resour. Res. 16, 731-739. Klotz, D., K. P. Seller, H. Moser, and F. Neumaier (1980). Disper- sivity and velocity relationships from lab and field experiments, J. Hydrol . 45, 169-184. Lallemand-Barres and Peaudecerf (1978). Recherche des relations entre la valeur de la dispersivite macroscopique d'un milieu aquifere ses autres caracteristiques et les conditions de mesure, Bulletin du BRGM, 2e Serie, Section III, n. 4. Lee, D. R., J. A. Cherry, and J. F. Pickens (1980). Groundwater transport of a salt tracer through a sandy lakebed, Limnol . Oceanogr. 25, 45-61. Matheron, G., and G. DeMarsily (1980). Is transport in porous media always diffusive? Water Resour. Res. 16, 901-917. Mercado, A. (1967). The spreading pattern of injected water in a perme- ability stratified aquifer, in Proc. Int. Assoc. Sci. Hydrol. Symp., Haifa, Publ. No. 72, pp. 23-26. Molinari, J. P., B. G. Plaudecerf, and M. Launay (1977). Essais con- joints en laboratoire et sur le terrain en vue d'une approche sin~plifie de la prevision des propogations des substances miscibles den les aquifers reels, in Proc. of the Symp. on Hydrodynamic Diffusion and Dispersion in Porous Media, Int. Assoc. for Hydraulic Research, Pavia, Italy, pp. 89-102. Neretnieks, I. (1980). Diffusion in the rock matrix: An important factor in radionuclide retardation'?J. Geophys. Res. 85, 4319-4397. Neretnieks, I., T. Eriksen, and P. Tahtnen (1982). Tracer movement in a single fissure in granitic rock: Some experimental results and their interpretation, Water Resour. Res. 18, 849-858. Neuman, S. P. (1982) Statistical characterization of aquifer hetero- geneities: An overview, in Recent Trends in Hydrogeology, T. N. Narasimhan, ea., Geol. Soc. Am. Spec. Pap. 189, pp. 81-102. 45 Neuzil, C. E., and J. V. Tracy (1981). Flow through fractures, Water Resour. Res. 17, 191-199. Pickens, J. F., and G. E. Grisak (1981a). Scale-dependent dispersion in a stratified aquifer, Water Resour. Res. 17, 1191-1212. Pickens, J. F., and G. E. Grisak (1981b). Modeling of scale-dependent dispersion in hydrogeologic systems, Water Resour. Res. 17, 1701- 1711. Schwartz, F. W. (1977). Macroscopic dispersion in porous media: The controlling factors, Water Resour. Res. 13, 743-752. SkibitzLie, H. E., and G. M. Robinson (1963). Dispersion in ground- water flowing through heterogeneous materials, U.S. Geol. Survey Prof. Pap. 386-B, 5 pp. Slichter, C. S. (1905). Field measurements of the rate of underground water, U.S . Geol . Surv . Water Su p ply Pa p . 140, pp. 9-85. Smith, L. (1981). Spatial variability of flow parameters in a stratified sand, J. Int. Assoc. Math. Geol. 13, 1-21. Smith, L., and F. W. Schwartz (1980). Mass transport, 1, A stochastic analysis of macroscopic dispersion, Water Resour. Res. 16, 303-313. Smith, L., and F. W. Schwartz (1981a). Mass transport, 2, Analysis of uncertainty in prediction, Water Resour. Res. 17, 351-369. Smith, L., and F. W. Schwartz (1981b). Mass transport, 3, Role of hydraulic conductivity data in prediction, Water Resour. Res., 17, 1463-1479. Sudicky, E. A., and J. A. Cherry (1979). Field observations of tracer dispersion under natural flow conditions in an unconfined sandy aquifer, Water Pollut. Res. Canada 14, 1-17. Sudicky, E. A., and E. O. Frind (1982). Contaminant transport in fractured porous media: Analytical solutions for a system of parallel fractures, Water Resour. Res. 18, 1634-1642. Tang, D. H., E. O. Frind, and E. A. Sudicky (1981). Contaminant transport in fractured porous media: Analytical solution for a single fracture, Water Resour. Res. 17, 555-564. Taylor, G. I. (1921). Diffusion by continuous move~nents, Math. Soc. Ser. 2, 20, 196-212. Taylor, G. I. (1953). The dispersion of matter in solvent flowing slowly through a tube, Proc. R. Soc. London, Ser. A 219, 189-203. Wang, H. F., and M. P. Anderson (1982). Introduction to Ground- water Modeling,: Finite Difference and Finite Element Methods, W. H. Freeman, San Francisco, Calif., 237 pp. Witherspoon, P. A. (1981). Effect of size on fluid movement in rock fractures, Geophys. Res. Lett. 8, 659-661. Witherspoon, P. A., J. S. Y. Wang, K. Iwai, and J. E. Gale (1980). Validity of cubic law for fluid flow in a deformable rock fracture, Water Resour. Res. 16, 1016-1024.