4 THE TECHNOLOGY BASE
A leading economic competitiveness issue pertaining to the mathematical sciences is technology transfer. The record is uneven, with technology transfer flourishing on some occasions and languishing on others. Technology transfer is an area of professional activity largely lacking in visibility, and for this reason, some of its successes are documented in this report. Also included is the history of one prominent failure of technology transfer.
Economic competitiveness, among other factors, requires a broad technology base from which to derive new methods of production, quantitative information (data) and analysis, and quality control methodology.
In this chapter, numerous examples show how the mathematical sciences have contributed to that technology base and helped to make possible the manufacture of new or improved goods, or the offering of a new or better service. In doing so, it is emphasized that the distinction between direct and indirect support, and between short- and long-range connections, cannot be drawn in a clear fashion. Consider the example of weather forecasts, clearly and naturally a part of the technology infrastructure. The forecasts depend on computer simulations and mathematical modeling, and thus derive in part from the mathematical sciences. Forecasts of wind currents and jet stream location are used in flight planning for commercial aircraft, and are as important a contributor to fuel economy as is the design of advanced wing foils (cited in §3.2). Forecasts are used by fishing fleets in deciding whether to extend their nets. Knowledge of the probability of precipitation is used by farmers in harvest planning. Prediction of severe weather patterns is used in planning to minimize losses from high
winds and from flooding due to high tides. Forecasts of temperature and humidity are used to minimize the economic cost and maximize the benefits of complying with environmental air quality regulations. From this example of weather forecasts, it becomes evident that there is not a sharp distinction between the technology base and direct applications.
The following discussion of the technology base does not focus narrowly on modeling and simulation. There is a fundamental significance to the mathematical way of thinking. Briefly, mathematics provides methods for organizing and structuring knowledge so that, when applied to technology, it allows scientists and engineers to produce systematic, reproducible, and transmittable knowledge. Analysis, design, modeling, simulation, and implementation then become possible as efficient, well-structured activities.
Similarly, the distinction between short- and long-term applications cannot be drawn unambiguously. In a series of cases, one finds the same subjects moving back and forth between theory and applications, and becoming richer with each transition, as the following examples illustrate:
-
Nearly integrable systems of differential equations and fiber optics;
-
Geometrical optics and the asymptotic solutions of differential equations;
-
Fourier analysis, group symmetries, and special functions;
-
Covariant differential geometry and elastic deformations; and
-
Fourier analysis on finite groups and the fast-Fourier-transform (FFT) algorithm.
The ability of the mathematical sciences to deliver short-term results with any degree of consistency depends crucially on support for their long-term development. Conversely, the more fundamental areas of the mathematical sciences are continually invigorated by interaction with applications. It is an almost universal experience that once an application succeeds, further progress depends on the development of new, and often fundamental, theories. This report endorses the principle that short-term applications and fundamental theories are virtually
inseparable. It does not attempt to make narrow distinctions within the technology base. Rather, the point of this chapter is to analyze areas of the mathematical sciences and to document their close connection to economic competitiveness, thereby establishing the importance of the technology base.
4.1 Technology Transfer
The technology transfer of importance to this report is the transfer of ideas, methods, and results from the mathematical sciences community to engineering and industrial groups for the purpose of improving the technical operation and economic competitiveness of U.S. industry. In view of the continuous web of ideas and values that make up the intellectual life of our nation, it seems most practical to promote the transfer of technology broadly to all segments of the economy, even though the concerns of this report relate most directly to support of the manufacturing sector.
Technology transfer is not usually recognized as an area of mathematics, and for this reason it is generally lacking in visibility. It is included here because of its importance to economic competitiveness and because mathematical scientists have extensive activities in this area. There are serious problems with technology transfer, problems that are by no means confined to the mathematical sciences alone. Unfortunately, the time required for transfer is long, commonly spanning one or more decades.
Historically, the transfer of technology from the statistical design of experiments to quality improvement in manufacturing has followed a tortuous path. In the 1920s, the British statistician and geneticist R. A. Fisher led the development of statistical theory and methods for experimentation. Fisher was stimulated largely by agricultural applications, and his ideas were rapidly adopted there and became extraordinarily successful.
Statisticians realized that these ideas also applied in industrial contexts. Statistical methods for experimental design were used by Tippett to improve productivity in the cotton and woolen industries in England, starting in the mid-1920s. Transfer of these ideas to manufacturing took place subsequently, but on a limited scale, largely confined to the chemical and pharmaceutical industries. Also, during the 1920s,
the foundations of statistical quality control were established at AT&T, in an effort spearheaded by Shewhart. In the 1950s, Deming, strongly influenced by Shewhart and the power of statistical quality control, brought the message of quality to Japan. His influence on Japanese manufacturing, and notably on the Japanese engineer Taguchi, was profound and was an important reason for the success Japan has had in industrial competition. Taguchi's contribution was to adapt the experimental design methodology, developed earlier in the United Kingdom and the United States, to problems of reducing variability in the performance of products, thereby increasing their quality. Concerns about America's competitiveness in the 1980s has led to the transfer, through Taguchi, of the methods of statistically planned experiments into the design and manufacture of products in a number of American industries. The basic ideas have been available since the 1920s, as have the initial successful applications. The time scale for the transfer of this technology is not yet completed, but it already spans 70 years.
Some of the common causes of delay in the transfer of technology may include the following:
-
Need to refine technology. Is the user or the originator to work out the details? Turnkey technology is the easiest to transfer.
-
Evaluation. Which of the many new ideas would actually be beneficial to users?
-
Communication. Ideas expressed in the technical language of the user are more readily adopted.
-
Learning. Time is required to learn a new technology and to adapt it to a new situation.
-
Collective decision making. Often a consensus is required among users before a technology is tried or adopted. This reduces risk but does introduce delay.
-
Responsibility. For the transfer of technology to succeed, the responsibility for the transfer is normally assumed by the groups or individuals who discovered the technology. Usually an active effort is required to accomplish the transfer.
-
Necessity. Failure of old technology rather than the superiority of the new is often the critical step for adoption of new technology. Demonstration of failure may be time-consuming.
-
Not invented here. Users have a variety of real and imagined
-
reasons for resisting ideas from the outside.
-
Multiple layers. Often there is a chain of groups through which the ideas and technology must pass, including multiple academic disciplines, industrial service groups, and various industrial management groups.
It is also appropriate to examine the structural contexts in which technology transfer has occurred. Technology transfer between the mathematical sciences and industry is extensive, and is documented in the rest of this report. To be successful, technology transfer must carry information in both directions. The mathematical scientist learns as much as he or she teaches. Usually technology transfer works best when both parties share a common goal. It depends fundamentally on the establishment of working relationships and trust. A few systematic examples of technology transfer are noted below.
The Seminar on Industrial Problems3 is held weekly at the Institute for Mathematics and its Applications (IMA) at the University of Minnesota. The speakers are from industry. The audience consists of IMA visitors and postdoctorates as well as graduate students and selected undergraduates from the University of Minnesota. The speakers present problems of a mathematical nature arising in their R&D activities. Subsequent to the presentation, there is usually a follow-up, and typically, within a period of several weeks to several months, many of the problems are partially or completely solved. Some of these problems lead to new and exciting mathematics. Here are a few examples considered by the Seminar on Industrial Problems.
-
Binary optics. Microelectronic techniques can be used to manufacture surfaces of optical substrates with stepped profile. Such optical devices can be used as lenses, avionic displays, and so on. The design
-
of the surface can be produced as software, but this step requires solving the Maxwell equations in the entire space with the surface to be designed as an interface between two optical media. Since the stepped profile does have corners, serious problems arise in trying to adapt traditional codes. An IMA team has found a new approach to solving the Maxwell equations, which leads to a very promising numerical method.
-
Electrophotography. Electrophotography is a process in which pictures are made of light and electricity. The common example is photocopying documents. One of the steps involved is creating a visual image from the electric image. Here the toner (ink) accumulates near the electric image of the dark spots of the document. The boundary of the toner's region is a "free boundary." The electric potential satisfies one partial differential equation outside the toner and another partial differential equation inside the toner. The potential is continuous with its first derivative across the free boundary, and its normal derivative vanishes on the free boundary. The mathematical problem represents an entirely new kind of free-boundary problem. An IMA team has shown that for some range of parameters, the problem has a unique solution and for another range of parameters, it has an infinite number of solutions. There are still many open questions regarding this problem. However, already at this stage certain important constants have been computed that may help the designer to improve the image of the photocopy.
-
Growth of crystals in solution. A large number of crystals lie in a solution within a photographic film. To achieve the best size distribution for a specific function of the film, one has to study the evolution of the crystals in time. This problem can be viewed as a dynamical system that approximates a conservation law with nonlinear nonlocal terms. The problem was considered by people at the IMA. Their analysis discovered the asymptotic size of the crystal grains; it also explained in what sense the dynamical system is a good approximation to the conservation law. So far only the case of crystals that are cube-like bodies has been considered. The next step will be to study a more realistic model where the crystals are cylinder-like.
Industrial mathematics conferences have been organized annually at the Rensselaer Polytechnic Institute. These conferences have an unusual format. The speaker, an industrial participant, presents a prob-
lem, and the conference participants, who are selected or self-selected for their interest in such events, attempt to figure out how to model the problem. They try to determine the basic variables and equations, the essential features of the problem, and the acceptable approximations. They discuss how to describe the problem through mathematical formulas. If this stage is successful, then discussion might continue on methods for the solution of the model equations. Several such problems will be considered in the course of the conference. A similar industrial clinic is organized at the Claremont Colleges; an instructor and a team of students spend typically one year working on a specific problem.
The Center for Quality and Productivity Improvement is an interdisciplinary center located at the University of Wisconsin. The staff of the center is evenly divided between statisticians and engineers. The center supports a large range of technology transfer activities, from conferences to guest lectures to consulting, and conducts a research program in quality and productivity improvement on which the technology transfer is based.
A consortium of industrial sponsors has been organized by the Institute for Oil Recovery and the Department of Mathematics at the University of Wyoming. The scientific program of the institute follows the research interests of its faculty in petroleum reservoir modeling and numerical simulation. Computational ideas and algorithms developed within the research programs of the institute are available to the industrial sponsors, including dynamically adaptive grids and characteristic methods of differencing.
At Duke University, a program was initiated in the modeling of granular flow. This problem had not been attempted previously by the mathematical community and looked rather disordered at the outset. Design engineers for grain silos had encountered various problems important to the design process that they did not understand. After some effort, it was discovered that the mathematical problems were quite interesting and were illustrative of the class of problems that change type from elliptic to hyperbolic. The change of type was associated with the formation of shear bands in the granular material, which was just the problem that had puzzled the design engineers.
A number of large industrial laboratories maintain in-house mathematics groups. These groups have similar technology transfer problems
and usually succeed by taking the responsibility upon themselves for the transfer of technology. Similarly, the national laboratories have developed algorithmic, computational, and software capabilities and technology, which have been transferred to U.S. industries. A very effective method of technology transfer is to educate students who will later find employment in industrial or national laboratories. Meetings of the mathematical sciences professional societies provide a forum for technology transfer, and in some cases attract engineers and mathematical scientists from industry.
Because of the central role of computing, software is an increasingly important mechanism for technology transfer. Well-designed software allows immediate application of new advanced algorithms and techniques in disparate fields. A common route for technology transfer involves implementation of a high-level computational algorithm in a computer code. Mathematica and Nastran provide examples. Argonne National Laboratory has pioneered with the establishment of a software library, Netlib, for the electronic exchange of software. It is known for its excellent quality, and a number of its offerings, such as LINPAK, are widely used.
Often, research groups in industry pick up on academic research codes and incorporate the ideas into their in-house production and simulation codes. The scientific computing language C++ began around 1980 as a research project at AT&T Bell Laboratories. A portable translator was distributed within the Bell Laboratories and to universities for a nominal cost, thereby encouraging experimentation by users and feedback to the designer. Today the estimated number of C++ users is 100,000. Similarly the statistical language S has grown from a research tool to a commercial product that is today the de facto standard among statisticians for both research and student training. Within AT&T, S has served as the medium for moving statistical methods from the research area into development, marketing, and manufacturing.
These examples show that it is possible for technology transfer to succeed. There are a variety of ways to transfer technology. Technology users can be canvassed, to determine their needs and interests; the problem can be selected in an area where users are known to be interested; and novel areas can be found, for which users and their prob-
lem must be identified. To ensure that technology transfer occurs, the mathematical scientists, engineers, manufacturers, and business leaders must accept the task to be accomplished and plan for the result.
4.2 Simulation and Computational Modeling
Mathematical and computational analysis is an essential tool in product design and system development. Oil exploration, automotive engine design, wing and fuselage design for aircraft, circuitry components for computers, finance, robotic control, the design of novel composite materials, and construction design provide only a few examples of this fact.
• Simulating the behavior and performance of equipment or systems on a computer enables the determination of the design parameters that will significantly improve performance, or even determine whether the "thing" will work. Simulation provides such information more quickly and cheaply than the classic construction and experimentation still commonplace in many industries.
One example is the megabit memory chip that was designed and tested in nine months at AT&T Bell Laboratories. Similar design speeds have been obtained by other manufacturers. Another example is the positioning of the engine nacelle on the Boeing 737 to increase lift significantly. The manufacturer of the 737 was able to obtain substantial improvements in performance while reducing the number of wind tunnel tests from more than 60 to about 10. Highly efficient methods of computational fluid dynamics lead to airplane geometries with optimal flight characteristics and lower fuel consumption (see Figure 4.1).
Complex processes are characterized by their many interacting sub-processes. They must be efficiently designed, built, modified, and maintained with sufficient flexibility to be viable in new, flexible manufacturing environments. These goals cannot be achieved without detailed analysis and simulation of the entire system to indicate sensitivities of process output to changes in interacting component subsystems.
Although engineering and scientific computing have become central tools of engineers and scientists over the past decades, there is a potential among U.S. industries for greatly increased utilization of

FIGURE 4.1 ONERA M6 wing attached to a cylindrical fuselage. This composite overlapping grid was generated using the program CMPGRD. These composite overlapping grids are used in modeling fluid flow around objects with complex geometrical structure. Some of their advantages over other methods are their smoothness and their ability to provide high resolution where it is needed, both of which are important for accurate modeling. The composite grid shown in this figure is used for modeling air flow around a wing. Reprinted, by permisssion, from [16]. Copyright ©1990 by Academic Press, Inc.
computers to reduce laboratory experimentation and testing (e.g., in pharmacology, design of materials, process design, and analysis of the total aerodynamical system of an aircraft).
The importance of scientific and engineering computing has been confirmed by numerous U.S. government-sponsored studies. The Critical Technologies Plan (see Appendix A.4) mandated by Congress identified 20 critical technologies, including the following five:
-
Simulation and modeling
-
Software producibility
-
Parallel computer architectures
-
Computational fluid dynamics
-
Semiconductor devices and microelectronic circuits
Simulation and modeling have a critical role among the remaining fifteen identified technologies. Simulation has been at the heart of progress in technology and science for many reasons, including the following:
-
Necessity. The cutting-edge problems that challenge engineers and scientists typically cannot be solved by other methods.
-
Availability. Raw computing power is enormous and increasing rapidly.
-
Feasibility. During the past several decades, there have been substantial advances in the mathematical methods and algorithmic development that unite science and technology with the computer.
Examples
Simulation technology has enriched the knowledge base and benefited the intuitive problem-solving approach used by practicing engineers. Absent such simulation, the available tools would be rather inadequate for the type of problems that are being addressed today. Aerospace and petroleum examples were mentioned earlier.
-
In the microelectronics industries, the design of new semiconductor devices and the circuitry employing them can be carried out only through simulation.
-
In the pharmaceutical industry, computational methods for understanding the structure of molecules (see Figure 4.2) are becoming the standard tools. The design of new drugs is widely expected to benefit greatly from a systematic use of simulation. Quantum chemistry depends heavily on large-scale high-performance computing, including simulation. Computational modeling in quantum chemistry will provide the scientific basis for new advances in pharmacology.
-
In the textile industry, the computerized layout of apparel cutting patterns to minimize waste is a problem in integer programming and optimization.
Resources
Only a decade ago, computational power was measured in megaflops (millions of floating point arithmetic operations per second). It is now measured in gigaflops (billions of floating point arithmetic operations per second) and will evolve to the multiteraflop range as powerful parallel computers come on line in the years ahead. Advances in graphics enable the user to comprehend pictorially massive amounts of data and results. Wideband networks are making supercomputing widely available to engineers and scientists at geographically remote locations. At the same time, powerful workstations provide desktop computational capability formerly available only on mainframes at a limited number of central locations.
Of equal importance to the raw computing power are advances being made in mathematical sciences, including the development of algorithms for parallel processing. In the past decade, knowledge of the behavior of the equations governing such vital areas as fluid dynamics and transport phenomena has increased dramatically. New algorithms are significantly improving the stability, accuracy, and speed of solutions of such equations.
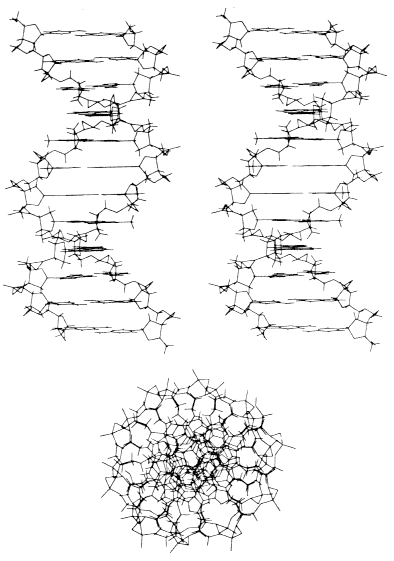
FIGURE 4.2 Computer simulation of a portion of a DNA strand, showing the three-dimensional helical form. The computation is based on the principle of minimization of an effective free energy. Computer simulation is an increasingly important method for determining the shape and structure of biological molecules and will be an increasingly powerful tool in biotechnology. Reprinted, by permission, from [13], Figure 12. Copyright ©1988 by John Wiley & Sons, Inc.
Requirements
Effective simulation depends on modeling, algorithms, and analytic understanding, as well as validation against reality. Analytic understanding is the subject of §§4.3 through 4.6. Modeling involves setting up mathematical equations whose solutions describe the behavior of the process to be modeled. The solutions must incorporate enough of the underlying science to ensure that results will be meaningful. The parameters in the equations must be observable or deducible from measurements and simple enough so their behavior can be understood. Finally, efficient and effective numerical methods for solving the equations must be developed and tested in each case.
Modeling is more than mathematical and numerical analysis—it must of necessity be an interdisciplinary effort requiring the cooperation of engineers and scientists who understand the problems and mathematicians who understand the computational and mathematical modeling process.
As technology advances and there is increased understanding, the mathematical model must be improved to represent more accurately the physical phenomena, with increases in complexity. For example, the so-called drift-diffusion equations for modeling the behavior of semiconductor devices have been very useful. However, as technology advances to the regime of submicron devices, those equations may cease to be accurate. Revision of the model to incorporate more details of the transport of electrons through a version of the Boltzmann equation or by Monte Carlo simulation is progressing. Radically new algorithms are needed at all levels to use high-performance parallel computers efficiently as well as to deal with problems of ever increasing complexity. Three-dimensional problems are orders of magnitude more complicated than two-dimensional ones. Simulation of a whole airplane is orders of magnitude more complicated than simulation of the wings. Understanding the structure and interactions of large organic molecules requires computational capability orders of magnitude larger than that required for simple molecules. System complexity will continue to increase as the underlying equations describing them incorporate more of the underlying science.
New numerical methods inherently suitable for parallel computing are needed to accommodate increasing computational demands. Such
methods will need to accommodate ''kernel computations,'' such as the solutions of systems of linear equations, the Fourier transform, and the eigenvalue and eigenvector calculations, in a structurally parallel way.
Input and output constitute another important area in which algorithmic advances are needed. The time it takes to input the geometry of the problem and generate the mesh on which many solution approaches depend is measured in weeks, whereas the time to perform the computing is measured in hours or minutes. To achieve large-scale simulation, such bottlenecks must be overcome. New methods for describing the geometry of the problem must be found. Better automatic methods to generate acceptable meshes for efficient and accurate numerical integration are urgently needed. The output of the results is equally important. Graphic representation of the results of the computations is mandatory if engineers and scientists are to make sense of them. This area of research is in its infancy, but the results are encouraging and give rise to realistic expectations that current obstacles will be overcome.
Large computer models are costly to run. The need to obtain information concerning the many parameters of the model requires efficient selection of parameter settings (inputs). This problem can be phrased as one of statistical experimental planning.
4.3 Statistical Quality Improvement
The methods and concepts of quality control and statistical design of experiments began in the 1920s. (See §4.1 for a brief history.)
Quality control began as a way to monitor or test output and thus to discard or repair defects. Statistical design of experiments in industrial contexts started as a way to identify causes of defects. The two areas have since been merged in many of their aspects. They have been transformed into a system for the building of quality into the design of products, the control of manufacturing processes to assure quality, and the installation of simple statistical tools at all stages of production to permit early detection and diagnosis of problems.
This change of emphasis was stressed by Deming in his now famous 14 points for creating quality products. Improvement is achieved by a careful study of processes and by finding and removing root causes for defects. Quality improvement is not a one-step process. It is an
ongoing, incremental process. Statistical methods of experimental design are used in a trouble-shooting mode. They are not restricted to a postmanufacture testing phase, but are used by engineers, foremen, and workers on the factory floor. Those closest to the problems are directly involved in their solution.
Quality improvement results in reduced wastage, loss, and scrap and, in contrast to traditional quality control measures, is generally a cost-reducing measure. These methods are not tied to unique cultural differences between national work forces. For example, a U.S. television manufacturer was acquired by Japanese owners. The facility had a product failure rate of 146 percent, meaning that most television sets required repair, and some required multiple repairs, before manufacture was complete. After introduction of quality improvement methods, the failure rate was reduced to 2 percent, with an increase in product quality and a decrease in manufacturing costs.
Statistical methods, to be used by factory workers, must be simple and robust. The methods are not a complex set of deductive rules, but rather are a simple set of tools, to be applied experimentally to diagnose problems. Technology transfer is here a central concern. Moreover, development of appropriate statistical tools for this context is a research question currently engaging U.S. statisticians. Statistical methods for design of experiments, such as factorial designs, blocking, and randomization, are well established in agriculture but less widely used in manufacturing. The selection of significant variables from among the less important ones, the reduction in the effective dimension of large or high dimensional data sets, and response surface methods are useful in data analysis. The value of these methods is greatly enhanced when developed into convenient and robust computer software, and supported by good graphical representations.
Quality improvement in manufacturing is not the end of the story. Quality is carried upstream to the design of products and the design of the manufacturing process. Quality by design, as this is called, requires collaboration among statisticians and engineers working with design, manufacturing, and quality. An example of an issue that arises in quality by design is the reduction of the variability of certain attributes of the product, as a function of the corresponding variability of the components. The manufacturing process provides an enormous wealth of
information about itself, which is normally not used in a serious way. Automated control provides a method for the use of this information in a self-learning or machine intelligence mode. Design variables for control of a chemical process (for example, temperature and pressure) might be specified initially through the solution of some model equation, which approximates the true manufacturing process. The role of automated control is to observe these control variables and ensure that they attain their desired values. However, one could also monitor the output for some measure of manufacturing quality and force the control variables to search in a small neighborhood of their specified design values for the optimum values, which give the best output.
Today, simulation models are prevalent and increasingly used to provide the data needed to achieve quality by design. Use of computer models in engineering design requires determination of many design parameters, often interacting in complicated ways. Statistical methods of experimental design; fitting of response surfaces in high dimensions, often with limited data; handling of large data sets; and statistical methods of data reduction are examples of the ideas and tools coming from statistics that will aid the design by simulation process, just as they have traditionally aided the experimental design process. What can be done for the design of products can also be transferred further "upstream" to the design of the manufacturing process.
Quality improvement is not the unique province of statistics. All the areas of the technology base (for example, simulation, modeling, and theory in engineering design) contribute to manufacturing quality.
4.4 Differential Equations
Differential equations are widely used in the modeling of natural phenomena. They are the basis of every one of the physical sciences and of the associated technology. Thus it is no surprise that they play a central role in the technology base required for economic competitiveness.
Asymptotics
Early in this century, boundary layer theory was developed as a powerful tool to attack nonlinear flow problems in a realistic way.
Asymptotic methods and singular perturbation theory provide insights into many critical phenomena in chemistry and physics, from shock waves to phase diagrams. Asymptotic theories depend on a small (or large) parameter and the possibly singular behavior that can result from small changes in a system. Usually, problems with this character are hard to handle, numerically, and special insight can be derived from analytic treatment. Stiff differential equations are one of the most successful theories of asymptotics. The equations have a very high technological significance in many areas, such as stability of chemical reactors, electrical and mechanical systems, and the design of semiconductors. Numerical algorithms, mathematical theory, and excellent software packages have been developed. Engineering-based CAD/CAM packages and computer codes depend on numerical algorithms based on the theory of stiff ordinary differential equations. Technology transfer has occurred rapidly in this area. Large systems of equations and parallel algorithms are still to be explored.
The geometric theory of diffraction is an approximation to the wave and Schrödinger equations. It has widespread application throughout physics and engineering and has been extended to apply to very general equations. Wavelets are a promising idea for the representation of solutions of differential equations. Fast potential algorithms give rapid solutions to important but special equations and are likely to become very important.
Nonlinear Phenomena
Most problems of interest and importance are nonlinear. Traveling wave pulses in fiber optics depend on nonlinearities in their governing equation to preserve their wave form. The equations come from a special class (integrable or nearly integrable equations). The theory of these equations depends on fairly esoteric mathematics, including analysis, algebra, and topology. A major breakthrough has been achieved in recent years in the development of this theory. Related equations arise in the description of water waves and other applications.
Nonlinear conservation laws are the basic equations of classical physics. They describe the interaction of nonlinear waves in a number of contexts with wide application to technology, including fluid dynamics, elasticity, oil reservoir flow, chemically reactive flows, and
phase transitions. The theory of free boundary problems describes a quite similar set of phenomena, but with more emphasis on the internal structure of the nonlinear waves, which often occur in highly localized and very thin fronts. New phenomena have recently been discovered that call into question accepted ideas and lead to the modification of widely used equations. Ideas from modern differential geometry have provided a very useful reformulation of the equations of elasticity, whereas topological concepts have been instrumental in understanding the bifurcations, or changes in structure of the solutions, as parameters are varied. These developments have considerable potential for application to technology and to science.
Inverse problems have wide application in technology; they arise in the image processing of CAT scan data (see Figures 4.3 a and b), in seismology, and in nondestructive testing. It is an area to which mathematicians have contributed extensively. Similarly, image processing and pattern recognition ideas often draw from methods in differential equations.
Stochastic Phenomena
Heterogeneous, chaotic, and stochastic solutions of differential equations are among the major challenges of this subject, as well as areas of active progress. The applications of such solutions are widespread. Consider first the case of composite materials, in which the variability is deliberate and is inserted on a controlled basis. Composites form the basis for high-technology design in aircraft, automobiles, machine tools, and many other areas. A common problem is to predict the strength and material properties of a complex material, with multiple layers, holes, or constituents mixed in a coarse-grained fashion. It is also necessary to design the material, i.e., the fine-grained layering, holes, and so on, to achieve optimal material properties, such as the strength-to-weight ratio (see Figure 4.4).
More commonly, the variability is not controlled but is imposed from the outside or arises spontaneously, from instabilities in the equations. Turbulence and multiphase mixing are examples. The technological examples are widespread and include the determination of drag or flow separation over an aircraft wing, the mixing of fuel and air in a carburetor, the breakup of a jet into droplets and spray, and the
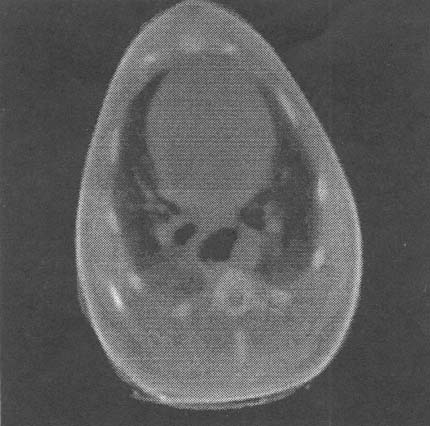
FIGURE 4.3a Improved image reconstruction methods (see Figure 4.3b) provide higher-contrast resolution of interfaces, in contrast to the resolution obtained with standard methods (Figure 4.3a). This improvement is based on new mathematical ideas and algorithms, which transform the unknown density function by a pseudodifferential operator and render the inverse problem local in terms of the tomographic data. The figures are reconstructions of the chest of a dog. The economic impact of this enhancement has been estimated at $100 million for coronary artery studies alone. Reprinted, by permission, from [14]. Copyright ©1991 by the Society for Industrial and Applied Mathematics.
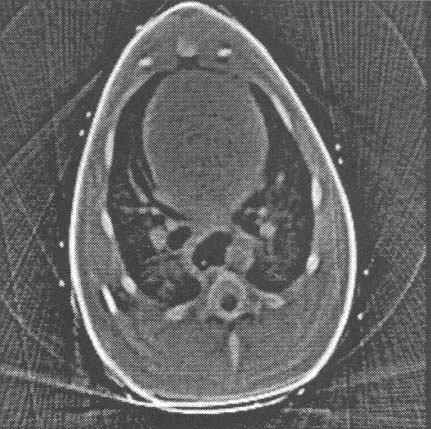
FIGURE 4.3b Improved image reconstruction methods for same image as in Figure 4.3a. Reprinted, by permission, from [14]. Copyright ©1991 by the Society for Industrial and Applied Mathematics.
mixing of the flame front in the turbulent flow in an engine cylinder. These problems are studied with a mixture of computational and statistical methods. Averaging is used to derive new equations in which the stochastic aspects have been removed and replaced by mean or effective quantities. Careful numerical and statistical studies provide a test of the validity of these averaging procedures. Interfaces between two fluids, when unstable, give rise to stochastic mixing phenomena. Frequently, this phenomenon has important economic implications, as in the solidification of alloys, where nonuniform mixing, or fingers, may degrade strength, or in oil recovery, where fingering results in poor recovery. Similar issues arise in many other technological contexts, such as the relation of material strength to microscopic descriptions involving lattice defects, voids, and microfractures and in the derivation of flow equations through porous media. To date, substantial progress has been made in the understanding of viscous flow through porous media, a necessary precondition for meaningful attempts at secondary and tertiary oil recovery. Also related are the propagation of waves in random media and localization theory, important for condensed matter physics. Mathematical scientists have been involved in the successful solution of problems in all of these areas.
Chaos theory has shown that simple-looking systems may have very complicated solutions, which appear to be stochastic in nature and may change in an irregular fashion from periodic or quasi-periodic behavior to more complex chaotic behavior in time.
Control Theory
For control theory, passive description of the solution is insufficient. Control theory has asymptotic, nonlinear, and stochastic aspects, as in the examples given above. The goal of the theory is to change (i.e., control or optimize) the solution, for example, by changing the equations or parts of the data that specify the solution. This is a common engineering problem: opening and closing valves and controlling speed or varying temperature to ensure that a process operates correctly. Control theory is thus basic to all automated manufacturing processes. Chemical plants often contain hundreds of control devices. Recently, advanced algorithms such as state estimators and multivariate controllers have been adopted. High volume and precision result

FIGURE 4.4 Visualization of plastic flow used for injection molding. The wedge-shaped glyph has a direction and length that indicate flow velocity. The velocity is confined to the horizontal plane but depends on height as well as position in the plane, which accounts for the vertical structure of the glyph. Stationary regions are indicated by a cylindrical glyph, and regions devoid of plastic have no glyph associated with them. Temperature and pressure are indicated by color shading, not shown here. Dynamics is indicated by animation. The top panel on the left shows the three basic glyphs (wedge, cylinder, and the absence of a glyph). The other three panels show single frames taken from the animation. These simulations were run on the CRAY XMP/48 supercomputer at the National Center for Supercomputing Applications at the University of Illinois at Champaign-Urbana. Reprinted, by permission, from [15]. Copyright ©1988 by the Society for Computer Simulation.
from automated hot strip mills in the steel industry. The control systems often use multilevel, multivariate adaptive control. The use of control theory and microprocessors in automobiles will increase greatly in the coming years. As a currently existing example, antilock brakes are based on feedback control. Automated control may allow operation in a regime that human control could not attain, as in the fly-by-wire control of advanced aircraft.
4.5 Optimization, Discrete, and Combinatorial Mathematics
Many scientific and engineering problems can be posed in terms of optimization, namely seeking the optimal value of some objective function by varying certain parameters. The definitions of the objective function and parameters depend on the problem. For example, the cost of a design can be minimized by an optimal selection of materials; the yield from a portfolio can be maximized by varying one's stock holdings. In most real problems, meaningful parameter values are restricted by constraints that arise from properties of the system or process to be optimized. For instance, physical laws or financial/ political considerations may need to be satisfied for the solution to be feasible.
Optimization problems can be categorized in several different ways, depending on the nature of the parameters, the special forms of the objective and/or constraint functions, problem size, connections among the variables, the level and quality of information, the desired accuracy, the computing resources available, and so on. The most efficient solution methods are specialized to exploit characteristics of specific problems.
Serious use of optimization to solve practical problems began during and after World War II and was made possible by the rapid development of computer technology. A measure of the enormous progress in optimization algorithms since that time is that algorithmic improvements in many areas have matched or even exceeded gains in computing power. For example, quasi-Newton methods, developed in the 1960s, require only first-derivative information but, close to the solution, converge very rapidly, whereas the only method previously available could display arbitrarily slow convergence or fail to converge even on simple problems.
Discrete optimization is a significant new aspect of optimization
that has been opened up by the advent of modern computers. Its problems involve choosing the best outcome from a huge collection of possibilities, such as the tour of service sites, which minimizes the distance traveled. These problems are extremely difficult to solve, because there is no global analysis or local measure, such as a gradient, to guide the convergence toward an optimal solution. Optimization problems arise in many practical situations, such as motion planning for a robotic machine tool.
Sequential Quadratic Programming Methods
Enormous progress has been made within the past 15 years in the development of algorithms for solving optimization problems that include nonlinear constraints. A great step forward has been the development of sequential quadratic programming (SQP) methods, which solve a sequence of simplified subproblems containing linearizations of the nonlinear constraints. SQP methods have been remarkably successful in solving problems that were considered intractable in the 1970s. Their success in solving well-known test problems led to the creation of reliable implementations in general-purpose software. The success of these codes then led to the development of SQP methods specialized for particular problems.
For example, in the 1980s the Electric Power Research Institute (EPRI) commissioned a project to apply state-of-the-art optimization methods to solve the important and troublesome optimal power flow (OPF) problem. The OPF problem has many forms, all of which involve minimizing a nonlinear function (say, the cost of maintaining and operating an electrical network), subject to nonlinear constraints representing the power flow equations as well as physical limitations on the system. The ''folklore'' prior to the 1980s was that OPF problems were "bumpy," i.e., had numerous local optima, and hence it was believed that problems of realistic size were extremely difficult, if not impossible, to solve. The "happy ending" is that these difficulties were shown to arise from inadequate numerical optimization methods rather than being inherent to the OPF problem. In fact, when a general-purpose SQP method was applied, the solutions were found to be well behaved and could be computed efficiently and reliably.
Based on this initial success, General Electric and other companies
that produce power network management systems now market software packages that apply specialized SQP methods to the OPF problem. Because large power systems are enormously expensive to operate and contain many fixed costs that cannot be lowered, any improvement in efficiency has a significant financial effect. For example, one power company reduced the power loss in its system by 3 percent per year, leading to an estimated annual savings of $2.5 million.
The scenario just described for the OPF problem illustrates a frequent pattern in the successful application of mathematical sciences: once a previously intractable problem has been solved, expectations rise accordingly.
Real-world optimization problems almost never arise in isolation, to be solved once and then to disappear. Rather, success with one problem leads its formulators to seek to solve larger and more complicated problems in the same vein or in closely related areas. In the case of the OPF, power engineers now want to solve ever-larger problems, to carry out operational planning under various contingencies, and to reoptimize the network in real time when changes in the system occur, such as weather-related damage to the power system.
Linear Programming
An area of great excitement in optimization since 1984 has been the development of interior methods to solve very large linear programming (LP) problems. Linear programming is a fundamental building block for most branches of optimization. It has a broad range of applications, for example, oil refinery planning, airline crew scheduling, and telephone routing. For nearly 40 years, the only practical method for solving these problems was the simplex method, which has been very successful for moderate-sized problems, but is incapable of handling very large problems.
Interior methods rely on more general nonlinear transformations and work efficiently on some large structured linear programs with which the simplex method has difficulty. Using interior methods, AT&T has been able to solve planning and routing problems that were previously unsolvable because of size—for example, long-range facility planning in the Pacific basin.
The development of interior methods has led to remarkable ad-
vances in the simplex algorithm. New implementations are competitive with interior-based methods on many problems, and either method can prove to be superior. This is an example of how results in one area of mathematics can encourage development in other areas. The net result is that large, important problems can now be solved.
Discrete Optimization
Applications of discrete optimization are revolutionizing the way products are manufactured, ordered, stored, and delivered. With proper mathematical scheduling techniques, one has prompt fulfillment of orders, with striking economic consequences. Until a few years ago, almost all shoes sold in this country were manufactured abroad. This is no longer the case, thanks to efficient computerized techniques for restocking inventories in a rapid and competitive way. These inventory methods have shifted the competitive balance in favor of domestic industry.
Efficient scheduling and routing of expensive human resources and equipment are allowing the private and public sectors to do more with less. With combinatorial optimization techniques, New York City reworked sanitation crew schedules to save $25 million a year with better service and more convenient work schedules. U.S. airlines need fewer planes and personnel to cover the same number of weekly flights and are better able to respond to weather disruptions through the use of advanced combinatorial algorithms for scheduling. The American Airlines computer-based reservation and scheduling scheme and the algorithms on which it is based are credited in the press as being a significant contributor to that carrier's competitive success. American Airlines, in cooperation with IBM, designed a mixed integer crew scheduling model at a scale that would have been unsolvable three years ago.
IBM's European manufacturing plants all have groups or access to groups that have been users of IBM's mathematical programming products for years. An example of the type of problem solved is the "implosion" problem providing a list of parts needed at various times in order to meet a production schedule. Availability of parts from various vendors may be part of the problem. Another type of problem, solved at GM for example, is a production allocation-distribution problem with allowances for changeovers, overtime, and layoffs at plants. At
one plant they reported that the use of this model saved more than $1 per car, which amounted to a considerable level of savings.
For the Weyerhaeuser Company, one of the largest forest products companies in the world, profit levels depend considerably on how trees are cut up into logs and how the resulting logs are allocated to different markets. These decisions about how to use raw materials are made by workers in the field, operating at high speed. The revenue Weyerhaeuser derives from any particular log depends on many factors: length, diameter, curvature, and knot and quality characteristics.
A decision simulator was developed to implement dynamic programming-based improvements in Weyerhaeuser's raw materials returns. The simulator provides the user with a way to cut and allocate tree stems, receive immediate feedback on the economic consequences of the decisions, and see for comparison the dynamic programming decisions and their economic consequences. Workers on site in forests and at mills quickly became comfortable with the system. Using the simulator, they continually improve their own decision-making capabilities. Operational benefits of the system have exceeded $100 million in increased profits.
Combinatorial optimization is a central methodology in theoretical computer science and in most large software systems. Although other countries equal or lead the United States in many aspects of computer memory and processor design, the United States still has a large lead in software and the underlying theory. In the last year, some Japanese computer firms established research centers in theoretical computer science in the United States, staffed by Americans.
Algebraic Methods
A major feature of twentieth-century technology has been the development and exploitation of new communications media. Mathematical laws governing the capacity of systems to transmit, store, and process information are the subject of information theory. Redundant signaling is necessary for reliable transmission, and coding theory is concerned with constructive methods of introducing redundancy—for example, the addition of a parity check to a binary word to detect a single bit error. Error-detecting and error-correcting codes are an integral and essential part not only of the modern telecommunications
industry, but also of every industry in which information is stored, retrieved, and transmitted. A scratched compact disc continues to "play true" because of an error-correcting code, which occurs similarly for disc drives, magnetic tapes, and all forms of stored and communicated data. The use of symbolic dynamics has allowed more efficient storage of data on discs, with perhaps a 5 percent improvement in a product with a $10 million annual market. The demand for protection of privacy and provision of electronic signatures generated by the spread of electronic communication networks has stimulated extensive research in cryptology. Cryptographic methods are already widely used for protection of automatic teller machine communications and for pay-TV access control. Very soon they will be used for protection of electronic mail and transmissions from portable telephones. Recent research has been extremely successful in developing fundamental new ideas, such as that of public-key cryptography, as well as in designing practical systems. Further work is necessary to find faster and even simpler systems that are still secure, since the schemes known at present often require excessive amounts of computing power.
4.6 Statistical and Probabilistic Models
Stochastic Modeling
Stochastic modeling is the study of phenomena in which "uncertainty" is caused by the inconsistency of natural phenomena or by sources that elude control. The uncertainty in stochastic models is recognized and included directly in the model as input, instead of the model being treated deterministically. Stochastic modeling areas such as simulation, queuing theory, dynamic programming, statistical quality control, and reliability have already been alluded to. These techniques have become an essential tool in business, government, and industry.
In a systematic effort to reduce inventories and manage assets, EPRI developed an industry-wide utility fuel inventory model using stochastic modeling. The task involved uncertainties due to supply disruptions and demand fluctuations. The inventory model balances a utility's customer service goals against these risks. The model is based on risk analysis, dynamic programming, and simulation, and enables a utility
to evaluate an array of fuel management policies in order to meet service goals in a cost-effective manner. This inventory model has been used by 79 utilities to realize annual savings of over $125 million.
An example of the use of stochastic modeling outside of the manufacturing context is given in a report of the President's Commission on Aviation Safety [17], issued in April 1988, on the strengths, weaknesses, and problems of the airspace system together with 15 recommendations for change. One of these recommendations stated that "Operations research [applied mathematics methods and models for solving complex optimization problems] should be recognized as a standard approach for problem solving in the FAA." As an example, when the safety of navigation standards over the North Atlantic was questioned by the International Federation of Airline Pilots Association in the 1960s, an operations research study, which included the assessment of collision risk, resulted in a resolution that both minimized cost and maximized safety.
Decision analysis was used to evaluate and select emission control equipment for three units of Ohio Edison's W. H. Sammis coal-fired power plant. With this technique, electrostatic precipitators were chosen over fabric filters, resulting in a savings of approximately $1 million. The modeling of the Long Island blood distribution system as an inventory problem, using Markov chains, and its optimal solution resulted in a reduction of wastage by 80 percent, which has translated into an annual savings of $500,000. Delivery costs were reduced by 64 percent, which has meant an annual savings of $100,000. Decision analysis, reliability theory, and Markov processes were used to plan and design the water supply system of the Palo Verde Nuclear Generating Station near Phoenix. A cost savings of approximately $20 million was achieved, and the reliability of an innovative water supply system was assured.
Spatial Statistics
Statistical variability can arise in observed data associated with locations in space, so that the random variable ξ = ξ(![]() ) is a function of the spatial coordinate
) is a function of the spatial coordinate ![]() . Such is the case with geostatistics, of importance to petroleum reservoir modeling and mining. The statistically most probable values of ξ, given partial geological data, are
. Such is the case with geostatistics, of importance to petroleum reservoir modeling and mining. The statistically most probable values of ξ, given partial geological data, are
constructed by kriging, which is a variance minimization algorithm. Further, representative variability can be added by the use of random fields, conditioned on the known data.
Agricultural field experiments depend on statistics for the analysis of data. The goal of these experiments is to compare different varieties of the same crop or different schedules for the application of fertilizer, water, and so on. Since the test plot will typically not be uniform with respect to other variables, such as sunlight or fertility, careful statistical design of the experiment and statistical analysis of the data are required. These are ongoing areas of statistical research, to which significant efforts are devoted. They have been highly successful and have been important contributors to the strong position in agricultural technology enjoyed by the United States.
Image enhancement and computer vision make use of random fields and spatial statistics. Commercial application of this technology includes biomedical devices, such as the CAT scan and automated medical diagnosis, and industrial devices, such as the design of intelligent robots and the use of ultrasound to test for defects in metal welds or pipe castings.
4.7 Manpower, Education, and Training
The mathematical sciences community has the primary responsibility for the collegiate mathematics education of engineers and scientists. It has provided significant portions of the intellectual leadership in efforts to revitalize education at the K-12 levels and has sole responsibility for graduate- and professional-level education in the mathematical sciences. Just at a time when increased use of mathematics across many disciplines has raised the requirements for mathematical reasoning on the part of students, there have been ongoing problems with the motivation of U.S. students to learn mathematics. These two events have prompted serious and high-level examination of the entire educational aspect of the mathematical sciences.
A major increase in instruction in necessary mathematical methods is occurring in contemporary higher education in the natural and social sciences, engineering, and business. For majors in the mathematical sciences, the departmental lines are disappearing. A recent survey of American universities showed that the enrollments in ad-
vanced mathematics courses taught outside the mathematical sciences departments exceed similar enrollments within those departments. In addition, the majority of those with a B.S. degree in mathematics who subsequently obtain a Ph.D. earn it in a field outside of mathematics. As one striking example of the blurring of departmental lines, more computer science faculty have Ph.D.s in mathematics than in computer science. This growth in the use of mathematics has occurred at more than the advanced level. Indeed, what was once considered advanced mathematical training is now becoming essential knowledge for many future blue-collar jobs. In Japan, working on an automobile assembly line requires that employees with only a high school diploma perform statistical quality control calculations.
American higher education has an unsurpassed reputation for producing creative researchers. The relatively few college students requiring very advanced mathematical training have been especially successfully educated. But the future challenge posed by large numbers of students in college (and, more importantly, in high school) needing much more mathematical training is made more difficult by the common U.S. assumption that most students lack the motivation to learn mathematics. Already the pipeline of students in mathematically oriented disciplines who are U.S. citizens or permanent residents is running low. Half or more of the Ph.D.s in mathematics and many engineering disciplines are being awarded to foreign nationals.
Heartening examples prove that students can be motivated to do much better: Jaime Escalante's Garfield High School students, publicized in the movie Stand and Deliver, and the mathematics majors of SUNY College at Potsdam, who number 20 percent of that college's baccalaureates (nationally, math majors account for about 1 percent of college graduates). The achievement of Escalante was given independent confirmation through U. Treisman's success at the University of California, Berkeley, with minority students taking calculus. Translating a few bright spots into a national agenda for excellence in mathematics education is the announced goal of the Mathematical Sciences Education Board of the National Research Council and of the joint Education Conference of the President and Governors. The importance of this mission cannot be overstated.
Besides the problem of improving students' motivation to learn
mathematics, there are difficult questions about how to teach mathematics. It is a challenge to find appropriate underlying themes on which to organize the teaching of mathematics more efficiently. There is already much more mathematics that busy students in the sciences should know than will fit into their schedules. In primary and secondary school, mathematics follows a relatively sequential program of integer addition to integer multiplication to fraction arithmetic to algebra to analytic geometry to calculus. But probability and statistics, matrix algebra, and computer-oriented discrete mathematics topics and diverse applications also demand attention. At the college level, the trail branches out in many directions. Efforts of the "New Math" in the 1960s to modernize school mathematics were largely a failure, although many of the country's best mathematical minds were involved. Unfortunately this failure halted for many years any further attempt to make the major changes required in mathematical education. Recent efforts such as the National Conference of Teachers of Mathematics (NCTM) standards [18] and the National Science Foundation/Mathematical Association of America Calculus Reform project show that mathematicians are now attacking these difficult educational issues once more.
There is currently substantial debate within collegiate mathematics departments concerning the required content of a major in mathematics. So many facets of both pure and applied mathematics exist that a consensus on what constitutes the central core of training in mathematics has yet to emerge. The explosion of new fields and new uses of mathematics continues to present serious educational challenges that must be addressed.
Because the mathematical sciences community has only recently returned to these educational issues in a serious way, because of the great importance of science and technical education to economic competitiveness and other important national issues, and because of the sizable fraction that mathematics occupies within science and technical education as a whole, there is a strong need for the mathematical sciences community to recognize the seriousness of the issues described in this report and to assume responsibility for further action.

































