Page 337
D
Technical Details of Power Calculations and Meta-Analyses
POWER CALCULATIONS
Many of the adverse events related to pertussis and rubella vaccines share the characteristic of rareness. Most of the events in question are infrequent to begin with, and the excess risk that may be associated with vaccination is small. As mentioned in Chapter 3, it is often difficult in such situations to distinguish scientifically between no excess risk and no detected excess risk. Because of the committee's focus on fairly characterizing the uncertainty in the available data, special attention was given to power analysis, a statistical tool that can help to distinguish between these two possibilities. This appendix describes and illustrates the power calculation methods used by the committee to take account of the diverse statistical methods used in the studies on which the analyses are based.
The results of epidemiologic studies are generally reported in terms of relative risks (RRs) or odds ratios. Because the odds ratio was considered to be an estimate of the RR in the context of this report (see Chapter 3), the term RR is used in the descriptive text to refer to both measures in the report of power analyses. For the purpose of these calculations, it was assumed that, in every study, the sampling distribution of the logarithm of the odds ratio or RR (noted as Y) has a normal distribution with a standard deviation equal to the estimated standard error (Fleiss, 1981, pp. 61-67). In order to calculate power statistics from published results, the committee took the following two steps.
Page 338
First, where possible, standard errors for Y were derived from confidence intervals reported by original investigators. In this way, variance reduction techniques such as matching of cases and controls are accurately reflected in the estimated standard error. In particular, if the reported odds ratio or RR is R, and the upper limit of its 95 percent confidence interval is U, the standard error was estimated as s = ln(U/R)/1.96. For studies in which no confidence interval was calculated by the original authors, the committee calculated an RR as appropriate and an associated confidence interval using standard methods for 2 x 2 tables (Fleiss, 1981, pp. 61-67) and applied the same procedure described above to estimate the standard error.
Second, 50 and 80 percent power levels for the RR were calculated as follows. Under the null hypotheses of no association, the expected value of Y, E(Y), is 0.0 and the critical point for a two-sided test with a = 0.05 is 1.96s. If E(Y) were equal to 1.96s, there would be a 50 percent chance that the test would detect an elevated risk; thus, the RR for which there is 50 percent power was calculated as e1.96s. To achieve 80 percent power, E(Y) must be 0.84s above the critical point, or 2.80s. Thus, the RR for which there is 80 percent power was calculated as e2.80s.
To illustrate this approach, Table D-1 shows the results of these calculations for the SONIC study relating DPT use to afebrile seizures (Gale et al., 1990; see also Table 4-5). The estimated RRs range from 0.5 to 0.8, and the upper confidence limits range from 1.1 to 1.5. On the basis of these results, the power calculations show that the SONIC study had a 50 percent chance of detecting an RR for afebrile seizures within 7 days of 3.0 and an 80 percent chance of detecting an RR within 7 days of 4.8. Thus, a relatively large increase in the risk of afebrile seizures could have gone unde-
|
TABLE D-1 Power Calculations for the SONIC Study Relating DPT Use to Afebrile Seizures |
|||||
|
Powerc |
|||||
|
Time Period |
RR |
Upper CIa |
sb |
50% |
80% |
|
Within 7 days |
0.5 |
1.5 |
0.56 |
3.00 |
4.80 |
|
Within 14 days |
.08 |
1.5 |
0.32 |
1.88 |
2.45 |
|
Within 28 days |
0.6 |
1.1 |
0.31 |
1.83 |
2.38 |
|
aCI, Confidence interval. |
|||||
Page 339
tected in a study of this size. The committee could only conclude that this study provided no evidence of a large effect.
A different approach was taken to calculate the power of the statistical tests used in a retrospective epidemiologic study by Shields and colleagues (1988). As described in Chapters 4 and 5 of this report, Shields and colleagues ascertained the age distribution of cases of SIDS and of a number of neurologic disorders in Denmark during two time periods with different vaccination schedules. During the 1967-1968 time period, DPT was given at ages 5, 6, 7, and 15 months; in 1972-1973, DPT was given at ages 5 and 9 weeks and 10 months. Shields and colleagues recorded the number of adverse events occurring in the following age intervals: 1 to 3, 4 to 8, 9 to 11, 12 to 14, 15 to 19, and 20 to 23 months. Although Shields and colleagues tested whether the entire distributions of cases differed between the two time periods, the committee's power calculations were based on a comparison of the proportions in two noncontinuous age groups.1 Group 1 was defined as age 4 to 8 months and age 12 or more months, so that a possible increase in the number of cases consistent with the 1967-1968 vaccination schedule could be detected. Group 2 was defined as ages 1 to 3 months and 9 to 11 months, so that a possible increase in the number of cases consistent with the 1972-1973 vaccination schedule could be detected.
The power calculations are based on the assumption that if there is an increase in the risk of the adverse event shortly following DPT vaccination, the proportion of cases in the time period in which most of the vaccinations take place should increase. More precisely, define pi as the expected number of cases in age group 1 in time period i, p0 as the expected proportion of non-vaccine-associated cases in the same group (independent of time period), and qi as the proportion of vaccinations in the same age group and time period. Furthermore, suppose that a proportion k/(1 + k) of the adverse events in an age-period group are caused by the vaccines so that the expected value of pi equals (p0 + qi k)/(1 + k). Under these assumptions, given qi and the number of vaccinations administered in each time period as reported by Shields and colleagues (1988), one can calculate the expected difference between the two time periods in the proportion of cases in age group 1, p2 - p1, its standard deviation, and thus the power of the test for a given value of k. Such calculations were performed for a range of appropri-
1 A more general version of the power calculations involving more than two groups was developed by Frederick Mosteller and Elizabeth Burdick of Harvard University (personal communication, 1991), and formed the mathematical basis of the simplified model used by the committee. The more complete model requires computer simulations for evaluation and is, thus, more complicated to implement. It was found, however, to yield results similar to those of the simplified model used here.
Page 340
ate values of k, and the values of k for which 50 and 80 percent powers were achieved were reported.
META-ANALYSES
Formal Analysis
As reported in Chapter 3, the committee found nine studies that offer some information on the timing of SIDS relative to vaccination. The following section describes in detail the methods used by the committee to perform a meta-analysis of these data. Part of the approach relies on standard methods for meta-analysis of clinical and epidemiologic data developed by DerSimonian and Laird (1986). But, because only four of the studies correct for the age pattern of SIDS (which would lead one to expect more SIDS cases in the first few days after vaccination than a uniform distribution would predict), an additional step was needed to adjust data from the poorly controlled studies.
The adjustment for the age pattern of SIDS was based on three studies that have proper controls for the age pattern of SIDS and roughly similar divisions of the time between vaccination and death: Griffin et al. (1988), Solberg (1985), and Walker et al. (1987). These studies indicate the number of observed and expected cases in three subdivisions of the (roughly) first month after vaccination: "early" is 0 to 3 days, "mid" is 4 to 7 days, and "late" is the rest of the month (which varies from 28 to 30 days). The study by Hoffman and colleagues (1987) has appropriate controls but is given in time intervals with breakpoints at 24 hours and 14 days, so it was not used in this part of the analysis.
In order to estimate an adjustment factor for the age pattern of SIDS, the fraction of expected cases in each period was compared to the fraction that would be expected if the SIDS deaths were uniformly distributed over time. The result is as expected: there are more deaths among the controls in the early and mid periods than a uniform distribution would predict. The ratios vary across the three studies, but all are in the predicted direction. The simple averages of the three ratios are as follows: early = 1.05, mid = 1.15, and late = 0.96.
These average ratios were then used to correct the five studies (Baraff et al., 1983; Bernier et al., 1982; Pollock et al., 1984; Taylor and Emery, 1982; Torch, 1982) that did not have appropriate controls, as follows. For each study, the number of cases that would have been expected in each interval under the uniform distribution was calculated first. Note that the "early" period is 0 to 2 days in one study, and the end of the "late" period ranges from 21 to 42 days. The average ratios from the first three studies were then applied to calculate an adjusted expected number of cases in each period.
Page 341
To summarize these results in a meta-analysis, the committee chose to use the DerSimonian and Laird (1986) approach to analyzing log odds ratios with appropriate sensitivity analyses for the major assumptions. The basic steps in this approach include (1) calculating an odds ratio for each study, comparing the proportion of deaths in the early period between cases and controls; (2) calculating a weighted average of the log odds ratios in which the weights reflect the variance of the individual estimates of the log odds ratios; and (3) calculating an additional weighted average based on a random-effects model, that is, assuming that the observed odds ratios are chosen at random from a population of odds ratios that would be obtained in similar studies. The DerSimonian and Laird approach also produces standard errors and confidence intervals for each weighted average. Because a number of statistical assumptions are possible, an analysis was performed to assess the sensitivity of the qualitative results to the assumptions.
The meta-analysis was based on the odds ratios that compared the number of deaths in the early period to the number in the early and late periods combined. Deaths in the mid period were excluded from the analysis because (1) the study of Hoffman and colleagues had no mid period, and (2) it was not clear whether mid-period deaths in the other studies should be aggregated into the early or late periods.
Because sample sizes in the studies of Taylor and Emery and Pollock and colleagues are so small (1 and 0 observed cases, respectively, in the early period), these two studies were not included in the analysis. Three alternative assumptions were made about the study of Hoffman and colleagues, which has two different control groups as well as a very different set of time breakpoints: (1) the results with both control groups are included as two separate studies, (2) only the results from the more highly matched control group B are included in the meta-analysis, and (3) no data from Hoffman and colleagues are included.
In four of the studies (Baraff et al., 1983; Bernier et al., 1982; Solberg, 1985; Torch, 1982) the expected numbers of cases are based on calculated distributions rather than on a sample of controls. In these cases, the committee assumed that only the observed proportion in the early period contributed to the standard error. This means that the confidence intervals from these studies understate the true uncertainty by an unknown amount. For the other three studies, the committee calculated standard errors without taking into account the matching and other variance reduction techniques that were actually used in the study. This implies that the resulting confidence intervals overstate the true uncertainty, again by an unknown amount.
The odds ratios for the individual studies, as shown in Figure D-l, range from 0.60 to 3.36. As Figure D-1 shows, the 95 percent confidence intervals for these odds ratios differ markedly from study to study. Some of the
Page 342
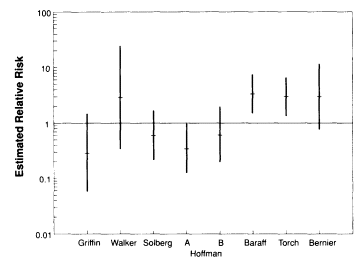
FIGURE D-1 Odds ratios and 95 percent
confidence intervals
for the risk of SIDS in the early period postvaccination for
the
seven studies included in the meta-analysis.
confidence intervals do not overlap, suggesting that a random-effects model is appropriate.
The results of the meta-analyses, shown in Figure D-2a, reflect the three assumptions about the study of Hoffman and colleagues laid out above and show the impact of choosing a fixed-effects or random-effects approach. Both assumptions have an impact on the calculations, but not enough to change the qualitative results. The decision to include or exclude the three less well controlled studies has somewhat more of an impact; if only the well-controlled studies are included in the meta-analysis, there is an almost significant inverse association between the vaccine and SIDS in the early period.
Figure D-2b shows the results of altering the categorization of deaths by time period. In the three studies that report on deaths after the first month, these are aggregated into the late period. The resulting meta-analyses differ little from those represented in Figure D-2a.
The committee also experimented with different adjustments for the age pattern of SIDS by varying the E/U ratio for the early period from 1.0 to 1.2 for the three studies with no internal controls. This change made very little difference in the results.
Thus, although the results depend somewhat on the statistical assumptions, in no case is there a significantly elevated average odds ratio for the
Page 343
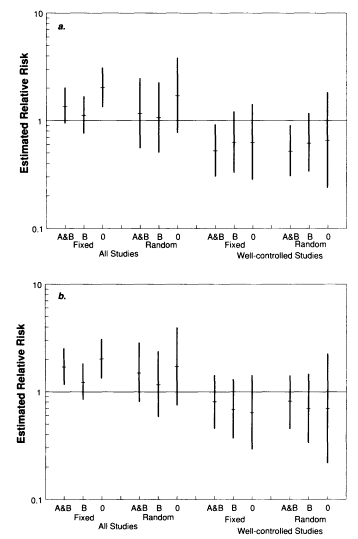
FIGURE D-2 a. Meta-analysis results comparing
the estimated
risk of SIDS in the early period postvaccination with that
in
the late part of the first month, under various assumptions:
(1) whether all studies or only well-controlled studies are
included in the meta-analysis, (2) whether a fixed- or a
random-effects model is assumed, and (3) whether the
meta-analysis includes results from the study of Hoffman et
al. (1987) based on age-matched controls (A) and age-,
race-,
and birth-weight-matched controls (B), on B alone, or on
neither (0). For each set of assumptions, the mean and 95
percent confidence interval from the meta-analysis are shown
on a logarithmic scale. b. Similar results comparing SIDS
deaths in the early period with deaths in the late period
plus
deaths after the end of the first month postvaccination.
Page 344
early period. Including the less well controlled studies, the average odds ratio is close to 1.0. Inclusion of only the well-controlled studies leads to a lower average odds ratio, under 0.6.
Informal Analysis
The committee felt that a formal meta-analysis as described above was not appropriate for the data on encephalopathy because of the relatively few cases recorded in studies other than the NCES. The committee did, however, make the following calculations to assess the consistency of data on encephalopathy from the other studies with those from the NCES.
Table D-2 lists the eight studies in which a number of vaccinated children in a defined population were monitored subsequent to vaccination. The number of children monitored and the number of encephalopathies recorded within 2 days (or 1 week, as explained in footnote a) are shown. The estimate of the total incidence in the 2 days postvaccination based on the data in all eight studies is 6.57 cases/864,041 children = 7.6 cases per million vaccinated children.
To determine the relative and attributable risks of encephalopathy following DPT immunization, the background incidence rate was estimated as follows. The four studies listed in Table 4-4 provide information on the total number of encephalopathy cases occurring in children of various ages.
|
TABLE D-2 Pooled Data for Encephalopathy Calculation |
||
|
Reference |
No. Children |
No. Cases |
|
Studies in defined populations |
||
|
Cody et al. (1981) |
15,752 |
0 |
|
Pollock and Morris (1983) |
||
|
Self-reports |
134,700 |
4 |
|
Hospital reports |
17,000 |
0 |
|
Pollock et al. (1984) |
6,004 |
1 |
|
Strom (1967) |
516,276 |
1 |
|
Long et al. (1990 |
538 |
0 |
|
Controlled studies |
||
|
Walker et al. (1988) |
26,600 |
0 |
|
Griffin et al. (1990) |
38,171 |
0 |
|
Gale et al. (1990) |
109,000 |
0.57a |
|
Total |
864,041 |
6.57 |
|
a There were two cases reported within I week of vaccination. Assuming a uniform distribution over the week, 2 x 2/7 = 0.57 cases were estimated to have occurred in the first 2 days. |
||
Page 345
Because Beghi and colleagues (1984) found that the incidence of encephalopathy was higher in the first year of life than in the second or third years, these data could not be combined without taking into account the differences in the ages of the children. Assuming that the ratio of incidence in the first year life to the incidence in the second and third years as estimated in the study by Beghi and colleagues (22/15.8, or 1.4) is correct, each year of observation beyond the first birthday is equivalent to 1/1.4, or approximately 0.7 years of experience before the first birthday. By using this figure, adjusted background incidence rates were calculated for each study in Table 4-4 and for the four studies together by dividing the number of cases recorded outside of the immediate postvaccination interval by the number of first-year-equivalent years of observation. By pooling the results of the four studies in Table 4-4, the estimated background incidence rate for encephalopathy is estimated to be 78 per million children per year, or 0.43 per million children per 2-day period.
By comparing the estimated total incidence in the 2 days postvaccination derived from all eight studies listed in Table D-2 with the estimated background incidence rate during this same period, the RR in the 2 days postvaccination can be estimated at 7.6 per million divided by 0.43 per million = 17.7. The attributable risk for encephalopathy is the difference between the total incidence and the background incidence: 7.6 per million - 0.43 per million = 7.2 per million. Assuming that children, on average, receive three immunizations, the estimated attributable risk of encephalopathy is 2.4 per million immunizations.
If the studies of Pollock and Morris (1983) and Strom (1967), which relied on spontaneous reports for ascertainment, are excluded, the RR estimate is 17.1 and the attributable risk estimate is 2.3 per million immunizations. Relying only on the data in controlled studies of well-defined populations (Gale et al., 1990; Griffin et al. 1990; Walker et al., 1988), the total incidence in the week following vaccination is 2 cases per 173,771 children = 11.5 cases per million vaccinated children. Using a background rate of 0.43 x 7/2 per million = 1.5 per million, the RR estimate is 7.6 and the attributable risk estimate is 3.3 per million immunizations.
REFERENCES
Baraff LJ, Ablon WJ, Weiss RC. 1983. Possible temporal association between diphtheria-tetanus toxoid-pertussis vaccination and sudden infant death syndrome. Pediatric Infectious Diseases 2:7-11.
Beghi E, Nicolosi AN, Kurland LT, Mulder DW, Hauser WA, Shuster L. 1984. Encephalitis and aseptic meningitis, Olmsted County, Minnesota, 1950-1981. I. Epidemiology. Annals of Neurology 16:283-294.
Bernier RH, Frank JA, Dondero TJ, Turner P. 1982. Diphtheria-tetanus toxoids-pertussis vaccination and sudden infant deaths in Tennessee. Journal of Pediatrics 101:419-421.
Cody CL, Baraff LJ, Cherry JD, Marcy SM, Manclark CR. 1981. Nature and rates of adverse
Page 346
reactions associated with DTP and DT immunizations in infants and children. Pediatrics 68:650-660.
DerSimonian R, Laird N. 1986. Meta-analysis in clinical trials. Statistics in Medicine 6:351-358.
Fleiss JL. 1981. Statistical Methods for Rates and Proportions. New York: John Wiley & Sons.
Gale JL, Thapa PB, Bobo JK, Wassilak SGF, Mendelman PM, Foy HM. 1990. Acute neurological illness and DTP: report of a case-control study in Washington and Oregon. In: Manclark CR, ed. Sixth International Symposium on Pertussis, Abstracts. DHHS Publication No. (FDA) 90-1162. Bethesda, MD: Public Health Service, U.S. Department of Health and Human Services.
Griffin MR, Ray WA, Livengood JR, Schaffner W. 1988. Risk of sudden infant death syndrome after immunization with the diphtheria-tetanus-pertussis vaccine. New England Journal of Medicine 319:618-623.
Griffin MR, Ray WA, Mortimer EA, Fenichel GM, Schaffner W. 1990. Risk of seizures and encephalopathy after immunization with the diphtheria-tetanus-pertussis vaccine. Journal of the American Medical Association 263:1641-1645.
Hoffman HJ, Hunter JC, Damus K, Pakter J, Peterson DR, van Belle G, Hasselmeyer EG. 1987. Diphtheria-tetanus-pertussis immunization and sudden infant death: results of the National Institute of Child Health and Human Development Cooperative Epidemiological Study of Sudden Infant Death Syndrome Risk Factors. Pediatrics 79:598-611.
Long SL, Deforest A, Smith DG, Lazaro C, Wassilak SGF. 1990. Longitudinal study of adverse reactions following diphtheria-tetanus-pertussis vaccine in infancy. Pediatrics 85:294-302.
Pollock TM, Morris J. 1983. A 7-year survey of disorders attributed to vaccination in North West Thames Region. Lancet 1:753-757.
Pollock TM, Mortimer JY, Miller E, Smith G. 1984. Symptoms after primary immunisation with DTP and with DT vaccine. Lancet 2:146-149.
Shields WD, Nielsen C, Buch D, Jacobsen V, Christenson P, Zachau-Christiansen B, Cherry JD. 1988. Relationship of pertussis immunization to the onset of neurologic disorders: a retrospective epidemiologic study. Journal of Pediatrics 113:801-805.
Solberg LK. 1985. DPT vaccination, visit to child health center and sudden infant death syndrome (SIDS): evaluation of DPT vaccination. Report to the Oslo Health Council 1985. (Available as NIH Library translation 85-152, Food and Drug Administration, Bethesda, MD.)
Strom J. 1967. Further experience of reactions, especially of a cerebral nature, in conjunction with triple vaccination: a study based on vaccinations in Sweden, 1959-1965. British Medical Journal 4:320-323.
Taylor EM, Emery JL. 1982. Immunisation and cot deaths (letter). Lancet 2:721.
Torch WC. 1982. Diphtheria-pertussis-tetanus (DPT) immunization: a potential cause of the sudden infant death syndrome (SIDS) (abstract). American Academy of Neurology, 34th Annual Meeting, April 25-May 1, 1982. Neurology 32(4, part 2):A169-170.
Walker AM, Jick H, Perera DR, Thompson RS, Knauss TA. 1987. Diphtheria-tetanus-pertussis immunization and sudden infant death syndrome. American Journal of Public Health 77:945-951.
Walker AM, Jick H, Perera DR, Knauss TA, Thompson RS. 1988. Neurologic events following diphtheria-tetanus-pertussis immunization. Pediatrics 81:345-349.










