William D. Kalsbeek1
This paper expands the discussion in Chapter 10 on the use of a multiple-frame approach to estimating the incidence of rape and sexual assault in household surveys of the Bureau of Justice Statistics. It explores the statistical rationale behind some initial findings on the relative statistical plausibility of a multiple-frame approach.2
BACKGROUND AND ASSUMPTIONS
1. The primary analysis objective is to estimate the proportion (P) of persons in the target population who have been a victim of a rape or sexual assault (RSA) in some calendar year.
2. The following two overlapping frames are involved in defining a dual-frame (DF) sample design that might be used to estimate P: (1) an administrative frame consisting of persons seen/treated/processed for their RSA during the same calendar year and (2) a standard area household frame of the residential population of the kind used for the NCVS.
________________
1Kalsbeek is a professor in the Department of Biostatistics at the University of North Carolina. He served as cochair of this panel.
2A presentation on the statistical issues in this appendix was presented at the Joint Statistical Meetings in Montreal in August 2013 (Kalsbeek, Spencer, and House, 2013), available http://www.amstat.org/meetings/jsm/2013/onlineprogram/AbstractDetails.cfm?abstractid=309226 [December 2013].
3. The administrative frame is a subset of the area household frame, and thus the two frames overlap. However, one can define two non-overlapping strata by considering those in the administrative frame to be one stratum and all members of the area household frame not included in the administrative frame to be the second stratum, implying that a sample for the second stratum selected from the area household frame would need to be screened to excluded members of the administrative frame. Formation of these two strata is the simplest frame construction arrangement for a dual-frame design and comparable to the frame structure of telephone sampling of landline and cell-only households (Hartley, 1962; Lohr, 2011).
4. The administrative frame might be chosen from any of the following sets of people who: (1) filed a crime complaint with the police or some other law enforcement agency, (2) were victims of RSA or aggravated assault when an accused perpetrator is charged with a crime and tried in the criminal justice system, (3) were treated for assault-related health consequences by a hospital emergency department, (4) were clients of victim support services (e.g., rape crisis center, domestic violence shelters, etc.), (5) were registered residents of Indian reservations, (6) were treated at Indian Health Services facilities, or (7) were patients of outpatient mental health clinics.
5. A simple form of sampling (i.e., simple random sampling with replacement, SRSWR) is applied separately to the administrative and the nonadministrative household strata.
6. The dual-frame sample design is seen as an alternative to a single-frame (SF) design but uses a standard area household frame as currently used in the NCVS. While more complex forms of stratified cluster sampling would be used with DF and SF designs, one assumes SRSWR sampling is applied to each frame, with the presumption that effects of greater sampling complexity would cancel, thus sustaining a comparison between the two design alternatives.
DETERMINING THE MOST COST-EFFICIENT SAMPLE ALLOCATION AMONG STRATA IN THE DUAL-FRAME DESIGN
One can consider the simplest case of multiframe sample design in which the set of population members comprising two overlapping frames is divided into two nonoverlapping sampling strata, as for instance with cell and landline frames in telephone sampling (Hartley, 1962; Lohr, 2011). In the situation described above, we have two nonoverlapping sampling strata formed by the members of: (1) the administrative frame (A), and (2) the nonadministrative household frame (HH) consisting of those members
of the HH frame who are not members of the administrative frame. Under this scenario one can observe the precision of a dual-frame estimator of the prevalence of rape and sexual assault on the basis of well-known properties of the analysis from a stratified sample.
For stratified SRSWR, the variance of the estimator, 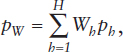 of P for the general case of selecting a sample of size n from H strata is
of P for the general case of selecting a sample of size n from H strata is
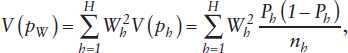
where for the h-th stratum: Wh = Nh/N is the proportion of the population, Ph is the proportion of victims of RSA among all Nh population members, and ph is the proportion of RSA victims among the nh sample members. If one defines Ch, the average cost of adding another survey respondent in the h-th stratum, then we can use the simple linear variable cost model, 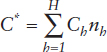 and the Cauchy-Schwartz inequality to establish the sample allocation that minimizes
and the Cauchy-Schwartz inequality to establish the sample allocation that minimizes ![]() The most cost-efficient sample allocation to the h-th stratum is thereby
The most cost-efficient sample allocation to the h-th stratum is thereby
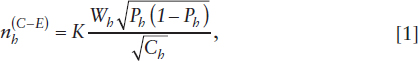
where 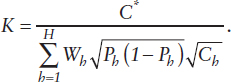
Applying the general result from Eq. [1] to the two-stratum setting of the dual frame,
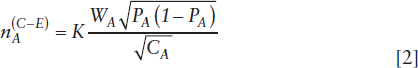
for the administrative stratum, and
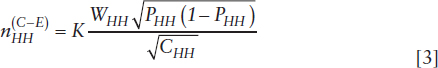
for the household stratum, where
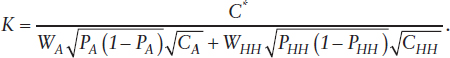
VARIANCE OF A DUAL-FRAME ESTIMATE BASED ON THE MOST COST-EFFICIENT ALLOCATION
The variance of pW for the stratified SRSWR with the most cost-efficient sample allocation (i.e., the nh(C–E)) for the case of H strata can be shown to be
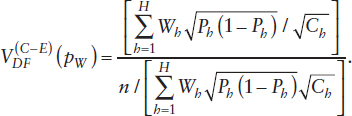
For the two-stratum case,
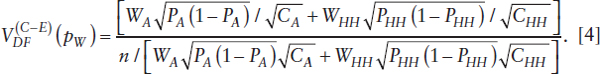
Dual-Frame vs. Single-Frame HH Area Household Frame Design
A cost-equivalent comparison of the dual-frame (DF) estimator with a single-frame (SF) estimator with a sample of size nSF = C*/CHH when the total variable cost of data collection for the SF design is C*. For design comparability one assumes SRSWR sampling from the household frame in which case the variance of the SF estimator (pHH) of P will be simply
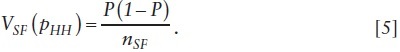
The variances of estimates of P by the DF and SF designs can be compared using the ratio

Other Comparison Indicators
1. Ratio of Average Unit Costs for the Two Dual-Frame Strata—This ratio depicts the ratio of the average cost of adding another respondent to the administrative stratum compared to the comparable average cost for the nonadministrative household stratum. This indicator is computed as
![]()
2. Ratio of Stratum RSA Rates for the Dual-Frame Design—Compared to an unstratified SRSWR design, Cochran (1977, Section 5.6) notes that when stratum unit costs are equal the relative effectiveness of the most cost-efficient stratum allocation for a stratified SRSWR depends on the extent of stratum differences in (i) Ph and (ii) the standard error of the RSA status (i.e., ![]() Differences in (ii) are especially pronounced for extremely small (or large) values of Ph, as is the case here with P being about 0.001 for the rate of RSA prevalence, and thus implying that PA >> PHH. The indicator used to measure the relative sizes of PA and PHH is
Differences in (ii) are especially pronounced for extremely small (or large) values of Ph, as is the case here with P being about 0.001 for the rate of RSA prevalence, and thus implying that PA >> PHH. The indicator used to measure the relative sizes of PA and PHH is
![]()
3. Extent of Oversampling Members of the Administrative Frame in the Dual-Frame Design—This is a descriptive indicator of the relatively greater sampling intensity in the administrative stratum compared to the household stratum in the DF design. The indicator is computed as
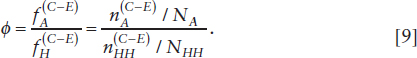
4. Percentage of Dual-Frame Sample from Administrative Stratum—Indicates how much of the total dual-frame sample (nDF) comes from the administrative frame. The indicator is computed as
5. Relative Size of the Dual-Frame Sample Compared to the Single- Frame Sample—Indicates the comparative sizes of the total sample sizes for the DF design (nDF) vs. the SF design (nDF). The indicator is computed as
![]()
6. Relative Standard Error of the Estimate for the Dual-Frame Design—Relative measure of the precision of the dual-frame estimate with the most cost-efficient stratum allocation. The indicator is computed as
EXAMPLE 1: [θ = CA/CHH = 2]
Suppose the following setting in which we are to compare the statistical quality of estimates from a DF design involving police records as the administrative source with comparable (and thus cost-equivalent) estimates from a household SF design as currently used in the NCVS. To determine the relative utility of DF and SF designs one might pose this question. How would the variance of a DF estimate of RSA prevalence (VDF(C-E) (pw)) compare with the variance of a comparable SF estimate (VSF(pHH)) obtained for the same cost?
To find an answer to this question within the context of the design assumptions, definitions, and theoretical findings described previously in this document, consider the following numerical values:
1. Police records are to be used to define an administrative stratum of crime victims, so specify the size of the administrative stratum as about NA = 140,000 by extrapolating to the total U.S. population the 1997 Uniform Crime Reports partial national count of 96,122 assaults/attempts to commit rape as reported on p. 25 of Crime in the United States 1997 (Federal Bureau of Investigation, 1997) at: http://www.fbi.gov/about-us/cjis/ucr/crime-in-the-u.s/1997/toc97.pdf
2. From an August BJS Selected Findings report by CM Rennison (Bureau of Justice Statistics, 2002b) at: http://bjs.ojp.usdoj.gov/content/pub/pdf/rsarp00.pdf, the NCVS estimated average annual number of RSAs reported to police (1992-2000) was about 116,300. Thus, the proportion of police records on assaults/attempts to commit rape that would turn out to be an RSA would be about PA = 116,300/140,000 = 0.83.3
3. Persons living at addresses define the household frame (as in the NCVS). According to Bureau of Justice Statistics (2008a) the total number of persons 12+ years of age is about N = 250,000,000 (in 2007), thus making the size of the household stratum NHH = N – NA = 249,860,000, and the proportion of the population in the administrative stratum will be about WA = 1 – WHH = 140,000/250,000,000 = 0.00056.
4. P = 0.001 based on figures from Criminal Victimization, 2007 (Bureau of Justice Statistics, 2008a), which can be found at http://bjs.ojp.usdoj.gov/content/pub/pdf/cv07.pdf.
5. Based on a 2009 FCSM Research Conference paper presented
________________
3If for confidentiality protection the types of crimes sampled through police records was broader, then PA would be lower, and perhaps much lower, than this value.
by Michael R. Rand of BJS (Rand, 2009) in (see pages 9 and 16 of this paper) at http://www.fcsm.gov/09papers/Rand_X-B.doc, funds available to conduct the NCVS in FY2009 amounted to C* = $26M, and about 150,000 NCVS interviews were completed in 2008. These figures imply an average cost per completed interview of about CHH = $26M/150000 = $173 for the household stratum.
Dual-Frame Design:
If the average per completed interview for the police records (administrative) stratum is two (2) times that of the household stratum (i.e., like the NCVS), then θ = CA/CM = 2 and thus CA = $346.
First determine the RSA rate for the household stratum as ![]() which makes PA = 0.83 larger than PHH by a factor of about
which makes PA = 0.83 larger than PHH by a factor of about ![]() The standard deviations of the 0/1 RSA status indicator for the two strata thus differ by a factor of
The standard deviations of the 0/1 RSA status indicator for the two strata thus differ by a factor of ![]() Because of these substantial stratum differences in Ph and
Because of these substantial stratum differences in Ph and ![]() one might expect from Eq. (5.37) in Cochran (1977) that a cost-efficient stratum allocation in this dual-frame context will produce substantially greater precision in estimates of P than a single-frame approach relying solely on household sampling. We will see this to be case below.
one might expect from Eq. (5.37) in Cochran (1977) that a cost-efficient stratum allocation in this dual-frame context will produce substantially greater precision in estimates of P than a single-frame approach relying solely on household sampling. We will see this to be case below.
Using Equations [2] and [3] above, we find that the most cost-efficient allocation of the dual-frame sample given C* for the police records stratum will be
and for the household stratum,
Thus, the total sample size for the DF design in this case would be
149,334, of which 955 (or about 0.6%) would be from the police records stratum.
The variance of the weighted estimate of P from the DF design based on this most cost-efficient sample allocation between strata will be
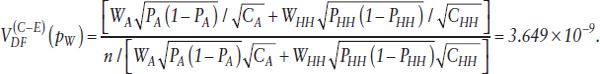
Cost-Equivalent Single-Frame Design:
Now turning our attention to the SF design, also with a budget of C* = $26M and CHH = $173, the sample size we can afford for the household frame is nSF = C*/ CHH = 150,289, which is only slightly greater that the total sample for the DF design. The variance of the single-frame estimate will therefore be
![]()
Cost-Equivalent Design Comparison:
Comparing the variances for RSA estimates from the DF and SF designs with C* = $26M, we have
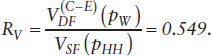
implying that the variance for the DF design is about 45% lower than the cost-equivalent variance for the SF design.
EXAMPLE 2: [θ = CA/CHH = 10]
Consider the same setting as above but where θ = CA/CHH = 10; i.e., where the average cost for the police records stratum is 10 times greater than for the household stratum (e.g., because it may be much more difficult to sample, recruit, and collect data from the sample obtained from police records). Here, the most cost-efficient allocation of the DF sample changes to nA(C–E) = 420 and nHH(C–E) = 146,086, and the variance ratio is Rv = 0.556, implying a 43% lower variance by the DF design.
1. An important factor in the much higher average unit cost for the police records stratum is the need to broaden the search for RSA cases beyond those persons reporting assaults/attempts to com-
mit rape (e.g., to also include aggravated assaults by a male on a female) so that, we note that the following changes in Rv when PA is smaller:
| PA | Rv | |
|
|
||
| 0.60 | 0.709 | |
| 0.50 | 0.768 | |
| 0.40 | 0.825 | |
| 0.30 | 0.879 | |
| 0.20 | 0.930 | |
These findings indicate that even at lower concentrations and substantially higher average unit costs for this administrative source, the dual-frame approach produces reasonable gains over a cost-equivalent single-frame approach.
2. I have produced a wider range of findings for all of the statistical and process indicators just computed to more broadly illustrate comparative results for the dual-frame approach versus a cost-equivalent single-frame approach when police records are the administrative frame source for the dual frame.
SOME FINAL THOUGHTS
Admittedly, the utility of the comparative findings in this document is somewhat limited by several simplifying assumptions I have made, particularly by (i) the use of a contrived two-stratum framework for the two overlapping frames of the dual-frame by screening out target population members from one frame in sampling the other, and (ii) the assumption of SRSWR sampling instead of further stratified multistage cluster sampling in each stratum,4 and (iii) considering only effects on sampling error instead of also including effects arising from other nonsampling sources errors such as nonresponse and measurement. Nonetheless, I believe that these preliminary findings strongly suggest that it would be worthwhile for BJS to more closely investigate the feasibility of using a dual-frame approach for estimating rates of RSA, particularly if these estimates are obtained from an independent RSA victimization survey as recommended by the panel. Finally, the panel’s suggestions accompanying a further investigation of the dual-frame might be to incorporate more realistic elements overlooked by my simplifying assumptions above.
________________
4Kalsbeek, Spencer, and House (2013) provide more information on the potential efficiency reductions expected from relaxing this assumption.










