SOLOMON LEFSCHETZ
September 3, 1884-October 5, 1972


BY PHILLIP GRIFFITHS, DONALD SPENCER, AND GEORGE WHITEHEAD1
SOLOMON LEFSCHETZ was a towering figure in the mathematical world owing not only to his original contributions but also to his personal influence. He contributed to at least three mathematical fields, and his work reflects throughout deep geometrical intuition and insight. As man and mathematician, his approach to problems, both in life and in mathematics, was often breathtakingly original and creative.
PERSONAL AND PROFESSIONAL HISTORY
Solomon Lefschetz was born in Moscow on September 3, 1884. He was a son of Alexander Lefschetz, an importer, and his wife, Vera, Turkish citizens. Soon after his birth, his parents left Russia and took him to Paris, where he grew up with five brothers and one sister and received all of his schooling. French was his native language, but he learned Russian and other languages with remarkable facility. From 1902 to 1905, he studied at the École Centrale des Arts et Manufactures, graduating in 1905 with the degree of mechanical engineer, the third youngest in a class of 220. His reasons for entering that institution were complicated, for as he said, he had been ''mathematics mad'' since he had his first contact with geometry at thirteen.
Since he was not a French citizen, he could neither see nor hope for a career as a pure mathematician. The next best thing was engineering because, as he believed, it used a lot of mathematics.
Upon graduating in 1905, Lefschetz decided to go to the United States, for a time at least, with the general purpose of acquiring practical experience. First, he found a job at the Baldwin Locomotive Works near Philadelpia. But he was particularly attracted to electrical engineering, which, at that time, was a nonexistent specialty at the École Centrale. In view of this, in January 1907 he became an engineering apprentice in a regular course at the Westinghouse Electric and Manufacturing Company in Pittsburgh. The course consisted of being shifted from section to section every few weeks. He wound up in the transformer testing section in the late fall of 1907, and in mid-November of that year, he was the victim of a testing accident, as a consequence of which he lost both hands.2 After some months of convalescence, he returned to the Westinghouse Company, where, in 1909, he was attached to the engineering department in the section concerned with the design of alternating-current generators.
Meanwhile, Lefschetz had become increasingly dissatisfied with his work there, which seemed to him to be extremely routine. So he resumed, first as a hobby, his mathematical studies that had been neglected since 1903. After a while he decided to leave engineering altogether and pursue mathematics. He left the Westinghouse Company in the fall of 1910 and accepted a small fellowship at Clark University, Worcester, Massachusetts, enrolling as a graduate student. The mathematical faculty consisted of three members: William Edward Story, senior professor (higher plane curves, invariant theory); Henry Taber (complex analysis, hypercomplex number systems); and Joseph de Perott (number
theory). At the École Centrale there were two professors of mathematics, Émile Picard and Paul Appel, and each had written a three-volume treatise: Analysis (Picard) and Analytical Mechanics (Appel). Lefschetz plunged into these and, with a strong French training in basic mathematics, was all set to attack a research topic suggested by Professor Story, namely, to find information about the largest number of cusps that a plane curve of given degree may possess. Lefschetz made an original contribution to this problem and obtained his Ph.D. summa cum laude in 1911. In the Record of Candidacy for the Ph.D., it is stated by Henry Taber that it was an "excellent examination, the best ever passed by any candidate in the department," and signed by him under the date June 5, 1911.
Clark University had a fine library with excellent working conditions, and Lefschetz made good use of it. By the summer of 1911 he had vastly improved his acquaintance with modern mathematics and had laid a foundation for future research in algebraic geometry. He had also become more and more closely associated with another mathematics student at Clark, Alice Berg Hayes, who became his wife on July 3, 1913, in North Brookfield, Massachusetts. She was to become a pillar of strength for Lefschetz throughout the rest of his life, helping him to rise above his handicap and encouraging him in his work.
Lefschetz' first position after Clark was an assistantship at the University of Nebraska in 1911; the assistantship was soon transformed into a regular instructorship. In 1913 he moved to the University of Kansas, passing through the ranks to become a full professor in 1923. He remained at the University of Kansas until 1924. Then, in 1924 came the call to Princeton University, where he was visiting professor (1924-25); associate professor (1925-27); full professor (1927-33); and from 1933 to 1953, Henry Burchard
Fine Research Professor, chairman of the Department of Mathematics 1945-53 and emeritus from 1953.
The years in the Midwest were happy and fruitful ones for Lefschetz. The almost total isolation played in his development "the role of a job in a lighthouse which Einstein would have every young scientist assume so that he may develop his own ideas in his own way."3 His two major ideas came to him at the University of Kansas.
The first idea is described by Lefschetz as follows. Soon after his doctorate he began to study intensely the two-volume treatise of Picard-Simart, Fonctions Algébriques de Deux Variables, and he first tried to extend to several variables the treatment of double integrals of the second kind found in the second volume. He was unable to do this directly, and it led him to a recasting of the whole theory, especially the topology.4 By attaching a 2-cycle to the algebraic curves on a surface, he was able to establish a new and unsuspected connection between topology and Severi's theory of the base, constructed in 1906, for curves on a surface. The development of these and related concepts led to a Mémoire, which was awarded the Bordin Prize by the French Academy of Sciences in 1919. The translated prize paper is given in the Bibliography (1921,3). The first half of the Mémoire, with some complements, is embodied in a famous monograph (1924,1).
The general idea for the second most important contribution also came to Lefschetz in Lawrence, Kansas, and it is the fixed-point theorem which bears his name. Almost all of Lefschetz' topology arose from his efforts to prove fixed-point theorems. In 1912, L. E. J. Brouwer proved a basic fixed-point theorem, namely, that every continuous transformation of an n-simplex into itself has at least one fixed point. In a series of papers, Lefschetz obtained a much more general result for any continuous transfor-
mation of a topological space X into itself where the restrictions on X were progressively weakened. In 1923, he proved the theorem for compact orientable manifolds and, by introducing relative homology groups, he extended it in 1927 to manifolds with boundary; his theorem then included Brouwer's. In 1927, he also proved it for any finite complex and, in 1936, for any locally connected topological space.
In the 1920s and 1930s, as a professor at Princeton University, Lefschetz was wholly occupied with topology, and he established many of the basic results in algebraic topology. For example, he created a theory of intersection of cycles (1925,1; 1926,1), introduced the notion of cocycle (which he called pseudo-cycle) and proved the Lefschetz duality theorem (see 1949,1 for an exposition of the fixed-point theorem and the duality theorem). His Topology was published in 1930 (1930,1), and his Algebraic Topology was published in 1942 (1942,1). The former was widely acclaimed and established the name topology in place of the previously used term analysis situs; the latter was less influential but secured the use of the name algebraic topology as a replacement for combinational topology.5
Lefschetz was an editor of the Annals of Mathematics from 1928 to 1958, and his influence dominated the editorial policy that made the Annals into a foremost mathematical journal.
In 1943 Lefschetz became a consultant for the U.S. Navy at the David Taylor Model Basin near Washington, D.C. There he met and worked with Nicholas Minorsky, who was a specialist on guidance systems and the stability of ships and who brought to Lefschetz' attention the importance of the applications of the geometric theory of ordinary differential equations to control theory and nonlinear mechanics. From 1943 to the end of his life, Lefschetz'
main interest was centered around ordinary nonlinear differential equations and their applications to controls and the structural stabilities of systems. Lefschetz was almost sixty years old when he turned to differential equations, yet he did original work and stimulated research in this field as a gifted scientific administrator.
In 1946, the newly established Office of Naval Research funded a project on ordinary nonlinear differential equations, directed by Lefschetz, at Princeton University. This project continued at Princeton for five years past Lefschetz' retirement from the university in 1953. Meanwhile, the Research Institute for Advanced Study was formed in Baltimore, Maryland, as a division of the Glen L. Martin Aircraft Company, and in 1957, Lefschetz established the Mathematics Center under the auspices of the institute and was entrusted with the recruitment of five mathematicians and about ten younger associates. He obtained the cooperation of Professor Lamberto Cesari of Purdue University and appointed Professor J. P. LaSalle of Notre Dame and Dr. J. K. Hale of Purdue to the group, the former as his second in command. After some six years it was necessary to transfer the center elsewhere, and the move, carried out by LaSalle, resulted in their becoming part of the Division of Applied Mathematics at Brown University. The group was later named the Lefschetz Center for Dynamical Systems. LaSalle was director and Lefschetz became a visiting professor, traveling there from Princeton once a week. Lefschetz continued his work at Brown until 1970, two years before his death.
In 1944, Lefschetz joined the Institute de Mathematicas of the National University of Mexico as a part-time visiting professor, and this connection continued until 1966. At the Institute, he conducted seminars, gave volunteer courses, and continued his research. He found a number of ca-
pable young men there and sent several of them to Princeton University for further advanced training up to the doctorate and beyond. From 1953 to 1966 he spent most of his winters in Mexico City.
Lefschetz received many honors. He served as president of the American Mathematical Society in 1935-36. He received the Bôcher Memorial Prize of the American Mathematical Society in 1924, and in 1970 he received the first award of the Steele Prize, also of the American Mathematical Society. He received the Antonio Feltrinelli International Prize of the National Academy of Lincei, Rome, in 1956; the Order of the Aztec Eagle of Mexico in 1964; and the National Medal of Science (U.S.) in 1964. He was awarded honorary degrees by the University of Prague, Prague, Czechoslavakia; University of Paris, Paris, France; the University of Mexico; and Brown, Clark, and Princeton universities. He was a member of the American Philosophical Society and a foreign member of the Academie des Sciences of Paris, the Royal Society of London, the Academia Real de Ciencias of Madrid, and the Reale Instituto Lombardo of Milan.
A symposium in honor of Lefschetz' seventieth birthday was held in Princeton in 1954,6 and in 1965 an international conference in differential equations and dynamical systems was dedicated to him at the University of Puerto Rico. The international Conference on Albegraic Geometry, Algebraic Topology and Differential Equations (Geometric Theory), in celebration of the centenary of Lefschetz' birth, was held at the Centro de Investigaci ón del IPN, Mexico City, in 1984.
LEFSCHETZ AND ALBEGRAIC GEOMETRY
In order to discuss Lefschetz' contributions to algebraic geometry, I shall first describe that field and its evolution
up until the period during which Lefschetz worked. Then I will give a somewhat more detailed description of some of his major accomplishments. I will conclude with a few observations about the impact of his work in algebraic geometry.
In simplest terms, algebraic geometry is the study of algebraic varieties. These are defined to be the locus of polynomial equations
Here the xi are coordinates in an affine space and the Pa are polynomials whose coefficients are in any field K For our purposes, it will be convenient to take K to be the complex numbers, as this was the case in classical algebraic geometry and in almost all of Lefschetz' work. It is worth noting, however, that he was one of the first to consider the case where K is an arbitrary algebraically closed field of characteristic zero. In fact, the so-called Lefschetz principle as expanded in his book Algebraic Geometry (1953, 1) roughly states that any result from the complex case remains valid in this more general situation.
In addition to using complex numbers, it is also convenient to add to the above locus the points at infinity. This is accomplished by homogenizing the polynomials Pa and considering the resulting locus V in the complex projective space PN defined by the homogenized equations. Two algebraic varieties V and V' are to be identified if there is a rational transformation
that takes V to V' and is generically one to one there. These are called birational transformations, and T estab-
lishes an isomorphism between the fields K(V') and K(V) of rational functions on V' and V, respectively.
In the nineteenth century the intensive study of algebraic curves —that is, algebraic varieties of dimension one—was undertaken by Abel, Jacobi, Riemann, and others. On an algebraic curve C given by a single affine equation,
in the plane, special objects of interest were the abelian integrals
where R(x,y) is a rational function. For example, the hyperelliptic integrals
are abelian integrals on the hyperelliptic curve y2 = (x-a1) (x-an) In addition to the indefinite integral (3), abelian sums
and periods
where γ is a closed path on C, were of considerable interest. A major reason for studying abelian integrals and their periods was that these provided an extremely interesting class of transcendental functions, such as the elliptic function p(u) defined up to an additive constant by
It was Riemann who emphasized that studying C up to birational equivalence is equivalent to studying the abstract Riemann surface ![]() associated to the curve (2). Assuming that f is irreducible, in modern terms
associated to the curve (2). Assuming that f is irreducible, in modern terms ![]() is a connected, complex manifold of dimension one for which there is a holomorphic mapping
is a connected, complex manifold of dimension one for which there is a holomorphic mapping
whose image is C and where π: ![]() → C is generically one to one. Viewed as an oriented real two-manifold, the Riemann surface
→ C is generically one to one. Viewed as an oriented real two-manifold, the Riemann surface ![]() has a single topological invariant, its genus g, and we have the familiar picture
has a single topological invariant, its genus g, and we have the familiar picture
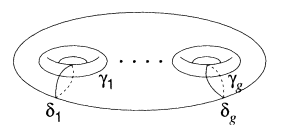
where δ1 δg, γ1γg form a canonical basis for H1(![]() , Z).
, Z).
The introduction of ![]() greatly clarifies the study of abelian integrals. For example, in terms of a local holomorphic coordinate z on
greatly clarifies the study of abelian integrals. For example, in terms of a local holomorphic coordinate z on ![]() , the rational differential ω = R(x,y)dx above is given by the expression
, the rational differential ω = R(x,y)dx above is given by the expression
where
is a meromorphic function. We then say ω is of the first kind if h(z) is holomorphic in all local coordinate systems, of the second kind if all residues c-1 = 0, and of the third kind otherwise. For example, assuming that the ai are distinct in (4), the holomorphic differentials on the hyperelliptic curve y2= (x-a1) (x-an) are given by abelian integrals (4) where R(x) is a polynomial of degree at most [n -1/2]. If the poles of ω are a finite set of points D, then the cycle γ is understood to be a class in H1(![]() -D,Z) and ω is of the second kind whenever its residues
-D,Z) and ω is of the second kind whenever its residues
are all zero. If S(x,y) is a rational function on C, then clearly the exact differential dS(x,y) is of the second kind.
Two results that relate the algebraic geometry and topology of an algebraic curve are these:
the vector space of differentials of the first kind has dimension equal to g; (5)
the vector space of differentials of the second kind modulo exact differentials has dimension equal to 2g = rank H1(![]() ,Z). (6)
,Z). (6)
As we shall see, by understanding the topology of an algebraic variety, Lefschetz was able to give far-reaching extensions of these results.
Toward the end of the nineteenth century, the study of algebraic curves was extended by Max Noether and others,
especially the Italian school led by Castelnuovo, Enriques, and Severi. In addition, these mathematicians and others began the systematic study of algebraic curves and algebraic surfaces from a projective or geometric point of view. To them, an algebraic surface S was the generic projection into P3 of a smooth algebraic surface ![]() lying in a PN. Thus, S is given by the single affine equation
lying in a PN. Thus, S is given by the single affine equation
and has singularities from a very short list of special types. A major result was that any algebraic surface has such a smooth model ![]() , and indeed an understanding was developed of all smooth models (in the case of curves, the Riemann surface
, and indeed an understanding was developed of all smooth models (in the case of curves, the Riemann surface ![]() is unique up to a biholomorphic transformation). Studying C or S by geometric methods operationally meant analyzing the various linear systems of divisors on the curve or surface. The specifics of these are not particularly relevant here; suffice it to say that little use was made of the topology and/or analysis on the variety.
is unique up to a biholomorphic transformation). Studying C or S by geometric methods operationally meant analyzing the various linear systems of divisors on the curve or surface. The specifics of these are not particularly relevant here; suffice it to say that little use was made of the topology and/or analysis on the variety.
Meanwhile, Picard and Poincaré in France had undertaken to extend results such as those in equations (5) and (6) to algebraic surfaces. Thus, they attempted to classify both single and double rational integrals

on the surface (7) in much the same way as had been done for curves. Here P, Q and R are rational functions of x, y, and z and it is assumed that the 1-form P dx + Q dy is closed, i.e., that
In this case we may speak both of the indefinite integral (8) and of its periods, as in the curve case. For the double integral (9), however, only its periods are defined. These are expressions
where γ is a closed 2-cycle in ![]() supported outside the singular locus of R dx dy.
supported outside the singular locus of R dx dy.
It is clear that the introduction of homology theory by Poincaré was essential for an understanding of rational integrals on a surface, and Poincaré's work on ''analysis situs'' was done while Picard was midstream in his own investigations. In what remains one of the "tour de forces" in the history of mathematics, over a period of about twenty years, Picard was able to arrive at a preliminary understanding of both single and double rational integrals on an algebraic surface. These investigations are detailed in the two volumes of Traité des Fonctions Algébriques de Deux Variables by Picard and Simart. There one may find a fairly complete extension (completed by Poincaré) of equations (5) and (6) to the rational integrals (8), an extension made possible by the understanding of the 1-cycles on an algebraic surface that was developed by Picard and by the theory of so-called normal functions due to Poincaré. For example, (5) becomes the statement that the number of closed, linearly independent holomorphic 1-forms on the surface is equal to the irregularity q, the irregularity being an algebro-geometric character that was later identified by Lefschetz as b1/2, where b1 = rank H1(![]() ,Z). In addition, by very lengthy arguments Picard was able to prove a number of results
,Z). In addition, by very lengthy arguments Picard was able to prove a number of results
concerning the double integrals (9). One of these may be explained as follows: We consider the affine algebraic surface S0 obtained by removing the hyperplane at infinity from S. Thus, S0 is the surface in C3 given by the polynomial equation (7). We then consider rational 2-forms
that are everywhere holomorphic on S0 and, therefore, that have their poles at infinity. These are then given by such expressions where R is a polynomial that has certain specified properties relative to the singularities of S0. Among such ω's are the exact differentials
where η = P dx + Q dy is a rational 1-form on S that is holomorphic on S0. Picard then proved that the pairing
between equivalence classes of such ω's modulo exact forms (10) and 2-cycles γ ∈ H2(S0,Z) modulo torsion cycles was nondegenerate. This is essentially equivalent to what is now known as the algebraic deRham theorem for algebraic surfaces.
As far as Picard and Poincaré were able to push things, certain difficulties remained. One was the relationship of the "curve at infinity"—i.e., S\S0—to the topology of S. In the third paragraph of his "A Page of Mathematical Autobiography" (1968, 2), Lefschetz refers to this when he says:
From the ρ0 formula of Picard, applied to a hyperelliptic surface Φ (topologically the product of 4 circles) I had come to believe that the second
Betti number R2(Φ) = 5, whereas clearly R2(Φ) = 6. What was wrong? After considerable time it dawned upon me that Picard only dealt with finite 2-cycles, the only useful cycles for calculating periods of certain double integrals. Missing link? The cycle at infinity, that is the plane section of the surface at infinity. This drew my attention to cycles carried by an algebraic surve, that is to algebraic cycles, and the harpoon was in!
Another difficulty, one that is totally unlike anything encountered in the study of rational integrals on curves, is that we may have a relation (10) where, for any η satisfying that equation, the poles of η are strictly longer than those of ω. In modern terminology, ω defines a class in H2(S0) that is nonzero but whose image vanishes in H2(S0\Do) for a suitable divisor Do on S.
It was at this stage that Lefschetz entered the picture. By systematically studying and understanding the topology of an algebraic surface, and also of a general n-dimensional algebraic variety, Lefschetz was able to solidify and considerably extend the results of Picard and Poincaré. In so doing, he once and for all established the principle that the understanding of the topology of an algebraic variety was central and essential in algebraic geometry. According to Hodge,7 "our greatest debt to Lefschetz lies in the fact that he showed us that a study of topology was essential for all algebraic geometers."
Before discussing the work of Lefschetz in more detail, I would like to remark that it was seeking a better understanding of Lefschetz' results on the topology of an algebraic variety that led Hodge to his work on harmonic integrals as detailed in his book The Theory and Applications of Harmonic Integrals (Cambridge, 1988). Subsequently, it is fair to say that algebraic geometry has been central to the development of mathematics in the last forty years, and that the strand of what might be called "transcendental algebraic geometry" as represented by Lefschetz and
Hodge is now completely interwoven into algebraic geometry and into the rest of mathematics.
Turning to Lefschetz' work in algebraic geometry, his approach to the study of the topology of an algebraic variety was typically direct and intuitive. He treated an algebraic variety as a concrete object and analyzed its topology directly. In modern terms, he realized a smooth n-dimensional ![]() by generally projecting it to a hypersurface V in Pn + 1 given by the affine equation
by generally projecting it to a hypersurface V in Pn + 1 given by the affine equation
Questions of singularities were by and large circumvented by suitably lifting various constructions on V up to ![]() . Now it was Picard who systematically analyzed the algebraic surface (7) by considering it as "fibred" by the ∞1 algebraic curves Cy given by
. Now it was Picard who systematically analyzed the algebraic surface (7) by considering it as "fibred" by the ∞1 algebraic curves Cy given by
This, in turn, was an extension of the classical method of studying the algebraic curve (2) by considering it as a branched covering over the x- axis. The analogue of branch points are then the singular curves Cy where the plane y = y is tangent to the surface f(x,y,z) = 0. Picard thus considered ![]() to be made up of the ∞l curves
to be made up of the ∞l curves ![]() yall but the singular ones having the picture above with retrosections δ1 δg, γ1 γg. The behavior of this topological picture was then analyzed. This method was then formalized and extended by Lefschetz, who proceeded to study the smooth variety
yall but the singular ones having the picture above with retrosections δ1 δg, γ1 γg. The behavior of this topological picture was then analyzed. This method was then formalized and extended by Lefschetz, who proceeded to study the smooth variety ![]() inductively by closely examining its hyperplane sections given by (11), together with Σ cixi = constant.
inductively by closely examining its hyperplane sections given by (11), together with Σ cixi = constant.
More specifically, choosing coordinates generically, we
consider the Lefschetz pencil of (n-1)-dimensional varieties Wt given by
The lifts ![]() of Wt to
of Wt to ![]() are then smooth except for a finite number of critical values t = t1, t = tN, where the hyperplane xn = tα is simply tangent to Wt at one finite point þα. In a suitable local analytic coordinate system z1, zn+1 in Pn+1 centered around þα, the Lefschetz pencil has the analytic equation
are then smooth except for a finite number of critical values t = t1, t = tN, where the hyperplane xn = tα is simply tangent to Wt at one finite point þα. In a suitable local analytic coordinate system z1, zn+1 in Pn+1 centered around þα, the Lefschetz pencil has the analytic equation
and from this a complete and explicit analysis of the topology of the ![]() as t → tα is possible. The result is that locally
as t → tα is possible. The result is that locally ![]() retracts onto the real n-sphere δt given by
retracts onto the real n-sphere δt given by
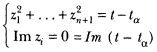
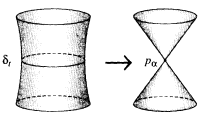
This cycle then shrinks to a point or vanishes as t → tα. All this may be pictured in the case n = 1 by
Assume now that, by an inductive procedure, the topological structure of the ![]() is known in a manner to be made
is known in a manner to be made
more explicit below. Next, picture the t-plane with slits drawn to the critical values
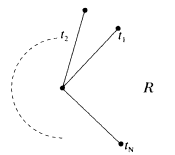
Over the simply connected region R on the t-sphere minus the slits, the family ![]() , t ∈ R is topologically trivial and is thus a product. More precisely, if we assume that inductively
, t ∈ R is topologically trivial and is thus a product. More precisely, if we assume that inductively ![]() , t ∈ R, has been represented as a real 2(n -1) cell et2n-2, with suitable identifications on the boundary, then the family et2n-2, t ∈ R, describes a 2n-cell e2n. The boundary of e2n consists of the family of boundaries of the et2n-2, which are assumed to be known inductively, together with the identifications that result from the identifications across the slits t0tα, as depicted above. These latter identifications are then known from a local analysis of the singularities around the points þα.
, t ∈ R, has been represented as a real 2(n -1) cell et2n-2, with suitable identifications on the boundary, then the family et2n-2, t ∈ R, describes a 2n-cell e2n. The boundary of e2n consists of the family of boundaries of the et2n-2, which are assumed to be known inductively, together with the identifications that result from the identifications across the slits t0tα, as depicted above. These latter identifications are then known from a local analysis of the singularities around the points þα.
In the case n = 1, the cells et2 are obtained by cutting the Riemann surface ![]() along the retrosections δ1 δg, γ1 γg. As t → tα we have a global picture
along the retrosections δ1 δg, γ1 γg. As t → tα we have a global picture
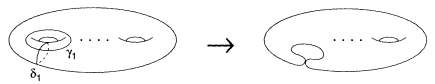
where the cycle δ1 vanishes. An explicit local analysis of this picture around t= tα gives the identification
to be made across the slit t0tα.
I have given this description not so much to attempt to reproduce Lefschetz as to illustrate his way of working, which, as mentioned, was concrete and direct. He had marvelous intuition, and so far as I know, all of the results he claimed in algebraic geometry have now been proved. When I was a graduate student at Princeton, it was frequently said that "Lefschetz never stated a false theorem nor gave a correct proof." In the case of the method of Lefschetz' pencils, it was later recognized that he was using t as a complex Morse function, log |t-t0| being the real Morse function, and this then led to the very beautiful derivation of Lefschetz' theorems, as given by Andreotti-Frankel (in Global Analysis, Princeton University Press, 1969).
These theorems may be summarized as follows: denote by ![]() a general smooth hyperplane section
a general smooth hyperplane section ![]() 0 of
0 of ![]() and consider the inclusion mapping
and consider the inclusion mapping
Then, to begin with, we have:
the mappings (12) are isomorphisms for i ≤n -2 and are subjective for i = n -1; (13)
for i = n -1, the kernel of j is generated by the vanishing cycles dα associated to the various critical points t = tα. (14)
These two results have the effect of reducing the topology of a variety below the middle dimension to that of its hyperplane sections. To understand the crucial middle ho-
mology group from the exact homology sequence of the pair (![]() ,
,![]() ) and assuming an inductive understanding of Hn (
) and assuming an inductive understanding of Hn (![]() ,Z), we need to understand the relative group Hn(
,Z), we need to understand the relative group Hn(![]() ,
,![]() ;Z) and this is given by the statement:
;Z) and this is given by the statement:
the group Hn(![]() ,
, ![]() ;Z) is generated by the relative cycles ∆α described by the locus of the vanishing cycle δt as t traverses the slit t0tα. (15)
;Z) is generated by the relative cycles ∆α described by the locus of the vanishing cycle δt as t traverses the slit t0tα. (15)
In addition to giving the δα and ∆α as generators of suitable groups, Lefschetz also gave the generators for the relations among these cycles and thereby arrived at a complete understanding of the Hi(![]() , Z) for i ≤ n. For i > n we consider the mappings
, Z) for i ≤ n. For i > n we consider the mappings
obtained by intersecting a cycle with k general hyperplane sections. Then we have
the mapping (16) is an isomorphism. (17)
This result, the so-called Hard Lefschetz Theorem, has an interesting history. To see what it means, we consider the case of algebraic surfaces. Over the punctured t-sphere B = P1\{t1, tN}, we have a family ![]() t, t ∈ B, of smooth algebraic curves. By transporting cycles
t, t ∈ B, of smooth algebraic curves. By transporting cycles ![]() t around closed loops on B, we obtain the so-called monodrony action of π1 (B) on H1(
t around closed loops on B, we obtain the so-called monodrony action of π1 (B) on H1(![]() ,Z). The effect of moving cycles around a critical point tα is given by the Picard-Lefschetz transformation
,Z). The effect of moving cycles around a critical point tα is given by the Picard-Lefschetz transformation
where γ · dα is the intersection number. It follows from (13) and (14) that H1 (![]() ) is isomorphic to
) is isomorphic to
This is just the space of invariant cycles, i.e., classes in H1(![]() ) that are invariant under the action of πl(B).
) that are invariant under the action of πl(B).
Given a 3-cycle Γ on ![]() that is in general position, the intersections
that is in general position, the intersections
give a family of cycles invariant under π1 (B) and the map L: H3 (![]() ) → H1(
) → H1(![]() ) is just Γ →
) is just Γ → ![]() 0= γ ∈ H1(
0= γ ∈ H1(![]() ) followed by the natural mapping H1(
) followed by the natural mapping H1(![]() ) → H1(
) → H1(![]() ). Conversely, if γ is an invariant cycle, then the locus Γ of its translates γt is a 3-cycle with Γ ·
). Conversely, if γ is an invariant cycle, then the locus Γ of its translates γt is a 3-cycle with Γ · ![]() = γ. Thus, the mapping L is subjective, and to prove that it is injective, we must show that
= γ. Thus, the mapping L is subjective, and to prove that it is injective, we must show that
an invariant, vanishing cycle is zero. (18)
It is easy to see that (18) is equivalent to the assertion
the intersection form on the space of vanishing cycles is nondegenerate, (18)'
and that, in turn, is a consequence of the action of
πl(B) on H1(![]() ) is semi-simple. (18)"
) is semi-simple. (18)"
Clearly, (18)-(18)" are global statements about monodrony, and although (18)" is true, the only existing proofs require the use of Hodge theory or its effective equivalent. This is a case in which Lefschetz' intuition was right on target, but the direct, geometric approach was insufficient to give a complete proof.
As a consequence of the results (13)-(17), Lefschetz deduced the properties
on the Betti numbers bi of a smooth n-dimensional variety. The first inequality in the case i = 0, n = 2 is a consequence of (18)', since an alternating bilinear form can be nondegenerate only on a vector space of even dimensions; the general case is proved by similar considerations.
The second inequality above arises from the following considerations. First, any k-dimensional subvariety ![]() ⊂
⊂ ![]() carries a fundamental cycle [
carries a fundamental cycle [![]() ] ∈ H2k(
] ∈ H2k(![]() ,Z).(Typically, Lefschetz considered this as obvious.) Second, for subvarieties
,Z).(Typically, Lefschetz considered this as obvious.) Second, for subvarieties ![]() 1 and
1 and ![]() 2 of complementary dimensions and meeting in isolated points, the algebro-geometric and topological intersection numbers are equal, namely
2 of complementary dimensions and meeting in isolated points, the algebro-geometric and topological intersection numbers are equal, namely
Finally, a general k-fold hyperplane section ![]() and a general (n-k)-fold hyperplane meet in a positive number of points, and consequently [
and a general (n-k)-fold hyperplane meet in a positive number of points, and consequently [![]() ] ≠ 0. The argument just given is clearly a special case of the Hard Lefschetz Theorem (16); the point of putting it here is that it explains how Lefschetz' attention was drawn to the part
] ≠ 0. The argument just given is clearly a special case of the Hard Lefschetz Theorem (16); the point of putting it here is that it explains how Lefschetz' attention was drawn to the part ![]() (
(![]() ,Z) of the homology of a smooth variety that is represented by algebraic cycles, i.e., by linear combinations of fundamental classes of k-dimensional algebraic subvarieties.
,Z) of the homology of a smooth variety that is represented by algebraic cycles, i.e., by linear combinations of fundamental classes of k-dimensional algebraic subvarieties.
Lefschetz was especially interested in the part ![]() (
(![]() ,Z) given by the fundamental classes of the divisors on
,Z) given by the fundamental classes of the divisors on ![]() . Here, his results were definitive. To state them we shall specialize to the case of algebraic surfaces, although every
. Here, his results were definitive. To state them we shall specialize to the case of algebraic surfaces, although every
thing extends to n-dimensions. Two divisors D1,D2 on an algebraic surface are said to be algebraically equivalent in case there is an algebraic family {Dl} of divisors parameterized by an auxilary variety ![]() and such that Di =Dλi for suitable points λ1,λ2 on
and such that Di =Dλi for suitable points λ1,λ2 on ![]() . It is clear that [Dl] = [D2] if D1 and D2 are algebraically equivalent, and Lefschetz proved the converse. This then established once and for all the so-called theory of the base and the finiteness of the rank p of the group of divisors modulo algebraic equivalence.
. It is clear that [Dl] = [D2] if D1 and D2 are algebraically equivalent, and Lefschetz proved the converse. This then established once and for all the so-called theory of the base and the finiteness of the rank p of the group of divisors modulo algebraic equivalence.
Now, this number p = H2alg (![]() ,Z) had been discussed by Picard in his attempt to classify the double integrals (9). Lefschetz was now able to give the generalization of (6) to double integrals by completing Picard's 'algebraic deRham' result to
,Z) had been discussed by Picard in his attempt to classify the double integrals (9). Lefschetz was now able to give the generalization of (6) to double integrals by completing Picard's 'algebraic deRham' result to
the dimension of the space of rational differentials ω = R(x,y)dx dy of the second kind modulo exact forms is equal to b-p. (20)
Put another way, Lefschetz was able to show that the occurrence of the relation (10) where poles (η) > poles (ω) was attributable to the nonhomologous algebraic 1-cycles on ![]() .
.
A related result, the famous Lefschetz (1,1) theorem, characterized the algebraic part H2alg (![]() ,z) of H2(
,z) of H2(![]() ,z). The result is:
,z). The result is:
A necessary and sufficient condition that a class Γ ∈ H2(![]() ,Z) be of the form Γ = [D] for (21)
,Z) be of the form Γ = [D] for (21)
some divisor D is
for all holomorphic two-forms ω on ![]() . The conjectured extension of (21) to higher dimensions and codimensions
. The conjectured extension of (21) to higher dimensions and codimensions
is due to Hodge, and it remains one of the major unsolved problems in algebraic geometry.
To conclude this section on Lefschetz and algebraic geometry, I would like to briefly comment on Lefschetz' subsequent influence on algebraic geometry. In the first forty or so years of the twentieth century there were two principal strands in algebraic geometry; one was the geometric approach of the Italian school, and the other was the transcendental approach as represented by Lefschetz and Hodge and continued by Kodaira and Spencer. In the last half-century a third strand, the algebraic approach of Weil, Zariski, and Grothendieck was added, and all three strands have now become intertwined. There is no better illustration of this than the Weil conjectures. These purely arithmetical statements were formulated by Weil, who also understood that they could be proved if a ''suitable'' cohomology theory could be developed for varieties defined over a field of finite characteristic. A suitable cohomology theory is essentially one for which Poincaré duality and the various Lefschetz theorems stated above, in particular the Hard Lefschetz Theorem, could be established. Such a cohomology theory was introduced by Grothendieck, and as is well known, the Weil program was completed by Deligne, who in effect used an inductive procedure reminiscent of the Lefschetz pencil method to prove an arithmetic analogue of the Hard Lefschetz Theorem.
When we look at algebraic geometry today, we not only see the intertwining of the historical strands within the field, but equally, we see algebraic geometry intertwined with the rest of mathematics and central to the ongoing developments of the field. One illustration of this is the use of algebraic geometry to generate solutions of special differential equations, both ordinary and partial. Here I mention the work originating from the Russian school that
constructs commuting integrals of special Hamiltonian dynamical systems from the Jacobian variety of algebraic curves, and the Atiyah-Hitchin-Drinfeld-Manin construction of special solutions to the Yang-Mills equations from suitable algebraic vector bundles. To some extent it may be said that we have come full circle to the historical roots of algebraic geometry in the study of special transcendental functions arising from abelian integrals, abelian sums, and periods as explained above. In all of these developments, the topological properties of algebraic varieties, as part of the infrastructure of algebraic geometry, play a central role.
I would like to mention a very beautiful recent development that exemplifies both a style and subject that are direct descendents of Lefschetz. This is the intersection homology theory of algebraic varieties due to Goresky-MacPherson, a theory that was designed to retain Poincaré duality and that reflects the topological properties of singularities in much the same way as ordinary homology, in the hands of Lefschetz, reflected the topology of smooth varieties. On reading the original paper of Goresky-MacPherson (Inventions Math., Vol 71, 1983) one cannot help but be struck by the similarity in viewpoint to Lefschetz.
Lefschetz' influence in algebraic geometry clearly places him in the tradition of Abel, Jacobi, Riemann, Poincaré, and Picard, whose works he drew so much from and extended in such a significant way. This influence is manifest today in his theorems, some of which were stated above, in the intertwining of topology and algebraic geometry, and in his overall approach to mathematics.
LEFSCHETZ THE TOPOLOGIST
Much of Lefschetz' work in topology is concerned with the notion of "fixed point." If f is a continuous mapping of a space X into itself, a fixed point of f is a point x such
that f(x) = x. The first important result of fixed-point theory was proved by L. E. J. Brouwer in 1912. It asserts that, if E is a closed n-cell, then every mapping of E into itself has (at least) one fixed point. This result becomes false if E is replaced by a space with a more complicated topological structure. For example, if S is the unit sphere in Euclidean (n + 1)-space and f is the antipodal map, given by the formula f(x) =-x for all points x of S, then f has no fixed points. On the other hand, any mapping of S into itself has a well-defined degree d(f) [intuitively, d(f) is the number of times that f maps S around itself; a more precise definition is given in the next paragraph]. It can be proved that any map whose degree is different from the degree (-1)n+1 of the antipodal map has a fixed point.
If X is a compact polyhedron and q is a non-negative integer, the q th homology group of X with rational coefficients is a rational vector space Hq(x) of finite dimension; and a map f: X → X induces a homomorphism fq: Hq(X) → Hq(X), which can be represented by a square matrix with rational (in fact, with integral) entries. If tq is the trace of this matrix, the Lefschetz number of f is the alternating sum L(f) of the integers tq. The homomorphisms fq depend only on the homotopy class of the map f and therefore the same is true for the Lefschetz number. In particular, if g is a sufficiently close approximation to f, then L(f) = L(g) When X is the n-sphere, the only nontrivial homology groups of X occur in dimensions o and n, and the latter groups are one-dimensional. Thus, to and tn are integers; in fact, to = 1 and tn = d(f), so that
Thus, the above result on self-maps of the n-sphere is subsumed in the Lefschetz Fixed-Point Theorem: If X is a
compact polyhedron and f: X → X a map such that L(f) ≠ 0, then f has a fixed point.
In his first proof of the fixed-point theorem in 1923 (1923, 1), Lefschetz made the additional assumption that X is an orientable closed n-manifold. One can approximate the map f by a map g that has only a finite number of fixed points and that is well-behaved near each fixed point x in the sense that g maps some neighborhood of x homomorphically upon another neighborhood. The index i(x) is then defined to be +1 or -1 according to whether g preserves or reverses orientation about x. The Cartesian square of X is an orientable (2n )-manifold Y, and the diagonal D and the graph G of g can be regarded as n-cycles in Y. Their intersection consists of all points (x,x) such that x is a fixed point of g; it is a zero-cycle y of Y whose Kronecker index I(y) is easily seen to equal the sum of the indices of the fixed points of g. But I(y) can be calculated in a different way, using the Künneth theorem on the homology groups of a product space and the Poincar é duality theorem in Y, with the result that I(y) = L(g). If f has no fixed points, we may assume that g has none either; then L(f) = L(g)= I(y) = 0.
While this proof is attractive, it suffers from the disadvantage that it fails to include the Brouwer theorem as a special case. This is because the n-cell is not a closed manifold, but rather a manifold with a boundary; and the above proof breaks down because of the failure of Poincaré duality for manifolds with a boundary. It was to remedy this situation that Lefschetz invented relative homology.
Like many other results of the time, the Lefschetz Duality Theorem was awkward to state because the correct concepts had not yet been developed. Expressed in modern language, it asserts that, if X is a (compact, oriented) n-manifold with regular boundary A, then the relative ho-
mology group Hq(X,A) is isomorphic with the cohomology group Hn-q( X). For the purpose of proving the fixed-point theorem, it suffices to know that the homology groups Hq(X,A) and Hn-q(X) are dual vector spaces. This was sufficient to modify the proof above to cover the case of manifolds with regular boundary, and this was done by Lefschetz in 1927 (1927, 2).
The importance of the Lefschetz duality theorem was not limited to this application. Of course, if A = Ø it reduces to the Poincaré duality theorem. On the other hand, if A is a subcomplex of a triangulation of the n-sphere S, and if U is a regular neighborhood of A, then S-U is a manifold with regular boundary b(U), to which we may apply the Lefschetz duality theorem to conclude that Hq[S-U,b(U)] and Hn-q (S-U) are isomorphic. Using standard (by now!) techniques of homology theory, we recover the Alexander duality theorem. Thus, the Lefschetz duality theorem appears as a unifying factor, connecting two important but apparently unrelated results.
Not content with this version of the fixed-point theorem, Lefschetz continued to seek generalizations. In 1928 Hopf had proved the theorem for arbitrary compacy polyhedra, but with some restriction on the map f. By 1934 Lefschetz had succeeded in removing the latter restrictions (1934,2), and by 1937 he was able to remove the hypothesis of triangulability of X, requiring instead that X be a compactum which is homologically locally connected in a suitable sense (1937,4).
The extensions of the fixed point theorem to more general spaces are not simply generalizations for their own sake. Indeed, fixed point theorems often appear in analysis as tools for proving existence theorems. To mention a very simple example, consider the ordinary first-order boundary problem
or, equivalently, the integral equation
The correspondence that associates to each function y the function defined by the right-hand side of the latter equation may be regarded as a mapping f of a suitable function space into itself. And a solution of the equation is nothing but a fixed point of f. To be sure, the function spaces appearing here and in other places in analysis are far from being compact, and so the Lefschetz theorem does not apply directly. Nevertheless, this point of view has been a very powerful one in modern analysis.
The importance of Lefschetz' work, however, is not limited to the study of fixed-point theorems. The notion of a fixed point of a map of a space into itself can be thought of as a special case of that of a coincidence. If f, g: X → Y are maps, a coincidence of f and g is a point x such that f(x) = g(x) If Y = X and f is the identify map, a coincidence of f and g is simply a fixed point of g. The graphs G(f) and G(g) of f and g are subspaces of X × Y, and the coincidences of f and g correspond to the intersection of their graphs. If X and Y are manifolds of dimensions m and n, respectively, then G(f) and G(g) may be regarded as m-cycles in the (m + n)-manifold X × Y. Now the theory of intersections in algebraic geometry was an old one; if U and V are subvarieties of an algebraic variety W, in general position, their intersection is a subvariety of dimension p + q-n, where p, q, and n are the dimensions of U, V, and W, respectively. This suggested to Lefschetz the idea of defining intersections in an orientable manifold M. This he succeeded in doing with the result that the graded
homology group of M is a ring, the intersection ring of M (1926,1).
All this took place before the discovery of cohomology. While Lefschetz did not define cohomology groups, he introduced pseudo-cycles in 1930 (1930,4). They were not defined intrinsically but, rather, were defined in terms of an embedding of the space in question in a sphere, and were used only as a tool for the proof of one of the versions of his fixed-point theorem. It was not until the late 1930s that the modern treatment of cohomology and cup products was given.
Other of Lefschetz' ideas that by now have thoroughly permeated the subject include singular homology theory and relative homology. While Lefschetz was not the first to use singular chains, his Colloquium Lectures (1930,1) gave the first formal treatment of the theory. His theory had some mild defects (the chain groups turned out not to be free), but these were corrected by Eilenberg in 1944, and the resulting theory has been of the greatest importance. As for relative homology groups, they are principal ingredients in the axiomatic treatment of the homology theory by Eilenberg and Steenrod, which has been so influential in the development of the subject in the last thirty or so years.
LEFSCHETZ AND ORDINARY DIFFERENTIAL EQUATIONS
Lefschetz was nearly sixty years old when he turned to differential equations, and he devoted the last twenty-five years of his life to the subject. He wrote over forty papers, articles, and books in this field and formed around him a vigorous and distinguished school, guiding and encouraging students and young mathematicians to work on problems of significance. In fact, he rekindled interest in a subject that had been nearly totally neglected in the United
States, and he recognized its mathematical importance and practical implications.
Although Lefschetz' own contributions to differential equations, control theory, and dynamical systems are not comparable to his great work in algebraic geometry and topology, he nevertheless wrote noteworthy original papers in these areas. His main interests centered around the theory of dissipative (as distinct from conservative) dynamical systems, including structural stability, and the resolution of singularities of critical points and bifurcating periodic orbits.
Dissipative dynamical systems are important in engineering problems where friction and resistance are essential ingredients. Such dynamical systems can be represented as vector fields on the phase-space manifold. Let S be the set of all C1 vector fields on a compact differentiable manifold M without boundary and assign to S the C1-topology. Two systems V1 and V2 of S are said to be qualitatively equivalent if there is a homomorphism of M mapping the unparameterized solution curves of V1 onto those of V2. A dynamical system V is called structurally stable if there is a neighborhood N of V in S such that each V1 ∈ N is qualitatively equivalent to V. Structurally stable differential systems are important in applied problems where the parameters of the physical process are known only approximately.
Lefschetz stimulated and guided work on these qualitative problems of global analysis. H. F. DeBaggis improved results of Pontryagin for the sphere S2 = M, and M. Peixoto proved that the structurally stable systems on a compact surface form an open dense subset of S. L. Markus proved that, on arbitrary n-dimensional manifolds M, a structurally stable system must necessarily have isolated and elementary critical points and periodic orbits.
Lefschetz was the first person from outside the former Soviet Union to recognize the importance of Liapunov's
stability theory, and he made an important contribution to the Lurie stability problem, one of the first applications of the Liapunov theory to a nonlinear control problem. He opened up the field of the mathematical theory of control, and in 1951, one of his students, Donald Bushaw, gave the first complete solution of a nontrivial problem in optimal control.
Among his other original contributions was his work on the behavior of solutions of analytic differential equations near an isolated singular point. He gave a complete characterization and a constructive procedure for obtaining all the solution curves of a two-dimensional system near an isolated critical point that pass through this critical point (1968,1). For a two-dimensional analytic system for which the coefficient matrix of the linear variational equation of an isolated critical point has both roots zero but is not identically zero, he proved that there can be at most a single nested oval of orbits (1958,1). He gave one of the best treatments of the method of determining the stability of an isolated equilibrium point of an n-dimensional system for which the linear variational equation has some zero roots(1961,1). He also studied the existence of periodic solutions of second- and higher-order nonlinear systems of differential equations (see 1943,2; 1954,2).
NOTES
1. Phillip Griffiths wrote the section on algebraic geometry, Donald Spencer wrote the sections on personal history and ordinary differential equations, and George Whitehead wrote the section on topology.
2. The date of the accident has been given incorrectly by several authors. The account of it here is taken from a communication by Lefschetz to the Academy dated January 8, 1954, and entitled "A Self Portrait," an unpublished document that was requested by A. Wetmore on behalf of the Academy.
3. From "A Self Portrait" (see note 2).
4. Topology can be described as the study of continuous functions, and it is customary to use the work "map" or "mapping" when referring to such functions.
5. F. Nebeker and A. W. Tucker, "Lefschetz, Solomon," in Dictionary of Scientific Biography, Supplement II, 1991.
6. Algebraic Geometry and Topology, a Symposium in Honor of S. Lefschetz, edited by R. H. Fox, D. C. Spencer, and A. W. Tucker, Princeton University Press, 1957, pp. 1-49.
7. Ibid, note 6.
BIBLIOGRAPHY OF S. LEFSCHETZ
1912 Two theorems on conics. Ann. Math. 14:47-50.
On the V33 with five nodes of the second species in S4. Bull. Am. Math. Soc. 18:384-86.
Double curves of surfaces projected from space of four dimensions Bull. Am. Math. Soc. 19:70-74.
1913 On the existence of loci with given singularities. Trans. Am. Math. Soc. 14:23-41. (Doctoral dissertation, Clark University, 1911.)
On some topological properties of plane curves and a theorem of M öbius. Am. J. Math 35:189-200.
1914 Geometry on ruled surfaces. Am. J. Math. 36:392-94.
On cubic surfaces and their nodes. Kans. Univ. Sci. Bull. 9:69-78.
1915 The equation of Picard-Fuchs for an algebraic surface with arbitrary singularities. Bull. Am. Math. Soc. 21:227-32.
Note on the n-dimensional cycles of an algebraic n-dimensional variety. R. C. Mat. Palermo 40:38-43.
1916 The arithmetic genus of an algebraic manifold immersed in another Ann. Math. 17:197-212.
Direct proof of De Moivre's formula. Am. Math. Mon. 23:366-68.
On the residues of double integrals belonging to an algebraic surface Quart. J. Pure Appl. Math. 47:333-43.
1917 Note on a problem in the theory of algebraic manifolds. Kans. Univ. Sci. Bull. 10:3-9.
Sur certains cycles à deux dimensions des surfaces algébriques. R. C. Accad. Lincei 26:228-34.
Sur les intégrales multiples des variétiés algébriques. C. R. Acad. Sci. Paris 164:850-53.
Sur les intégrals doubles des variétiés algébriques. Annali Mat. 26: 227-60.
1919 Sur l'analyse situs des variétiés algébriques. C. R. Acad. Sci. Paris 168:672-74.
Sur les variétiés abéliennes. C. R. Acad. Sci. Paris 168:758-61.
On the real folds of Abelian varieties. Proc. Natl. Acad. Sci. U.S.A. 5:103-6.
Real hypersurfaces contained in Abelian varieties. Proc. Natl. Acad. Sci. U.S.A. 5:296-98.
1920 Algebraic surfaces, their cycles and integrals. Ann. Math. 21:225-28. (Correction, Ann. Math. 23:333.)
1921 Quelques remarques sur la multiplication complexe. Comptes Rendus du Congrès International des Mathématiciens, Strasbourg, September 1920. Toulouse: É. Privat.
Sur le théorème d'existence des fonctions abéliennes. R. C. Accad. Lincei 30:48-50.
On certain numerical invariants of algebraic varieties with application to Abelian varieties. Trans. Am. Math. Soc. 22:327-482.
1923 Continuous transformations of manifolds. Proc. Natl. Acad. Sci. U.S.A. 9:90-93.
Progrès récents dans la théorie des fonctions abéliennes. Bull. Sci. Math. 47:120-28.
Sur les intégrales de seconde espèce des variétiés algébriques. C. R. Acad. Sci. Paris 176:941-43.
Report on curves traced on algebraic surfaces. Bull. Am. Math. Soc. 29:242-58.
1924 L'analysis situs et la géométrie algébrique. Collection de monographies publiée sous la direction de M. Émile Borel. Paris: Gauthier-Villars. (New edition, 1950.)
Sur les integrals multiples des variétiés algébriques. J. Math. Pure Appl. 3:319-43.
1925 Intersections of complexes on manifolds. Proc. Natl. Acad. Sci. U.S.A. 11:287-89.
Continuous transformations of manifolds. Proc. Natl. Acad. Sci. U.S.A. 11:290-92.
1926 Intersections and transformations of complexes and manifolds. Trans. Am. Math. Soc. 28:1-49.
Transformations of manifolds with a boundary. Proc. Natl. Acad. Sci. U.S.A. 12:737-39.
1927 Un théorème sur les fonctions abélinnes. In Memorian N. I. Lobatschevskii, pp. 186-90. Kazan, USSR: Glavnauka.
Manifolds with a boundary and their transformations. Trans. Am. Math. Soc. 29:429-62, 848.
Correspondences between algebraic curves. Ann. Math. 28:342-54.
The residual set of a complex on a manifold and related questions Proc. Natl. Acad. Sci. U.S.A. 13:614-22, 805-7.
On the functional independence of ratios of theta functions. Proc. Natl. Acad. Sci. U.S.A. 13:657-59.
1928 Transcendental theory; singular correspondences between algebraic curves; hyperelliptic surfaces and Abelian varieties. In Selected Topics in Algebraic Geometry, vol. 1, chapters 15-17, pp. 310-95. Report of the Committee on Rational Transformations of the National Research Council, Washington. NRC Bulletin no. 63. Washington, D.C.: National Academy of Sciences.
A theorem on correspondence on algebraic curves. Am. J. Math. 50:159-66.
Closed point sets on a manifold. Ann. Math. 29:232-54.
1929 Géométrie sur les surfaces et les variétiés algébriques. Mémorial des Sciences Mathématiques, Fasc. 40. Paris: Gauthier-Villars.
Duality relations in topology. Proc. Natl. Acad. Sci. U.S.A. 15:367-69.
1930 Topology. Colloquium Publications, vol. 12. New York: American Mathematical Society.
Les transformations continues des ensembles fermés et leurs points fixes. C. R. Acad. Sci. Paris 190:99-100.
(With W. W. Flexner.) On the duality theorems for the Betti numbers of topological manifolds Proc. Natl. Acad. Sci. U.S.A. 16:530-33.
On transformations of closed sets. Ann. Math. 31:271-80.
1931 On compact spaces. Ann. Math. 32:521-38.
1932 On certain properties of separable spaces. Proc. Natl. Acad. Sci. U.S.A. 18:202-3.
On separable spaces. Ann. Math. 33:525-37.
Invariance absolute et invariance relative en géométrie algébrique. Rec. Math. (Mat. Sbornik) 39:97-102.
1933 On singular chains and cycles. Bull. Am. Math. Soc. 39:124-29.
(With J. H. C. Whitehead.) On analytical complexes. Trans. Am. Math. Soc. 35:510-17.
On generalized manifolds. Am. J. Math. 55:469-504.
1934 Elementary One- and Two-Dimensional Topology. Princeton, N.J.: Princeton University. (Mimeograph.)
On locally connected and related sets. Ann. Math. 35:118-29.
1935 Topology. Princeton, N.J.: Princeton University. (Mimeograph.)
Algebraicheskaia geometriia: metody, problemy, tendentsii. In Trudy Vtorogo Vsesoiuznogo Matematischeskogo S''ezda, Leningrad, 24-30 June 1934, vol. 1, pp. 337-49. Leningrad-Moscow.
Chain-deformations in topology. Duke Math. J. 1:1-18.
Application of chain-deformations to critical points and extremals Proc. Natl. Acad. Sci. U.S.A. 21:220-22.
A theorem on extremals. I, II. Proc. Natl. Acad. Sci. U.S.A. 21:272-74. On critical sets. Duke Math. J. 1:392-412.
1936 On locally-connected and related sets (second paper). Duke Math. J. 2:435-42.
Locally connected sets and their applications. Rec. Math. (Mat. Sbornik) 1:715-17.
Sur les transformations des complexes en sphères. Fund. Math. 27:94-115.
Matematicheskaia deiatel'nost'v Prinstone. Usp. Mat. Nauk 1:271-73.
1937 Lectures on Algebraic Geometry. Part 1. 1936-37. Princeton, N.J.: Princeton University Press. (Planograph.)
Algebraicheskaia geometriia. Usp. Mat. Nauk 3:63-77.
The role of algebra in topology. Bull. Am. Math. Soc. 43:345-59.
On the fixed point formula. Ann. Math. 38:819-22.
1938 Lectures on Algebraic Geometry. Part 2. 1937-38. Princeton, N.J.: Princeton University Press.
On chains of topological spaces. Ann. Math. 39:383-96.
On locally connected sets and retracts. Proc. Natl. Acad. Sci. U.S.A. 24:392-93.
Sur les transformations des complexes en sphères (note complèmentaire). Fund. Math. 31:4-14.
Singular and continuous complexes, chains and cycles. Rec. Math. (Mat. Sbornik) 3:271-85.
1939 On the mapping of abstract spaces on polytopes. Proc. Natl. Acad. Sci. U.S.A. 25:49-50.
1941 Abstract complexes. In Lectures in Topology; The University of Michigan Conference of 1940, pp. 1-28. Ann Arbor: University of Michigan Press.
1942 Algebraic Topology. Colloquium Publications, vol. 27. New York: American Mathematical Society.
Topics in Topology. Annals of Mathematics Studies, no. 10. Princeton, N.J.: Princeton University Press. (A second printing, 1951.)
Émile Picard (1856-1941): Obituary. American Philosophical Society Yearbook 1942, pp. 363-65.
1943 N. Kryloff and N. Bogoliuboff. Introduction of Nonlinear Mechanics. Annals of Mathematics Studies, no. 11. Translation by S. Lefschetz. Princeton, N.J.: Princeton University Press.
Existence of periodic solutions for certain differential equations Proc. Natl. Acad. Sci. U.S.A. 29:29-32.
1946 Lectures on Differential Equations. Annals of Mathematics Studies, no. 14. Princeton, N.J.: Princeton University Press.
1949 Introduction to Topology. Princeton Mathematical Series, no. 11. Princeton, N.J.: Princeton University Press.
A. A. Andronow and C. E. Chaikin. Theory of Oscillations. English language edition ed. S. Lefschetz. Princeton, N.J.: Princeton University Press.
Scientific research in the U.S.S.R.: Mathematics. Am. Acad. Polit. Soc. Sci. Ann. 263:139-40.
1950 Contributions to the Theory of Nonlinear Oscillations, ed. S. Lefschetz. Annals of Mathematics Studies, no. 20. Princeton, N.J.: Princeton University Press.
The structure of mathematics. Am. Sci. 38:105-11.
1951 Numerical calculations in nonlinear mechanics. In Problems for the Numerical Analysis of the Future, pp. 10-12. National Bureau of Standards, Applied Math. Series, no. 15. Washington, D.C.: U.S. Government Printing Office.
1952 Contributions to the Theory of Nonlinear Oscillations, vol. 2, ed. S. Lefschetz. Annals of Mathematics Studies, no. 29. Princeton, N.J.: Princeton University Press.
Notes on differential equations. In Contributions to the Theory of Nonlinear Oscillations, vol. 2, pp. 67-73.
1953 Algebraic Geometry. Princeton Mathematical Series, no. 18. Princeton, N.J.: Princeton University Press.
Algunos trabajos recientes sobre ecuaciones diferenciales. In Memoria de Congreso Cientifico Mexicana U.N.A.M., Mexico, vol. 1, pp. 122-23.
Las grades corrientes en las matemáticas del siglo XX. In Memoria de Congreso Cientifico Mexicana U.N.A.M., Mexico, vol. 1, pp. 206-11.
1954 Russian contributions to differential equations. In Proceedings of the Symposium on Nonlinear Circuit Analysis, New York, 1953, pp. 68-74. New York: Polytechnic Institute of Brooklyn.
Complete families of periodic solutions of differential equations Comment Math. Helv. 28:341-45.
On Liénard's differential equation. In Wave Motion and Vibration Theory, pp. 149-53. American Mathematical Society Proceedings of Symposia in Applied Math., vol. 5. New York: McGraw-Hill.
1956 On a theorem of Bendixson. Bol. Soc. Mat. Mexicana 1:13-27.
Topology, 2nd ed. New York: Chelsea Publishing Company. (Cf. 1930,1.)
1957 On coincidences of transformations. Bol. Soc. Mat. Mexicana 2:16-25.
The ambiguous case in planar differential systems. Bol. Soc. Mat. Mexicana 2:63-74.
Withold Hurewicz. In memoriam. Bull. Am. Math. Soc. 63:77-82.
Sobre la modernizacion de la geometria. Rev. Mat. 1:1-11.
Differential Equations: Geometric Theory. New York: Interscience.(Cf. 1962,1.)
1958 On the critical points of a class of differential equations. In Contributions to the Theory of Nonlinear Oscillations, vol. 4, pp. 19-28. Princeton, N.J.: Princeton University Press.
Liapunov and stability in dynamical systems. Bol. Soc. Mat. Mexicana 3:25-39.
The Stability Theory of Liapunov. Lecture Series no. 37. College Park, Md.: University Institute for Fluid Dynamics and Applied Mathematics.
1960 Controls: An application to the direct method of Liapunov. Bol. Soc. Mat. Mexicana 5:139-43.
Algunas consideraciones sobre las matemáticas modernas. Rev. Unión Mat. Argent. 20:7-16.
Resultados nuevos sobre casos criticos en ecuaciones diferenciales Rev. Unión Mat. Argent. 20:122-24.
1961 The critical case in differential equations. Bol. Soc. Mat. Mexicana 6:5-18.
Geometricheskaia Teoriia Differentsial'nykh Uravnenii. Moskva: Izd-vo Inostrannoi Lit-ry. (Translation of 1957,5.)
(With J. P. LaSalle.) Stability by Liapunov's Direct Method. New York: Academic Press.
(With J. P. LaSalle.) Recent Soviet contributions to ordinary differential equations and nonlinear mechanics. J. Math. Anal. Appl. 2:467-99.
1962 Differential Equations: Geometric Theory, 2nd rev. ed. New York: Interscience.
(Ed. with J. P. LaSalle.) Recent Soviet Contributions to Mathematics. New York: Macmillan.
1963 On indirect automatic controls. Trudy Mezhdunarodnogo Simpoziuma po Nelineinym Kolebaniyam, pp. 23-24. Kiev: Izdat. Akad. Ukrain. SSR.
Some mathematical considerations on nonlinear automatic controls. In Contributions to Differential Equations, vol. 1, pp. 1-28. New York: Interscience.
Elementos de Topologia. Ciudad de México: Universidad Nacional Autónoma de México.
(Ed. with J. P. LaSalle.) Proceedings of International Symposium on Nonlinear Differential Equations and Nonlinear Mechanics, Colorado Springs, 1961. New York: Academic Press.
1964 Stability of Nonlinear Automatic Control Systems. New York: Academic Press.
1965 Liapunov stability and controls. SIAMJ. Control Ser. A 3:1-6.
Planar graphs and related topics. Proc. Natl. Acad. Sci. U.S.A. 54:1763-65.
Recent advances in the stability of nonlinear controls. SIAM Rev. 7:1-12.
Some applications of topology to networks. In Proceedings of the Third Annual Allerton Conference on Circuit and System Theory, pp. 1-6. Urbana: University of Illinois.
1966 Stability in Dynamics. William Pierson Field Engineering Lectures, March 3, 4, 10, 11, 1966. Princeton, N.J.: Princeton University School of Engineering and Applied Science.
1967 Stability of Nonlinear Automatic Control Systems. Moscow: Izdat. ''Mir." (A translation of 1964,1, in Russian.)
1968 On a theorem of Bendixson. J. Diff. Equations, 4:66-101.
A page of mathematical autobiography. Bull. Am. Math. Soc. 74:854-79.
1969 The Lurie problem on nonlinear controls. In Lectures in Differential Equations, ed. A. K. Aziz, vol. 1, pp. 1-19. New York: Van Nostrand-Reinhold.
The early development of algebraic geometry. Am. Math. Mon. 76:451-60.
Luther Pfahler Eisenhart, 1876-1965: A Biographical Memoir. Bio-
graphical Memoirs, vol. 40, pp. 69-90. Washington, D.C.: National Academy of Sciences.
1970 Reminiscences of a mathematical immigrant in the United States. Am. Math. Mon. 77(4).
1971 The early development of algebraic topology. Bol. Soc. Brasileira Mat. 1:1-48.
AUXILIARY REFERENCES
R. C. Archibald, A Semicentennial History of the American Mathematical Society, I, New York, 1938, pp. 236-40.
Algebraic Geometry and Topology, a Symposium in Honor of S. Lefschetz , edited by R. H. Fox, D. C. Spencer, and A. W. Tucker, Princeton University Press, 1957, pp. 1-49.
Selected Papers by S. Lefschetz, including the book I 'analysis situs, Chelsea Publishing Company, Bronx, New York, 1971.
Sir William Hodge, "Solomon Lefschetz, 1884-1972," in Biographical Memoirs of Fellows of the Royal Society, 19, London, 1973; reprinted in Bulletin of the London Mathematical Society, 6 (1974), pp. 198-217 and in The Lefschetz Centennial Conference, I, Mexico 1984, D. Sunderaraman, ed., published as Contemporary Mathematics, 58.1, American Mathematical Society, 1986, pp. 27-46.
J. K. Hale and J. P. La Salle, The Contribution of Solomon Lefschetz to the Study of Differential Equations, typed manuscript prepared for Hodge in writing the above article.
J. P. La Salle, "Memorial to Solomon Lefschetz," in IEEE Transactions on Automatic Control, vol. AC-18 ( 1973), pp. 89-90.
Lawrence Markus, "Solomon Lefschetz, an Appreciation in Memoriam," Bull. Am. Math. Soc., vol. 79 ( 1973), pp. 663-80.
William Hodge, "Solomon Lefschetz, 1884-1972," in Yearbook of the American Philosophical Society ( 1974), pp. 186-93.
"Lefschetz, Solomon," in National Cyclopedia of American Biography, 56 ( 1975), James T. White and Co., Clifton, New Jersey, pp. 503-4.
F. Nebeker and A. W. Tucker, "Lefschetz, Solomon" in Dictionary of Scientific Biography, Supplement II, 1991.












































