Mathematics Curriculum, Teacher Professionalism, and Supporting Policies in Korea and the United States: Summary of a Workshop (2015)

4
DEVELOPMENT OF INSTRUCTIONAL MATERIALS IN KOREA

A group consisting of Kyong Mi Choi of the University of Iowa, Kyeong-Hwa Lee of Seoul National University, Kyungmee Park of Hongik University, and Ji Won Son of the University of Tennessee at Knoxville collaborated on presentations given by Son and Choi that focused on three questions.

1. What is the role of learning trajectories in the development of curriculum?
2. How are curricular tasks designed and what criteria are used?
3. How do you assure procedural competency and conceptual understanding in the design of the curriculum?

Learning Trajectories in the Development of Curriculum

Ji Won Son presented the group’s discussion of learning trajectories. She noted that since Martin Simon introduced the term “learning trajectory” in 1995, the idea of learning trajectories has gained attention in the United States and Korea as a way to focus research on learning in the service of curriculum, instruction, and assessment. In particular, this is a way to bring coherence between learning and curriculum. For example, the Common Core State Standards for Mathematics document states:

In the group’s opinion, no specific term for learning trajectories exists in Korean mathematics education, but the ideas that underlie the notion of learning trajectory are not new (Empson, 2011).

In 1995, Simon described learning trajectories as having three components:

1. A set of mathematical goals.
2. A clearly marked developmental path.
3. A coherent set of instructional tasks or activities.

Similar components occur in the Korean national curriculum, Son said. The curriculum articulates the goals for student learning based on the big ideas of mathematics and thoroughly describes them. The curriculum and textbooks include descriptions of students’ thinking as they learn to achieve specific goals in mathematical domains within and across grade levels. Also, the curriculum presents developmental paths, describing a typical learning route children follow in

developing understanding of skills related to a particular mathematical goal. In Korea, the developmental path is called GaeNyumdo (“concept map”). The curriculum specifies sets of instructional tasks or activities aligned with the mathematical goals and developmental path.

Son gave examples of each, beginning with developmental paths for number and operation at the elementary level, focusing on fraction multiplication. Fraction multiplication is a grade 5 topic. But before learning fraction multiplication, students need to learn addition, subtraction, and multiplication with whole numbers, as shown in Figure 4-1. Figure 4-1 describes a curricular path, but at the same time emphasizes horizontal connections among various topics, including number and geometry. Table 4-1 shows some associated tasks and goals.

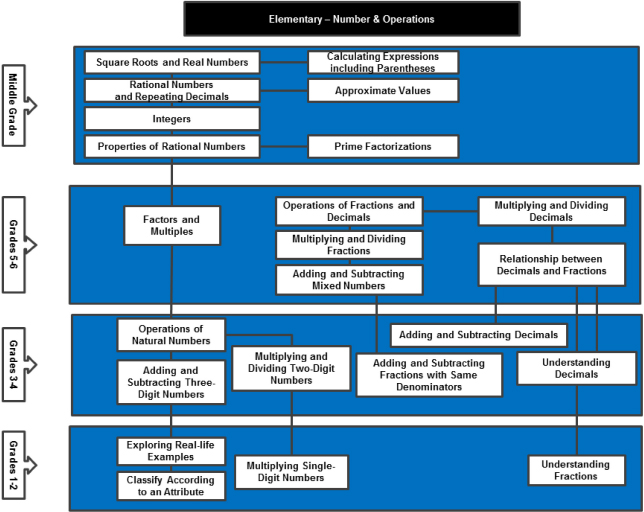
FIGURE 4-1 Curricular path showing connections among various topics. The developmental path is called GaeNyumdo (“concept map”).
SOURCE: Kyong Mi Choi, Kyeong-Hwa Lee, Kyungmee Park, and Ji Won Son.

TABLE 4-1 Grade 5 Fraction Multiplication

Understanding fraction multiplication is broken down into three goals: understanding it as repeated addition, as an operator, and as finding a product of fractions. She provided a second example of GaeNyumdo at the secondary level, focusing on number and operation, and showing horizontal and vertical connections (see Figure 4-2), as well as goals and instructional tasks to teach irrational numbers (see Table 4-2).

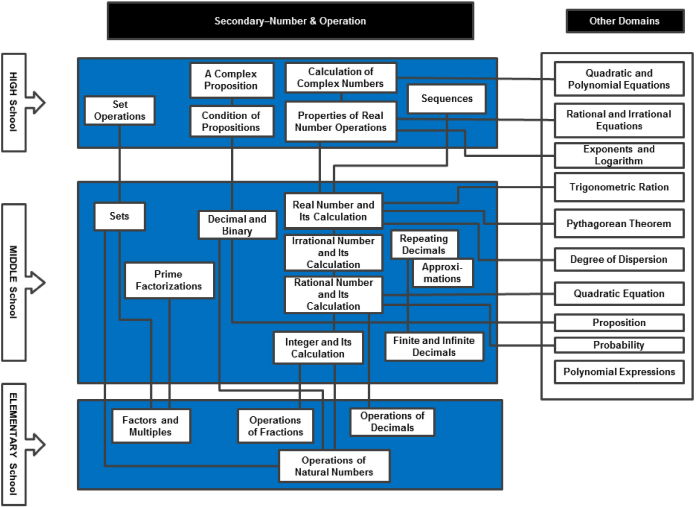
FIGURE 4-2 GaeNyumdo showing connections.
SOURCE: Kyong Mi Choi, Kyeong-Hwa Lee, Kyungmee Park, and Ji Won Son.

TABLE 4-2 Secondary: Irrational Numbers

Developmental Path (Mathematical Goals)	Instructional Tasks
1. To understand that there are numbers that are not rational; to know that they are called irrational.	A length of a side of a square is 1 cm. Can you express the length of its diagonal as a quotient of integers?
2. To understand and make rational approximations of irrational numbers in order to compare sizes of irrational numbers.	Locate each of the following on a number line:
3. To find sums and products of rational and irrational numbers.	For a rectangle whose length is and width is , what would be the area of the rectangle? Would the product of two irrational numbers always be rational (or irrational)? Explain.

Son stated that her group thought that learning trajectories showed how students’ conceptions developed—vertically and horizontally—by providing natural developmental building blocks from one level to the next. These help teachers and curriculum developers to assess, teach, and sequence activities. In particular, Korean mathematics textbooks provide GaeNyumdo at the end of the unit. These help teachers pose questions such as the following:

• What does this student understand?
• What could this student learn next and how could they learn it?

Dealing with such questions helps a teacher to consider learning trajectories.

Task Design

Kyong Mi Choi described features of instructional task design. Tasks are developed by teams of mathematicians, mathematics educators, and mathematics teachers to ensure mathematical correctness, and to consider how learners understand mathematics and possible misconceptions.

Tasks have five core elements: intuitive exploration, explanation, examples, practice, and extension. To promote intuitive exploration, tasks borrow concepts from everyday life, fill in a missing piece of reasoning, or use mathematical knowledge from earlier grades. For example, the Korean words for “territory” and “region” are the same. To familiarize students with the mathematical meaning of “region,” a Korean traditional door invokes students’ prior knowledge of a related meaning.

(After the presentation, Mi-Kyung Ju remarked that relating mathematical terminology to familiar words is important for equity because terminology is often borrowed from Chinese, and children from less educated families are less likely to be familiar with Chinese.)

The goal of explanation is to inform students so that they can figure out principles and meaning. Explanation includes defining mathematical terms and focusing on mathematical structures to be able to conceptualize, find algorithms, or contextualize. Core ideas and relevant background information are provided.

Example involves having students work through a typical example that reflects the core idea, justifying each step. Students reflect on mathematical processes, reasoning, and writing solutions correctly.

In speaking of practice, Choi quoted Confucius: “Is it not a pleasure after all to practice in due time what one has learned?” (Analects of Confucius, I.1). Practice allows students to make “new” knowledge their own by emulating and repeating what they have learned. Changes of mathematical structures when practicing enable students to reason mathematically and to make it a habit to apply relevant previous knowledge. Choi remarked that practice may be a factor in the superior mathematics performance shown by Korean students in international studies.

Extension gives students opportunities to explore different aspects that might have been overlooked or omitted. Students are encouraged to use multiple perspectives through problem solving, reasoning, and communication to connect mathematics and real-life activities. Choi noted that this focuses on objectification of mathematical content and process.

Procedural Competency and Conceptual Understanding

Ji Won Son described Korean approaches to assuring procedural fluency and conceptual understanding in the design of the curriculum. Conceptual understanding means comprehension of the meaning of mathematical concepts and operations. Procedural fluency refers to students’ skill in carrying out procedures flexibly, accurately, and appropriately (Kilpatrick, Swafford, and Findell, 2001). In particular, the National Council of Teachers of Mathematics stresses that instruction should begin with a conceptual rationale for procedures, as the algorithms alone do not help students think about the operations and what they mean.

However, in teaching and learning of operations, Korean curriculum and instruction aims to develop conceptual understanding and procedural fluency simultaneously (Son, 2011, 2012) by use of the following four approaches:

1. Instructional tasks in each lesson are designed based on the three-step method:
   1. Develop the meaning of the operation.
   2. Develop strategies for computing.
   3. Practice strategies and strategy selection.
2. Use a variety of representational models in a systematic way.

3. Encourage various types of computational strategies using distributive, associative, and commutative rules.
4. Use estimation frequently as basis for mathematical learning.

For example, when teaching fraction multiplication, the first emphasis is on repeated addition. Korean students solve problems using “area models” as sectors of disks. In Korea, “area models” may be disks and sectors of disks, while in the U.S., “area models” tend to be rectangles (perhaps composed of smaller rectangles).

Different representations are used in accordance with the three different meanings of fraction multiplication.

1. Repeated addition: area model.
2. Multiplication as operator: measurement and set model.
3. Taking a part of a part of a whole: area model.

To encourage use of various computational strategies, textbooks provide various methods for calculation, ask students to decide which are more efficient, and provide ways of making calculations easier (e.g., canceling before multiplying), and emphasize the use of the distributive property. Typically U.S. textbooks provide only one reduction method or none, Son stated, but Korean mathematics textbooks provide at least three reduction methods.

Use of estimation is frequent in order to help students understand concepts as well as to develop procedural fluency. Before asking the exact answer, textbooks ask students to estimate.¹ For example: Estimate how much this is: ½ × ⅓. Why do you think so?

Son ended the session with a summary. Korean curriculum and instruction provides opportunities to learn concepts and procedures simultaneously, rather than sequentially, by providing multiple computational strategies, using different types of representational models, making connections among ideas, and using number relations.

Comments

The discussion of developing instructional materials in Korea generated a variety of comments, many of which are given below.

Estimation

• Koreans found that when teaching estimation and fractions, they are trying to have students sense without calculating and develop the habit of thinking before calculating. Educators found that, with a little practice, children develop such a sense of estimation very fast, a lot faster than adults.

__________________

¹ The comments at the end of this chapter describe the different types of estimation and give some details about related mathematical goals.

Spiral curriculum

• Koreans have carefully implemented a spiral curriculum, starting in grade 2, with some preparatory work in grade 1, and it goes on until grade 5, instead of teaching fractions in the fifth grade like other countries. The Korean system indicates that a spiral structural approach functions better to teach mathematical content in a systematic, coherent, and consistent way.
• Both the United States and Korea follow spirals, but they may have different cycle lengths. Comparing the Korean with the Chinese curriculum, China deals with each topic in greater depth, more intensively. Therefore, the Chinese have fewer topics per grade than Koreans. In addition, the Chinese model is more linear than the Korean.

Teacher’s manuals

• The teacher’s manual in Korea does not seem to have the “Bible” status that textbooks do. Some teachers follow the teacher’s manual with fidelity and some use it as a reference. There are many aspects of teaching that change spontaneously, even planned learning trajectories.
• Korean teachers are used to this lesson structure: introduce the idea of the lesson, develop ideas, and close the lesson. The textbook structure uses this format because teachers use it. Each textbook may take different approaches, but each lesson has a clear format: approach ideas, have students practice, then wrap up. Korean textbooks are very compact. More exercises, activity sheets, or tasks are provided by teacher’s manuals, the teacher community, or curricular resources. In lessons, variation occurs in the selection of approaches, choice of tasks, and how the lesson is wrapped up, so the use of different textbooks does not matter to teachers.
• Korean teachers are required to do demonstration lessons where they show understanding of both horizontal and vertical trajectories. The beginning of the teacher’s manual gives vertical trajectories for all six grades and prior knowledge at the beginnings of each unit. Teachers do the homework of reading the descriptions in the teacher’s manual. Teachers have the belief that they can teach well only if they know what children learned previously, what they have to learn in this lesson, and what they will have to learn in the next lesson. Teachers do their homework sincerely and faithfully in preparing lessons, and analyze trajectories and apply those well in teaching.
• In the teacher’s manual, Koreans explain why they put a particular task in a particular place, and give possible situations that could lead students to misunderstandings and the actions teachers can take in these situations.

Cognitive demand of Korean school mathematics

• Koreans made changes between the seventh curriculum and the 2007 revision, when they added differentiated workbooks according to student level. The textbook is aimed at average students, and the workbook is a supplement for upper- and lower-level students. In the 2009 revision, they decided not to use workbooks for the secondary level. Instead, they decided to raise demand in the textbook with higher-level questions.
• In Korea, the secondary level is worse than the elementary level in terms of cognitive demand and transparency in the teacher’s manual.