Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction (2013)

Below is the uncorrected machine-read text of this chapter, intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text of each book. Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.

92 7.1 Overview This chapter provides detailed illustrative examples to demonstrate the full range of appli- cability of the Level I probability-based scour estimates using the procedures presented in Chapter 5. Given the unique nature of any bridge-stream intersection, these examples illus- trate application of the methodology for a wide variety of bridge-stream scenarios in a range of physiographic regions across the country. The five bridge sites selected cover a wide variety of situations, including bridges over navigable waterways where pier scour predominates, single-span bridges where contraction and/or abutment scour occur, and bridges where all three scour components are evident. Although these are realistic examples using actual bridges, some conditions have been changed for purposes of illustration. 7.2 Example Bridge No. 1: Maryland Piedmont Region Location: Maryland Physiographic region: Piedmont Bridge length: Existing bridge: 44 ft; replacement bridge: 55 ft No. spans: 1 ADT: 7,801 Main channel width: 33 ft River planform: Meandering, moderately sinuous (1.06–1.25) 100-year discharge: 4,530 ft3/sec 100-year depth: 7.5 ft approach flow depth in main channel 7.7 ft at upstream face, main channel 100-year velocity: 5.9 ft/sec approach velocity in main channel upstream 10.7 ft/sec at the upstream internal bridge section Hydraulic model: 1-D (HEC-RAS) Pier type/geometry: N/A Bed material: Gravel Abutment type/location: Vertical/South abutment set back 5 ft; North abutment in the low flow channel; replacement abutments will be wingwall configuration. Purpose of study: Bridge replacement Example Bridge No. 1 presents the Level I analysis method to provide probability values and scour factors for a bridge located in the Piedmont physiographic region of Maryland (see Figure 7.1). The site currently consists of a single-span, two-lane bridge with a history of C H A P T E R 7 Illustrative Examples

Illustrative Examples 93 contraction and abutment scour. The bridge has been rated as scour critical, has scour coun- termeasures, and is scheduled for replacement. For the new bridge, no overtopping or pressure flow occurs in the 100-year design scour event. For the 100-year design scour event, a desired total scour reliability index, b, of 3.0 is assumed for this example. This b corresponds to a 99.86% probability of non-exceedance during the design event. The calculations presented in this example are for the proposed replacement bridge. Step 1. Perform hydrologic, hydraulic, and design-equation scour computations using appropriate methods. a. Hydrologic analysis: USGS regional regression relationships for the Maryland Piedmont and Blue Ridge regions were used to develop the estimate of the 100-year design flood. For the 100-year event, the regression equation is: ( ) ( ) ( )= + +− −Q 1,471.1 DA LIME 1 FOR 1100 0.617 0.154 0.045 where: Q100 = Estimate of 100-year flood discharge (cfs) DA = Watershed drainage area (sq. mi.) LIME = Percentage of carbonate/limestone rock in watershed FOR = Percentage of forest cover in watershed Using the USGS regression equation and the watershed characteristics upstream of the bridge, the 100-year design discharge at this site is estimated to be 4,530 ft3/sec. b. Compute abutment scour: The NCHRP Project 24-20 live-bed approach for estimating total scour at the abutment was used to determine a scour depth of 8.6 ft. The NCHRP approach includes contraction scour plus the local scour at the abutment toe. Because both abutments of the new bridge will be in close proximity to the channel banks, the total scour depth is approximately the same for the left and right sides. (a) Upstream channel (b) Downstream face Figure 7.1. Example Bridge No. 1.

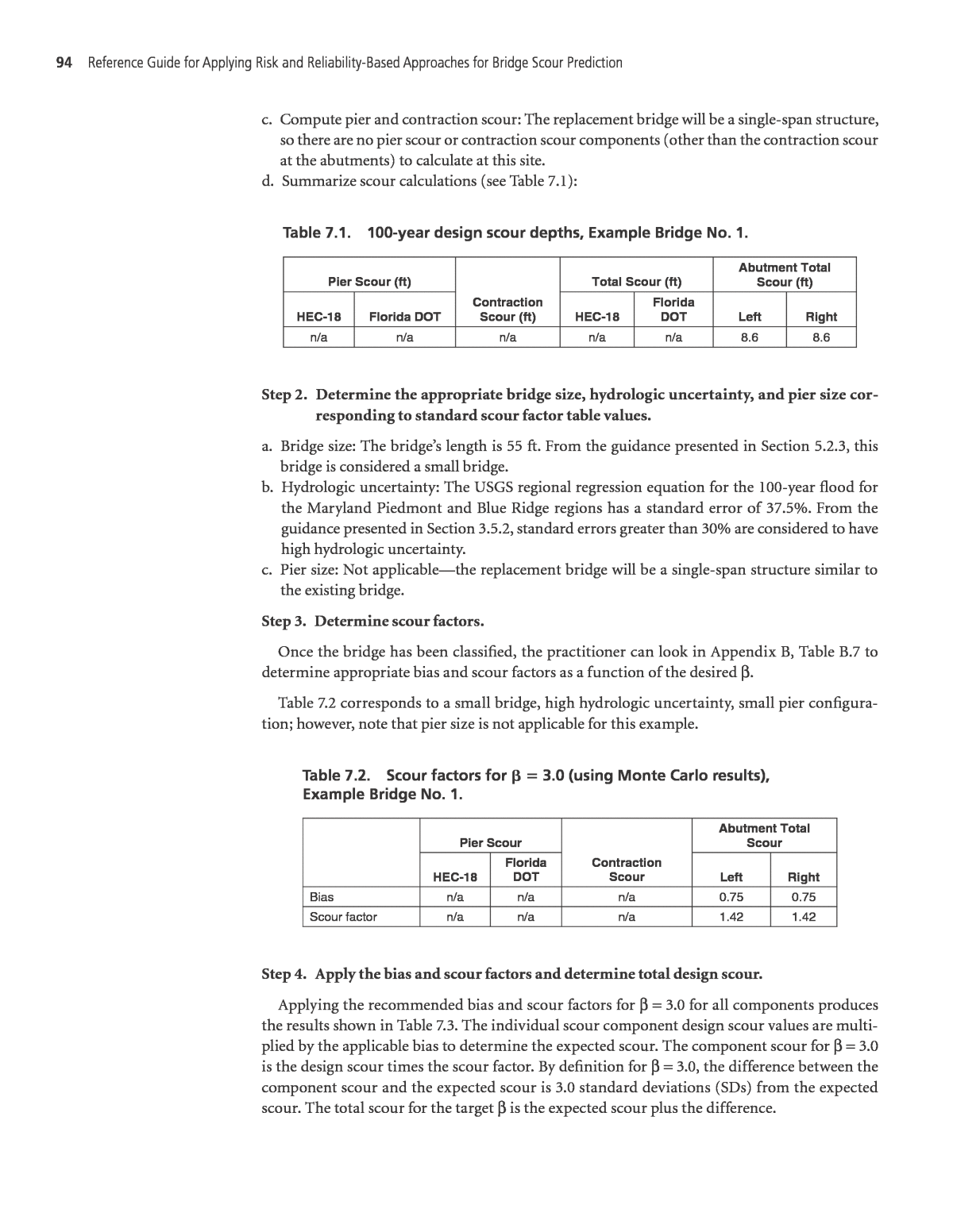
94 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction Step 2. Determine the appropriate bridge size, hydrologic uncertainty, and pier size cor- responding to standard scour factor table values. a. Bridge size: The bridge’s length is 55 ft. From the guidance presented in Section 5.2.3, this bridge is considered a small bridge. b. Hydrologic uncertainty: The USGS regional regression equation for the 100-year flood for the Maryland Piedmont and Blue Ridge regions has a standard error of 37.5%. From the guidance presented in Section 3.5.2, standard errors greater than 30% are considered to have high hydrologic uncertainty. c. Pier size: Not applicable—the replacement bridge will be a single-span structure similar to the existing bridge. Step 3. Determine scour factors. Once the bridge has been classified, the practitioner can look in Appendix B, Table B.7 to determine appropriate bias and scour factors as a function of the desired b. Table 7.2 corresponds to a small bridge, high hydrologic uncertainty, small pier configura- tion; however, note that pier size is not applicable for this example. Pier Scour Contraction Scour Abutment Total Scour HEC-18 Florida DOT Left Right Bias n/a n/a n/a 0.75 0.75 Scour factor n/a n/a n/a 1.42 1.42 Table 7.2. Scour factors for b 5 3.0 (using Monte Carlo results), Example Bridge No. 1. Pier Scour (ft) Contraction Scour (ft) Total Scour (ft) Abutment Total Scour (ft) HEC-18 Florida DOT HEC-18 Florida DOT Left Right n/a n/a n/a n/a n/a 8.6 8.6 Table 7.1. 100-year design scour depths, Example Bridge No. 1. c. Compute pier and contraction scour: The replacement bridge will be a single-span structure, so there are no pier scour or contraction scour components (other than the contraction scour at the abutments) to calculate at this site. d. Summarize scour calculations (see Table 7.1): Step 4. Apply the bias and scour factors and determine total design scour. Applying the recommended bias and scour factors for b = 3.0 for all components produces the results shown in Table 7.3. The individual scour component design scour values are multi- plied by the applicable bias to determine the expected scour. The component scour for b = 3.0 is the design scour times the scour factor. By definition for b = 3.0, the difference between the component scour and the expected scour is 3.0 standard deviations (SDs) from the expected scour. The total scour for the target b is the expected scour plus the difference.

Illustrative Examples 95 7.3 Example Bridge No. 2: Nevada Great Basin Subregion Location: Nevada Physiographic region: Intermontane basins and plateaus; Great Basin Subregion Bridge length: 210 ft No. spans: 3 ADT: 1,300 (2001) Main channel width: 208 ft River planform: Sinuous (1.06–1.25) 100-year discharge: 31,150 ft3/s 100-year depth: 19.6 ft 100-year velocity: 11.7 ft/s Hydraulic model: 1-D (HEC-RAS) Pier type/geometry: 1.7 ft wide by 44 ft long concrete wall piers on 19 ft wide pile caps (exposed) Bed material: Sand with gravel Abutment type/location: Spill-through abutments at channel banks Purpose of study: Scour evaluation and countermeasure selection for a plan of action Example Bridge No. 2 presents the Level I analysis method to provide probability values and scour factors for a bridge located in the Great Basin physiographic region of Nevada (see Figure 7.2). The example bridge is 210 ft long with two concrete wall piers on spread Contraction Pier Scour Scour Total Scour Abutment Total Scour HEC-18 Florida DOT HEC-18 Florida DOT Left Right Design scour (ft) n/a n/a n/a n/a n/a 8.6 8.6 Bias 0.75 0.75 Expected scour (ft) 6.5 6.5 Scour factor 1.42 1.42 Component scour for = 3.0 (ft) 12.2 12.2 Difference from expected (ft) 5.7 5.7 Total scour for = 3.0 (ft) 12.2 12.2 Table 7.3. 100-year scour results for b 5 3.0 (using Monte Carlo results), Example Bridge No. 1. Figure 7.2. Example Bridge No. 2 (looking downstream).

96 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction footings. Because of long-term degradation at this site, the spread footings are now exposed above the stream bed. The abutments are of spill-through configuration located at the chan- nel banks. No overtopping or pressure flow occurs in the 100-year design scour event. For the 100-year design scour event, a desired total scour reliability index, b, of 2.5 is assumed for this example. This b corresponds to a 99.38% probability of non-exceedance during the design event. Step 1. Perform hydrologic, hydraulic, and design-equation scour computations using appropriate methods. a. Hydrologic analysis: Bulletin 17B methods were used to determine the design scour event dis- charge, the expected value of the natural logarithm transform of discharge, and the SD of the uncertainty about that expected value for a given recurrence interval. The resulting discharges and summary statistics are presented in Table 7.4. Annual Exceedance Discharge (cfs) p(X > x) T (years) Bulletin 17B Estimate 95% Confidence Limits Lower Upper 0.1 10 10,400 6,720 18,530 0.04 25 17,300 10,560 34,110 0.02 50 23,690 13,910 49,970 0.01 100 31,150 17,630 69,810 0.005 200 39,720 21,740 94,050 0.002 500 52,810 27,750 133,500 Table 7.4. Hydrologic data from Bulletin 17B analysis of bridge site (n 5 17 years), Example Bridge No. 2. Pier Scour (ft) Contraction Scour (ft) Total Scour (ft) Abutment Total Scour (ft) Left Right 28.9 1.7 30.6 2.4 3.3 Table 7.5. 100-year design scour depths, Example Bridge No. 2. b. Design-equation scour computations using the HEC-18 method for pier scour, the HEC- 18 method for contraction scour, and the NCHRP Project 24-20 method as presented in HEC-18 for abutment scour were computed for this example. Table 7.5 presents the results of these computations. Step 2. Determine the appropriate bridge size, hydrologic uncertainty, and pier size cor- responding to standard scour factor table values. a. Bridge size: The example bridge’s length is 210 ft. From the guidance presented in Section 5.2.3, this bridge is best represented as a medium bridge. b. Hydrologic uncertainty: To establish the relative hydrologic uncertainty of this bridge, it is necessary to estimate the COV associated with the uncertainty of the discharge estimate for the design scour event. 1. The lognormal distribution of hydrologic uncertainty is determined from the 95% confi- dence limit discharge values as follows. The hydrologic uncertainty of a given Bulletin 17B

Illustrative Examples 97 discharge estimate is assumed to be lognormally distributed. Consequently, given the 95% upper and 95% lower confidence limits (see Section 3.5.2), ln Q ln Q 2 ln Q ln Q 2Z COV upper lower upper lower c ( ) ( ) ( ) ( ) µ = + σ = − = σ µ 2. For a 95% confidence limit, Zc = 1.645 (see Appendix A). From the hydrologic analysis, the upper and lower 95% confidence limits for the 1% exceedance probability event (i.e., the 100-year flood) are: Q 69,810 cfs, Q 17,360 cfs, and Z 1.645 upper lower c = = = 3. Substituting values for Qupper, Qlower, and Zc into these equations, ln 69,810 ln 17,360 2 10.46 ln 69,810 ln 17,360 2 1.645 0.423 COV 0.423 10.46 0.0404 ( ) ( ) ( ) ( ) ( ) µ = + = σ = − = = = Compare the computed COV with Table 7.6 (reproduced from Table 3.4) for the 1% exceed- ance probability event: Annual Exceedance Discharge COV (lognormal) p(X > x) T (years) Low Medium High 0.04 25 0.009 0.014 0.018 0.02 50 0.010 0.015 0.019 0.01 100 0.011 0.016 0.021* 0.005 200 0.012 0.017 0.022 0.002 500 0.013 0.018 0.023 *Bolding shows where the COV for Example Bridge No. 2 falls within the table. These numbers indicate Example Bridge No. 2 has high hydrologic uncertainty. Table 7.6. Hydrologic uncertainty as function of annual exceedance probability (reproduced from Table 3.4), Example Bridge No. 2. This bridge has high hydrologic uncertainty. c. Pier size: Because the pile caps are exposed above the stream bed, their width (19 ft) is com- pared to the values in Table 7.7 (reproduced from Table 5.1). This bridge has large piers for a bridge of its type.

98 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction Consequently, this bridge is best classified as a medium bridge with high hydrologic uncer- tainty and large pier size for the Level I analysis. However, the 19 ft wide pile cap is signifi- cantly larger than the 4.5 ft large pier assumed for a medium bridge, suggesting that this bridge may be a candidate for a Level II analysis. Step 3. Determine scour factors. Once the bridge has been classified, the practitioner can look in Appendix B, Table B.18 to determine appropriate bias and scour factors as a function of the desired b. Table 7.8 corresponds to a medium bridge with high hydrologic uncertainty and large pier size. Bridge Type Pier Size (ft) Small Medium Large Small 1 2 3 Medium 1.5 3 4.5* Large 3 6 9 *Bolding shows where the pier size for Example Bridge No. 2 falls within the table. This medium-size bridge has a large pier size. Table 7.7. Representative bridge pier size as a function of bridge type (reproduced from Table 5.1), Example Bridge No. 2. Pier Scour Contraction Scour Abutment Total Scour Left Right Bias 0.68 0.92 0.75 0.75 Scour factor 0.97 2.21 1.48 1.48 Table 7.8. Scour factors for b 5 2.5 (using Monte Carlo results), Example Bridge No. 2. Pier Scour Contraction Scour Total Scour Abutment Total Scour Left Right Design scour (ft) 28.9 1.7 30.6 2.4 3.3 Bias 0.68 0.92 0.75 0.75 Expected scour (ft) 19.7 1.6 21.3 1.8 2.5 Scour factor 0.97 2.21 1.48 1.48 Component scour for = 2.5 (ft) 28.0 3.8 3.6 4.9 Difference from expected (ft) 8.3 2.2 8.6 1.8 2.4 Total scour for = 2.5 (ft) 29.9 3.6 4.9 Table 7.9. 100-year scour results for b 5 2.5 (using Monte Carlo results), Example Bridge No. 2. Step 4. Apply the bias and scour factors and determine total design scour. Applying the recommended bias and scour factors for b = 2.5 for all components produces the results shown in Table 7.9. The individual scour component design scour values are multi- plied by the applicable bias to determine the expected scour. Total expected scour is the sum of expected pier and contraction scour. The component scour for b = 2.5 is the design scour times the scour factor. By definition for b = 2.5, the difference between the component scour and the expected scour is 2.5 standard deviations from the expected scour.

Illustrative Examples 99 The total scour difference from expected is the square root of the sum of the squares of the component scour differences (pier and contraction scour). The total scour for the target b is the expected plus the difference as shown in Table 7.9. 7.4 Example Bridge No. 3: California Pacific Mountains Subregion Location: California Physiographic region: Pacific mountains; Great Valley Subregion Bridge length: 1,200 ft No. spans: 10 ADT: 11,800 (2009) Main channel width: 607 ft River planform: Meandering, highly sinuous (>1.26) 100-year discharge: 140,000 ft3/s 100-year depth: 24 ft 100-year velocity: 12.04 ft/s Hydraulic model: 1-D (HEC-RAS) Pier type/geometry: 2 column bents, 6-foot diameter columns @ 24 ft OC Bed material: Fine to coarse sand Abutment type/location: Spill-through abutments set back on floodplain Purpose of study: Scour evaluation Example Bridge No. 3 presents the Level I analysis method to provide probability values and scour factors for a bridge located in the Pacific Mountain physiographic region of California (see Figure 7.3). The example bridge is a 1,200 ft long bridge with 6 ft diameter drilled shaft interior bents and set back, spill-through type abutments. No overtopping or pressure flow occurs in the 100-year design scour event. For the 100-year design scour event, a desired total scour reliability index, b, of 2.5 is assumed for this example. This b corresponds to a 99.38% probability of non-exceedance during the design event. Note: For illustrative purposes, in this example pier scour is calculated using both the HEC-18 and Florida DOT methods. Step 1. Perform hydrologic, hydraulic, and design-equation scour computations using appropriate methods. a. Hydrologic analysis: Bulletin 17B methods were used to determine the design scour event dis- charge, the expected value of the natural logarithm transform of discharge, and the SD of the Figure 7.3. Example Bridge No. 3 (looking upstream).

100 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction b. Design-equation scour computations using the HEC-18 and Florida DOT methods for pier scour, the HEC-18 method for contraction scour, and the NCHRP Project 24-20 method as presented in HEC-18 for abutment scour were computed for this example. Table 7.11 presents the results of these computations. Annual Exceedance Discharge (cfs) p(X > x) T (years) Bulletin 17B Estimate 95% Confidence Limits Lower Upper 0.1 10 92,050 79,470 110,600 0.04 25 112,000 94,920 138,700 0.02 50 126,300 105,700 159,500 0.01 100 140,000 115,800 179,900 0.005 200 153,300 125,500 200,200 0.002 500 170,300 137,700 226,600 Table 7.10. Hydrologic data from Bulletin 17B analysis of bridge site (n 5 49 years), Example Bridge No. 3. Pier Scour (ft) Contraction Scour (ft) Total Scour (ft) Abutment Total Scour (ft) HEC-18 Florida DOT HEC-18 Florida DOT Left Right 13.7 11.2 5.3 19.0 16.5 11.0 6.7 Table 7.11. 100-year design scour depths, Example Bridge No. 3. Step 2. Determine the appropriate bridge size, hydrologic uncertainty, and pier size cor- responding to standard scour factor table values. a. Bridge size: The example bridge’s length is 1,200 ft. From the guidance presented in Sec- tion 5.2.3, this bridge is best represented as a large bridge. b. Hydrologic uncertainty: To establish the relative hydrologic uncertainty of this bridge it is necessary to estimate the COV associated with the uncertainty of the discharge estimate for the design scour event. 1. The lognormal distribution of hydrologic uncertainty is determined from the 95% confi- dence limit discharge values as follows. The hydrologic uncertainty of a given Bulletin 17B discharge estimate is assumed to be lognormally distributed. Consequently, given the 95% upper and 95% lower confidence limits (see Section 3.5.2), ln Q ln Q 2 ln Q ln Q 2Z COV upper lower upper lower c ( ) ( ) ( ) ( ) µ = + σ = − = σ µ uncertainty about that expected value for a given recurrence interval. The resulting discharges and summary statistics are presented in Table 7.10.

Illustrative Examples 101 2. For a 95% confidence limit, Zc = 1.645 (see Appendix A). From the hydrologic analysis, the upper and lower 95% confidence limits for the 1% exceedance probability event (i.e., the 100-year flood) are: Q 179,900 cfs; Q 115,800 cfs; and Z 1.645 upper lower c = = = 3. Substituting values for Qupper, Qlower, and Zc into these equations, ln 179,900 ln 115,800 2 11.88 ln 179,900 ln 115,800 2 1.645 0.1339 COV 0.1339 11.88 0.0113 ( ) ( ) ( ) ( ) ( ) µ = + = σ = − = = = Compare the computed COV with Table 7.12 (reproduced from Table 3.4) for the 1% exceedance probability event: Annual Exceedance Discharge COV (Lognormal) p(X > x) T (years) Low Medium High 0.04 25 0.009 0.014 0.018 0.02 50 0.010 0.015 0.019 0.01 100 0.011* 0.016 0.021 0.005 200 0.012 0.017 0.022 0.002 500 0.013 0.018 0.023 *Bolding shows where the COV for Example Bridge No. 3 falls within the table. These numbers indicate that Example Bridge No. 3 has low hydrologic uncertainty. Table 7.12. Hydrologic uncertainty as a function of annual exceedance probability (reproduced from Table 3.4), Example Bridge No. 3. Bridge Type Pier Size (ft) Small Medium Large Small 1 2 3 Medium 1.5 3 4.5 Large 3 6* 9 *Bolding shows where the pier size for Example Bridge No. 3 falls within the table. This large bridge has a medium pier size. Table 7.13. Representative bridge pier size as a function of bridge type (reproduced from Table 5.1), Example Bridge No. 3. This bridge has low hydrologic uncertainty. c. Pier size: Compare the bridge pier size (6 ft diameter) to Table 7.13 (reproduced from Table 5.1). This bridge has medium piers for a bridge of its type.

102 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction Consequently, this bridge is best classified as a large bridge with low hydrologic uncertainty and medium pier size for the Level I analysis. Step 3. Determine scour factors. Once the bridge has been classified, the practitioner can look in Appendix B, Table B.20 to determine appropriate bias and scour factors as a function of the desired b. Table 7.14 corresponds to a large bridge with low hydrologic uncertainty and medium pier size. Pier Scour Contraction Scour Abutment Total Scour HEC-18 Florida DOT Left Right Bias 0.68 0.75 0.93 0.76 0.76 Scour factor 0.95 1.08 2.04 1.66 1.66 Table 7.14. Scour factors for b 5 2.5 (using Monte Carlo results), Example Bridge No. 3. Pier Scour Contraction Scour Total Scour Abutment Total Scour HEC-18 Florida DOT HEC-18 Florida DOT Left Right Design scour (ft) 13.7 11.2 5.3 19.0 16.5 11.0 6.7 Bias 0.68 0.75 0.93 0.76 0.76 Expected scour (ft) 9.3 8.4 4.9 14.2 13.3 8.4 5.1 Scour factor 0.95 1.08 2.04 1.66 1.66 Component scour for = 2.5 (ft) 13.0 12.1 10.8 18.3 11.1 Difference from expected (ft) 3.7 3.7 5.9 7.0 7.0 9.9 6.0 Total scour for = 2.5 (ft) 21.2 20.3 18.3 11.1 Table 7.15. 100-year scour results for b 5 2.5 (using Monte Carlo results), Example Bridge No. 3. Step 4. Apply the bias and scour factors and determine total design scour. Applying the recommended bias and scour factors for b = 2.5 for all components produces the results shown in Table 7.15. The individual scour component design scour values are multi- plied by the applicable bias to determine the expected scour. Total expected scour is the sum of expected pier and contraction scour. The component scour for b = 2.5 is the design scour times the scour factor. By definition for b = 2.5, the difference between the component scour and the expected scour is 2.5 standard deviations from the expected scour. The total scour difference from expected is the square root of the sum of the squares of the component scour differences (pier and contraction scour). The total scour for the target b is the expected plus the difference, as shown in Table 7.15. 7.5 Example Bridge No. 4: Missouri Interior Lowlands Subregion Location: Missouri Physiographic region: Interior lowlands; Dissected Till Plains Subregion Bridge length: 1,715 ft

Illustrative Examples 103 No. spans: 7 ADT: 94,470 (2006) Main channel width: 1013 ft River planform: sinuous (>1.25) 100-year discharge: 401,000 ft3/s 100-year depth: 55.1 ft 100-year velocity: 9.8 ft/s (avg. channel) Hydraulic model: 1-D (HEC-RAS) Pier type/geometry: Proposed bridge: 11 ft diameter drilled shafts with cap Bed material: Poorly graded sand (SP) Abutment type/location: Spill-through abutments on floodplain Purpose of study: New bridge Example Bridge No. 4 presents the Level I analysis method to provide probability values and scour factors for a new bridge located in the interior lowlands, Dissected Till Plains physio- graphic subregion of Missouri (see Figure 7.4). The bridge will be a 1,715 ft long cable-stayed bridge with a large pylon in the main channel and approach bents on the overbanks. The abut- ments are of spill-through configuration set well back from the main channel. No overtopping or pressure flow occurs during the 100-year design flood. For the 100-year design scour event, a desired total scour reliability index, b, of 3.0 is assumed for this example. This b corresponds to a 99.86% probability of non-exceedance. Step 1. Perform hydrologic, hydraulic, and design-equation scour computations using appropriate methods. a. Hydrologic analysis: The Missouri River and its major tributaries are highly regulated by a large number of water supply, flood control, and navigation projects constructed over the last century and operated by various state and federal agencies. In 2004, the USACE completed the Upper Mississippi River System Flow Frequency Study (USACE 2004). That study developed methodologies to allow the USACE to reconstruct a 100-year period of annual peak flows at selected locations in the system as if all the currently-existing projects were in place and operating since the year 1898. The USACE study used data from numerous gages, reservoir operation rules, reservoir routing, and unsteady channel flow routing procedures to develop an annual peak flow series at the bridge. Appendix E, Kansas City District Hydrology and Hydraulics of that study pro- vides the reconstructed flow series for the Missouri River at Kansas City for the 100-year period from 1898 through 1997. Figure 7.4. Example Bridge No. 4 (looking upstream).

104 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction b. Design-equation scour computations using the HEC-18 method for pier scour, the HEC-18 method for contraction scour, and the NCHRP Project 24-20 method as presented in HEC-18 for abutment scour were computed for the 100-year scour design flood in this example. The pier scour calculations are calculated for the large pylon in the main channel. Both left and right abutments are located outside the existing levees; therefore, no abutment scour is antici- pated. Table 7.17 presents the results of these computations. Annual Exceedance Discharge (cfs) p(X > x) T (years) Special Study Estimate 95% Confidence Limits Lower Upper 0.01 100 401,000 350,000 458,000 Table 7.16. Hydrologic data from site-specific analysis of bridge site (n 5 100 years), Example Bridge No. 4. Pier Scour (ft) Contraction Scour (ft) Total Scour (ft) Abutment Total Scour (ft) Left Right 44.1 2.3 46.4 0.0 0.0 Table 7.17. 100-year design scour depths, Example Bridge No. 4. For this special study, site-specific methods were used to determine the flood frequency relationships for floods of various return periods. The 100-year discharges and summary statistics are presented in Table 7.16. Step 2. Determine the appropriate bridge size, hydrologic uncertainty, and pier size cor- responding to standard scour factor table values. a. Bridge size: The example bridge’s length is 1,715 ft. From the guidance presented in Sec- tion 5.2.3, this bridge is best represented as a large bridge. b. Hydrologic uncertainty: To establish the relative hydrologic uncertainty of this bridge, it is necessary to estimate the COV associated with the uncertainty of the discharge estimate for the design flood event. 1. The lognormal distribution of hydrologic uncertainty is determined from the 95% con- fidence limit discharge values as follows. The hydrologic uncertainty of a given discharge estimate (in this case, from a special study which does not correspond to a strict Bulle- tin 17B analysis) is assumed to be lognormally distributed. Consequently, given the 95% upper and 95% lower confidence limits (see Section 3.5.2), ln Q ln Q 2 ln Q ln Q 2Z COV upper lower upper lower c ( ) ( ) ( ) ( ) µ = + σ = − = σ µ

Illustrative Examples 105 2. For a 95% confidence limit, Zc = 1.645 (see Appendix A). From the hydrologic analysis, the upper and lower 95% confidence limits for the 1% exceedance probability event (i.e., the 100-year design flood) are: Q 458,000 cfs; Q 350,000; and Z 1.645 upper lower c = = = 3. Substituting values for Qupper, Qlower, and Zc into these equations, ( ) ( ) ( ) ( ) ( ) µ = + = σ = − = = = ln 458,000 ln 350,000 2 12.90 ln 458,000 ln 350,000 2 1.645 0.082 COV 0.082 12.90 0.0064 Compare the computed COV with Table 7.18 (reproduced from Table 3.4) for the 1.0% exceedance probability event: Annual Exceedance Discharge COV (lognormal) p(X > x) T (years) Low Medium High 0.04 25 0.009 0.014 0.018 0.02 50 0.010 0.015 0.019 0.01 100 0.011* 0.016 0.021 0.005 200 0.012 0.017 0.022 0.002 500 0.013 0.018 0.023 *Bolding shows where the COV for Example Bridge No. 4 falls within the table. These numbers indicate that Example Bridge No. 4 has low hydrologic uncertainty. Table 7.18. Hydrologic uncertainty as a function of annual exceedance probability (reproduced from Table 3.4), Example Bridge No. 4. Bridge Type Pier Size (ft) Small Medium Large Small 1 2 3 Medium 1.5 3 4.5 Large 3 6 9* *Bolding shows where the pier size for Example Bridge No. 4 falls within the table. This large bridge has a large pier size. Table 7.19. Representative bridge pier size as a function of bridge type (reproduced from Table 5.1), Example Bridge No. 4. This bridge has low hydrologic uncertainty. c. Pier size: The 11 ft width of the drilled shaft piles beneath the main channel pylon is com- pared to the values in Table 7.19 (reproduced from Table 5.1). This bridge has large piers for a bridge of its type.

106 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction Consequently, this bridge is best classified as a large bridge with low hydrologic uncer- tainty and large pier size for the Level I analysis. Step 3. Determine scour factors. Once the bridge has been classified, the practitioner can look in Appendix B, Table B.21 to determine appropriate bias and scour factors as a function of the desired b. Table 7.20 corresponds to a large bridge with low hydrologic uncertainty and large pier size. Pier Scour Contraction Scour Abutment Total Scour Left Right Bias 0.68 0.93 0.76 0.76 Scour factor 0.99 2.37 1.96 1.96 Table 7.20. Scour factors for b 5 3.0 (using Monte Carlo results), Example Bridge No. 4. Pier Scour Contraction Scour Total Scour Abutment Total Scour Left Right Design scour (ft) 44.1 2.3 46.4 0.0 0.0 Bias 0.68 0.93 Expected scour (ft) 30.0 2.1 32.1 Scour factor 0.99 2.37 Component scour for = 3.0 (ft) 43.7 5.5 Difference from expected (ft) 13.7 3.4 14.1 Total scour for = 3.0 (ft) 46.2 Table 7.21. 100-year scour results for b 5 3.0 (using Monte Carlo results). Step 4. Apply the bias and scour factors and determine total design scour. Applying the recommended bias and scour factors for b = 3.0 for all components produces the results shown in Table 7.21. The individual scour component design scour values are multi- plied by the applicable bias to determine the expected scour. Total expected scour is the sum of expected pier and contraction scour. The component scour for b = 3.0 is the design scour times the scour factor. By definition for b = 3.0, the difference between the component scour and the expected scour is 3.0 standard deviations from the expected scour. The total scour difference from expected is the square root of the sum of the squares of the component scour differences (pier and contraction scour). The total scour for the target b is the expected plus the difference as shown in Table 7.21. 7.6 Example Bridge No. 5: South Carolina Atlantic Coastal Plain Subregion Location: South Carolina Physiographic region: Atlantic coastal plain; Sandhills subregion Bridge lengths: Main channel: 1,950 ft; west relief: 520 ft; east relief: 520 ft No. spans: 13, 8, 8 ADT: 7,450 (2009) Main channel width: 320 ft

Illustrative Examples 107 River planform: Meandering, low sinuosity (< 1.06) 100-year discharge: 249,100 ft3/s total (181,900 ft3/s main channel, 36,000 ft3/s west relief, and 31,200 ft3/s east relief) 100-year depth: 54 ft maximum 100-year velocity: 3.3 ft/s average in main channel bridge opening Hydraulic model: 2-D (FESWMS FST-2DH) Pier type/geometry: Existing bridge: Drilled shafts with webwalls Proposed replacement bridge: 7 ft diameter drilled shafts main channel and 20 in. columns at the two relief bridges Bed material: Sandy clay (CL) and sandy silt (ML) Abutment type/location: Spill-through abutments set back on floodplains Purpose of study: Bridge replacement Example Bridge No. 5 presents the Level I analysis method to provide probability values and scour factors for a bridge located in the Atlantic coastal plain physiographic region of the Sandhills subregion of South Carolina (see Figure 7.5). The site includes a main channel bridge and two relief bridges. No overtopping or pressure flow occurs in the 100-year design event. For the 100-year design scour event, a desired total scour reliability index, b, of 2.0 is assumed for this example. This b corresponds to a 97.72% probability of non-exceedance during the design event. Figure 7.6 illustrates the velocity contours from a 2-D hydraulic model of the 100-year flood at this site, showing the main bridge and the two relief bridges. Step 1. Perform hydrologic, hydraulic, and design-equation scour computations using appropriate methods. a. Hydrologic analysis: Bulletin 17B methods were used to determine the design scour event dis- charge, the expected value of the natural logarithm transform of discharge, and the SD of the uncertainty about that expected value for a given recurrence interval. The resulting discharges and summary statistics are presented in Table 7.22. Figure 7.5. Example Bridge No. 5 (main channel looking upstream). Annual Exceedance Discharge (cfs) p(X > x) T (years) Bulletin 17B Estimate 95% Confidence Limits Lower Upper 0.1 10 139,000 125,000 157,000 0.04 25 178,800 159,000 206,000 0.02 50 212,400 185,000 252,000 0.01 100 249,100 214,000 301,000 0.005 200 287,800 244,000 354,000 0.002 500 351,800 293,000 443,000 Table 7.22. Hydrologic data from Bulletin 17B analysis of bridge site (N 5 75 years), Example Bridge No. 5.

108 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction b. Design-equation scour computations using the HEC-18 method for pier scour, the HEC-18 method for contraction scour, and the NCHRP Project 24-20 method as presented in HEC-18 for abutment scour were computed for this example. Table 7.23 presents the results of these computations. Bridge Pier Scour (ft) Contraction Scour (ft) Total Scour (ft) Abutment Total Scour (ft) Left Right Main 9.9 3.4 13.3 4.6 8.8 West relief 5.4 3.7 9.1 14.5 9.8 East relief 5.8 4.5 10.3 12.8 15.5 Table 7.23. 100-year design scour depths, Example Bridge No. 5. Figure 7.6. 2-D model of bridge site (velocity contours shown), Example Bridge No. 5. Step 2. Determine the appropriate bridge size, hydrologic uncertainty, and pier size cor- responding to standard scour factor table values. a. Bridge size: The example bridges are 1,200 ft, 520 ft, and 520 ft long. From the guidance pre- sented in Section 5.2.3, each bridge is best represented as a large bridge. b. Hydrologic uncertainty: To establish the relative hydrologic uncertainty of this bridge exam- ple, it is necessary to estimate the COV associated with the uncertainty of the discharge esti- mate for the design scour event. 1. The lognormal distribution of hydrologic uncertainty is determined from the 95% confi- dence limit discharge values as follows. The hydrologic uncertainty of a given Bulletin 17B

Illustrative Examples 109 discharge estimate is assumed to be lognormally distributed. Consequently, given the 95% upper and 95% lower confidence limits (see Section 3.5.2), ln Q ln Q 2 ln Q ln Q 2Z COV upper lower upper lower c ( ) ( ) ( ) ( ) µ = + σ = − = σ µ 2. For a 95% confidence limit, Zc = 1.645 (see Appendix A). From the hydrologic analysis, the upper and lower 95% confidence limits for the 1% exceedance probability event are: Q 301,000 cfs; Q 214,000 cfs; and Z 1.645 upper lower c = = = 3. Substituting values for Qupper, Qlower, and Zc into these equations, ln 301,000 ln 214,000 2 12.4443 ln 301,000 ln 214,000 2 1.645 0.103688 COV 0.103688 12.4443 0.0083 ( ) ( ) ( ) ( ) ( ) µ = + = σ = − = = = Compare the computed COV with Table 7.24 (reproduced from Table 3.4) for the 1% exceedance probability event: Annual Exceedance Discharge COV (lognormal) p(X > x) T (years) Low Medium High 0.04 25 0.009 0.014 0.018 0.02 50 0.010 0.015 0.019 0.01 100 0.011* 0.016 0.021 0.005 200 0.012 0.017 0.022 0.002 500 0.013 0.018 0.023 *Bolding shows where the COV for Example Bridge No. 5 falls within the table. These numbers indicate that Example Bridge No. 5 has low hydrologic uncertainty. Table 7.24. Hydrologic uncertainty as function of annual exceedance probability (reproduced from Table 3.4), Example Bridge No. 5. This bridge has low hydrologic uncertainty. c. Compare the bridge pier size (7 ft diameter and 20 inch diameter) to Table 7.25 (reproduced from Table 5.1). The main channel bridge has medium piers and the two relief bridges have small piers.

110 Reference Guide for Applying Risk and Reliability-Based Approaches for Bridge Scour Prediction Consequently, the main channel bridge is best classified as a large bridge, low hydrologic uncertainty, medium pier size, and the two relief bridges are best classified as large bridge, low hydrologic uncertainty, small pier size for the Level I analysis. Step 3. Determine scour factors. Once the bridge has been classified, the practitioner can look in Appendix B, Table B.19 and Table B.20, to determine appropriate bias and scour factors as a function of the desired b. Table 7.26 provides bias and scour factors corresponding to a large bridge with low hydro- logic uncertainty and medium pier size (for the main bridge) and also for a large bridge with low hydrologic uncertainty and small pier size (for the relief bridges). Step 4. Apply the bias and scour factors and determine total design scour. Applying the recommended bias and scour factors for b = 2.0 for all components pro- duces the results shown in Tables 7.27, 7.28, and 7.29 for the specific bridges. The individual scour component design scour values are multiplied by the applicable bias to determine the expected scour. Total expected scour is the sum of expected pier and contraction scour. The component scour for b = 2.0 is the design scour times the scour factor. By definition for b = 2.0, the difference between the component scour and the expected scour is 2.0 SDs from the expected scour. The total scour difference from expected is the square root of the sum of the squares of the component scour differences (pier and contraction scour). The total scour for the target b is the expected scour plus the difference as shown in the tables. HEC-18 Pier Scour Contraction Scour Abutment Total Scour LB, LH, MP LB, LH, SP Left Right Bias 0.68 0.68 0.93 0.76 0.76 Scour factor 0.90 0.89 1.77 1.43 1.43 Table 7.26. Scour factors for b 5 2.0 (using Monte Carlo results), Example Bridge No. 5. *Bolding shows where the pier sizes for Example Bridge No. 5 fall within the table. The main channel bridge in this example has medium piers, and the two relief bridges have small piers. Bridge Type Pier Size (ft) Small Medium Large Small 1 2 3 Medium 1.5 3 4.5 Large 3 6* 9 Table 7.25. Representative bridge pier size as a function of bridge type (reproduced from Table 5.1), Example Bridge No. 5.

Illustrative Examples 111 HEC-18 Pier Scour Contraction Scour Total Scour Abutment Total Scour Left Right Design scour (ft) 9.9 3.4 13.3 4.6 8.8 Bias 0.68 0.93 0.76 0.76 Expected scour (ft) 6.7 3.2 9.9 3.5 6.7 Scour factor for target 0.90 1.77 1.43 1.43 Component scour for target (ft) 8.9 6.0 6.6 12.6 Difference from expected (ft) 2.2 2.8 3.6 3.1 5.9 Total scour for target (ft) 13.5 6.6 12.6 Table 7.27. 100-year scour results for main channel bridge and b 5 2.0, Example Bridge No. 5. HEC-18 Pier Scour Contraction Scour Total Scour Abutment Total Scour Left Right Design scour (ft) 5.4 3.7 9.1 14.5 9.8 Bias 0.68 0.93 0.76 0.76 Expected scour (ft) 3.7 3.4 7.1 11.0 7.5 Scour factor for target 0.89 1.77 1.43 1.43 Component scour for target (ft) 4.8 6.6 20.7 14.0 Difference from expected (ft) 1.1 3.2 3.4 9.7 6.5 Total scour for target (ft) 10.5 20.7 14.0 Table 7.28. 100-year scour results for west relief bridge and b 5 2.0, Example Bridge No. 5. HEC-18 Pier Scour Contraction Scour Total Scour Abutment Total Scour Left Right Design scour (ft) 5.8 4.5 10.3 12.8 15.5 Bias 0.68 0.93 0.76 0.76 Expected scour (ft) 3.9 4.2 8.1 9.7 11.8 Scour factor for target 0.89 1.77 1.43 1.43 Component scour for target (ft) 5.2 8.0 18.3 22.2 Difference from expected (ft) 1.2 3.8 4.0 8.6 10.4 Total scour for target (ft) 12.1 18.3 22.2 Table 7.29. 100-year scour results for east relief bridge and b 5 2.0, Example Bridge No. 5.