5
Validity of the Achievement Levels
Chapter 4 examined evidence of the reliability of the outcomes of NAEP’s 1992 achievement-level settings, that is, the consistency and stability of the cut scores over different conditions. In this chapter, we focus on evidence of the validity of the achievement levels, following the definition in the most recent edition of Standards for Educational and Psychological Testing (hereafter referred to as Standards; American Educational Research Association et al., 2014, p. 11): “the degree to which evidence and theory support the interpretations of test scores for the proposed uses of tests.” More simply, validity refers to the extent to which test results mean what they are intended to mean and can legitimately be used in the way they are intended to be used.
This chapter begins with a short section on the concept of validity and validation. The next two major sections discuss the processes used by NAEP to assess content-related validity and criterion-related validity. The final section presents the committee’s conclusions about both kinds of validity.
CONCEPTS OF VALIDITY AND VALIDATION
Content and Criterion Validity Evidence
In the context of setting standards for NAEP, content-related validity evidence focuses on the extent to which the achievement levels and exemplar items reflect the content and skills embodied in the assessment
framework. Criterion-related validity evidence focuses on the relationships between the achievement levels and other similar measures external to NAEP.
We consider the available information in light of the Standards (American Educational Research Association et al., 1985, 1999, 2014) and best practices in place in 1992 and now.
With regard to evidence of content-related validity, the 1985 Standards offered very little in the context of standard setting. The most relevant was Standard 8.6:
Results from certification tests should be reported promptly to all appropriate parties, including students, parents, and teachers. The report should contain a description of the test, what is measured, the conclusions and decision that are based on the test results, the obtained score, information on how to interpret the reported score, and any cut score used for classification.
The 1999 version included the following guidance relevant to achievement levels, in Standard 8.8:
When score reporting includes assigning individuals to categories, the categories should be chosen carefully and described precisely. The least stigmatizing labels, consistent with accurate representation should always be assigned,
The 2014 version was much more explicit with regard to supporting intended inferences, in Standard 8.7:
When score reporting assigns scores of individual test takers into categories, the labels assigned to the categories should be chosen to reflect intended inferences and should be described precisely.
With regard to evidence of criterion-related validity, the 1985 Standards did not explicitly call for such studies, but it did provide some guidance, in Standard 1.23:
When a test is designed or used to classify people into specified alternative treatment groups (such as alternative occupational, therapeutic, or educational programs) that are typically compared on a common criterion, evidence of the test’s differential prediction for this purpose should be provided.
The 1999 and 2014 versions were almost identical and more explicit about the need for evidence of criterion-related validity, in Standard 5.23:
When feasible and appropriate, cut scores defining categories with distinct substantive interpretations [1999: should be established on the basis of] should be informed by sound empirical data concerning the relation of test performance to the relevant criteria.
Evolution of the Concepts of Validity and Validation
The theoretical conception of validity has changed over time. Between 1920 and 1950, evidence of criterion validity was regarded as the “gold standard” (Angoff, 1988; Kane, 2006; Cronbach, 1971; Moss, 1992; Shepard et al., 1993). Validation was to address the question of how well a test estimates the criterion, in which a criterion was defined in terms of performance on the actual tasks (Cureton, 1951, which was the first issue of Educational Measurement). A test was considered valid for any criterion for which it provided accurate estimates (Gulliksen, 1950). In the influential Essentials of Psychological Testing, Cronbach (1949) organized validity in terms of two kinds of evidence: “logical,” based on judgment, and “empirical,” based on correlations between test scores and some other measure. By the early 1950s, measurement theorists expanded the concept of validity to include content validity (see Kane, 2006), and, shortly thereafter, construct validity (American Psychological Association, 1954).
Initially, content-, construct-, and criterion-related validity were regarded as three distinct types. And criterion-related validity was further divided, temporally, into relationships with current measures (concurrent validity) and relationships with future measures (predictive validity). By the 1980s, the measurement field had moved toward a unitary conception of validity in which construct validity was central (e.g., Cronbach, 1980). Messick (1989, p. 19) described this concept: “[V]alidity is a unitary concept in the sense that score meaning (as embodied in construct validity), underlies all score-based inferences.” This conception is still in place, although validity evidence may be classified into types or sources, such as content related or criterion related. Over time, measurement theorists have further clarified that it is the interpretations and uses that need to be validated, not the test itself.
The process by which these proposed interpretations and uses are evaluated is called validation. Validation proceeds in the same way as the scientific process of hypothesis testing. It requires the formulation of hypotheses (or claims) to be based on the test results and gathering evidence to evaluate the tenability of those claims. Some (e.g., Cronbach, 1980; Messick, 1989; Kane, 2006) describe it as an argument-based approach. That is, validation involves developing a scientifically sound argument to support the intended interpretation of test scores and their relevance to the proposed use, as discussed in the Standards (American Educational Research Association et al., 1999, p. 9). The measurement field also recognizes that validation should include efforts to challenge proposed interpretations and to consider competing interpretations.
Over time, there has been increasing recognition that validation is an ongoing process: it does not stop after one or two studies are completed. Moreover, it does not yield an unequivocal “yes” or “no” answer, such as
that a test is or is not valid. Collecting and evaluating validity evidence is continual: at any time, evidence about validity may be strengthened or refuted as new findings are reported. Messick (1989, p. 13) captures this view:
Because evidence is always incomplete, validation is essentially a matter of making the most reasonable case to guide both current use of the test and current research to advance understanding of what the test score means.
This idea is captured in the current Standards in which validation is defined as the process of “accumulating relevant evidence to provide a sound scientific basis for the proposed score interpretations” (American Educational Research Association et al., 2014, p. 11).
The above very brief discussion merely touches the surface of the wealth of literature in the field of measurement on validation.1 We provide this brief history to make two points. First, the concept of validity has evolved since the 1992 standard settings, and it continues to evolve. As a consequence, standards and expectations for validity evidence have also evolved. Second, sources of data have expanded since 1992, and they, too, continue to expand. The studies conducted in 1992 made use of the available information and drew conclusions accordingly. Since then, however, new sources with new kinds of data and new ways to analyze them have produced new evidence. In the sections below, we discuss both the evidence that was collected in 1992 for the NAEP standard setting and the conclusions drawn about it, as well as evidence that has been collected since then and how it might affect those conclusions.
CONTENT-RELATED VALIDITY EVIDENCE
Content-related validity evidence for the NAEP achievement levels is presented in the ACT documentation and technical reports (ACT, Inc., 1993a, 1993b, 1993c, 1993d, 1993e; Allen et al., 1996, App. H) and in the NAEd background studies and summary report (Shepard et al., 1993). These studies consisted of reviews by subject-matter experts. The reviews focused on the congruence of the achievement-level descriptors (ALDs) and the exemplar items to each other and to the content frameworks. Although these reviews are publicly available, we note that the documentation is uneven: some documentation is very thorough and clear; other documentation is quite vague. It is difficult to reconstruct the processes and decisions behind these studies, along with the sequencing and over-
__________________
1 For more detailed histories, see Cronbach (1980), Messick (1989), Kane (2006), and Zeiky (2001, 2012).
sight. Some appear to have been conducted independently by ACT or by the National Academy of Education (NAEd); others reflect collaboration. This lack of clarity is important because, as detailed below, the two groups drew different conclusions about the adequacy of the descriptors and the extent of congruence among the descriptors, the exemplar items, and the frameworks.
Given that these events occurred more than 24 years ago, it is not possible to fully characterize and understand the deliberations behind the decisions. We are hesitant to make judgments about the rationale for decisions made long ago; at the same time, we acknowledge that some of the issues raised at that time warranted further investigation. For the most part, the content-related studies were designed to answer the following kinds of questions (ACT, Inc., 1993c):
- How well do the achievement-level descriptors reflect the assessment frameworks for reading and mathematics?
- How well do the achievement-level descriptors reflect the items in the 1992 assessments?
- How does one know that students with NAEP scores at or above the cut score associated with a particular achievement level can do the kinds of things that the achievement-level descriptors say they should be able to do?
- Are the exemplar items good indicators of the types of knowledge and skills students should demonstrate?
For both reading and mathematics, the original standard settings were conducted by ACT with 60-62 panelists over the course of 5 days (see Chapter 4). During the final stage of the process, the panelists drafted descriptors for their respective content areas (reading or mathematics) for each achievement level and each grade, and they selected exemplar items to illustrate these descriptors.
For the validation reviews, panels of experts were convened for each content area. The composition of the new panels was somewhat different from the original ones: as detailed in Chapter 4, they included some of the original panelists and new subject-matter experts.
Several key issues are important for understanding the purpose and results of these reviews. For NAEP, prior to the process of setting cut scores, the ALDs were interpreted as aspirational: that is, they define the things that students should know and be able to do. Once the standard setting was completed, the draft descriptors were revised and exemplar items were selected to reflect the things students at each level actually know and can do.
The selection of exemplar items—sometimes called item mapping—
relies on both expert judgment and empirical probability estimates. For each test question, every examinee has some chance of responding correctly, depending on her or his level of proficiency in the subject area. Item response theory procedures allow researchers to estimate the probability of an examinee with a certain level of proficiency responding correctly to each item. These estimates are called response probabilities. For a given test item, depending on its characteristics, examinees with a low level of proficiency have a low chance of answering correctly, and examinees with a high level of proficiency have a much higher chance of answering correctly.
The idea of item mapping is to find items that students at one level can answer correctly (say, two-thirds of the time or more) while students at the next lower level cannot. For example, for a given item, a response probability of 0.67 associated with a certain level of proficiency means that examinees with that level of proficiency have a 67 percent chance of answering the item correctly. The items can be mapped to the achievement level at which the likelihood of a correct response is 0.67. Thus, the exemplar items demonstrate the kinds of tasks that students with proficiency at the cut score are likely to get correct (e.g., two out of three times). Together, the ALDs and exemplar items are intended to provide concrete information to help users interpret and understand the achievement levels.
CONTENT-RELATED EVIDENCE FOR MATHEMATICS
In 1992, three expert panel reviews were convened for mathematics, two described in ACT, Inc. (1993c) and another described by Silver and Kenny (1993). That is, there were three sets of the descriptors: the original developed by the standard setting panelists; the revisions made by the expert review panel; and the final done by the National Assessment Governing Board (NAGB). Tables 5-1a, 5-2a, and 5-3a in the Annex to this chapter show those versions for grades 4, 8, and 12, respectively, for each level (Basic, Proficient, Advanced).
Since 1992, there have been two additional changes in ALDs. A new mathematics framework was developed for the 2005 assessment: it included mathematical reasoning at all grade levels and proficiency levels. At that time, the cut scores for 12th-grade mathematics were reset, and new descriptors were developed. An evaluation of this standard setting is reported in Buckendahl et al. (2009). The 2005 framework for grade 12 was adjusted a few years later to incorporate measures of academic preparedness for college. At that time, a full standard setting was not done, but an expert review of ALDs was conducted. Each of the expert reviews is discussed below.
The 1992 Assessment
Review of the Descriptors and Exemplar Items from the Standard Setting
ACT, Inc. (1993c) provides details of the first expert review. Of the 18 panelists that participated in the review, 10 had participated in the original standard setting, and 8 were new. Panelists who had participated in the standard setting had been selected from among the teachers for each of the three grade levels at the original standard setting. The additional 8 panelists were nominated by stakeholder groups—the National Council for Teachers of Mathematics and the Mathematical Sciences Education Board.
The review was scheduled over 3 days, and the documentation includes details about the overall plan and agenda, which included a series of group and independent exercises. The documentation notes that, while completing the first exercise, the review leaders sensed that some panelists were uncomfortable with the descriptors (ACT, Inc., 1993c, p. 5-8). Panelists commented that the descriptions were ‘’inappropriate,” “not useful,” and ‘’indefensible.” Tension between the panelists from the original standard setting and the new panelists was also evident. Rather than force completion of the process as planned, the staff decided to depart from the schedule and address the group’s concerns.
The documentation provides highlights from these discussions. In general, panelists indicated that the descriptors could be improved with editing and agreed to work on them. The group established guidelines for acceptable revisions: the descriptions could be edited so that consistency across achievement levels within a grade would be enhanced, the consistency across grade levels within each achievement level would be enhanced, and the terminology used would be more clearly communicated to diverse audiences. The group also agreed on boundaries: the panelists would not change any descriptor in such a manner that it would alter the conceptualization of skills and knowledge associated with performance at each specific grade and achievement level. Panelists worked together in grade groups and later came together to review the work across grade levels. Panelists who had participated in the original standard setting were “leaders” of the groups and served as resources for determining whether the suggested changes were within the agreed guidelines. By the end of the meeting, panelists agreed on wording for the descriptors: the changes can be seen in Tables 5-1a, 5-2a, and 5-3a, in the “revised” columns.
Copies of the revised descriptions were then sent to all panelists who had participated in the original standard setting process. They reviewed the revised versions and responded to several evaluation questions, including whether they could support the revised descriptions or whether
the revised descriptions represented a change in the level of student performance they expected when rating items. The ACT documentation characterized the reviews as generally positive: 35 percent positive, 53 percent mostly positive, 6 percent mostly negative, and 6 percent negative (ACT, Inc., 1993c). No additional information is provided in the ACT documentation.
As part of this meeting, panelists also reviewed the exemplar items selected during the standard setting. ACT documentation notes that panelists were given sets of released items from the 1992 mathematics assessment. These items had been classified as Basic, Proficient, and Advanced according to guidelines recommended by NAGB’s Technical Advisory Committee on Standard Setting (ACT, Inc., 1993c, pp. 5-9). Panelists were given a form that could be used to decide whether an item should be included as an exemplar of an achievement level.
Working in grade groups, the panelists agreed on several items to include as exemplars for each achievement level. The numbers of items varied, and there was some difficulty in reaching agreement on items for some achievement levels, particularly the advanced level. Three panel members said that none of the released items adequately represented the 12th-grade advanced achievement level. They then reviewed the entire 1992 item pool and concluded that the types of items they had been looking for were not in the item pool. As a result of this additional review, these participants gave support to the selections put forth by the entire group.
The entire group then reviewed the selections made by the three grade groups. Items that were common to more than one grade (e.g., the 4th and 8th grades or the 8th and 12th grades) occasionally required negotiations to determine which grade should use the item as an exemplar. These decisions were forged by the representatives of the grade levels involved and agreed to by all panelists. The items selected in this way were included with the revised descriptions that were sent to the original panelists for evaluation and approval.
Review of the Revised Descriptors
The second expert review is documented in Silver and Kenney (1993). The purpose of this review was to evaluate the revised ALDs. Panelists included 14 mathematics education professionals, none of whom had been involved in the original standard setting or ACT’s expert reviews.
This panel participated in an item classification exercise: panelists compared the mathematics items to the revised descriptors and classified each as Basic, Proficient, or Advanced. Results were used to calculate a
cut-score interval for each level and grade.2 The resulting cut scores were then compared with the official mathematics cut scores. The newly developed cut scores did not line up with those from the original mathematics standard setting: in all but one of the comparisons, the NAGB cut score was outside the range of (higher or lower than) the cut scores generated by the expert panel.
The same panelists completed a second exercise in which they were asked to discuss (1) the extent to which the descriptors reflects professionally defensible expectations for student performance in mathematics at each grade level and (2) the extent to which the descriptors and exemplar items communicated information about student performance to various constituencies. Silver and Kenney (1993, p. 237) summarized these discussions:
The group consensus was that there were serious gaps and inconsistencies—not only within descriptions at a particular grade level, but also between the descriptions across grade level. Moreover, there was consensus that there was a mismatch between the descriptors and the items.
The panelists agreed that exemplar items were critical to understanding the achievement levels, but their review of the released items was generally negative (Silver and Kenney, p. 238).
Silver and Kenny highlighted two findings. First, the two versions of ALDs differed in nontrivial ways: the original version more closely matched the 1992 framework and items; the revised version better represented mathematics achievement aspirations that match contemporary thinking. Second, they cautioned against “retrofitting” achievement levels to a test that was not originally designed to be reported with respect to such descriptions. They concluded (Silver and Kenney, 1993, p. 242): “It is not possible to recommend without reservation that the descriptions, exemplars, and [cut scores] be used to report the test results.” This information was provided to NAGB for consideration in determining the final version of the descriptors.
Review of NAGB’s Proposed Descriptors
NAGB, in its role as the oversight policy body for NAEP, was responsible for the final decision about the cut scores and the descriptors. As described in Chapter 4, NAGB decided to lower the cut scores for mathematics by 1 standard error. NAGB also proposed revisions to the descrip-
__________________
2 For details, see Silver and Kenney (1993, p. 234).
tors, which would then be the final version (see Tables 5-1a, 5-2a, and 5-3a in the Annex to this chapter).
To obtain validity evidence on the revised descriptors, ACT conducted another expert panel review (ACT, Inc., 1993c). The purpose of this review was to determine whether people were likely to make appropriate inferences about student performance on the basis of the proposed final version of the descriptors for reporting the 1992 NAEP results. The review involved a classification exercise like that conducted by Silver and Kenny (1993). Eleven panelists participated in the review: 6 had participated in the original standard setting and ACT’s review of the original descriptors; 5 were new and had been recommended by the stakeholder groups consulted for the first review—the National Council of Teachers of Mathematics, the Mathematical Sciences Education Board, and the Council of Chief State School Officers. Panelists were asked to sort the pool of mathematics items into achievement levels using the new NAGB-proposed final version of the descriptors.
Overall, panelists agreed on the classification of about 60 percent of the items at all three grade levels, and they assigned items to achievement levels based on the descriptors. After the meeting, the researchers conducted statistical analyses to evaluate student performance on these items. They examined performance of students with NAEP scores in the score intervals for each achievement level. They found that students at each achievement level had an average percentage correct of about 65 percent for items mapped to that achievement level.3
From this analysis, the researchers concluded that the NAGB-proposed final descriptors in mathematics were reasonably clear and that the cut scores reflect the kinds of achievement included in the descriptors (ACT, Inc., 1993c, p. 5-19). These descriptors appear in the Annex: see Tables 5-1a, 5-2a, and 5-3a.
The 2005 Assessment: Revisions to Grade-12 Achievement-Level Descriptors
As noted above, a new framework for grade-12 mathematics was developed for the 2005 assessment, and a new standard setting was conducted. The new framework increased the emphasis on conceptual understanding and reasoning, especially in content other than geometry, and it increased the focus on algebra and on data analysis and probability. The ALDs for grade 12 were revised accordingly to reflect these changes: “deductive reasoning” is in the descriptor for Proficient, and there are
__________________
3 This analysis used complex item response theory procedures. See Chapter 5 of ACT, Inc. (1993c) for details.
three mentions of reason or reasoning in the descriptor for Advanced (see Table 5-3a). At the same time, the descriptors for grades 4 and 8 were not changed, although the expanded explanations were revised slightly. In the expanded explanation of Proficient at grade 8, “reason” or “reasoning” is mentioned twice in the descriptors, and it is mentioned once in the final sentence of the expanded explanation for Advanced at grade 8. This difference in what was and was not changed in the mathematics descriptors raises questions about the extent to which the framework for grades 4, 8, and 12 continues to represent a coherent progression of mathematics knowledge, as reflected in contemporary thinking in mathematics education (see Daro et al., 2011; Schmidt et al., 2002, 2005; Watanabe, 2007).
The 2009 Assessment: Revisions to Grade-12 Achievement-Level Descriptors4
The framework for grade-12 mathematics was revised for the 2009 assessment. This change was prompted by the desire to measure the extent to which 12th-grade students are prepared for postsecondary education and training. However, it was decided that the revision did not warrant a whole new standard setting. Instead, NAGB conducted an evaluation of the alignment of the grade-12 mathematics items to the existing ALDs. Through this “anchor study,” the descriptors could be revised as needed to ensure they were aligned with the items in the item pool (which, in turn, were intended to be aligned with the revised framework), but an interruption in the trend line could be avoided.
The anchor study proceeded in four stages, as described by Pitoniak et al. (2010, p. 14):5
First, statistical analyses were conducted to determine the items that anchored to different achievement-level ranges. Second, a panel of mathematics experts was convened. They reviewed all items that anchored to each of the three achievement level ranges and wrote individual descriptions of the mathematics skills measured by each item. The panel then created summary descriptions of what students in different achievement-level ranges knew and could do based on the items anchored to each level. Third, the panel evaluated the alignment of the summary descriptions to the policy-level definitions and the 2005 achievement-level descriptions. Fourth, the panelists drafted achievement-level descriptions.
__________________
4 This text was revised after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
5 Details about this study appear in Pitoniak et al. (2010).
Statistical Analyses
As noted above, the first step involved conducting statistical analyses to map (or anchor) the items to the existing achievement levels. This process is described below.
- Using plausible value estimates (see Chapter 1), assign individual test takers to achievement levels.
- Compute the probability of each student in that achievement level answering each item correctly (or, for an open-ended question, reaching a given score level).
- Average the probabilities for students within a given level to yield the anchoring probability used in the study for that item (or score level). Each item (or score level) will then have four probabilities: one each for Below Basic, Basic, Proficient, and Advanced.
- Map items to achievement levels. For this study, an item was considered to map to the achievement level for which the probability of a correct response averaged across students at that achievement level is 0.67 or higher.
The mapping process also used a statistic called the discrimination index. This statistic provides an overall sense of how well a given item distinguishes between two adjacent achievement levels. For this study, discrimination indices were calculated for each item at each of the three named achievement levels using the following steps:
- Determine the probability of a correct response for students at one achievement level.
- Determine the probability of a correct response for students at the next lower achievement level.
- Subtract the two probabilities to get the difference.
- Prepare a cumulative distribution of these differences for all of the items.
- Identify the items that map to the anchor achievement level that also meet the discrimination criterion. For this study, the criterion was the 40th percentile; thus, an item was considered to be sufficiently discriminating if the difference in probability of a correct response at the anchor level and the next lowest achievement level is greater than or equal to the 40th percentile in the cumulative distribution of differences.
Table 5-1 shows the results from this analysis. The top half of the table provides counts and percentages of items that mapped to an achievement level. The bottom half of the table provides similar information for
items that did not map. The final column shows that 24 items anchored at the Basic level, 68 at the Proficient level, and 79 at the Advanced level. Overall, a total of 171 items (approximately 76%) mapped to one of the achievement levels, and 54 items (approximately 24%) did not map to any achievement level.
Items may not map to an achievement level for one of two reasons: they fail to meet the response-probability criterion for any of the levels, or they fail to meet the discrimination criterion. The first cell in the lower half of the table shows that 7 items did not map because they were too easy. That is, the score at which a test taker had a 67 percent chance of answering correctly was lower than the cut score for basic, in this case, below 141. In addition, the table also shows that 38 items (17%) did not map because they were too difficult. That is, the score at which a test taker had a 67 percent chance of answering correctly was higher than the cut score for advanced.
Other items met the response-probability criterion but did not meet the discrimination criterion. Approximately 4 percent of items fell in this category.
TABLE 5-1 Anchor Study Results for 2009 Grade-12 Mathematicsa
| Description | Total | |
|---|---|---|
| Count | Percentage | |
| Items That Anchored at Basic, Proficient, or Advanced | ||
| Anchored at Basic | 24 | 11 |
| Anchored at Proficient | 68 | 30 |
| Anchored at Advanced | 79 | 35 |
| Items That Did Not Anchor Due to Response-Probability Criterion | ||
| Anchored Below Basic | 7 | 3 |
| Did not anchor because too difficult | 38 | 17 |
| Items That Did Not Anchor Due to Discrimination Criterion (but met response-probability criterion) | ||
| Did not anchor at Basic | 0 | 0 |
| Did not anchor at Proficient | 7 | 3 |
| Did not anchor at Advanced | 2 | 1 |
| All Items | 225 | |
NOTES: Because responses to some items were scored at multiple levels (polytomously), column totals may be greater than the number of items in the assessment. Detail may not sum to totals because of rounding. See text for explanation.
aThis table was added after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
SOURCE: Adapted from Pitoniak et al. (2010, Table 1).
Expert Review
A six-member panel of mathematics experts was convened to review the scale anchoring analysis and produce written descriptions of the knowledge and skills displayed by students within each achievement-level range. Two members were high school teachers, four were university-level faculty members, and the sixth member was “president of a national mathematics organization” (Pitoniak et al., 2010, p. 5). After an initial set of training procedures, panelists reviewed the items and described the skills demonstrated by students responding correctly to each item (or at different levels, for polytomous items), referred to as item-level descriptions. The items were grouped according to the achievement level they mapped to. For each achievement level, panelists examined all of the item-level descriptions and developed a summary of the knowledge and skills demonstrated at the level, referred to as the anchor descriptions.
Panelists were then asked to compare the anchor descriptions for each achievement level to (1) the NAEP policy-level definitions and (2) the 2005 grade-12 mathematics ALDs. For each of these documents, panelists provided an initial rating of the alignment between their summaries and the specific document using a scale to indicate whether the alignment was weak, moderate, or strong. Panelists discussed their ratings and then, on their own, provided a second rating without further group discussion.
Alignment of the anchor summaries to the policy-level definitions was rated as moderate to strong for Basic, moderate for Proficient, and weak to moderate for Advanced. Alignment of the anchor summaries to the 2005 ALDs was rated as moderate to strong for all achievement levels. At the end of the anchor study, panelists prepared and settled on draft descriptions for each of the achievement levels.
Panelists also responded to three evaluation questions about their level of satisfaction with the item-level descriptors, the anchor descriptions for each achievement level, and the final ALDs. On a scale that ranged from very dissatisfied to very satisfied, all of the panelists reported they were satisfied or very satisfied with the results. Five of the six were very satisfied with the ALDs.
The last step was to revise, review, and finalize the ALDs. After the meeting, NAGB obtained public comment on the anchor descriptions drafted by the panelists. Public comments were shared with the panelists, and the panelists worked together to revise them. A final version was approved by NAGB’s Committee on Standards, Design, and Methodology at its May 2010 board meeting. These ALDs appear in the Annex to this chapter.
CONTENT-RELATED EVIDENCE FOR READING
Chapter 5 of the documentation of the 1992 standard setting for reading (ACT, Inc., 1993c) discusses the results of expert reviews of the ALDs, and Appendix F of the technical report for the 1994 administrations (Allen et al., 1996) presents results from a study to examine the congruence between the item pool and the ALDs.
The 1992 Assessment
Review of the Descriptors from the Standard Setting
A total of 19 panelists participated in the initial review—10 from the original standard setting and 9 new panelists who were state-level reading curriculum supervisors or assessment directors or university faculty teaching in disciplines related to the subject area (see Allen et al., 1996, App. F).
The reading panelists completed tasks similar to those done by the mathematics panelists. They compared the original descriptors with the original policy definitions, the reading framework, and across grade levels. They were asked to make recommendations about ways in which the descriptors could be improved. The group suggested very few changes. Pearson and DeStefano (1993) indicated that there was some concern that this was due to influence from panelists who had participated in the original standard setting, because they were heavily invested in the earlier version.
Panelists were asked to respond to six questions related to the appropriateness of the descriptors before and after revisions were made. Panelists said that the descriptors were more than “somewhat professionally defensible” before revision and “very professionally defensible” after revision. Panelists also said that the original descriptors communicated more than “somewhat well” to educators and “somewhat well” to the public and “very well” to both groups after revision. Panelists said that the descriptors reflected appropriate content for the grade more than “somewhat well” before being revised and “very well” after revision. Panelists also said the descriptors reflected more than “somewhat well” the proper sequence of skills both within and across grades before being revised and ‘’very well” after being revised.
After completing revisions to the descriptors, panelists were asked to respond to a second questionnaire, which asked them to evaluate the descriptors in terms of the NAGB policy definitions of the achievement levels and of the framework. The results indicated that panelists judged the revised descriptors to be very consistent with the NAGB generic
definitions and more than “somewhat consistent” with the 1992 NAEP reading framework.
Review of the Alignment of the Item Pool and the Descriptors
A total of 58 reading professionals (teachers and nonteacher educators) were assembled to review the descriptors in relation to the 1992 reading item pool. The panelists were assigned to two different task groups, which used different procedures for their rating process. One group used a procedure called item difficulty categorization; the other used a procedure called judgmental item categorization.6
The item-difficulty categorization procedure examined the level of support for the descriptors as justified by empirical performance data for the NAEP items. The items were selected for each achievement level using a response probability criterion of 0.50 at the lower borderline score. These were called “can do” items. The items not meeting the same probability criterion at the upper borderline score for the level were categorized as “can’t do” items. Those items meeting the probability criterion anywhere in the range of scores for a level—from the lower borderline to the upper borderline—were called “challenging items.” Panelists were trained to examine the items in each of the three categories and determine whether or not the cognitive demand of the item matched the skills and knowledge identified in the descriptors. Mismatches were identified and later resolved or accounted for through a grade-level procedure involving the other group (which used the judgmental-item categorization).
The judgmental-item categorization procedure asked panelists to assign items to levels on the basis of their judgment of where each belonged given the ALDs. Items were assigned to the lowest level of performance required to respond correctly. This assignment was done in two rounds: The first round collected independent judgments; the second involved group discussion, with the goal of reaching consensus on the judgments.
The two groups then reconvened to discuss their findings. The goal of this final discussion was to reach general agreement on the extent of agreement between the descriptors and the item pool. The committee could not locate any details about this evaluation or its results. The process is summarized in Allen et al. (1996, App. F, p. 797): “[O]n the basis of the validation process only one recommendation was made by the panelists to improve the [descriptors] and bring them more in line with
__________________
6 This process was similar to that used for the grade-12 mathematics anchor study, described above. See Donahue et al. (2010).
performance data.” The recommended change was to include an ability to make inferences in the descriptor of the Basic level at each grade.
The 2009 Assessment7
Revisions to the Reading Framework
The framework first adopted for reading in 1992 was in place through the 2007 reading assessment. In line with evolving understanding in the field of reading, the framework was changed for the 2009 reading assessment, and that version remains in place. The current framework conceptualizes reading as an active and complex process that involves (1) understanding written text, (2) developing and interpreting meaning, and (3) using meaning as appropriate to the type of text, purpose, and situation.
Point (3) reflects a substantial change in the understanding of reading. Earlier conceptions treated comprehension as an endpoint. It is now conceptualized to include a reader’s act not only of constructing meaning, but also of using the meaning that is constructed through reading. That is, one reads both to comprehend and to use what is comprehended for further understanding. The changes to the framework were foundational. For reasons described in Chapter 7 (both empirical and judgment based), these changes did not lead to a new standard setting. However, the ALDs were revised, as shown in Tables 5-4a, 5-5a, and 5-6a. The revisions were based on anchor studies like those described above for grade-12 mathematics.
Statistical Analyses
The same methods described earlier for grade-12 mathematics were used for the statistical part of the reading anchor studies. The same criteria were set for the response probability value and the discrimination index used to map items onto specific achievement levels. The analyses were done for all three grades, and results appear in Table 5-2. For this analysis, the authors did not distinguish between the two criteria in reporting the numbers and percentages of items as in Table 5-1a, so it is not clear whether an item failed to anchor due to difficulty level or to discrimination level. However, 27 percent, 16 percent, and 18 percent of the items did not anchor to an achievement level, respectively, for grades 4, 8, and 12.
__________________
7 This text was revised after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
TABLE 5-2 Numbers and Percentages of NAEP Reading Items Anchoring across Categoriesa
| Grade and Category | Totalb | |
|---|---|---|
| Count | Percentage | |
| Grade 4 | ||
| Anchored Below Basic | 4 | 2.9 |
| Anchored at Basic | 33 | 23.7 |
| Anchored at Proficient | 43 | 30.9 |
| Anchored at Advanced | 21 | 15.1 |
| Did not anchor | 38 | 27.3 |
| Total Number of Items | 139 | |
| Grade 8 | ||
| Anchored Below Basic | 17 | 9.3 |
| Anchored at Basic | 64 | 35.0 |
| Anchored at Proficient | 45 | 24.6 |
| Anchored at Advanced | 27 | 14.8 |
| Did not anchor | 30 | 16.4 |
| Total Number of Items | 183 | |
| Grade 12 | ||
| Anchored Below Basic | 12 | 6.5 |
| Anchored at Basic | 62 | 33.3 |
| Anchored at Proficient | 55 | 29.6 |
| Anchored at Advanced | 24 | 12.9 |
| Did not anchor | 33 | 17.7 |
| Total Number of Items | 186 | |
NOTES: Because responses to some items were scored at multiple levels, column totals may be greater than the number of items in the assessment. The numbers may not sum to the totals because of rounding. See text for explanation.
aThis table was added after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
bThe vocabulary-only blocks were not included in this study.
SOURCE: Adapted from Donahue et al. (2010, Tables 1, 2, and 3).
Expert Review
This part of the study for reading proceeded in the same way as that for mathematics: three six-member panels of experts were convened—one for each grade. For each grade, at least two panelists were university-level reading faculty members and at least two were top-rated reading classroom teachers at the grade level. Eighteen panelists were recruited, but two were unable to participate (one for the 4th-grade panel and one for the 8th-grade panel). The 16 panelists worked in grade groups to develop item-level descriptions and anchor descriptions for each achievement level. For reading, panelists made three comparisons—between the anchor descriptions and (1) the policy-level definitions, (2) the 1992
ALDs, and (3) the 2009 preliminary achievement-level descriptions that were developed along with the framework to guide item development. Findings were as follows:
- Alignment of the anchor descriptions to the policy definitions: Most panelists rated the alignment as moderate or strong. However, one-third of the grade-12 panelists (2 of 6) rated the alignment to be weak at the Advanced level.
- Alignment of the anchor descriptions to the 1992 ALDs: Most panelists rated the alignment to be moderate to weak. The lowest ratings were for 4th grade, where all five panelists rated alignment to be weak at the Basic level, and three of the five panelists rated it to be weak at the Advanced level.
- Alignment of the anchor descriptions to the 2009 preliminary ALDs: Most panelists rated the alignment to be moderate or strong for 8th and 12th grade. But for 4th grade, none of the panelists thought the alignment was strong. For the Basic level, all the panelists judged it to be moderate; at the Proficient level, two panelists rated it as moderate, and three judged it as weak; for the Advanced level, one panelist rated it as moderate, and four rated it as weak.
These alignment ratings—considered jointly with the extent of items that did not anchor (27%)—suggest that additional work is needed to align the descriptions with the item pool, particularly at grade 4.
Panelists were asked to complete a final evaluation to indicate their overall satisfaction with the results. Most panelists said they were satisfied or very satisfied with the item-level descriptors and the anchor-based summaries, although for each comparison, two panelists were neutral. With regard to the achievement-level descriptions, all five grade-8 panelists were very satisfied, and four of the six grade-12 panelists were satisfied (one was very satisfied, one was neutral). Only two of the grade-4 panelists were satisfied (two were neutral, and one was dissatisfied).
Finally, as with mathematics, the revised descriptions were circulated for public comment. A subset of individuals who had participated in the anchor studies (two for each grade) reviewed the comments and made the changes they deemed appropriate. The revised versions were then reviewed by all of the anchor-study panelists, which resulted in adjustments to the descriptions until all of the panelists were comfortable with the result. A final version was approved by the NAGB’s Committee on Standards, Design, and Methodology at their March 2010 board meeting. These ALDs appear in the Annex to this chapter.
CRITERION-RELATED VALIDITY EVIDENCE
Criterion-related evidence usually consists of comparisons with indicators separate from the assessment of the content and skills that are measured by the assessment, in this case, other measures of achievement in reading and mathematics. The goal is to help to evaluate the extent to which achievement levels are reasonable and set at an appropriate level.
It can be challenging to identify and collect the kinds of data that are needed to evaluate criterion-related validity. It is somewhat less difficult for assessments that report scores for individuals than for assessments that report only group-level results. For the former, special studies can focus on achievement-related measures, such as course-taking patterns, grades, classroom assessments, and teacher ratings. For the latter, like NAEP, individuals are not identified or classified into achievement levels: instead, the percentages of students scoring at each achievement level are estimated. The difficulty of collecting evidence of criterion-related validity for NAEP has been documented in prior evaluations (e.g., Shepard et al., 1993; Hambleton et al., 2009; ACT, Inc., 1993c). The ACT reports that document the validity of the achievement levels do not include results from any studies that compared NAEP achievement levels to external measures. It is not clear why NAGB did not pursue such studies. In contrast, the NAEd reports include a variety of such studies.
The NAEd evaluators relied on some existing data, including the International Assessments of Education Progress (IAEP) of mathematics for 13-year-olds; advanced placement (AP) tests; college admissions tests, such as SAT; and state assessments. The NAEd evaluators also conducted a special study in which 4th- and 8th-grade teachers classified their own students into the achievement-level categories by comparing the ALDs with the student’s classwork. This study used a contrasting groups standard setting procedure (see Cizek, 2001, 2012).8
Buros Institute evaluators (Buckendahl et al., 2009) made use of some of the same data sources as NAEd in evaluating the reasonableness and criterion-related validity of the achievement levels, including performance on AP tests; college admission tests; the international assessments in place by that time (IAEP was only administered in 1988 and 1991): mathematics and reading tests for 15-year-olds on the Programme for International Student Assessment (PISA) examination; and grade-4 and grade-8 results for the mathematics component of the Trends in International Mathematics and Science Study (TIMSS).9
We drew from similar sources for our evaluation and present trends
__________________
8 For details on these studies, see McLaughlin et al. (1993) and Shepard et al. (1993).
9 For details on these studies, see Buckendahl et al. (2009c).
when available. Below we compare (1) NAEP grade-4 and grade-8 achievement-level results in mathematics with the international benchmarks for the mathematics literacy component of TIMSS in the same grades; (2) NAEP grade-8 achievement-level results in reading and mathematics with international benchmarks for the mathematics literacy and reading literacy tests on PISA for 15-year-olds; (3) NAEP achievement levels in grades 4 and 8 with those set by states; and (4) NAEP grade-12 achievement-level results in mathematics and reading with results from the AP tests in calculus and English. With regard to college admissions tests, we focus on recent research on setting each test’s benchmark for college readiness.
Comparisons with International Assessments
The United States participates regularly in both PISA and TIMSS, which are administered to samples of students and, like NAEP, report group-level results rather than scores for individuals. Both also report results for the participating countries, with countries rank ordered by summary measures of their students’ performance.
U.S. Results on PISA
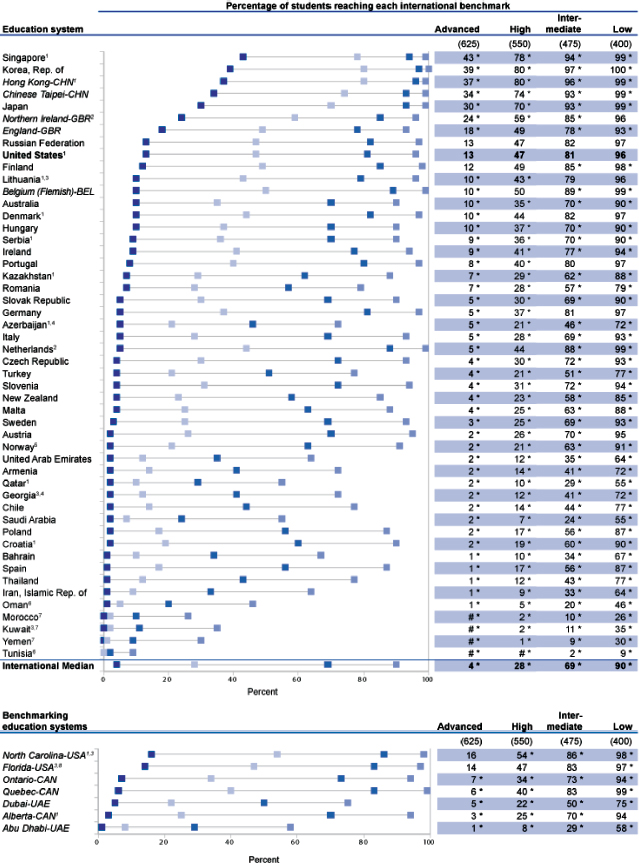
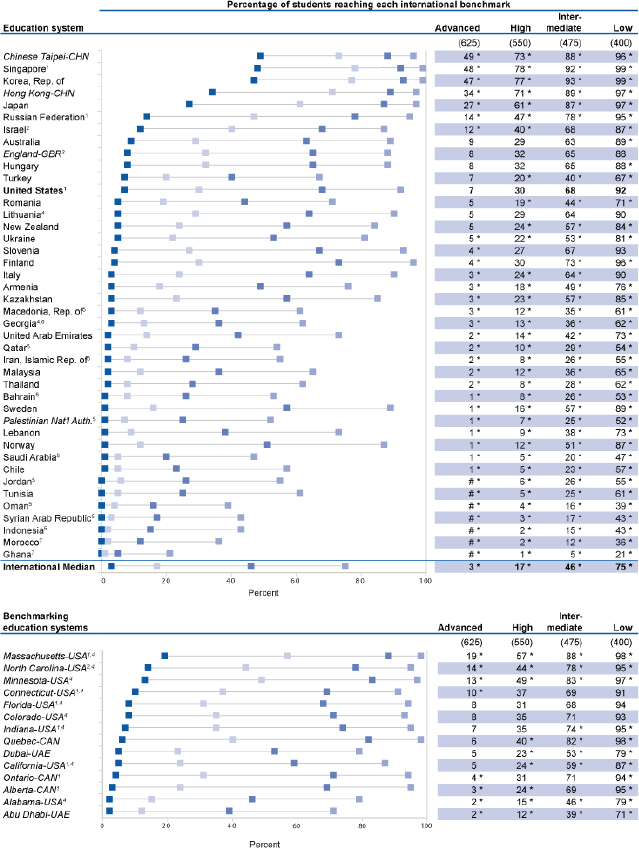
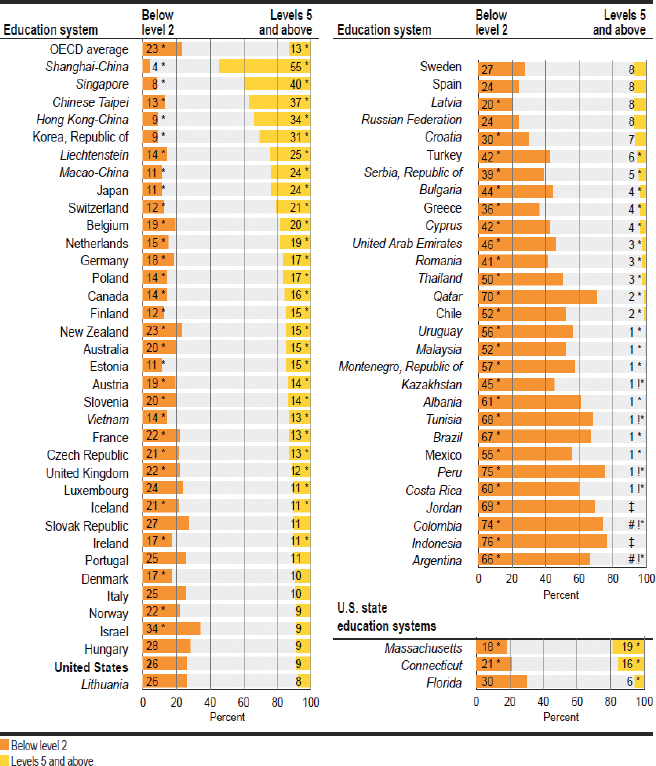
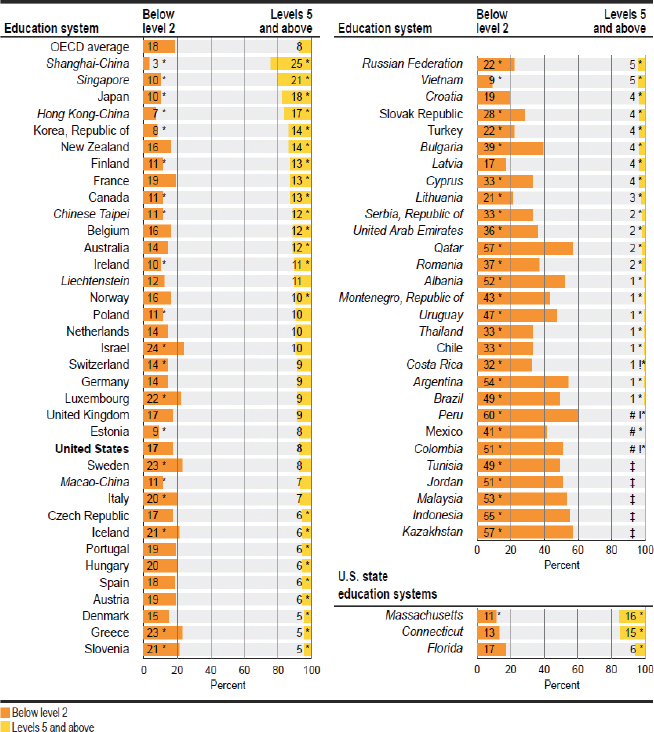
PISA is given to 15-year-olds around the world and assesses both mathematics literacy and reading literacy. Scores are reported on a scale of 1 to 1,000. On the most recent PISA results (2012), U.S. students averaged a score of 481 in mathematics literacy, which places them 35th of 65 countries, just below the Slovak Republic and just above Lithuania. In reading, the U.S. students averaged 498, placing the United States 23rd, just below the United Kingdom and just above Denmark.10 PISA also reports results that are based on proficiency levels, ranging from 1 to 6: they are not labeled, but descriptors are provided (OECD, 2014). PISA reports highlight the percentages of students in each country who score below level 2 and at level 5 and above. In 2012, 9 percent of U.S. students scored at level 5 or above in mathematics literacy: see Figure 5-1. This result can be compared with NAEP results from 2011 and 2013, where the percentages scoring at the advanced level were 8 and 9 percent, respectively. Similarly, 8 percent of U.S. students scored at level 5 or higher for reading literacy: see Figure 5-2. This result can be compared with the advanced level for NAEP 2011 and 2013, where the percentages scoring at the advanced level were 3 and 4 percent, respectively.
__________________
10 More than 500,000 students participated from 65 countries, all 34 in the OECD and 31 others, which together represented 80 percent of the world’s economy (OECD, 2014).
NOTES: Education systems are ordered by 2012 percentages of 15-year-olds in levels 5 and above. To reach a particular proficiency level, a student must correctly answer a majority of items at that level. Students were classified into mathematics proficiency levels according to their scores. Exact cut scores are as follows: below level 1 (a score less than or equal to 357.77); level 1 (a score greater than 357.77 and less than or equal to 420.07); level 2 (a score greater than 420.07 and less than or equal to 482.38); level 3 (a score greater than 482.38 and less than or equal to 544.68); level 4 (a score greater than 544.68 and less
SOURCE: U.S. Department of Education (2012).
U.S. Results on TIMSS
TIMSS is given to representative samples of 4th- and 8th-grade students around the world.11 It assesses both mathematics and science and reports results as average scale scores and levels. The scale score ranges from 1 to 1,000. Data are available by country for 1995, 2007, and 2011 for grade 4 and grade 8. The average scores for 4th graders for those 3 years were, respectively, 518, 529, and 541. U.S. students ranked 8th. The average scores for 8th graders were, respectively, 492, 508, and 509. U.S. students ranked 7th.
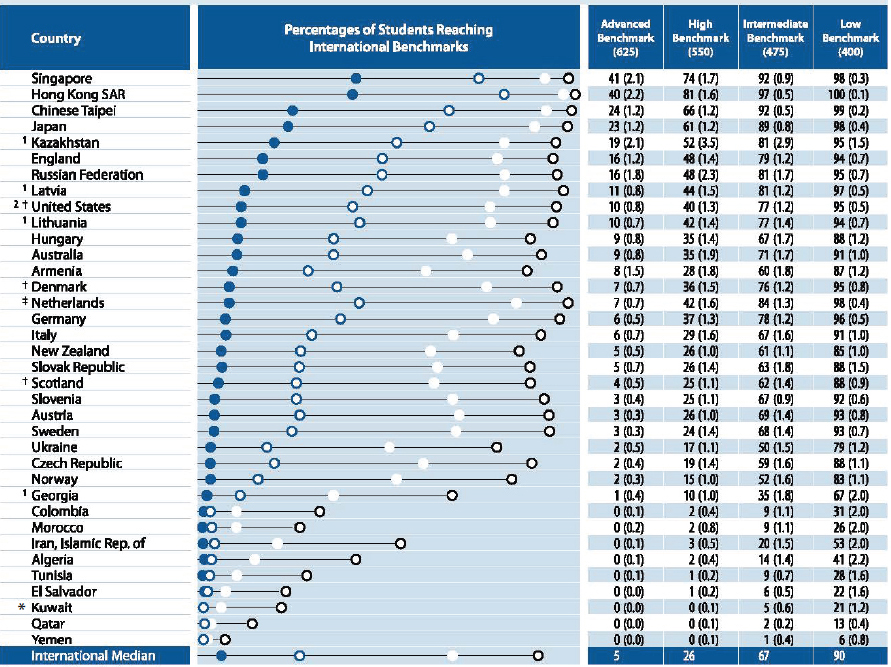
Like PISA, TIMSS has set benchmarks. There are four levels, labeled advanced, high, intermediate, and low. Figures 5-3 and 5-4 show the percentages of students at each of the levels for 2011, and Figures 5-5 and 5-6 show them for 2007. For those years, 13 percent of 4th graders and 7 percent of 8th graders scored at the advanced level; these results compare with 7 percent of 4th graders and 8 percent of 8th graders who were at the advanced level in mathematics on NAEP in 2011.
Table 5-3 summarizes these comparisons for both TIMSS and PISA.
__________________
11 Fourth-grade students from 57 countries and 8th-grade students from 56 countries participated in the 2011 TIMSS (Provasnik et al., 2012).
NOTES: Education systems are ordered by 2012 percentages of 15-year-olds in levels 5 and above. To reach a particular proficiency level, a student must correctly answer a majority of items at that level. Students were classified into reading proficiency levels according to their scores. Exact cut scores are as follows: below level 1b (a score less than or equal to 262.04); level 1b (a score greater than 262.04 and less than or equal to 334.75); level 1a (a score greater than 334.75 and less than or equal to 407.47); level 2 (a score greater than 407.47 and less than or equal to 480.18); level 3 (a score greater than 480.18 and less than or equal to 552.89); level
SOURCE: U.S. Department of Education (2012).
Linking TIMSS and PISA Results to NAEP
The results discussed above show how U.S. students do on international assessments. They provide data that are useful comparisons with NAEP, particularly in judging the reasonableness of the percentages of students that score at the Proficient and Advanced levels. It is also useful to consider how students in other counties would do on NAEP. That is, if one of the purposes of setting performance standards for NAEP is to establish expectations at which U.S. students will be competitive with those in other countries, it is reasonable to ask to what degree the standards represent achievement levels that are actually attained by students in those countries. Given the differences in TIMSS and PISA results between students in other countries and U.S. students, one would expect greater percentages of students in countries such as Singapore and China to perform at the Advanced and Proficient levels. However, if it turned out that only small percentages of students in other countries attained these NAEP levels, then one could conclude that they had been set unreasonably high.
Since the time of the NAEd evaluation, new methods have been developed to investigate these questions (e.g., Beaton and Gonzalez, 1993; Johnson and Siengondorf, 1998; Pashley and Phillips, 1993). They rely on statistical procedures called “linking” and estimate how students in other countries would perform on NAEP. Using linking methods, researchers have “mapped” data from international assessments to the NAEP score scale and estimated students’ scores on TIMSS and PISA that would be
SOURCE: U.S. Department of Education (2011a).
SOURCE: U.S. Department of Education (2011b).
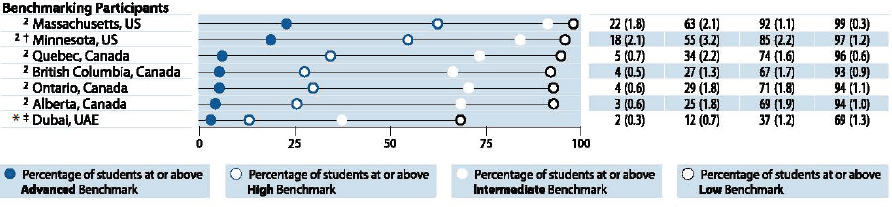
NOTES: †Met guidelines for sample participation rates only after replacement schools were included (see Appendix A). ‡Nearly satisfied guidelines for sample participation rates only after replacement schools were included (see Appendix A). 1National Target Population does not include all of the International Target Population defined by TIMSS (see Appendix A). 2National Defined Population covers 90 percent to 95 percent of National Target Population (see Appendix A). *Kuwait and Dubai, UAE tested the same cohort of students as other countries, but later in 2007, at the beginning of the next school year. ()Standard errors appear in parentheses. Because results are rounded to the nearest whole number, some totals may appear inconsistent.
SOURCE: Mullis et al. (2008, Exhibit 2.2, p. 70). Reprinted with permission from the International Association for the Evaluation of Educational Achievement.
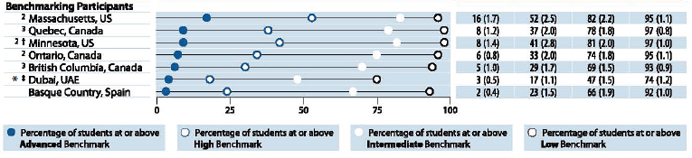
NOTES: †Met guidelines for sample participation rates only after replacement schools were included (see Appendix A). ‡Nearly satisfied guidelines for sample participation rates only after replacement schools were included (see Appendix A). Did not satisfy guidelines for sample participation rates (see Appendix A). 1National Target Population does not include all of the International Target Population defined by TIMSS (see Appendix A). 2National Defined Population covers 90 percent to 95 percent of National Target Population (see Appendix A). 3National Defined Population covers less than 90 percent of National Target Population (but at least 77%, see Appendix A). *Kuwait and Dubai, UAE tested the same cohort of students as other countries, but later in 2007, at the beginning of the next school year. ()Standard errors appear in parentheses. Because results are rounded to the nearest whole number, some totals may appear inconsistent.
SOURCE: Mullis et al. (2008, Exhibit 2.2, p. 71). Reprinted with permission from the International Association for the Evaluation of Educational Achievement.
TABLE 5-3 Percentages of U.S. Students Who Scored in the Top Categories on TIMSS, PISA, and NAEP: 2007, 2011, 2012
| Grade, Subject, and Assessment | Highest Levela | Two Highest Levelsb | ||||
|---|---|---|---|---|---|---|
| 2007 | 2011 | 2012 | 2007 | 2011 | 2012 | |
| Grade-4 Mathematics | ||||||
| TIMSS | 10 | 13 | n/ac | 40 | 47 | n/a |
| NAEP | 6 | 7 | n/a | 39 | 40 | n/a |
| Grade-8 Mathematics | ||||||
| TIMSS | 6 | 7 | n/a | 31 | 30 | n/a |
| PISA | n/a | n/a | 9 | n/a | n/a | n/a |
| NAEP | 7 | 8 | n/a | 32 | 35 | n/a |
| Grade-8 Reading | ||||||
| PISA | n/a | n/a | 8 | n/a | n/a | n/a |
| NAEP | 3 | 3 | n/a | 31 | 34 | n/a |
NOTE: NAEP = National Assessment of Educational Progress, PISA = Programme for International Student Assessment, TIMSS =Trends in International Mathematics and Science Study.
aHighest level for TIMSS and NAEP is “advanced.” PISA reports the top-level results as “5 and higher.”
bTwo highest levels for TIMSS are “advanced” and “high.” For NAEP, two highest levels are “Proficient” and “Advanced.” PISA reports level results at 5 and higher or 2 and lower; results for two highest levels were not available.
cn/a: Not available because test was not administered in this year.
roughly equivalent to the cut scores on NAEP for similar grades and subject areas. Once the TIMSS and PISA cut scores are determined, it is possible to calculate the percentage of students in other countries who would likely score at each of the NAEP achievement levels.
The committee cautions that linking is not an exact science, and there can be a considerable amount of error associated with the estimated cut scores. Various linking methods carry different assumptions—the more stringent the assumptions, the more robust the results (if the assumptions are met). The most robust method of linking is called equating: it produces results for the two tests that are considered interchangeable. Other methods are less robust, but make possible more comparisons between test results. These methods are called calibration, concordance, vertical scaling, projection, and moderation.12 Results from two international mapping studies are available, one by Phillips (2007) and another by Hambleton et al. (2009).
__________________
12 These methods are too complex to fully describe here: for details, see Kolen and Brennan (2004) and Holland and Dorans (2006).
Phillips applied linking procedures (moderation) that were developed in Johnson and Siengondorf (1998). He used NAEP score data from 2000 and TIMSS score data from 1999 to estimate the TIMSS scores that were equivalent to the NAEP cut scores. He then calculated the percentage of students at each NAEP achievement level for the students in each TIMSS country: that is, the results show the percentage of students in each country that would be projected to score at each achievement level on NAEP. He repeated this analysis with TIMSS score data from 2003 (although the linking was conducted with NAEP 2000 score data). Hambleton and colleagues used a similar but a more robust linking method than Phillips (equipercentile equating), and they used data for the same year to develop the link, 2003.
Both sets of analyses applied these cut scores to score data from TIMSS and PISA and estimated the percentages of students at the NAEP Advanced and Proficient achievement levels: see Tables 5-4 and 5-5, respectively, for Hambleton and colleagues and for Phillips. Countries are rank ordered by their estimated performance: in Table 5-4 by the percentage of students in the advanced level; in Table 5-5 by the percentage of students at or above the Basic level.
The two analyses show fairly consistent results, with the same set of countries appearing in the top 10. Both also show that students in other countries are projected to do very well on NAEP. As many as 40.6 percent of students in Singapore are projected to score at the Advanced level. Along with Singapore, the analyses project that at least 20 percent of students from four other countries—Hong Kong, the Republic of Korea, Chinese Taipei, and Japan—would score at the advanced level. The United States’ ranking is much lower: 11th for the Hambleton and colleagues analysis (Table 5-4), with 28.8 percent scoring proficient or above and 5.4 percent scoring Advanced; and 14th in the Phillips analysis (Table 5-5), with 26 percent scoring Proficient or above and 5 percent scoring Advanced and above.
Similar findings were found by Hambleton and colleagues (2005) for a NAEP-PISA link: see Table 5-6. The top country is Belgium, projected to have 49.7 percent of students at Proficient or above and 16.8 percent of students at Advanced. The top five countries have a minimum of 46.7 of their students scoring at Proficient or above and at least 13.0 percent at the Advanced level (Belgium, Netherlands, Republic of Korea, Japan, and Finland). The United States ranked 26th, with 29 percent at the Proficient or above level and 5.0 percent at the Advanced level.
Taken together, these results confirm that not only do the students in other countries score significantly higher than U.S. students on TIMSS and PISA but also they would outscore U.S. students on the nation’s own national assessment.
TABLE 5-4 International Comparisons of Students at NAEP Proficient or Above and Advanced Achievement Levels in 2003 Based on Link to TIMSS 2003: Grade-8 Mathematics (in percentage)
| Country | Proficient or Above | Advanced |
|---|---|---|
| Singapore | 76.8 | 40.6 |
| Chinese Taipei | 66.1 | 35.1 |
| Korea, Republic of | 69.8 | 31.7 |
| Hong Kong | 73.0 | 26.5 |
| Japan | 61.7 | 21.1 |
| Hungary | 40.5 | 9.3 |
| Netherlands | 44.3 | 7.8 |
| Belgium | 46.5 | 7.3 |
| Estonia | 38.8 | 7.2 |
| Slovak Republic | 30.6 | 6.3 |
| United States | 28.8 | 5.4 |
| Australia | 29.1 | 5.2 |
NOTES: Countries are ranked in order by the percentage of students at the Advanced level. NAEP = National Assessment of Educational Progress, TIMSS = Trends in International Mathematics Science Study.
SOURCE: Data from Hambleton et al. (2009).
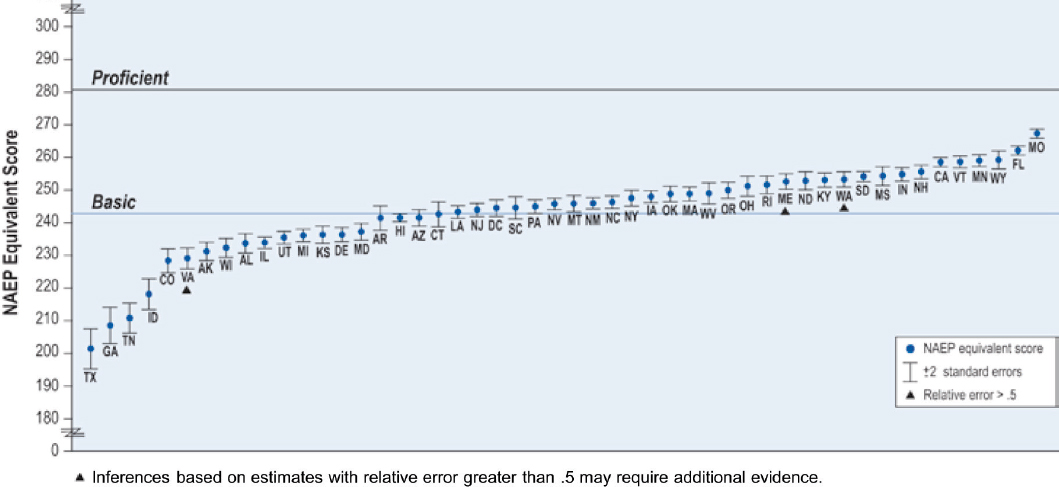
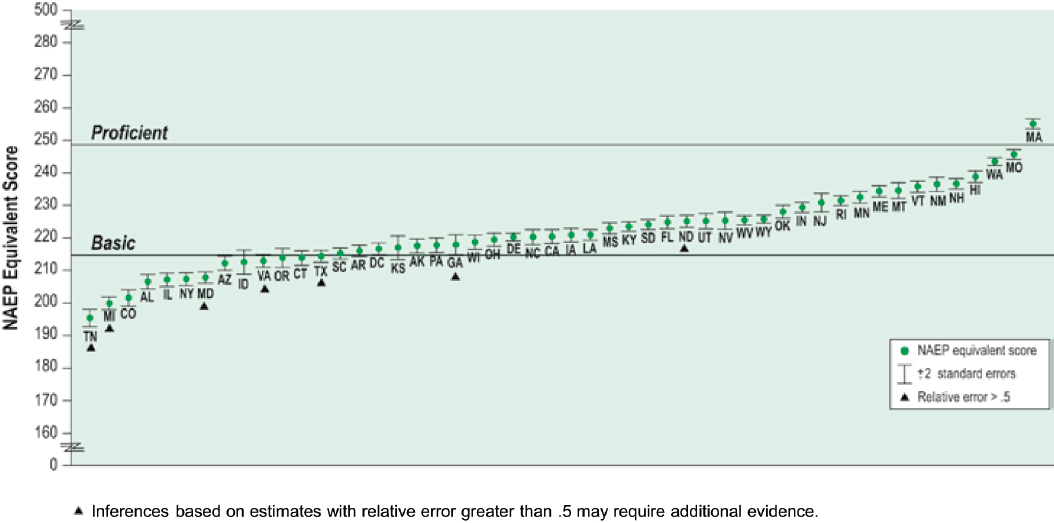
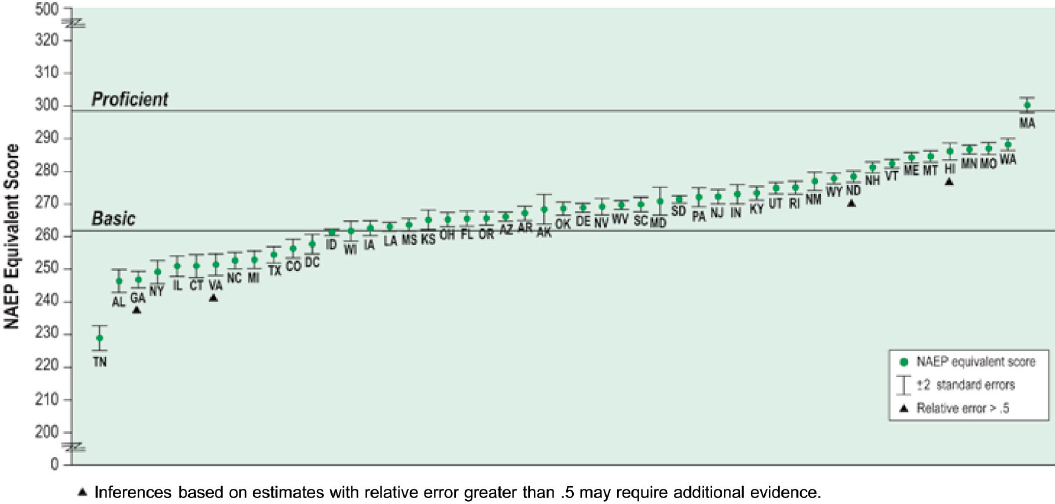
Comparison with State Proficiency Standards
A major development subsequent to the setting and early evaluations of the 1992 NAEP standards was the passage in 2001 of the No Child Left Behind Act (NCLB), which required each state to set and report proficiency standards in reading and mathematics for grades 3 through 8 and once for high school. The process used by each state to set and adopt performance-level standards for its assessments was subject to peer review and approval by the U.S. Department of Education. A wide variety of standard setting processes were used, most eventually receiving approval under peer review.
Beginning with NAEP results from 2003, the National Center for Education Statistics (NCES) conducted a series of studies that mapped each state’s grade-4 and -8 reading and mathematics proficiency levels to the NAEP scale. The mapping was based on the kinds of linking procedures described above (for details, see Phillips, 2007; Bandeira de Mello et al., 2009). For each state, the analyses estimated a point on the NAEP scale that was roughly equivalent to the state’s standards; these estimates are not exact and the extent of error associated with each is reported. This mapping was designed as a mechanism to evaluate the extent to which state standards reflected the same rigor as NAEP standards, and it was used as a policy lever to encourage states to set challenging standards for their students. As such, it is useful for making comparisons, but it cannot be construed as independent evidence documenting the reasonableness of
the NAEP achievement levels: similarities are expected by design. Nonetheless, it is informative to examine the extent of comparability between states’ standards and NAEP.
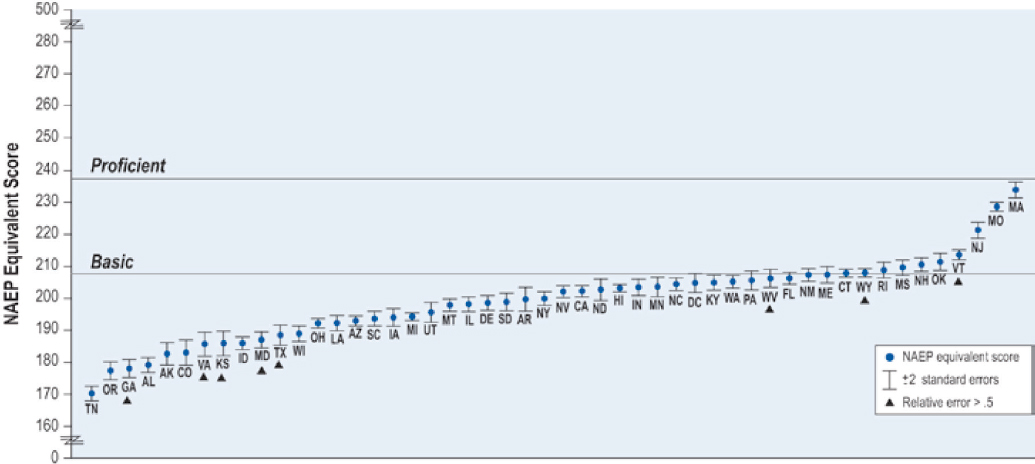
With that caveat in mind, the committee examined the most recent mapping results for grades 4 and 8 in reading and mathematics. This information is summarized in Table 5-7, which shows the numbers of states setting a proficiency level within the score range for each of the NAEP achievement levels from each of the three most recent state mapping studies (2009, 2011, 2013). For the most recent year (2013), in mathematics, five states’ grade-4 standards were in NAEP’s Proficient ranges (i.e., their minimum scores were at or above the NAEP minimum for Proficient), as were three states’ grade-8 standards. In reading, two states’ proficiency standards were in NAEP’s Proficient range. In many cases, the NAEP scale equivalent for state standards, especially in grade-4 reading, mapped below the NAEP achievement level for Basic.
Figures 5-7 through 5-10 show plots of the results by state, that is, each state’s cut score for proficient (as projected on the NAEP scale), along with the error/variance associated with these estimates.
There may well be valid reasons for state standards to be somewhat below NAEP’s. The NAEP achievement levels, as established in 1992, were intended to be somewhat “aspirational,” that is, oriented toward what students might eventually achieve. The state achievement levels are used for current school accountability and so may be more descriptive than aspirational. Thus, differences in what educators think students should know and be able to do may reflect differences in the uses of these results. In addition, states’ conceptions of proficiency is related to grade level on the state’s curriculum and content standards; in contrast, NAEP’s assessment frameworks are not designed to be representative of any specific curriculum. NAEP’s achievement-level standards may thus reflect a broader and more challenging range of content than states’ assessments.
In the comparison of NAEP and states’ standards, grade-4 reading stands out as somewhat of an outlier. For all of the other grades and subjects, the majority of states set proficiency cut points somewhere between the NAEP Basic and Proficient cut points. For grade-4 reading, the majority of states set Proficient cut points below the NAEP Basic cut point. Thus, the state mapping results suggest that the NAEP Proficient standard for grade-4 reading may be higher than what educators currently believe is required for proficiency in this grade and subject.
Comparisons with Advanced Placement Tests
The AP program provides curricular materials to enable high schools to offer college-level course work to high school students. Examinations
TABLE 5-5 Percentage of Students at or Azbove Basic, Proficient, and Advanced in Grade-8 2003 TIMSS Mathematics: Estimated by Linking the Grade-8 2000 NAEP Mathematics Achievement Levels to the Grade-8 1999 TIMSS Mathematics Scale
| Nation | Percentage at or Above Basic | Margin of Error for Basic | Percentage at or Above Proficient | Margin of Error for Proficient | Percentage at or Above Advanced | Margin of Error for Advanced |
|---|---|---|---|---|---|---|
| Singapore | 96+ | 1.5 | 73+ | 4.6 | 35+ | 6.4 |
| Hong Kong, SAR | 95+ | 1.7 | 66+ | 5.5 | 24+ | 6.0 |
| Korea, Republic of | 92+ | 1.8 | 65+ | 4.6 | 29+ | 5.4 |
| Chinese Taipei | 88+ | 2.4 | 61+ | 4.5 | 30+ | 5.0 |
| Japan | 90+ | 2.3 | 57+ | 5.1 | 20+ | 4.7 |
| Belgium (Flemish) | 82+ | 3.7 | 40 | 5.6 | 9 | 3.0 |
| Netherlands | 83+ | 4.0 | 38 | 6.2 | 7 | 3.0 |
| Hungary | 77 | 3.9 | 37 | 5.1 | 9 | 2.9 |
| Estonia | 82+ | 4.0 | 36 | 5.8 | 6 | 2.6 |
| Slovak Republic | 68 | 4.5 | 28 | 4.5 | 6 | 2.1 |
| Australia | 67 | 4.9 | 27 | 4.7 | 5 | 2.2 |
| Russian Federation | 69 | 4.8 | 27 | 4.8 | 5 | 2.0 |
| Malaysia | 70 | 5.1 | 26 | 5.0 | 4 | 1.9 |
| United States | 67 | 4.7 | 26 | 4.4 | 5 | 1.9 |
| Latvia | 70 | 4.9 | 25 | 4.8 | 4 | 1.8 |
| Lithuania | 66 | 4.7 | 24 | 4.3 | 4 | 1.7 |
| Israel | 63 | 4.6 | 24 | 4.0 | 5 | 1.8 |
| England | 65 | 5.4 | 22 | 4.7 | 4 | 1.8 |
| Scotland | 65 | 5.2 | 22 | 4.4 | 3 | 1.5 |
| New Zealand | 63 | 5.6 | 21 | 4.7 | 3 | 1.8 |
| Sweden | 66 | 5.2 | 21 | 4.3 | 3 | 1.3 |
| Serbia | 54- | 4.5 | 19 | 3.2 | 4 | 1.3 |
| Slovenia | 63 | 5.2 | 19 | 4.0 | 2 | 1.1 |
| Romania | 53- | 5.0 | 18 | 3.6 | 4 | 1.5 |
| Armenia | 54 | 4.8 | 18 | 3.4 | 3 | 1.2 |
| Italy | 58 | 5.2 | 17 | 3.7 | 2 | 1.2 |
| Bulgaria | 53 | 5.2 | 17 | 3.6 | 3 | 1.3 |
| Moldova, Republic of | 46- | 5.2 | 12- | 2.9 | 1 | 0.9 |
| Cyprus | 45- | 4.7 | 11- | 2.5 | 1 | 0.6 |
| Norway | 46- | 5.6 | 9- | 2.5 | 1- | 0.5 |
| Macedonia, Republic of | 35- | 4.4 | 8- | 2.1 | 1 | 0.6 |
| Jordan | 31- | 4.3 | 7- | 1.9 | 1- | 0.5 |
| Egypt | 25- | 3.6 | 5- | 1.4 | 1- | 0.4 |
| Indonesia | 26- | 4.2 | 5- | 1.7 | 1- | 0.5 |
| Palestinian Nat’l. Auth. | 20- | 3.1 | 4- | 1.1 | 0- | 0.3 |
| Lebanon | 30- | 5.3 | 3- | 1.4 | 0- | 0.2 |
| Iran, Islamic Republic of | 22- | 4.0 | 2- | 0.9 | 0- | 0.1 |
| Chile | 16- | 3.2 | 2- | 0.8 | 0- | 0.2 |
| Bahrain | 19- | 3.4 | 2- | 0.7 | 0- | 0.1 |
| Philippines | 15- | 3.3 | 2- | 1.0 | 0- | 0.2 |
| Tunisia | 16- | 4.1 | 1- | 0.5 | 0- | 0.0 |
| Morocco | 11- | 2.9 | 1- | 0.4 | 0- | 0.0 |
| Botswana | 8- | 2.1 | 0- | 0.3 | 0- | 0.0 |
| Saudi Arabia | 3- | 1.0 | 0- | 0.3 | 0- | 0.1 |
| Ghana | 4- | 1.6 | 0- | 0.3 | 0- | 0.0 |
| South Africa | 2- | 0.8 | 0- | 0.2 | 0- | 0.0 |
NOTES: The nations have been rank ordered based on percentage estimated to be proficient. The margin of error in the percentages for country j includes sampling error, σSEj, and linking error, σLEj. The overall error is ![]() . A plus (+) or minus (–) indicates the 95 percent confidence level that the nation’s percentage at and above the projected achievement level is greater or less than that in the United States. TIMSS =Trends in International Mathematics and Science Study.
. A plus (+) or minus (–) indicates the 95 percent confidence level that the nation’s percentage at and above the projected achievement level is greater or less than that in the United States. TIMSS =Trends in International Mathematics and Science Study.
SOURCE: Philips (2007, Table 10, pp. 14-15). Copyright © 2007 American Institutes for Research, Washington, D.C. Reprinted with permission.
TABLE 5-6 International Comparisons of Students at Proficient or Above and Advanced on NAEP 2003, Based on Link to PISA for 2003: Grade-8 Mathematics
| Country | Proficient or Above | Advanced |
|---|---|---|
| Belgium | 49.7 | 16.8 |
| The Netherlands | 50.6 | 15.2 |
| Korea, Republic of | 52.6 | 15.1 |
| Japan | 50.6 | 15.0 |
| Finland | 52.9 | 13.5 |
| Switzerland | 46.7 | 13.0 |
| New Zealand | 45.1 | 12.5 |
| Australia | 45.9 | 11.5 |
| Canada | 48.3 | 11.4 |
| Czech Republic | 41.7 | 10.6 |
| Germany | 39.5 | 9.0 |
| Denmark | 40.7 | 8.7 |
| Sweden | 38.3 | 8.6 |
| Israel | 41.5 | 8.3 |
| Great Britain | 38.1 | 8.1 |
| Austria | 37.5 | 7.9 |
| France | 40.0 | 7.8 |
| Slovak Republic | 33.9 | 6.4 |
| Norway | 32.6 | 5.8 |
| Hungary | 31.3 | 5.7 |
| Ireland | 34.3 | 5.5 |
| Luxembourg | 32.2 | 5.5 |
| Poland | 30.2 | 5.3 |
| United States | 29.0 | 5.0 |
| Spain | 28.2 | 5.0 |
NOTES: Countries are ranked in order by the percentage of students at the Advanced level. NAEP = National Assessment of Educational Progress, PISA = Programme for International Student Assessment.
SOURCE: Data from Hambleton et al. (2009).
are then offered to evaluate students’ level of achievement on this material. These AP tests are often cited by advocates for education standards as positive examples of challenging syllabus-driven examinations (see, e.g., Shepard et al., 1993, p. 92). The AP courses and tests most closely related to NAEP reading are English language and composition and English literature and composition. For NAEP mathematics, calculus is the most closely related to two AP courses: AB, which is designed to be equivalent to a one-semester college calculus course, and BC, which includes all
TABLE 5-7 States’ Standards for “Proficient” Mapped to Each NAEP Achievement Level: Mathematics and Reading, Grades 4 and 8
| Subject, Grade, and Achievement Level | 2009 | 2011 | 2013 |
|---|---|---|---|
| Mathematics | |||
| 4th Grade | |||
| Proficient | 1 | 1 | 5 |
| Basic | 43 | 45 | 42 |
| Below Basic | 6 | 5 | 4 |
| Total | 50 | 51 | 51 |
| 8th Grade | |||
| Proficient | 1 | 2 | 3 |
| Basic | 38 | 37 | 38 |
| Below Basic | 9 | 10 | 8 |
| Total | 48 | 49 | 49 |
| Reading | |||
| 4th Grade | |||
| Proficient | 0 | 0 | 2 |
| Basic | 15 | 20 | 23 |
| Below Basic | 35 | 31 | 26 |
| Total | 50 | 51 | 51 |
| 8th Grade | |||
| Proficient | 0 | 0 | 1 |
| Basic | 35 | 36 | 40 |
| Below Basic | 15 | 15 | 10 |
| Total | 50 | 51 | 51 |
NOTES: Each cell is a count of the number of states. NAEP = National Assessment of Educational Progress.
SOURCE: Data from Bandeira de Mello et al. (2015).
of AB plus additional topics and is equivalent to a full year of college calculus.13
The AP tests are scored on a scale from 1 to 5, with a score of 3 or higher recommended for college credit at many colleges. We compared the percentages of students who scored of 3 or higher and 4 or higher on each AP test with the percentages of students who scored at the Proficient and Advanced levels on NAEP: see Tables 5-8 and 5-9. It is important to note that the percentages of students shown in the tables do not represent the percentages of AP test takers that scored at each level: rather, they
__________________
13 For details, see http://apcentral.collegeboard.com/apc/public/courses/220300.html [March 2016].
SOURCE: Bandeira de Mello (2011).
SOURCE: Bandeira de Mello (2011).
SOURCE: Bandeira de Mello (2011).
SOURCE: Bandeira de Mello (2011).
represent the percentages of high school graduates in the respective year who scored at each AP level.14
Reporting the number as a percentage of the national population of high school graduates enables comparisons with the percentage of sampled students who took NAEP reading and mathematics tests and scored at the Proficient and Advanced level. It also replicates the analysis that Shepard and colleagues (1993) reported for the 1992 results, thus allowing comparisons with the baseline in 1992.15
For mathematics, Table 5-8 compares data for 3 years: 2005, 2009, and 2013.16 Overall, the percentage of students scoring in the advanced level on NAEP is lower than the percentage of students scoring 3 or higher or 4 or higher for each year shown. The differences are in the range of 2 to 3 percentage points.
For reading, Table 5-9 shows data for the 4 years that NAEP has administered the test between 1992 and 2013. Overall, the percentage of students scoring at the advanced level on NAEP is considerably lower than the percentage of students scoring 3 or higher on the AP exams. The differences are on the order of 4 to 9 percentage points. Comparisons with the percentage scoring 4 or higher are closer to the NAEP results, differing by 1 or 2 percentage points. For the most part, these are relatively small differences that might be explained by the differences in the characteristics of the populations. Students in the AP population have chosen to take the exam; often, they have also just completed the relevant coursework, and they have an incentive to do well and obtain college credit. None of these factors applies for the NAEP samples, and in particular, there have long been concerns about the extent to which 12th-grade students are motivated to perform well on NAEP.
Comparisons with College Admissions Tests
NAEd examined the relationships between results for grade 12 for NAEP and the SAT. The NAEd studies looked specifically at certain points on each test’s score scale that the researchers judged were commensurate
__________________
14 The sources for the AP score distributions for 2005, 2009, 2013, and 2015, respectively, are shown here: http://media.collegeboard.com/digitalServices/pdf/research/national_summary_2005.xls [August 2016]; http://media.collegeboard.com/digitalServices/pdf/research/2009/NATIONAL_Summary_09.xls [August 2016]; http://media.collegeboard.com/digitalServices/pdf/research/2013/STUDENT-SCORE-DISTRIBUTIONS-2013.pdf [August 2016]; and https://secure-media.collegeboard.org/digitalServices/pdf/research/2015/Student-Score-Distributions-2015.pdf [August 2016].
15 See http://nces.ed.gov/programs/digest/d13/tables/dt13_219.10.asp [January 2016].
16 These dates were selected because the grade-12 mathematics framework and achievement levels were changed in 2005, so the trend line begins then.
TABLE 5-8 Comparison of Advanced Placement Test Results in Calculus with NAEP Achievement-Level Results for Grade-12 Mathematics: Percentage of High School Graduates Achieving Each Score, Compared to the Percentage of Students at Proficient and Advanced for NAEP
| AP Test Score | 2005 | 2009 | 2013 | 2015 |
|---|---|---|---|---|
| 1 | 1.7 | 2.0 | 2.9 | 3.5 |
| 2 | 1.1 | 1.2 | 1.1 | 1.1 |
| 3 | 1.4 | 1.7 | 1.1 | 2.3 |
| 4 | 1.5 | 1.7 | 2.0 | 2.1 |
| 5 | 2.0 | 2.5 | 3.4 | 3.6 |
| Cumulative Percentage Scoring 3 or Higher | 4.9 | 5.9 | 6.5 | 8.0 |
| Cumulative Percentage Scoring 4 or Higher | 3.5 | 4.2 | 5.4 | 5.7 |
| NAEP Results | ||||
| Percentage Proficient and Above | 23.0 | 26.0 | 26.0 | 25.0 |
| Percentage Advanced | 2.0 | 3.0 | 3.0 | 3.0 |
NOTES: Calculus includes both AP levels; see text for discussion. The AP results are shown for the years in which the NAEP grade-12 mathematics assessment was given. The percentages shown do not represent the percentage of AP test takers that scored at each level. Instead, they represent the percentages of high school graduates in the respective year who scored at each AP level. AP = Advanced Placement, NAEP = National Assessment of Educational Progress.
SOURCE: Data from the College Board (2009, 2013, 2015).
with Proficient- and Advanced-level work. Since then, the College Board (which administers the SAT) and ACT, Inc. have determined benchmarks on their respective exams that can be interpreted as readiness for college. Both organizations define college readiness as a function of the likelihood of obtaining a specific grade-point average (e.g., 4.00, 3.00) in first-year credit-bearing courses.17
In a special set of NAGB-sponsored studies, NAEP reading and mathematics scores were linked to SAT verbal and mathematics scores so that a NAEP college readiness benchmark could be set for each assessment. The intent of this study was to statistically relate NAEP and the SAT and use that relationship to identify a reference point or range on the NAEP
__________________
17 For details see ACT, Inc. (2013), Allen and Sconing (2005), and Wyatt et al. (2011).
TABLE 5-9 Comparison of Advanced Placement Test Results in English with NAEP Achievement-Level Results for Grade-12 Reading: Percentage of High School Graduates Achieving Each Score, Compared to the Percentage of Students at Proficient and Advanced for NAEP
| AP Test Score | 1992 | 2005 | 2009 | 2013 |
|---|---|---|---|---|
| 1 | 0.2 | 1.5 | 2.2 | 3.3 |
| 2 | 1.7 | 5.0 | 6.0 | 7.8 |
| 3 | 2.1 | 5.3 | 6.1 | 7.6 |
| 4 | 1.1 | 2.9 | 4.0 | 4.4 |
| 5 | 0.6 | 1.2 | 1.8 | 2.3 |
| Cumulative Percentage Scoring 3 or Higher | 3.8 | 9.4 | 11.9 | 14.6 |
| Cumulative Percentage Scoring 4 or Higher | 1.7 | 4.1 | 5.8 | 6.7 |
| NAEP Results | ||||
| Percentage Proficient and Advanced | 40.0 | 36.0 | 38.0 | 37.0 |
| Percentage Advanced | 4.0 | 5.0 | 5.0 | 5.0 |
NOTES: The AP results combine English literature and language. The AP results are shown for the years in which the NAEP grade-12 reading assessment was given. The percentages shown do not represent the percentage of AP test takers that scored at each level. Instead, they represent the percentages of high school graduates in the respective year who scored at each AP level. AP = Advanced Placement, NAEP = National Assessment of Educational Progress.
SOURCE: Moran et al. (n.d.).
12th-grade reading and mathematics scales associated with the College Board’s preparedness benchmarks on the SAT reading and mathematics measures, specifically a score of 500 (see Moran et al., n.d.).
To accomplish this linking, NAGB entered into an agreement with the College Board to obtain SAT scores for public school students who were in 12th grade in 2009 and had taken the SAT by June 2009. The SAT data were matched, using identifiers provided by the College Board, to performance records of students who participated in the 2009 NAEP grade-12 assessments in reading and mathematics. Limiting the study to public school students resulted in NAEP samples of 49,000 in reading and 46,000 in mathematics.
For each student in the matched (linking) sample, scores were available from one or more administrations of the SAT, which included separate scores for critical reading and mathematics. The scale scores for each section range from 200 to 800 in 10-point increments. The critical reading and mathematics scores from each student’s highest composite SAT score were used in this study because these are the SAT scores most likely to be considered in college admissions.
The first set of analyses focused on evaluating two methods to statistically link SAT and NAEP scores. Given that the two assessments measure somewhat different skills and knowledge, the more robust linking procedure, equating, was inappropriate. The researchers used two alternative methods—projection and concordance. They compared the accuracy of the two methods and the extent to which the assumptions for each were met. Reading met the assumptions for projection but not for concordance because the correlation between NAEP reading and SAT critical reading was too low (r = .74). Mathematics met the assumptions for both because the correlation between NAEP and SAT mathematics was higher (r = .91).
The second set of analyses focused on applying the linking procedures to estimate the “equivalent” scale score on NAEP reading and mathematics. The researchers reported results for both linking methods, but with cautions for the linking for reading. Table 5-10 shows the results for both linking procedures.
Results from the projection analyses are shown at the top portion of the table. Column 2 shows the NAEP scale score in mathematics mapped to the SAT benchmark score of 500, and column 4 shows similar information for reading. Three values are reported from the projection analysis: the NAEP score at which 50 percent of SAT test takers score 500 or above; the NAEP score at which 67 percent of SAT test takers score 500 or above; and the NAEP score at which 80 percent of SAT test takers score 500 or above. The different percentages (50, 67, and 80, respectively) reflect different judgments about the accuracy of predictions.18 For mathematics, an NAEP score of 169 represents the point at which 67 percent of SAT takers scored at or above 500. For reading, this same score was 313.
Table 5-10 also shows the range of scores when the analyses were done by racial and ethnic group (columns 3 and 5). For the benchmark score of 169 in mathematics, the range was 164-175, or 11 points. For reading, the range for a benchmark score of 313 was wider at 26 points (302-328).
__________________
18 The higher the percentage, the more likely the prediction will be accurate and the student will do well. Choosing a percentage requires judgments about how much accuracy is needed and the associated consequences of making erroneous decisions.
TABLE 5-10 Grade-12 NAEP Mathematics and Reading Scale Scores Associated with SAT College Readiness Criteria: Results from Two Linking Procedures, Projection Analysis and Concordance Analysis
| Mathematics | Reading | |||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| Percentage of Students Scoring at or Above 500 on SAT | Scale Score for Total Group | Range of Scale Scores for Subgroups | Scale Score for Total Group | Range of Scale Scores for Subgroups |
| Results from Projection Procedure: | ||||
| 50 | 164 | 159-170 | 302 | 290-318 |
| 67 | 169 | 164-175 | 313 | 302-328 |
| 80 | 175 | 169-181 | 325 | 314-338 |
| Results from Concordance Procedure: | ||||
| SAT score of 500 | 165 | 162-168 | 303 | 296-313 |
NOTES: See text for discussion. The NAEP cut scores for Proficient are 176 for mathematics and 302 for reading. NAEP = National Assessment of Educational Progress, SAT = Scholastic Aptitude Test.
SOURCE: Adapted from Moran et al. (n.d., Tables 1 and 2).
The bottom portion of the table shows the results from the concordance analyses, and for comparison, the NAEP cut score for Proficient is shown in the third row. These analyses involved statistical procedures that are too complex for the purposes of this report. Interested readers are referred to Moran et al. (2012) for details.19
Setting Benchmarks Based on External Criteria
Using the results from the studies described above, NAGB has now determined scale scores associated with academic preparedness on the mathematics and reading assessments, for which it adopted a definition of college readiness (Fields, 2013, p. v).
Academic preparedness for college refers to the reading and mathematics knowledge and skills needed to qualify for placement into entry-level, credit-bearing, non-remedial courses that meet general education degree requirements in broad access 4-year institutions and, for 2-year institutions, for entry level placement, without remediation, into degree-bearing programs designed to transfer to 4-year institutions.
__________________
19 See http://www.nagb.org/content/nagb/assets/documents/what-we-do/preparednessresearch/statistical-relationships/SAT-NAEP_Linking_Study.pdf [April 2016].
The academic preparedness scores are 163 for mathematics (on a 0-300 scale) and 302 for reading (on a 0-500 scale). These scores can be compared to the NAEP cut scores for Proficient. For mathematics, the score of 163 is 13 points lower than the Proficient cut score of 176. For reading, the score of 302 is the same as the cut score for Proficient.
Establishing “benchmarks,” such as these indicators of academic preparedness, can help to define the achievement levels more concretely. For example, the academic preparedness score for reading is at the cut score for Proficient, offering the possibility of interpreting Proficient as college ready, although research would be needed to evaluate the validity of that interpretation. The academic preparedness score for mathematics falls at the upper end of the Basic achievement level (7 points below proficient). This is a puzzling finding that we think needs further research.20 Nonetheless, we endorse this line of research that connects NAEP performance to important external criteria.
CONCLUSIONS
Content-Related Validity Evidence
ACT conducted studies to collect evidence of content validity for the achievement levels and exemplar items. The content experts that participated in these studies suggested changes to the ALDs and exemplars. The descriptors were further revised by NAGB, and the official versions are quite different from the ones used for setting the cut scores. There were differences of opinion on the extent to which the final descriptors were aligned with the framework, the item pool, and contemporary thinking about mathematics and reading subject matter. The grade-12 ALDs for mathematics were changed in 2005, but related changes were not made for grades 4 and 8, suggesting a break in the continuum of skills across the grades. For the 2009 assessment, the ALDs were again changed for grade-12 mathematics and for all grades in reading. Results from the anchor studies indicate that many of the grade-12 mathematics items did
__________________
20 NAGB’s decision to report academic preparedness, and the evidence complied to support this decision, reinforce educators’ prior judgment about what grade-12 students need to know and be able to do with respect to reading. The level set by educators in 1992 matches well the College Board’s college readiness benchmark using SAT scores. For mathematics, differences between the NAEP Proficient level and the College Board college-readiness level may indicate that educators aimed a bit high when they reset standards for the 2005 grade-12 mathematics assessment, but it may also reflect ambiguity as to what constitutes college readiness in mathematics. While reading is basic for virtually all college majors, the level of mathematics required for success in science, technology, engineering, and mathematics majors may, in fact, be considerably higher than the level required for success in other majors.
not anchor to any achievement level because they were too difficult (17%). For 4th-grade reading, results indicate that more than a quarter (27.4%) of the items did not anchor to an achievement level.
On these issues, we draw two conclusions.
CONCLUSION 5-1 The studies conducted to assess content validity are in line with those called for in the Standards for Educational and Psychological Testing in place in 1992 and currently in 2016. The results of these studies suggested that changes in the achievement-level descriptors (ALDs) were needed, and they were subsequently made. These changes may have better aligned the descriptors to the framework and exemplar items, but as a consequence, the final ALDs were not the ones used to set the cut scores. Since 1992, there have been additional changes to the frameworks, item pools, assessments, and studies to identify needed revisions to the ALDs. But, to date, there has been no effort to set new cut scores using the most current ALDs.21
CONCLUSION 5-2 Changes in the National Assessment of Educational Progress mathematics frameworks in 2005 led to new achievement-level descriptors and a new scale and cutscores for the achievement levels at the 12th grade, but not for the 4th and 8th grades. These changes create a perceived or actual break between 12th-grade mathematics and 4th- and 8th-grade mathematics. Such a break is at odds with contemporary thinking in mathematics education, which holds that school mathematics should be coherent across grades.
Criterion-Related Validity Evidence
CONCLUSION 5-3 The Standards for Educational and Psychological Testing in place in 1992 did not explicitly call for criterion-related validity evidence for achievement-level setting, but such evidence was routinely examined by testing programs. The National Assessment Governing Board did not report information on criterion-related evidence to evaluate the reasonableness of the cut scores set in 1992. The National Academy of Education evaluators reported four kinds of criterion-related validity evidence, and they concluded that the cut scores
__________________
21 This text was revised after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
were set very high. We were not able to determine whether this evidence was considered when the final cut scores were adopted for the National Assessment of Educational Progress.
We endorse the line of research that connects NAEP performance to important external criteria. Connecting NAEP performance to external criteria, possibly by predicting performance on external criterion measures, could enhance understanding of the NAEP achievement levels. As described above, the achievement levels are currently set judgmentally through a process in which participants decide—without any reference to external criteria—what students should know and be able to do at given points in their school careers, namely grades 4, 8, and 12. The resulting achievement levels are evaluated by a set of studies to ensure they are internally valid (consistent with ALDs) and demonstrate appropriate relationships with other measures of the same construct. However, this kind of evaluation is not the same as focusing on prediction, particularly prediction of important benchmarks and milestones.
Beaton and colleagues (2012) discuss the use of a predictive approach to determine achievement levels, an approach that places a high priority on the external validity of the cut scores in relation to predetermined criteria. The college readiness benchmark is designed as a point on the NAEP scale at which students are predicted to perform at a given level in their first year of college. Other benchmarks would also be useful, such as the score or score range on NAEP at which students are predicted to meet the international benchmarks set by TIMSS and PISA (which in turn reflect global competitiveness).
Beaton and colleagues suggest other external criteria to consider. For grade-4 mathematics, for example, they suggest that performance in grade-5 mathematics would seem the most logical criterion. Similarly, for grade-8 reading, performance in grade-9 English-language arts would seem to be the most logical criterion. A similar approach has been used in New York to define achievement levels related to probability of success at the next level.22
The groundwork for these kinds of studies has not yet been done but is well worth pursuing. To our knowledge, there have been no studies that examine the extent to which performance on the grade-4 NAEP mathematics assessment predicts performance in grade-5 mathematics, or the
__________________
22 July 1, 2010, memorandum to then-Commissioner David Steiner from Howard Ever-son regarding Relationship of Regents ELA and Math Scores to College Readiness Indicators. Available: http://usny.nysed.gov/scoring_changes/MemotoDavidSteinerJuly1.pdf [March 2017]. July 2, 2010, memorandum to then-Commissioner David Steiner from David Liebowitz and Dan Koretz regarding 8th-Grade Math and ELA Cut Scores. Available: http://usny.nysed.gov/scoring_changes/Grade_8_Cut_Scores_July2.pdf [March 2017].
extent to which grade-8 performance predicts high school performance, such as being on track to be ready for college. These studies would require assessments in grades that are not currently tested by NAEP. But if measures were developed, the criterion-related information the studies would generate would be enormously useful for understanding NAEP results.
CONCLUSION 5-4 Since the National Assessment of Educational Progress (NAEP) achievement levels were set, new research has investigated the relationships between NAEP scores and external measures, such as academic preparedness for college. The findings from this research can be used to evaluate the validity of new interpretations of the existing performance standards, suggest possible adjustments to the cut scores or descriptors, and or enhance understanding and use of the achievement-level results. This research can also help establish specific benchmarks that are separate from the existing achievement levels. This type of research is critical for adding meaning to the achievement levels.
ANNEX: ACHIEVEMENT-LEVEL DESCRIPTORS23
The six tables in this Annex show the various versions of the achievement-level descriptors for mathematics and reading for grades 4, 8, and 12 for Basic, Proficient, and Advanced levels.
__________________
23 This text was revised after the report was initially transmitted to the U.S. Department of Education; see Chapter 1 (“Data Sources”).
TABLE 5-1a Achievement-Level Descriptors for 4th-Grade Mathematicsa
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Basic level signifies some evidence of conceptual and procedural understanding in the five NAEP content areas of Numbers & Operations; Measurement; Geometry; Data Analysis. Statistics, and Probability; and Algebra and Functions. Understanding simple facts and single-step operations are included at this level, as is the ability to perform simple computations with whole numbers. This level shows a partial mastery of estimation, basic fractions, and decimals relating to money or the number line; it shows an ability to solve simple real-world problems involving measurement, probability, statistics, and geometry. At this level, there is a partial mastery of tools such as four-function calculators and manipulatives (geometric shapes and rulers). Written responses are often minimal, perhaps with a partial response and lack of supportive information. |
Basic-level students exhibit some evidence of conceptual and procedure understanding in the five NAEP content areas. At the fourth-grade level, algebra and functions are treated in informal and exploratory ways often through the study of patterns. Basic-level students estimate and use basic facts to perform simple computations with whole numbers. These students show some understanding of fractions and decimals. They solve simple real-world problems in all areas. These students use, although not always accurately, four-function calculators, rulers, and geometric shapes. Written responses are often minimal and lack supporting information. |
| Official—1992 | |
| Fourth-grade students performing at the Basic level should show some evidence of understanding the mathematical concepts and procedures in the five NAEP content areas. Fourth graders performing at the Basic level should be able to estimate and use basic facts to perform simple computations with whole numbers; show some understanding of fractions and decimals; and solve some simple real-world problems in all NAEP content areas. Students at this level should be able to use—though not always accurately—four-function calculators, rulers, and geometric shapes. Their written responses are often minimal and presented without supporting information. | |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Proficient level signifies consistent demonstration of the integration of procedural knowledge and conceptual understanding as applied to problem solving in the five NAEP content areas of Numbers and Operations; Measurement; Geometry; Data Analysis, Statistics, and Probability; and Algebra and Functions. The Proficient level indicates an ability to perform computation and estimation with whole numbers, to identify fractions, and to work with decimals involving money or the number line. Solving real-world problems involving measurement, probability, statistics, and geometry is an important part of this level. This level signifies the ability to use, as tools, four-function calculators, rulers, and manipulatives (geometric shapes). It includes the ability to identify and use pertinent/appropriate information in problem settings. The ability to make connections between and among skills and concepts emerges at this level. Clear and organized written presentations, with supportive information, are typical. And, there is an ability to explain how the solution was achieved. |
Proficient-level students consistently integrate procedural knowledge and conceptual understanding as applied to problem solving in the five NAEP content areas. Using whole numbers, they estimate, compute, and determine whether their results are reasonable. They have a conceptual understanding of fractions and decimals. Solving real-world problems in all areas is important at this level. Proficient students appropriately use four-function calculators, rulers and geometric shapes. These students use problem-solving strategies such as identifying and using appropriate information. [Problem-solving strategies include identification and use of appropriate information.] They present organized written solutions with supporting information and explain how they were achieved. |
| Official—1992 | |
| Fourth-grade students performing at the Proficient level should consistently apply integrated procedural knowledge and conceptual understanding to problem solving in the five NAEP content areas. Fourth graders performing at the Proficient level should be able to use whole numbers to estimate, compute, and determine whether results are reasonable. They should have a conceptual understanding of fractions and decimals; be able to solve real-world problems in all NAEP content areas; and use four-function calculators, rulers, and geometric shapes appropriately. Students performing at the Proficient level should employ problem-solving strategies such as identifying and using appropriate information. Their written solutions should be organized and presented both with supporting information and explanations of how they were achieved. | |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Advanced level signifies the integration of procedural knowledge and conceptual understanding as applied to problem solving in the five NAEP content areas of Numbers and Operations; Measurement; Geometry; Data Analysis, Statistics, and Probability; and Algebra and Functions. This is evidenced by divergent and elaborate written responses. The Advanced level indicates and ability to solve multistep and nonroutine real-world problems involving measurement, probability, statistics, and geometry, and an ability to perform complex tasks involving multiple steps and variables. Tools are mastered, including four-function calculators, rulers, and manipulatives (geometric shapes). This level signifies the ability to apply facts and procedures by explaining why as well as how. Interpretations extend beyond obvious connections and thoughts are communicated clearly and concisely. At this level, logical conclusions can be drawn and complete justifications can be provided for answers and/or solution processes. |
Advanced-level students integrate procedural knowledge and conceptual understanding as applied to problem solving in the five NAEP content areas. They solve complex and nonroutine real-world problems in all areas. They have mastered the use of tools such as four-function calculators, rulers, and geometric shapes. Advanced-level students draw logical conclusions and justify answers and solution processes by explaining the “why” as well as the “how.” Interpretations extend beyond obvious connections and thoughts are communicated clearly and concisely. |
| Official—1992 | |
| Fourth-grade students performing at the Advanced level should apply integrated procedural knowledge and conceptual understanding to problem solving in the five NAEP content areas. Fourth graders performing at the Advanced level should be able to solve complex and nonroutine real-world problems in all NAEP content areas. They should display mastery in the use of four-function calculators, rulers, and geometric shapes. These students are expected to draw logical conclusions and justify answers and solution processes by explaining why, as well as how, they were achieved. They should go beyond the obvious in their interpretations and be able to communicate their thoughts clearly and concisely. | |
aSee Allen et al. (1999, App. F).
TABLE 5-2a Achievement-Level Descriptors for 8th-Grade Mathematicsa
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| Students performing at the Basic level should begin to describe objects, to process accurately and elaborate relationships, to compare and contrast, to find patterns, to reason from graphs, and to understand spatial reasoning. This level of partial mastery signifies an understanding of arithmetic operations on whole numbers, decimals, fractions, and percents, including estimation. Problems that are already set up are generally solved correctly, as are one-step problems. However, problems involving the use of available data, and determinations of what is necessary and sufficient to solve the problem, are generally quite difficult. Students should select appropriate problem-solving tools, including calculators, computers, and manipulatives (geometric shapes) to solve problems from the five content areas. Students should also be able to use elementary algebraic concepts and elementary geometric concepts to solve problems. This level indicates familiarity with the general characteristics of measurement. Students at this level may demonstrate limited ability to communicate mathematical ideas. |
Basic-level students exhibit evidence of conceptual and procedural understanding. These students compare and contrast, find patterns, reason from graphs, and understand spatial reasoning. This level of performance signifies an understanding of arithmetic operations, including estimation, on whole numbers, decimals, fractions, and percents. Students complete problems correctly with the help of structural prompts such as diagrams, charts, and graphs. As students approach the Proficient level, they will solve problems involving the use of available data and determine what is necessary and sufficient for a correct solution. Students use problem-solving strategies and select appropriate tools, including calculators, computers, and manipulatives (geometric shapes) to solve problems from the five content areas. Students use fundamental algebraic and informal geometric concepts to solve problems. Students at this level demonstrate limited skills in communicating mathematically. |
| Official—1992 | |
| Eighth-grade students performing at the Basic level should exhibit evidence of conceptual and procedural understanding in the five NAEP content areas. This level of performance signifies an understanding of arithmetic operations—including estimation—on whole numbers, decimals, fractions, and percents. Eighth graders performing at the Basic level should complete problems correctly with the help of structural prompts such as diagrams, charts, and graphs. They should be able to solve problems in all NAEP content areas through the appropriate selection and use of strategies and technological tools—including calculators, computers, and geometric shapes. Students at this level also should be able to use fundamental algebraic and informal geometric concepts in problem solving. As they approach the Proficient level, students at the Basic level should be able to determine which of available data are necessary and sufficient for correct solutions and use them in problem solving. However, these 8th graders show limited skill in communicating mathematically. |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| Proficient-level students apply mathematical concepts consistently to more complex problems. They should make conjectures, defend their ideas, and give supporting examples. They have developed the ability to relate the connections between fractions, percents, and decimals, as well as other mathematical topics. The Proficient level denotes a thorough understanding of the arithmetic operations listed at the Basic level. This understanding is sufficient to permit applications to problem solving in practical situations. Quantity and spatial relationships are familiar situations for problem solving and reasoning, and this level signifies an ability to convey the underlying reasoning skills beyond the level of arithmetic. Ability to compare and contrast mathematical ideas and generating examples is within the Proficient domain. Proficient-level students can make inferences from data and graphs; they understand the process of gathering and organizing data, calculating and evaluating within the domain of statistics and probability, and communicating the results. The Proficient level includes the ability to apply the properties of elementary geometry. Students at this level should accurately use the appropriate tools of technology. |
Proficient-level students apply mathematical concepts and procedures consistently to complex problems. They make conjectures, defend their ideas, and give supporting examples. They have developed the ability to relate the connections between fractions, percents, and decimals, as well as other mathematical topics, such as algebra and functions. The Proficient level denotes a thorough understanding of the arithmetic operations listed at the Basic level. This understanding is sufficient to permit applications to problem solving in practical situations. Quantity and spatial relationships are familiar situations for problem solving and reasoning, and students at this level convey the underlying reasoning skills beyond the level of arithmetic. Proficient-level students compare and contrast mathematical ideas and generate their own examples. These students make inferences from data and graphs; they understand the process of gathering and organizing data, calculating, evaluating, and communicating the results within the domain of statistics and probability. Students at this level apply the properties of informal geometry, and accurately use the appropriate tools of technology. |
| Official—1992 | |
| Eighth-grade students performing at the Proficient level should apply mathematical concepts and procedures consistently to complex problems in the five NAEP content areas. Eighth graders performing at the Proficient level should be able to conjecture, defend their ideas, and give supporting examples. They should understand the connections between fractions, percents, decimals, and other mathematical topics such as algebra and functions. Students at this level are expected to have a thorough understanding of Basic-level arithmetic operations—an understanding sufficient for problem solving in practical situations. Quantity and spatial relationships in problem solving and reasoning should be familiar to them, and they should be able to convey underlying reasoning skills beyond the level of arithmetic. They should be able to compare and contrast mathematical ideas and generate their own examples. These students should make inferences from data and graphs; apply properties of informal geometry; and accurately use the tools of technology. Students at this level should understand the process of gathering and organizing data and be able to calculate, evaluate, and communicate results within the domain of statistics and probability. |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Advanced level is characterized by the ability to go beyond recognition, identification, and application of mathematical rules in order to generalize and synthesize concepts and principle. Generalization often takes shape through probing examples and counterexamples and can be focused toward creating models. Mathematical concepts and relationships are frequently communicated with mathematical language, using symbolic representations where appropriate. Students at the Advanced level consider the reasonableness of an answer, with both number sense and geometric awareness. Their abstract-thinking ability allows them to create unique problem-solving techniques and explain the reasoning processes they followed in reaching a conclusion. These students can probe through examples and counterexamples that allow generalization and description of assumptions with models and elegant mathematical language. |
Advanced-level students go beyond recognition, identification, and application of mathematical rules in order to generalize and synthesize concepts and principles. Generalization often takes shape through probing examples and counterexamples and can be used to create models. Mathematical concepts and relationships are frequently communicated with mathematical language, using symbolic representations where appropriate. Students at the Advanced level consider the reasonableness of an answer, with both number sense and geometric awareness. Their abstract thinking allows them to create unique problem-solving techniques and explain the reasoning processes they followed in reaching a conclusion. These students probe examples and counter examples that allow generalization and description of assumptions with models and elegant mathematical language. |
| Official—1992 | |
| Eighth-grade students performing at the Advanced level should be able to reach beyond the recognition, identification, and application of mathematical rules in order to generalize and synthesize concepts and principles in the five NAEP content areas. Eighth graders performing at the Advanced level should be able to probe examples and counterexamples in order to shape generalizations from which they can develop models. Eighth graders performing at the Advanced level should use number sense and geometric awareness to consider the reasonableness of an answer. They are expected to use abstract thinking to create unique problem-solving techniques and explain the reasoning processes underlying their conclusions. | |
aSee Allen et al. (1999, App. F).
TABLE 5-3a Achievement-Level Descriptors for 12th-Grade Mathematicsa
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Basic level represents understanding of fundamental algebraic operations with real numbers, including the ability to solve two-step computational problems. It also signifies an understanding of elementary geometrical concepts such as area, perimeter, and volume, and the ability to make measurements of length, weight, capacity, and time. Also included in the Basic level is the ability to comprehend data in both tabular and graphical form and to translate between verbal, algebraic, and graphical forms of linear expression. Students at this level should be able to use a calculator appropriately. |
Basic-level students demonstrate procedural and conceptual knowledge in solving problems in the five NAEP content areas. They use estimation to verify solutions and determine the reasonableness of the results to real world problems. Algebraic and geometric reasoning strategies are used to solve problems. These students recognize relationships in verbal, algebraic, tabular, and graphical forms. Basic-level students demonstrate knowledge of geometric relationships as well as corresponding measurement skills. Statistical reasoning is applied to the organization and display of data and to reading tables and graphs. These students generalize from patterns and examples in the areas of algebra, geometry, and statistics. They communicate mathematical relationships and reasoning processes with correct mathematical language and symbolic representations. Calculators are used appropriately to solve problems. |
| Official—1992 | |
| Twelfth-grade students performing at the Basic level should demonstrate procedural and conceptual knowledge in solving problems in the five NAEP content areas. Twelfth-grade students performing at the Basic level should be able to use estimation to verify solutions and determine the reasonableness of results as applied to real-world problems. They are expected to use algebraic and geometric reasoning strategies to solve problems. Twelfth-grade students performing at the Basic level should recognize relationships presented in verbal, algebraic, tabular, and graphical forms; and demonstrate knowledge of geometric relationships and corresponding measurement skills. They should be able to apply statistical reasoning in the organization and display of data and in reading tables and graphs. They also should be able to generalize from patterns and examples in the areas of algebra, geometry, and statistics. At this level, they should use correct mathematical language and symbols to communicate mathematical relationships and reasoning processes and use calculators appropriately to solve problems. |
|
| Official—2005 | |
| Twelfth-grade students performing at the Basic level should be able to solve mathematical problems that require the direct application of concepts and procedures in familiar situations. Twelfth-grade students should be able to perform computations with real numbers and estimate the results of numerical calculations. These students should also be able to estimate, calculate, and compare measures and identify and compare properties of two- and three-dimensional figures, and solve simple problems using two-dimensional coordinate geometry. At this level, students should be able to identify the source of bias in a sample and make inferences from sample results; calculate, interpret, and use measures of central tendency; and compute simple probabilities. They should understand the use of variables, expressions, and equations to represent unknown quantities and relationships among unknown quantities. They should be able to solve problems involving linear relations using tables, graphics, or symbols, and solve linear equations involving one variable. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Basic level should be able to solve mathematical problems that require the direct application of concepts and procedures in familiar mathematical and real-world settings. Students performing at the Basic level should be able to compute, approximate, and estimate with real numbers, including common irrational numbers. They should be able to order and compare real numbers and be able to perform routine arithmetic calculations with and without a scientific calculator or spreadsheet. They should be able to use rates and proportions to solve numeric and geometric problems. At this level, students should be able to interpret information about functions presented in various forms, including verbal, graphical, tabular, and symbolic. They should be able to evaluate polynomial functions and recognize the graphs of linear functions. Twelfth-grade students should also understand key aspects of linear functions, such as slope and intercepts. These students should be able to extrapolate from sample results; calculate, interpret, and use measures of center; and compute simple probabilities. Students at this level should be able to solve problems involving area and perimeter of plane figures, including regular and irregular polygons, and involving surface area and volume of solid figures. They should also be able to solve problems using the Pythagorean theorem and using scale drawings. Twelfth graders performing at the Basic level should be able to estimate, calculate, and compare measures, as well as to identify and compare properties of two- and three-dimensional figures. They should be able to solve routine problems using two-dimensional coordinate geometry, including calculating slope, distance, and midpoint. They should also be able to perform single translations or reflections of geometric figures in a plane. |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Proficient level represents mastery of fundamental algebraic operations and concepts with real numbers, and an understanding of complex numbers. It also represents understanding of polynomials and their graphs up to the second degree, including conic sections. The elements of plane, solid, and coordinate geometry should be understood at the Proficient level. The Proficient level includes the ability to apply concepts and formulas to problem solving. Students at this level should demonstrate critical thinking skills. The Proficient level also represents the ability to judge the reasonableness of answers and the ability to analyze and interpret data in both tabular and graphical form. Basic algebraic concepts, measurement, and constructive geometry concepts are mastered at this level. |
Proficient-level students integrate mathematical concepts and procedures consistently to more complex problems in the five NAEP content areas. They demonstrate an understanding of algebraic reasoning, geometric and spatial reasoning, and statistical reasoning as applied to other areas of mathematics. They perform algebraic operations involving polynomials, justify geometric relationships, and judge and defend the reasonableness of answers in real-world situations. These students analyze and interpret data in tabular and graphical form. Proficient-level students understand and use elements of the function concept in symbolic, graphical and tabular form. They make conjectures, defend their ideas, and give supporting examples. |
| Official—1992 | |
| Twelfth-grade students performing at the Proficient level should consistently integrate mathematical concepts and procedures to the solutions of more complex problems in the five NAEP content areas. Twelfth graders performing at the Proficient level should demonstrate an understanding of algebraic, statistical, and geometric and spatial reasoning. They should be able to perform algebraic operations involving polynomials; justify geometric relationships; and judge and defend the reasonableness of answers as applied to real-world situations. These students should be able to analyze and interpret data in tabular and graphical form; understand and use elements of the function concept in symbolic, graphical, and tabular form; and make conjectures, defend ideas, and give supporting examples. | |
| Official—2005 | |
| Twelfth-grade students performing at the Proficient level should be able to select strategies to solve problems and integrate concepts and procedures. These students should be able to interpret an argument, justify a mathematical process, and make comparisons dealing with a wide variety of mathematical tasks. They should also be able to perform calculations involving similar figures including right triangle trigonometry. They should understand and apply properties of geometric figures and relationships between figures in two and three dimensions. Students at this level should select and use appropriate units of measure as they apply formulas to solve problems. Students performing at this level should be able to use measures of central tendency and variability of distributions to make decisions and predictions, calculate combinations and permutations to solve problems, and understand the use of the normal distribution to describe real-world situations. Students performing at the Proficient level should be able to identify, manipulate, graph, and apply linear, quadratic, exponential, and inverse functions (y = k/x); solve routine and nonroutine problems involving functions expressed in algebraic, verbal, tabular, and graphical forms; and solve quadratic and rational equations in one variable and solve systems of linear equations. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Proficient level should be able to recognize when particular concepts, procedures, and strategies are appropriate, and to select, integrate, and apply them to solve problems. They should also be able to test and validate geometric and algebraic conjectures using a variety of methods, including deductive reasoning and counterexamples. Twelfth-grade students performing at the Proficient level should be able to compute, approximate, and estimate the values of numeric expressions using exponents (including fractional exponents), absolute value, order of magnitude, and ratios. They should be able to apply proportional reasoning, when necessary, to solve problems in nonroutine settings, and to understand the effects of changes in scale. They should be able to predict how transformations, including changes in scale, of one quantity affect related quantities. These students should be able to write equivalent forms of algebraic expressions, including rational expressions, and use those forms to solve equations and systems of equations. They should be able to use graphing tools and to construct formulas for spreadsheets; to use function notation; and to evaluate quadratic, rational, piecewise-defined, power, and exponential functions. |
| At this level, students should be able to recognize the graphs and families of graphs of these functions and to recognize and perform transformations on the graphs of these functions. They should be able to use properties of these functions to model and solve problems in mathematical and real-world contexts, and they should understand the benefits and limits of mathematical modeling. Twelfth graders performing at the Proficient level should also be able to translate between representations of functions, including verbal, graphical, tabular, and symbolic representations; to use appropriate representations to solve problems; and to use graphing tools and to construct formulas for spreadsheets. Students performing at this level should be able to use technology to calculate summary statistics for distributions of data. They should be able to recognize and determine a method to select a simple random sample, identify a source of bias in a sample, use measures of center and spread of distributions to make decisions and predictions, describe the impact of linear transformations and outliers on measures of center, calculate combinations and permutations to solve problems, and understand the use of the normal distribution to describe real-world situations. Twelfth-grade students should be able to use theoretical probability to predict experimental outcomes involving multiple events. These students should be able to solve problems involving right triangle trigonometry, use visualization in three dimensions, and perform successive transformations of a geometric figure in a plane. They should be able to understand the effects of transformations, including changes in scale, on corresponding measures and to apply slope, distance, and midpoint formulas to solve problems. |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
| The Advanced level represents mastery of trigonometric, exponential, logarithmic, and composite functions, zeros and inverses of functions, polynomials of the third degree and higher, rational functions, and graphs of all of these. In addition, the Advanced level represents mastery of topics in discrete mathematics including matrices and determinants, sequences and series, and probability and statistics, as well as topics in analytic geometry. The Advanced level also signifies the ability to successfully apply these concepts to a variety of problemsolving situations. |
Advanced-level students consistently demonstrate the integration of procedural and conceptual knowledge, as well as the synthesis of ideas, in the five NAEP content areas. Advanced-level students understand the function concept, and they compare and apply the numeric, algebraic, and graphical properties of functions. They apply and connect their knowledge of algebra, geometry, and statistics to solve problems in more advanced areas of continuous and discrete mathematics. Advanced-level students formulate generalizations using examples and counterexamples to create models. In communicating their mathematical reasoning, these students demonstrate clear, concise, and correct use of mathematical symbolism and logical thinking. |
| Official—1992 | |
| Twelfth-grade students performing at the Advanced level should consistently demonstrate the integration of procedural and conceptual knowledge and the synthesis of ideas in the five NAEP content areas. Twelfth-grade students performing at the Advanced level should understand the function concept; and be able to compare and apply the numeric, algebraic, and graphical properties of functions. They should apply their knowledge of algebra, geometry, and statistics to solve problems in more advanced areas of continuous and discrete mathematics. They should be able to formulate generalizations and create models through probing examples and counterexamples. They should be able to communicate their mathematical reasoning through the clear, concise, and correct use of mathematical symbolism and logical thinking. |
|
| Official—2005 | |
| Twelfth-grade students performing at the Advanced level should demonstrate in-depth knowledge of the mathematical concepts and procedures represented in the framework. Students should be able to integrate knowledge to solve complex problems and justify and explain their thinking. These students should be able to analyze, make and justify mathematical arguments, and communicate their ideas clearly. Advanced-level students should be able to describe the intersections of geometric figures in two and three dimensions, and use vectors to represent velocity and direction. They should also be able to describe the impact of linear transformations and outliers on measures of central tendency and variability, analyze predictions based on multiple datasets, and apply probability and statistical reasoning in more complex problems. Students performing at the Advanced level should be able to solve or interpret systems of inequalities and formulate a model for a complex situation (e.g., exponential growth and decay) and make inferences or predictions using the mathematical model. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Advanced level should demonstrate in-depth knowledge of and be able to reason about mathematical concepts and procedures. They should be able to integrate this knowledge to solve nonroutine and challenging problems, provide mathematical justifications for their solutions, and make generalizations and provide mathematical justifications for those generalizations. These students should reflect on their reasoning, and they should understand the role of hypotheses, deductive reasoning, and conclusions in geometric proofs and algebraic arguments made by themselves and others. Students should also demonstrate this deep knowledge and level of awareness in solving problems, using appropriate mathematical language and notation. Students at this level should be able to reason about functions as mathematical objects. They should be able to evaluate logarithmic and trigonometric functions and recognize the properties and graphs of these functions. They should be able to use properties of functions to analyze relationships and to determine and construct appropriate representations for solving problems, including the use of advanced features of graphing calculators and spreadsheets. |
| These students should be able to describe the impact of linear transformations and outliers on measures of spread (including standard deviation), analyze predictions based on multiple datasets, and apply probability and statistical reasoning to solve problems involving conditional probability and compound probability. Twelfth-grade students performing at the Advanced level should be able to solve problems and analyze properties of three-dimensional figures. They should be able to describe the effects of transformations of geometric figures in a plane or in three dimensions, to reason about geometric properties using coordinate geometry, and to do computations with vectors and to use vectors to represent magnitude and direction. |
aFor Pre-Standard Setting Draft, Post-Standard Setting Draft, and Official 1992, see Allen et al. (1999, App. F). For Official 2005, see http://nces.ed.gov/nationsreportcard/mathematics/achieveall.aspx#grade12 [September 2016]. For Official 2009, see http://nces.ed.gov/nationsreportcard/pubs/main2009/2011455.aspx [September 2016].
TABLE 5-4a Achievement-Level Descriptors for 4th-Grade Readinga
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Basic performance in reading should include
|
Basic performance in reading should include
|
| Official—1992 | |
| Fourth-grade students at the Basic level should demonstrate an understanding of the overall meaning of what they read. When reading text appropriate for fourth graders, they should be able to make relatively obvious connections between the text and their own experiences. For example, when reading literary text, they should be able to tell what the story is generally about, provide details to support their understanding, and be able to connect aspects of the stories to their own experiences. When reading informational text, Basic-level fourth graders should be able to tell what the selection is generally about or identify the purpose for reading it; provide details to support their understanding; and connect ideas from the text to their background knowledge and experiences. |
|
| Official—2009 | |
| Fourth-grade students performing at the Basic level should be able to locate relevant information, make simple inferences, and use their understanding of the text to identify details that support a given interpretation or conclusion. Students should be able to interpret the meaning of a word as it is used in the text. | |
| When reading literary texts such as fiction, poetry, and literary nonfiction, fourth-grade students performing at the Basic level should be able to make simple inferences about characters, events, plot, and setting. They should be able to identify a problem in a story and relevant information that supports an interpretation of a text. When reading informational texts such as articles and excerpts from books, fourth-grade students performing at the Basic level should be able to identify the main purpose and an explicitly stated main idea, as well as gather information from various parts of a text to provide supporting information. |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Proficient performance in reading should include
|
Proficient performance in reading should include
|
| Official—1992 | |
| Fourth-grade students performing at the Proficient level should be able to demonstrate an overall understanding of the text, providing inferential as well as literal information. When reading text appropriate to fourth grade, they should be able to extend the ideas in the text by making inferences, drawing conclusions, and making connections to their own experiences. The connection between the text and what the student infers should be clear. For example, when reading literary text, Proficient-level fourth graders should be able to summarize the story, draw conclusions about the characters or plot, and recognize relationships such as cause and effect. When reading informational text, Proficient-level students should be able to summarize the information and identify the author’s intent or purpose. They should be able to draw reasonable conclusions from the text, recognize relationships such as cause and effect or similarities and differences, and identify the meaning of the selection’s key concepts. |
|
| Official—2009 | |
| Fourth-grade students performing at the Proficient level should be able to integrate and interpret texts and apply their understanding of the text to draw conclusions and make evaluations. When reading literary texts, such as fiction, poetry, and literary nonfiction, fourth-grade students performing at the Proficient level should be able to identify implicit main ideas and recognize relevant information that supports them. Students should be able to judge elements of author’s craft and provide some support for their judgment. They should be able to analyze character roles, actions, feelings, and motivations. When reading informational texts such as articles and excerpts from books, fourth-grade students performing at the Proficient level should be able to locate relevant information, integrate information across texts, and evaluate the way an author presents information. Student performance at this level should demonstrate an understanding of the purpose for text features and an ability to integrate information from headings, text boxes, graphics and their captions. They should be able to explain a simple cause-and-effect relationship and draw conclusions. |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Advanced performance in reading should include
|
Advanced performance in reading should include
|
| Official—1992 | |
| Fourth-grade students performing at the Advanced level should be able to generalize about topics in the reading selection and demonstrate an awareness of how authors compose and use literary devices. When reading text appropriate to fourth grade, they should be able to judge texts critically and, in general, give thorough answers that indicate careful thought. For example, when reading literary text, Advanced-level students should be able to make generalizations about the point of the story and extend its meaning by integrating personal experiences and other readings with the ideas suggested by the text. They should be able to identify literary devices such as figurative language. When reading informational text, Advanced-level fourth graders should be able to explain the author’s intent by using supporting material from the text. They should be able to make critical judgments of the form and content of the text and explain their judgments clearly. |
|
| Official—2009 | |
| Fourth-grade students performing at the Advanced level should be able to make complex inferences and construct and support their inferential understanding of the text. Students should be able to apply their understanding of a text to make and support a judgment. When reading literary texts, such as fiction, poetry, and literary nonfiction, fourth-grade students performing at the Advanced level should be able to identify the theme in stories and poems and make complex inferences about characters’ traits, feelings, motivations, and actions. They should be able to recognize characters’ perspectives and evaluate characters’ motivations. Students should be able to interpret characteristics of poems and evaluate aspects of text organization. When reading informational texts, such as articles and excerpts from books, fourth-grade students performing at the Advanced level should be able to make complex inferences about main ideas and supporting ideas. They should be able to express a judgment about the text and about text features and support the judgments with evidence. They should be able to identify the most likely cause given an effect, explain an author’s point of view, and compare ideas across two texts. |
aFor Pre-Standard Setting Draft, Post-Standard Setting Draft, and Official 1992, see Allen et al. (1996, App. F). For Official 2009; see https://nces.ed.gov/nationsreportcard/reading/achieve.aspx [September 2016].
TABLE 5-5a Achievement-Level Descriptors for 8th-Grade Readinga
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Basic performance in reading should include
|
Basic performance in reading should include
|
| Official—1992 | |
| Eighth-grade students performing at the Basic level should demonstrate a literal understanding of what they read and be able to make some interpretations. When reading text appropriate to eighth grade, they should be able to identify specific aspects of the text that reflect the overall meaning, recognize and relate interpretations and connections among ideas in the text to personal experience, and draw conclusions based on the text. For example, when reading literary text, Basic-level eighth graders should be able to identify themes and make inferences and logical predictions about aspects such as plot and characters. When reading informative text, they should be able to identify the main idea and the author’s purpose. They should make inferences and draw conclusions supported by i nformation in the text. They should recognize the relationships among the facts, ideas, events, and concepts of the text (e.g., cause and effect and chronological order). When reading practical text, they should be able to identify the main purpose and make predictions about the relatively obvious outcomes of procedures in the text. |
|
| Official—2009 | |
| Eighth-grade students performing at the Basic level should be able to locate information; identify statements of main idea, theme, or author’s purpose; and make simple inferences from texts. They should be able to interpret the meaning of a word as it is used in the text. Students performing at this level should also be able to state judgments and give some support about content and presentation of content. When reading literary texts, such as fiction, poetry, and literary nonfiction, eighth-grade students performing at the Basic level should recognize major themes and be able to identify, describe, and make simple inferences about setting and about character motivations, traits, and experiences. They should be able to state and provide some support for judgments about the way an author presents content and about character motivation. When reading informational texts such as exposition and argumentation, eighth-grade students performing at the Basic level should be able to recognize inferences based on main ideas and supporting details. They should be able to state and provide some support for judgments about the way an author presents content and about character motivation. They should be able to locate and provide relevant facts to construct general statements about information from the text. Students should be able to provide some support for judgments about the way information is presented. |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Proficient performance in reading should include
|
Proficient performance in reading should include
|
| Official—1992 | |
| Eighth-grade students performing at the Proficient level should be able to show an overall understanding of the text, including inferential as well as literal information. When reading text appropriate to eighth grade,· they should extend the ideas in the text by making clear inferences from it, by drawing conclusions, and by making connections to their own experiences—including other reading experiences. Proficient-level eighth graders should be able to identify some of the devices authors use in composing text. For example, when reading literary text, students at the Proficient level should be able to give details and examples to support themes that they identify. They should be able to use implied as well as explicit information in articulating themes; to interpret the actions, behaviors, and motives of characters; and to identify the use· of literary devices such as personification and foreshadowing. When reading informative text, they should be able to summarize the text using explicit and implied information and support conclusions with inferences based on the text. When reading practical text, Proficient-level students should be able to describe its purpose and support their views with examples and details. They should be able to judge the importance of certain steps and procedures. |
|
| Official—2009 | |
| Eighth-grade students performing at the Proficient level should be able to provide relevant information and summarize main ideas and themes. They should be able to make and support inferences about a text, connect parts of a text, and analyze text features. Students performing at this level should also be able to fully substantiate judgments about content and presentation of content. When reading literary texts, such as fiction, poetry, and literary nonfiction, eighth-grade students performing at the Proficient level should be able to make and support a connection between characters from two parts of a text. They should be able to recognize character actions and infer and support character feelings. Students performing at this level should be able to provide and support judgments about characters’ motivations across texts. They should be able to identify how figurative language is used. When reading informational texts such as exposition and argumentation, eighth-grade students performing at the Proficient level should be able to locate and provide facts and relevant information that support a main idea or purpose, interpret causal relations, provide and support a judgment about the author’s argument or stance, and recognize rhetorical devices. |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Advanced performance in reading should include
|
Advanced performance in reading should include
|
| Official—1992 | |
| Eighth-grade students performing at the Advanced level should be able to describe the more abstract themes and ideas of the overall text. When reading text appropriate to eighth grade, they should be able to analyze both meaning and form and support their analyses explicitly with examples from the text; they should be able to extend text information by relating it to their experiences and to world events. At this level, student responses should be thorough, thoughtful, and extensive. For example, when reading literary text, Advanced-level eighth graders should be able to make complex, abstract summaries and theme statements. They should be able to describe the interactions of various literary elements (i.e., setting, plot, characters, and theme) and to explain how the use of literary devices affects both the meaning of the text and their responses to the author’s style. They should be able to analyze and evaluate the composition of the text. When reading informative text, they should be able to analyze the author’s purpose and point of view. They should be able to use cultural and historical background information to develop perspectives on the text and be able to apply text information to broad issues and world situations. |
|
| When reading practical text, Advanced-level students should be able to synthesize information that will guide their performance, apply text information to new situations, and critique the usefulness of the form and content. | |
| Official—2009 | |
| Eighth-grade students performing at the Advanced level should be able to make connections within and across texts and to explain causal relations. They should be able to evaluate and justify the strength of supporting evidence and the quality of an author’s presentation. Students performing at the Advanced level also should be able to manage the processing demands of analysis and evaluation by stating, explaining, and justifying. When reading literary texts, such as fiction, literary nonfiction, and poetry, eighth-grade students performing at the Advanced level should be able to explain the effects of narrative events. Within or across texts, they should be able to make thematic connections and make inferences about characters feelings, motivations, and experiences. When reading informational texts such as exposition and argumentation, eighth-grade students performing at the Advanced level should be able to infer and explain a variety of connections that are intratextual (such as the relation between specific information and the main idea) or intertextual (such as the relation of ideas across expository and argument texts). Within and across texts, students should be able to state and justify judgments about text features, choice of content, and the author’s use of evidence and rhetorical devices. |
aFor Pre-Standard Setting Draft, Post-Standard Setting Draft, and Official 1992, see Allen et al. (1996, App. F). For Official 2009, see https://nces.ed.gov/nationsreportcard/reading/achieve.aspx [September 2016].
TABLE 5-6a Achievement-Level Descriptors for 12th-Grade Readinga
| BASIC | |
|---|---|
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Basic performance in reading should include
|
Basic performance in reading should include
|
| Official—1992 | |
| Twelfth-grade students performing at the Basic level should be able to demonstrate an overall understanding and make some interpretations of the text. When reading text appropriate to 12th grade, they should be able to identify and relate aspects of the text to its overall meaning, recognize interpretations, make connections among and relate ideas in the text to their personal experiences, and draw conclusions. They should be able to identify elements of an author’s style. For example, when reading literary text, 12th-grade students should be able to explain the theme, support their conclusions with information from the text, and make connections between aspects of the text and their own experiences. When reading informational text, Basic-level 12th graders should be able to explain the main idea or purpose of a selection and use text information to support a conclusion or make a point. They should be able to make logical connections between the ideas in the text and their own background knowledge. When reading practical text, they should be able to explain its purpose and the significance of specific details or steps. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Basic level should be able to identify elements of meaning and form and relate them to the overall meaning of the text. They should be able to make inferences, develop interpretations, make connections between texts, and draw conclusions; and they should be able to provide some support for each. They should be able to interpret the meaning of a word as it is used in the text. When reading literary texts, such as fiction, literary nonfiction, and poetry, twelfth-grade students performing at the Basic level should be able to describe essential literary elements such as character, narration, setting, and theme; provide examples to illustrate how an author uses a story element for a specific effect; and provide interpretations of figurative language. When reading informational texts, such as exposition, argumentation, and documents, twelfth-grade students performing at the Basic level should be able to identify the organization of a text, make connections between ideas in two different texts, locate relevant information in a document, and provide some explanation for why the information is included. |
| PROFICIENT | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Proficient performance in reading should include
|
Proficient performance in reading should include
|
| Official—1992 | |
| Twelfth-grade students performing at the Proficient level should be able to show an overall understanding of the text, which includes inferential as well as literal information. When reading text appropriate to 12th grade, they should be able to extend the ideas of the text by making inferences, drawing conclusions, and making connections to their own personal experiences and other readings. Connections between inferences and the text should be clear, even when implicit. These students should be able to analyze the author’s use of literary devices. When reading literary text, Proficient-level 12th graders should be able to integrate their personal experiences with ideas in the text to draw and support conclusions. They should be able to explain the author’s use of literary devices such as irony or symbolism. When reading informative text, they should be able to apply text information appropriately to specific situations and integrate their background information with ideas in the text to draw and support conclusions. When reading practical texts, they should be able to apply information or directions appropriately. They should be able to use personal experiences to evaluate the usefulness of text information. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Proficient level should be able to locate and integrate information using sophisticated analyses of the meaning and form of the text. These students should be able to provide specific text support for inferences, interpretative statements, and comparisons within and across texts. When reading literary texts such as fiction, literary nonfiction, and poetry, twelfth-grade students performing at the Proficient level should be able to explain a theme and integrate information from across a text to describe or explain character motivations, actions, thoughts, or feelings. They should be able to provide a description of settings, events, or character and connect the description to the larger theme of a text. Students performing at this level should be able to make and compare generalizations about different characters’ perspectives within and across texts. When reading informational texts including exposition, argumentation, and documents, 12th-grade students performing at the Proficient level should be able to integrate and interpret texts to provide main ideas with general support from the text. They should be able to evaluate texts by forming judgments about an author’s perspective, about the relative strength of claims, and about the effectiveness of organizational elements or structures. Students performing at this level should be able to understand an author’s intent and evaluate the effectiveness of arguments within and across texts. They should also be able to comprehend detailed documents to locate relevant information needed for specified purposes. |
| ADVANCED | |
| Pre-Standard Setting Draft | Post-Standard Setting Draft |
Advanced performance in reading should include
|
Advanced performance in reading should include
|
| Official—1992 | |
| Twelfth-grade students performing at the Advanced level should be able to describe more abstract themes and ideas in the overall text. When reading text appropriate to 12th grade, they should be able to analyze both the meaning and the form of the text and explicitly support their analyses with specific examples from the text. They should be able to extend the information from the text by relating it to their experiences and to the world. Their responses should be thorough, thoughtful, and extensive. For example, when reading literary text, Advanced-level 12th graders should be able to produce complex, abstract summaries and theme statements. They should be able to use cultural, historical, and personal information to develop and explain text perspectives and conclusions. They should be able to evaluate the text, applying knowledge gained from other texts. |
|
| When reading informational text, they should be able to analyze, synthesize, and evaluate points of view. They should be able to identify the relationship between the author’s stance and elements of the text. They should be able to apply text information to new situations and to the process of forming new responses to problems or issues. When reading practical texts, Advanced-level 12th graders should be able to make a critical evaluation of the usefulness of the text and apply directions from the text to new situations. |
|
| Official—2009 | |
| Twelfth-grade students performing at the Advanced level should be able to analyze both the meaning and the form of the text and provide complete, explicit, and precise text support for their analyses with specific examples. They should be able to read across multiple texts for a variety of purposes, analyzing and evaluating them individually and as a set. When reading literary texts such as fiction, poetry, and literary nonfiction, 12th-grade students performing at the Advanced level should be able to analyze and evaluate how an author uses literary devices, such as sarcasm or irony, to enhance and convey meaning. They should be able to determine themes and explain thematic connections across texts. When reading informational texts, twelfth-grade students performing at the Advanced level should be able to recognize, use, and evaluate argumentation and expository text structures and the organization of documents. They should be able to critique and evaluate arguments and counterarguments within and between texts, and substantiate analyses with full and precise evidence from the text. They should be able to identify and integrate essential information within and across documents. |
aFor Pre-Standard Setting Draft, Post-Standard Setting Draft, and Official 1992, see Allen et al. (1996, App. F). For Official 2009; see https://nces.ed.gov/nationsreportcard/reading/achieve.aspx [September 2016].