2
The Scientific Case for an Electron-Ion Collider
This chapter reviews in detail the fundamental scientific issues that would be addressed by an electron-ion collider (EIC).
THE ORIGIN OF MASS
The majority of the visible mass of the universe resides in the two types of nucleons—protons and neutrons. Nucleons are made of massless gluons and almost massless quarks. In the Standard Model of particle physics, the masses of quarks, just like the mass of the electron, arise through their coupling to the Higgs field. Excitations of this field, Higgs particles, have recently been observed at the Large Hadron Collider (LHC). This observation has confirmed the basic Higgs mechanism. However, while the Higgs mechanism can explain all of the mass of the electron, it accounts for only a small part of the mass of the nucleon—namely, that associated with the masses of quarks.
The remainder of the mass of the nucleon is encoded in a slight rearrangement of Einstein’s relation E = mc2. In relativistic theories, mass is given by m = E/c2, and the energy of the quark and gluon fields contributes to the mass of the nucleon. Quantum fields are richer than classical fields, because the vacuum of the theory is not empty, but filled with quantum fluctuations of particles and antiparticles. These fluctuations contribute to the energy of empty space. The nucleon is a state
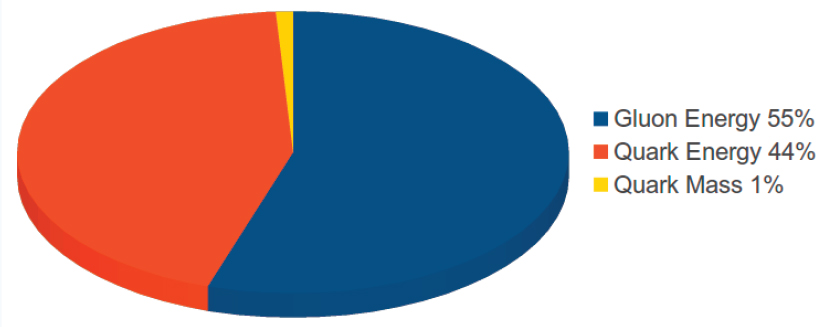
defined by its quantum numbers: baryon number,1 electric charge, and spin, and its mass is determined by the difference in the energy between a quantum state containing a single nucleon and the energy of the vacuum.
The minimum configuration of quarks that can provide the quantum numbers of the nucleon is called the “valence quark content.” In the proton, the valence content is two up quarks and one down quark. Because quarks and gluons are light, and because the coupling between valence quarks and gluons is strong, valence quarks are surrounded by a large number of sea quarks (quark-antiquark pairs) and gluons. An inventory2 of the mass of the nucleon is shown in Figure 2.1. The contribution of the valence up and down quark masses is less than 1 percent. The remainder of the mass is associated with the energy of the highly relativistic quark and gluon fields. One can observe that the largest contribution to the mass of the proton originates from the gluon field energy. In this sense, the source of visible mass in the universe is not the Higgs field, but the gluon field.
Conducting a thought experiment allows an exploration of the mass of the proton by ionizing it, removing sea quarks and gluons from the valence quark core, and carefully monitoring the binding energies in the process. As explained in
___________________
1 “Baryon number” is a conserved quantity that ensures that the proton cannot decay into a positron and a photon. In the Standard Model of particle physics, each quark carries baryon number 1/3.
2 This inventory is based on data from deep-inelastic scattering (DIS). In particular, using relativistic invariance, one can relate the momentum fraction carried by quarks and gluons to the total quark and gluon energy. See X. Ji, 1995, A QCD analysis of the mass structure of the nucleon, Phys. Rev. Lett. 74:1071.
Chapter 1, confinement implies that this experiment cannot be realized. Instead, the EIC will explore the contents of the proton using a well-understood probe, the photon. In high-energy collisions of virtual photons and nucleons, the quark and gluon fields in the nucleon manifest themselves as quark and gluon “partons” (see Box 1.1 in Chapter 1). By selecting the energy and resolution of the virtual photon, an EIC can address different regions of Bjorken x (explained in Box 1.3 in Chapter 1) going from the regime of moderate x dominated by valence quarks to the small x regime controlled by sea quarks and gluons. These types of experiments have been carried out before, but the EIC will add several new dimensions by studying the distribution of partons in the plane transverse to the motion of the nucleon, and by determining their transverse motion (see Box 2.1). These measurements will provide tomographic images of nucleons and nuclei. These images can be used to study several profound questions about the structure of the nucleon and the nucleus. First, as a function of Bjorken x, what is the relative spatial size of the valence quark, sea quark, and gluon distributions? Second, what is the spatial structure of the different contributions, shown in Figure 2.1, to the energy density and pressure forces in the nucleon? Lastly, what is the spatial distribution of gluons in a large nucleus?
Imaging Quarks and Gluons
Tomographic images of both quarks and gluons in the nucleon are enabled by advances in quantum chromodynamics (QCD) theory since the mid-1990s combined with the unique capabilities of an EIC. First, the advances in theory that facilitate measurements of the transverse position of partons are described.
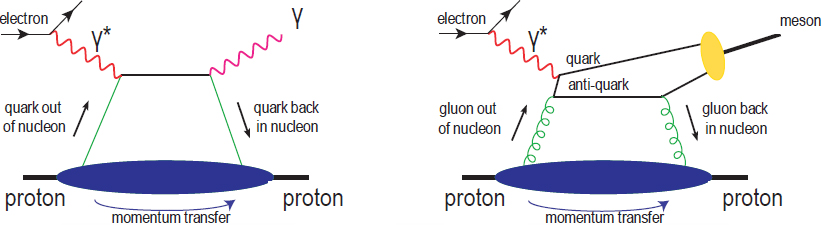
The two prototype reactions that have been analyzed are called deeply virtual Compton scattering and deeply virtual meson production (see Figure 2.2). The following text will refer to these processes as real photon and meson production in electron scattering. In real photon production, the incoming electron produces a high-energy virtual photon that interacts with the target nucleon or nucleus just as it does in deep-inelastic scattering (DIS). However, instead of destroying the target, the nucleon is left intact, and a real photon is produced. In real meson production, the final state consists of the target nucleon as well as a quark-antiquark bound state, such as a vector meson. The virtual photon is characterized by its resolution and energy, as in DIS, but there is an additional kinematic observable, the momentum transfer between the initial and final state proton. The crucial advance in QCD theory is the observation that the dependence of the cross section on the momentum transfer contains information about the transverse position of the struck parton.
Real photon production directly determines the transverse position of quarks. Information on the gluon distribution can be obtained from real meson produc-
tion. The interpretation of this process is most direct when the focus is on the production of a heavy-quark bound state like the J/ψ, a charm-anticharm state, or the Upsilon (Υ), a bottom-antibottom pair. In this case, the dominant process is shown in the right panel of Figure 2.2, where the virtual photon produces a quark-pair that interacts with the target via two-gluon exchange. Gluonic density
profiles are also obtained independently through varying the probe resolution Q2 in real photon production. The combination of real photon and meson production therefore provides an important cross-check on transverse gluon profiles. Exploratory studies of real photon production were carried out at the ZEUS and then H1 experiments at the Hadron-Electron Ring Accelerator (HERA), at Thomas
Jefferson National Accelerator Laboratory (JLab) with a 6 GeV electron beam on a fixed proton target, at the HERA Measurement of Spin (HERMES) experiment at Deutsches Elektronen-Synchrotron (DESY), and at the Common Muon and Proton Apparatus for Structure and Spectroscopy (COMPASS) experiment at the European Organization for Nuclear Research (CERN). These experiments suffered from limited statistics or kinematic reach. In the near future, JLab, with its 12 GeV-energy high-luminosity upgrade, will provide high-precision images of the valence quark region.
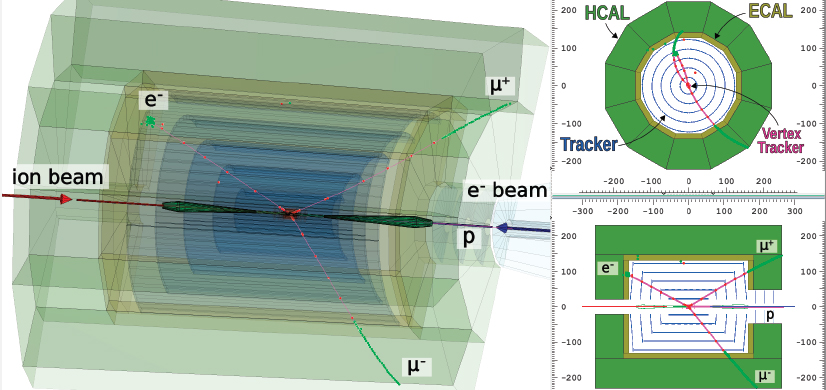
An EIC would dramatically improve on these measurements, via detailed images of gluonic profiles and would also offer a path to determine the orbital contribution of sea quarks and gluons to the nucleon spin. The counter-propagating electron and hadron beams configuration of an EIC is the most efficient means to achieve high energy and high resolution for a given energy of the electron or hadron beam. The collider geometry also has significant advantages in terms of the detector geometry (see Figure 2.3). In a fixed target experiment, all reaction products end up in a narrow region of the detector along the beam line, making it difficult to clearly separate and measure the deflected electron and the target nucleon or its decay products. In a colliding beam detector, the reaction products are clearly separated in the laboratory, enabling precise measurements of the kinematic variables on which tomographic images are based. Furthermore, carefully designed forward detection of the recoiling particles, the proton in the case of Figure 2.2, can select the desired exclusive reaction.
The scientific program of an EIC will be enabled by a unique combination of three crucial variables—energy, luminosity, and polarization—combined with the
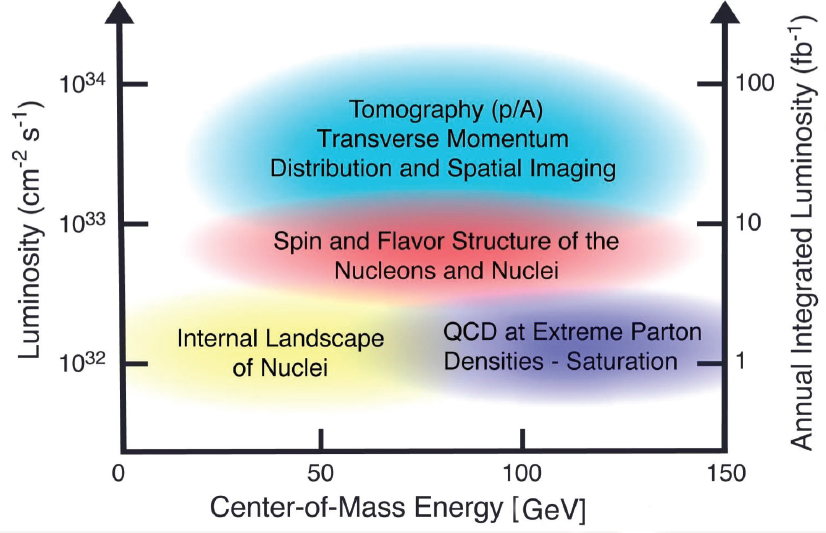
ability to collide electrons with both nucleons and nuclei. Polarization, or alignment of spins, is needed to access the carriers of spin and angular momentum in the proton. The energy-luminosity regimes required to fully explore the central pillars of an EIC science program, determining the origins of the mass and spin-flavor composition of the proton, imaging the spatial and momentum distribution of their partons (quarks and gluons), and studying dense gluon matter, are indicated in Figure 2.4.
High energy is needed to produce high-resolution images of the partons in nucleons and nuclei that carry a small fraction x of the momentum of the target. This regime is dominated by gluons and sea quarks. High energy also provides large kinematic coverage, which is crucial in extracting gluon distributions. Lastly, high energy provides access to the regime of very high gluon density, a new frontier in QCD.
Luminosity determines the rate at which collisions occur. High luminosity is needed because parton imaging is based on the detection of very specific final states,
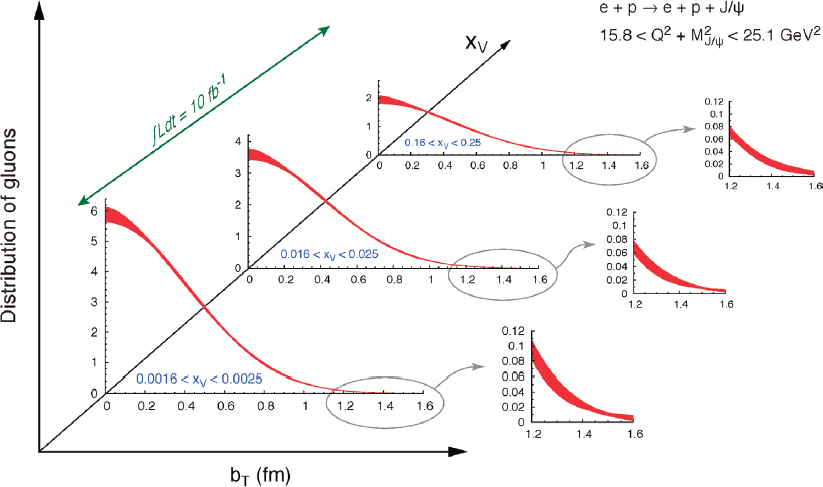
such as an intact nucleon combined with a final state photon or vector meson, that occur in only a small fraction of all reactions. Parton imaging also requires an accurate determination of not only total interaction rates, but of the dependence of these rates on the deflection angles of all scattered particles, for which large luminosity is also needed. Figure 2.4 indicates both the instantaneous luminosity as well as the annual integrated luminosity (for running time of 107 seconds per year, a 30 percent duty factor) that can be achieved. It is the latter that ultimately controls the experimental uncertainty. Figure 2.5 shows the accuracy of the transverse gluon profiles that can be obtained from J/ψ production using an integrated luminosity of 10 fb–1. Note the precision that can be achieved at large transverse radii bT, which is important for understanding the way in which confinement of quarks and gluons is reflected in the transverse spatial profile of parton distributions.
3D Imaging in Momentum
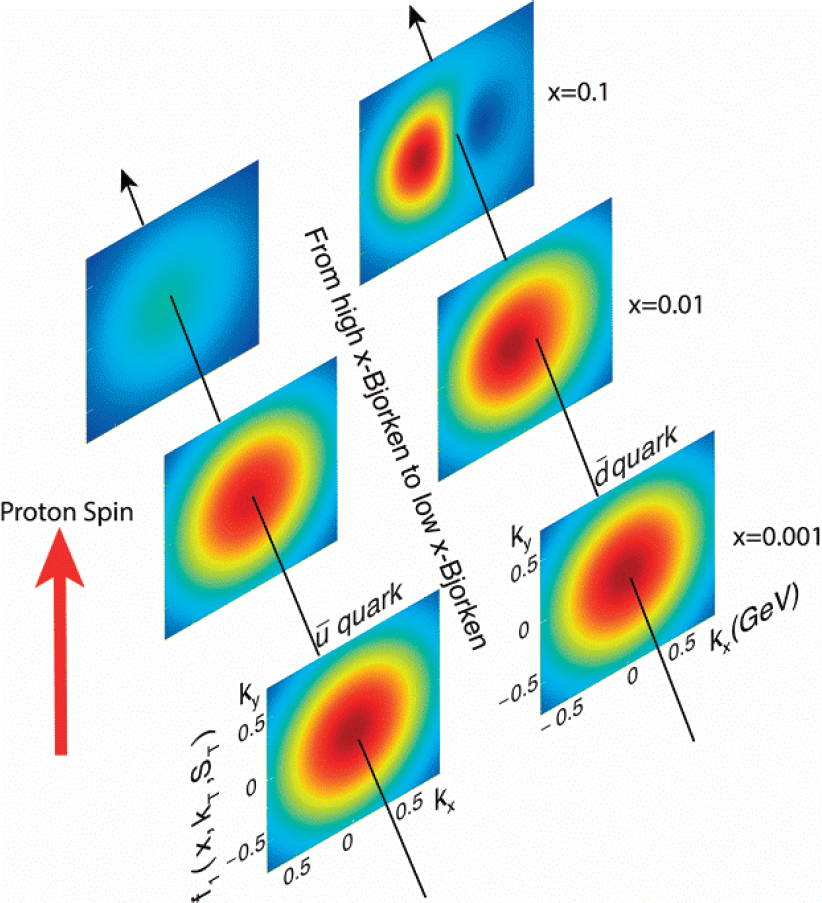
An important complement to the program of imaging the transverse position of partons is the determination of transverse motion. Combined with the dependence on longitudinal motion encoded in Bjorken x, transverse momentum distributions (TMDs) provide a three-dimensional (3D) picture of the nucleon in momentum space. Due to the uncertainty principle, the transverse momentum of partons is related to the characteristic size of the quantum mechanical fluctuation from which it originated. Transverse momentum imaging therefore constrains the possible evolution of color fluctuations with Bjorken x, going from the valence sector at large x to the sea quark and gluon regime at small x. In the small x regime, the results provide important information about the limit of high gluon density, discussed in the last section of this chapter. In a polarized proton, one also expects that the orbital motion of partons is correlated with the spin direction, leading to correlations among spin, transverse motion, and transverse position.
The transverse dynamics of partons can be accessed using a process called semi-inclusive deep-inelastic scattering (SIDIS). As in DIS, the target nucleon is
destroyed, but at least one of the outgoing hadrons is detected. These reactions are referred to as coincidence experiments, because the outgoing hadron (typically a meson) is detected in coincidence with the scattered electron. Information about the transverse motion of partons is encoded in the transverse momentum of the produced hadron. Coincidence scattering is most powerful when combined with polarization, which is discussed in the following section.
THE ORIGIN OF SPIN
Spin is a fundamental property of elementary particles. Matter particles, like electrons and quarks, have a spin or an intrinsic angular momentum equal to ħ/2, where ħ is Planck’s fundamental constant. (For simplicity, the ħ is not written further, leaving it tacitly understood, and the nucleon is referred to, for example, as having spin ½.) Force carriers, like photons and gluons, have spin 1. Composite particles acquire angular momentum from a combination of the fundamental spins and orbital angular momentum of their constituents. Nucleons are bound states of quarks and gluons with total spin ½; the total angular momentum of a nucleon is the sum of the spin and orbital angular momenta of the quarks and gluons they contain. Similarly, the total angular momentum of nuclei is the sum of the spin and orbital motion of nucleons, and in atoms it is the combination of nuclear angular momentum with the spin and orbital motion of electrons.
Charged particles, or neutral particles made of charged constituents, have magnetic moments that in the absence of external electromagnetic fields are aligned with the direction of spin. The fact that protons and neutrons behave as magnets is of great technological importance. For example, the magnetic moment of the proton is the basis of magnetic resonance imaging (MRI). In a magnetic field, protons with spin aligned or anti-aligned with the field have different energy, and this energy difference can be probed using radio frequency (RF) fields.
Gluon Spin and Orbital Angular Momentum
The textbook picture of the spin of the proton is that of three spinning valence quark tops. The total spin ½ is obtained because two of the valence quarks are aligned, and the third one is anti-aligned with the spin of the proton. This simple picture qualitatively accounts for the magnetic moments of the proton and the neutron. It explains, for example, why the neutron, despite its vanishing electric charge, has a nonzero magnetic moment. However, the valence quark picture fails to account for more detailed studies of the spin structure of the nucleon. Beginning in the late 1970s experiments at Stanford Linear Accelerator Center (SLAC), CERN, DESY, and JLab studied DIS using polarized protons. These experiments determine the net polarization of quarks along the direction of the spin of proton.
In units of the total spin ½ of the proton, the valence quark picture predicts that this polarization should be 100 percent. In fact, it was found that the quark polarization is only about 30 percent. The remainder of the spin must reside in orbital angular momenta of quarks and gluons or gluon polarization.
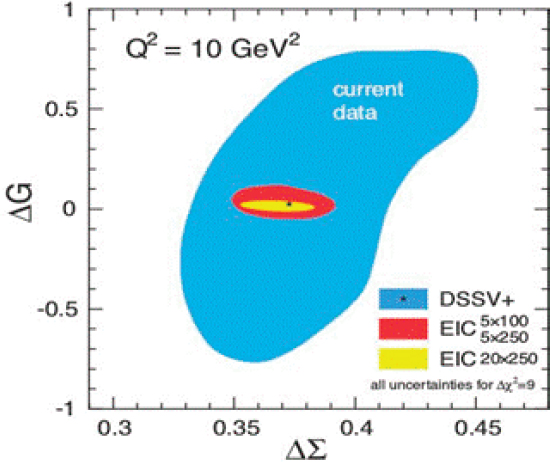
This observation has motivated a broad program aimed at measuring other contributions to the total spin of the proton. Exploratory measurements of the quark orbital angular momentum in the valence quark regime are an important part of the physics program at the 12 GeV upgrade of JLab. Polarized proton-proton collisions at the Relativistic Heavy Ion Collider (RHIC) have provided the first evidence for a nonvanishing gluon spin polarization in the proton. A central goal of the EIC program is to provide a determination of the gluon spin contribution and its orbital angular momentum. The uncertainties in the gluon spin contribution will be dramatically reduced (see Figure 2.6). These measurements would be based on the resolution dependence of polarized DIS. This dependence arises from quark and gluon partons radiating additional partons. When a polarized gluon radiates a quark-antiquark pair, the spin orientation of the gluon is transferred to
the quark and the antiquark. This effect can be measured using polarized electron scattering with a polarized proton beam.
The orbital angular momentum of gluons can be probed via the exclusive measurements described in Figure 2.2. Precise knowledge of the spin of gluons combined with sum rules of the generalized parton distributions (GPDs) determined in these measurements offer the possibility of isolating the contribution to the nucleon spin of the orbital angular momentum of gluons.
Transverse Motion in Polarized Nucleons
The dynamics of spin-orbit correlations in QCD can be studied using the transverse momentum distribution of partons in a transversely polarized proton, one with its spin direction orthogonal to its direction of motion. Consider a nucleon as shown in Figure 2.1.1 with its spin instead in the y-direction. If part of the spin is carried by orbital motion, then this will be reflected at the parton level by a correlation between momentum in the x-direction, and position in the z-direction. In coincidence experiments this relationship can manifest itself as a correlation between the transverse spin of the nucleon and the direction of motion of the observed hadron. This type of observable is referred to as a “spin asymmetry” in a coincidence experiment.
For spin-orbit correlations to manifest themselves as spin asymmetries, a second ingredient is required. As explained in Box 2.2, this second prerequisite is that the struck parton acquires a quantum-mechanical phase from traveling through the color field of the nucleon. As a consequence, spin asymmetries probe the dynamics of QCD in novel ways. Pioneering studies of spin asymmetries in coincidence experiments were carried out in fixed-target experiments at HERMES, COMPASS, and the JLab 6 GeV facility. Figure 2.7 shows transverse momentum profiles extracted from a global fit to existing data, the distribution of unpolarized u and d sea quarks in a polarized proton. A very important result was observed: Whereas d quarks in the proton show strong spin-orbit correlations, the corresponding effects in the u quark sector are weak. It was also observed that spin-orbit effects are large in the valence regime, but disappear in the low x regime.
An EIC would improve on these experiments in several ways. It would significantly extend the kinematic coverage of spin asymmetries in terms of Bjorken x, transverse momentum, and resolution. This extended range will allow detailed tests of QCD in terms of spin-orbit effects and color phases (see Box 2.2). An EIC would for the first time measure spin asymmetries in the gluon sector. Currently, nothing is known about spin-orbit correlations of gluons.
GLUONS IN NUCLEI
An EIC would be able to study the gluons that bind quarks and antiquarks into nucleons and nuclei with unprecedented precision. A central goal of such studies is to explore the limit of low Bjorken x, where the number of gluons in the target
is very large. Here, the description of the nucleus in terms of colored degrees of freedom is expected to simplify dramatically, and discovery of a new type of state composed of dense gluon matter is also expected. An EIC would also be able to explore modifications of the quark distributions in nuclei, as explained in more detail in Box 2.3.
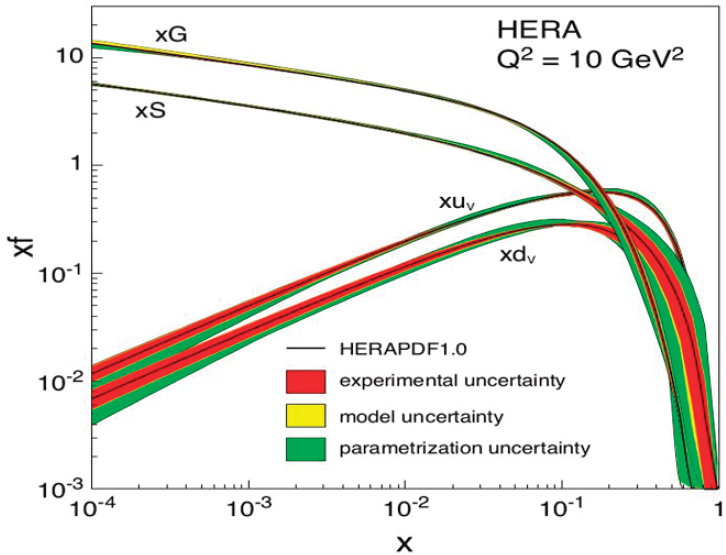
There are several strategies for turning beams of electrons into calibrated probes of nuclear gluons. The first of these methods, based on measurements of the evolution of the quark distribution as a function of resolution, was previously used at other electron machines. As the resolving power of the virtual photon is increased, it becomes sensitive to quark-antiquark fluctuations at shorter distances. In protons and nuclei, these pair fluctuations are produced by gluons, so that a measurement of the change of the quark distribution with scale probes the gluon distribution. Figure 2.8 shows a summary of parton distributions obtained at HERA. It can be observed that the number of gluons grows significantly in the low x, high-energy regime; low x matter is gluonic matter.
This method has a number of limitations. It assumes that the interactions between quarks and gluons are sufficiently weak that one can compute the rate at which quark-antiquark pairs are radiated by gluons. This assumption is questionable in the regime of small x, where the gluon density is large, as well as in the regime of low Q2, where the interaction is strong. An EIC would employ a new and independent method, based on measuring the cross section of longitudinally polarized photons. This cross section vanishes in the simple quark-parton model, but it is not zero if gluon constituents or gluonic interactions are taken into account. A measurement of the longitudinal DIS cross section on the nucleon requires varying the energy of the electron and hadron beams, and there has been only one previous attempt, also from HERA, to measure this cross section. An EIC would perform systematic measurements of the longitudinal photon cross section in both nucleons and nuclei. These measurements would not only constrain the distribution of gluons, but also test theories of the interaction of virtual photons with dense gluon matter, in particular the dipole picture discussed below. An EIC would significantly extend measurements of nuclear parton distribution functions in the low x regime.
Measurements of nuclear structure functions address a very fundamental question about the properties of nuclei in QCD: To what extent is a nucleus just a collection of individual nucleons? Existing determinations of the parton distribution in the valence quark regime show a depletion with respect to the expectation for a noninteracting system of nucleons, an observation believed to reflect the effects of nuclear binding (the European Muon Collaboration [EMC] effect). Nuclear gluon distributions are very poorly constrained at present. Future experiments at an EIC would measure these functions and study how the gluon field of an individual nucleon is modified by its interaction with other nucleons in the nucleus.
The most striking conclusion one might draw from the measurements of the
gluon distribution shown in Figure 2.8 is that the number of gluon grows, apparently without bound, in the low x limit. Clearly, at some point, however, the density becomes so large that gluons lose their individual identity and are strongly overlapping. Where this happens, as a function of Bjorken x, depends on the resolution, because gluons have a spatial extent determined by the resolution Q2. One can therefore ask, for a given value of Bjorken x: Below what resolution scale is the number density so large that gluons are no longer independent? This scale is called the “saturation scale,” Qs.
An important new regime in which nuclear physics becomes simple but the full richness of QCD is retained arises if the saturation scale is large. In this limit,
asymptotic freedom predicts that the interaction strength is weak, but the large gluon density implies that the gluon self-interaction, which is a central feature of QCD, is crucial. This regime is referred to as “dense saturated gluon matter.”3 If Qs
___________________
3 This state is frequently described as a color glass condensate, where “glass” refers to slowing of the time evolution in a fast-moving nucleus by Lorentz time dilation, and “condensate” indicates that the phase space density of gluons is very high. The existence and the properties of this state are a direct consequence of the field equations of QCD. In the limit of large occupation number, these equations are approximately classical. Classical QCD has no intrinsic scale, and the color glass condensate leads to simple scaling relations for cross sections and particle production rates. It also provides initial conditions for the production of a quark-gluon plasma in heavy ion collisions. In collisions of two
is much bigger than typical hadronic energy scales, then the properties of saturated gluon matter depend only on Qs and not on details of the nucleon or nucleus that is being probed.
Producing dense, saturated gluon matter requires high energy and small x. Estimates of the saturation scale at HERA, which collided protons and electrons at a center-of-mass energy of 318 GeV, give a value around 1 GeV, which is not much larger than typical hadronic energy scales. The EIC will operate at lower energy, but it will provide a new lever arm, the ability to accelerate nuclei, enabling it to explore the saturation regime. At high energy, the nucleus is Lorentz contracted along the
___________________
ions, the kinetic energy of the gluons is thermalized, and the dense gluon component evolves into a hot gluon plasma. Gluons in the plasma radiate quark-antiquark pairs, and the equilibrium state becomes a hot quark-gluon plasma that cools and decays into hadrons. The hot quark-gluon plasma is currently being studied at RHIC and LHC, but the dense gluonic system that provides the initial state can be studied only at an EIC.
direction of motion, and the effective gluon density increases as the nuclear radius, proportional to the cube root of the mass number A of the nucleus. Empirical studies of the growth of the gluon distribution provide an estimate of the effective gain in center-of-mass energy afforded by the ability to accelerate heavy nuclei.4 These studies indicate that saturation effects at an EIC are equivalent to those at an electron-proton collider operating at an energy A½, or about 15 times higher.5
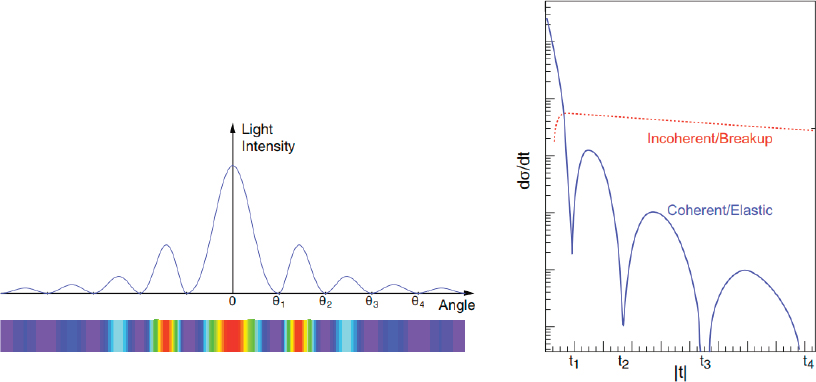
An important aspect of saturation effects in DIS at an EIC is the role of “diffractive scattering.” Diffraction is a well-known effect in optics. When light waves encounter an obstacle with a sharp boundary, they are bent around the object and produce an interference pattern on a screen located behind the obstacle (see the left panel of Figure 2.9). For a given wavelength of the light, the distance between the minima is determined by the size of the object. Diffraction is also observed
___________________
4 See, for example, E. Aschenauer et al., The electron-ion collider: Assessing the energy dependence of key measurements, arXiv:1708.01527.
5 There is some uncertainty in the value of the saturation scale, and there is no definitive theoretical prediction for how large Qs has to be for the full simplicity of the saturation picture to manifest itself. However, much of the experimental program, measuring nuclear effects in the gluon distribution function, studying diffractive scattering in the regime of high gluon density, and mapping the gluon distribution in the transverse plane, does not depend on any particular picture of QCD in the regime of high gluon density.
in the scattering of highly energetic particles on nuclear targets in the limit that the interaction is strong and the projectile is strongly absorbed by the target. If the target is a completely absorbing black disk, then the total cross section is twice the geometric cross section of the target; half of the cross section is due to diffractive scattering.
The high-energy limit of nuclear DIS can be viewed as a process in which the virtual photon produces a quark-antiquark pair with a color dipole moment that interacts with the nuclear target (see Figure 2.10). In the low x regime, the target is dense gluonic matter and the probability for absorbing the quark-antiquark dipole will be large, and may approach unity. This implies that a significant part of the total cross section is diffractive scattering. Experimentally, one observes reactions in which the target nucleus remains intact, called “coherent diffraction,” or reactions in which the target is excited, but there is a large separation in the detector between the decay products of the struck quark and the remnants of the nucleus. The latter events are called “incoherent diffraction.”
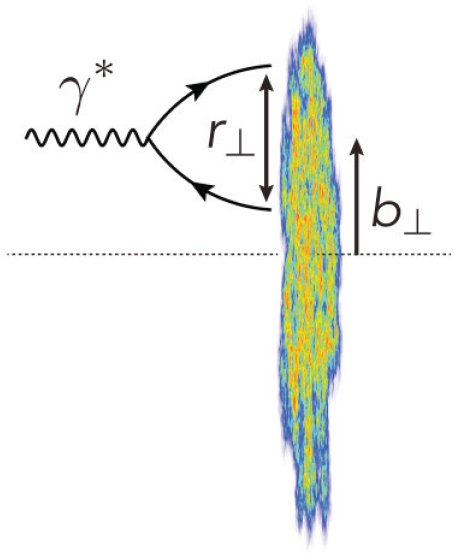
 . The dipole interacts with the Lorentz-contracted gluon field of the nucleus at an impact parameter b
. The dipole interacts with the Lorentz-contracted gluon field of the nucleus at an impact parameter b . The figure also indicates that the color field is fluctuating, and that the boundary of the nucleus is not sharp. SOURCE: E. Aschenauer et al., 2017, The electron-ion collider: Assessing the energy dependence of key measurements, arXiv:1708.01527.
. The figure also indicates that the color field is fluctuating, and that the boundary of the nucleus is not sharp. SOURCE: E. Aschenauer et al., 2017, The electron-ion collider: Assessing the energy dependence of key measurements, arXiv:1708.01527.Diffraction in QCD is a more complicated process than diffraction in optics. If the resolution of the photon is larger than the saturation scale, then the dipole probe of the gluon field is small, and the absorption cross section is small. This means that the target is black at low resolution and gray at high resolution. Also, the nucleus does not have a sharp boundary; it is black in the center and gray near the boundary. Lastly, the nucleus is a quantum system, and the gluon density fluctuates. The nucleus has black spots that fluctuate from event to event.
These complications provide important opportunities. The fact that the blackness of the target depends on resolution implies that the saturation scale can be measured using the dependence of the diffractive cross section on the resolution scale and the nuclear mass number. The observation that the nucleus has a diffuse boundary means that the transverse location of gluons in the nucleus can be mapped. Lastly, the fact that the blackness of the target fluctuates can be used to extract shape fluctuations of the nucleon and correlations between nucleons in the target.
The picture of DIS based on the dipole picture—that the virtual photon turns into a quark-antiquark color dipole—predicts the energy and nuclear mass dependence of diffractive DIS. The diffractive cross section rises steeply with energy at low energy, but becomes an approximately constant fraction of the total cross section in the regime that an EIC would explore. A substantial increase in the rate of diffraction is achieved by going to nuclear targets. At a given energy, nuclear targets contain more gluons and are closer to the black disk limit. The blackness of the target decreases as the resolution is increased, but diffraction is expected to persist at high Q2. This is a reflection of the large saturation scale: gluons are tightly packed, and the target appears black even if the resolution is high. An EIC will enable detailed studies of the dependence on nuclear mass number, the resolution of the virtual photon, and the mass of the diffracted object. These results will test the universality of the dipole model—the assumption that a single dipole cross section can account for many different observables. They will determine the gluon density and therefore the saturation scale in the target and study the onset of gluon self-interaction effects that come into play as the dipole cross section approaches the black disk limit.
The right panel of Figure 2.9 shows a prediction of the diffraction pattern that is expected to emerge in the coherent production of J/ψ mesons. One clearly observes the minima and maxima that are characteristic of diffraction. One also sees that the pattern is expected to disappear if the target nucleus is excited, as shown in the incoherent/breakup curve. The interference patterns are governed by quantum mechanics, and the quantum mechanical rules for combining amplitudes imply that the difference between coherent and incoherent diffraction can be related to fluctuations of the gluon density.
The power of this result is illustrated in Figure 2.11, which shows a model of
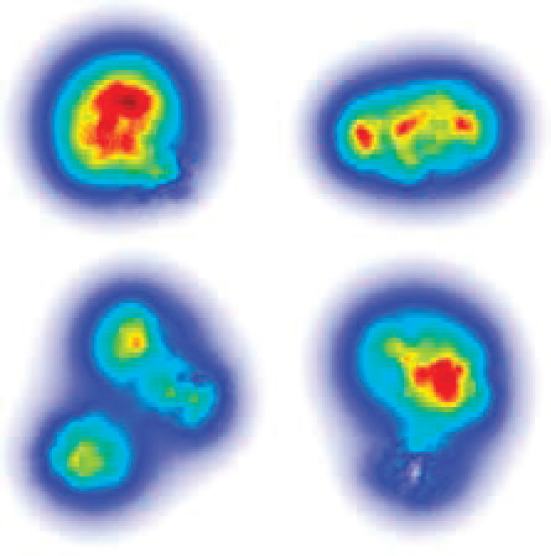
gluon fluctuations in the proton. It was generated using existing data on J/ψ production on the proton. One can observe dramatic fluctuations in the shape of a single proton and that these fluctuations are quite different from what one would expect for a simple bound state of three constituent quarks. This is a far cry from early models of the proton. At low resolution, one expects to see correlations of nucleons in nuclei, and at fine resolution, one will determine fluctuations in the number of valence partons and fluctuations in the color field surrounding these partons. An EIC would be able to explore the power spectrum of fluctuations in nuclei and nucleons in detail and revolutionize the understanding of the emergence of matter from quantum fields of colored quarks and gluons.






















