2
Plenaries
Five plenaries provided workshop participants with an in-depth look at emerging areas of research. In particular, speakers explored how thermal conduction and energy conversion were previously understood; recent experiments that have evolved understanding of the basic physics involved; and how new discoveries might translate into applications in energy, materials, quantum technologies, and other areas. Plenary speakers were Kamran Behnia, École Supérieure de Physique et de Chimie Industrielles de la Ville de Paris (ESPCI); Sean Hartnoll, Stanford University; N. Phuan Ong, Princeton University; Lucile Savary, École Normale Supérieure (ENS); and Joseph P. Heremans, The Ohio State University. Each talk was followed by a brief question-and-answer period, and speakers participated in a full open discussion at the end of the workshop.
THERMAL TRANSPORT AND QUASIPARTICLE HYDRODYNAMICS
Kamran Behnia, ESPCI
Behnia set the stage with a brief history of the field of thermal and electrical conduction; discussed how different scientific branches view transport; and addressed the hydrodynamics of phonons, electron hydrodynamics, and a possible boundary to thermal diffusivity.
Thermal and Electrical Conduction
After the work of Seebeck and Fourier in the early 19th century came the Drude model, around the turn of the 20th century. Following the kinetic theory of gases’ expression, k = 1/3 C v l, which models thermal conduction, the Drude model relates the thermal conductivity k to three properties: specific heat per volume C, average velocity of the electrons v, and their mean free path l. Heat conduction in insulators, which follows the same expression but for phonons (lattice vibrations), produces a curve whose peak of thermal conductivity as a function of temperature is a compromise of those three temperature dependencies of C, v, and l. In the low-temperature limit, the mean free path becomes as large as the sample size. Therefore, the Drude model implies that the bigger the solid, the higher the peak of the thermal conductivity.
A more sophisticated model, according to Behnia, is the Boltzmann-Peierls transport equation, which is now possible to solve exactly in a given solid thanks to progress in numerical calculations and has recently been used increasingly. For example, a 2013 paper1 showed that there is almost perfect agreement between thermal conductivity as calculated theoretically and as measured experimentally in the case of simple semiconductors.
Condensed Matter and Fluid Mechanics
Behnia explained that transport is viewed differently between the fields of condensed matter physics, which deals with solids, and fluid mechanics, which deals with hydrodynamics. Condensed matter physicists often use concepts such as “electron liquid” or “phonon gas.” But the flow in these fluids is very different from the flow as understood in fluid mechanics. In the Boltzmann formalism, collisions impede the flow, which is very different from the picture given by the Navier-Stokes equation. Condensed matter physicists know that in solids there is a lattice (with possible defects), and collisions of quasi-particles can limit the flow of energy. In fluid mechanics, there is no lattice and the flow is not limited by collisions (which therefore conserves momentum). As a result, one uses the Navier-Stokes equation instead of the Boltzmann-Peierls. Dissipation arises because of viscosity rather than because of quasiparticle collisions with a lattice.
Decades ago, Gurzhi suggested that in some solids, within a finite temperature window, heat transport by phonons and charge transport by electrons can become hydrodynamic.2 This idea led to two fields of contemporary research on hydrodynamics of electrons and phonons.
___________________
1 L. Lindsay, D.A. Broido, and T.L. Reinecke, 2013, Ab initio thermal transport in compound semiconductors, Physical Review B (87) 165201, https://link.aps.org/doi/10.1103/PhysRevB.87.165201.
2 R.N. Gurzhi, 1968, Hydrodynamic effects in solids at low temperature, Soviet Physics Uspekhi (11:2), https://iopscience.iop.org/article/10.1070/PU1968v011n02ABEH003815/meta.
Phonon Hydrodynamics
Behnia explained that ballistic transport is a prerequisite for observing hydrodynamics. While phonon ballistic transport is the default case in an insulator, electron ballistic transport requires extremely clean samples. For phonon hydrodynamics to exist among the ballistic and diffusive regimes, there should be a specific hierarchy between three types of scattering processes: normal, resistive, and boundary. Momentum is conserved in a normal collision but is lost in a resistive collision, and boundary scattering refers to the scattering by the edges. Hydrodynamic flow occurs when the normal scattering time is much shorter than the resistive scattering time, and the boundary scattering time lies between the two. This hierarchy of time scales allows phonons to exchange momentum by normal collisions during their trajectory. Gurzhi’s work started phonon hydrodynamics, as reviewed in a 1974 paper by Beck and colleagues3 and revived by Cepellotti and colleagues, who predicted that phonon hydrodynamics is possible in graphene even at room temperature.4
There are two signatures of phonon hydrodynamics per Behnia: Poiseuille flow, which is when a macroscopic flow of heat has a distribution determined by the sample boundaries akin to the laminar flow of liquid in a pipe, and second sound, which is the wavelike propagation of a heat pulse. Both Poiseuille flow and second sound are corrections to diffusive flow in a limited temperature window. It is not possible to cancel the diffusive flow because resistive scattering never vanishes. It is also important to note that individual phonons traveling ballistically are not hydrodynamic.
Behnia noted that, theoretically, the Poiseuille flow of phonons corresponds to a thermal conductivity that evolves as fast as T8. While such a phenomenon has not been observed by experiment, thermal conductivity evolving faster than specific heat as a function of temperature has been observed in several solids (e.g., in crystals of 3He and 4He, bismuth, and very recently strontium titanate5 and black phosphorus6) and has been interpreted as a signature of the Poiseuille flow. The work on strontium titanate is especially interesting because it shows all of the transport regimes clearly, in Behnia’s opinion.
___________________
3 H. Beck, P.F. Meier, and A. Thellung, 1974, Phonon hydrodynamics in solids, physica status solidi (a) (24:11), https://doi.org/10.1002/pssa.2210240102.
4 A. Cepellotti, G. Fugallo, L. Paulotta, M. Lazzeri, F. Mauri, and N. Mazari, 2015, Phonon hydrodynamics in two-dimensional materials, Nature Communications (6) 6400, https://doi.org/10.1038/ncomms7400.
5 V. Martelli, J.L. Jiménez, M. Continentino, E. Baggio-Saitovitch, and K. Behnia, 2018, Thermal transport and phonon hydrodynamics in strontium titanate, Physical Review Letters (120) 125901, https://link.aps.org/doi/10.1103/PhysRevLett.120.125901.
6 Y. Machida, A. Subedi, K. Akiba, A. Miyake, M. Tokunaga, M. Tokunaga, Y. Akahama, K. Izawa, and K. Behnia, 2018, Observations of Poiseuille flow of phonons in black phosphorus, Science Advances (4:6), https://doi.org/10.1126/sciadv.aat3374.
The theoretical superlinear size dependence of thermal conductivity mentioned in the previous paragraph is a consequence of the parabolic profile of fluid velocity inside a pipe. Phonon viscosity, on the other hand, is not homogeneous. A non-Newtonian fluid will instead give a flat profile with a different flow, which Behnia believes could account for the small corrections in the hydrodynamic regimes.
The second signature of phonon hydrodynamics is second sound, a wavelike propagation of temperature. It was first observed in 1944 by Peshkov in superfluid helium.7 In the 1950s, it was discovered that the same hierarchy of scattering rates that leads to the Poiseuille flow of phonons should give rise to second sound in insulating solids.8 Second sound has been observed in multiple systems since then, including recently in graphite at much higher temperatures than seen in other systems.9
Behnia stressed that the hydrodynamic regime is fragile. It is not a zero-temperature phenomenon. Since the rate of resistive and normal scattering can never differ by orders of magnitude, it only occurs in a limited temperature window and is a small correction to the diffusive flow. However, it provides a potentially groundbreaking opportunity to get to quantum turbulence through enhancing the Reynolds number, he said.
Electron Hydrodynamics
Electron hydrodynamics is harder to observe because the samples have to be extremely pure to meet the ballistic regime.
An examination of thermal transport data allows a fresh look at the study of electron hydrodynamics. In particular, the finite-temperature deviation from the Wiedemann-Franz law is traditionally associated with the way in which elastic scattering affects thermal and electrical transport. However, it can be used to distinguish between momentum-scattering and momentum-relaxing collisions between electrons, which both vary as the square of temperature, albeit with different prefactors.
___________________
7 V. Peshkov, 1944, Second sound in helium II, Journal of Physics (8) 381-389.
8 R.A. Guyer and J.A. Krumhansl, 1966, Solution of the linearized phonon Boltzmann equation, Physical Review (148) 766, https://link.aps.org/doi/10.1103/PhysRev.148.766.
9 S. Huberman, R.A. Duncan, K. Chen, B. Song, V. Chiloyan, Z. Ding, A.A. Maznev, G. Chen, and K.A. Nelson, 2019, Observation of second sound in graphite at temperatures about 100K, Science (364:6438) 375-379, https://doi.org/10.1126/science.aav3548.
A Possible Bound to Thermal Diffusivity
Behnia recounted that it has been observed that metals whose resistivity increases linearly with temperature have similar scattering rates. This led to the suggestion that there is a previously unknown bound to the diffusivity of quasiparticles in metals.10 Charge diffusivity corresponds to resistivity, while thermal diffusivity corresponds to thermal conductivity. It is not a priori given that both diffusivities (charge and thermal) will be subjected to the bound. Behnia said that examining available data suggests that such a bound holds also for phonons in insulators, if one replaces Fermi velocity with sound velocity.
Behnia concluded by summarizing the main points of his talk: In some solids, within a specific temperature range below the peak in conductivity, phonon flow is strengthened by collisions. This range is the Gurzhi hydrodynamic regime. Some collisions occur close to a structural instability, and such a proximity may enhance normal scattering. Electron-hole compensation can boost this. Last, he proposed that available data suggest there exists a universal lower bound to thermal diffusivity.
Q&A
A participant asked if there was a material that could have only hydrodynamic phonon transport. Behnia answered that he could not envision such a material, because the ballistic regime is unavoidable owing to the impossibility of a particle traveling from one side of the sample to the other without colliding with other particles. When asked if electron entanglement was a possibility, Behnia replied that there is a debate about viscosity of electrons and entanglement, especially in a Fermi gas.
Another participant asked what the two fluids in phonon second sounds are. Behnia replied that the phonon gas has two components. Phonons that suffer normal collisions do not lose momentum, while those suffering resistive collisions lose momentum. These two components can be considered the counterparts of the two fluids of the superfluid.
In response to a question about the thermal diffusivity of glasses, Behnia noted that thermal diffusivity decreases with warming in a glass.
___________________
10 S.A. Hartnoll, 2015, Theory of universal incoherent metallic transport, Nature Physics (11) 54-61.
THERMAL TRANSPORT BEYOND THE QUASIPARTICLE PARADIGM
Sean Hartnoll, Stanford University
Hartnoll introduced quasiparticles, challenged the current thinking on their existence, and discussed bounds on diffusivity and a concrete model for non-quasiparticle diffusion.
Quasiparticles
Fourier noted long ago that heat is as fundamental to life as gravity, and heat is everywhere. Diffusion theory describes thermal transport, but does not give the expression for actual diffusivity. To learn that, Hartnoll explained that physicists developed a microscopic theory for thermal and electrical conduction of quasiparticles. If those quasiparticles carry charge and heat, then it should also be possible to calculate the Lorentz ratio, L, the ratio of thermal conductivity to electron conductivity.
Many studies have shown that the survival of quasiparticles at low energies and long wavelengths is nontrivial, and does not always happen. Hartnoll noted that non-quasiparticle physics can lead to concepts that would be impossible in the context of quasiparticles, such as those particles with very high figures of merit ZT = S2/L, where L is low and S, the Seebeck coefficient, is high.
Hartnoll pointed to several studies supporting this idea. As early as 1994, Allen et al. showed an absence of quasiparticles if the mean free path is shorter than the particle wavelength or less than the lattice spacing.11 More recent work found T-linear regimes with mean free paths again shorter than lattice spacing (Figure 2.1)12 and that, when the mean free path is too short, thermal diffusivity is reminiscent of electrical diffusivity in “bad” metals, which also have short mean free paths.13 Finally, it has been shown that it is possible to violate the Wiedemann-Franz (WF) law, because if WF was true, the electronic contribution would be larger than the total thermal conductivity, which is impossible.14
Physics without quasiparticles brings many new questions, according to Hartnell, such as: How can we determine diffusivity in the absence of quasiparticles?
___________________
11 P.B. Allen, X. Du, L. Mihaly, and L. Forro, 1994, Thermal conductivity of insulating Bi2Sr2YCu2O8 and superconducting Bi2Sr2CaCu2O8: Failure of the phonon-gas picture, Physical Review B (49) 9073, https://link.aps.org/doi/10.1103/PhysRevB.49.9073.
12 J. Zhang, E.M. Levenson-Falk, B.J. Ramshaw, D.A. Bonn, R. Liang, W.N. Hardy, S.A. Hartnoll, and A. Kapitulnik, 2017, Anomalous thermal diffusivity in underdoped YBa2Cu3O6+x, PNAS (114:21) 5378-5383, https://doi.org/10.1073/pnas.1703416114.
13 J. Zhang, E.D. Kountz, E.M. Levenson-Falk, D. Song, R.L. Greene, and A. Kapitulnik, 2018, Thermal diffusivity above Mott-Ioffe-Regel limit, eprint at arXiv, https://arxiv.org/abs/1808.07564.
14 S. Lee, K. Hippalgaonkar, F. Yang, J. Hong, C. Ko, J. Sun, K. Liu, et al., 2017, Anomalously low electronic thermal conductivity in metallic vanadium dioxide, Science (355:6323) 371-374, https://doi.org/10.1126/science.aag0410.
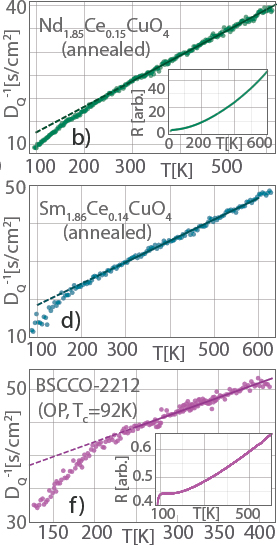
What concepts can replace the quasiparticle velocity, lifetime, and mean free path? Can we look beyond single particle excitations? Hartnoll presented two possibilities to reorient the current thinking: the idea of bounds on diffusivity and a concrete model for non-quasiparticle diffusion.
Bounds on Diffusivity
Diffusivity has bounds, Hartnoll argued, similar to how heat engines are bound by the theories of thermodynamics. The bounds may not explain how a given material works—they do not provide a working model—but they provide constraining parameters. In the same way that heat engines are constrained by efficiency, the key constraints for diffusivity are conservation laws and locality, he said. Hartnoll’s published bound is that diffusion is constrained by microscopic velocity and thermalization time and does not depend on quasiparticles (Figure 2.2).15
___________________
15 P.T. Brown, D. Mitra, E. Guardavo-Sanchez, R. Nourafkan, A. Reymbaut, C.D. Hébert, S. Bergeron, 2018, Bad metallic transport in a cold atom Fermi-Hubbard system, eprint at arXiv, https://arxiv.org/abs/1802.09456.
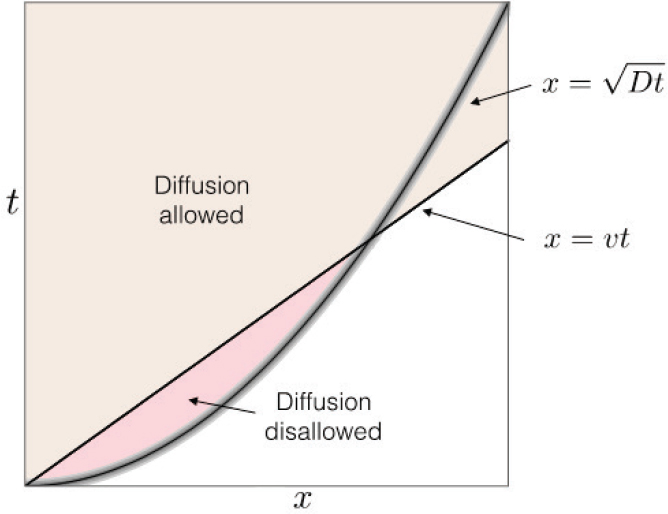
Diffusivity is the process of perturbations dispersing in a medium. Some perturbations decay quickly, while others live much longer. However, the total energy in the system is conserved. Low-energy, very-long-wavelength perturbations also occur, and they decay slowest. In diffusion, these long-amplitude and long-wavelength perturbations limit transport, according to Hartnoll. Correlation functions of conserved densities about thermal equilibrium are strongly constrained.
According to Fourier’s law, temperature diffuses. Temperature must be defined by a local thermal equilibrium, which takes time to establish itself; this local thermalization time is the time scale over which everything (except the perturbations) has decayed. Once at the locally defined temperature, diffusion happens, but its value is determined by the “fast” dynamics of the Lieb-Robinson (LR) velocity, which describes how quickly signals can transmit in a quantum mechanical system. Hartnoll explained that LR velocity connects the concepts of locality and quantum mechanics and can constrain diffusion, because a local temperature has to be established before diffusion can start, so diffusion cannot happen too quickly. In fact, diffusivity has to be less than thermalization time times the LR velocity squared.
A Model for Non-Quasiparticle Diffusion
Hartnoll offered a solvable, realistic model of non-Boltzmann transport for non-quasiparticle diffusion. It is possible to find non-Boltzmann transport at very high temperatures in the Hubbard model. The Boltzmann regime is valid in a Hubbard model, but it is possible to undo Hubbard’s approximation and allow exponential interactions between sites, instead of onsite. The mathematics of this process is different, but it is possible to use “small t” perturbation theory and create inhomogeneous distributions of charge. This results in hopping in an emergent disordered landscape, allowing the energy change between neighboring parts to take a continuum of values.16
Hartnoll explained that this process creates a way to calculate diffusivity as a function of temperature as well as the Lorentz ratio, whose value is extremely small, because at high temperatures, heat current and electrical current are proportional to each other.
Future Challenges
Several challenges emerge when moving beyond quasiparticles, although Hartnoll expressed confidence they will be overcome. First, phonons are absent from his model for non-quasiparticle diffusion, but they are important for two reasons. One, LR velocity is not fully defined for every situation. It may be possible to use butterfly velocity instead, which is connected to quantum chaos. Two, high temperatures are more complicated for the model with phonons included. Second, the bound arising from Hartnoll’s model does not reveal what the thermalization time actually is, and it will be necessary to determine when this time scale will be relevant.
The cancellation leading to the WF violation occurs when the electrical and heat currents become proportional. It can also happen in a naturally deep hydrodynamic regime, where both the electrical and heat currents are proportional not to each other, but to a collective velocity field, which Hartnoll and his team recently demonstrated and which could also violate the Lorentz ratio.17 It is also important to note that these diffusions are represented by a classical process and nonlinear equations, even though they emerge from a quantum system, and there can be normal, very small fluctuation effects, which could be controlled by thermal diffusion.18
___________________
16 C.H. Mousatov, I. Esterlis, and S.A. Hartnoll, Bad metallic transport in a modified Hubbard model, eprint at arXiv, https://arxiv.org/abs/1803.08054.
17 R. Mahajan, M. Barkeshli, and S.A. Hartnoll, 2013, Non-Fermi liquids and the Wiedemann-Franz law, Physical Review B (88) 125107, https://link.aps.org/doi/10.1103/PhysRevB.88.125107.
18 X. Chen-Lin, L.V. Delacretaz, and S.A. Hartnoll, 2019, Theory of diffusive fluctuations, Physical Review Letters (122) 091602, https://link.aps.org/doi/10.1103/PhysRevLett.122.091602.
Wrapping up, Hartnoll emphasized that quantum materials without quasiparticles are a logical possibility, and he suggested they must be pursued to advance quantum technology. Another logical possibility is exotic materials with extremely low Lorentz ratios, he noted. Diffusion could have bounds related to the LR velocity and thermalization times. High-temperature expansions will give a clear model for non-Boltzmann transport, and going forward, all of these ideas must be extended to include phonons, he said.
Q&A
In response to a question, Hartnoll replied that it is possible to tailor the lattice distance to lower the mean free path, and added that this brings up the question of how to build non-quasiparticle systems. The most promising current idea is a phonon band structure, he said. Ideally, scientists should find an absence of quasiparticles in a material deep into the hydrodynamic regime, but it is still not known how to do that. Hartnoll expressed uncertainty about whether accomplishing that could enable room-temperature superconductors, but he pointed out that, for unknown reasons, high-temperature superconductors have a very short mean free path.
Hartnoll also clarified that the Lorentz ratio is the same throughout this process, and ideally the thermal conductivity value, Kappa, should be the same for both electrons and phonons, which could be the case very deep in the hydrodynamic regime. Behnia agreed with this assessment, although Hartnoll added that this is only one avenue to explore, and not necessarily the best one. Other materials or models could work, and results seen at high temperatures could potentially extend to lower temperatures.
Behnia asked for clarity about upper and lower bounds, and Hartnoll replied that his unproven, though strong, conjecture is that the lower bound to diffusivity is inspired by lower bounds of viscosity. Because the upper bound is qualitatively different, there is less evidence for it. He added that understanding the thermoelectric figure of merit, ZT, enables new lines of inquiry; other participants noted that the maximum record for ZT in the literature is 2.8.
Hartnoll concluded by noting that heat was not being treated as a wave but as a collective, whether it is a field or excitation, because these are not single electrons or single phonons.
THERMAL HALL EFFECT FROM NEUTRAL SPIN EXCITATIONS IN FRUSTRATED QUANTUM MAGNETS
N. Phuan Ong, Princeton University
Ong discussed applying the thermal Hall effect as a potentially important transport probe to investigate the state of matter called quantum spin liquids (QSLs).
In particular, he discussed the notion of topological order, different QSLs, and the properties of the pyrochlores Tb2Ti2O7 and Yb2Ti2O7 and a new cobalt-based candidate QSL, Na2BaCo(PO4)2.
Topological Order
Topological order is a fundamental property of new phases of quantum matter that lie outside the purview of the Landau paradigm. Unlike well-studied many-body states such as superconductivity and ferromagnetism, the spin liquid state does not have an obvious order parameter. Instead, it features a highly entangled ground state that cannot be described by a product-state (Hartree Fock) wave function, Ong said. The ground state is predicted to display novel topological excitations that are strongly nonlocal. For example, although the spins lack long-range order, changing one spin affects millions of spins. These theoretical ideas have been around for some time, but have not been experimentally verified, Ong noted. The entangled ground state is promising for applications in topological quantum computing.
Ong described several examples of topological excitations. A Haldane-gap material, for example, is composed of an array of spin S = 1 chains. At low temperatures, an energy gap appears in the spin excitation spectrum, despite the absence of an order parameter. The fractional quantum Hall effect is a highly entangled, many-body ground state. Two important models for gapped QSLs are the Toric code model and the Kitaev hexagonal spin-exchange model.19,20 Kitaev’s 2003 and 2006 papers, which inform much of this work, introduced many of the concepts (Majorana particles, visons, spinons, fusion rules, braiding rules) widely used in topological quantum computing today, Ong noted.21
Ong said research on topological order has sparked renewed interest in Anderson’s 1971 theory in which resonating valence bonds (RVB) are central to the spin-liquid state.22 Anderson also proposed in 1987 that the RVB state is the underlying mechanism for high-temperature superconductivity in the cuprates.23
___________________
19 L. Savary and L. Balents, 2017, Quantum spin liquids: A review, Reports on Progress in Physics (80) 016502, https://doi.org/10.1088/0034-4885/80/1/016502.
20 Y. Zhou, K. Kanoda, and T.-K. Ng, 2017, Quantum spin liquid states, Reviews of Modern Physics (89) 025003, https://link.aps.org/doi/10.1103/RevModPhys.89.025003.
21 A.Yu. Kitaev, 2003, Fault-tolerant quantum computation by anyons, Annals of Physics (303:1) 2-30, https://doi.org/10.1016/S0003-4916(02)00018-0.
22 P.W. Anderson, 1973, Resonating valence bonds: A new kind of insulator? Materials Research Bulletin (8:2) 153-160, https://doi.org/10.1016/0025-5408(73)90167-0.
23 P.W. Anderson, 1987, The resonating valence bond state in La2CuO4 and superconductivity, Science (235:4793) 1196-1198, https://doi.org/10.1126/science.235.4793.1196.
Roughly, he regards the RVB state as a superposition of many configurations in which every spin forms a singlet pair with a neighbor.24
Quantum Spin Liquids
The majority of magnetic materials undergo a phase transition to an ordered state (ferromagnetic, antiferromagnetic, or spiral) at a (Curie) temperature reliably estimated from the spin exchange energy derived from the high-temperature susceptibility. Ong explained that in an interesting subgroup, however, spins fail to order even when cooled well below the estimated Curie temperature because of a phenomenon called geometric frustration. At very low temperatures, the spins stubbornly resist ordering, but the wave function of the sample is strongly entangled. This is called the quantum spin liquid (QSL).
There are several classes of QSLs, including topological spin liquids, gapped liquids, and gapless liquids obtained by projection of the Fermi liquid wave function (gapless liquids specifically feature a spinon Fermi surface). To date, the QSL state has been investigated mostly by spectroscopic techniques (e.g., neutron scattering) and thermodynamic experiments (magnetization and heat capacity), according to Ong. These techniques measure the spectra at equilibrium. In order to probe excitations, one must apply a weak driving “field” to drive the system slightly off equilibrium, and measure the “current” carried by the excitations in a transport experiment. To this end, thermal Hall conductivity has emerged as a very promising transport probe. The QSL materials are electrically insulating, so to study the spin excitation currents, it is necessary to measure the heat currents (as opposed to charge currents). The difficulty therein is that the observed thermal conductivity is overwhelmingly dominated by the uninteresting phonon current (the heat current conveyed by lattice vibrations).
To overcome this obstacle, Ong’s lab and others have used the thermal Hall effect to isolate the spin excitations. An applied magnetic field (not too strong) “deflects” the spin current sideways to produce the Hall signal. The phonon current that is unaffected by the field does not contribute to the Hall signal. Now, semi-classically, the ordinary spin excitations in a ferromagnet (called spin waves or magnons) are not deflected sideways by a magnetic field (being charge neutral, they do not sense the Lorentz force). In a growing group of frustrated quantum magnets, there exists a large thermal Hall effect that must arise from spin excitations in the candidate QSL state. In a QSL, the origin of the transverse heat current is not the Lorentz force but a topological field called the Berry curvature, which acts on mobile excitations like an effective magnetic field, even when they are charge
___________________
24 L. Savary and L. Balents, 2017, Quantum spin liquids: A review, Reports on Progress in Physics (80) 016502, https://doi.org/10.1088/0034-4885/80/1/016502.
neutral. Another recent development that Ong considers exciting is the report of a quantized thermal Hall conductivity in a material α-RuCl3 previously identified as a candidate Kitaev spin exchange system.25
Ong suggested that a promising hunting ground for QSLs is the region of the phase diagram in which an external magnetic field is just sufficient to suppress long-range order in antiferromagnets based on a triangular or Kagome lattice. Several promising QSLs have been discovered over the past 10 years. The most well known is Herbertsmithite (ZnCu3(OH)6Cl2), which has a Kagome lattice. However, crystals of this material tend to have significant lattice disorder caused by the exchange of copper and zinc atoms.
Pyrochlores: Tb2Ti2O7 and Yb2Ti2O7
Ong described several pyrochlores, which are composed of two interpenetrating networks of vertex-shared tetrahedra (all pyrochlores have the stoichiometry 2-2-7). Viewed along the body diagonal of the unit cell (111), the lattice has the Kagome structure. At very low temperatures, some pyrochlores exhibit spin-ice behavior, with a highly degenerate ground state that displays extensive spin entropy (analogous to water ice). Other pyrochlores are QSL candidates at low temperatures. An advantage of pyrochlores is that very pure crystals can be grown. This enables the important quantum effects inherent to geometric frustration to be distinguished from classical lattice disorder effects.
The first QSL pyrochlore to exhibit a thermal Hall effect was Tb2Ti2O7. Measurements by Hirschberger et al. uncovered a large thermal Hall conductivity which increased monotonically with decreasing temperature (Figure 2.3).26 This thermal Hall signal—presumably arising from the intrinsic Berry curvature in the QSL state—is suppressed in a strong magnetic field that destroys the QSL state altogether by aligning the spins. This early result, in combination with recent results, suggests an overall picture for the excitations in a class of gapped QSLs, Ong noted.
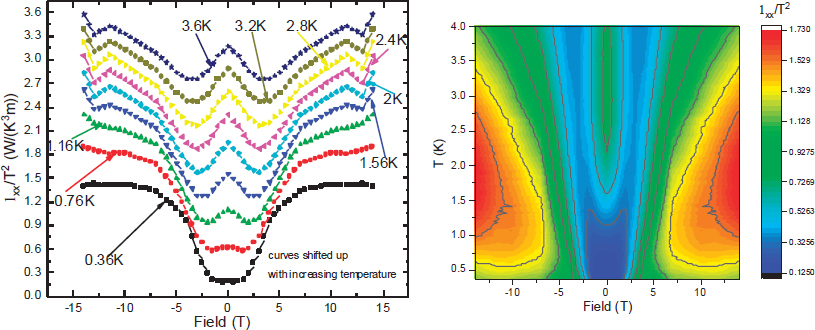
Experiments on a second pyrochlore, Yb2Ti2O7, reveals an even larger thermal Hall effect. At very low temperatures (0.4 K), ordering occurs, but a weak magnetic field kills the antiferromagnetic state to realize a strongly frustrated QSL state at low temperatures. Using crystals of exceptional quality, Scheie et al. found a very
___________________
25 Y. Kasahara, K. Sugii, T. Ohnishi, M. Shimozawa, M. Yamashita, N. Kurita, H. Tanaka, et al., 2018, Unusual thermal Hall effect in a Kitaev spin liquid candidate α−RuCl3, Physical Review Letters (120) 217205, https://link.aps.org/doi/10.1103/PhysRevLett.120.217205.
26 M. Hirschberger, J.W. Krizen, R.J. Kava, and N.P. Ong, 2015, Large thermal Hall conductivity of neutral spin excitations in a frustrated quantum magnet, Science (348:6230) 106-109, https://doi.org/10.1126/science.1257340.
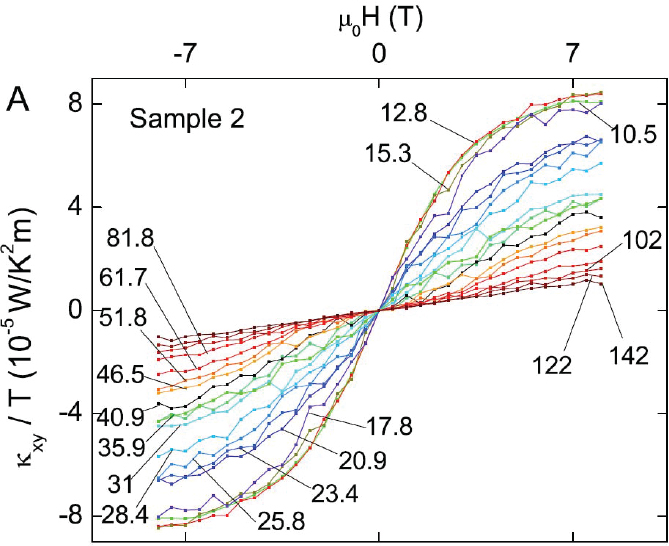
large Hall signal.27 Again, the QSL state is destroyed if the field is too strong. An interesting new feature is that the thermal Hall effect changes sign with field (Figure 2.4). The reason for the sign change is still being researched. Future studies are planned for temperatures below 100 millikelvin.
A New Candidate QSL: Na2BaCo(PO4)2
Na2BaCo(PO4)2 is a cobalt-based triangular lattice frustrated magnet. It is a layered material with spin-1/2 cobalt ions occupying the sites of a triangular lattice. The spin exchange is highly anisotropic, with strong in-plane exchange and weak interlayer exchange. The material resists ordering even at very low temperatures, displaying very large magnetocaloric effects related to weak coupling between the spin excitations and the phonons.
___________________
27 A. Scheie, J. Kindervater, S. Säubert, C. Duvinage, C. Pfleiderer, H.J. Changlani, and S. Zhang, 2017, Reentrant phase diagram of Yb2Ti2O7 in a <111> magnetic field, Physical Review Letters (119) 127201, https://link.aps.org/doi/10.1103/PhysRevLett.119.127201.
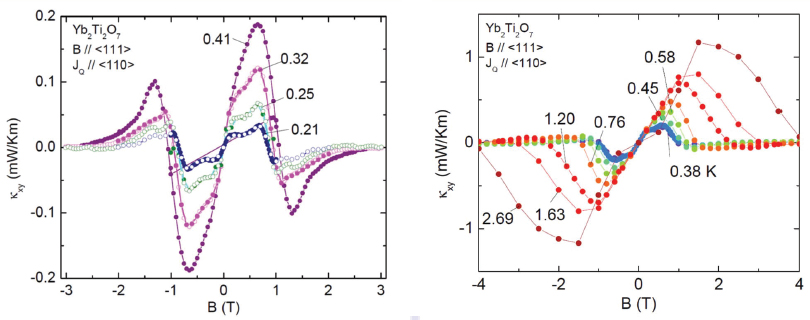
This new QSL candidate is even more promising than the pyrochlores discussed above, Ong said, but as with the earlier pyrochlores, a strong magnetic field kills the QSL state of interest. Deep in the QSL state, the heat current carried by the spin excitations approaches a very small value as the temperature is decreased to 0.3 Kelvin in a weak magnetic field. However, if the field is raised above 3 Teslas, the QSL state is destroyed and the spin thermal conductivity steeply rises to a large value compatible with ordinary spin waves (magnons).
Ong explained further that at fields below 3 Teslas and low temperatures, the system is highly frustrated but reveals unusual excitations.28 The most interesting feature is the appearance of a sizable thermal Hall effect in the weak-field region. The Hall signal grows linearly with magnetic field until the QSL state is destroyed, whereupon the thermal Hall effect disappears (Figure 2.5).29
In summary, Ong reiterated that experiments among different QSLs are slowly paving the way for the thermal Hall effect to be an effective transport probe. Although there remain many unresolved issues, the emerging pattern is that as the temperature is lowered to the QSL state, spin excitations become strongly localized (i.e., there is poor heat conductance by the spin excitations). However, a large Hall signal appears that possibly originates from chiral edge conduction. The spins also have massive entropy, yet become increasingly decoupled from the phonon bath. In all cases, a large magnetic field kills the QSL state as well as the Hall signal, to leave ordinary spin waves.
___________________
28 R. Zhong, S. Guo, G. Xu, Z. Xu, and R.J. Cava, 2019, Strong quantum fluctuations in a quantum spin liquid candidate with a Co-based triangular lattice, PNAS 116, 14505-14510, doi/10.1073/pnas.1906483116.
29 T. Gao et al., 2019, in preparation.
Q&A
Asked why the conductivity was so low when the symmetry is deliberately broken, Ong replied that although there are several theories, researchers do not fully understand heat current behavior. So far, Ong believes that the most promising theory, based on topological notions, is that the heat current carried by spin excitations is confined to the edges of the crystal, which define a closed loop. In an applied temperature gradient, the heat current carried by the transverse edge at the warm end is larger than its opposite counterpart at the cool end. The difference of the transverse currents immediately yields a thermal Hall effect.
Another participant asked how defects could affect this work, and if lanthanides were a potentially promising material. Ong answered that the most important property is whether a material can demonstrate geometric frustration.
Asked if there was a relationship between the thermal Hall angle and sample quality, Ong further elaborated on the problem of analyzing the heat transport experiments on QSL materials. Experiments measuring the spin thermal Hall conductance are at an early stage, and much remains to be understood. As for the mechanism, Ong’s best guess is that the chiral edge effect in combination with the Berry curvature seems especially promising. The heat transport by spin excitations in QSL is an inherently quantum mechanical effect. Nevertheless, some intuition may be gained from a Boltzmann equation approach if one amends the standard semiclassical equations of motion to include Luttinger’s “anomalous velocity” term (which invokes Berry curvature). This approach suggests that pristine sample quality (hence long mean free path) improves the ability to detect the thermal Hall signal. However, intuitions derived from the Boltzmann equation approach have intrinsic limitations.
QUANTIZATION OF THE THERMAL HALL CONDUCTIVITY AT SMALL HALL ANGLES
Lucile Savary, École Normale Supérieure (ENS)
Savary discussed experiments in thermal Hall conductivity that have led to new understandings of Hall plateaus, the discovery of potential new states of matter, realization of the Kitaev model, and opportunities to go beyond Kitaev. Experiments with thermal transport are bringing researchers closer to probing new states of matter, but there are still many unanswered questions.
Transport Experiments
Transverse transport, a transverse response to a longitudinal perturbation, can be used to demonstrate that new phases of matter exist. In thermal transport, Hall conductivity and its anti-symmetrized version of the off-diagonal conductivity can uncover properties of these new phases, according to Savary.
Experiments in this realm either apply a thermal gradient to a sample or thread an electrical current through a system to achieve a solution to Fourier’s law, which relates the energy current to the temperature gradient through the thermal conductivity tensor. In these experiments, the magnetic field is also perpendicular to the plane of the sample, and through the Lorentz force that field can bend the orbit of electrons, inducing a perpendicular electrical field that is used to measure Hall conductivity.30
Hall Plateaus
Applying larger magnetic fields results in striking Hall conductivity plateaus, Savary said, and a dissipation-free system where the longitudinal resistivity is zero, despite the electrical field being applied. Therefore, in this case, the Hall angle is 90 degrees. These plateaus are important because the result is quantized and doesn’t depend on experimental details such as sample size, shape, disordering, or ordering. That independence signifies that something fundamental is happening, Savary posited, although what that is is still unknown.
This particular Hall effect appears only in systems with some disorder, because the Hall conductivity is proportional to the Chern number of the filled bands, which is a topological (or nonlocal) property independent of system details. The
___________________
30 M. Ye, G.B. Halász, L. Savary, and L. Balents, 2018, Quantization of the thermal Hall conductivity at small Hall angles, Physical Review Letters (121) 147201, https://link.aps.org/doi/10.1103/PhysRevLett.121.147201.
fact that it is nonlocal and can be probed with thermal transport is crucial, Savary said. Hall conductivity is proportional to a topological property, and that is consistent with its isentropicness. It is also completely unrelated to any loss of entropy, which is consistent with the fact that Hall conductivity can be quantized, she added.
Discovering New States
Researchers are now working to discover whether this knowledge can be used to unambiguously find new magnetic phases with nonlocal properties. New phase discoveries are important to the study of new quantum materials, because in the most highly entangled, nonlocal, nonclassical phases, nonlocal excitations appear that cannot be probed easily. In fact, they can appear only because of the high degree of entanglement.
In a resonating valence bond state, for example, many singlets cover a lattice in a superposition, and some fractional particles can emerge, which are called spinons. They cannot be created locally, and because all probes typically are local, it is very hard to find this phase, despite many years of experimental and theoretical work in quantum magnetism.
While there are system-dependent ways to probe a QSL once it is found, there is no generic, unambiguous way to accomplish this, Savary said. There are measures of entanglement, such as entanglement entropy, but they are not accessible to these experiments. To determine if a QSL is in a highly entangled state, a case-by-case basis must be used because different spin liquids require different techniques, although some chiral spin liquids are easy to find because they have edge modes that give rise to thermal Hall conductance. Non-Abelian states, on the other hand, can be quantized at half-integers, which enables some information collection.
Both QSLs and non-Abelian states are very difficult to find, according to Savary. There are only a few potential platforms where they exist, and even fewer candidate materials in which they can be found. One platform is spin liquids in a magnetic field, and there may also be some fractional quantum Hall states that are non-Abelian. This is cutting-edge work, and finding a QSL or non-Abelian state would represent a great advance, Savary noted.
The Kitaev Model and Beyond
In 2003, Kitaev proposed a rich isotropic model for realizing various types of QSLs on a honeycomb lattice with the exact solution in terms of Majorana fermions.31 As a function of the different coupling constants, there were three dif-
___________________
31 A.Yu. Kitaev, 2003, Fault-tolerant quantum computation by anyons, Annals of Physics (303:1) 2-30, https://doi.org/10.1016/S0003-4916(02)00018-0.
ferent phases: gapless QSL, gapped QSL, and, most interestingly in Savary’s view, gapless bulk Majoranas that acquire a gap from a time-reversal braking perturbation from which half-quantized thermal conductivity arises. After an enormous amount of experimental and theoretical work, the Kitaev model was realized in actual materials.32
The model was created with other materials, but research is now under way with ruthenium trichloride (RuCl3), which has much lower energy scales that make it easier to study, Savary said. However, RuCl3 has magnetic order in the zero field, and to get to the QSL phase, there must be none. It may be possible to achieve an intermediate QSL phase before a paramagnetic phase, but the two phases are very hard to distinguish.
Kasahara et al. were able to measure thermal Hall conductivity in RuCl3 because they applied the magnetic field at a slight angle, and they observed a plateau with the half-quantized value, even at fairly high temperatures.33 Savary emphasized that these results are highly significant because, if confirmed, it will be the first unambiguous discovery of a QSL with non-Abelian anyons in the electrical insulating phase, and one with Majoranas at nearly 5 K, a much higher temperature than any system so far.
Unfortunately, she noted, there are some problems with the results. The longitudinal conductivity was much higher than Hall conductivity, which means the gradient was not at a constant temperature, which is important yet impossible when such a large gradient in one direction is needed. Also, the results suggest that there is no coupling, yet the leads are in fact coupled.
Savary and her team conducted a further experiment, with several different linearized equations and boundary conditions, and reached several conclusions.34 First, the Majorana phonon coupling induces a transverse phonon current which is transferred to the Majoranas. Also, owing to the phase-based constraints, phonon-Majorana coupling, crucial to the quantized Hall effect, becomes less than T-6, and the measured thermal Hall conductivity vanished at zero temperature, which was unexpected. At a lower temperature, therefore, the result is unmeasurable, she said, and without enough spin-phonon coupling, there will be no quantized Hall effect. Not only does spin-phonon coupling preserve the thermal Hall effect, it in fact allows it to exist.
___________________
32 G. Jackeli and G. Khaliullin, 2009, Mott insulators in the strong-spin orbit coupling limit: from Heisenberg to a quantum compass and Kitaev models, Physical Review Letters (102) 017205, https://link.aps.org/doi/10.1103/PhysRevLett.102.017205.
33 Y. Kasahara, T. Ohnishi, Y. Mizukami, O. Tanaka, S. Ma, K. Sugii, N. Kurita, 2018, Majorana quantization and half-integer thermal Hall effect in a Kitaev spin liquid, Nature (559) 227-231, https://doi.org/10.1038/s41586-018-0274-0.
34 Y. Vinkler-Aviv and A. Rosch, 2018, Approximately quantized thermal Hall effect of chiral liquids coupled to phonons, Physical Review X (8) 031032, https://link.aps.org/doi/10.1103/PhysRevX.8.031032.
Q&A
Asked about making new 3D materials that work in the plane, instead of perpendicular to it, Savary answered that working with these materials is more akin to 2D physics, for example with RuCl3, which has many isolated layers, but phonon conductivity could occur along the Z direction. Another participant observed that theoretical translations of experiments can sometimes help. Savary agreed, and she explained that her results are similar to the current being threaded in the X direction, noting that it does not change the results. The participant then asked why left-right phonon imbalance has zero thermal Hall effect, instead of just a very small one. Savary replied that it is because it is only an approximation. The real number is 10-3 lower, and the real reason for the transverse Hall conductivity is the temperature imbalance that is caused by the coupling to the phonons, she clarified.
Another participant asked if the Hall effect had a signature in the thermal magnetoresistance. Savary expressed uncertainty, but speculated that it would be a change of very small magnitude, and the direction and sign of this change are not immediately evident.
THERMAL SPIN TRANSPORT: SPIN-SEEBECK AND MAGNON DRAG EFFECTS
Joseph P. Heremans, The Ohio State University
To frame his talk, Heremans noted that about 95 percent of the world’s energy comes from thermal processes, so even a slight improvement in the energy efficiency of transforming heat to work has an enormous engineering impact. Thus, improving energy efficiency is a prime motivation for research on heat engines (devices that convert heat energy to work). Heremans noted that whereas heat is the random motion of particles, quasiparticles, or other entities, work is directed motion. Every heat engine converts random motion into unidirectional motion, essentially functioning as rectifiers.
Heremans’s talk explored opportunities for improving thermoelectric heat engines, spin-based energy conversion, and magnon-drag thermopower.
Solid-State Energy Conversion Technologies
Solid-state technologies for energy conversion surpass classic mechanical engines by having no moving parts and unlimited lifetimes. Heremans described experiments with several such technologies. While magnetocaloric and electrocaloric heat engines offer promise, both require adequate solid-state heat switches,
magnetocaloric technologies require a magnetic field, and electrocaloric technologies have little power.
Thermoelectric heat engines, for their part, offer advantages of high power density and ease of control, but have stalled at a maximum value of about ZT = 2, despite Glenn Slack’s 1995 prediction that the devices would reach a ZT of 4.35 This disparity underscores the need for fundamentally new ideas and approaches in order for thermoelectrics to advance. The ZT of a thermoelectric generator is a measurement of the thermal efficiency of that generator in terms of a fraction of the Carnot efficiency: a thermoelectric with a ZT of 1 can have a thermal efficiency about 13 percent of the Carnot efficiency; a ZT of infinity would characterize a generator that meets the Carnot efficiency.
Heremans discussed three possible routes toward increased ZT, suggested by equations in which the figure of merit appears as a function of the square of the Seebeck coefficient, S, also known as the thermoelectric power or thermopower, and of the conduction electrons’ thermal conductivity (κE) and the lattice thermal conductivity (κL). One expression for ZT, modified according to the Wiedemann-Franz law, can be written as follows:
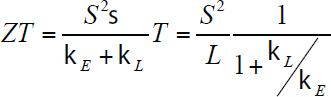
where T is the absolute temperature, σ is the electrical conductivity of the solid, and L is the Lorentz ratio. L is more or less a universal constant for electrons in a solid, unless they undergo collisions that change their energy and entropy.
The first route to improved ZT lies in minimizing κL. Heremans explained that because the amorphous limit on κL essentially has been reached, further minimizing κL looks like an avenue of research that will yield diminishing returns over time.
However, a second route to improved ZT may be offered by reducing the Lorentz ratio, as noted by Sean Hartnoll. But to have hope for progress on this route, it would be necessary to break the quasiparticle picture associated with the Lorentz ratio—that is, that the heat carried by quasiparticles must be related to the charge carried by the same particles.
The third route to higher ZT would be to develop materials with a high Seebeck coefficient (or thermopower) and, simultaneously, a high number of conduction electrons so that κE is large and σ is large. However, Heremans noted that the Mott relation and Fermi-Dirac statistics pose a problem for this approach. The Pauli exclusion principle (and thus Fermi-Dirac statistics) limits the number of degrees
___________________
35 G.A. Slack, 1995, in CRC Handbook of Thermoelectrics (ed. D.M. Rowe), 407, CRC Press.
of freedom of fermions, such as charge carriers, and this limits the amount of entropy they are allowed, which limits their thermopower.
Spin-Based Energy Conversion
To study the spin-Seebeck effect (first reported in 200836), Heremans and colleagues coated a ferromagnet with a layer of platinum and heated it from the bottom. The resulting temperature gradient causes an upward flow of quasiparticles known as magnons, which are spin waves resulting from the continually precessing magnetization of the ferromagnet. Because the magnetization only precesses counterclockwise, it provides the needed rectification: the magnons thereby can induce a spin polarization of the electrons in the platinum.
Heremans explained that as the flowing magnons meet the metal layer, the conservation of angular momentum forces their spins’ angular momentum to transfer to conduction electrons in the metal, giving rise to an inverse spin-Hall voltage that drives an electron current in the platinum, providing thermopower. This setup attains a spin-Seebeck effect of 2 mV/K in InSb, when the InSb electrons are spin polarized by an external magnetic field. Using aluminum instead of Pt as contact to the InSb shrinks the effect by an order of magnitude, because the electrons in aluminum do not give rise to an inverse spin-Hall effect; in that case, the voltage is only due to the thermoelectric voltage in the InSb. These experiments and others have demonstrated the spin-Seebeck effect in other types of materials, including several types of ferromagnets, an antiferromagnet, and a paramagnet, as well as in ferromagnetic and diamagnetic (in the presence of an external field) semiconductors.37
Heremans posited that these studies suggest a new approach to boosting the Seebeck coefficient of metals (Figure 2.6). In the single electron picture, thermopower is the entropy per particle. However, because of limitations on fermions from the Pauli exclusion principle and the Mott relation, thermopower decreases as more and more electrons are involved. Not so for magnons. They are bosons, so an unlimited number of them can occupy the same energy level. Applying a temperature gradient to a magnonic population produces magnonic thermopower, a shift in the magnon chemical potential. The ratio of that chemical potential over the temperature gradient is simply the specific heat per particle, independent of the number of particles involved. So, a large number of magnons will make that chemical potential large, something that cannot be done with electrons, Heremans noted.
___________________
36 K. Uchida, S. Takahashi, K. Harii, J. Ieda, W. Koshibae, K. Ando, S. Maekawa, and E. Saitoh, 2008, Observation of the spin Seebeck effect, Nature (455:7214) 778-781, https://doi.org/10.1038/nature07321.
37 C.M. Jaworski, J. Yang, S. Mack, D.D. Awschalom, J.P. Heremans, and R.C. Myers, 2010, Observation of the spin-Seebeck effect in a ferromagnetic semiconductor, Nature Materials (9:11) 898-903, https://doi.org/10.1038/nmat2860.
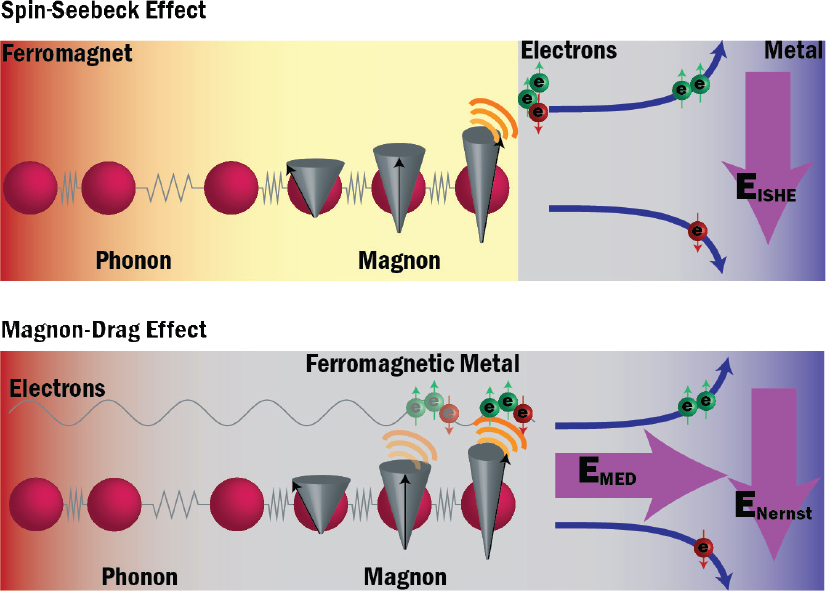
In a magnon-drag experiment, the advective process happens inside a homogeneous material. Here, the conservation of linear momentum impels a moment to the electrons from the magnon flux, which gives rise to a voltage directly, the magnon-drag thermopower. In principle, the conservation of spin angular momentum should give rise to a transverse voltage in ferromagnets with strong spin-orbit coupling as well, but experimental proof for that effect has not yet been found. See S.R. Boona, R.C. Myers, and J.P. Heremans, 2014, Spin calitronics, Energy and Environmental Science (7), 885. SOURCE: Joseph P. Heremans, The Ohio State University, presentation to the workshop on April 11, 2019.
Another experiment on thermally driven spin currents showed that one can separate magnon thermal conductivities by applying magnetic fields at low temperature, according to Heremans. He said this shows another reason why these spin-current and heat-current effects can be large,38 adding that they are also Onsager reversible.39
Magnon Drag Thermopower
Heremans noted that another thermally driven spin effect that can produce work is magnon drag, which physicists identified in the 1960s. In a ferromagnetic metal, when flows of magnons or electrons occur because of temperature differences, these flows can exert drag on each other and cause magnons to transfer to electrons the linear momentum that they have acquired from phonons, creating additional thermopower 10 times larger than the electronic thermopower itself. They also can transfer spin-angular momentum, which, in theory, should boost the anomalous Nernst effect, although that effect has not yet been seen experimentally.
Heremans and colleagues fleshed out a hydrodynamic theory of magnon-drag thermopower indicating that the thermopower is proportional to the magnon specific heat. The theory provides a way of measuring the efficiency of transferring linear momentum from magnons to electrons through collisions. In ferromagnetic metals rich in mobile electrons like elemental iron or cobalt, magnons collide mostly with those charge carriers. While the calculated power factors are high (the power factor is S2σ, and measures the power density of a thermoelectric generator), so is thermal conductivity, and so the ZT is not good. In cobalt, the power factor is about 5 times greater than in classical semiconductors.
Heremans’s group also is investigating manganese telluride, in collaboration with Oak Ridge National Laboratory and the Chinese Academy of Sciences. The material is hexagonal with a nickel arsenide structure. It is an antiferromagnet below room temperature, where it displays a known large magnon-drag thermopower. However, the group found they could get a ZT of 1 or higher in it. Findings of particular interest emerged when the researchers raised the structure’s temperature above its magnetic ordering (Néel) temperature of approximately 307 K. One would expect this transition to disrupt the magnetic order, dropping thermopower to the level at which diffusion alone creates flows, Heremans noted. Instead, the thermopower remained 2 to 10 times higher than expected from diffusion. Based on these results, Heremans proposed that magnon drag persisted in the paramagnetic state.
___________________
38 C.M. Jaworski, R.C. Myers, E. Johnston-Halperin, and J.P. Heremans, 2012, Giant spin Seebeck effect in a non-magnetic material, Nature (487:7406) 210-213, https://doi.org/10.1038/nature11221.
39 J. Flipse, F.K. Dejene, D. Wagenaar, G.E.W. Bauer, J. Ben Youssef, and B.J. Van Wees, 2014, Observation of the spin Peltier effect for magnetic insulators. Physical Review Letters (113:2) 027601, https://dx.doi.org/10.1103/PhysRevLett.113.027601.
Based on data collected by Raphael Hermann of Oak Ridge National Laboratory, Heremans suggested that thermal fluctuations of magnetization in the paramagnetic regime still look to electrons like magnons, so they still drag. This suggests paramagnetic semiconductors are a good platform for thermoelectrics research, Heremans said, adding that while there are no ferromagnetic semiconductors at room temperature, there are many paramagnetic ones. This opens a new direction in the quest for high-ZT thermoelectric materials, which had always avoided paramagnetic semiconductors because of their low mobilities. It is now known that the higher thermopower may more than compensate for that drawback, Heremans said.
Heremans pointed to experiments on the semiconductor indium antimonide to illustrate that thermal measurements can be used to analyze phonon physics. Although phonons are not associated with magnetic effects, researchers found that phonon interactions with the crystal lattice could result in thermal magnetoresistance in the presence of a magnetic field. Phonons perturbed conduction electrons in the semiconductor’s valence bands, causing local variations in the material’s diamagnetic susceptibility, leading to local fluctuation of magnetization and to small magnetic forces on nearby lattice atoms. Because the change in magnetization took place over just a tiny fraction of an Angstrom, the gradient in magnetization, which determines the magnetic force, was large enough to produce a force on the atoms. This, in turn, affects phonon scattering on other phonons and reduces thermal conductivity.40
Wrapping up, Heremans called for more work on topological insulators and hybridized magnon-phonon systems and for advancing technologies such as solid-state refrigeration; waste heat scavenging; and thermal diodes, switches, and regulators. He recommended a 2013 paper by Martin Maldovan, then of MIT and the Georgia Institute of Technology, discussing acoustic and thermal cloaking, hypersonic phononic crystals, and more.41
Circling back to unidirectional heat propagation with which he began his talk, Heremans highlighted a 2014 paper proposing possible phonon modes capable of one-way propagation and cited the edge modes from Lucile Savary’s work as potentially capable of providing such unidirectionality, if they could be isolated.42
___________________
40 H. Jin, O.D. Restrepo, N. Antolin, S.R. Boona, W. Windl, R.C. Myers, and J.P. Heremans, 2015, Phonon-induced diamagnetic force and its effect on the lattice thermal conductivity, Nature Materials (14:6) 601-606, https://doi.org/10.1038/nmat4247.
41 M. Maldovan, 2013, Sound and heat revolutions in phononics, Nature (503:7475) 209-217, https://dx.doi.org/10.1038/nature12608.
42 C.L. Kane and T.C. Lubensky, 2014, Topological boundary modes in isostatic lattices, Nature Physics (10:1), 39-45, https://doi.org/10.1038/nphys2835.
Q&A
Heremans fielded several questions related to the materials his group used in spin-Seebeck experiments. Platinum is a standard, he noted, and his team wanted a solid in which they knew the magnitude of the spin-Hall angle. They used aluminum, which has no spin-Hall effect, to prove that the effect they observed was related to the spin signal coming from InSb.
Another participant asked Heremans why the drag in the paramagnetic regime depends on carrier density whereas the Néel temperature does not. Heremans confirmed that the drag scales with carrier density in the antiferromagnetic regime, but apparently much less so in the paramagnetic regime. He confirmed that the answer to that question is not known today. He then pointed to a different mystery about the drag under those conditions: the lack of temperature dependence. He noted that his group currently has no model for the magnon-drag thermopower in the paramagnetic regime.


























