4
Foundations of Quantum Information Science and Technology
INTRODUCTION
Quantum information science and engineering is a rapidly developing interdisciplinary field of science and technology, drawing from various subfields of physical science, computer science, mathematics, and engineering, which addresses how the fundamental laws of quantum physics can be exploited to achieve dramatic improvements in how information is acquired, transmitted, and processed. Its importance has been emphasized recently by the U.S. government through the National Quantum Initiative Act. This chapter focuses on the question of how the exquisite control of individual atoms and photons described in Chapter 3 can be brought to bear on quantum technologies for information processing. In the language of Chapter 3, a quantum information processor is essentially a quantum many-body system, far from equilibrium, whose initial state and subsequent time evolution dynamics we can control with extreme precision, and whose final quantum state can be measured (“readout”) with high fidelity. Different time evolution under external control of the quantum system corresponds to running different programs (executing quantum algorithms) on the computer. The final step of measurement provides the answer to the calculation.
Theoretical research carried out over the past two decades indicates that large-scale quantum computers may be capable of solving some otherwise intractable problems with far-reaching applications in, for example, cryptology, chemistry, materials science, and fundamental physical science. These developments have stimulated a worldwide effort to build quantum machines using a variety of physical
platforms, such as trapped ions, neutral atoms, superconducting circuits, spins of electrons and nuclei, and photons. The key challenges in the quest to implement scalable quantum information processors are associated with the contradicting requirements of combining excellent isolation from the environment with the ability to control strong, coherent, and programmable interactions and single-shot readout of the many-body system. The fundamental ideas of fault tolerance, established over the past two decades, suggest that it should be possible in principle to realize large-scale quantum machines despite imperfections in the individual components. Building a large-scale fault-tolerant universal quantum computer is the grand challenge of the field. However, it is currently unclear if and how this goal can be achieved within any realistic physics setting. The 2019 National Academies of Sciences, Engineering, and Medicine report Quantum Computing: Progress and Prospects1 discusses the current state of the art and the challenges that lie ahead.
The power of quantum computers resides in the subtle interplay between the unique resources of superpositions and entanglement (discussed further below), in ways that are not yet fully understood. Information is physical, and binary information (bits representing zeros and ones) is stored in the two (on/off) states of transistors in ordinary computer chips. In a quantum computer, information is stored in quantum bits (qubits). A qubit is any quantum system with two discrete states. A simple example would be an atom either in its lowest energy state (ground state) or a particular excited state. Another example would be a state containing either 0 or 1 photons of some particular energy. Qubits can be in superposition states in which we are uncertain whether they will yield 0 or 1 when measured (and indeed the measurement results are ineluctably random—a feature that can be used to make true random number generators). At first glance, this appears to be a major bug, not a feature. However, it is now understood that (very crudely speaking) qubits have the potential to be 0 and 1 simultaneously, creating a kind of quantum parallelism that is one of the sources of power of the quantum computer. The other distinctly quantum resource is entanglement, which will be described further below.
Even though recent experimental advances already allow for unprecedented new insight into the physics of complex quantum many-body systems, it is currently unclear if large-scale quantum processors can be used to obtain substantial speed-up over classical computers for any practical tasks apart from simulating complex quantum systems and Shor’s factoring algorithm. This is a key challenge that theoretical quantum computer science must address in the coming decade. It seems virtually certain that the small-scale quantum computers that are beginning to become available will allow numerous people from a variety of disciplines to start playing with them and coming up with new and unexpected ideas for how best to
___________________
1 National Academies of Sciences, Engineering, and Medicine, 2019, Quantum Computing: Progress and Prospects, The National Academies Press, Washington, DC.
operate them and improve their performance, just as occurred in the early history of classical computation. Frustration with the extreme difficulty of programming early classical computers using electrical plug boards and patch cords led directly to the invention of the von Neumann architecture in which data and instructions are stored in memory in the same way, so that programs could modify their own instructions. If we are fortunate, the next decade will lead to analogous breakthroughs in the quantum computation domain.
In this chapter, the committee discusses key ideas and hardware-level techniques for understanding fundamental principles behind creating, quantifying, and controlling quantum entanglement and universal control of many-body quantum systems, as well as for development of technological platforms for quantum information processing and simulation, quantum communication networks, and the application of quantum information ideas for enhanced sensing and measurement.
Ideas, techniques, and methods of atomic, molecular, and optical (AMO) physics are at the forefront of this exciting frontier involving building, studying, and applying large-scale controlled quantum systems. Experimental efforts to manipulate large-scale quantum systems are achieving steadily improving results. AMO systems and techniques played a pioneering role and continue to play a leading role in this field. Programmable quantum systems of up to about 50 quantum bits have been realized using trapped ions, neutral atoms, and superconducting circuits. Ion trap quantum computers represent the gold standard of qubit coherence and quantum control, and were recently used to realize sophisticated algorithms for quantum chemistry. Recent developments involving realization of programmable neutral atom arrays in various spatial dimensions, and quantum operations using controlled excitations into atomic Rydberg states, demonstrate the promise for high-fidelity control of systems composed of hundreds of qubits. Furthermore, atom-photon interfaces are being developed, which convert “stationary qubits”—for example, stored in atoms as quantum memory—to “flying qubits” represented by microwave or optical photons propagating—for example, in waveguides—as building blocks for both local and wide-area quantum networks. This implementation of coherent quantum operations in quantum networks provides a basis for fault-tolerant quantum communication including quantum repeaters (QRs), and the potential for scaling up quantum computers in modular architectures. The extensions of the methods originally developed in the AMO community to solid-state systems, such as circuit quantum electrodynamics (QED), play a central role in the most advanced superconducting quantum computer realizations. In particular, they form the basis for recently demonstrated promising approaches for quantum error correction.
At the same time, the fundamental concepts of quantum entanglement and quantum coherence now play central roles in almost all subfields of physical science. Aside from setting the stage for quantum technologies, research on quantum entanglement, quantum information processing, and quantum error correction is
also establishing new tools and approaches for deepening our understanding of fundamental physical phenomena. For example, in quantum condensed-matter physics, concepts arising from the study of quantum entanglement have spurred the development of powerful methods for classifying quantum phases of matter and more efficient schemes for simulating entangled quantum many-body systems using conventional classical computers. In addition, ideas from quantum information theory and quantum entanglement theory may deepen our understanding of the quantum structure of spacetime.
In the next decade, these experimental and theoretical methods will allow researchers to start implementing and testing novel quantum algorithms for diverse scientific applications, and to explore practical methods for quantum error correction and fault tolerance. They could enable the first realizations and tests of quantum networks with applications to long-distance quantum communication and nonlocal quantum sensing. In addition, controlled quantum systems are already being exploited in some of the world’s most precise atomic clocks, and in magnetic sensors that achieve an unprecedented combination of sensitivity and spatial resolution. Meanwhile, as already mentioned in Chapter 3, new experimental tools are being harnessed to simulate models of quantum many-body physics that are beyond the reach of today’s digital computers.
Exciting new scientific opportunities are arising at the interface of AMO physics, quantum information science, device engineering, condensed-matter physics, and high-energy physics: this new scientific interface is by now often referred to as quantum information science and engineering. For example, advances in precision measurements exploiting quantum coherence and entanglement may enable unprecedented tests of fundamental symmetries of the universe as well as new strategies for probing dark matter and dark energy (see also Chapter 6). Quantum simulators and quantum computers may provide new insights regarding the behavior of strongly correlated many-body systems and strongly coupled quantum field theories relevant to high-energy particle physics as well as condensed matter. Furthermore, concepts from particle physics and quantum field theory may suggest new applications for quantum computers, and new ways to make quantum systems more robust against noise. From this perspective, this chapter plays an important role connecting basic tools of quantum control for photons and atoms presented in Chapters 2 and 3 to some emerging applications presented in Chapters 5, 6, and 7.
UNDERSTANDING, PROBING, AND USING ENTANGLEMENT
Entanglement is the most precious property and resource of quantum physics, and fundamentally distinguishes quantum physics from classical physics. It occurs when two or more objects possess certain correlations, which cannot be explained classically in terms of local hidden variables or quantum-mechanically in terms
of product states or mixtures thereof. In the context of quantum technologies, entanglement is a resource in the sense that the more entanglement, the better one can perform particular tasks such as quantum communication or computation. This is why the study and quantification of entanglement plays a central role in quantum information theory, the discipline that develops the theory behind applications of quantum physics to the transmission and processing of information.
Entanglement of simple systems, composed of only a few objects, is by now relatively well understood. For pure states (i.e., states of systems not entangled with external environmental degrees of freedom inaccessible to the experimenter), the presence or absence of entanglement can be easily certified. Regarding the quantification, the situation is more complex. For two systems, the entanglement is properly quantified by the entropy of entanglement, E, which measures how mixed the local (reduced) states are in terms of the von Neumann entropy. The maximally entangled states of two qubits (so-called Bell states) possess one unit of entanglement; the entanglement of other states is related to that unit in the sense that they can be converted to Bell states at a ratio given by E. For multipartite states, the situation is more complicated, as one can define different measures, and there is not even a partial order with respect to any of them—that is, one state can be more entangled than another according to one measure, but less according to a different measure. In that case one typically considers the pragmatic approach of operational measures, which are task dependent, meaning that they are defined according to the advantage they yield for a given informational task. For mixed states, the situation is even more intricate. While it is possible to determine whether states are entangled or not, in some cases it may become a difficult computational task. The quantification faces the same problems as for pure states. Despite a lot of progress made over the past decade, the theory of entanglement is still not fully established.
The past 10 years have experienced substantial progress in probing entanglement in experiments. First, different strategies have been proposed to detect the presence of that intriguing property in few- or even many-body systems. These strategies have been widely used in a variety of experiments in order to benchmark their performance, or to certify their quantumness. Experiments with tens of trapped ions, atoms, superconducting qubits, and other systems have witnessed the presence of the strongest forms of entanglement, while other experiments with many particles (for instance, atomic ensembles with millions of atoms) have also detected some weak forms of entanglement. Each of these can be considered as a “tour de force” in experimental physics, and have successfully demonstrated that close theory-experiment connection can lead to rapid progress.
Apart from the development of a deeper understanding of entanglement as well as its quantification as a resource, there remain important challenges for future research. On the experimental side, there is the demonstration of higher levels of entanglement with different technologies, as well as the possibility to entangle more
objects together strongly (for example, in so-called Greenberger–Horne–Zeilinger [GHZ] states). An experimental challenge would be to create such a state of N qubits, or N00N states of photons, which are useful in the context of parameter estimation, metrology, and sensing. (So-called N00N states are maximally entangled states consisting of a coherent superposition of two possibilities: N photons in mode 1 and 0 photons in mode 2, superposed with 0 photons in mode 1 and N photons in mode 2. The origin of the name can be seen in the standard quantum notation for such a state: |N0>+|0N>.) From the theory side, finding new applications of entanglement would be highly desirable. Nowadays, we know of only a few tasks for which quantum properties (and, in particular, entanglement) can improve performance. Among these are cryptography, random number generation, quantum computing, and sensing. However, there may be many other realms where entanglement provides an advantage over classical limits. The further development of the theory of entanglement may well lead to such applications in the next decade.
In the past few years, we have witnessed how the notion of entanglement has gone beyond quantum information theory and had a strong impact in other areas of physics. For instance, it has been found that in the quantum ground state, and as long as interactions are local, entanglement is relatively scarce in nature as it typically fulfills a so-called area law. In brief, this means that the entanglement (or, more precisely, the quantum mutual information) of a region with respect to its complement scales with the surface area of the region and not with the volume. This occurs in many domains of physics, including atomic, condensed-matter, and high-energy, and has striking consequences. This implies that the corresponding states can be efficiently described in terms of tensor networks, a new language that allows one to overcome the exponential growth of information that is normally required to describe and deal with such systems and that prevents the analysis of quantum many-body systems in general. Thus, a great challenge of entanglement theory is to help to develop algorithms that allow one to address physics questions that cannot be attacked with classical (super) computers. Furthermore, the study of entanglement has expanded to other areas of physics including quantum gravity, where several theories have recently emerged that connect entanglement with other concepts. In particular, entanglement is at the core of the so-called firewall paradox (of black holes), and it has been used to devise toy-models (of condensed-matter many-body theories) and to understand some aspects of holographic principles (in theories of gravity), and is possibly even connected to the emergence of the geometry of spacetime itself. In particular, entanglement has established a common language in all those communities, and it is expected to shed new light in different areas of physics.
It is important to emphasize that recent advances in realizing quantum machines allow one to study the fundamental aspects of quantum entanglement in the laboratory. In particular, the experimental systems described in this chapter allow researchers to experimentally probe various aspects of quantum many-body
systems using trapped ions and neutral atoms. In addition, the completion of several “loophole free” experimental tests of Bell inequalities,2 described below in the section “Bell Inequalities, Quantum Communication, and Quantum Networks,” was one of the highlights of the past decade. These sophisticated tests were made possible by remarkable experimental advances, which in turn play a crucial role in quantum technologies. Furthermore, Bell tests are also used in the very core of some quantum technologies, such as Device Independent Quantum Key Distribution (DIQKD), and ultimate quantum random number generators (QRNGs).
CONTROLLING QUANTUM MANY-BODY SYSTEMS
AMO systems provide one of the most advanced and promising ways to implement controlled quantum systems. Ideas, techniques, and methods developed in the framework of AMO define the forefront of building, studying, and applying large-scale quantum information processing, and also have a profound impact in helping develop a similar level of control in solid-state systems. Individual atoms, first of all, host the most pristine qubits found in nature. Atoms, by their very nature, are identical, and when isolated from detrimental effects of the environment using well-developed atomic techniques of trapping and cooling, provide us with large-scale quantum registers of identical qubits. When atomic qubits are represented by appropriate internal energy levels within individual atoms, they are essentially atomic clocks and hence enjoy the attributes of high-performance frequency standards. Second, the long tradition in AMO of precision measurement has provided the community with the tools, including lasers and microwave fields, which provide the necessary control techniques to manipulate atoms and their interaction, as well as high-fidelity readout, fulfilling the stringent requirements of control of engineered large-scale quantum matter. In an effort to scale quantum devices to an increasing number of quantum particles, atomic physics has the unique advantage that sophisticated quantum error correction techniques might not be as much the limiting requirement as in other physical settings—even though the development of these techniques is one of the key challenges in the field. Last, atomic systems provide natural quantum interfaces, or transducers, where “stationary qubits” stored in atomic quantum memory are interfaced with, for example, optical or microwave photons as “flying qubits,” as required in building “on chip,” intra-laboratory, or wide-area quantum networks.
Below, recent highlights are presented demonstrating the progress, future promise, and challenges associated with quantum control of large-scale, many-body atomic systems. Ion trap quantum systems have long represented the gold standard
___________________
2 A. Aspect, Viewpoint: Closing the door on Einstein and Bohr’s quantum debate, Physics 8:123, 2015, 10.1103/Physics.8.123.
of qubit coherence and quantum control. Recently, they were used to realize sophisticated quantum algorithms. New developments involving realization of configurable neutral atom arrays in various spatial dimensions, and quantum operations using controlled excitations into atomic Rydberg states, demonstrate the promise for high-fidelity control of systems composed of hundreds of qubits. At the same time, the extension of the methods originally developed in the AMO community to solid-state systems, such as circuit QED, play a central role in the most advanced solid-state quantum computer realizations. Last, AMO methods and techniques are employed for controlling electronic and spin degrees of freedom of atom-like impurities in solid-state systems, with applications ranging from implementation of quantum networks to nanoscale quantum sensing.
Trapped Ion Quantum Computing
For the past two decades, trapped atomic ions have been among the most advanced candidates for the implementation of quantum processors (see Figure 4.1). Following very early proposals and demonstrations of controllable quantum entanglement operations in the mid-1990s, there are now more than 50 teams investigating trapped ion entanglement and quantum computing architectures in academic institutions, national laboratories, and industrial organizations around the world. In addition to the continued refinement of fundamental entanglement operations and protocols with trapped ions, this platform is becoming systematized and controlled by agile hardware interfaces and software technology in a way that is moving toward practical quantum computation. This is catalyzed by the fact
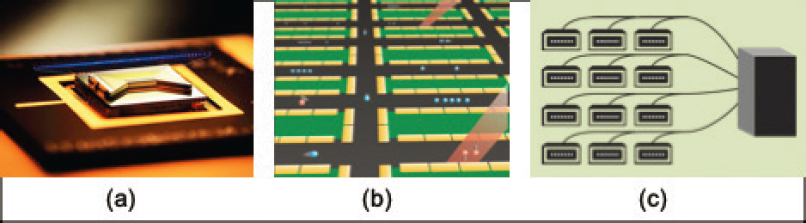
that the scaling of trapped ion quantum computers does not rely on new physics or even breakthroughs, but on the engineering, systemization, and improved performance of their controllers. Importantly, it appears likely that trapped ion quantum computers will be able to scale to dimensions well beyond those needed for quantum advantage in practical problems, that is, demonstrating tasks beyond what can be achieved efficiently on classical devices.
As noted above, individual trapped and laser-cooled atoms and ions host the most pristine qubits found in nature, and the highest performing individual atomic clock systems are based on atomic ions. By virtue of their electrical charge, individual atomic ions can be isolated and manipulated in space with exquisite precision. By applying external electromagnetic fields from nearby arrays of electrodes inside a vacuum chamber, individual atomic ions can be confined or trapped for indefinite periods of time The most popular atomic ion species used for quantum computing purposes are those with single valence electronic configurations such as Be+, Ca+, and Yb+, whose essential attributes are the required laser wavelengths for cooling and manipulation, the electronic structure of the atom—primarily its nuclear spin and ancillary electronic energy levels—and the atomic mass.
When laser-cooled, a collection of trapped atomic ion qubits forms a crystal, and established techniques using lasers and microwaves allow the initialization and measurement of quantum states within trapped ion qubits with nearly perfect fidelity. Moreover, following classic nuclear magnetic resonance (NMR) and atomic clock techniques using microwaves or optical fields, individual qubit operations such as single-qubit gates or rotations, can be achieved with greater than 99.99 percent fidelity.
The Coulomb interaction between atomic ions in a crystal leads to strongly coupled normal modes of motion, much like an array of pendula connected by springs. These modes can be utilized as information buses to generate programmable entanglement between the qubits. The generation of entangled quantum logic gates between trapped ion qubits relies on qubit state-dependent forces (from applied optical or microwave fields). The fidelity of two-qubit gates has reached the 99.9 percent level using both optical and microwave fields, and is currently limited by mechanisms such as spontaneous emission or motional decoherence during the gate, residual intensity fluctuations of the control beams, stability of the frequency of the motional modes, and the decoherence of the qubit itself. It is important to realize that the error budgets in these systems are well characterized, and research efforts continue to improve gate performance in these systems.
Based on the high-fidelity component operations demonstrated to date, small-scale ion trap systems have been assembled in which a universal set of quantum logic operations can be implemented on small qubit systems in a programmable manner, forming the basis of a general-purpose quantum computer. While the performance of individual quantum logic operations in these fully functional
systems tends to lag behind the state-of-the-art demonstrations at the component level of just two qubits, the larger systems can exhibit a wide variety of quantum algorithms and tasks that comprise some of the largest and most complex quantum computer systems operated to date. For instance, small-scale trapped ion systems have been used to implement Grover’s search algorithm, Shor’s factoring algorithm, the Deutsch-Jozsa algorithm, quantum Fourier transform, the Bernstein-Vazirani algorithm, the quantum hidden shift algorithm, quantum error correction and detection codes, and quantum simulation tasks.
While it appears possible to scale a trapped ion quantum computer to 30-100 qubits in a single crystal, it may prove difficult to push well beyond this level given technical limitations such as trap potential fluctuations and other slowly varying control parameters. However, there are many opportunities to scale trapped atomic ions using more modular approaches. At the lowest level, a very large chain can be rigidly displaced through an interaction/control zone much like a tape moves across a head in a classical Turing machine. The physical shuttling of atomic ions through separated trapping zones in sufficiently complex trap electrode geometries is a promising method for a modular quantum computer architecture, sometimes called a “quantum CCD,” as shown in Figure 4.1(b). This may require multiple species of trapped ions for sympathetic cooling after splitting/merging chains, and also cryogenic (4 K) environments to maintain low pressure and long-chain lifetime. Great progress has been achieved in the ability to integrate quantum gate operations with shuttling between collections of trapped ion qubits. This has been demonstrated so far on the level of a few ions, and one of the future challenges is scaling to many thousands of qubits on a single chip using this method.
A higher level of modularity may be afforded by exploiting the interface between trapped ion qubit memories and flying photonic qubits, as depicted in Figure 4.1(c). Here, certain “communication” qubits in a chain are linked to other such qubits in a spatially separated chain, perhaps on another ion trap chip, or in a separate vacuum chamber over longer distances. This architecture follows closely the multicore architecture adopted by classical computing processors, and follows from the generalization that complexity demands modularity.
In general, the scaling of qubits toward a useful large-scale quantum computer requires that both qubits and gate quality do not degrade with increasing size of the system. Given pairwise gate operations between qubits, it might be expected that with N qubits, we will require N2 coherent gate operations. This would call for either error correction before N gets too large or for gate fidelities to be improved as 1-1/N2. Not only is this a scaling benchmark that allows full entanglement within a system, but also many applications demand this form of scaling. This evolution of the technology is particularly challenging, as larger quantum systems generally couple more strongly to their environment. At present, trapped ions are among the leading platforms for quantum information processing having achieved full quantum control for 20 and
more qubits. In the foreseeable future, atomic ion qubits will be limited mainly by their controllers. In addition, the error modes of trapped ion devices are well understood, offering great confidence that trapped ion quantum computers will indeed scale to dimensions far beyond what is achieved in present experiments.
From Quantum Computers to Programmable Quantum Simulators
Programmable quantum simulators (PQSs) have recently emerged as a new paradigm in quantum information processing. In contrast to the universal quantum computer, PQSs are nonuniversal quantum devices with restricted sets of quantum operations, which however can be naturally scaled to a large number of qubits. PQSs are experimental platforms that are able to produce families of interesting quantum states by letting large collections of particles interact in a precise fashion, thus generating potentially large-scale entanglement. The resulting quantum many-body states can be further manipulated via precise single-particle control. The quantum states produced in this way are thus programmable in the sense that they are parametrized by control parameters provided by the experimentalist (such as duration and strength of the interaction, and degree of single-particle rotations). In contrast to universal quantum computing, generation of these quantum states is not universal—that is, they belong to a restricted class of states, yet they are the ones for which interesting applications exist (to be discussed below). PQS platforms can be viewed as an interpolating step between dedicated, single-purpose quantum simulators and fully fledged universal quantum computers. As more and more refined control is developed, PQS platforms can be expected to bridge and ultimately close the gap between these two notions.
Significant progress has been made in the development of PQSs. The specialization of these platforms to a single task endows them with relatively good scaling properties compared to universal quantum computing devices such as quantum computers, not only regarding the number of particles or qubits, but also in the fidelity of quantum operations they can perform. Furthermore, imaging methods such as quantum gas microscopes for optical lattices or the spin readout of trapped ions and atomic arrays provide detailed access to the properties of the quantum states at single-particle resolution. Repetition rates of the experimental cycles have increased tremendously, enabling large numbers of experiments to be performed in short times. Particular examples of PQS platforms are, for instance, linear arrays of trapped ions, as discussed in the previous section (see Figure 4.1), and arrays of trapped atoms in optical tweezers that can be excited to the Rydberg state (see below, and Figures 4.3, 4.5, and 4.6a,b). Both platforms realize controllable Ising-type interactions that can be switched on and off at will.
All of these recent advances have opened the door to novel applications, beyond traditional analog quantum simulation for which the platforms were originally intended. A key example is the use of the PQS as a quantum co-processor in a hybrid
classical-quantum feedback loop. The PQS is employed in its role as a quantum state generator, controlled by a classical computer that attempts to steer the resulting quantum state toward a desired target state. The targeted state can be the ground state of a physical model (see Box 4.1). An alternative application would be to encode an optimization problem in the many-particle state and let the quantum
system generate approximate solutions using the Quantum Approximate Optimization Algorithm (QAOA). In both cases, many short experiments with only modest requirements on coherence time are performed, and the resulting state is measured frequently. At each step, a cost function is evaluated from the measurements, which the classical computer attempts to optimize variationally in a feedback loop.
Future experimental efforts should continue to improve the quality of available PQS platforms by increasing the coherence times and the number of particles and extending the set of available controls. Improved repetition rates of experiments would be beneficial for the use of PQSs in variational settings. The latter point is particularly relevant for itinerant atomic systems, such as fermionic atoms in optical lattices (see Chapter 3), whose application in a variational optimization context could open interesting perspectives to address long-standing equilibrium problems in quantum chemistry, condensed-matter, and high-energy physics. Theoretical efforts should be directed at quantifying the computational power of PQS platforms in the context of solving optimization problems, and exploring how PQSs could function as modular building blocks for a future generation of quantum simulators and quantum computers. A further theoretical focus area is the development of novel applications of the quantum states produced by PQS, for instance in quantum metrology.
Controllable, coherent many-body systems can provide insights into the fundamental properties of quantum matter, can enable the realization of new quantum phases, and could ultimately lead to computational systems that outperform existing computers based on classical approaches. Recently several experimental groups in the United States and France developed and demonstrated a powerful new method for creating controlled many-body quantum matter that combines deterministically prepared, reconfigurable arrays of individually trapped cold atoms in one, two, and three spatial dimensions with strong, coherent interactions enabled by excitation to Rydberg states (see, e.g., Figure 4.2).
For example, recent experiments realized programmable quantum spin model with tunable interactions and system sizes of up to 51 qubits. This work already led to the discovery of a new class of quantum many-body states that challenge traditional understandings of thermalization in isolated quantum systems, and has triggered extensive new theoretical investigations into these so-called quantum many-body scars. Using the same platform and applying it to the study of condensed-matter models, these experiments observed quantum phase transitions into spatially ordered states that break various discrete symmetries. The experimental study of quantum critical dynamics within this platform offered the first experimental verification of the quantum Kibble-Zurek hypothesis, and showed its application to exotic, previously unexplored models such as the chiral clock model. In addition, a similar platform was recently utilized for realization of symmetry-protected topological phases of matter.
Apart from studies of many-body quantum physics, recent experiments demonstrated the suitability of the platform for quantum computation by overcoming
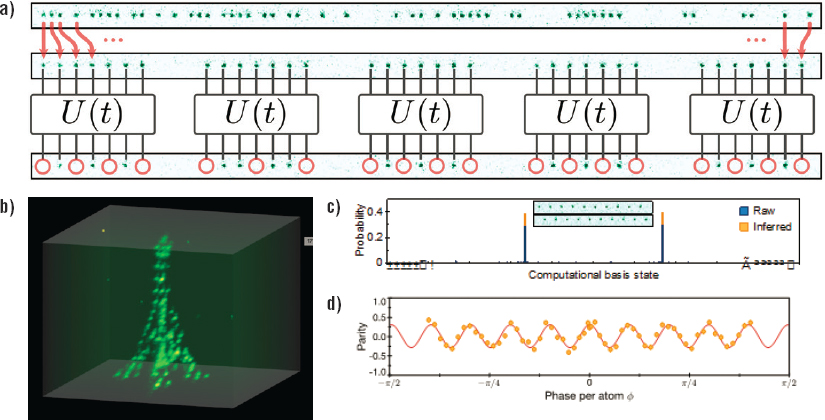
several long-standing limitations in quantum control of cold atoms. High-fidelity single-qubit rotations and quantum state detection has been demonstrated. In addition, the preparation of high-fidelity entangled states has been demonstrated, establishing neutral atoms as a competitive platform for quantum information processing. Most recently, this system has been used by Harvard-Massachusetts Institute of Techology (MIT) collaboration to realize GHZ entangled states of 20 atoms, which is the largest N-particle entangled state of individually measured particles to date. At the time of the writing, high-fidelity multi-qubit operations have been realized by the groups at Harvard/MIT and Wisconsin using this approach. Last, recent theoretical work demonstrated that this approach is well suited for realization and testing of quantum algorithms for solving complex combinatorial optimization problems, paving the way toward exploring the first real-world applications of quantum computers.
Before concluding, the committee notes that this is a very rapidly growing area of research. Very recently, a number of new systems involving optical tweezer arrays have been demonstrated. These include new experiments involving realization of tweezer arrays with alkaline-earth atoms such as strontium and ytterbium, as well as polar molecules (see Chapter 3). These platforms hold promise for many potential applications, ranging from high-fidelity quantum information processing and quantum simulations to quantum metrology.
Cavity and Circuit QED
QED is the theory of the interaction of light quanta (photons) with electrons and atoms. As described below, one of the exciting developments in the past 15 years has been the movement of ideas from AMO physics and quantum electrodynamics into the world of condensed-matter physics.
QED correctly predicts many subtle phenomena and is widely considered to be the most successful and most precisely tested theory in all of science. One of its most fundamental predictions is that atoms placed into excited states are unstable and will spontaneously fluoresce—that is, decay to a lower energy state by emitting one or more photons. This useful phenomenon is crucial for many technologies including computer screens and other types of optical displays.
Ordinarily, photon modes of all possible wavelengths (and hence energies) are available, and thus the atom can always find a mode of the correct energy into which it can decay. In cavity QED, one modifies the photon modes available to the atom by placing it between two highly reflecting mirrors to form a resonant cavity that can support only modes of certain discrete wavelengths. Cavity QED allows one to engineer the photon environment seen by the atom and thereby either enhance or suppress its decay rate. These so-called Purcell effects have been observed in optical and microwave cavities but are typically rather weak and limited by the small size of the atom and the small wavelength of light relative to the large electromagnetic mode volume of the resonator.
Inspired by ideas from condensed-matter physics and electrical engineering radio filter theory, AMO scientists have in recent decades made great progress in creating optical resonators with very small mode volume—comparable to the volume associated with a single wavelength of the light emitted by the atom. One way to accomplish this is by custom design of so-called photonic bandgap materials. These structures can be engineered to efficiently couple the light emitted by a single atom (or color center defect in a solid) into an optical fiber for purposes of quantum control, communication, and information processing. Since the relevant scale against which to measure cavity mode dimension is the wavelength of the photons it traps, one can effectively decrease the mode volume by moving to atoms that emit and absorb long wavelength microwave photons rather than short wavelength
optical photons. Serge Haroche shared the 2012 Nobel Prize for his work on cavity QED of Rydberg atoms passing through a microwave resonator.
Rydberg atoms are ordinary atoms with one electron excited to a large orbit around the nucleus. Here “large” means about 104 atomic diameters or 10−6 m. In the past 20 years, condensed-matter physicists have gone even further by constructing artificial atoms out of superconducting Josephson junction circuits. These millimeter-size objects are visible to the naked eye and contain trillions of electrons. However, because of their superconductivity, the electrons in these circuits move coherently in unison, allowing the “atoms” to have quantized energy spectra simpler even than hydrogen. Because of their enormous size, these quantum objects interact very strongly with electromagnetic waves. In free space, these “atoms” spontaneously decay very rapidly by emitting microwave photons. However, unlike the case with optical photons, one can completely enclose these “atoms” inside a superconducting box that effectively acts like a nearly perfectly reflecting set of microwave mirrors fully surrounding the “atom.” This makes it almost impossible for the “atom” to spontaneously decay (because the microwave photons keep getting reflected back and cannot escape), thereby extending the lifetime of the artificial atoms through the Purcell effect by a factor of 103. With this strong lifetime enhancement, artificial atoms have coherence times relative to their transition frequencies that are comparable to the hydrogen atom. The Purcell effect can also be used to shorten the lifetime by placing the atom in resonance with the cavity. A spectacular example of this is recent work using a resonant cavity to dramatically enhance the spontaneous emission rate of donor electron spins in silicon by a factor of nearly 1012, thereby shortening the spin relaxation time by a factor of 103. One application of this enhanced dissipation is spin reset in magnetic resonance experiments and qubit control experiments.
The fact that a cm-scale microwave cavity can have a mode volume considerably smaller than a cubic wavelength further enhances the coupling of the artificial atom to photons trapped in the cavity. The coupling is so strong that even when the “atom” and cavity are detuned in frequency from each other by 20 percent, the second-order effects of the “atom” virtually emitting and quickly reabsorbing photons to and from the cavity yields an ultrastrong dispersive interaction H = χσza†a, where σz describes the state of the (two-level) “atom” and ![]() ≡ a†a represents the number of photons in the cavity. The meaning of this dispersive interaction is that the transition frequency of the “atom” suffers a quantized “light shift” for each additional microwave photon present in the cavity. It also means that the cavity has two different resonance frequencies depending on whether the “atom” is in its ground or excited state. Remarkably, the dispersive coupling χ can be three orders larger than the linewidths (decay rates) of both the cavity and the “atom,” placing this system in a completely new regime of nonlinear quantum optics at the single-photon level.
≡ a†a represents the number of photons in the cavity. The meaning of this dispersive interaction is that the transition frequency of the “atom” suffers a quantized “light shift” for each additional microwave photon present in the cavity. It also means that the cavity has two different resonance frequencies depending on whether the “atom” is in its ground or excited state. Remarkably, the dispersive coupling χ can be three orders larger than the linewidths (decay rates) of both the cavity and the “atom,” placing this system in a completely new regime of nonlinear quantum optics at the single-photon level.
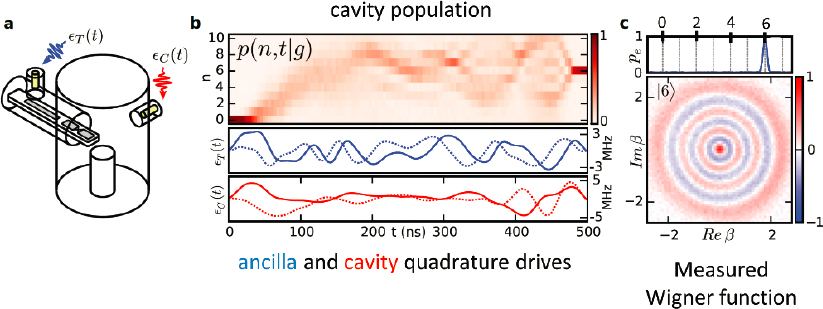
This ultrastrong coupling relative to dissipation permits universal control of the combined qubit-cavity system. One can readily make quantum nondemolition (QND)
measurements of photon number: measure the photon number parity ![]() = eiπa†a (without measuring the photon number), and using these parity measurements, carry out complete state tomography through direct measurement of the Wigner function (a quasi-probability distribution in phase space). These capabilities go far beyond what is possible in ordinary quantum optics where the nonlinear interactions of light and matter are much weaker relative to the dissipation. Figure 4.3 illustrates these quantum control and measurement capabilities.
= eiπa†a (without measuring the photon number), and using these parity measurements, carry out complete state tomography through direct measurement of the Wigner function (a quasi-probability distribution in phase space). These capabilities go far beyond what is possible in ordinary quantum optics where the nonlinear interactions of light and matter are much weaker relative to the dissipation. Figure 4.3 illustrates these quantum control and measurement capabilities.
This powerful ability to control quantum states opens up a new regime of strong nonlinear quantum optics at the single-photon level. It permits creation of error-correctable logical qubits, not from material objects, but rather from superpositions of different numbers of microwave photons. These “photonic logical qubits” are the first qubits in any technology to reach the breakeven point for error correction (where the lifetime of the quantum information encoded in the logical qubit exceeds that of any individual physical qubit). Other recent advances include deterministic teleportation of quantum gates on logical qubits, and novel new entangling gates such as the exponential-SWAP gate that acts on two microwave resonators by performing a coherent superposition of swapping and not swapping the contents of the two resonators. These capabilities advance the possibility of gate-based photonic quantum computing and also of simulating the many-body dynamics of interacting bosons. An exciting new direction would be using an array
of microwave cavities to simulate the fractional quantum Hall effect for bosons in the parameter regime where the excitations are Majorana zero-modes obeying non-Abelian statistics. Another exciting new direction that is now rapidly blossoming is “quantum acoustics,” in which one can use similar techniques to create, control, and measure individual quanta of sound (mechanical vibrations).
CONTROLLED MANY-BODY SYSTEMS FOR QUANTUM SIMULATIONS
Simulating Quantum Dynamics of Many-Body Systems
Quantum simulation of complex many-body systems was the original context in which Richard Feynman proposed building programmable quantum machines. The motivation was that exact classical computation or simulation of quantum dynamics becomes extremely challenging even for a modest-size quantum system. In fact, it is virtually impossible to exactly compute the dynamics of coupled qubits with system sizes exceeding around 50 quantum bits. These considerations make it very challenging to study non-equilibrium dynamics of closed quantum systems. Central to such systems is the dynamics of entanglement growth that creates nontrivial quantum correlations that cannot be captured by simple theories. Recent experimental advances involving programmable quantum simulators already allow researchers to carry out quantum simulations with system sizes that cannot be handled classically, and to gain unprecedented insights into the physics of such systems.
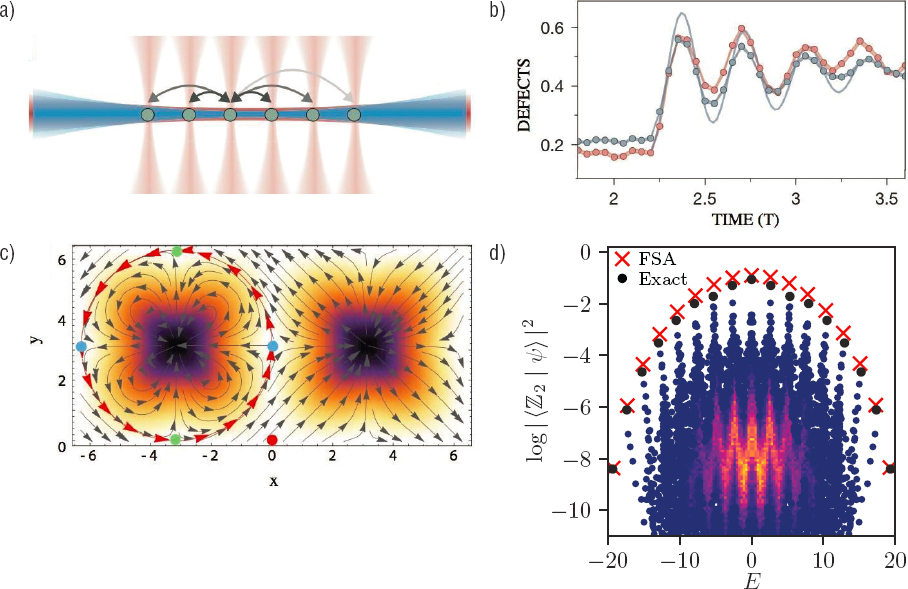
One example involves understanding of non-equilibrium quantum phases. This is especially challenging since, almost by definition, the equations of motion of an out-of-equilibrium system are constantly in flux. For instance, in the case of periodically driven (Floquet) systems, these equations of motion are periodic, but the non-equilibrium system is generically expected to absorb energy from the driving field (so-called Floquet heating) until it approaches a featureless infinite temperature state, thus preventing any nontrivial quantum ordering. Part of the success of experimentally realizing non-equilibrium phases of matter is owed to the theoretical development of strategies to prevent such Floquet heating (including most notably many-body localization; see Chapter 3 for additional discussion). One recent example of an intrinsically non-equilibrium phase realized in the laboratory is the discrete time crystal (see Box 4.2), whose ordering spontaneously breaks the time translation symmetry of the underlying drive. The period of the resulting discrete time crystal is quantized to an integer multiple of the drive period, and arises from collective synchronization. Another recent example involves experimental discovery of so-called quantum many-body scars, involving special slowly thermalizing trajectories in many-body Hilbert space of constrained, strongly interacting systems, which are accompanied by nonmonotonic slow entanglement growth (see Figure 4.4).
From Many-Body Physics to Lattice-Gauge Theories and High-Energy Physics
During the past decade, the development of atomic quantum simulators has been mainly driven by the attempt to gain insight into strongly correlated many-body systems of condensed-matter physics. Physically interesting quantum many-body systems, which cannot be solved with classical simulation methods, have become accessible to analog or digital quantum simulation with cold atoms, molecules, and ions. In the future, quantum simulators may also enable us to address currently unsolvable problems in particle physics, including the real-time evolution of the hot quark-gluon plasma emerging from a heavy-ion collision or the deep interior of neutron stars.
The phenomena in condensed-matter and high-energy physics the committee wants to address are described by gauge theories, and the challenge is thus the development of quantum simulators for gauge, and in particular, lattice-gauge theories—that is, gauge theories discretized on a lattice. In particle physics, Abelian and non-Abelian gauge fields mediate the fundamental strong and electroweak forces between quarks, electrons, and neutrinos. In atomic and molecular physics, electromagnetic Abelian gauge fields are responsible for the Coulomb forces that bind electrons to atomic nuclei. In condensed-matter physics, besides the fundamental electromagnetic field, effective gauge fields may emerge dynamically at low energies. Examples of phenomena, which can be understood in a lattice gauge language include anyonic statistics of quasiparticles in quantum-Hall systems, or quantum spin liquids, which may arise in geometrically frustrated antiferromagnets. Furthermore, universal topological quantum computation is based on non-Abelian Chern-Simons gauge theories. Box 4.3 illustrates the basic features of lattice-gauge theories with the example of quantum spin-ice as a frustrated spin-model in condensed-matter physics, and 1D QED, the so-called Lattice Schwinger Model.
While quantum simulation of gauge theories is fundamental, it is challenging to implement lattice-gauge models with atomic setups (and other platforms). The Hamiltonians for gauge models to be realized in the atomic laboratories are complex (see, e.g., Figure 4.3.1b), and often do not have a natural counterpart in atomic lattice models—for example, the familiar Hubbard models with cold bosonic and fermionic atoms in optical lattices. Instead, these models are obtained only as emergent lattice-gauge models in atomic models—that is, as effective models in the low-energy sector with high-energy degrees of freedom integrated out. However, designing such effective Hamiltonians for analog quantum simulation comes at a price: not only is it nontrivial to engineer the required gauge-invariant Hamiltonian couplings from the available atomic resources, but also the resulting energy scales of these effective theories can be small, with corresponding stringent
requirements for temperature and decoherence times in experiments. Numerous theory proposals have been made in recent years to implement analog quantum simulation of Abelian and non-Abelian lattice-gauge theories for spin models, and with fermionic and bosonic atomic mixtures in specially engineered lattice geometries. However, an experimental realization of analog quantum simulation of lattice-gauge theories remains an outstanding challenge.
Quantum simulation can be implemented not only as an analog simulation but also as a digital quantum simulation. For example, the time evolution generated by a (potentially complex) Hamiltonian can be decomposed into Trotter steps—that is, essentially using a universal quantum computer to propagate the quantum many-body problem. Real-time dynamics for a Lattice Schwinger Model has been studied with a trapped-ion quantum processor (see Figure 4.5). The committee emphasizes, however, that this programming of complex many-body dynamics on a universal quantum computer is expensive, and for present devices is restricted to a small number of qubits and Trotter steps (four qubits, and four Trotter steps). Scaling digital quantum computations and simulations to a large number of qubits, and in a fault-tolerant way, is again one of the outstanding challenges for the future.
There is a third method of quantum simulation of complex many-body problems: variational quantum simulation. Refer to the section “From Quantum Computers to Programmable Quantum Simulators” earlier in this chapter for a description of this technique.
Applications to Quantum Chemistry
In the early 20th century, the new field of quantum chemistry was formed by the interaction of chemists, physicists, applied mathematicians, and computer scientists. One hundred years later, we have seen the birth of quantum information for quantum chemistry, building on discoveries at the nexus between modern theoretical physical chemistry and the new ideas emerging from quantum information theory and its foundations in quantum physics and computer science. For the past two decades, research has been focused on (1) elucidating the role of quantum information in molecular systems and using this to solve outstanding problems in chemistry, (2) re-envisioning quantum spectroscopy and control, and (3) constructing and utilizing quantum information processors and developing applications for these in chemistry.
Today, many theoretical/computational chemists rely on large computational packages such as GAMESS and GAUSSIAN and other software packages that in part employ extremely efficient Gaussian integral evaluations. To achieve chemical accuracy (1 kcal/mol or fewer) in a systematic way, they rely on using either variational expansion methods such as multi-configuration self-consistent field or
configuration interaction methods with large basis sets or perturbative expansions such as Coupled Cluster (e.g., CCSDT) and many-body perturbation theory such as MP3. Supplementing these methods, Density Functional Theory and to a lesser extent a variety of forms of quantum Monte Carlo have become popular in certain circles. Despite the progress in developing such electronic structure methods, many important problems in chemistry such as the prediction of chemical reactions and the description of excited electronic states, transition states, and ground states of transition-metal complexes that are essential for material design, although doable by these methods, remain challenging. The accuracy requirements for prediction (and identification) of spectra of atoms and molecules relevant to astrophysics are even more demanding (i.e., much better than 0.01 cm−1 uncertainty in inverse wavelength). At present theorists are using a combination of empirical fitting methods and tuning molecular potential energy surfaces to fit spectra. Substantial improvements in the accuracy of ab initio calculations need to be achieved and represent an important challenge for the future.
Bringing techniques from quantum information into the picture may enable treatment of some of these hard problems. Based on the different variations of the phase estimation algorithm, mappings to Ising Hamiltonians, the variational quantum eigensolver (VQE), and other quantum simulation techniques, scientists have been able to obtain results with modest accuracy using up to six qubits on several experimental platforms (photonic quantum computer, NMR, ion trap, and superconducting-based qubits) for small molecules such as H2, BeH2, LiH, and H2O. The big question is how to proceed to perform electronic-structure calculations for large chemical systems! Recently, Reiher et al. showed how quantum computers (with about 110 logical qubits) can be used to elucidate the reaction mechanism for biological nitrogen fixation in nitrogenase, by augmenting classical calculation of reaction mechanisms with reliable estimates for relative and activation energies that are beyond the reach of traditional methods. One can assume that treating complex chemical systems in the field of catalysis, drug design, cluster optimization, and so on will need at least hundreds of logical error-corrected qubits (thousands to millions of physical qubits!). To address these challenges, a number of exciting research directions are currently being explored. These include the following:
- Developing hybrid quantum-classical algorithms: The initial development of VQE is a good example in this direction: one uses a quantum device to evaluate the expectation value of the objective function depending on parameters that are optimized through classical methods. See, for example, Box 4.1, earlier in this chapter.
- Developing quantum machine learning: Combining machine learning techniques with quantum algorithms. The initial development of the Boltzmann machine for quantum simulations is a good example in this direction.
- Designing quantum algorithms relevant to chemistry based on d-level systems qudits (where “d” is an integer greater than two) instead of qubits. Initial ideas of exploiting a natural mapping between vibrations in molecules and photons in waveguides is a good example of simulating the vibrational quantum dynamics of molecules using programmable photonic chips based on qudits.
- More broadly exploiting quantum information ideas for chemistry: This has led to progress in quantifying entanglement in chemical reactions and complex biological systems. However, how to measure entanglement between electrons in chemical reactions is still a challenge. Also, how the quantum resources of interference, superposition, and entanglement can assist in quantum control of chemical reactions is still at an early stage.
BELL INEQUALITIES, QUANTUM COMMUNICATION, AND QUANTUM NETWORKS
From Bell Inequalities to Quantum Communication
Quantum theory predicts that reality is not nearly as simple as one might have imagined. In particular, it predicts that physical quantities observable in experiments do not have values until they are measured. Einstein identified, and famously objected to, this feature of the theory. However John Bell devised an experimental “Bell inequality” test that only the quantum theory could pass and any classical theory (in which observables have values before they are measured) must fail. In addition to being of profound importance to our understanding of the nature of physical reality, Bell inequalities are now becoming critical system engineering tests that certify a computer is truly quantum, certify true random number generation, and certify the security of encryption and communication.
Experimental tests of Bell inequalities have played an important role in the emergence of quantum information, by drawing the attention of physicists to the revolutionary character of entanglement. One can find a witness of this role in the paper by Feynman considered a founding paper of quantum computing,3 in which he writes: “I’ve entertained myself always by squeezing the difficulty of quantum mechanics into a smaller and smaller place, so as to get more and more worried about this particular item. It seems to be almost ridiculous that you can squeeze it to a numerical question that one thing is bigger than another. But there you are—it is bigger than any logical argument can produce.” Although he does not give any reference, Feynman clearly refers to Bell inequality violations.
___________________
3 R.P. Feynman, Simulating physics with computers, International Journal of Theoretical Physics 21:467-488, 1982.
Bell inequalities4,5 refer to the strong correlations between measurements on two quantum objects initially prepared together in an entangled state—for instance, polarization measurements of two photons emitted in opposite directions. The violation of Bell inequalities means that it is impossible to understand these correlations by invoking unknown common properties, properties not part of the standard quantum formalism (e.g., local supplementary parameters or “hidden variables”), determined at the preparation and carried along separately by each subsystem. Such models, widely used in classical science, allow one to explain, for instance, correlations of some diseases of identical twins, who carry along the same set of chromosomes. Renouncement of the corresponding worldview, known as “local realism” and advocated by Einstein, was considered surprising enough to demand experimental tests. In fact, situations in which Bell inequalities are predicted to be violated by quantum systems are so rare that specific experiments had to be designed to perform the tests. And some now widely used quantum technologies, such as efficient sources of pairs of entangled photons, were developed to make these tests possible.
Almost immediately after the first convincing tests, in the 1970s, showing that quantum mechanics remains valid even in extreme situations where Bell inequalities are violated, questions were raised about possible loopholes in the tests, with two main targets: (1) the detection loophole—that is, the fact that detectors with limited sensitivity, which miss a significant fraction of the photons, leave open the possibility of some classes of local supplementary parameters; and (2) the locality loophole—that is, the fact that in order to prevent any possible unknown interaction between the separated objects, one should make relativistically independent measurements, in which the settings of the instruments and the measurements themselves are separated by a space-like interval, so that no interaction obeying the impossibility to propagate faster than light could interfere with the test. The locality loophole, the most important according to Bell, was addressed as early as 1982, and its closure was confirmed by several later experiments. The detection loophole, on the other hand, could be closed only with the development of new detectors with efficiencies close to 100 percent, in the 2010s. Closing the two loopholes in the same experiment demanded a new generation of experimental setups, and eventually happened in 2015. After decades of discussions, controversies, and experimental advances, it is hard not to admit that entanglement is real, and as weird as Einstein, Schrödinger, Feynman, and others thought it to be.
Beyond their role in the emergence of quantum information, Bell inequalities are directly involved in quantum cryptography, and specifically quantum key
___________________
4 J.S. Bell, On the Einstein-Podolsky-Rosen paradox, Physics 1:195-200, 1964.
5 J.S. Bell, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, 2004 (revised edition).
distribution (QKD). The basic problem addressed by QKD is to distribute to two spatially separated partners, Alice and Bob, two identical random sequences of zeros and ones. Alice and Bob will then use them as a key to encode and decode messages. The protocol, known as a “one-time pad,” is mathematically proven secure, provided that the key is used only once, for a message not longer than the key. One of the methods used to generate safely, at a distance, the two identical random sequences of zeros and ones, is based on pairs of entangled photons, which yield random but identical results if Alice and Bob choose identical settings for their measurement devices. The whole protocol demands that Alice and Bob choose at random various settings among a small list of predetermined values. After completing the measurements, they exchange information, on a public channel, about what were the chosen settings, and about some results. This allows them to select the cases of identical settings and to identify the identical keys, but other settings allow them to make a test of Bell inequalities. If they find a violation, they can be sure that there is no eavesdropper (Eve) on the line, spying on their exchange of quantum information.
Many sophisticated protocols have been elaborated based on the idea that a Bell test is a way to check whether information could be obtained by a spy. In principle, such a verification is device independent, meaning that it suffices to find a violation of a Bell inequality to be sure that no information has been obtained by Eve, independently of a detailed knowledge of the employed apparatuses. Surprisingly, this kind of idea also applies to other protocols, such as the famous BB84 protocol, or continuous variables protocols, which do not use sources of entangled photon pairs. Many sophisticated protocols have been developed to take account of the imperfections of real devices in the search for practical device-independent QKD (meaning that the performance of the devices is such that they can be certified, via Bell inequality tests, safe to use even if provided by a third party). One can expect that these ideas will yield realizations of quantum cryptography devices even safer than the systems already commercially available.
One could consider these efforts to be pointless, since we have today classical cryptographic protocols, for instance the famous Rivest-Shamir-Adleman (RSA) cryptosystem, which were considered safe until recently. But we also know that RSA can be broken by Shor’s algorithm on a quantum computer, or could be broken if an adversary would find a mathematical algorithm for a classical computer allowing that individual to speed up the decomposition of a large number into its prime factors, or if the adversary had computers more powerful than ours. This may well happen in the future, which means that present encrypted messages, saved blindly today, could be deciphered a few years from now. There are many domains, from diplomacy to industrial processes, where this would be detrimental even with long delays. In contrast, intercepted messages encrypted with quantum cryptography promise to remain impossible to decipher forever, or at least as long as the basic laws of quantum physics remain valid. This is not a small advantage.
Among the advances in quantum technologies stimulated by the loophole-free tests of Bell inequalities, one in particular deserves special mention: the entanglement of two quantum bits separated by more than 1 km. Although the present entanglement rate is extremely low, it demonstrates the possibility to entangle quantum memories at a significant distance. Such memories will be essential in future quantum networks.
Nevertheless, a major problem remains to be solved: how to create and maintain entanglement at large distance, say, more than 50 km. At such a distance, even the best optical fibers have too strong attenuation, and it would be necessary to rejuvenate a pair of entangled photons with a series of QRs spaced at shorter distances along the way. Although several setups have been proposed, and some of their elements have been experimentally demonstrated, no practical QR exists today. Various systems are under study, in AMO physics and in condensed-matter laboratories, as described in the following section. For the time being, expedients must be used. One approach consists of building every 50 km a “trusted node”—that is, a building controlled by trusted guards, where the quantum information is converted to classical information and then resent in a rejuvenated quantum form. While this approach can possibly be used for some specific applications, over limited distances, it does not provide a true quantum security guarantee, does not allow for the distribution of superposition states, and can hardly be generalized to the scale of the world. More interestingly, pairs of entangled photons sent from a satellite (acting as a trusted node) have been distributed over distances on the order of 1,000 km,6 since they suffer from absorption only in the atmospheric part of the photon trajectories. This approach is currently limited by several factors, including low quantum key generation rate, and a number of major engineering challenges that must be overcome to achieve large-scale practical application.
Another application of the Bell tests, less cited but important, is the validation of a genuine random number generator (RNG). A possible definition of a genuine RNG is one whose output cannot be known by anybody before it is delivered. Measurements on only one of the components of an entangled pair fulfill that condition, if a Bell test shows a violation of Bell inequalities, since then we know that there cannot be a local supplementary parameter determining the result of the measurement. This is another example of a device-independent certification based on the Bell inequalities test.
Long-Distance Quantum Communication and Applications of Distributed Entanglement
As mentioned above, efficient quantum communication over long distances (≥1,000 km) remains an outstanding challenge due to attenuation and operation
___________________
6 J. Yin, Y. Cao, Y.-H. Li1, S.-K. Liao, L. Zhang, J.-G. Ren, W.-Q. Cai, et al., Satellite-based entanglement distribution over 1200 kilometers, Science 356:1180-1184, 2017.
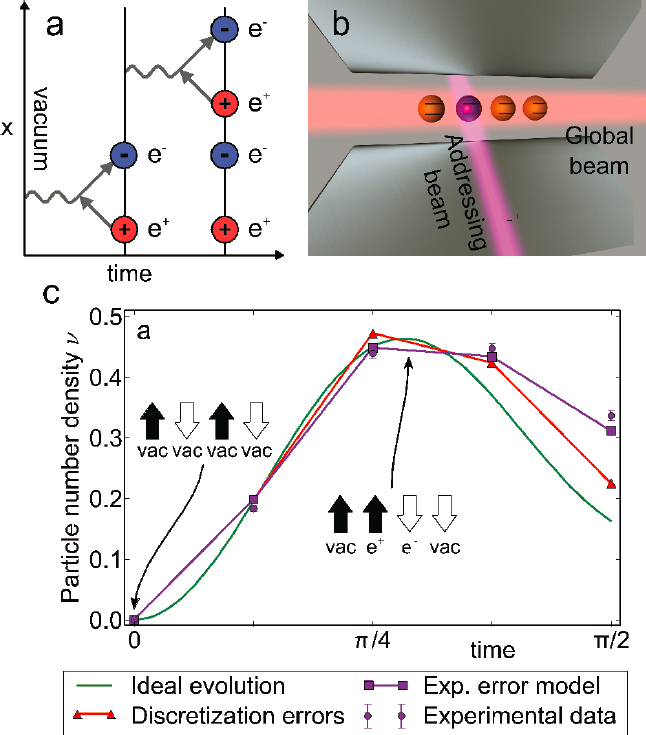
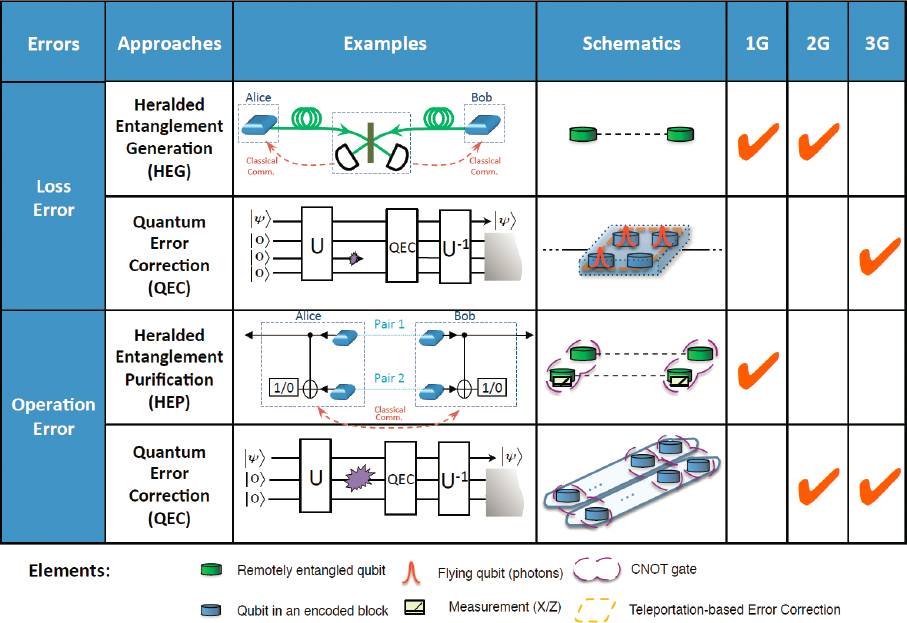
errors accumulated over the entire communication distance. To overcome these challenges, QRs have been proposed for fiber-based long-distance quantum communication. The essence of QRs is to divide the total distance of communication into shorter intermediate segments connected by QR stations, in which loss errors and operation errors can be suppressed, by applying error detection (e.g., heralded entanglement generation and purification) or even error correction operations. Based on the methods adopted to suppress loss and operation errors, various QRs can be classified into three different generations (types), as shown schematically in Figure 4.6. These various QRs can significantly reduce the temporal resource overhead associated with extending the distance of the generated entanglement, from exponential to polynomial or even poly-logarithmic scaling with distance, while maintaining a reasonable physical resource requirement.
The capability of generating long-distance entanglement with QRs opens many new promising applications. Global-scale privacy-related protocols can be implemented, such as sharing of classical or quantum secrets, schemes for verifiable multiparty agreement, anonymous transmission, secure delegated quantum computing using network-based untrusted servers, and even blind computation wherein algorithms are performed directly on encrypted data. In addition, other related interesting applications have been proposed outside the domain of cryptography. For example, we can build long-baseline optical telescopes to improve astronomical observations and improve the synchronization and security of quantum networks of clocks.
To physically implement QRs, it will be advantageous to take a hybrid approach, as other physical platforms might provide better quantum memory and quantum gates than photonic systems. The hybrid approach often requires the quantum system to have (1) a quantum interface to reliably couple to the fiber optical modes, (2) good heralded quantum memory for storage and entanglement purification, and (3) the capability of quantum gates for quantum error detection/correction. Note that the quantum memory requirement varies for different generations of QRs. The implementation of quantum gates can be nondeterministic—for example, operations based on heralded partial Bell measurements. Recently, there have been significant advances in developing such hybrid quantum systems, based on trapped ions, neutral atoms, color defect centers, quantum dots, rare-earth ions, superconducting devices, and so on.
The outstanding challenge is to develop a hybrid quantum system that can simultaneously fulfill all these requirements with high fidelity and efficiency. There is now a broad effort across various promising physical platforms to first demonstrate QRs. The trapped-ion platform (with good memory and reliable gates) has recently improved the optical coupling efficiency by orders of magnitude, so that it can generate entanglement faster than the observed decoherence, overcoming the resource scaling requirement for quantum networks. Atomic ensembles with Rydberg
interactions not only have good optical coupling, but also Rydberg-induced photon-photon interactions for deterministic gates to enhance the efficiency of QR nodes. Various quantum transducers for microwave-optical conversion are actively being pursued using various hybrid systems, which will extend superconducting quantum information processing capability from microwave to optical photons for quantum networks. Nanophotonic devices coupled to cold atoms or atom-like solid-state quantum emitters can efficiently guide the emitted photons to optical fibers with extremely high efficiency (>95 percent), enabling access to individual rare-earth ion quantum memories, demonstrated at Princeton University, or even providing controlled interactions between pairs of color centers, demonstrated at Harvard. In particular, integrated quantum network nodes combining all necessary ingredients have been demonstrated recently using silicon-vacancy centers in diamond. Most recently, this system was used by the Harvard University-Massachusetts Institute of Technology collaboration to demonstrate memory-enhanced quantum communication. Specifically, a single solid-state spin memory integrated in a nanophotonic diamond resonator was used in a proof-of-concept experiment to implement asynchronous Bell-state measurements, a key element of QR. This enabled a four-fold increase in the quantum communication rate of over the loss-equivalent direct-transmission method while operating megahertz clock rates. In the coming decade these approaches will likely result in realization and testing of medium-scale, functional quantum network prototypes that extend the range of quantum communication.
QUANTUM INFORMATION SCIENCE FOR SENSING AND METROLOGY
Realization of Spin Squeezing
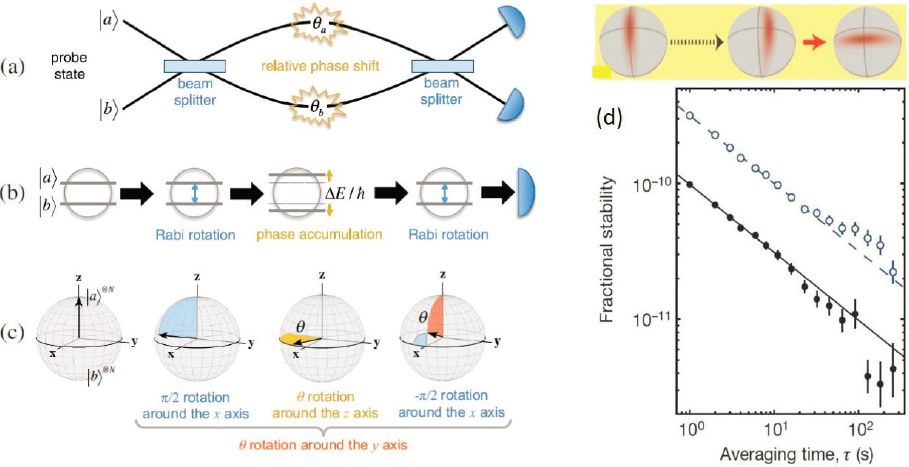
Many precision measurements in atomic physics are carried out in the form of a frequency measurement of the phase evolution speed between two atomic states (see also Chapter 6). When the measurement is performed with many independent particles to increase the signal-to-noise ratio, the precision increases as the square root of the particle number, a situation referred to as the standard quantum limit (SQL). The SQL can be overcome by using many-atom entangled states to perform the measurement. With suitably chosen states, the measurement precision can be significantly better than the SQL, and in principle approach the Heisenberg limit, where the precision improves linearly with the particle number. Highly useful entangled states are squeezed spin states (SSSs), in which the uncertainty in one variable of interest is reduced at the expense of another variable that does not affect the measurement precision to lowest order. SSSs can be directly used as input states to a standard metrology procedure (such as Ramsey sequence; see Figure 4.7), yielding lower quantum noise than a corresponding sequence with an
unentangled coherent spin state (CSS). In Bose-Einstein condensates, SSSs can be prepared using state-dependent collisions. Another possibility, more suitable for precision measurements, is optical preparation, in which a mode of a light field acts as an intermediary that creates an effective spin-dependent atom-atom interaction.
To make the interaction as coherent and strong as possible, an optical resonator enclosing the ensemble can be used. In this way, spin squeezing approaching 20 dB has been realized. This number corresponds to a reduction of the variance by a factor 100 below the SQL, which, under ideal circumstances, would enable a reduction of the measurement time to reach a given precision by the same factor.
SSSs can in principle be used to improve any quantum measurement based on interference—for example, Ramsey-type measurements. A particularly interesting possibility is the application to optical-lattice clocks, that are already achieving precision at the low 10−17/Hz1/2 level at JILA and NIST, and fractional accuracies at the 10−18 level, and that are operating at or near the SQL. Here SSSs could usher
in a new generation of clocks, where many-body entangled states can further increase the precision by one or two orders of magnitude, leading to, for example, gravitational-red-shift sensitivity at the millimeter scale. Other promising applications of SSSs include atom interferometry to achieve unprecedented signal-to-noise ratio for precision tests and measurements of fundamental constants.
New Applications of Quantum Sensing
In recent years, solid-state atom-like quantum systems have attracted intense interest as precision quantum sensors with wide-ranging applications in both the physical and life sciences. Most prominently, nitrogen-vacancy (NV) color centers in diamond provide an unprecedented combination of nanoscale spatial resolution and sensitivity to electromagnetic fields and temperature, while operating over a wide range of temperatures from cryogenic to well above room temperature in a robust, solid-state system. Importantly, since NV centers are atomic-size defects and can be localized very close to the diamond surface, they can be brought to within a few nanometers of the sample of interest, greatly enhancing the sample’s magnetic or electric field at the position of the NV sensor and enabling nanometer-scale spatial resolution. For magnetic field sensing, one optically measures the effect of the Zeeman shift on the NV ground-state spin levels. Similarly, NV-diamond can provide nanoscale electric field sensing via a linear Stark shift in the NV ground-state spin levels induced by interactions with the crystalline lattice and can provide nanoscale temperature sensing via a change in the zero-magnetic-field splitting between the NV spin levels. In addition, NV-diamond has other enabling properties for both physical and life science applications, including the following: fluorescence that typically does not bleach or blink; ability to be fabricated into a wide variety of forms such as nanocrystals, atomic force microscope tips, and bulk chips with NVs a few nanometers from the surface or uniformly distributed at high density; compatibility with most materials (metals, semiconductors, liquids, polymers, etc.); benign chemical properties; and good endocytosis with no known cytotoxicity for diamond nanocrystals and other structures used in sensing and imaging of living biological cells and tissues.
Applications of NV-diamond quantum sensors are rapidly advancing and diversifying, with translation of the technology into other fields accelerating and commercialization under way. Some recent highlights and their future potential are outlined here. NMR detection of a single protein and MRI of a single proton with angstrom resolution may lead to structure determination of individual proteins and other materials of interest with atomic-scale resolution (see Box 4.4). Noninvasive sensing and imaging of biomagnetism in living cells and whole animals with submicron resolution—for example, see Figure 4.8—provides a powerful new platform for studies in cell biology, genetics, brain function and disease, as well as lab-on-a-chip bioassays. In vivo nanodiamonds, which have been used to map temperature and
chemical changes in living human cells, have the potential for guiding thermoablative therapy for tumors and other lesions, and in the longer term may be used to monitor and even repair in vivo damage at the cellular and molecular level. Mapping of heterogeneous magnetic materials within primitive meteorites and early Earth rocks (>4 billion years old) with micron resolution is already providing key advances in the understanding of the formation of the solar system and Earth’s geodynamo.
Similarly, imaging patterns of nanoscale magnetic fields is being successfully applied to a wide variety of advanced materials such as magnetic insulators undergoing spin injection, skyrmions, graphene, spin-torque oscillators, and canted antiferromagnets. This method may fill a critical technical need in the exploration and targeted development of smart materials for challenges in energy, the environment, information processing, and more. Recent work has also realized discrete time crystals in NV-diamond: this new form of matter may enable further advance in NV-diamond sensors by greatly extending the coherence time of dense NV ensembles. In addition, robust bulk diamond and nanodiamond sensors are being developed for extreme environments, which could provide unique tools for sensing buried ordinance and natural resources, as well as navigation, including underground, deep underwater, in conditions of extreme heat, radiation, pressure, and so on.
GRAND CHALLENGES AND OPPORTUNITIES
Grand Challenge: Realization of Large-Scale Quantum Machines and Networks
How do we build nearly perfect large-scale quantum machines out of a collection of imperfect parts? How do we nearly perfectly control these systems with imperfect controllers? The quantum states that give quantum machines their extraordinary
powers are at the same time much more fragile than the states of classical machines. Furthermore, if we measure a quantum state, the very act of observation “collapses” that state. Thus, the task of fault-tolerant design is vastly more subtle and challenging than it is in traditional classical systems design. It is a remarkable fact that, with certain assumptions on the noise and error model, it is mathematically proven that fault tolerance is possible in principle. For quantum computing, this can be achieved by creating logical qubits that encode quantum information in entangled states of multiple physical qubits. To drive down the error rate, one can concatenate this procedure by building higher-level logical qubits from groups of lower-level logical qubits. Under concatenation, the error rate falls extremely rapidly. Unfortunately, the count of hardware parts rises exponentially with concatenation depth. The technological challenge at this stage of development is that we neither have access to exponentially large numbers of high-quality components nor the ability to control and measure them. It is possible that this challenge can be met head on through engineering, but an important intellectual challenge is to develop completely new ideas that will allow us to avoid the hardware count explosion and achieve practical fault tolerance in a manner that is much more “hardware efficient.”
A related aspect of this grand challenge is the problem of navigating inside the enormous state space of quantum machines, measuring and controlling where the system is in this space and verifying that the quantum error-correction protocols and other processes are working as planned. In addition to Hamiltonian engineering, one must be able to control and engineer the dissipation in the system. Naively, dissipation is bad for quantum coherence, but new ideas and experiments are beginning to appear for using dissipation to stabilize and enhance coherence.
A third aspect is to connect quantum machines through quantum networks and to invent hybrid systems for transduction between different hardware platforms and signal modalities. For example, cryogenic superconducting microwave quantum circuits offer great advantages for universal control of complex photon states, while fiber optics offers the ability to transmit information over large distances at room temperature. In the past decade, promising first steps were taken toward transducers that can reversibly and noiselessly convert quantum information across the five-orders-of-magnitude frequency gap between the optical and microwave domains, but much remains to be done in the next decade. At the same time, recently demonstrated techniques for efficient interfacing between single photons and long-lived memories associated with spin states of individual quantum emitters will need to be developed and deployed for realization and testing of quantum networking protocols.
Grand Challenge: Applications of Large-Scale Quantum Machines
Experimental efforts to manipulate large-scale quantum systems are achieving steadily improving results: systems involving approximately 100 strongly interacting,
controllable quantum particles with large-scale entanglement are becoming an experimental reality. What can such quantum machines do both in principle and in practice? Can they provide a useful quantum advantage for real-world problems in areas such as computation, simulation, and communication? For example, even though recent advances already allow for unprecedented new insight into the physics of complex quantum many-body systems, it currently remains an open question if, and to what extent, large-scale quantum computers can be used to obtain meaningful speed-up for any practically relevant tasks apart from Shor’s factoring algorithm. At the same time, while it is well-known that networks of quantum systems can potentially be used for nonlocal distribution of quantum entanglement, it is currently unclear how to implement any practically relevant applications beyond quantum key distribution, and to what extent they might work without error correction.
Addressing these exciting challenges will likely require coordinated effort across several subfields of physics, computer science, mathematics, chemistry, engineering, and materials science. New, efficient quantum algorithms for solving scientific and computational problems need to be developed and adopted for specific hardware implementations. Hybrid approaches combining state-of-the-art classical and quantum computational approaches also need to be explored. Most importantly, advances in building quantum machines should allow researchers to implement and test novel quantum algorithms for diverse scientific applications, and to explore practical methods for quantum error correction and fault tolerance. They could enable the first realizations and tests of quantum networks with applications to long-distance quantum communication and nonlocal quantum sensing.
Grand Challenge: New Fundamental Science with Programmable Many-Body Systems and Quantum Simulators
The fact that the number of possible quantum states of a system grows exponentially with system size presents enormous challenges for the use of conventional computers to carry out numerical predictions of the properties of many-body systems and lattice-gauge theories of interest in condensed-matter, nuclear, and high-energy physics. We are just entering an exciting new era in which programmable quantum simulators are beginning to be used to elucidate the properties of important models and make new discoveries of great interest in these fields.
How do we make these quantum simulators fully programmable, large-scale, and also very high-fidelity (e.g., through quantum error correction and fault-tolerant quantum gate operations)? Quantum simulators offer the advantage of extraordinary experimental access through direct measurement techniques to the quantum state of the system being simulated. In particular, they allow one to measure the most fundamental properties of quantum many-body systems such as
quantum entanglement and to explore fundamentally new phenomena away from equilibrium. However, many-body systems can be characterized not only by local order parameters that are easily measurable, but often by subtle nonlocal many-body correlations associated with hidden underlying characteristics—for example, the correlations that are associated with spin liquids. Much more work remains to be done to develop measurement techniques for these important but subtle quantities. Efforts combining the most advanced quantum and classical methods (such as those combining quantum simulators and classical and quantum machine learning) should be pursued.
As discussed further in Chapter 7, AMO physics produces new tools and measurement techniques that have broad impact in other fields of fundamental science as well as practical applications with economic impact. In particular, quantum matter and quantum sensors are playing an important role in the elucidation of new science in biology, medicine, cosmology, astrophysics, condensed-matter, geophysics, and other fields. The next decade will bring numerous additional opportunities for new science as well as new near-term applications.
Quantum Information and AMO Physics: New Opportunities
The above considerations, consistent with Quantum Computing,7 make it clear that despite major progress across several disciplines of physical, engineering, and computer science, the field of quantum information science and engineering is still in its early stages of development, with major outstanding challenges not only involving practical realization and applications of large-scale quantum machines, but of fundamental science as well. It is clear that AMO systems, methods, and techniques are uniquely suited to addressing these challenges in the coming decade, and will likely play a pivotal role in both basic science explorations and developing the first applications of quantum machines. The key distinguishing feature of AMO systems is a combination of an excellent degree of coherence and well-developed quantum control techniques that can be directly extended to medium-scale systems involving tens to hundreds of identical qubits without need for complex quantum error correction. In the coming decades, these systems and techniques should allow researchers to explore classically intractable problems in quantum dynamics, explore outstanding questions in physics of high-temperature superconductivity and in spin liquids, allow realization and testing of quantum optimization algorithms, and investigate hardware-efficient approaches to quantum error correction.
To support this assessment, the committee provides a brief summary of the most recent developments in the field, described in this chapter, that have occurred
___________________
7 National Academies of Sciences, Engineering, and Medicine, 2019, Quantum Computing: Progress and Prospects, The National Academies Press, Washington, DC.
since Quantum Computing was published in 2019, and the corresponding near-term opportunities that they open up.
Strings of trapped ions represent both a leading platform for universal quantum computation, and as a programmable analog quantum simulator. Experimentally, system sizes of 53 qubits have been built. Gate fidelities have improved to 99.9(1) percent, and operating speeds have increased to the microsecond scale. A central issue is scalability, and going from 1D to 2D ion-trap arrays. These advances in ion-trap quantum computing have enabled the implementation of a plethora of routines and algorithms. This includes repetitive error correction and encoding and operations in topological codes. With increasing numbers of qubits, routines are required to characterize, verify, and validate the performance of ion-trap devices. Prominent examples for such verification routines with trapped ions are scalable benchmarking, scalable tomography, and methods that work with incomplete data. On the quantum computing side, this provides a basis for the implementation of numerous algorithms and digital simulations such as Shor’s algorithm, Bernstein-Vazirani, and the Hidden Shift algorithm. Furthermore, ion-trap quantum computer architecture has been used to implement digital quantum simulation. Particularly promising are variational quantum algorithms for quantum chemistry, and the recent implementation of variational quantum simulation of ground and excited states of lattice models. As discussed earlier in Box 4.1, this latter experiment demonstrated verification—that is, an error bar for variational energies was computed on the quantum machine.
Rydberg atom arrays emerged, based on the experiments carried out over the past 2 years, as a leading platform for quantum information processing and simulations. As discussed in the section “Controlled Many-Body Systems for Quantum Simulations,” specific highlights include realization of a programmable quantum spin model with tunable interactions and system sizes of up to 51 qubits, and its use for probing the Kibble-Zurek mechanism, quantum critical dynamics, topological physics, discovery of quantum many-body scars, and, most recently, realization of a 20-atom GHZ state, the largest GHZ state demonstrated to date. This approach opens up unique opportunities for realizing deep quantum circuits with coherent systems consisting of hundreds of qubits in two or three spatial dimensions, with applications ranging from testing quantum algorithms and exploring efficient approaches for quantum error corrections, to realization of quantum machine learning models and generation of large-scale entangled states for quantum metrology. In particular, programmable quantum simulators based on trapped ions and neutral atoms hold great promise for simulating complex systems ranging from spin liquids to lattice-gauge theories. They appear to be particularly suitable for implementation of variational and quantum-classical algorithms, leading the search for first useful applications of quantum processors.
As described in the section “Long-Distance Quantum Communication and Applications of Distributed Entanglement,” integrated quantum network nodes have
been demonstrated recently using trapped cold atoms and ions, and color centers in diamond. In particular, quantum nodes combining all necessary ingredients—from efficient quantum-optical interfaces to long-lived memory and multiqubit operations—have been demonstrated recently using atom-like silicon vacancy centers in diamond. Proof-of-concept demonstration of emory-enhanced quantum communication has been carried out using system. These developments open up unique opportunities for realization of QRs for long-distance communication and for exploring new applications of quantum networks. In addition, these quantum networks provide a viable route for scaling up quantum processors to large-scale devices, by connecting small-scale quantum computers via quantum channels, thereby allowing quantum computation or simulation on quantum networks. It is one of the key features of atomic quantum hardware that quantum processors, involving local quantum memory and gate operations, representing the nodes of the quantum network, combine naturally with atom-photon quantum interfaces, enabling the needed conversion of “stationary” atomic to “flying” photonic qubits.
Recent advances demonstrating >20 dB spin squeezing, as well as in controlling coherent dynamics of strongly correlated systems, open the door for exciting applications of entangled states in quantum metrology. Exciting avenues range from the use of spin squeezing and entanglement to further improve the state-of-the-art optical atomic clocks, to realization of quantum sensor networks, and the use of strongly correlated states in systems ranging from ultracold atoms to solid-state atom-like systems to enable novel sensing functionalities and applications. Last, we expect that in the coming decade quantum sensors based on atom-like solid-state systems will be deployed for addressing long-standing goals such as single-molecule NMR and for realization of practical applications such as biomedical diagnostics and MRI on a chip.
Based on ideas from AMO physics, continuous-variable quantum information processing is making significant progress in the domain of microwave photons coupled to Josephson junction electrical circuit elements acting as artificial atoms. The first error-corrected logical qubit quantum memory to exceed the break-even point (i.e., achieve lifetime extension) for quantum error correction encoded the quantum information in a Schrödinger cat state of microwave photons (see the section “Cavity and Circuit QED”). A controlled-NOT entangling gate on two logically encoded photonic qubits was used for the first deterministic gate teleportation experiment. The one- and two-logical-qubit gate operations that have been developed for these cases are particular to the logical encoding used. The universal code agnostic entangling E-SWAP gate has recently been demonstrated for the first time and used to entangle two microwave cavities each holding a variety of different photon states. In addition, two superconducting qubits at opposite ends of a 78-cm microwave transmission line have been entangled with high fidelity. These advances represent substantial first steps toward construction of a modular architecture for quantum computation using error-corrected logical qubits that do not require vast overhead.
FINDINGS AND RECOMMENDATIONS
Finding: There are many possible systems and platforms for construction of quantum machines. The technology development is still at a very early stage and the state of the art is evolving very rapidly.
Finding: The federal government has decided to pursue a “science first” policy for quantum information science.
Recommendation: In support of the National Quantum Initiative, federal funding agencies should broadly support the basic research underlying quantum information science.
Recommendation: Academia and industry should work together to enable, support, and integrate cutting-edge basic research, complemented by focused engineering efforts for the most advanced quantum information science platforms.
Recommendation: The Department of Energy and other federal agencies should encourage medium-scale collaborations in quantum information science among academia, national laboratories, and industry.
Finding: The Department of Defense has a long history of supporting AMO research as part of its mission. This has been richly rewarded by numerous developments including the laser, GPS, optics, and a multitude of sensors. More recently, the National Institute of Standards and Technology and the National Science Foundation have joined with the Department of Defense, leading to the emergence and nurturing of all aspects of QIS. Most recently, the Department of Energy is expected to play a major role in the National Quantum Initiative.
Recommendation: (a) The Department of Defense (DoD) should continue both this foundational support for novel developments and the exploitation of the resulting technologies. (b) U.S. funding agencies participating in the National Quantum Initiative (NQI) should collaborate with each other and with DoD to build on the long history in quantum information science when developing their plans under NQI. (c) The Department of Energy and its laboratories should develop strong collaborations with leading academic institutions and other U.S. funding agencies to realize the full potential of quantum information science.










































