3
EXAMPLES OF CONSTRUCTIVE CROSS-FERTILIZATION BETWEEN THE MATHEMATICAL SCIENCES AND CHEMISTRY
Use of Statistics to Predict the Biological Potency of Molecules Later Marketed as New Drugs and Agricultural Chemicals
Because the search for new drugs or pesticides typically involves the investigation of thousands of compounds, many research investigators have sought computer methods that would correctly forecast the biological properties of compounds before their synthesis. Box 3.1 describes how searches for new drugs or pesticides are done. There are four well-documented cases of the use of computer methods, particularly quantitative structure-activity relationship (QSAR) methods, as an integral part of the design of compounds that are now marketed as drugs or agrochemicals. Not only are these compounds commercial successes for the companies that developed them, but they benefit mankind by aiding in the treatment of disease or increasing the food supply. This viewpoint has been so successful that recently a company, Arris, was founded to incorporate the direct involvement of mathematicians in the development of proprietary drug design software.
The Hansch-Fujita QSAR method (Hansch and Fujita, 1964) was developed in the early 1960s and has become widely used by medicinal and agricultural chemists. In this method, one first describes each molecule in terms of its physical properties and then uses statistical methods to uncover the relationship between some combination of these physical properties and biological potency.
Usually in QSAR methods the relationships are examined with multiple linear or nonlinear regression, classical multivariate statistical techniques. However, discriminant analysis, principal components regression, factor analysis, and neural networks have been applied to these problems as well. More recently, the partial least squares (PLS) method (Wold et al., 1983) has found wide use in both QSAR and analytical chemistry. Although PLS was originally developed by a statistician for use in econometrics, its widespread utility in chemistry has prompted additional statistical research to improve its speed and its ability to forecast the properties of new compounds, and to provide mechanisms to include nonlinear relationships in the equations.
Recently, Boyd described four cases in which QSAR and other computer analysis led to a commercial product (Boyd, 1990). He documented each case carefully by correspondence with the original inventors. The first is the antibacterial compound norfloxacin marketed for human therapy in Japan, the United States, and other countries. It is up to 500 times more potent than previously marketed compounds of this class. Additionally, it is effective against Pseudomonas, a difficult organism to control. Norfloxacin and its subsequent derivatives achieve a clinical efficacy of approximately 90%. Norfloxacin was designed at the Kyorin Pharmaceutical Company in Japan from a traditional QSAR analysis that used regression analysis of about 70 compounds.
The second and third QSAR-designed molecules to reach the market are both herbicides. Metamitron, discovered by Bayer AG in Germany, was based on a QSAR that involved the multiple linear regression analysis of 22 compounds. In 1990 it was the best seller in Europe for the protection of sugar beet crops. The other herbicide, bromobutide, has been marketed in Japan since 1987. It was developed at Sumitomo Chemical Company in Japan based on QSAR analysis of 74 compounds.
The final example concerns the fungicide myclobutanil, which entered the European market in 1986 for the treatment of grape diseases and was introduced to the U.S. market in 1989. It was developed by Rohm and Haas in the United States. The design of myclobutanil involved traditional
|
BOX 3.1 Rational Drug Design The traditional discovery of new drugs is an empirical process that starts with a compound of marginal biological activity. This "lead" compound either is discovered serendipitously by the random screening of a large number of compounds (often obtained from libraries of previously synthesized molecules) or is obtained by preparing analogues of a natural ligand (i.e., a small molecule such as a hormone that binds to a biomacromolecule such as an enzyme). Chemical intuition and experience as well as ease of synthesis serve to suggest other closely related molecules (analogues) for synthesis. This process is iterative and continues until a compound is discovered that not only possesses the requisite activity toward the target but also possesses minimal activity toward other biomacromolecules (i.e., it is selective and nontoxic). The compound must also have a desirable duration of action in a suitable dosage form, its synthesis must not be too costly so that its use will be cost-effective, it must be patentable, etc. This process can take many years, can cost millions of dollars, and often does not result in a marketed product. Any method that would make this process more efficient is clearly useful. Thus, chemists in the pharmaceutical industry have sought a more rational procedure for the discovery and design of new drugs. If the three-dimensional structure of the target biomacromolecule has been determined (e.g., by using X-ray diffraction or nuclear magnetic resonance spectroscopic techniques), a technique that has been termed structure-based drug design can be used for the design of new molecules with the potential to become useful therapeutic agents. If the three-dimensional structure of the target is unavailable, then a hypothetical model is formulated with the goal of describing the molecular features required if a particular compound is to elicit a desired biological response. This model, of course, can be validated only after a number of compounds have been synthesized and tested for their biological activity so that a statistical relationship between biological activity and physical molecular properties (i.e., a quantitative structure-activity relationship, or QSAR) can be established. Nonetheless, such a model is highly useful for focusing the synthetic effort on compounds that have the greatest chance of exhibiting increased biological activity. Rational drug design is heavily dependent on computational chemistry techniques, and advances in rational drug design are tightly coupled to advances in new algorithms for computer-assisted molecular modeling. To design a new ligand for a biomacromolecule of interest using the three-dimensional structure of the target biomacromolecule as a guide, the structure of the target must have been found with sufficient resolution to be of utility. One must then attempt to predict the bound geometry and intermolecular interactions responsible for the high binding affinity of novel potential ligands (or molecular fragments) associated with the biomacromolecular target. Computer algorithms have been developed over the past few years that aid in the identification of potential docking modes. These algorithms have also been used to identify, from three-dimensional databases, molecules that can potentially dock (and hence bind) to a biomacromolecular target. The prediction of biological activity of a potential ligand prior to synthesis represents another essential activity for the structure-based design of new drugs. This endeavor represents an enormous challenge for structure-based drug design, but some progress has been made using statistical mechanics-based free energy perturbation techniques that involve computer simulations employing molecular dynamics or Monte Carlo methods or by using QSAR methods that rely on the three-dimensional properties of the bound ligand. In spite of the obstacles associated with employing an analytical approach to the design of new drugs, rational drug design has, nonetheless, been of enormous utility to the pharmaceutical industry. The QSAR method has played a rule in the development of a number of drugs currently undergoing clinical trials and there are marketed products for which QSAR has been instrumental. A number of potential drugs that have been discovered using structure-based drug design techniques are currently under preclinical or clinical investigation for the treatment of diseases that include cancer, AIDS, rheumatoid arthritis, psoriasis, and glaucoma. |
QSAR on 67 compounds and three-dimensional molecular modeling to explain the QSAR and to provide a model of how the compounds bind to their biological target.
Although these successes are real accomplishments, researchers in medicinal and agricultural chemistry would like to extend the methods to more cases; such extensions create an opportunity for creative mathematical insights. The thrust of new research in QSAR has been to calculate the descriptors of the molecules from their three-dimensional arrangements of atoms and electrons in space (Kubinyi, 1993). The problem is that one of the popular methods, the comparative molecular field analysis (CoMFA), generates thousands of descriptors for each molecule, whereas the dataset typically contains biological activity for only 10 to 30 members. While partial least squares can properly handle such data, it is sensitive to random noise, with the result that the true signal may be masked by irrelevant predictors. QSAR workers need a new method to analyze matrices with thousands of correlated predictors, some of which are irrelevant to the end point. This is an opportunity for a mathematical scientist to contribute an original approach to an important problem.
The new company Arris was founded on the basis of a close collaboration of mathematicians and theoretical chemists. They have produced QSAR software that examines the three-dimensional properties of molecules using techniques from artificial intelligence (Jain et al., 1994). The initial results from this work are promising and suggest that further improvements in three-dimensional QSAR could result from additional collaborations between mathematicians and theoretical chemists.
References
Boyd, D.B., 1990, Successes of Computer-Assisted Molecular Design, Reviews in Computational Chemistry, VCH Publishers, New York, pp. 355–371.
Hansch, C., and T. Fujita, 1964, Rho sigma pi analysis: A method for the correlation of biological activity and chemical structure, Journal of the American Chemical Society 86:161–162.
Jain, A., K. Koile, and D. Chapman, 1994, Compass: Predicting biological activities from molecular surface properties; Performance comparisons on a steroid benchmark, Journal of Medicinal Chemistry 34:2315–2327.
Kubinyi, H., ed., 1993, 3D QSAR in Drug Design: Theory, Methods, and Applications, ESCOM, Leiden.
Wold, S., H. Marten, and H. Wold, 1983, The multivariate calibration problem in chemistry solved by the PLS method, Matrix Pencils (Lecture Notes in Mathematics), Springer-Verlag, Heidelberg, pp. 286–293.
Numerical Analysis
Since much of current computational chemistry is based on numerical computation, it is not surprising to find successful transfers of information from the numerical analysis community to computational chemistry. Subroutine packages such as LINPACK, EISPACK, and those in the NAG and IMSL libraries codify algorithms for solving linear equations and eigenproblems, developed by the numerical linear algebra community over a period of decades. These software packages provided reliable and well-documented solutions to common mathematical problems with a fixed and well-defined user interface. The internal details of these components have been enhanced from time to time, for example, through the use of the basic linear algebra subroutines (BLAS) that allowed computer vendors to optimize performance to some extent without requiring significant changes to the source code of these packages. This allowed them to be used effectively on vector supercomputers when they were introduced. Many of the EISPACK routines were incorporated into widely used
quantum chemistry packages such as GAMESS, HONDO, MELD, and COLUMBUS when these packages were "vectorized."
Recent advances in parallel computing have allowed much larger problems to be addressed cost-effectively. The LAPACK project funded by the National Science Foundation (NSF) has developed software for solving linear equations on modern high-performance computers (Demmel et al., 1993). The Defense Department's Advanced Research Projects Agency is funding a similar project called PRISM to develop scalable implementations of an eigensolver based on the invariant subspace decomposition approach (ISDA), as well as parallel implementations of fundamental linear algebra operations such as band reduction, tridiagonalization, and matrix multiplication.
A more recent advance in numerical analysis is the method of multipole expansions for computing long-range forces, such as Coulombic forces, more efficiently through the use of very accurate simplified approximations (Draghicescu, 1994) in the far field. This has been applied successfully in molecular dynamics with implementations for both sequential and parallel computers (Ding et al., 1992a,b).
Many computational chemistry codes have been adapted to work efficiently on parallel computers by a variety of techniques. Much of this has been achieved by modifying programs and data structures using techniques from computer science (Plimpton and Hendrickson, 1994). However in other codes, new parallel algorithms have been developed. For example, grid-based electrostatics
|
BOX 3.2 Research Opportunities in Parallel Computing Considerable opportunities for advances remain regarding parallel computation that could impact computational chemistry. For example, multigrid methods solve grid-based electrostatics problems in an optimal amount of work (and storage) on sequential computers. That is, the unknown potential can be determined on a grid of n points in O(n) work and storage. However, the standard adaptation of multigrid methods to parallel computers is not optimally efficient. A significant theoretical problem is whether a solution technique exists that uses only O(n/p)work on a parallel computer with p processors. |
calculations (Davis et al., 1990) provide one of the most difficult simulations to parallelize with full efficiency, due to the long-range interactions implicit in such partial differential equations (see Box 3.2). No part of the problem domain can be treated independently of any other, and so there is no natural parallelism in such problems. Like many algorithms in scientific computation, parallelism must be created at the expense of communication between processors that would be absent in the uniprocessor implementation.
Despite the inherent difficulties in parallelizing such problems, novel domain decomposition methods have provided effective parallel iterative methods (Ilin et al., 1995). These techniques allow extremely large problems to be solved in a moderate amount of time on massively parallel processors. They have been incorporated into the computer code UHBD, which has been used effectively to study biomedically significant enzymes in different ways, providing critical insight into the discovery of new behavior (Gilson et al., 1994) and even allowing the engineering of new, more effective enzymes (Getzoff et al., 1992).
References
Davis, M.E., J.D. Luty, B.A. Allision, and J.A. McCammon, 1990, Electrostatics and diffusion of molecules in solution: Simulations with the University of Houston Brownian Dynamics program, Computer Physics Communications 62:187–197.
Demmel, James W., Michael T. Heath, and Henk A. van der Vorst, 1993, Parallel numerical linear algebra, Acta Numerica 3:111–197.
Ding, Hong-Qiang, Naoki Karasawa, and William A. Goddard III, 1992a, The reduced cell multipole method for Coulomb interactions in periodic systems with million-atom unit cells, Chemical Physics Letters 196:610.
Ding, Hong-Qiang, Naoki Karasawa, and William A. Goddard III, 1992b, Atomic level simulations on a million particles: The cell multipole method for Coulomb and London nonbond interactions, J. Chemical Physics 97:4309–4315.
Draghicescu, C.I., 1994, An efficient implementation of particle methods for the incompressible Euler equations, SIAM J. Numer. Anal. 31:1090–1108.
Getzoff, Elizabeth D., Diane E. Cabelli, Cindy L. Fisher, Hans E. Parge, Maria Silvia Viezzoli, Lucia Banci, and Robert A. Hallewell, 1992, Faster superoxide dismutase mutants designed by enhancing electrostatic guidance, Nature 358:347–351.
Gilson, M.K., T.P. Stratsma, J.A. McCammon, D.R. Ripoll, C.H. Faerman, P.H. Axelsen, I. Silman, and J.L. Sussman, 1994, Open "back door" in a molecular dynamics simulation of acetylcholinesterase, Science 263:1276–1278.
Ilin, A., B. Bagheri, L.R. Scott, J.M. Briggs, and J.A. McCammon, 1995, Parallelization of Poisson Boltzmann and Brownian Dynamics calculation, in Parallel Computing in Computational Chemistry, T.G. Mattson, ed., ACS Books, Washington, D.C.
Plimpton, S., and B. Hendrickson, 1994, A New Parallel Method for Molecular Dynamics Simulation of Macromolecular Systems, Report 94–1862, Sandia National Laboratories, Albuquerque, N. Mex.
Distance Geometry
The idea of modeling complex molecules by using residue-residue cartesian distances as a guide for understanding the nature of protein folding and energetics stimulated work in the early 1970s (Kuntz, 1975; Liljas and Rossman, 1975). It was clear, though, that more mathematical machinery was needed. The area of distance geometry already existed in the work of Blumenthal (1970), while closely related mathematics, called multidimensional scaling, was developed by Kruskal and Wish (1978) and incorporated into advanced statistical packages. In essence, distance geometry is a method to work in spaces with greater than three dimensions, allowing distance constraints to be satisfied that could not be satisfied in three dimensions. Distance geometry helps one move from collections of distances between points to possible coordinates for these points. It also helps one distinguish important information from the standard restrictions imposed on us by living in three dimensions.
Tools were developed to go from upper and lower bound distances to three-dimensional structures, a process that required projecting an object from many-dimensional space into three. A seminal paper explored what distance information was needed to determine a three-dimensional structure to a given resolution (Havel et al., 1979), and later work concluded that a large amount of imprecise data could be sufficient to determine a macromolecular structure to a high resolution (Havel et al., 1983). This was the time when nuclear magnetic resonance (NMR) spectroscopists were beginning to be able to extract atom-atom distances for matter in solution, which could then be compared with those that could be found in the crystal by X-ray diffraction (Havel and Wuthrich, 1985). Distance geometry or
|
BOX 3.3 Protein Microtutorial Proteins are large molecules composed of smaller chemical units (residues), the 20 naturally occurring amino acids, stably linked together in an ordered linear sequence. The amino acids possess distinct sizes, shapes, and mutual interactions. Consequently, the ordered sequence (denoted by "primary structure" of the protein) controls physical and biological properties. In its simplest form, "the protein folding problem" consists in predicting the three-dimensional stable shape of protein molecules from the primary structure, to facilitate understanding those physical and biological properties. While the fixed chemical structure of proteins constrains most of their chemical bond lengths and the angles between neighboring chemical bonds to lie within tight limits, a substantial number of degrees of freedom describing the local amino acid packing ("secondary structure") and the overall three-dimensional shape of the protein (its "tertiary structure'' or ''conformation") remain to be determined. It is believed that the conformation holds the key to physical and biological properties. An experimentally important type of information relevant to a protein's preferred conformation is a set of distances between selected amino acids. The folded conformation of a protein is analogous to the posture of a human body. Body motion at skeletal joints plays the rule of protein backbone and amino acid side chain folding degrees of freedom. Given a selected set of distances between skeletal joints, for instance, one might be able to infer what posture the human subject had adopted or at least to rule out several possibilities. Similarly, distance geometry for proteins can be used to reconstruct their three-dimensional conformation. |
the related approach to refine the molecule in real space (Braun and Go, 1992) turned out to be useful methods to turn NOE (nuclear Overhauser effect) distances into three-dimensional structures. Distance geometry has continued to be a key tool in the NMR spectroscopist's arsenal, providing not only the structures, but also a quantitation of how accurately they are known.
Distance geometry is an important technique in computational chemistry. The focus of the original work was to predict protein structure from amino acid sequence (see Box 3.3) and work continues along these lines using residue-residue potentials (Maiorov and Crippen, 1992). The use of distance geometry in NMR structure determination is mentioned above. Distance geometry has also been used as a tool in the development of QSARs in macromolecule-ligand binding (Ghose and Crippen, 1990) and in a docking procedure to find different orientations that ligands can have when bound to macromolecules (Kuntz et al., 1982).
An example of this last use of distance geometry is its application to the intermolecular docking of a small molecule to a protein, similar to what was done to produce the cover illustration. Distance geometry is applied by setting the distances between interacting atoms to their ideal intermolecular distance (in contrast to the bond length). The result is a general program for solving conformational problems involving one or more molecules with implicit interatomic constraints taken from the given molecular structure and explicit distance constraints added by the user. A program by Blaney et al. (1990), for example, allows one to solve model building problems on complex molecular systems that are very difficult or impossible to solve by conventional methods.
Distance geometry has also been used to establish which, if any, three-dimensional conformations of a set of molecules can be superimposed. One treats the whole ensemble of molecules simultaneously with intermolecular distances set to zero if the atoms are
Docking is the fitting and binding of small molecules (ligands) at the active sites of biomacromolecules (e.g., enzymes and DNA).
to be superimposed or to infinity if they need not be. This has become a useful method for analyzing three-dimensional structure-activity relationships (Sheridan et al., 1986).
In summary, distance geometry is a general and powerful tool for creating three-dimensional structures, usually by going into a higher-dimensional space and then projecting into three dimensions. Its power lies in exploring "conformational" space (the universe of all possible spatial arrangements of a molecule) and assessing how convincingly the data (often experimental) have implied the structure. It has been applied in this guise to structures from small organic ring systems to proteins in the ribosomal machinery. It is clearly an area in which a fundamental technique from mathematics was brought to bear in important areas of structural chemistry and biochemistry (Crippen and Havel, 1988).
Given the importance of all areas in which distance geometry has been applied to date (protein folding, ligand docking, conformational analysis), future development in this area is likely to be important for computational chemistry (Crippen, 1991). Some of the remaining major mathematical research challenges in distance geometry applied to chemistry include (1) the need to develop improved sampling algorithms (e.g., partial metrization); (2) the need for practical algorithms to solve tetrangle and higher-order inequalities; (3) the need to develop biased sampling approaches that avoid previously sampled configurations; and (4) energy embedding—given a pairwise potential, how can one best solve for the global minimum in N-1 space and then "squeeze" the system down to 3-space? A perspective on some of these challenges is given in recent reviews (Crippen, 1991; Blaney and Dixon, 1994).
References
Blaney, J.M., and J.S. Dixon, 1994, Distance geometry in molecular modeling, in Reviews in Computational Chemistry, vol. 5, K.B. Lipkowitz and D.B. Boyd, eds., VCH Publishers, New York, pp. 299–335.
Blaney, J.M., G.M. Crippen, A. Dearing, and J.S. Dixon, 1990, DGEOM program #590, Quantum Chemistry Program Exchange, Bloomington, Ind.
Blumenthal, C.M., 1970, Theory and Applications of Distance Geometry, Chelsea Publishing Co., Bronx, N.Y.
Braun, W., and N. Go, 1985, Calculation of protein conformations by proton-proton distance constraints: A new efficient algorithm, J. Mol. Biol. 186:611–626.
Crippen, G.M., 1991, Chemical distance geometry—current realization and future projection, J. Math. Chem. 6:307–324.
Crippen, G.M., and T.F. Havel, 1988, Distance Geometry and Molecular Conformation, Research Studies Press, John Wiley & Sons, New York.
Ghose, A.K., and G.M. Crippen, 1990, Modeling the benzodiazepine receptor binding site by the general three-dimensional quantitative structure-activity relationship method REMOTEDISC, Mol. Pharm. 37:725–734.
Havel, T.F., and K. Wuthrich, 1985, An evaluation of the combined use of nuclear magnetic resonance and distance geometry for the determination of protein conformations in solution, J. Mol. Biol. 182:281–294.
Havel, T.F., G.M. Crippen, and I.D. Kuntz, 1979, Effects of distance constraints on macromolecular conformation. II. Simulation of experimental results and theoretical predictions, Biopolymers 18:73–81.
Havel, T.F., I.D. Kuntz, and G.M. Crippen, 1983, The theory and practice of distance geometry, Bull. Math. Biol. 45:665–720.
Kruskal, J.B., and M. Wish, 1978, Multidimensional Scaling, Sage Publishing, Beverly Hills, Calif.
Kuntz, I.D., 1975, An approach to the tertiary structure of globular proteins, J. Am. Chem. Soc. 97:4362–4366.
Kuntz, I.D., J.M. Blaney, S.J. Oatley, R. Langridge, and T.E. Ferrin, 1982, A geometric approach to macromolecule-ligand interactions, J. Mol. Biol. 161:269–288.
Liljas, A., and M. Rossman, 1975, Recognition of structural domains in globular proteins, J. Mol. Biol. 85:177–181.
Maiorov, V.M., and G.M. Crippen, 1992, Contact potential that recognizes the correct folding of globular proteins, J. Mol. Biol. 227:876–888.
Sheridan, R.P., R. Nilakantan, J.S. Dixon, and R. Venkataraghaven, 1986, The ensemble approach to distance geometry: Application to the nictotinic pharmacophore, J. Med. Chem. 29:899–906.
Mathematics and Fullerenes
The structures and properties of the fullerene molecules—"buckyballs" (see Figure 3.1) and related highly symmetric carbon molecules that are roughly spherical—have been linked with some very central areas of mathematics.1 Topology can provide insights into the types of such structures that can and cannot exist; the symmetries of the molecules, which underlie some of their interesting properties, are naturally described with group theory; and graph theory can give insight concerning the vibrational modes of such molecules.
The prototypical buckyball molecule, C60, is composed of 60 carbon atoms linked into a shape reminiscent of a soccer ball, mathematically known as a truncated icosahedron. Other fullerenes that have been observed are composed of more than 60 carbons, except for one member of the family that contains only 44. The "surfaces" of all members are composed solely of pentagons and hexagons and share the property that each vertex connects exactly three edges. (This latter property follows from the chemical bonding of carbon atoms.) Such polyhedral surfaces are subject to a classic topological relationship derived by Euler:
where the summation is over all faces of the polyhedron and fn is the number of faces with n sides. This expression leads immediately to a property observed in all the fullerenes observed so far in the laboratory: since n is found experimentally to take only the values 5 or 6, f5 must equal 12. In addition, the formula puts no restrictions on f6, and indeed a variety of fullerene molecules with a variety of numbers of hexagonal "faces" have been synthesized.
Group theory provides a methodological way of cataloging the vibrational symmetries of fullerenes, which can be linked to measurable energy spectra. There are 174 vibrational modes for a C60 molecule, but only 46 of these are potentially distinguishable. Group theoretic arguments based on irreducible representations and Schur's lemma pare this number dramatically, explaining why the observed infrared spectrum contains just four absorption lines. The same principles applied to the
scattering measured by Raman spectroscopy explain why that spectrum should have exactly 10 lines.
Graph theory is applied to fullerenes via Hückel theory, which forms the basis of an algorithm linking stability properties to the eigenvalues of a so-called adjacency matrix (representing, in this case, which pairs of carbons are bonded). Computation of the eigenvalues would be straightforward, at least for the smaller fullerenes, but more understanding comes about through mathematical analysis. Again by using Schur's lemma and other tools of group theory, the adjacency matrix can be decomposed into much smaller blocks that are amenable to providing clearer insight. For C60 this technique has led to closed-form solutions of certain matrices (Chung et al., 1993), which in turn suggest that C60 has a stability even greater than that of benzene.
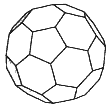
Figure 3.1 A buckyball.
References
Chung, F., and S. Steinberg, 1993, Mathematics and the buckyball, American Scientist 81:56–71.
Chung, F.R.K., D. Rockmore, and S. Steinberg, 1993, The symmetry and spectrum of the buckyball, 1993, preprint.
Quasicrystals
Interatomic and intermolecular forces have traditionally been central concerns in chemistry, not only because of the useful properties that they produce, but also because the crystallography that emerges from those forces when matter is solidified has been a dominant tool for structural analysis (see the section on X-ray crystallography below). Consequently, any striking deviation from conventional expectation about what interatomic or intermolecular forces can yield as solid-state ordering automatically concerns chemical researchers. The recently discovered quasi-crystalline state falls in this category.
That quasicrystals—orientationally ordered solids with local fivefold (or other classically unorthodox) symmetry but no spatial periodicity—really existed was demonstrated by Cahn et al. (1988) and Gratias et al. (1988). Their data were obtained from X-ray and neutron diffraction of Al73Mn21Si6 single-phase icosahedral powder and were analyzed by Patterson analysis. Their work showed that the data were best considered as representing a "cut" of a periodic six-dimensional Patterson function. This work led to the definition of quasicrystals by the "cut-and-projection" method.
What is very interesting and perhaps not so well known is that Meyer (1972), 16 years earlier and motivated by problems in number theory, had built a mathematical structure that he called a "pseudolattice," which turns out to be the correct mathematical tool for the study of quasicrystals. Meyer's work establishes the basic harmonic analysis for quasicrystals In his book, he studied socalled Pisot and Salem numbers, which can be defined as follows: A Pisot number θ is a root of a polynomial with integer coefficients of degree m such that if θ2, ..., θm are the other roots, then |θi| < 1, i = 2, ..., m. A Salem number is defined in the same way, but some of the inequalities are replaced by equalities.
One of the relations between Pisot or Salem numbers and quasicrystals is the following. Let Λ ![]() Rn be a quasicrystal. If θ > 1 and θΛ
Rn be a quasicrystal. If θ > 1 and θΛ ![]() Λ, then θ is either a Pisot or a Salem number. Conversely, if θ is either a Pisot or a Salem number, then there exists a quasicrystal Λθ
Λ, then θ is either a Pisot or a Salem number. Conversely, if θ is either a Pisot or a Salem number, then there exists a quasicrystal Λθ![]() Rn such that θΛ
Rn such that θΛ ![]() Λ.
Λ.
In order to establish that result, Meyer had to establish a theory of harmonic analysis for quasicrystals.
Recently, Moody and Patera (1993) have used fairly sophisticated Lie group and Lie algebra ideas to study families of quasicrystals. In their work the mathematics has been used as a means of unifying various physical models of quasicrystals into one consistent picture.
References
Cahn, J.W., D. Gratias, and B. Mozer, 1988, Patterson Fourier analysis of the icosahedral (A1, Si)-Mn alloy, Physical Review B 38:1638–1642.
Gratias, D., J.W. Cahn, and B. Mozer, 1988, Six-dimensional Fourier analysis of the icosahedral Al73Mn21Si6 alloy, Physical Review B 38:1643–1646.
Meyer, Y., 1972, Algebraic Numbers and Harmonic Analysis, North Holland Press. Amsterdam.
Moody, R.V., and J. Patera, 1993, Quasicrystals and icosians, J. Phys. A. Math. Gen. 26:28–29.
Chemical Topology
Topology is a branch of mathematics that studies properties of objects that do not change when the object is elastically deformed. Topology allows stretching, shrinking, twisting—any sort of elastic deformation short of breaking and reassembling the object. The basic idea in topology is to relax the rigid Euclidean notion of congruence and replace it with more flexible notions of equivalence. A flexible molecule in solution does not maintain a fixed three-dimensional configuration. Such a molecule can assume a variety of configurations (referred to as "conformation" by chemists), driven from one to the other by thermal fluctuations, solvent effects, experimental manipulation, and so on. For small molecules with complicated molecular graphs, topology can aid in the prediction and detection of various types of spatial isomers (Walba, 1985; Simon, 1986; Walba et al., 1988). Recent triumphs in the chemical synthesis of molecules with novel topology include the molecular trefoil knot (Dietrich-Buchecker and Sauvage, 1989) (Figure 3.2) and the five interlocked rings of the self-assembling compound "olympiadane" (Amabilino et al., 1994). For larger molecules, given an initial topological state, one can identify all possible attainable configurations of the molecule and can detect when an agent (chemical or biological) has intervened to change the topological state (Wasserman and Cozzarelli, 1986).
Combinatorics, Graph Theory, and Chemical Isomer Enumeration
In the nineteenth century, Arthur Cayley produced a body of work involving the enumeration of certain types of trees (connected acyclic 1-complexes); some of the enumerated trees corresponded to the number of certain (combinatorially possible) chemical compounds (Cayley, 1857, 1877). This correspondence is obtained by abstracting a chemical molecule as a molecular graph; the vertices are the atoms, and the edges are the covalent bonds, with protons (hydrogen atoms) usually suppressed. Structural isomers correspond to the (abstract) isomorphism types of these graphs. Enumeration of isomorphism types uses group theory (permutation groups) to count the intrinsic (internal) symmetries of these graphs. This work was continued and expanded in the twentieth century by Polya (Polya and
Read, 1987) and others (Balaban, 1976).
A benefit to chemistry of combinatorial enumeration is that one can build a (mathematically) complete list of molecular graphs satisfying certain similarity (homology) parameters of chemical interest. As discussed in the section of this chapter beginning on page 37, the mathematical enumeration of possibilities is just the first in a series of steps that must be taken in order to extract chemically useful information (i.e., which of the molecular graphs are chemically realizable). Of those that are realizable, how does one store representative graphs in a database in a manner in which chemically relevant queries are feasible? The abstract (intrinsic) isomorphism type of a molecular graph carries little information about the three-dimensional (extrinsic) configuration, and hence the reactivity, of chemical realizations. How does one derive three-dimensional information from an abstract one-dimensional graph?
Figure 3.2 A synthetic trefoil. Reprinted, by permission, from Dietrich-Buchecker and Sauvage (1989). Copyright 1989 by VCH Publishers, Inc.
Analysis of Molecular Spectra by Using Cayley Trees
The high-resolution electronic spectra of polyatomic molecules are often very complex, consisting of many thousands of lines; yet they often contain significant information about molecular vibration/rotation structure and intramolecular dynamics. Traditionally this information has been extracted by assigning quantum numbers to lines based on an assumed zeroth-order Hamiltonian. However there are many molecules for which the choice of zeroth-order Hamiltonian is not clear, or for which the spectra are so strongly perturbed from a known zeroth-order Hamiltonian that it is not clear how or if a spectrum can be assigned. Statistical methods have been used to analyze these spectra, but most spectra contain information beyond the simple statistical limit. Another approach is to examine coarse-grained spectra (Gomez Llorente et al., 1989), as such spectra sometimes reveal hidden structure associated with short-time molecular dynamics that can easily be interpreted.
Recently there has been interest in using the methods of graph theory, in particular Cayley trees, to study complex spectra (Davis, 1993). The basic idea is to use the spectra to construct trees by coarse-graining the spectra over a hierarchy of time scales. An analysis of the statistical properties of these trees using methods taken from the cluster analysis literature (Gordon, 1987; Jain and Dubes, 1988) then provides a systematic way of locating hidden structure in the spectra. In addition, when quantum eigenstates are available for the spectra being studied, it is possible to use the trees to determine "smoothed" states that represent the underlying vibrational dynamics responsible for the hidden structure. This also provides a short time picture of the vibrational motions of the highly excited molecule, and in many cases it is possible to relate this to the underlying classical description of the vibrational motions, including features such as periodic orbits, bottlenecks to intramolecular vibrational redistribution, and Fermi resonances.
Group Theory, Topology, Geometry, and Stereochemistry
Stereochemistry studies the spatial configuration of molecules. To enumerate and distinguish stereoisomers, one must study symmetries of the molecule in 3-space (Cotton, 1971; Fujita, 1991).
Which of the intrinsic symmetries of the molecular graph are realizable by chemically reasonable spatial transformations? Of particular interest in this situation is the notion of chirality (see Figure 3.3). A molecule in space is chiral if it is not equivalent to the configuration obtained by a flexible transformation plus reflection in a plane.
Apart from energy minimization questions, the enumeration of spatial configurations and physical symmetries and chirality of relatively small molecules requires group theory, geometry, and topology. For small molecules, group theory is useful in distinguishing stereoisomers obtained by ligand substitution and in the study of dynamic symmetry of fluxional molecules (Longuet-Higgins, 1963; Smeyers, 1992). Group theory techniques include representation theory, group characters, and so on. Group theory has also been applied to quantum chemical problems such as symmetry-adapted functions for molecular orbital theory, ligand field theory, and molecular vibrations (Cotton, 1971; National Research Council, in preparation). By using group theory and representation theory, symmetry-invariant properties of physical interest can be studied (Kramer and Cin, 1980). Mulliken (1933), for example, used ideas from finite point groups and molecular orbital theory to assign "term symbols" (i.e., irreducible representation labels) to many excited states of small, highly symmetrical molecules.
Figure 3.3 A chiral pair of synthetic Möbius molecules. Reprinted from Simon (1992) by permission of the American Mathematical Society.
New techniques for the efficient computation of the fast Fourier transform (FFT) for finite groups (Gordon, 1987; Diaconis and Rockmore, 1990) have potential applications in molecular spectroscopy and in understanding the symmetry of nonrigid molecules. The unitary group has been used in electronic structure theory to develop formulas for matrix elements, perturbation expansions, and coupled cluster expansions of the Hamiltonian written in second quantized form. For larger, more flexible molecules, the descriptive and computational ability of topology can be used to find topological barriers to the interconversion of a pair of spatial configurations or to the interconversion of protons in the molecule. Given the completely flexible equivalences of topology, in which energy, bond lengths, divalent vertices, and so on are disregarded, if two spatial molecular configurations (or specific atoms in the configuration) are topologically inequivalent, then they are physically inequivalent. Knowledge of the topological inequivalence of certain protons is useful in the analysis of NMR spectra (Walba, 1985; Walba et al., 1988). Topological considerations are sometimes very effective in detecting chirality of chemical compounds (Walba, 1985; Simon, 1986).
Topology of Polymers
Macromolecules such as synthetic polymers and biopolymers such as DNA, RNA, and proteins are very flexible and can exhibit high degrees of spatial complexity. Synthetic polymers can be very large, in some cases having on the order of 106 monomers in a polymer strand (e.g., polystyrene). Biopolymers (DNA, RNA, proteins) can also be extremely large, having hundreds to thousands of monomers. For example, in prokaryotes, DNA plasmids are on the order of 104 nucleotides, and
bacterial chromosomes are on the order of 105 nucleotides. The effects of microscopic topological entanglement (knotting and linking) of polymer strands in a polymer melt are believed to be trapped by quenching (driving off the solvent, or cooling) and (in principle) will be observable in the macroscopic physical and chemical properties of the quenched polymer network (Edwards, 1968; Flory, 1976; deGennes, 1984).
Polymers in dilute solution can be modeled by means of self-avoiding walks on a lattice or piecewise-linear curves in 3-space. The lattice spacing serves to simulate volume exclusion; in the piecewise-linear case, volume exclusion can be modeled by assigning thickness to the linear segments of the chain. The degree of entanglement complexity of a polymer with itself (knotting) or with other polymers (linking) is believed to play a significant rule in many physical and chemical processes, such as crystallization behavior and rheological properties (Edwards, 1968; Flory, 1976; deGennes, 1984). A linear polymer can be modeled as a self-avoiding walk (SAW) on the simple cubic lattice Z3; a ring polymer can be modeled as a self-avoiding polygon (SAP) on Z3. One can experimentally generate randomly embedded ring polymers by performing a cyclization (random closing) reaction on a dilute family of linear polymers of the same length N (Shaw and Wang, 1993; Rybenkov et al., 1993). A fundamental mathematical problem is to describe the yield of such a reaction: What is the distribution of knots and links produced by a random closing reaction, as a function of the length N and the concentration of linear substrate? A long-standing fundamental conjecture in this area was the Frisch-Wasserman-Delbruck (FWD) conjecture (Frisch and Wasserman, 1961; Delbruck, 1962): The probability that a random polygon contains a knot tends to one as the number of edges tends to infinity.
The FWD conjecture was recently solved with the development of a rigorous proof of the asymptotic inevitability of knotting (Soteros et al., 1992). The mathematical quantization of topological entanglement for short chains can be done by Monte Carlo simulation (Klenin et al., 1988). In Monte Carlo simulations, knotting and linking of random chains are computed in various models that include volume exclusion and some energetic terms; rigorous results in various models include the asymptotic inevitability of knotting in random chains and the (at least linear) growth of certain entanglement parameters with chain length. Monte Carlo simulation can also elucidate dynamic chemical phenomena such as electrophoresis (Slater and Noolandi, 1986) and adsorption (Smit and Siepmann, 1994). Recent striking advances in observation techniques such as fluorescence microscopy for single DNA molecules (Bustamante et al., 1990) make possible the verification and fine tuning of some of these mathematical theories of molecular conformation and dynamic molecular properties.
Knots, Links (Catenanes), and DNA
Mathematics and molecular biology continue to benefit from productive interaction, as described in the upcoming report Calculating the Secrets of Life (National Research Council, in press). One area of interaction is in the topology and geometry of DNA, because the spatial configuration of biopolymers is intimately related to function. For example, the DNA of all organisms has a complex and fascinating topology. Duplex DNA consists of a pair of DNA backbone strands (each strand is an alternating linear arrangement of sugar and phosphate moieties), and attached to each backbone are the nucleotides adenine, thymine, cytosine, and guanine. Adeninc (A) binds only to thymine (T) by means of a double hydrogen bond, and cytosine (C) binds only to guanine (G) by means of a triple hydrogen bond; the bonded pairs A-T and C-G are called base pairs. The hydrogen bonds form the rungs of a ladder, and this ladder is twisted in space in the form of a right-hand helix (the usual Crick-Watson model for the primary structure of the double helix). In the double helix, one backbone strand winds around the other on the average of every 10.5 base pairs. The human genome is on the order of 3 × 109 base pairs, which amounts to some 3 × 108 interwindings. So, human
chromosomal DNA can be viewed as two very long curves that are intertwined millions of times, linked to other curves, tied into knots, and subjected to four or five successive orders of coiling to convert it into a compact form for information storage. For information retrieval and cell viability, some geometric and topological features must be introduced, and others quickly removed. Some enzymes maintain the proper geometry and topology by passing one strand of DNA through another via an enzyme-bridged transient break in the DNA; these enzymes play crucial rules in cell metabolism, including segregation of daughter chromosomes at the termination of replication, and in maintaining proper in vivo (in the cell) DNA topology. Other enzymes break the DNA apart and recombine the ends by exchanging them. These enzymes regulate the expression of specific genes, mediate viral integration into and excision from the host genome, mediate transposition and repair of DNA, and generate antibody and genetic diversity. These enzymes perform incredible feats of topology at the molecular level; the description and quantization of spatial configuration and enzyme action require the language and computational machinery of geometry (White, 1992; Wolffe, 1994) and topology (Sumners, 1992).
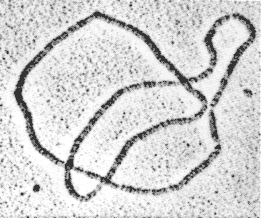
Figure 3.4 A DNA trefoil. Courtesy of N.R. Cozzarelli and A. Stasiak.
In the topological approach to enzymology (Wasserman and Cozzarelli, 1986), the topological invariance of knotted (see Figure 3.4) and catenated DNA during experimental work-up and the computational power of topology are exploited to capture information on enzyme action. For in vitro (in a test tube) experiments, an enzyme extracted from living cells is reacted with circular DNA substrate produced by cloning techniques. The enzyme reaction produces a topological signature in the form of an enzyme-specific family of supercoiled DNA knots and links (catenanes). By observing changes in DNA geometry (supercoiling, or interwinding of the DNA upon itself) and topology (knotting and linking) by means of gel electrophoresis and electron microscopy of the reaction products, the enzyme mechanism can be characterized mathematically (Sumners, 1992). Because of the enormous variety of knot and catenane structure, fine details of DNA structure and enzyme action can be selectively assayed.
References
Amabilino, D.B., P.R. Ashton, A.S. Reder, N. Spencer, and J.F. Stoddart, 1994, Olympiadane, Angewandte Chemie (Int. Eng. Ed.) 33:1286–1290.
Balaban, A.T., 1976, Chemical Applications of Graph Theory, Academic Press, London.
Bustamante, C., S. Gurrieri, and S.B. Smith, 1990, Observation of single DNA molecules during pulsed-field gel electrophoresis by fluorescence microscopy, Methods: A Companion to Methods in Enzymology 1:151–159.
Cayley, A., 1857, On the theory of analytic forms called trees, Phil. Mag. 13:172–176.
Cayley, A., 1877, On the number of univalent radicals CnH2n+1, Phil. Mag. Series 5, (3):34–35.
Cotton, F.A., 1971, Chemical Applications of Group Theory, Wiley-Interscience, New York.
Davis, M.J., 1993, Hierarchical analysis of molecular spectra, J. Chem. Phys. 98:26–14.
deGennes, P.G., 1984, Tight knots, Macromolecules 17:703–704.
Delbruck, M., 1962, Knotting problems in biology, in Mathematical Problems in the Biological Sciences (Proceedings of Symposia in Applied Mathematics, vol. 14), American Mathematical Society, Providence, R.I., pp. 55–63.
Diaconis, P., and D. Rockmore, 1990, Efficient computation of the Fourier transform for finite groups, J. Am. Math. Soc. 3:297–332.
Dietrich-Buchecker, C.O., and J.P. Sauvage, 1989, A synthetic molecular trefoil knot, Angewandte Chemie (Int. Eng. Ed.) 28:189–192.
Edwards, S.F., 1968, Statistical mechanics with topological constraints: II., J. Phys. A. 1:15–28.
Flory, P.J., 1976, Statistical thermodynamics of random networks, Proc. R. Soc. Lond. A 351:351–380.
Frisch, H.L., and E. Wasserman, 1961, Chemical topology, J. Am. Chem. Soc. 83:3789–3795.
Fujita, S., 1991, Symmetry and Combinatorial Enumeration in Chemistry, Springer-Verlag, Berlin.
Gomez Llorente, J.M., J. Zakrzewski, H.S. Taylor, and K.C. Kulander, 1989, Spectra in the chaotic region: Methods for extracting dynamic information, J. Chem. Phys. 90:150–518.
Gordon, A.D., 1987, Parsimonious trees, Classification 4:85–101.
Jain, A.K., and R.C. Dubes, 1988, Algorithms for Clustering Data, Prentice Hall, Englewood Cliffs, New Jersey.
Klenin, K.V., A.V. Vologodskii, V.V. Anshlevich, A.M. Dykhne, and M.D. Frank-Kamenetskii, 1988, Effect of excluded volume on topological properties of circular DNA, J. Biomol. Str. Dyn. 5:1173–1185.
Kramer, P., and M.D. Cin, eds., 1980, Groups, Systems and Many-Body Physics, Vieweg and Sohn Verlagsgesellschaft mbH, Braunschweig.
Longuet-Higgins, H.C., 1963, The symmetry groups of non-rigid molecules, Molec. Phys. 6: 445–460.
Mulliken, R.S., 1933, Electronic structures of poly-atomic molecules and valence IV electronic states, quantum theory of the double bond, Phys. Rev. 43:279–302.
National Research Council, 1995, Calculating the Secrets of Life, National Academy Press, Washington, D.C., in press.
National Research Council, in preparation, Group Theory: The Language of Symmetry in Science and Technology, National Academy Press, Washington, D.C.
Polya, G., and R.C. Read, 1987, Combinatorial Enumeration of Groups, Graphs, and Chemical Compounds, Springer-Verlag, New York.
Rybenkov, V.V., N.R. Cozzarelli, and A.V. Vologodskii, 1993, Probability of DNA knotting and the effective
diameter of the DNA double helix, Proc. Nat. Acad. Sci. USA 90:5307–5311.
Shaw, S.Y., and J.C. Wang, 1993, Knotting of a DNA chain during ring closure, Science 260: 533–536.
Simon, J., 1986, Topological chirality of certain molecules, Topology 25:229–235.
Simon, J., 1992, Knots and chemistry, in New Scientific Applications of Geometry and Topology (Proceedings of Symposia in Applied Mathematics, vol. 45), American Mathematical Society, Providence, R.I., pp. 97–130.
Slater, G.W., and J. Noolandi, 1986, On the reptation theory of gel electrophoresis, Biopolymers 25:431–454.
Smeyers, Y.G., 1992, Introduction to group theory for non-rigid molecules, Adv. in Quantum Chemistry 24.
Smit, B., and J.I. Siepmann, 1994, Simulating the adsorption of alkanes in zeolites, Science 264:1118–1120.
Soteros, C.E., D.W. Sumners, and S.G. Whittington, 1992, Entanglement complexity of graphs in Z3, Math. Proc. Camb. Phil. Soc. 111:75–91.
Sumners, D.W., 1992, Knot theory and DNA, in New Scientific Applications of Geometry and Topology (Proceedings of Symposia in Applied Mathematics, vol. 45), American Mathematical Society, Providence, R.I., pp. 39–72.
Walba, D., 1985, Topological stereochemistry, Tetrahedron 41:3161–3212.
Walba, D.M., J. Simon, and F. Harary, 1988, Topicity of vertices and edges in the Mobius ladders; A topological result with chemical implications, Tetrahedron Lett. 29:731–734.
Wasserman, S.A., and N.R. Cozzarelli, 1986, Biochemical topology: Applications to DNA recombination and replication, Science 232:951–960.
White, J.H., 1992, Geometry and topology of DNA and DNA-protein interactions, in New Scientific Applications of Geometry and Topology (Proceedings of Symposia in Applied Mathematics, vol. 45), American Mathematical Society, Providence, R.I., pp. 17–37.
Wolffe, A.P., 1994, Architectural transcription factors, Science 264:1100–1101.
Graph Theory
Application of Graph Theory to Organizing Chemical Literature
To organize the chemistry literature for research or patent purposes, it is essential that scientists be able to search this literature by the chemical features of interest as well as with traditional text queries. Accordingly, a body of experience has been developed for using computers to recognize either total chemical structures or parts of them from an input structural diagram and to quickly identify in databases of millions of compounds those that match the search criteria (Ash et al., 1985). Currently there are several large comprehensive chemical databases such as those maintained by Chemical Abstracts (Dittman et al., 1983) and the Beilstein Institute. (The Chemical Abstracts substance database, for example, contains information on 13 million substances, including molecular formulas and structure diagrams where available.) Chemical and pharmaceutical companies maintain such chemical information databases of their own compounds using either commercial (e.g., MDLI,
DARC, Daylight) or self-written software.
A key element to the success of such chemical information systems was the recognition that a two-dimensional chemical structure diagram can be treated as a labeled graph (Sussenguth, 1965). Many algorithms and concepts from graph theory (Harary, 1976) have been applied to chemical information problems, for example, the concepts of graph isomorphism to identify whether a particular compound is in a database and subgraph isomorphism to identify compounds that contain substructures of interest, algorithms to detect the smallest set of smallest rings as an aid to unique atom numbering heuristics, and subgraph (''clique-detection''—see Box 3.4) algorithms to detect the maximum common substructure in two molecules. These ideas have recently been extended to provide rapid searches of databases of tens to hundreds of thousands of molecules to find those that match a three-dimensional query—typically based on distances, angles, and torsions between points in the stored three-dimensional structure of the molecules (Borman, 1989; Bures et al., 1994). Generally there are between 4 and 20 distance and angle constraints to be matched in a three-dimensional query: the number of hits decreases with the number of constraints. Recently, commercial programs have been updated to include consideration of conformational flexibility.
Graph algorithms are used increasingly to solve similar problems in molecular modeling and computational chemistry (Martin et al., 1992). For example, to use a molecular mechanics program to optimize a molecular structure, each atom must be assigned an atom type based on its substructural environment. Chemical information tools are used to recognize such substructures. Modeled three-dimensional structures are stored in a chemical information database with the result that it is easy to find a prebuilt analogue of a new compound one wishes to build. Others have devised programs that build three-dimensional structures of molecules from their two-dimensional structures by finding the maximum common overlapping substructures in a database of three-dimensional structures and piecing these together (Wipke and Hahn, 1988; Leach et al., 1990).
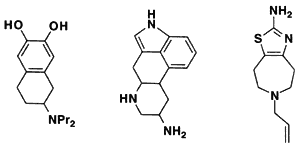
Methods based on graph theory have also been used to find common three-dimensional features within a set of molecules (Crandell and Smith, 1983; Brint and Willett, 1987; Martin et al., 1993). In particular, the Bron-Kerbosh clique-detection algorithm has been found to be especially fast (Brint and Willett, 1987). Such common three-dimensional features might represent a pharmacophore, the set of three-dimensional features that determines whether or not a molecule will show a particular biological activity. For example, Figure 3.6 depicts three different molecules that activate the D2 dopamine receptor. The figure shows that although these molecules look different in two dimensions, in three dimensions they share the arrangement of a hydrogen bond donor, its projection to a receptor hydrogen bond acceptor, a positively charged nitrogen, and its projection to an anionic site on the receptor (Martin et al., 1993).
Two-dimensional structures describe the connectedness of the atoms in a molecule. The training of a chemist involves learning how to translate these two-dimensional pictures into chemical properties. Thus, an OH means one thing to a chemist, but something different to other folks. Since molecules are really three-dimensional (with added dimensions of properties), it is important to translate the two-dimensional structure into three dimensions for computer processing. People have used the same type of graph-processing algorithms to detect parts of molecules that have certain three-dimensional properties and to then glue the three-dimensional pieces together much as when using a Tinkertoy. The methods are expert systems in that they use other knowledge, not first principles. They operate by using graph-matching ideas.
Clique-detection methods are also used to propose docking orientations of small molecules to macromolecules (Kuntz et al., 1982; Kuhl et al., 1984; Smellie et al., 1991; Kuntz, 1992). The computer program DOCK searches databases of tens of thousands of molecules to find those that fit into a macromolecular binding site of known three-dimensional structure (Kuntz, 1992). A number of structurally novel enzyme inhibitors have been identified by this means.
|
BOX 3.4 Clique Detection In graph theory terms, a clique is a subgraph in which every node is connected to every other node. For three-dimensional molecular structures, the nodes of the graph might typically be the atoms of the structure labeled according to atomic symbol and the edges are the distances between the points. Clique-detection algorithms find cliques in an input graph that match a clique in a reference graph. That is, they find corresponding points in the two three-dimensional structures such that corresponding points are of the same type in the two structures and all corresponding interpoint distances are identical within some tolerance. In Figure 3.5, two different cliques in the same molecule are indicated, as is one clique of a second molecule. As shown, the matching cliques in the two molecules can be superimposed. Notice that the points do not superimpose exactly since the lengths of the edges need only be identical within some tolerance. |
A molecule with a clique marked.
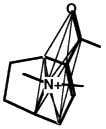
Another clique in the same molecule.
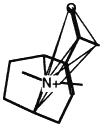
A second molecule with a clique marked.
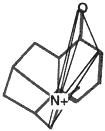
The two molecules superimposed over their matching cliques. The corresponding atoms are in shaded ellipsoids.
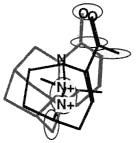
Figure 3.5 The basic operation of clique detection.
In general, these advances have not been the result of active collaborations between graph theorists and chemical information specialists. Rather, the chemical information specialists have followed the graph theory literature, and when a particular concept or algorithm seemed the appropriate solution for some problem, they would attempt to implement it. Sometimes this meant waiting until a graduate student with the particular skills was available. For example, in the case of the Ullman subgraph isomorphism algorithm (Ullman, 1976), Peter Willett suspected that it would be an improvement over the one used in chemical information systems at that time, and several graduate
2D chemical structures of three molecules that activate the D2 receptor.
3D overlay of these molecules in the proposed pharmacophore map. The points for superposition are marked with an arrow.
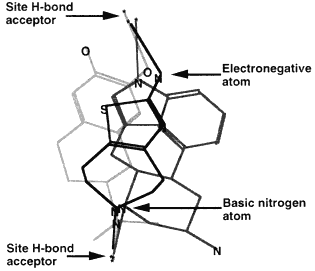
Figure 3.6 Development of a pharmacophore map. Reprinted (with adaptions) by permission from Martin et al. (1993). Copyright 1993 by ESCOM Science Publishers B.V.
students tried to implement it. It was not successfully implemented, however, until Andrew Brint, who was well trained in mathematics, took up the challenge. Since that time, 1986, the Ullman subgraph isomorphism algorithm has replaced the previous algorithms in all commercial chemical information systems (Willett, 1987).
Application of Graph Theory to Representation of Chemical Reactions
The synthesis of organic chemicals is an art that takes many years of training and experience to master. There are two aspects to synthesis: design of the synthetic pathway (what precursors and general reaction conditions will be used) and laboratory execution of the actual synthesis. Experienced synthetic chemists design the synthesis of new molecules based on their knowledge of the hundreds of types of reactions that can be done, their limitations in terms of the other structural features of the molecules that will survive the reaction conditions, and the usual success of the reactions in terms of side products and yield.
The complication with using the computer to aid in this process is that synthetic organic chemists
rely primarily on information contained in two-dimensional chemical structure diagrams. A chemical reaction is simply a transformation of one diagram into another by combining and transforming starting materials into products. Hence, the expertise is organized intellectually in pictures, not numbers. The key insight that these structure diagrams can be described as labeled graphs enabled the use of the computer to process structure diagrams.
Computer programs for designing the synthesis of compounds also rely heavily on these algorithms (Wipke et al., 1978; Wipke and Rogers, 1984; Hanessian et al., 1990; Pensak and Corey, 1977; Johnson et al., 1992; Gasteiger et al., 1992). For example, it is essential to detect the smallest set of smallest rings since these form the basis of the synthetic strategy. Structure searching is used to ascertain if a proposed precursor is commercially available. Substructure searching identifies labile bonds to be broken in a retrosynthetic fashion. Maximal common subgraph algorithms have been used on the two-dimensional structures of products and reactants to perceive the part of a molecule unchanged in a chemical reaction (McGregor and Willett, 1980)—what is common between product and reactant is unchanged.
Two approaches have been used to apply the computer to the design of chemical syntheses. The first simply catalogues literature chemical reactions, transformations, with the associated starting materials and product(s), conditions, yield, and literature reference. For this application, the chemical reaction can be input as normally written and the computer can be used to detect which parts of the molecule are not changed. By definition, then, the parts of the molecular graph that change represent the chemical reaction. The unchanged parts represent the chemical context in which the reaction occurs. In graph theory terms, the unchanged parts are the maximum common subgraph of the reactants and products. The second type of computer program to aid the planning of synthesis involves the actual disconnection of the synthetic target into the proposed starting materials. Such computer programs treat molecules as labeled graphs but use rules encoded by experts to guide the proposed synthetic route. Because of the large number of rules to be encoded, such retrosynthetic programs are much less complete and of less general use than the reaction library programs.
References
Ash, J.E., S.E. Chubb, S.E. Ward, S.M. Welford, and P. Willett, 1985, Communication, Storage and Retrieval of Chemical Information, Ellis Horwood, Chichester.
Borman, S., 1989, Software adds new dimension to structure searching, Chemical and Engineering News 67:28–32.
Brint, A.T., and P. Willett, 1987, Algorithms for the identification of three-dimensional maximal common substructures, J. Chemical Information and Computer Sciences 27:152–158.
Bures, M.G., Y.C. Martin, and P. Willett, 1994, Searching techniques for databases of three-dimensional chemical structures, Topics in Stereochemistry, E.L. Eliel and S.H. Wilen, eds., John Wiley & Sons, New York, pp. 467–511.
Crandell, C.W., and D.H. Smith, 1983, Computer-assisted examination of compounds for common three-dimensional substructures, J. Chemical Information and Computer Sciences 23:186–197.
Dittmar, P.G., N.A. Farmer, W. Fisanick, R.C. Haines, and J. Mockus, 1983, The CAS ONLINE Search System. I. General system design and selection, generation and use of search screens, J. Chemical Information and Computer Sciences 23:93–102.
Gasteiger, J., W.-D. Ihlenfeldt, R. Fick, and J.R. Rose, 1992, Similarity concepts for the planning of organic reactions and syntheses, J. Chemical Information and Computer Sciences 32:700–712.
Hanessian, S., J. Franco, G. Gagnon, D. Laramee, and B. Laroche, 1990, Computer-assisted analysis and perception of stereochemical features in organic molecules using the CHIRON program, J. Chemical Information and Computer Sciences 30:413–425.
Harary, F., 1976, An exposition of graph theory, Chemical Applications of Graph Theory, A.T. Balaban ed., Academic Press, London, pp. 59.
Johnson, A.P., C. Marshall, and P.N. Judson, 1992, Starting material oriented retrosynthetic analysis in the LHASA program: 1. General description, J. Chemical Information and Computer Sciences 32:411–417.
Kuhl, F.S., G.M. Crippen, and D.K. Friesen, 1984, A combinatorial algorithm for calculating ligand binding, J. Comput. Chem. 5:24–34.
Kuntz, I.D., 1992, Structure-based strategies for drug design and discovery, Science 257:1078–1082.
Kuntz, I.D., J.M. Blaney, S.J. Oatley, R. Langridge, and T.J. Ferrin, 1982, A geometric approach to macromolecule-ligand interactions, J. Mol. Biol. 161:269–288.
Leach, A.R., D.P. Dolata, and K. Prout, 1990, Automated conformational analysis and structure generation: Algorithms for molecular perception, J. Chemical Information and Computer Sciences 30:13–16.
Martin, Y.C., 1992, 3D database searching in drug design, J. Medicinal Chemistry 35:2145–2154.
Martin, Y.C., K.-H. Kim, and M.G. Bures, 1992, Computer-assisted drug design in the 21st century, in Medicinal Chemistry in the 21st Century C.G. Wermuth, N. Koga, H. König, and B.W. Metcalf, eds., Blackwell, Cambridge, Mass., pp. 295–317.
Martin, Y.C., M.G. Bures, E.A. Danaher, J. DeLazzer, I. Lico, and P.A. Pavlik, 1993, A fast new approach to pharmacophore mapping and its application to dopaminergic and benzodiazepine agonists, J. Computer-Aided Molecular Design 7:83–102.
McGregor, J.J., and P. Willett, 1980, Use of a maximal common subgraph algorithm in the automatic identification of the ostensible bond changes occurring in chemical reactions, J. Chemical Information and Computer Sciences 21:137–140.
Pensak, D.A., and E.J. Corey, 1977, LHASA—logic and heuristics applied to synthetic analysis, Computer Assisted Organic Synthesis, ACS Symposium Series, Vol. 61, American Chemical Society, Washington D.C., pp. 132.
Smellie, A.S., G.M. Crippen, and W.G. Richards, 1991, Fast drug-receptor mapping by site-directed distances: A novel method of predicting new pharmacological leads, J. Chemical Information and Computer Sciences 31:386–392.
Sussenguth, E.H., 1965, A graph-theoretic algorithm for matching chemical structures, J. Chemical Documentation 5:36–43.
Ullman, J.R., 1976, An algorithm for subgraph isomorphism, J. ACM 16:31–42.
Willett, P., 1987, Similarity and Clustering in Chemical Information Systems, Research Studies Press, Letchworth.
Wipke, W.T., and D. Rogers, 1984, Artificial intelligence in organic synthesis, SST: Starting material selection strategies; An application of superstructure search, J. Chemical Information and Computer Sciences 24:71–81.
Wipke, W.T., and M.A. Hahn, 1988, AIMB: Analogy and intelligence in model building. System description and performance characteristics, Tetrahedron Computer Methodology 1:141.
Wipke, W., G.I. Ouchi, and S. Krishnan, 1978, Simulation and evaluation of chemical synthesis, SECS, Artificial Intelligence 11:173.
X-Ray Crystallography
An excellent source on the topic of X-ray crystallography is the article by Nobel laureate Herbert A. Hauptman (1990), from which the following is excerpted with permission of Plenum Publishing Corporation.
"It was recognized almost from the beginning that the diffraction pattern, the directions and intensities of the X-rays scattered by a crystal, is uniquely determined by the crystal structure; which is to say that if one knew the crystal structure—the arrangement of the atoms in the crystal—then one could calculate the diffraction pattern completely. It turns out that, conversely, diffraction patterns determine, in general, unique crystal and molecular structures, although this fact was not known until many years later. In short, the information content of a typical molecular structure coincides precisely with the information content of its diffraction pattern. It is a measure of the great advances made by the new science of X-ray crystallography that, nowadays, one can routinely transform the information content of a diffraction pattern into a molecular structure, at least for the so-called "small" molecules, that is those consisting of some 150 or fewer non-hydrogen atoms.
"Since X-rays, like ordinary visible light, are electromagnetic waves, they have a phase as well as an intensity, just as any other wave disturbance. In order to work backwards, from diffraction patterns to crystal and molecular structures, it turns out to be necessary to measure not only the intensities of the X-rays scattered by the crystal but their phases as well. However, the phases cannot be measured in the ordinary kind of diffraction experiment; they appear to be irretrievably lost. Only the intensities can be directly measured. This then gives rise to the central problem of X-ray crystallography, the so-called phase problem, how to deduce the values of the phases of the X-rays scattered by a crystal when only their intensities are known . . . .
"Because the needed phase information was lost in the diffraction experiment, it was thought that one could use arbitrary values for the phases associated with the measured intensities of the scattered X-rays. In this way one obtains a myriad of different crystal structures, all consistent with the known intensities. It therefore came to be generally believed that a procedure for going directly from the measured intensities to crystal structures could not, even in principle, be devised. By the same thinking, the problem of deducing the values of the individual phases from the diffraction intensities, the so-called phase problem, was also thought to be unsolvable, even in principle. It wasn't until the early 1950's, through the exploitation of special properties of molecular structures and through a simple mathematical argument, that these erroneous conclusions were finally refuted.
''My work on this problem started in 1948 about a year after I joined the Naval Research Laboratory in Washington, D.C. and initiated my collaboration with Jerome Karle. . . . The
first important contribution that Karle and I made was the recognition that it would be necessary to exploit prior structural knowledge to transform the phase problem from an unsolvable one to one that was solvable, at least in principle. Our first step in this direction was to exploit the nonnegativity of the electron density function p(r). Before our analysis was complete, however, David Harker and John Kasper [1948] published their famous paper . . . in which they derived inequalities in which the measured intensities restrict the possible values of the phases. This was a very mysterious paper, because nowhere in it does there appear any explicit mention of the basis for the inequality relations, and indeed the most important fact is conspicuous by its absence. It is simply that the electron density function is nonnegative everywhere. This fact is, however, implicit in Harker and Kasper's work. In very short order Karle and I completed our own analysis and derived the complete set of inequality relationships based on the nonnegativity of the electron density function [Karle and Hauptman, 1950] . . . . It includes the Harker-Kasper inequalities as a special case, and many others besides. Although the complete set of inequalities greatly restricts the values of the phases, the relations appear to be too intractable to be useful in applications, except for the simplest structures, and their potential has never been fully exploited . . . .
"Beyond any doubt our most important contribution during the early 1950's was the introduction of probabilistic techniques—in particular, use of the joint probability distribution of several diffraction intensities and the corresponding phases—as the central tool in the solution of the phase problem [Hauptman and Karle, 1953]. . . . We assumed to begin with that all positions of the atoms in the unit cell of the crystal were equally likely, or, in the language of mathematical probability, that the atomic position vectors were random variables, uniformly and independently distributed. With this assumption the intensities and phases of the scattered X-rays, as functions of the atomic position vectors, are also random variables, and one can use the methods of modern mathematical probability theory to calculate the joint probability distribution of any collection of intensities and phases. A suitably chosen joint probability distribution leads directly to the conditional probability distribution of a specified structure invariant, assuming again an appropriately chosen set of diffraction intensities. The conditional distribution in turn leads to the structure invariant, an estimate of which is given, for example, by its most probable value. Once one has a sufficiently large number of sufficiently reliable estimates of structure invariants, one can use standard techniques to calculate the values of the individual phases, provided that the process incorporates a recipe for specifying the origin.
"Although probabilistic methods played an essential rule in the development of the direct method and provided it with its logical foundation, it must also be pointed out that nonprobabilistic methods also played an important part . . . . In particular the well known Sayre equation, a relationship of fundamental importance among measured magnitudes and unknown phases, continues to be useful to the present day and lies at the heart of some of the more successful computer programs for solving crystal structures.
"I cannot conclude this brief account of the early history of the direct methods of X-ray crystallography without also describing the reception this work received at the hands of the crystallographic community. This was, simply, extreme skepticism, if not outright hostility. . . .
"Today some 100,000 molecular structures are known, most determined by the direct methods, and about 5,000 new structures are added to the list every year. It is no exaggeration to say that modern structural chemistry owes its existence to this development . . . .
"Work on the phase problem continues to this day and applications to structures of ever increasing complexity continue to be made. It still appears that progress is made only in proportion to our ability to bring more powerful mathematical techniques to bear on this fascinating problem."
Remark
The committee can only add its belief that the last quoted sentence from Hauptman's account has wide applicability to problems of chemical interest, some of which are described in the next chapter.
References
Harker, D., and J.S. Kasper, 1948, Acta Crystallogr. 1:70.
Hauptman, H.A., 1990, History of x-ray crystallography, Struct. Chem. 6:617–620.
Hauptman, H., and J. Karle, 1953, Solution of the Phase Problem 1. The Centrosymmetric Crystal, American Crystallographic Association Monograph No. 3, Polycrystal Book Service, Dayton, Ohio.
Karle, J., and H. Hauptman, 1950, Acta Crystallogr. 3:181.
























