Nonlinear Shallow-Water Flow on Deck Coupled with Ship Motion
Z.-J.Huang, C.-C.Hsiung (Technical University of Nova Scotia, Canada)
Abstract
Shallow water wave equations are employed to study the problem of nonlinear water flow on deck. The Flux-Difference Splitting method is devised to solve the nonlinear shallow water flow equations numerically. The finite difference scheme is a second-order Total Variation Diminishing scheme which is able to tackle discontinuities in the flow and gives satisfactory results. The nonlinear ship motions with considering water flow on deck are solved in the time domain. The flow patterns are validated against published model test data. Ship motions with water on deck are computed and discussed.
Introduction
The effect of water flow on deck on ship motion, especially for small vessels with open deck and RO-RO ferries, is very important for safe operations in waves (Caglayan and Storch, 1982; Grochowalski, 1989). Its effect on the roll motion of a ship has two folds. The first is the damping effect which will reduce or increase the roll motion depending on positive or negative damping (Van Den Bosch, 1966). The other is the change of GZ values in statical stability and consequently the resonant frequency of roll response is modified. In addition, the phase difference between water sloshing and roll motion is very important for the roll motion prediction. When the hydraulic jump or the bore is developed, its position affects the heeling moment exerted on the ship.
Dillingham (1981) initiated the numerical computation of the nonlinear shallow water flow on a two-dimensional deck using Random Choice method. In the numerical computation, the analytical solution of a local Riemann problem in each spatial interval was first constructed. Then a random sampling procedure was applied to find an random abscissa in each interval. A piecewise constant numerical solution was found by substituting the abscissa into the local analytical solution. Pantazopoulos (1988) extended this method to a three-dimensional deck space. Huang and Hsiung (1994) introduced the Flux-Difference Splitting method to tackle the shallow water flow problem. The governing equations and the numerical method was first developed for the 2-D case (Huang and Hsiung, 1994), and later was extended to the 3-D case (Huang and Hsiung, 1995). This method was developed based on the same idea in the flux-vector splitting method which was originally introduced by Steger and Warming (1981) to compute the shock wave in a shock tube and later applied to hydraulics by others (e.g. Alcrudo et al., 1992). Based on this approach, the effect of water flow on deck on the motions of fishing vessels was investigated by Huang (1995).
Lee and Adee (1994) computed the motions of a cylinder in sway, roll and heave including the free water on deck. The equations of ship motion of the frequency domain were solved in the time domain in regular beam seas. The hydrodynamic forces on the hull were obtained from a 2-D strip theory in the frequency domain and the forces resulted from in the water flow on deck were obtained from the 2-D Random Choice method given by Dillingham (1981). Armenio et al. (1994) solved the equation of one degree roll motion in regular waves. The linear viscous damping was adopted and the frequency domain hydrodynamic forces were used in the equation of ship motion. The 2-D sloshing of water on deck was obtained from a Navier-Stokes slover.
The time domain Green function has been ap-
plied to the ship motion problem (e.g. King, et al., 1988). Lin and Yue (1994) extended this method to large amplitude ship motions. The exact hull surface boundary condition was satisfied on the instataneous wetted surface under the incident wave profile. The local incident wave elevations were used to transform the hull geometry and the free surface into a computational domain so that the transient Green function method could be applied. Another approach was adopted by de Kat and Paulling (1989) and by Magee (1994), in which the Froude-Krylov force and restoring force were calculated based on the instataneous wetted hull surface under the incident wave profile while linear radiated and diffracted wave forces were employed.
Typically, for the deck flow computation, the classical first order schemes have a strong dissipative effect on the numerical solution and the second order schemes produce numerical results with spurous oscillations near the discontinuity. In this paper, the governing equations of nonlinear shallow water flow on deck are derived in the flux vector form and are solved numerically by flux-Difference Splitting method. The Superbee flux limiter has been employed in the algorithm and the finite difference scheme is a second-order Total Variation Diminishing scheme which gives satisfactory results without non-physical spurious oscillations and is able to capture the hydraulic bore. The Fractional Step method is used so that solutions of the shallow water equation can be obtained by solving two sets of one-dimensional differential equations. The hydrodynamic forces caused by water flow on deck is considered in the time domain equation of ship motions. The time domain added mass, hydrodynamic damping and hydrodynamic restoring force coefficients are calculated using the impulse potential (King, et al., 1988). The equations of ship motion also include the nonlinear Froude-Krylov forces, nonlinear restoring forces and nonlinear viscous roll damping. However, the linear radiated and diffracted wave forces are used. Our approach can be summarized as follows:
-
the time domain added mass, hydrodynamic restoring force and damping force coefficients are computed using the impulse potential function (linear);
-
linear diffracted wave forces and retardation functions are computed based on the frequency domain diffracted wave forces and damping coefficients, respectively (linear);
-
F-K forces and hydrostatic restoring forces are computed at the instantaneous position (nonlinear);
-
forces due to water flow on deck, viscous damping, resistance, cross-flow drag, thrust, rudder and maneuvering forces are included (nonlinear); and
-
nonlinear equations of ship motion solved in the time domain.
The present work has been applied to fishing vessels with shallow draft. Computations of water flow on deck and ship motions are compared with model test results.
Ship Motion in the Time Domain
Three coordinate systems are employed for the the ship motion analysis as shown in Fig.1.
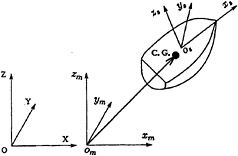
Fig. 1 Coordinate Systems for Ship Motions
OXYZ is the space-fixed coordinate system with the OXY plane on the calm water surface and the OZ axis be positive upwards. The second coordinate system omxmymzm is a moving system which moves with the same steady forward speed as the ship in OX direction. The omxmym plane always coincides with the OXY plane, the omxm axis is in the same direction as the OX axis and the omzm axis is positive upwards. The third coordinate system osxsyszs is fixed on the ship with the osxsys plane coincident with the OXY plane when the ship is at its static equilibrium position, and the oszs axis is positive upwards.
The oscillatory ship motion are described in the omxmymzm system. The ship motions are repre-
sented by (ξ1, ξ2,ξ3,e1,e2,e3), in which, (ξ1,ξ2,ξ3) are the displacements of the centre of gravity, and (e1,e2,e3) are the Eulerian angles of the ship in space. The Eulerian angles are the measurements of the ship's rotation about the axes which pass througth the centre of gravity of the ship. The instantaneous translational velocities of ship motion in the directions of osxs, osys and oszs are u1, u2 and u3, respectively, and the rotational velocities about axes parallel to osxs, osys and oszs and passing through the centre of gravity are u4, u5 and u6, respectively. The equations of ship motion are:
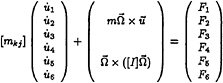
(1)
where ![]() [Πkj] is the generalized mass matrix:
[Πkj] is the generalized mass matrix:
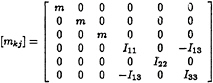
(2)
and [I] is the moment of inertia matrix
(3)
in which m is the mass of the ship, Ikk (k=1,2,3) denote the moments of inertia of the ship, and Ikj(k≠j) are the products of inertia of the ship. The total external forces on the ship are
(4)
where ![]() are the restoring forces;
are the restoring forces; ![]() are nonlinear Froude-Krylov forces;
are nonlinear Froude-Krylov forces; ![]() the diffracted wave forces;
the diffracted wave forces; ![]() the radiated wave forces;
the radiated wave forces; ![]() the viscous damping forces;
the viscous damping forces; ![]() the nonlinear forces due to water flow on deck; and the force component
the nonlinear forces due to water flow on deck; and the force component ![]() may include the hydrodynamic maneuvering forces, the rudder force, propeller thrust, viscous resistance and cross-flow drag.
may include the hydrodynamic maneuvering forces, the rudder force, propeller thrust, viscous resistance and cross-flow drag.
The ship translational displacements (ξ1,ξ2,ξ3)T in the steady moving system and the Eulerian angles (e1,e2,e3)T are solved from:
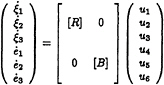
(5)
where matrices [B] and [R] are defined as follows:
(6)
(7)
and ci=cos ei, si=sin ei, and ti=tan ei for i=1,2,3.
The ship motions in the time domain are solved simultaneously from twelve equations in both (1) and (5). At each time step, the motion velocities in the ship-fixed coordinate system are obtained by integrating (1) with the velocities at the previous time step as the initial conditions. The ship motion displacements are solved from (5) in the steady moving coordinate system.
Since the ship motion at a new time step, which is unknown, is required to compute the forces (e.g. the restoring force has to be calculated with the ship motion displacement), the linear prediction of stochastic theory is adopted to determine the ship motion for the force computation. With the predicted ship motion at t=tn+1, the external forces are evaluated. Then, the ship motion is solved numerically from the first order ordinary differential equations (1) and (5) by the Extrapolation method (Magee, 1994).
Nonlinear Shallow Water Flow on Deck
Governing Equations
The flux difference splitting method has been developed for computing the shallow water flow in a three dimensional deck space (Huang and Hsiung, 1994,1995; Huang, 1995). The ship motions of six degrees of freedom has been considered in
the numerical scheme for the deck flow. The coordinate system oxyz for water flow on the three dimensional deck is shown in Fig.2.
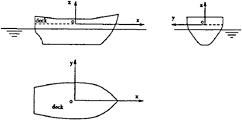
Fig. 2 Coordinate System for Deck Flow
It is fixed on the deck space with oxy attached on the deck bottom plane. The oz axis is positive upward and the origin o is at the centre of the deck bottom.
The continuity equation and Euler's equations of motion can be written as follows:
(8)
(9)
where ![]() u, v and w are velocity components of the water particles in x-, y- and z- directions, respectively, measured at point in space from the field point of view; p is the pressure; and
u, v and w are velocity components of the water particles in x-, y- and z- directions, respectively, measured at point in space from the field point of view; p is the pressure; and
(10)
![]() and (xg,yg,zg) is the coordinate of the centre of gravity of the ship in the oxyz system.
and (xg,yg,zg) is the coordinate of the centre of gravity of the ship in the oxyz system.
On the free surface, the kinematic condition is:
(11)
and the dynamic free surface condition is:
p=0 on z=ζ (12)
It is assumed that the deck bottom surface is flat and the wall of the deck is vertical. The boundary conditions are:
![]() on the deck wall and bottom (13)
on the deck wall and bottom (13)
If the water depth is shallow compared with the horizontal dimension of the deck space, it can be assumed that w is a small quantity compared with u and v; and the dependence of u and v on z may be ignored, i.e. u=u(x,y,t) and v=v(x,y,t). Let q=gζ, then the governing equations can be expressed in a vector form:
(14)
in which,
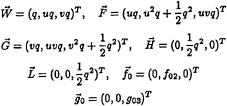
where D22=1+q2/g+qq3/g2, E33=1+r2/g+ qr3/g2, f02=qq0+q2q1/g, and g03=qr0+q2r1/g,
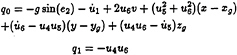
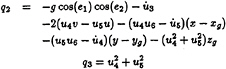
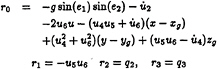
The derivatives of flux vectors ![]() and
and ![]() can be expressed in terms of the derivatives of vector
can be expressed in terms of the derivatives of vector ![]() as follows:
as follows:
where [Ji], i=1,2,3,4, are the Jacobian matrices. The eigenvalues of the Jacobian matrix [J1] are:
and the eigenvectors:
The eigenvalues of the Jacobian matrix [J2] are:
and the eigenvectors:
Finally, the governing equation is reconstructed into the following form:
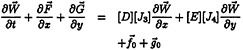
(15)
In the numerical computation, the governing equation can be split into two equations using the Fractional Step method as given by Yanenko (1971) as:
(16)
and
(17)
and these two one-dimensional equations are solved for each time step.
The Flux Difference Splitting Scheme
The deck is divided into m×n nodes. The approximate Jacobian matrices ![]() and
and ![]() are so constructed that
are so constructed that
In the present study, the differences of ![]() and
and ![]() are approximated as follows:
are approximated as follows:
and
Also, the vectors at the right hand sides of equations (16) and (17) are projected into the eigenvector space as follows:
and
The finite difference equations can be derived as follows:
(18)
and
(19)
where ![]() and
and ![]() With the Superbee limiter (Roe, 1985),
With the Superbee limiter (Roe, 1985), ![]() it follows that
it follows that
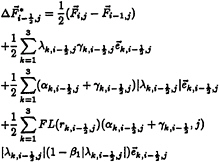
(20)
Similarly, ![]() and
and ![]() can be derived. The mathematical details are given by Huang (1995).
can be derived. The mathematical details are given by Huang (1995).
In the numerical computation, for each time step, equation (18) is first solved along the x-direction by assuming that ![]() and
and ![]() and they are constants for
and they are constants for ![]() and y=yj, for j=1,2,…,n. Solutions at this stage, u′, v′ and q′, are obtained, and
and y=yj, for j=1,2,…,n. Solutions at this stage, u′, v′ and q′, are obtained, and ![]() and
and ![]()
can be calculated. Furthermore, equation (19) is solved along the y-direction by assuming that ![]() and
and ![]() and they are constants for
and they are constants for ![]() and x=xi, for i=1,2,…,m.
and x=xi, for i=1,2,…,m.
Computation of Forces
Forces Caused by Water Flow on Deck
As soon as the water depth and the water particle velocity are computed, the pressure on deck can be obtained as follows:
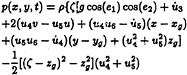
(21)
Then forces and moments caused by water flow on deck are calculated by integrating the pressure over the deck area.
Nonlinear Froude-Krylov Forces
At each time instant, the ship motions (ξ1,ξ2,ξ3, e1,e2,e3) are solved from equations (1) and (5). Making use of the Euleran angles (e1,e2,e3), the ship-fixed coordinate system and the steady moving coordinate system can be related as:
(22)
where (xsg,ysg,zsg) are the coordinates of the centre of gravity of the ship in the ship-fixed coordinate system. Also, we have
X=Ut+xm, Y=ym and Z=zm (23)
where U is the forward speed of the ship.
The wave profile ζ0(X,Y,t) can be computed using equation (??). All the nodal points on the ship hull and deck are transformed into the OXYZ coordinate system using equations (22) and (23). If a nodal point is below the free surface ζ0(X,Y,t), then we compute the pressure at this point:
P(X,Y,Z,t)=Ps(X,Y,Z,t)+Pd(X,Y,Z,t) (24)
where, the static pressure is:
Ps(X,Y,Z,t)=–ρg[Z–ζ0(X,Y,t)] (25)
and the dynamic pressure is:
(26)
In this work, quadrilateral panels are used to discretize the ship hull surface. It is assumed that at the instant tn, there are N(tn) wetted panels on the hull surface and the deck space. The mean pressure on a panel is:
(27)
where pj is the pressure at a nodal point of the panel. The nonlinear restoring forces are computed as follows:
(28)
where ΔSj is the area of the jth panel and nk,j is the kth component of the unit normal on the jth panel. The nonlinear Froude-Krylov forces are:
(29)
where the subscript “d” indicates the dynamic pressure.
The irregular waves are expressed in the spacefixed coordinate system, OXYZ. They are represented by superposition of finite number of regular sinusoidal waves. The incident wave potential of the irregular wave field is given as follows:
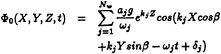
(30)
where aj is the amplitude of the jth regular wave, ωj is the frequency of the jth regular wave, kj=![]() is the wave number and δj is the random phase lag of the jth regular wave. The phase lag δj follows a uniform distribution over [0,2π]. For practical computation, the number of wave components Nw is approximatly 25. Wave spectra, such as Pierson-Moskowitz, JONSWAP, Bretschnerder, Ochi-Hubble six parameter, or measured spectrum, can be used in generating irregular waves for the computer simulation.
is the wave number and δj is the random phase lag of the jth regular wave. The phase lag δj follows a uniform distribution over [0,2π]. For practical computation, the number of wave components Nw is approximatly 25. Wave spectra, such as Pierson-Moskowitz, JONSWAP, Bretschnerder, Ochi-Hubble six parameter, or measured spectrum, can be used in generating irregular waves for the computer simulation.
Forces due to the Radiated and Diffracted Waves
The impulse response function method given by Cummins (1962) is used to describe the radiated wave forces on the ship hull. The radiated wave potential is caused not only by the oscillatory velocity but also by the oscillatory displacement which changes the position of the body in the steady flow field. The force due to radiated waves can be expressed as follows:
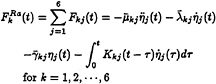
(31)
where ![]() kj is the time domain added mass of the ship,
kj is the time domain added mass of the ship, ![]() is the time domain hydrodynamic damping,
is the time domain hydrodynamic damping, ![]() kj is the coefficient of the time domain hydrodynamic restoring force. These coefficients are computed from the impulsive potentials (King, et al., 1988). Kkj(t) is the retardation function which is obtained by:
kj is the coefficient of the time domain hydrodynamic restoring force. These coefficients are computed from the impulsive potentials (King, et al., 1988). Kkj(t) is the retardation function which is obtained by:
(32)
where B(ij(ωe) is the damping coefficients in the frequency domain which is computed using the panel method (Hsiung and Huang, 1991).
In order to compute the hydrodynamic damping and hydrodynamic restoring coefficients, the m-terms have been calculated. To avoid the direct evaluation of the second derivatives, an integral equation method has been applied to the 2-D body by Wu (1991). Computations were carried for a 3-D body by Huang and Hsiung (1993) based on the double-body flow potential ![]() . Applying the Green theorem, the following integral equation can be obtained for the m-terms:
. Applying the Green theorem, the following integral equation can be obtained for the m-terms:
(33)
(34)
and
(35)
where ![]()
![]() is the field point,
is the field point, ![]() is the source point,
is the source point, ![]()
![]() and
and ![]() is the source strength. The m-terms: m4, m5 and m6 can be computed directly using m1, m2 and m3 (Newman, 1978).
is the source strength. The m-terms: m4, m5 and m6 can be computed directly using m1, m2 and m3 (Newman, 1978).
The diffracted wave force in irregular waves may be obtained as:
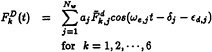
(36)
where ![]() is the amplitude and
is the amplitude and ![]() d,j is the phase lag of the diffracted wave force, respectively. They are computed in the frequency domain using the panel method (Hsiung and Huang, 1991).
d,j is the phase lag of the diffracted wave force, respectively. They are computed in the frequency domain using the panel method (Hsiung and Huang, 1991).
Viscous Roll Damping Moment
Various forms of formulation of the roll damping moment have been applied to the nonlinear roll motion, such as the linear plus quadratic model, the linear plus cubic model, etc (Haddara and Bass, 1990). Special attention should be paid on the choice of the form of damping coefficients for small vessels. Roll decay tests have been carried out for five inshore fishing vessels (Peng, et al., 1995). This type of fishing boat has a big skeg with flat bottom near the stern, as well as low L/B ratio and a shallow draught. Different forms of damping moment were applied to fit the roll decay curves based on the energy balance method. It has been realized that the evaluation of roll damping of this type of vessel is more difficult than conventional ships, such as cargo ships or frigates. In general, the roll damping coefficients are roll angle dependent and the following formulas are applied:
(37)
or
(38)
where ![]() is the natural frequency of the ship in roll.
is the natural frequency of the ship in roll.
Resistance, Cross-Flow Drag and Thrust
In this work, resistance model test results are used for inshore fishing vessels (Lacy, 1995). Models were also towed transversely in the tank in order to measure the cross-flow drag (Huang, 1995). Test results are used in the numerical simulation of the vessel motions.
If there is no test data available, empirical formulas, such as those given by Holtrop amd Mennen (1982), are used for resistance estimation. The cross-flow drag and moment can be calculated by:
(39)
and
(40)
where Cd(xs) is the sectional cross-flow drag coefficient, T(xs) is the local draft of the ship and v2(xs) is the transverse relative velocity between the hull and the water particle of the local crossflow.
The thrust and torque of the propeller can be estimated from the available propeller charts as:
(41)
and
(42)
where tp is the thrust deduction fraction, np the revolution of the propeller per minute, Dp the propeller diameter, J the advancing coefficient, KT the thrust coefficient and KQ the torque coefficient.
Maneuvering Forces
The following nonlinear lateral force and turning moment are adopted in the seakeeping computation (Kijima et al., 1990):
(43)
and
(44)
where L is ship length, d is ship draft, ![]() and
and ![]() In computation,
In computation, ![]() is the instantaneous relative velocity beteen the ship and the calm water in the x-direction, and u2 the instantaneous sway velocity. The hydrodynamic derivatives Y′s and N′s are determined by empirical formulas or from test results.
is the instantaneous relative velocity beteen the ship and the calm water in the x-direction, and u2 the instantaneous sway velocity. The hydrodynamic derivatives Y′s and N′s are determined by empirical formulas or from test results.
Rudder Forces and Autopilot
It is defined that the rudder angle δ is positive when the rudder is turned to the port side. From the paper by Kijima et al. (1990), the normal force acting on the rudder can be evaluated by:
(45)
where ![]() is the aspect ratio of the rudder, Ar the rudder area of single side, Vr the relative velocity of the water particle to the rudder, and δe the effective rudder angle:
is the aspect ratio of the rudder, Ar the rudder area of single side, Vr the relative velocity of the water particle to the rudder, and δe the effective rudder angle:
(46)
Suppose that the normal force acts on the pressure point Crud on the rudder, the rudder force components can be obtained as follows:
(47)
(48)
(49)
and
(50)
where lx and lz are horizontal and vertical distances between the pressure point Crud and the centre of gravity, respectively; Ucx and Ucy are the longitudinal and lateral components of current, respectively.
If the autopilot is considered, the following formula is recommended:
(51)
where ![]() is the yaw gain,
is the yaw gain, ![]() is the yaw rate gain, and δ0 is the threshold value of yaw beyond which the rudder is activated.
is the yaw rate gain, and δ0 is the threshold value of yaw beyond which the rudder is activated.
Results and Discussion
First, we present the computed motion results of fishing vessel A. Motion tests of a free-running model of this vessel in a wave tank have been conducted. Heave acceleration, roll angle and pitch angle are measured; and wave slopes, 2ζ0/λ, up to 0.09 are used, where λ is the incident wave length and ζ0 is the incident wave amplitude. The principal dimensions of the model are given in Table 1 and the panelized hull up to waterline and bulwark are given in Fig.3 and Fig.4, respectively. It represents thousands of fishing vessels on the eastern seaboard of Canada. These vessels have very shallow draft, large skeg, flat bottom near the stern, as well as low length to beam ratio. The vessels are very stiff in waves, the typical full-scale natural period is only about 3 sec.
Table. 1 Characteristics of Fishing Vessel A
|
Length, Loa (m) |
1.846 |
|
Maximum beam, B (m) |
0.717 |
|
Mean draft, D (m) |
0.187 |
|
Volume ∇ (m3) |
0.0663 |
|
Radius of gyration rxx (m) |
0.236 |
|
Radius of gyration ryy (m) |
0.430 |
|
L.C.G. (m) (from F.P.) |
0.996 |
|
V.C.G. (m) (from baseline) |
0.378 |
|
Natural roll period T0 (sec) |
1.150 |

Fig. 3 Panelized Hull up to Waterline
At a nominal forward speed of 5 knots, comparison between computed results and the measurements are given in Fig.5 and Fig.6 for the double amplitudes of heave acceleration and pitch motion. The double amplitude of heave acceleration is normalized by ![]() and the double pitch amplitude by 2kζ0. The computed results agree well with the model test results.
and the double pitch amplitude by 2kζ0. The computed results agree well with the model test results.
Fig. 4 Panelized Hull up to Bulwark
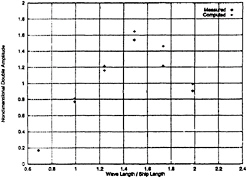
Fig. 5 Heave Acceleration in Head Seas
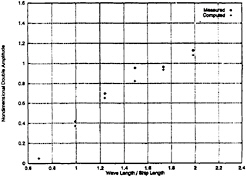
Fig. 6 Pitch Motion in Head Seas
The nondimensional double amplitude of roll in beam seas with a nominal forward speed of 5 kts is given in Fig.7. Time histories of the measured and computed roll motions are shown in Fig.8, in
which λ/L=1.5 and wave height 0.62 m. Both computed and measured roll have a mean heel angle towards the incident waves.
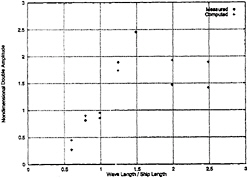
Fig. 7 Nondimensional Roll Motion in Beam Seas
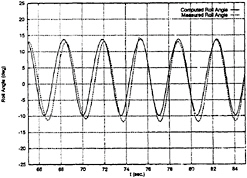
Fig. 8 Roll Time History in Beam Seas
Water flow on deck, which is subjected to roll excitation, is computed. The deck is 0.91 m wide. Numerical results are compared with experimental data given by Adee and Caglayan (1982). At the frequency 1.57 rad/sec which is close to one half of the first resonant frequency, roll amplitude 9.5 deg, water depth 7.62 cm, the computed and measured wave motions are shown in Fig. 9. For an amplitude 5.0 deg and a frequency 2.07 rad/sec, which is close to the primary resonant frequency, the wave profiles at t=3.0 sec is shown in Fig.10 where the water depth is 5.08 cm. A bore can be clearly observed there. For the roll amplitude 7.5 deg and the exciting frequency 3.644 rad/sec, which is one and a half of the primary resonant frequency, water depth 5.08 cm, the numerical results and measured data are shown in Fig.11.
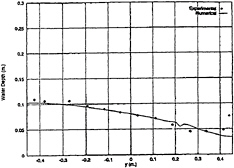
Fig. 9 Wave Profile, a4=9.5 deg, ω=1.57 rad/sec, t=2.0 sec
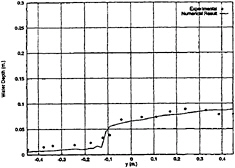
Fig. 10 Wave Profile, a4=5 deg, ω=2.07 rad/sec, t=3.0 sec
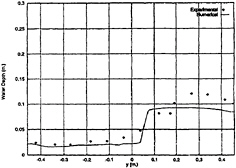
Fig. 11 Wave Profile, a4=7.5 deg, ω=3.644 rad/sec, t=2.0 sec
For an amplitude 7.5 deg and a frequency 4.71 rad/sec, which is close to the second resonant frequency, the wave profiles at t=3 sec is given in Fig.12. Two bore can be clearly observed in the computed results.
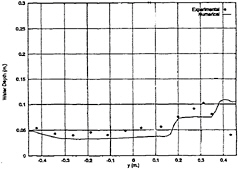
Fig. 12 Wave Profile, a4=7.5 deg, ω=4.712 rad/sec, t=3 sec
The wave motion and the velocity distribution under the excitation of multi-degrees of freedom of ship motions are more complicated than those under the roll excitation only. Some characteristics of the wave motion can be found from numerical computations. Computed results are given below for a deck well of 1 m by 0.8 m with the water depth 10 cm. The rotation pivot is assumed to be located at the centre of the bottom surface. The primary resonant frequencies are ω0x=3.11 rad/sec in the longitudinal direction and ω0y=3.89 rad/sec in the transverse direction, respectively. Fig.13 and Fig.14 show the wave profile and the velocity distribution, respectively, under the coupled roll and pitch excitation. The roll and pitch amplitudes are 5 deg and frequencies 4.0 rad/sec which are close to the first resonant frequency. The time instant is 4.0 sec. In addition to the two bores which are caused by rolling and pitching, an oblique bore is produced by the interaction of two bores. The wave in the deeper water region travels faster than that in the shallower region. From Fig.14, the particles near the oblique bore have greater speed than those in the other part of the deck.
As the frequency of deck oscillation is close to the second resonant frequency 2ω0y, ω=7.8 rad/sec, the wave pattern at t=2 sec is shown in Fig.15.
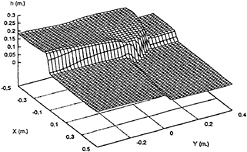
Fig. 13 Wave Pattern due to Roll and Pitch, t=4.0 sec, ω=4.0 rad/sec
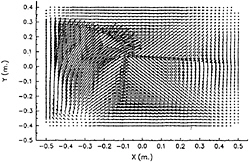
Fig. 14 Velocity Distribution due to Roll and Pitch, t=4.0 sec, ω=4.0 rad/sec
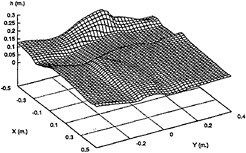
Fig. 15 Wave Pattern due to Roll and Pitch, t=2.0 sec, ω=7.8 rad/sec
The wave motion due to the coupled surge and sway excitation is shown in Fig.16. The surge
and sway amplitudes and frequencies are 2 cm and 6 rad/sec, respectively. Again, two bores can be clearly observed. However, the bores are not so steep as those caused by the roll and pitch motion near the first resonant frequency ω0y.
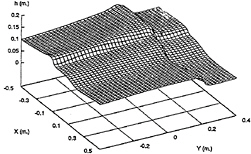
Fig. 16 Wave Pattern due to Surge and Sway, t=1.5 sec, ω=6.0 rad/sec
In the computation of ship motion with water on deck, fishing vessel B, which is similar to fishing vessel A in hull geometry, is used in this paper. The boat is 12.5 m long, 4.2 m wide with a draft 1.47 m. Its displacement is 22.78 m3. The deck size is 4 m by 3 m. The amount of water trapped on deck is assumed to be 15%V0 and 25%V0, where V0 is the intact vessel volume displacement. The corresponding water depths in the deck well are 0.285 m and 0.475 m, respectively.
Ship motions in six-degrees-of-freedom have been computed, all motions are couled on another. The heave, roll and pitch motions with and without 15%V0 water on deck are shown in Fig.17, Fig. 18 and Fig.19. It is assumed that the boat is in its upright position initially and has zero forward speed in beam seas. The wave length equals the boat length. With water on deck, the heave motion shown in Fig.17 has a component of constant sinkage due to the water weight, and its amplitude and frequency are similar to those without water on deck. Small variations of the heave amplitude can be observed. From Fig.18 and Fig.19, the roll and pitch amplitudes are increased compared with those without water on deck. Nonlinear roll and pitch motions are observed in the predicted time history. It seems that the boat oscillates about a bias heel angle towards the lee side or the weather side. But most time it is towards the lee side. No clear patterns of roll motion can be found.
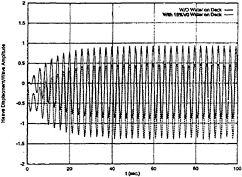
Fig. 17 Heave Motion, ω=2.2 rad/sec, β=90 deg, U=0 kts
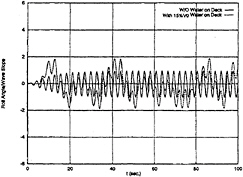
Fig. 18 Roll Motion, ω=2.2 rad/sec, β=90 deg, U=0 kts
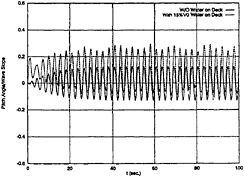
Fig. 19 Pitch Motion, ω=2.2 rad/sec, β=90 deg, U=0 kts
Keeping all other parameters the same as in the above case except increasing water on deck
25%V0, the predicted roll and pitch motions are given in Fig.20, and Fig.21, respectively. The roll motion in Fig.20 shows a period-tripling oscillation caused by the water flow on deck. Also, the roll amplitude is enlarged. A mean trim exists in the pitch motion with water on deck as shown in Fig.21. The pitch frequency is not changed compared with that of no water on deck. However, the nonlinear effects due to the water flow on deck and nonlinear coupling effect between roll and pitch (the nonlinear coupling effect is from the nonlinear equations of ship motion, the restoring force and the Froude-Krylov force) can be found in the pitch response time history. The pitch motion amplitude is increased.
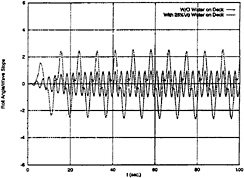
Fig. 20 Roll Motion, ω=2.2 rad/sec, β=90 deg, U=0 kts
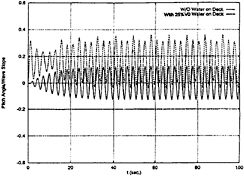
Fig. 21 Pitch Motion, ω=2.2 rad/sec, β=90 deg, U=0 kts
From above computations, it can be seen that the water flow on deck definitely affects the roll motion and that the pitch motion is not only affectes by the water flow on deck but also coupled with roll motion. Further computations were carried out for the boat at a forward speed of 5 knots with heading 45 deg and wave frequency 2.2 rad/sec. The roll and pitch motions with 25%V0 water on deck are shown in Fig.22 and Fig.23, respectively. A steady trim and amplitude variations are found in the pitch motion, and there is no frequency shift. The roll motion is periodic, and the period three and a half of wave excitation period. The roll amplitude is magnified.
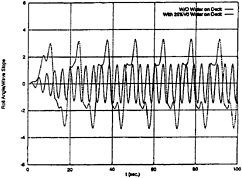
Fig. 22 Roll Motion, ω=2.2 rad/sec, β=45 deg, U=5 kts
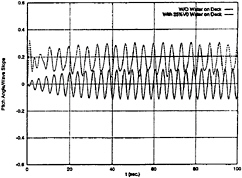
Fig. 23 Pitch Motion, ω=2.2 rad/sec, β=45 deg, U=5 kts
In this particular case, the resonant frequency of water sloshing inside the deck is much lower than the roll natural frequency, the water flow on deck may increase the roll motion amplitude and can alter the frequency of roll motion.
Conclusions
Equations of nonlinear ship motions are solved in the time domain. The linear radiated and diffracted wave forces are employed, however, other forces, such as nonlinear Froude-Krylov forces, deck flow forces and maneuvering forces are included in the equations. This method is applied to compute motions of fishing vessels of shallow draft. The computed results show good agreement with model test results.
The Flux-Difference Splitting method has been devised to study the shallow water flow on deck. It provides a tool to look into the hydrodynamic characteristics of the complicated deck flow phenomina and to investigate the effect of water depth and deck geometry. It can capture the steep wave front accurately. From the point of view of computing time required in simulation, it is faster than the Navier-Stokes solver. The nonlinear wave motion on deck is dominated by the water depth, deck width, position of rotation pivot, as well as the frequency and amplitude of excitation. When the excitating frequency is close to the primary resonant frequency, a single bore is generated and it travels back and forth in the deck well. Near the second resonant frequency, one or two bores can be observed.
For the small fishing vessels, the first resonant frequency of deck flow is within the frequency range of the major part of wave energy in irregular waves, therefore with water on deck a bore would occur. Nonlinear motion responses due to the water flow on deck have been observed. The vessels under investigation are “stiff” in roll, the first natural frequency of water sloshing inside the deck is much lower than the roll natural frequency. The water flow on deck actually increases the roll motion amplitude and the frequency of roll motion is also changed. The roll motion with multiple period of the incident waves has also been observed in the computation.
Acknowledgments
The authors are grateful for the research supports from Transport Canada, and Natural Sciences and Engineering Research Council of Canada.
References
Adee, B.H. and Caglayan, I., “The Effects of Free Water on Deck on the Motions and Stability of Vessels”, Proceedings of the Second International Conference on Stability of Ships and Ocean Vehicles, Tokyo, Japan, 1982.
Alcrudo, F., Garcia-Navaro, P. and Saviron, J-M., “Flux Difference Splitting for 1D Open Channel Flow Equations”, International Journal for Numerical Methods in Fluids, Vol. 14, 1992.
Armenio, V., Cardo, A.La Rocca, M., and Mele, P., “Numerical Prediction of Roll Motion of a Ship with Liquids on Board in Regular Waves from Different Directions”, Proceedings of the Fifth International Conference on Stability of Ships and Ocean Vehicles, Melbourne, Florida, 1994.
Caglayan, I. and Storch, R.L., “Stability of Fishing Vessels with Water on Deck: A Review”, Journal of Ship Research, Vol. 26, No. 2, June 1982.
Cummins, W.E., “The Impulse Response Function and Ship Motions,” Schiffstechnik, Vol. 9, 1962.
de Kat, Jan O. and Paulling, J.R., “The Simulation of Ship Motions and Capsizing in Servere Seas,” Transactions, SNAME, Vol. 97, 1989.
Dillingham, J., “Motion Studies of a Vessel with Water on Deck”, Marine Technology, Vol. 18, No. 1, 1981.
Grochowalski, S., “Investigation into the Physics of Ship Capsizing by combined Captive and Free Running Tests”, Transactions, SNAME, 1989.
Haddara, M.R. and D.W.Bass, “On the form of Roll Damping Moment for Small Fishing Vessels”, Ocean Engineering, Vol. 17, No 6, 1990.
Holtrop, J. and Mennen, G.G.J., “An Approximate Power Prediction Method”, International Ship Building Progress, No. 335, Vol. 29, 1982.
Hsiung, C.C. and Huang, Z.J., “Comparision of the Strip Theory and the Panel Method in Computing Ship Motion with Forward Speed”, Proceedings of Symposium on Selected Topics of Marine Hydrodynamics, St. John's, Nfld, 1991.
Huang, Z.J., Nonlinear Shallow Water Flow on Deck and Its Effect on Ship Motion, Ph. D. Thesis, Technical University of Nova Scotia, Halifax, Nova Scotia, 1995.
Huang, Z.J. and Hsiung, C.C., “Nonlinear Shallow Water Flow on the Three-Dimensional Deck”,
Proceedings of the Tenth International Workshop on Water Waves and Floating Bodies, Oxford, U. K., April 1995.
Huang, Z.J. and Hsiung, C.C., “Application of the Flux Difference Splitting Method to Compute Nonlinear Shallow Water Flow on Deck”, Proceedings of the Fifth International Workshop on Water Waves and Floating Bodies, Kuju, Oita, Japan, April 1994.
Huang, Z.J. and Hsiung, C.C., “An Improved 3-D Panel Method to Compute m-Terms for Ship Motion”, Proceedings of the Second Canadian Marine Dynamics Conference, Vancouver, B.C., August 1993.
Kijima, K., Katsuno, T., Nikiri, Y. and Furukawa, Y., “On the Maneuvering Performance of a Ship with the Parameter of Loading Condition”, Journal of the Society of Naval Architects of Japan, Vol. 168, 1991.
King, B.K., Beck, R.F. and Magee, A. R., “Seakeeping Calculations with Forward Speed Using Time Domain Analysis ”, Proceedings of the Seventeenth Symposium on Naval Hydrodynamics, The Hague, Netherland, 1988.
Lacy, G. “Comparison of the Resistance Characteristics of Five Inshore Fishing Vessels”, Proceedings of the Third Canadian Marine Hydrodynamics and Structures Conference , Halifax, Nova Scotia, August 1995.
Lee, K. and Adee, B., “Numerical Analysis of a Vessel's Dynymic Responses with Water Trapped on Deck”, Proceedings of the Fifth International Conference on Stability of Ships and Ocean Vehicles, Melbourne, Florida, 1994.
Lin, W.M. and Yue, D.K., “Large Amplitude Motions and Wave Loads for Ship Design”, Proceedings of the Twentieth Symposium on Naval Hydrodynamics, Santa Barbra, California, 1994.
Magee, A., “Seakeeping Applications Using a Time-Domain Method”, Proceedings of the Twentieth Symposium on Naval Hydrodynamics, Santa Barbra, California, August, 1994.
Newman, J.N., “The Theory of Ship Motions,” Advances in Applied Mechanics, Vol. 18, 1978.
Pantazopoulos, M.S., “Three-dimensional Sloshing of Water on Deck”, Marine Technology, Vol. 25, 1988.
Peng, H., Lacy, G., Huang, Z.J. and Hsiung, C. C., “Nonlinear Roll Damping of Nova Scotia Inshore Fishing Boat”, Proceedings of the Twenty-Fourth American Towing Tank Conference, Texas A & M University, College Station, Texas, November 1995.
Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P., Numerical Recipes (Fortran), Cambridge University Press, 2nd Edition, 1992.
Roe, P.L., “Some Contributions to the Modelling of Discontinuous Flows”, Lectures in Applied Mathematics, Vol. 22, American Mathematical Society, 1985.
Steger, J. and Warming, R.F., “Flux-Vector Splitting of the Inviscid Gas Dynamic Equations with Application to Finite-Difference Methods”, Journal of Computational Physics, Vol. 40, 1981.
Van der Bosch, J.J. and Vugts, J.H., “On Roll Dampping by Free-Surface Tanks”, Transactions, RINA, Vol. 108, 1966.
Wu, G.X., “A Numerical Scheme for Calculating the mj-terms in Wave-Current-Body Interaction Problem', Applied Ocean research, Vol. 13, No. 6 , December 1991.
Yanenko, N.N., The Method of Fractional Steps, Springer-Verleg, New York, 1971.















