Coupled Hydrodynamic Impact and Elastic Response
D.-J.Kim,1 W.Vorus,2 A.Troesch,2 R.Gollwitzer3
(1University of Pusan, Korea; 2University of Michigan, USA; 3Naval Surface Warfare Center [Panama City], USA)
ABSTRACT
A theoretical model for hydrodynamic impact of hulls with hard chines is described. Two distinct conditions are considered: one in the initial stages of impact where the jet-head travels along the hull towards the chine and one in the later stages of impact where the jet-head leaves the body at the chine and outwardly travels across the water surface. Numerical calculations of the hull impact force and acceleration are given and compared with experimental drop test results. The model is then extended to include an internal body, supported by springs and dashpots. The mass of the impacting hull and the mass of the internal body form a two body system subject to the external force of the fluid. The motion of the masses are coupled through the hydrodynamic boundary value problem to form a time dependent hydroelastic impact model. Results applicable to shock mitigation and shock isolation studies are given.
INTRODUCTION
The hydroelastic behavior of high speed craft in a seaway is becoming an important design consideration as hull scantlings are made lighter in a never-ending search for weight reduction. This optimization of hull strength is occurring at the same that time vessel speeds are increased due to extended performance demands. In addition to structural considerations, the high speed and resulting high acceleration environment affect human performance and comfort. Severe shock loads certainly cause a reduction in operating personnel effectiveness and can result in potentially severe injury.
The accurate prediction of hull loads and responses during impact, though, requires the solution of coupled external hydrodynamic and internal elasto-dynamic problems. In previous impact loading calculations (e.g. Yamamoto et al., 1980, Meyerhoff and Schlachter, 1980, and Belik et al, 1988), either the hydrodynamic force was decoupled from structural response by assuming constant-velocity water entry, or simplistically coupled hydroelastic models were used where the hydrodynamic load was treated as quasi-steady. Recent works by Kvålsvold and Faltinsen (1993) and Kvålsvold et al (1995) have shown that the impact-initiated dynamic response of an elastic structure can be an important factor in changing local pressures and thus hull girder loads. The coupling between the hydrodynamics and an internal structural response has also been investigated in shock mitigation studies where biodynamic human response was a primary consideration (e.g. Gollwitzer and Peterson, 1995, 1996). These more recent efforts demonstrate the importance of a validated, general time-dependent, impact theory to which hull structural response can be coupled.
Starting with von Karman (1929) and Wagner (1932, 1933), the hydrodynamic impact problem has been investigated in various forms for years. However, the different theories are approximations and forced compromises reflecting the inherent difficulty of the problem. Traditionally, the analysis has either been conducted in two dimensions using a nonlinear free surface boundary condition without gravity, or in three dimensions using a simplified pressure release condition, i.e. ![]() =0 on z =0. Some recent representative examples of these two different approaches are Cointe (1991), Zhao and Faltinsen (1992, 1993) and Vorus (1992, 1996) for the two dimensional solutions and Troesch and Kang (1986 and 1988) for the simplified three dimensional
=0 on z =0. Some recent representative examples of these two different approaches are Cointe (1991), Zhao and Faltinsen (1992, 1993) and Vorus (1992, 1996) for the two dimensional solutions and Troesch and Kang (1986 and 1988) for the simplified three dimensional
solution. These papers did not couple the elastic response of the hull with the hydrodynamic problem.
The following sections will present the theory of transient impact, experimental validation, and numerical calculations of coupled wedge impact with elastic hull response. A time-dependent free surface impact boundary value problem (Vorus 1992, 1996) will be used to estimate the impact load acting on a rigid, constant deadrise section. The paper will discuss the significant difficulties associated with solving the fully nonlinear boundary value problem when time dependent spray sheets are present and assumptions based upon similarity flows are no longer valid. In addition, the impact problem for a finite wedge where the wedge surface becomes vertical at a hard chine will be briefly reviewed (Vorus, 1996). Comparisons between theory and experiments will also be presented. The experiments involve the drop testing of nearly prismatic sections of typical planing hulls. The analysis is then extended to include the coupling of a discrete mass attached to the rigid hull by springs and dashpots. This model has direct application to the shock problem associated with high speed planing vessel impact in waves. Numerical studies are presented which show the effect of different parameter values in system mass ratio, stiffness, and damping on maximum acceleration response.
THEORETICAL MODELING OF IMPACT
The characteristics of the flow during impact, which include the hull pressure distribution, jet velocity, and free surface deformation, change dramatically as the jet head passes over severe hull geometric variations. When the jet head reaches a location on the hull's surface where the surface curvature exceeds that which would normally occur in an unrestrained jet, such as at a chine, the pressure drops significantly. See Figure 1 for a schematic defining the “chines dry” and “chines wet” stages of impact. A variation of the model described in the following paragraphs (Vorus, 1992, 1996) has been compared extensively with steady planing pressure distributions (Lai and Troesch, 1995) which include the essential characteristics of impact hydrodynamics. A summary of the impact model is reviewed here briefly for completeness. Details can be found in Vorus (1996).
The theoretical formulation of Vorus (1992, 1996) can be viewed as a solution to the complete two dimensional nonlinear impact initial-boundary value problem in all respects except that the nonlinear boundary conditions are satisfied on the horizontal axis. This is argued to be consistent to lowest order in the flatness limit. Physically, as the cylinder flattens toward coincidence with the horizontal axis, the boundary conditions more and more accurately apply on the axis, implying a limit of geometric linearity. However, with increasing flatness, the transverse flow velocity tends toward infinity over the entire material contour (except with a singular zero at the plane of symmetry for symmetric impact). This implies the limiting condition of uniform hydrodynamic nonlinearity. The theory is therefore mixed: It is geometrically linear in that the boundary conditions are satisfied on the horizontal axis, but it is hydrodynamically nonlinear in that the large transverse perturbation velocity is fully retained in the axis boundary conditions.
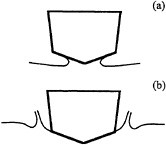
Figure 1: Definition of “chines dry” (a) and “chines wet” (b) impact phases
The mathematics problem is defined with the aid of Figure 2. Although depicted on Figure 2 as a semi-infinite wedge, the cylinder contour is of arbitrary shape and can include a hard chine where separation is forced to occur. The impact velocity V(t) is also arbitrary and can include, for example, forced deceleration which also produces contour flow separation, as is demonstrated in Vorus (1996).
Referring to Figure 2, the principal solution unknowns are the zero pressure point offset zc(t), the jet head offset zb(t) and the jet velocity distribution, Vs(z,t), between zc(t) and zb(t). A multi-layered nonlinear iteration is required in computing these unknowns starting from an initial condition corresponding to the self-similar semi-infinite wedge at the initial impact velocity V(0). The solution equations that must be iterated derive from the nonlinear boundary conditions satisfied on the axis segments indicated in Figure 2 b.
The dynamic boundary condition of zero pressure on the jet head free vortex sheet leads to a one-dimensional Burger's equation in terms of the Vs(z,t) and zc(t) unknowns:
(1)
Here ζ=z/zc, τ is nondimensional time, and b= zb/zc. As shown in Vorus (1996), Eq. (1) can be solved analytically by Galaen transformation to express Vs=Vs(ζ, τ; zc(τ)) on the free sheet. The solution to Eq. (1) assures that the pressure is constant on 1≤ζ≤b(τ). The condition that the value of the constant be zero is assured by:
(2)
In Eq. (2), the free sheet normal velocity Vn is taken as 0 or 1 depending on whether at τ the chine is unwetted or wetted, respectively.
Equation (2) and the solution to Eq. (1) provide two conditions on the unknowns zc(t), zb(t), and Vs(z,t) in zc<z≤zb. Vs(zc,t), the velocity entering the jet head, is the boundary condition in Eq. (1) and must be considered to be a fourth unknown.
The integral equation formed from the cylinder kinematic boundary condition is of the Carleman type, which is inverted analytically to produce the contour vortex strength, γc=–2Vs in 0≤z≤zc(τ) in terms of the principal unknowns as:
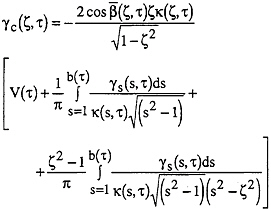
(3)
The two new terms in (3) are both unknown functions at time τ:
![]() where β(ζ,τ) is the spatially variable contour deadrise angle at τ in 0≤ζ≤1.
where β(ζ,τ) is the spatially variable contour deadrise angle at τ in 0≤ζ≤1.
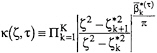 is from a K-element piecewise linear discretization of the cylinder contour at τ in 0≤ζ≤1 with the
is from a K-element piecewise linear discretization of the cylinder contour at τ in 0≤ζ≤1 with the ![]() and
and ![]() being the element end-point offsets and angles, respectively, as developed in Vorus (1996).
being the element end-point offsets and angles, respectively, as developed in Vorus (1996).
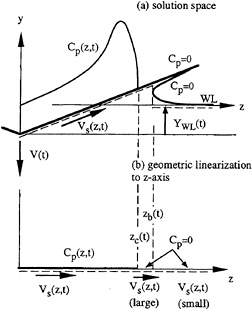
Figure 2: Solution space and unknowns
Equation (3) is singular at z=zc(ζ=1). Removal of the singularity requires that the first two terms in the bracket be collectively zero:
(4)
Equation (4) is a velocity continuity condition, in the sense of a “Kutta Condition,” providing with Eqns. (1) and (2) a third relationship among the four unknowns.
For the chine-wetted penetration phase of the cylinder immersion, with zc(τ) known and equal to the chine offset Zch the formulation is theoretically complete with Eq. (4). Equations (1), (2), and (4) determine the remaining principal unknowns γs(ζ,τ), γs(1,τ), and zb(τ) uniquely, given the values at the time of chine-wetting. For the initial chine-unwetted flow however, zc(τ) is an additional independent unknown, and an additional condition is required.
By Figure 2a, the velocity of the jet head, zb(t), is jump discontinuous from a large value on the cylinder contour to a small (higher order) value on the free-surface at the jet-head. However, the cylinder and free-surface contours must be continuous at zb(t) for the chine unwetted flow zc(t)≤Zch. The displacement continuity condition is obtained by integrating the kinematic boundary condition in time and solving the resulting Carleman integral equation for a displacement vortex strength:
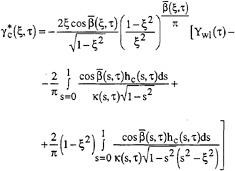
(5)
As with Eq. (3), the singularity in the first two bracketed terms of this solution must be removed to achieve the required displacement continuity. There results the fourth and final condition on the unknowns:
(6)
where hc(s,τ) in Eq. (6) is the cylinder contour elevation above the baseline from the plane of symmetry to the jet head, s=1. Ywl(τ) is the distance above the baseline to the undisturbed water surface and is just the integral of V(τ) in time. Both hc(s,τ) and Ywl(τ) are known functions at time τ.
The four generally unknown functions zc(t), zb(t), Vs(zc,t) in zc<z<zb, and Vs(zc,t) are iterated forward in time using Eqns. (1), (2), (4), and (6). Since all integral equation inversions have been performed analytically and the spatial integrations have been performed semi-analytically in terms of special functions, the numerical computations required with this highly nonlinear problem are stable and well behaved even with relatively course discretization. The numerical analysis employed to date is outlined in Vorus (1996); all the numerical results exhibited there were executed on a 16 mHz desk-top computer.
Once the four solution variables have been determined for any time, back substitution into Eq. (3) (with the singular terms removed) gives the cylinder contour vortex strength:
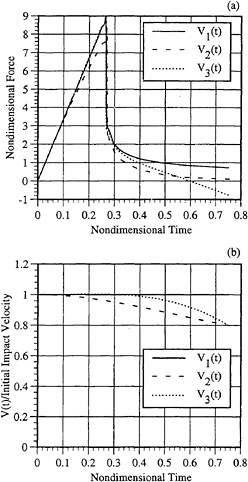
Figure 3: Impact force ![]() vs time (τ) for prescribed time varying impact velocities (a)
vs time (τ) for prescribed time varying impact velocities (a) ![]() vs τ. (b) Prescribed V(t) vs τ. Deadrise=20 degrees
vs τ. (b) Prescribed V(t) vs τ. Deadrise=20 degrees
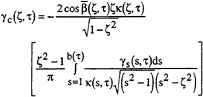
(7)
In a standard manner, the contour vortex strength, Eq. (7), is applied with the unsteady Bernoulli equation to produce the cylinder pressure distributions and the impact forces of primary interest.
Typical results for impact forces on a twenty degree wedge with non-constant impact velocity are presented in Figures 3 and 4. The nondimensional form of the impact force, ![]() and time, τ, are defined below as follows:
and time, τ, are defined below as follows:
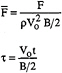
(8)
where B (=2 Zch) is the hull beam at the chine and the initial impact velocity is Vo. Four different prescribed velocities were used to calculate the impact forces. These prescribed velocities possess attributes of velocities shown in the coming sections where rigid body equations of motion are coupled with impact hydrodynamics. Three of the less severe velocity changes (characteristic of heavily loaded hulls during drop tests) are shown in Figure 3. The first velocity, V1, is constant for reference. The other two velocities, V2(t) and V3(t), are reduced 20%, one gradually (i.e. V2) and one quickly (i.e. V3). The large drop in impact force at an approximate value of τ=0.265 is due to the transition from chines dry to chines wet flow as the jet head passes the chine. The solution becomes square root singular at that instant, but of course integrable. The different accelerations produce significantly different impact forces, with the sharpest deceleration leading to negative impact loads.
In Figure 4, the velocity, V4(t), is reduced quickly to 30% of the initial value. This would be characteristic of lightly loaded hulls during drop tests. The large reduction in velocity produces a significantly smaller maximum impact force (but not necessarily lower accelerations, as will be demonstrated later) which occurs not at the instant of chines wetting, but rather at some time before. Of particular interest is the negative impact force during the chines-wetted phase of the impact. This “suction force” is due to the reduced momentum of the jet and downward momentum of the surrounding fluid. The velocity of the jet, Vjet(t) (=Vs(Zch,t)), is also shown in Figure 4 b. During the initial stages of impact, the jet velocity for a twenty degree deadrise hull is approximately eight times the impact velocity. Once the jet head clears the chine, Vjet(t) decreases significantly, actually becoming less than the magnitude of the downward velocity of the hull.
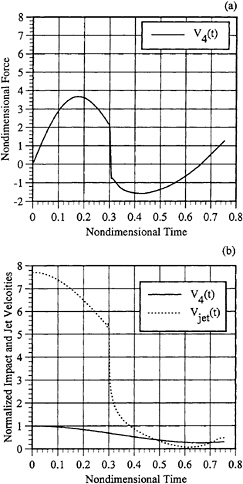
Figure 4: Impact force ![]() and jet head velocity for a prescribed time varying impact velocity (a)
and jet head velocity for a prescribed time varying impact velocity (a) ![]() vs τ. (b) Prescribed V(t) and Vjet(t) vs τ. Deadrise=20 degrees
vs τ. (b) Prescribed V(t) and Vjet(t) vs τ. Deadrise=20 degrees
EXPERIMENTAL VALIDATION PROGRAM
Objectives and Application
Drop tests were conducted at the Coastal Systems Station (CSS), Dahlgren Division, Panama City, Florida. These types of tests have been shown to be vital to the ongoing CSS shock mitigation program, and are expected to be useful in conjunction with future shock mitigation investigations. Within the CSS program, the data have been used for initial, qualitative evaluation and identification of shock mitigation concepts, for calibrating and validating the 2-D vertical water-entry model, and for validating evolving 2-D cylinder impact theories. The application to qualitative evaluation and identification of shock mitigation concepts is justified in part by the observed similarity between at-sea measurements of high-speed-vessel acceleration time histories, and those of boat-segment drop tests for approximately similar hull geometries and vertical entrance velocities. The most important and relatively long term application of drop test data, however, is calibration and validation of the 2-D components within evolving wave-to-wave planing boat theories.
Facility, Model Description, and Procedures
All test drops were conducted in the above ground test pool in Building 319 at CSS. The test tank is a fresh water pool that measures 40.0 ft (12.2 m) long by 15.0 ft (4.6 m) wide by 16.5 ft (5.0 m) deep. The water depth was reduced to 11.25 ft (3.43 m) to minimize the amount of water splashing out of the pool during water impact. The test models were lifted above the water surface by an overhead crane, and dropped into the center of the water surface. The temperature of the water varied slightly as the ambient temperature in the building varied. The average temperature for all drops was within 70 degrees F±5 degrees F. Water density differences were insignificant and consequently no corrections for density were made in the data.
Drops were made of prismatic and non-prismatic hull segments and aluminum and fiber reinforced plastic hull segments. Also two full-length scale model hulls were dropped: a baseline hull and a hull with a shock mitigation system installed. This paper will presents results of the aluminum full-scale prismatic hull segments. A more detailed discussion of all drops is given by Gollwitzer and Peterson (1996).
The aluminum hull segments represent longitudinal segments of a full scale hard-chine hull about 40 ft (12.2 m) long overall. The baseline test segment was a prismatic 23 deg deadrise segment without strakes, 3.4 ft (1.04 m) long as measured longitudinally along the keel, with a chine beam of 5.0 ft (1.52 m). A variation of the baseline segment with strakes added parallel to the keel was also tested.
A test fixture served as the central hardware interface for the testing. The test hull bottom, the drop sling arrangement, and the accelerometers were mounted to the test fixture to form the complete hull segment which weighed 916 lb (4.07 kN). The drop test fixture and hull bottom were essentially structures assembled from plates of aluminum. Longitudinal and transverse plates were welded into the drop test fixture for stiffening, reducing the contribution of structural elastic effects to the total measured accelerations during water-entry impact.
A four-leg sling was used to connect the test segment to an overhead crane. One leg of the sling was secured to each of the four corners of the test fixture. For each drop, the four legs were fitted into a quick-release mechanism attached to the overhead crane hook. The segment was hoisted by the crane to the desired drop height. The data collection process was initiated, a verbal countdown was made, and the fixture was dropped by opening the quick-release hook.
Other impact tests have used vertical rails to ensure the vertical drop orientation of the test fixture (e.g. Chuang, 1970). Mechanical guides were not used here after three-axis accelerometer measurements confirmed that the free drops were indeed vertical. The models were dropped from heights of 2, 4, 6, and 8 ft (0.61, 1.22, 1.83 and 2.44 m) above the water surface. Other varied parameters were the mass and the trim angle of the models.
Instrumentation
Hull mounted accelerometers were used in the experimental part of this shock and vibration study, primarily to enable comparisons between laboratory measurements and previously acquired at-sea data. The signals in both sets of tests were digitally recorded.
Both piezoelectric and piezoresistive accelerometers were used for this investigation to measure the full range of accelerations and the full frequency response of interest. Hermetically sealed accelerometers were chosen to reduce the harmful effects of the test environment. The piezoresistive accelerometers were Entran Inc. semiconductor Wheatstone bridge instruments, Model EGA3 series. Their nominal sensitivity was 0.5 mV/g with a range of ±500 g's and a nominal resonant frequency of 3000
Hz. Low frequency resolution is effectively unlimited. The piezoelectric accelerometers were Dytran Instruments Inc. low impedance quartz crystal and seismic mass transducers, Model 3100 series. Their nominal sensitivity was 50 mV/g with a range of ±100 g's. Low frequency response was 1 Hz±10 % at 5% down.
All accelerometers used for these tests measured 0 g when at rest. All reported accelerations are referenced to 0 g for the test segment floating in static equilibrium.
The accelerometers were secured in the longitudinal, transverse, and vertical directions to a solid mounting block. The mounting block was placed at the top center of the drop test fixture, which was the location of the longitudinal and transverse centers of gravity of the test segment. The analog voltage signals from the accelerometers were transmitted by hard wire to Ectron Model 562 analog amplifiers. The amplifiers provided wideband frequency response to 80 kHz and supply voltage to the accelerometers of 10.00 V±0.002 V. Data were sampled at a 200 microsecond sample rate and recorded by a Nicolet Model 310 Digital Oscilloscope and a TEAC digital tape recorder, Model RD-200T, with a 200 KHz low pass anti-aliasing filter. A desktop personal computer was used to process the collected data using in-house software. A more detailed discussion of the instrumentation is included in Gollwitzer and Peterson (1996).
Discussion of the Experimental Results
Two typical acceleration time histories are presented here, one for the constant deadrise section without strakes, Figure 5, and one for a similar section with strakes, Figure 6. Numerical results based upon the theory of Eqns. (1)–(7), where V(τ) is determined from ![]() are also plotted for comparison.
are also plotted for comparison.
In Figure 5, the results for the constant deadrise section without strakes are shown. The vertical axis is the acceleration in g's and the horizontal axis is the elapsed time in seconds. The solid line represents the filtered (cutoff frequency= 200Hz) experimental acceleration and the dashed line represents the theoretical equivalent.
Generally, the unfiltered data of the constant deadrise section without strakes indicates mechanical frequency components at about 20 Hz and 60 Hz superimposed on the basic hydrodynamic shock record. An impulse test of the model indicated the fundamental frequency of the test fixture to be 63 Hz. For reference, a human is susceptible to motion sickness at frequencies between about 0.2 Hz and 1 Hz (ISO 2631 Part 3). The spine of the seated human is susceptible to discomfort and injury at frequencies from about 4 Hz to 8 Hz, and the lower extremities of a standing human are susceptible to discomfort and
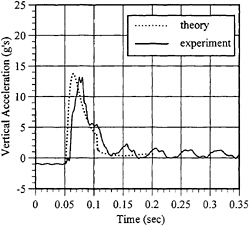
Figure 5: Experimental (solid line) and theoretical (dashed line) impact accelerations in g's for a twenty three degree deadrise (nominal) hull section. No strakes attached. Drop height=8.0 ft (2.438 m)
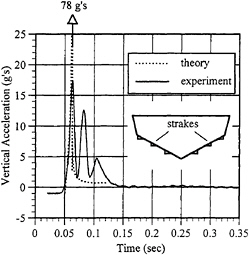
Figure 6: Experimental (solid line) and theoretical (dashed line) impact accelerations in g's for a twenty eight degree deadrise (nominal) hull section. With strakes attached. Drop height=8.0 ft (2.438 m)
injury at frequencies as high as 30 to 40 Hz (ISO 2631 Part 1). The model scale time histories shown in Figures 5 and 6 were digitally filtered at 200 Hz. This filtering frequency captures the relevant human body discomfort and injury dynamics while eliminating contaminating high frequency noise effects.
In Figure 6, the results for the constant deadrise section with strakes are shown. A significant characteristic of the experimental curve is the large drop in acceleration when the jet head reaches the first strake and the flow effectively becomes chines-wet-type-flow until reattachment. The cycle is repeated as the jet head advances toward the next strake. At present, the theoretical model is only valid up to the first strake. The model assumed that the flow became chines wet after the first strake and remain separated which is clearly not the case. The time to reach the first strake edge is approximately predicted, but the maximum acceleration is severely over-predicted due to the high rate of change of locally decreasing deadrise. This is an area of ongoing research.
For the constant deadrise section without strakes, the distinct phases of the individual shock event can be seen in the Figure 5. The water re-entry shock pulse is shown in the time histories by the rapid rise from –1 g up to the peak amplitude and the subsequent fall back towards 0 g. The rise time is approximately 20 msec, and the fall time is approximately 50 msec, producing a total pulse duration of about 70 msec. The submergence/emergence phase occurs for about 500 msec after the water re-entry shock phase.
The impact of the hull segment with strakes as shown in Figure 6 is significantly different from the time history shown in Figure 5. An examination of the geometry of the strakes and the boat velocities at water entry indicates that multiple peaks in the acceleration time histories are caused by the strakes entering the water. The drop tests indicate that strakes shorten the duration but increase the amplitudes of the shocks. Care must be taken in the positioning of the strakes so as to not excite hull or human resonant frequencies during impact.
Based upon the above comparisons between theory and experiment, we conclude that the theory predicts hydrodynamic impact characteristics for constant deadrise shapes, both up to and beyond the point where the jet head reaches the chine. The magnitude of the maximum acceleration is slightly over predicted and the rise time is slightly offset. The elastic response of the test section certainly plays a role in defining the impact characteristics, but without an extensive structural analysis, this role is difficult to quantify. For sections with strakes, there are discernible differences between theory and experiment. More work is clearly needed to describe the impact of sections with locally large slope changes leading to separation and then re-attachment.
IMPACT OF A MULTI-DEGREE-OF-FREEDOM BODY
This part of the paper examines the effect of variable impact velocity on multi-degree of freedom bodies experiencing slam conditions. An obvious application of this analysis is the design of shock mitigating devices for occupants of high speed vessels. A simplified lumped-mass model for the hull structure is assumed. The time-dependent free surface impact boundary value problem (Vorus 1992, 1996) described in the first sections of this paper has been used to estimate the impact load acting on an externally rigid, finite beam, constant deadrise section.
The system equations of motion can include a finite number of discrete masses attached to the rigid hull by springs and dashpots. The mass of the impacting hull and the mass of the internal body form a time dependent hydroelastic impact model. See Figure 7 for a schematic of the two degree model considered here. Since the solution is presented as the time integration of the equations of motion, the internal stiffness and damping can be nonlinear functions of the relative displacement and velocity. In this work, the system damping and stiffness are linearized as shown in Eq. (9).
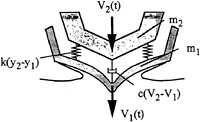
Figure 7: Schematic of coupled hydroelastic impact model with variable impact velocity.
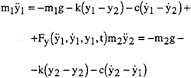
(9)
where the hydrodynamic impact force, ![]() is determined from the theory governed by Eqns. (1–7). This dynamic multi-body model has been incorporated into the hydrodynamic impact simulator forming a coupled hydroelastic analysis program. The time dependent impact velocity is not prescribed, but rather the solution of Eq. (9).
is determined from the theory governed by Eqns. (1–7). This dynamic multi-body model has been incorporated into the hydrodynamic impact simulator forming a coupled hydroelastic analysis program. The time dependent impact velocity is not prescribed, but rather the solution of Eq. (9).
A characteristic beam loading parameter, ![]() is defined, where m1 is the mass per unit length of the impacting hull bottom and m2 is the mass per unit length of the suspended interior mass. The impact velocity is represented by the parameter H/B, where B is the beam of the section and H is the drop height. The initial impact velocity, Vo, then is given by
is defined, where m1 is the mass per unit length of the impacting hull bottom and m2 is the mass per unit length of the suspended interior mass. The impact velocity is represented by the parameter H/B, where B is the beam of the section and H is the drop height. The initial impact velocity, Vo, then is given by ![]()
Time dependent, single degree-of-freedom impact
Before the dynamic effect of an interior oscillating mass is examined, the infinite spring constant case is investigated first. This will provide a basis for describing the effects of mass and stiffness parameter variations on the maximum acceleration, the maximum impact force, and the times to maximum impact force and chines wetting.
In Figure 8, a plot of the nondimensional maximum acceleration of the section and the beam loading parameter, α, is given for two values of the H/B parameter, 1.0 and 1.6 respectively. There is a slight drop height dependence in the results due to the relative contribution of the buoyancy term to the velocity squared term in Bernoulli's equation, depending upon the immersion of the section. Since the connecting spring constant is infinite, large values of α represent the limit of constant velocity impact, a typical assumption of classic impact analysis. The acceleration (deceleration) is in the nondimensional form ![]() where
where
For small values of α, there is a large increase in maximum acceleration (i.e. maximum deceleration) for decreasing α and for values of α> 2, the relative change rapidly decreases, asymptoting to –g as α → ∞. Generally, the maximum acceleration occurs prior to chine wetting for small values of α, and corresponds to when the jet head reaches the chine for large values of α (see Figures 3 and 4). From this figure, we can conclude that when the mass is relatively small the acceleration, or deceleration, is large.
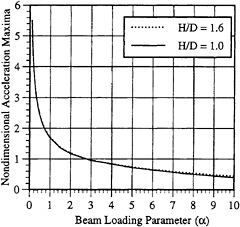
Figure 8: Maximum impact accelerations ![]() as a function of the beam loading parameter, α, and drop heights. H/B=1.0 (solid line), 1.6 (dashed line). Infinite spring constant. Deadrise=23 deg.
as a function of the beam loading parameter, α, and drop heights. H/B=1.0 (solid line), 1.6 (dashed line). Infinite spring constant. Deadrise=23 deg.
In Fig.9, representative nondimensional dynamic force coefficient time histories for two different mass parameters are shown. The nondimensional form of the impact force, ![]() and time, τ, are defined above in Eqns. (8). Even though the maximum deceleration for α=0.1, as shown in Fig.8, is approximately ten times the maximum deceleration for α=10.0, the relative impact force for the lighter hull is an order of magnitude smaller. This suggests that light craft may experience accelerations that are potentially damaging to humans while heavier, better riding craft experience large local structural loads. Chine wetting for α=0.1 occurs at approximately τ=1.41 and for α=10.0 occurs at approximately τ=0.314. Generally, when the mass parameter is larger, it follows that the deceleration is relatively smaller, the value of the force coefficient is relatively greater, and the effect of chine wetting is more pronounced.
and time, τ, are defined above in Eqns. (8). Even though the maximum deceleration for α=0.1, as shown in Fig.8, is approximately ten times the maximum deceleration for α=10.0, the relative impact force for the lighter hull is an order of magnitude smaller. This suggests that light craft may experience accelerations that are potentially damaging to humans while heavier, better riding craft experience large local structural loads. Chine wetting for α=0.1 occurs at approximately τ=1.41 and for α=10.0 occurs at approximately τ=0.314. Generally, when the mass parameter is larger, it follows that the deceleration is relatively smaller, the value of the force coefficient is relatively greater, and the effect of chine wetting is more pronounced.
The nondimensional time of the maximum acceleration, τmax, and the nondimensional time of the chine wetting, τwet, are plotted together in Fig. 10. When the mass parameter α, is small the chine
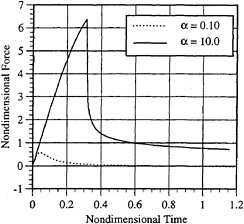
Figure 9: Impact force time histories ![]() for two values of the beam loading parameter, α=0.1 (dashed line) and 10.0 (solid line). H/B=1.0. Infinite spring constant. Deadrise=23 deg.
for two values of the beam loading parameter, α=0.1 (dashed line) and 10.0 (solid line). H/B=1.0. Infinite spring constant. Deadrise=23 deg.
wetting time occurs after the time of maximum acceleration. As α approaches zero, which would be the case for lightly loaded hulls, chine wetting does not occur. When α is large, the maximum acceleration coincides with the time of chine wetting. This is analogous to heavily loaded hulls where the assumption of constant velocity impact is most nearly valid.
Time dependent, two degree-of-freedom impact
Based upon these results, two mass parameter values are chosen as α=0.3 and α=2.5 for the finite spring constant case. (The experimental test hull had a value of α=0.587.) From Figure 10, the nondimensional chine wetting times for the infinite spring constant case with these two values of α are approximately 0.66 and 0.37 respectively. Three representative values of the spring constant are calculated so that one of the system natural periods (i.e. ![]() ) are 0.1 (relatively very stiff), 1 (relatively moderately stiff), and 5 (relatively soft), times the chine wetting time, twet. The damping coefficient is selected such that the damping ratio is 0.01. Here the damping ratio is defined as
) are 0.1 (relatively very stiff), 1 (relatively moderately stiff), and 5 (relatively soft), times the chine wetting time, twet. The damping coefficient is selected such that the damping ratio is 0.01. Here the damping ratio is defined as ![]() (An investigation into the influence
(An investigation into the influence
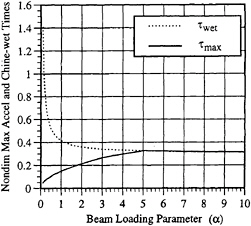
Figure 10: Time of maximum acceleration (solid line) and time of chine wetting (dashed line) as a function of the beam loading parameter, α. H/B=1.0. Infinite spring constant. Deadrise=23 deg.
of damping was carried out. As expected, for light damping the actual value of the damping ratio had little effect on the maximum values and general character of the responses.) To find the effect of mass distribution on acceleration of coupled body motion, another parameter, the mass distribution ratio (m2/m1), is defined.
In Figure 11 acceleration time histories of the coupled body for a constant mass distribution ratio of m2/m1=1.0 are given. Three different system stiffness' corresponding to values of Tn/twet=0.1, 1, and 5 are shown. The value of the mass parameter is α=2.5. In the large spring constant case (Tn/twet=0.1) there seems to be little phase shift in the two accelerations of m1 and m2 until chine wet conditions are reached. After chine wetting, the time histories exhibit typical lightly damped free vibration behavior where the masses then oscillate 180 degrees out of phase. In the intermediate stiffness case (Tn/twet=1.0), the interior sprung mass experiences a dynamic overshoot of approximately 80%. In the soft system case (Tn/twet=5.0), the sprung mass experiences the lowest acceleration on a much expanded time scale. The time history also suggests that the largest
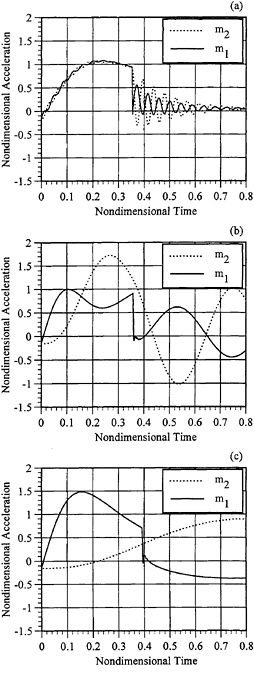
Figure 11: Impact acceleration time histories ![]() for three spring constants. Deadrise=23 deg. (a) Tn/twet=0.1. (b) Tn/twet=1.0. (c) Tn/twet=5.0. H/B=1.6. m2/m1=1.0. α=2.5.
for three spring constants. Deadrise=23 deg. (a) Tn/twet=0.1. (b) Tn/twet=1.0. (c) Tn/twet=5.0. H/B=1.6. m2/m1=1.0. α=2.5.
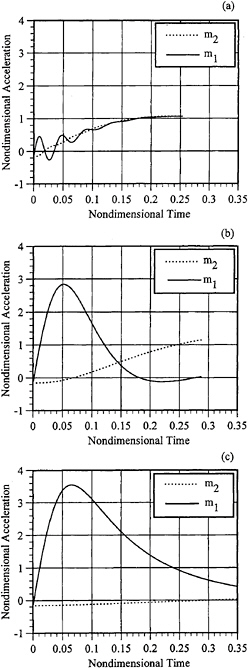
Figure 12: Impact acceleration time histories for three spring constants. (a) Tn/twet =0.1. (b) Tn/twet=1.0. (c) Tn/twet= 5.0. H/B=1.6. m2/m1=10. α= 2.5. Deadrise=23 deg.
relative displacement occurs during the soft system impact. For all three cases, increased damping would be particularly effective in reducing the acceleration. In general, for a given drop height which is equivalent to specified loading condition, the acceleration can be decreased by selection of a proper mass/stiffness distribution of the two bodies.
Acceleration time histories are shown in Figure 12 for a mass distribution ratio of m2/m1 =10.0. Here the time histories for the two suffer systems are stopped at chine wetting due to numerical convergence difficulties in the time integration routines. Generally, the results have similarities to the results shown in Figure 11 with the exception that the interior mass experiences a significant reduction in acceleration. A possible shock mitigation device suggested by the plots would be a heavy inner hull attached by springs to a much lighter outer skin.
In Figures 13 and 14, the acceleration time history results for a mass parameter of α=0.3 are shown. The mass distribution ratios, m1/m2, are 1.0 and 10.0 respectively. These time histories are typical of lightly loaded craft impacting the water surface. The trends are the same as the previous results of Figures 11 and 12 but the magnitude of accelerations, particularly the impacting mass m1, is greater by approximately a factor of three.
SUMMARY AND CONCLUSIONS
The paper has shown results of variable speed impact and hydroelastic impact for systems such as that illustrated in Figure 7. Both experimental and theoretical results are presented. The theory, strictly valid in the limit of flat hulls, is based upon a geometrically linear but hydrodynamically nonlinear model. Important factors in the determining the severity of impact accelerations are hull geometry, hull weight, initial impact velocity, and ratios of internal/external masses and system internal stiffness. Generally, light craft experience high accelerations, but low impact forces and heavier, better riding craft experience large local structural loads but low accelerations. Shock mitigation, or the study of shock mitigation devices, involves the solution of coupled hydrodynamic and elastic problems. Results given here have demonstrated the potential for reducing impact accelerations through proper choice of mass distributions and system natural frequencies.
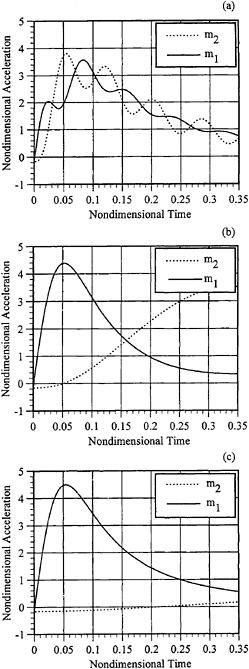
Figure 13: Impact acceleration time histories for three spring constants. (a) Tn/twet= 0.1. (b) Tn/twet=1.0. (c) Tn/twet= 5.0. H/B=1.6. m2/m1=1.0. α= 0.3. Deadrise=23 deg.
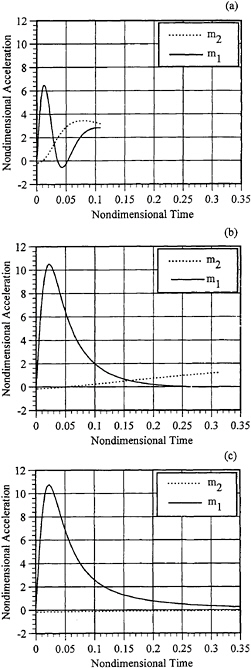
Figure 14: Impact acceleration time histories for three spring constants. (a) Tn/twet= 0.1. (b) Tn/twet=1.0. (c) Tn/twet= 5.0. H/B=1.6. m2/m1=10.0. α=0.3. Deadrise=23 deg.
ACKNOWLEDGMENTS
This work has been supported by the Korea Science and Engineering Foundation, the Office of Naval Research under Contracts DOG-G-N00014 –94– 1–0652 and DOD-G-N0014–95–1–1124 with program managers Dr. Peter Majumdar, Dr. Edwin Rood and Dr. Thomas Swean, respectively, the Michigan Sea Grant College Program, projects R/T-27, R/T-30 under grant number NA89AA-D-SG083, NOAA, U.S. Dept. of Commerce, and the University of Michigan, Office of the Vice President for Research Program to Promote International Partnerships.
REFERENCES
1. Belik, O., Bishop, R.E.D., and Price, W.G., “Influence of Bottom and Flare Slamming on Structural Responses,” Trans. RINA, Vol. 130, 1988.
2. Chuang, S.-L., “Investigation of Impact of Rigid and Elastic Bodies with Water,” DTNSRDC Report No. 3248, 1970.
3. Cointe, R., “Free Surface Flows Close to a Surface Piercing Body,” Math. Approaches in Hydrodynamics, Soc. Ind. Appl. Maths., 1991, pp. 319–334.
4. Gollwitzer, R.M. and Peterson, R.S., “Repeated Water-Entry Shock Mitigation for High Speed Planing Boats, ” Proceedings, 66th Shock and Vibration Symposium, Oct. 30—Nov. 1, 1995, Biloxi, MS.
5. Gollwitzer, R.M. and Peterson, R.S., “Drop Tests and Planing Boat Modeling,” Proceedings, Small Craft Symposium, May 15–17, 1996, University of Michigan, Ann Arbor, MI.
6. Kvålsvold, J. and Faltinsen, O.M., “Hydroelastic Modeling of Slamming Against the Wetdeck of a Catamaran, ” Proc., FAST '93, Yokohama, Japan, Vol. 1, December 1993, pp 681–697.
7. Kvålsvold, J., Faltinsen, O.M., and Aarsnes, J., “Effect of Structural Elasticity on Slamming Against Wetdecks of Multihull Vessels.” Proc., PRADS '95, Seoul, Korea, Vol. 1, September 1995, pp 684–699.
8. Lai, C. and Troesch, A.W., “Modeling Issues Related to the Hydrodynamics of Three Dimensional Steady Planing.” Jour. of Ship Research, Vol. 39, No. 1, 1995, pp. 1–24.
9. Meyerhoff, M. and Schlachter, G., “An Approach for the Determination of Hull Girder Loads in a Seaway Including Hydrodynamic Impacts,” Ocean Engineering, Vol. 7, 1980.
10. Troesch, A.W. and Kang, C.-G, “Hydrodynamic Impact Loads on Three-Dimensional Bodies.” 16th Symposium on Naval Hydrodynamics, University of California, Berkeley, 1986.
11. Troesch, A.W. and Kang, C.-G., “Evaluation of Impact Loads Associated with Flare Slamming,” SNAME STAR Symposium, Pittsburgh, 1988.
12. von Karman, T. “The Impact on Seaplane Floats During Landing.” NACA TN 321, 1929.
13. Vorus, W.S., “An Extended Slender Body Model for Planing Hull Hydrodynamics,” presented at the SNAME Great Lakes and Great Rivers Section Meeting , Cleveland, January 23, 1992.
14. Vorus, W.S., “A Flat Cylinder Theory for Vessel Impact and Steady Planing Resistance, ” June, Journal of Ship Research, 1996.
15. Wagner, H., “Über Stoss-und Gleitvorgänge an der Oberflächen von Flüssigkeiten.” Z. Angew. Math. Mech. 12, 1932.
16. Wagner, H. “Planing of Watercraft,” NACA TN 622, 1933.
17. Yamamoto, Y., Fujino, M., and Fukasawa, T., “Motion and Longitudinal Strength of a Ship in Head Sea and the Effects of Nonlinearities,” Naval Architecture and Ocean Engineering, Society of Naval Architects of Japan, Vol. 18, 1980.
18. Zhao, R. and Faltinsen, O., “Water Entry of Two-Dimensional Bodies,” Seventh International Workshop on Water Waves and Floating Bodies, Val de Reuil, France, May 24–27, 1992.
19. Zhao, R. and Faltinsen, O., “Water Entry of Two-Dimensional Bodies,” Journ. Fluid Mech., 246, 1993, pp. 593–612.














