Large-Eddy Simulation of the Vortical Motion Resulting from Flow over Bluff Bodies
S.Jordan (Naval Undersea Warfare Center [Newport], USA)
ABSTRACT
The focus of the present investigation is resolution of the vortical motion within the near wake of two example bluff bodies. Specifically, the mixing of the secondary eddies and primary Strouhal vortex frequencies in the separated shear layer of a circular cylinder and the subsequent vortical motion in the near wake are numerically investigated using the large-eddy simulation (LES). These LES investigations were performed at Reynolds numbers (Re) of 5600 and 8000. Preliminary results of a NACA 0018 hydrofoil is also presented. The vortical flow of the hydrofoil was simulated at Re= 25000 and an angle-of-attack of 7.5 degrees. The governing LES equations were formulated in curvilinear coordinates to accommodate the nonorthogonal grids. A corresponding generalized dynamic model is developed for the sub-grid scale turbulence. At the cylinder sub-critical Reynolds number of 8000, the LES results showed that laminar separation is quickly succeeded by Tollmien-Schlichting instabilities, secondary eddies and finally the formation of the primary Strouhal vortex. Through the separated shear layer, the LES results showed a range of transition wave frequencies that dominated the high-frequency components of the pressure spectrum compared to the low frequency component of the Strouhal vortex. The results also showed several modes of mixed transition and Strouhal frequencies. At Re=5600, the LES results showed good comparisons to the published experimental data in terms of the time-averaged pressure distribution along the cylinder periphery, the shedding frequency, the vortex detection frequency, and the overall characteristics of the Strouhal vortices in the near wake. The results also showed streamwise filaments that connect subsequent Strouhal vortices. The time-averaged Reynolds stress results of the formation region reveal symmetric characteristics similar to published experimental data at the sub-critical Reynolds number of 140,000. The LES results of the hydrofoil showed laminar separation of the upstream upper boundary layer followed by transition to turbulence and reattachment near the beginning of the trailing edge.
INTRODUCTION
Many engineering problems within the Navy involve very complicated flow behaviors that cannot be accurately simulated using simple computational methods. In addition, the physical geometries are generally quite arbitrary and require special attention when attempting to predict the associated flow. In most problems, the flow is unsteady, incompressible and very turbulent. Traditionally, numerical simulations of these flows are performed using the Reynolds-averaged Navier-Stokes (RANS) equations with a general purpose phenomenological model to fully represent the turbulence. The available turbulence models vary extensively in complexity; in particular, from simple algebraic eddy viscosity relationships to complex formulations involving several additional differential equations. In each model, values for the empirical constants are supplied from turbulent flows that are usually fundamentally simpler than the complexity of the problem at hand. Consequently, a RANS simulation can not be expected to give accurate predictions of the fine-scale turbulent physics using these general purpose models.
A viable alternative for numerical simulation of complex turbulent flows is the large-eddy simulation (LES). This approach is gaining popularity over the traditional RANS simulation. The LES success rests primarily on the rapid advancements in supercomputer technology as well as the recent developments in the methodology itself. Unlike the full-scale modeling inherent in a RANS technique, the LES method requires resolution of the dominate energy-bearing scales of the turbulent field while modeling only the remaining finer eddies which tend toward homogeneous and isotropic characteristics. Demarcation between the resolved and modeled scales is formally instituted by spatially filtering the basic governing equations of the fluid motion. In most computations however, this filter is actually treated implicitly through the spatial resolution of the implemented grid. Those physics lying beneath the grid resolution embody the subgrid scales (SGS) of the turbulent field and usually encompass most of the equilibrium range of the kinetic energy. Under this premise of an energy balance, today's SGS models are much simpler in form and better delineate the turbulent physics of their assigned scales as opposed to the typical full-turbulence models used in the RANS computations.
Studies of the turbulent vortical formation behind bluff bodies and the subsequent transport of the vorticity downstream has many important and practical Naval implications. Resolution of the turbulent vortical characteristics within the bluff body wake poses an excellent challenge for the large-eddy simulation. Except for only minor dispersion, the large scale motion usually remains strongly coherent for many characteristic lengths downstream of the bluff body. Since the impetus of LES is full resolution of the large scale motion, the results can provide specific information regarding the cyclic formation and downstream transport of the vortical motion including the local turbulent physics.
The formation and the downstream transport of the Strouhal vortices in the near wake of a circular cylinder is an excellent example of a difficult bluff body flow. The vortices themselves derive most of their large-scale vorticity from the separated shear layers and they organize downstream to form the well-known Karman vortex street. The upper and lower separated shear layers constitute the transverse outer regions of the formation regime. Both layers lie between the point of separation and the initial formation of the shed Strouhal vortices. Besides these shear layers, the fluctuating base pressure near the downstream stagnation location contributes to the Strouhal vortex formation as well. A sketch illustrating these features is depicted in Figure 1.
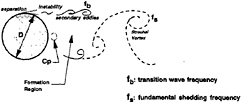
Figure 1: Sketch of the Primary Strouhal Vortex and Secondary Eddies in the Cylinder Wake Formation Region.
Our understanding of the cylinder shear layer physics improved significantly due to the experimental investigation by Bloor (1), Unal and Rockwell (2) and Wei and Smith (3). Bloor hypothesized that transition from laminar separation to turbulent vortex formation occurs within the separated boundary layer. This process occurs in two phases. Soon after separation, two-dimensional small-scale instabilities arise within the separated layer that amplify into Tollmien-Schlichting waves and eventually lead to turbulence. Due to the three-dimensional nature of the flow, these instabilities experience substantial spanwise distortion which also contribute to the transition mechanism. Unal and Rockwell also found high-frequency instabilities to exist, but for only Re≥1900 with pronounced amplification at specific Reynolds numbers of Re= 3400 and Re=5040. At the latter Re in particular, they showed the spectral amplitudes to vary significantly across the shear layer at the predominant frequencies of the small-scale instabilities as well as the frequencies of the much larger scale Strouhal vortex.
Through flow visualization testing, Wei and Smith proposed a different phenomena for the separated shear layer physics. They observed creation of small-scale secondary vortices between separation and the initial large-scale Strouhal vortex formation. These secondary structures evolve from the same two-dimensional instabilities described by Bloor. The Strouhal vortices receive the majority of their vorticity from the secondary structures which
in-turn originate further upstream from the vorticity contained in the separated boundary layer. One primary difference between the Strouhal and shear layer structures is the minor influence of the rear base pressure on the secondary vortex formations. In the spanwise direction, the secondary vortices distort to periodic cellar structures that align themselves streamwise. Wei and Smith attributed the alignment to some feedback mechanism delivered from the downstream to upstream structures. At the higher Reynolds numbers within the intermediate range, the cellar structures become less pronounced and highly irregular.
The phenomena occurring in the separated shear layers just described as well as the organized vortex formation and subsequent downstream motion in the near wake is the subject of the present LES investigation. Only a few LES investigations have been previously reported of the cylinder separated shear layers and near wake flow. The first was a two-dimensional study by Song and Yuan (4) at a high Reynolds number. Since vortex stretching strongly dominates the turbulent production in the near wake (5), their simulation appears quite inadequate for capturing the important scales of the turbulent physics. Braza et al. (6,7) reported mixing layer eddies and pressure-frequency spectra of the cylinder shear layers, but their computations were also two-dimensional. Besides obviously ignoring important three-dimensional contributions to the streamwise maturity of the secondary eddies, pressure predictions near rear stagnation are always overpredicted thereby lengthening the formation region of the primary vortices. Another study was reported by Kato et al. (8) who concentrated on predicting the aerodynamic noise in the near wake using the finite element method. Their LES results served as input into the Lighthill-Curle equation for predicting the radiated far field acoustic pressures. However, due to their simple subgrid-scale turbulence model and their relatively coarse mesh of the wake region, agreement with the experimental data in terms of the spectral physics was obtained only at the low frequency levels.
In the following work, results from large-eddy simulations will be presented at a Reynolds number of 8000 to investigate the mixing of frequencies in the formation region due to the primary Strouhal vortex and the separated shear-layer secondary eddies. Results from a simulation at Re=5600 will also be presented of the organized vortex motion in the near wake of the circular cylinder with special emphasis placed on the turbulent statistics of the formation region. These Reynolds numbers are based on the cylinder diameter (D) and the uniform freestream velocity (U∞) and are both sub-critical, meaning that the boundary layer at separation is strictly laminar. At these Reynolds numbers, the shedding of the primary shed vortices occurs at a dimensionless frequency (Strouhal number, St) of approximately 0.21; St=f D/U∞. Experimental measurements of the near wake turbulent statistics at a Reynolds number of 5600 were published by Zhou and Antonia ( 9). They reported the near wake as being fully turbulent over a downstream distance (x) ranging from 10 to 60 diameters referenced to the cylinder center. Over that range, their data showed little variation in the cross-sectional area of the primary vortices.
Finally, the preliminary results of the fine-scale turbulent motion resulting from trailing edge separation of the boundary layer of a hydrofoil will close the presentation and discussion of this paper. To adequately resolve the near wake flow of these geometries, non-orthogonal grid topologies were implemented. The corresponding equations were therefore solved in a curvilinear coordinate framework. Additionally, the dynamic subgrid scale turbulence model of Germano et al. (10) was reformulated for application in the curvilinear space. Since non-orthogonal topologies are often necessary to properly resolve the flow characteristics in many complex domains like the cylinder and hydrofoil wake, this LES formulation with the dynamic model has extensive applicability.
FORMULATION
Extension of the LES strategy to non-orthogonal grids was presented in detail by Jordan (11). For brevity, an abbreviated version will be described. Transformation of the Navier-Stokes equations to curvilinear coordinates where the Cartesian velocity components are the primary dependent variable has the form
(1)
(2)
The contravariant velocity components (Uk) are defined here as ![]() The Jacobian
The Jacobian ![]() of
of
the transformation appears in the formulation to place it in strong conservation-law form (12). To derive the corresponding LES equations, each term in equation (1) must be filtered (designated by an overbar). Except for convection, these terms commute with the filtering process to yield an analog set of equations in curvilinear coordinates that appear as
(3)
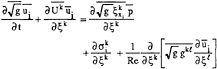
(4)
The subgrid scale (SGS) stress tensor ![]() is defined in terms of the Cartesian and contravariant velocity components as
is defined in terms of the Cartesian and contravariant velocity components as ![]()
For the cylinder and hydrofoil formation regions, the LES system of equations in (3 and 4) was time-advanced according to a variant of the fractional-step method (13). The convective terms were spatially discretized by third-order upwind-biased finite differences while the diffusive terms were differenced by second-order central differences. All terms in pressure-Poisson 's equation were central differenced to the second order. Strong coupling between the pressure and velocity components was maintained through a fourth-order accurate compact differencing scheme for the pressure gradient in the velocity update equation. Details of the solution methodology, along with several test cases, were reported by Jordan and Ragab (14). The method is second-order accurate in both space and time.
DYNAMIC SUBGRID SCALE MODEL
To generalize the dynamic model by Germano et al. (10) for the cylinder application, the model was mathematically transformed to the computational space. This transformation was first reported by Jordan and Ragab (14). The SGS stress tensor in terms of the Cartesian velocity components is defined as
(5)
Removal of the metrics from the filtering process provides a definition for ![]() as
as
(6)
which in terms of its Cartesian counterpart τij is defined by ![]() Using this expression, a generalized dynamic model (GDM) for the SGS stress tensor was defined as
Using this expression, a generalized dynamic model (GDM) for the SGS stress tensor was defined as
(7)
where C is Smagorinsky's constant. The turbulent eddy viscosity is defined as ![]() where
where ![]()
![]() and the strain-rate tensor
and the strain-rate tensor ![]() in the computational space is computed according to
in the computational space is computed according to
(8)
The resolvable strain-rate field ![]() in the computational space is
in the computational space is ![]() By combining this transformation with equation (8), the complete definition for
By combining this transformation with equation (8), the complete definition for ![]() is
is
(9)
where ![]()
![]()
The procedures of Germano et al. (10) and Lilly (15) were used by Jordan and Ragab (14) to derive an expression for Smagorinsky's coefficient in the GDM. To implement their procedures directly the metrics were kept as part of the filtering process. An expression for Smagorinsky's coefficient in the computational space was obtained by filtering the governing LES equations in curvilinear coordinates a second time (by the test filter) to produce terms similar to those obtained by Germano et al. in the Cartesian coordinate system. In the computational space however, two new resolvable stress tensors arose. These two tensors are the:
Reynolds stress tensor ![]() where
where
(10)
and a Leonard tensor ![]() defined as
defined as
(11)
Consistent with the model scaling law for ![]() the stress tensor
the stress tensor ![]() was modeled as
was modeled as
(12)
Using the identity ![]() the resolvable tensor
the resolvable tensor ![]() in the computational space became
in the computational space became
(13a)
(13b)
Following the least-squares minimization procedure of Lilly (15), the GDM coefficient in equation (7) appeared as
(14)
where the tensorial components in ![]() and
and ![]() are given in equations (11) and (13b), respectively. For the present computations, the tensors
are given in equations (11) and (13b), respectively. For the present computations, the tensors ![]() and
and ![]() were determined through application of a box filter. Negative values of the coefficient were truncated to zero, therefore all backscatter effects were eliminated.
were determined through application of a box filter. Negative values of the coefficient were truncated to zero, therefore all backscatter effects were eliminated.
RESULTS AND DISCUSSION
Simulation of the cylinder flow was focused specifically on resolving the separated shear layer physics and the formation and transport of the Strouhal vortices. To establish sufficient grid resolution near the cylinder surface, comparisons were made to the experimental results reported by Bouard and Coutanceau (16) of the early wake formation. According to Bouard and Coutanceau, the structural characteristics of the early wake formation behind the circular cylinder are similar for 1000<Re<10000. Specifically, they visualized the early time evolving profiles of the exterior wake boundary and measured the horizontal velocity along the downstream centerline axis. LES computations were compared to those experimental measurements to help estimate the grid resolution that is required adjacent to the cylinder surface for the present study at the lower Reynolds numbers.
If a 2D simulation is performed of the cylinder wake flow at these sub-critical Reynolds numbers, one will grossly over-predict both the minimum and the base pressure coefficients along the cylinder surface. The base pressure coefficient (Cp)b in this case refers to the local region directly behind the cylinder. In view of the experimental data, this parameter strongly correlates with the formation length, strength and Strouhal number of the primary shed vortices. Typically, a 2D simulation underpredicts the vortex formation length while over-predicting the strength and the shedding frequency of the vortices. Resolving the correct base pressure is therefore a minimum prerequisite of the field spacing. In our simulations, we found 16 points in the spanwise direction sufficient to satisfy this requirement at the lowest possible computational cost. Moreover, our results will show that this spanwise resolution was also adequate to capture the large-scale three-dimensionality of the near wake flow.
The final grid was 241×241×16 (x,y,z directions). Along the cylinder surface, the distribution of points was Δs ![]() 0.011π within the upstream laminar boundary layer and Δs
0.011π within the upstream laminar boundary layer and Δs ![]() 0.007π within the turbulent wake. Normal to the cylinder surface, the spacing in wall units was <Δy+> = ±4. In the spanwise direction, the grid point spacing was uniform at Δz
0.007π within the turbulent wake. Normal to the cylinder surface, the spacing in wall units was <Δy+> = ±4. In the spanwise direction, the grid point spacing was uniform at Δz ![]() 0.04π.
0.04π.
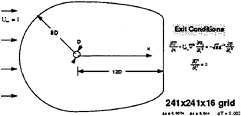
Figure 2: Grid and Flow Conditions for the LES Simulation of the Circular Cylinder.
The flow was impulsively started with unit velocity, zero reference pressure and a fixed nondimensional time step of ΔT=0.0005; T=tU∞/D. After the initial transients (T=0.05), new velocity and pressure conditions were imposed at exit. Specifically, a zero tangential pressure gradient condition was enforced along the downstream grid boundary while a combination of the continuity and Euler equations were found satisfactory to exit the shed vortices with minimum distortion. The inner boundary which is the cylinder surface was always no-slip and the upstream centerline axis was a branch cut. The spanwise boundaries were periodic.
These above conditions are illustrated in Figure 2. It should be noted that unlike some previous works, vortex shedding was not artificially initiated by numerically inducing a slight twist to the cylinder. For the present simulation, shedding of the Strouhal vortices was allow to occur naturally through time evolution of an unstable wake.
A comparison of the experimental measurements (16) and the present numerical results at the span's mid-plane is shown in Figure 3 for Re= 3000 and a non-dimensional time T=2.5. Their agreement is acceptable for the horizontal velocity profile. The computation under-predicted the minimum horizontal velocity component by 6 percent, but the overall error is just under 5 percent. This error is due principally to the rapid growth of the main eddies just prior to this instance in time that demands a very fine grid resolution to sufficiently resolve the associated gradients.
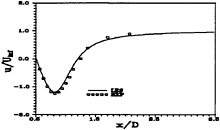
Figure 3: Comparison of LES Results and Experimental Data (16) of the Circular Cylinder. Profiles Depict Downstream Horizontal Velocity at T=2.5.
A useful quantity for visualizing the large-scale three-dimensional structures of the near wake is the helicity ![]() A typical snapshot is shown in Figure 4 which depicts isosurfaces of this parameter taken from the LES results at Re=5600. The snapshot clearly shows elongated large-scale streamwise structures connecting the alternating shed vortices. Gerrard (17) regularly observed these filaments in his flow visualization experiments and termed them as “fingers”. These intermediate structures persist downstream and posses a high degree of streamwise vorticity, but low streamwise velocity. In terms of the helicity quantity, they are apparently on the same local scale as the adjacent Strouhal vortices which by comparison contain a high degree of spanwise vorticity, but low spanwise velocity. The fingers themselves comprise pairs of counter-rotating vortices which is a circumferential plane of the cylinder.
A typical snapshot is shown in Figure 4 which depicts isosurfaces of this parameter taken from the LES results at Re=5600. The snapshot clearly shows elongated large-scale streamwise structures connecting the alternating shed vortices. Gerrard (17) regularly observed these filaments in his flow visualization experiments and termed them as “fingers”. These intermediate structures persist downstream and posses a high degree of streamwise vorticity, but low streamwise velocity. In terms of the helicity quantity, they are apparently on the same local scale as the adjacent Strouhal vortices which by comparison contain a high degree of spanwise vorticity, but low spanwise velocity. The fingers themselves comprise pairs of counter-rotating vortices which is a circumferential plane of the cylinder.

Figure 4: Typical Snapshot of the Three-Dimensionality of the Cylinder Wake.
As mentioned earlier, the experimental measurements of Zhou and Antonia (9) detected an exponentially downstreamn decay of the peak vorticity of the Strouhal vortices. A two-dimensional snapshot of these vortices is shown in Figure 5 and represents spanwise averages of the z-component of the vorticity vector. Their time-averaged decay (23 cycles) is plotted in Figure 7 along with the streamwise variation reported by Zhou and Antonia. Using both the numerical and experimental results, the peak vorticity (ωp) decays according to ωp=6exp(–0.056x) over the wake region 5≤x≤60.
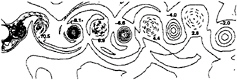
Figure 5: Typical Snapshot of the Vorticity in the Near Wake at Re=5600.
In contrast to their relative size, the detection frequency of the Strouhal vortices displayed considerable variability. Figure 6 is a good illustration of this characteristic where a nonuniform streamwise and relative transverse spacing can easily be seen between subsequent vortices. This distribution was typical throughout the wake region and provides an explanation for detecting the large
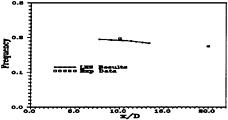
Figure 6: Time Averaged Downstream Decay of the Vortex Detection Frequency.
disparity in the relative frequency. However, time-averaging (23 cycles) this frequency reveals a near linear downstream decay as shown in Figure 6 over the entire wake region of interest (8≤x≤60) when the current results are combined with the experimental data (9).
Time traces of the lift and the drag force coefficient over approximately 23 shedding cycles along with their corresponding spectral components are shown in Figure 8. The dominate peak in the lift spectra occurs at the fundamental frequency which identifies the Strouhal frequency (fs) of the oscillation. The value of fs=0.21 shown in the spectra is close to the measurement of 0.205 as reported by Zhou and Antonia (9), and it characterizes one complete shedding cycle (actually two vortices). The other peaks in the lift frequency spectra are of minor consequence which echoes the modulating appearancee of the respective time trace. Conversely, the time signal of the drag force coefficient displays periods of intermittency and bursting phenomena which can largely be attributed to the numerous mixed modes occurring in the separated shear layers (2). The corresponding frequency spectra reflect these characteristics by indicating dominate peaks at several frequencies and over broader bandwidths. Inasmuch as the periodicity of the drag coefficient should be ideally equal to one-half that of the lift, its fundamental frequency is expected to be near 2fs (or ![]() 0.42) with modes (m/n)fs (n,m=1, 2, 3···) signifying various harmonics and subharmonics. In Figure 8c, the predominate modes of the drag frequency spectra follow this criteria approximately with the strongest peak occurring at 2fs. The existence of this peak supports the conclusion drawn by Karniadakis and Triantafyllou (18), that the absolute instability which accounts for the low-frequency shedding of the large-scale vortices persists and dominates those disturb-
0.42) with modes (m/n)fs (n,m=1, 2, 3···) signifying various harmonics and subharmonics. In Figure 8c, the predominate modes of the drag frequency spectra follow this criteria approximately with the strongest peak occurring at 2fs. The existence of this peak supports the conclusion drawn by Karniadakis and Triantafyllou (18), that the absolute instability which accounts for the low-frequency shedding of the large-scale vortices persists and dominates those disturb-
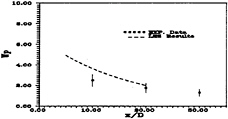
Figure 7: Time Average Decay of Peak Vorticity Within Strouhal Vortices.
ances associated with the transitional and the full turbulent regimes of the near wake.
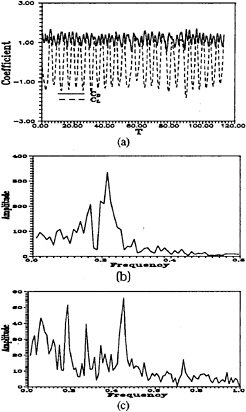
Figure 8: Lift and Drag Force Profiles and Corresponding Amplitudes Over 23 Shedding Cycles; (a) Time Traces, (b) Lift Force Amplitudes and (c) Drag Force Amplitudes
Along the cylinder surface, the local mean and root-mean-square (rms) pressure results are compared in Figure 9 to the time-averaged experimental data published by Norberg (19). As previously discussed, the spatial resolution in the spanwise direction was governed principally by achieving good agreement with the experimental data in terms of the base (and minimum) pressure coefficients. Although the maximum rms magnitudes are slightly over-predicted, the overall results are also in good qualitative agreement with the experimental data. The corresponding mean drag force coefficient is 1.18 which is the same value obtained after time-averaging the trace data shown in Figure 8a.
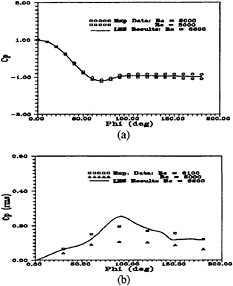
Figure 9: Comparisons of (a) Mean and (b) RMS Pressure Distributions Along the Cylinder Surface to Experimental Measurements (19)
As discussed earlier, past experimental observations and measurements conclude that the most fundamental physics of Strouhal vortices originate from the region immediately behind the cylinder. Consequently, by verifying our LES predictions of these basic physics, we can now investigate the mean turbulent energy production ![]() –P
–P![]() in the formation region where no conclusive data currently exists;
in the formation region where no conclusive data currently exists; ![]() .
.
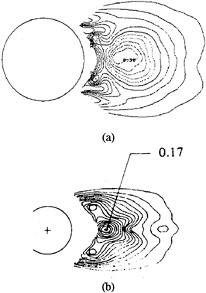
Figure 10: Contours of Turbulent Production in the Formation Region; (a) LES Results at Re=5600 and (b) Experimental Data (5) at Re=140,000.
Figure 10 shows the computed contours of production in the formation region along with the corresponding globally averaged experimental data of Cantwell and Coles (5) at Re=140,000. The qualitative agreement between the two figures further suggests that both of these sub-critical Reynolds numbers do indeed share similar turbulent physics within the formation region. Each figure indicates negligible production levels beyond 2–3 diameters downstream. The highest production levels for the Re=5600 simulation occur along the horizontal centerline axis approximately 1.11 diameters downstream compared to 1.17 diameters at Re=140,000. Two additional peak levels of lesser magnitude are also shown that are symmetric about the formation region centerline. At Re=140,000, these lower levels arise at an angle approximately 60 degrees (origin at the highest peak location and measured from the centerline axis) compared to an contours inside the formation region as shown in angle of 50 degrees for the present Re=5600 results.
Presentation of the LES results at Re=8000 begins with a typical snapshot of the vorticity Figure 11 where the dashed contours denote negative
vorticity. The contours appear to verify the three progressive phenomena of the separated shear layer as described by Wei and Smith (3) that lead to formation of the turbulent vortex; namely, laminar separation, T-S instability waves and secondary eddy formation. Moreover, the contours also show the turbulent vortex deriving the majority of its vorticity from the secondary eddies.
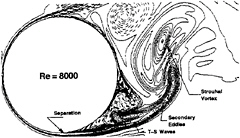
Figure 11: Snaphot of the Vorticity Contours Inside the Cylinder Formation Region (Re=8000).
According to the experimental relationships (1,3), a range for the transition wave frequency at Re =8000 is 2.52≤fb≤2.93. By scanning the pressure-frequency spectra for peak amplitudes over this range, one should be able to discern a region within the shear layer where transition initiates. Shown in Figure 12 is the distribution of the peak amplitudes found in the spectra over the range of fb given. The figure clearly suggests a zone of laminar flow as depicted by the low level and widely distributed contours of the peak amplitudes. Construction of an imaginary radial line with θ= 125° (measured from upstream stagnation) is possible that delineates the limit of laminar flow or the initiation of transition. This line is drawn as dashed in the figure. If a data point is selected to the left of this line, the predominant subharmonics of the Strouhal frequency fs should be identifiable with little mixing of fb. In Figure 13a, the pressure spectrum at coordinates (8.34, 8.45) in fact shows these subharmonics (nfs) with fs=0.112.
Although Figure 12 indicates two areas of highest peak amplitude in the formation region, only one can be perceived as within the separated shear layer. This maximum occurs at coordinates (8.61, 8.45). The mixing of secondary and Strouhal frequencies can be studied along development of the
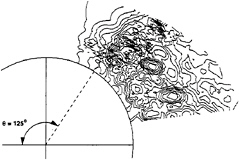
Figure 12: Distributions of the Maximum Peak Amplitude of the Secondary Eddies in the Formation Region.
separated shear layer by simply examining specific data points along a horizontal line through this peak. We begin in the laminar flow zone at point (8.34, 8.45) which is adjacent to the cylinder surface. The pressure spectrum in Figure 13a at this point is clearly indicative of deterministic physics. Further downstream at point (8.40, 8.45) which is still within the shear layer, the transition wave frequency appears and some minor mixing with the Strouhal frequency (fb- 2fs for example in Figure 13b). This point lies slightly to the right of the radial line in Figure 12. The ratio fb/fs is 11.57 which falls within the range 10.12≤fb/fs≤11.78 as determined from Bloor (1) and Wei and Smith (3), respectively. At the highest peak amplitude in the shear layer (8.61, 8.45), the mixing of fb and fs become more salient as indicated in Figure 13c by the significant amplitudes in the pressure spectrum at predominant modes of nfs±mfb. Notice that subharmonics of fb in both samples are not indicated which agrees with experimental measurements (2). Much further downstream within the shear layer where the flow has fully transitioned to turbulent, the mixing of frequencies is much less discernible as expected. As shown in Figure 13d at sample point (9.00, 8.45), the amplitudes have diminished and the frequency bandwidths have widen significantly at the predominant modes shown further upstream. These series of sample points show good agreement with the shear layer physics hypothesized by Bloor (1) and Wei and Smith (2).
Investigations of the turbulent vortical motion resulting from trailing edge separation of the hydrofoil were performed at Re=25,000. A C-grid
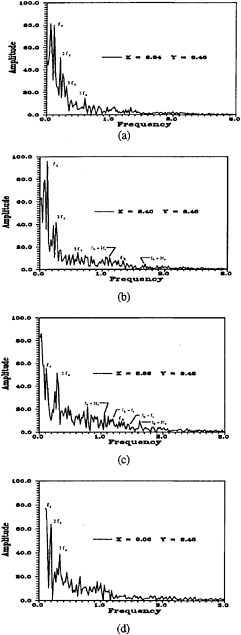
Figure 13: Pressure-Frequency Spectra at Various Grid Points Within the Separated Shear Layer; (a) x=8.34,y=8.45, (b) x=8.40,y=8.45, (c) x=8.61, y=8.45 and (d) x=9.00, y=8.45.
389×89×16 which had line clustering along the hydrofoil surface provided the best discretization strategy. The spanwise boundaries were assumed to be periodic. Expect for the downstream boundary and the hydrofoil surface (no-slip), unit velocity and potential flow conditions were applied along the other external grid boundaries. Conservation of energy across the downstream branch-cut was verified by examining the spectral energy content of the turbulent fluctuating quantities. The turbulent vortices exited without loss of peak vorticity through transformation of Euler's equation combined with continuity.

Figure 14: Flow Characteristics on Upper Surface of a NACA 0018 Hydrofoil at Re=25,000 and Angle-of-Attack of 7.5 degrees.
The hydrofoil was subjected to a 0° and a 7.5° angle-of-attack (AOA). Both upstream conditions produced trailing edge separation, but of different physical character. At AOA=0°, both of the upper and lower laminar boundary layers separated along the trailing edges and then quickly transitioned to the generation of turbulent vortices. The interplay between the separated regions produced asymmetric oscillatory separation points on the hydrofoil surfaces. At AOA=7.5° (Figure 14), a separation bubble was produced through laminar separation along the upper surface followed by reattachment due to an abrupt transition to turbulence of the separated free-shear layer. However, the now turbulent boundary layer separated further downstream along the trailing edge. These physics have been verified qualitatively through corresponding experimental flow visualization testing. Qualitative verification of these LES computations to previously published data is currently underway.
CONCLUDING REMARKS
The impetus of the present large-eddy simulation (LES) was to investigate the turbulent physics of the near wake behind a circular cylinder and a NACA hydrofoil. The governing LES equations and subgrid-scale (SGS) turbulence model were formulated in curvilinear coordinates where both the Cartesian and the contravariant velocity components were utilized to dynamically evaluate the model coefficient. Initially, we computed the early evolution of the near wake at a Reynolds number of 3000. Based on this study, the following concluding remarks are offered:
-
The primary Strouhal vortices were shed at a non-dimensional frequency of 0.21. Their time-averaged peak vorticity (ωp) exponentially decayed with downstream distance with a near linear decline of their local detection frequency over the near wake region of interest 5≤x≤60; specifically, ωp=6exp(–0.056x).
-
Between subsequent shed vortices are pairs of connecting intermediate structures (or “fingers”).
-
The root-mean-square (rms) pressure results along the cylinder surface compared reasonably well with the experimental data (9), although the maximum rms magnitude which occurred at an angle near 90° from upstream stagnation was slightly over-predicted.
-
The distribution of the turbulent production within the formation region was symmetric and maximum levels occurred along the centerline axis. The distributions compared qualitatively well with the published experimental data (5) at a much higher sub-critical Reynolds number of 140,000. This agreement indicates that each wake flow share similar structural dynamics.
-
The transition waves in the shear layer dominated the high-frequency component (fb) of the pressure spectrum whereas the Strouhal vortex comparatively occurred at low frequencies (fs).
-
Simulation results in the form of pressure time traces and the corresponding spectra at specific points through the shear layer showed amplified peaks in the spectra easily distinguishable at modes of mixed frequencies nfs±mfb. No subharmonics of fb were detected.
-
The ratio of fb/fs through the shear layer was found to be approximately 11.57. This value falls within the range of the relationships based on the published experimental evidence (3).
-
Preliminary LES results of a NACA 0018 hydrofoil showed laminar separation of the upstream upper boundary layer followed by transition to turbulence in the separated shear layer and finally reattachment near the beginning of the trailing edge.
ACKNOWLEDGMENTS
The author gratefully acknowledges the support of the Office of Naval Research (Dr. L.P. Purtell, Scientific Officer) and the Independent Research Program (Dr. S.Dickinson Coordinator) at the Naval Undersea Warfare Center Division Newport.
REFERENCES
1. Bloor, M.S., 1964, “The Transition to Turbulence in the Wake of a Circular Cylinder,”, Journal of Fluid Mechanics, Vol. 19, pp. 290.
2. Unal, M.F. and Rockwell, D., 1988, “On Vortex Formation from a Cylinder. Part 1. The Initial Stability, ” Journal of Fluid Mechanics, Vol. 190, pp. 491–512.
3. Wei, T. and Smith, C.R., 1986, “Secondary Vortices in the Wake of Circular Cylinders,” Journal of Fluid Mechanics, Vol. 169, pp. 513–533.
4. Song, C.C.S. and Yuan, M., 1990, “Simulation of Vortex-Shedding flow About a Circular Cylinder at High Reynolds Number,” Journal of Fluids Engineering, Vol. 112, pp. 155–163.
5. Cantwell, B. and Coles, D., 1983, “An Experimental Study of Entrainment and Transport in the Turbulent Near Wake of a Circular Cylinder,” Journal of Fluid Mechanics, Vol. 136, pp. 321–374.
6. Braza, M., Chassaing, P. and Minh, H. H., 1990, “Prediction of Large-Scale Transition Features in the Wake of a Circular Cylinder,” Physics of Fluids, A. 2, pp. 1461–1470.
7. Braza, M., Persillon, H. and Sers, F., 1993, “Prediction of Certain transition Characteristics in the Wake of a Circular Cylinder in Free and Forced Flow,” IUTAM Symposium on Bluff-Body Wakes, Dynamics and Instabilities, ed. Eckelmann et al., Springer-Verlag, pp. 279–284.
8. Kato, C., Iida, A., Takano, Y.Fujita, H. and Ikegawa, M., 1993, “Numerical Prediction of Aero-dynamic Noise Radiated from Low Mach Number Turbulent Wake,” AIAA 93–0145.
9. Zhou Y. and Antonia, R.A., 1993, “A Study of Turbulent Vortices in the Near Wake of a Cylinder,” Journal of Fluid Mechanics, Vol. 253, pp. 643–661.
10. Germano, M., Piomelli, U., Moin, P., and Cabot W.H., 1991, “A Dynamic Subgrid-Scale Eddy Viscosity Model,” Physics of Fluids, A. 3, pp. 1760–1765.
11. Jordan, S.A., 1994, “The Large-Eddy Simulation of Incompressible Flows in Simple and Complex Geometries,” Ph.D. Dissertation, Virginia Polytechnic Institute and State University.
12. Vinokur, M. 1974, “Conservative Form of Gas Dynamics Equations,” La Recherche Aerospatiale, No. 1974–1, pp. 65–68.
13. Kim, J. and Moin, P., 1985, “Application of a Fractional-Step Method to Incompressible Navier-Stokes Equations,” Journal of Computational Physics, Vol. 59, pp. 308–310.
14. Jordan, S.A. and Ragab, S.A., 1994, “An Efficient Fractional-Step Technique for Unsteady Three-Dimensional Flows,” Journal of Computational Physics, (accepted).
15. Lilly, D.K., 1992, “A Proposed Modification of the Germano Subgrid-Scale Closure Method, ” Physics of Fluids, A. 4, pp. 633–635.
16. Bouard, R. and Coutanceau, M., 1980, “The Early Stage of Development of the Wake Behind an Impulsively Started Cylinder for 40<Re <104,” Journal of Fluid Mechanics, Vol. 101, pp. 583–607.
17. Gerrard, J.H., “The Wakes of Cylindrical Bluff Bodies at Low Reynolds Number,” Phil. Transactions Royal Society of London, Vol. 288, pp. 351–382.
18. Karniadakis, G.E. and Triantafyllou, G.S., 1992, “Three-Dimensional Dynamics and Transition to Turbulence in the Wake of Bluff Bodies,” Journal of Fluid Mechanics, Vol. 238, pp. 1–30.
19. Norberg, C., 1992, “Pressure Forces on a Circular Cylinder in Cross Flow,” IUTAM Symposium on Bluff-Body Wakes, Dynamics and Instabilities, ed. Eckelmann et al., Springer-Verlag, pp. 275–278.












