The Forces Exerted by Internal Waves on a Restrained Body Submerged in a Stratified Fluid
N.Gavrilov, E.Ermanyuk, I.Sturova (Lavrentyev Institute of Hydrodynamics, Russia)
ABSTRACT
This paper presents the results of experimental and theoretical studies of forces exerted by plane internal waves on the horizontal elliptic cylinder in the case of stratification simulating a pycnocline.
The experiments were performed in a test tank filled with two layers of miscible fluids. The upper layer was distilled water, the lower layer was a glycerine solution in water. The elliptic cylinder was positioned normally to the side walls of the test tank. In its cross-section the small axis was directed upwards and the ratio between axes was 2:1. The basin was equipped with both a wave maker and a wave breaker. The variable experimental parameters included: the amplitude and length of waves, the distance from the cylinder centre to the free surface, and the pycnocline thickness. The incident internal wave in experiments was represented by the first mode.
The linear 2-D problem of internal wave scattering on a restricted cylinder is considered theoretically. The fluid is assumed to be nonviscous, incompressible and composed of three layers (the upper and lower layers are homogeneous and the middle layer is linearly stratified), which provides an approximate model of the experimental conditions. The Boussinesq approximation is used. For the sharp pycnocline, the methods developed for surface waves are applied to study the forces acting on a body fully submerged in the fluid layer of constant density. The method of coupled finite elements is most efficient for solving the present problem. For a body partially submerged in the middle layer, the problem is solved approximately. The comparison between theoretical and experimental data is presented.
1.
INTRODUCTION
Exploration of the Ocean has stimulated the study of environmental factors acting on marine structures and deep-submersibles. A particular feature of real sea is the presence of vertical density gradient resulting from variation of temperature and salinity with depth. It is well-known that vertical density stratification allows internal waves to arise under the action of surface waves, tides, variation of atmospheric pressure, etc. (see, for example, Phillips [1], Miropolsky [2]). For submerged technical objects, short-period internal waves are of particular interest. These waves are typical for thermocline stratification.
In the case of a body located in homogeneous fluid layer, the action of internal waves is closely analogous to the action of surface waves but for the difference of characteristic time- and length-scales. The amplitude of internal waves may be as much as 5–10 times greater than the amplitude of surface waves. The frequency of short internal waves is less than the frequency of surface waves by 1.5–2 orders of magnitude. In the region of variable density, the dynamic interaction of body and waves is complicated by buoyancy-driven effects that have no direct analogy in the domain of surface waves.
Scattering of surface waves on restricted submerged bodies has been much studied theoretically and experimentally. In contrast, the investigation of internal wave scattering is not yet sufficiently advanced though the loads induced by internal waves on marine structures and submerged vehicles are quite essential as demonstrated by field and laboratory experiments (see, for example, Ermanyuk & Sturova [3], Razumeenko [4]).
In most cases, natural pycnocline structure is approximated as a two-layer fluid with a step change of density at the interface. However, a realistic smooth density variation gives rise to new physical effects that are beyond the domain of two-layer model.
The present paper deals with theoretical and experimental study of forces exerted by internal waves on horizontal elliptic cylinder in the case of stratification characterized by the presence of a finite region of high density gradient.
2.
EXPERIMENTS
The experiments were carried out in a test tank (4.5×0.2×0.6m) filled with stratified two-layer fluid. The density of the upper layer (distilled water) was ρ1=0.999g/cm3, the density of the lower layer (glycerine—water solution) was ρ2=1.011g/cm3. The experimental installation is shown in Fig.1. The waves were generated by heaving motion of a semi-cylinder 1. The test-tank was equipped with a wave-breaker 2. The elliptic cylinder 3 of 3cm minor axis and axis ratio 2:1 was mounted on the 2-component hydrodynamic scales 4 so that the gaps between the ends of the cylinder and the walls of the test tank did not exceed 0.1cm. The minimum natural frequency of scales was 2.4Hz. The maximum wave frequency throughout the experiments was 0.21Hz. The loads acting on the cylinder were transmitted to flexible elements 5 by the system of strings 6 and streamlined arms 7. The deformations of elements were measured by induction displacement sensors. As the maximum amplitude of wave loading in experiments did not exceed 1.1·10–3N, the corresponding displacement
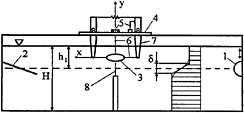
Fig. 1.
of the cylinder under the action of waves was less than 5 · 10–3mm. A series of experiments was undertaken to study the influence of streamlined arms on the accuracy of force measurements. The corresponding error was found to be less than 0.5%.
In the reference frame with the origin taken at free surface (the y-axis points upwards), the measured density distribution closely matched the following relation:
(1)
where ρ0=(ρ1+ρ2)/2, ε=(ρ2–ρ1)/ρ1,h1 is the depth of the upper layer, δ is the parameter characterizing the thickness of the region of large density gradient (pycnocline). The total depth of fluid was H=45cm.
The parameters of wave motion were measured by resistive wave gauges 8 of length greater than the overall pycnocline thickness which is equal 3δ for the density distribution (1). The time-dependent output w(t) of the wave gauges may be written as the integral of local conductivity variations over the length of probes. As the local conductivity is directly proportional to local density, the integral looks as follows:
(2)
where w0 is dimensional constant, η(y) is the distribution of local vertical displacements of fluid particles, y1,y2 are the ordinates of the ends of the probe, f(t) is the harmonic function of time. The function η(y) reaches its maximum ηm at
the middle of pycnocline for the first mode of internal waves. The function dρ/dy is appreciable only within the region of thickness δ. In this region η(y) ≈ ηm in the test range of wave frequency. Thus, to a high degree of accuracy the integral (2) is the measure of an average of local wave amplitudes over δ. The influence of other parameters on the output of the wave-gauges was taken into account by dynamic calibration; to do this, the response of the wave-gauges undergoing vertical oscillations of known amplitude and frequency was measured in the test range of δ. Analog outputs of wave and force measuring systems were converted to digital and analyzed by specialized computer.
Strictly speaking, the oscillations of the wave maker generate all the modes of wave motion. However, when the amplitude of the heave motion of the semi-cylinder used as the wave maker is small and its diameter is large compared to the pycnocline thickness, the high modes are weakly generated and quickly decay with distance. The test section was spaced at 1.8m from the wave maker. The visual examination of the wave pattern clearly indicated that the incident wave motion in experiments was represented by the first mode. To analyze the experimental data, the dispersion relation (see, Phillips [1]) was used:
ω2=εgk/[kγ+coth kh1+coth k(H–h1)], (3)
where k is the wave number, ω is the wave frequency, γ is the characteristic thickness of the pycnocline. The measurements showed that this dispersion relation agrees well with the experimental data under condition γ=δ.
In the fluid system described, the forces exerted on the elliptic cylinder by internal waves of the first mode depend on the following non-dimensional parameters:
where b is the minor axis of elliptic cylinder, η is the amplitude of internal waves, h is the distance from the cylinder centre to the free surface, v is the kinematic viscosity.
The value H/b=15 was kept constant. Three typical locations of the cylinder were studied: ![]()
![]() (in the middle of the upper layer),
(in the middle of the upper layer), ![]() (in the upper layer close to the interface),
(in the upper layer close to the interface), ![]() (in the lower layer close to the interface). For each location of the cylinder, parameter
(in the lower layer close to the interface). For each location of the cylinder, parameter ![]() varied in the range
varied in the range ![]() The variation of
The variation of ![]() resulted from diffusion of glycerine.
resulted from diffusion of glycerine.
For each set of parameters ![]() and
and ![]() the loads on the cylinder were measured depending on the amplitude and the length of incident waves. These parameters varied in the ranges: 0.05<
the loads on the cylinder were measured depending on the amplitude and the length of incident waves. These parameters varied in the ranges: 0.05<![]() <0.4;
<0.4; ![]() The wave steepness ηk was less than 0.08.
The wave steepness ηk was less than 0.08.
The above-mentioned experimental conditions imply low values of Keulegan-Carpenter numbers. As it is shown by Sarpkaya [5], Chaplin [6], a variation of Stokes number β does not affect the wave loading under these conditions. Furthermore, in the present experiments parameter β varied in a narrow range from 20 to 30. The kinematic viscosities of upper and lower layers differed only by 10%.
The amplitudes of loads were normalized to the scale of inertial forces ρ0S![]() and ρ0S
and ρ0S![]() so that
so that
Cx=Fx/ρ0S![]() , Cy=Fy/ρ0S
, Cy=Fy/ρ0S![]() , (4)
, (4)
where ![]() ,
, ![]() are the amplitudes of local horizontal and vertical accelerations of fluid particles calculated at y=–h,S is the cross-sectional area of elliptic cylinder, Fx and Fy are the amplitudes of horizontal and vertical loads acting on a cylinder of unit length.
are the amplitudes of local horizontal and vertical accelerations of fluid particles calculated at y=–h,S is the cross-sectional area of elliptic cylinder, Fx and Fy are the amplitudes of horizontal and vertical loads acting on a cylinder of unit length.
The application of the first-order theory of Phillips [1] combined with dispersion relation (3) gives the following estimate of amplitudes of local accelerations:
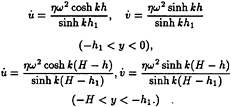
(5)
The normalization (4) provides a simple representation of experimental data for a body located in fluid layer of constant density in the case of dominant inertial forces (see, for example, Chaplin [6], Ermanyuk & Sturova [3]). In the region of density variation, the total wave induced loads depend on inertial, damping and buoyancy forces. However, to separate the components of total measured force, one should formulate a number of additional assumptions. Because of this, the normalization (4) is used for all the experimental data obtained. It should be kept in mind that relations (5) give overestimated values of local accelerations for fluid particles located in the pycnocline. In this case, these relations should be considered only as formal normalization parameters.
The experimental results for a cylinder located in the upper layer at ![]() are shown in Fig.2 representing the dependencies of Cx and Cy on the non-dimensional wave number
are shown in Fig.2 representing the dependencies of Cx and Cy on the non-dimensional wave number ![]() at different
at different ![]() Hereinafter, the sets of data a) and b) correspond to Cx and Cy, respectively. In this series, any action of buoyancy force is excluded. However, the presented data show essential dependence of the force coefficients on the pycnocline thickness δ.
Hereinafter, the sets of data a) and b) correspond to Cx and Cy, respectively. In this series, any action of buoyancy force is excluded. However, the presented data show essential dependence of the force coefficients on the pycnocline thickness δ.
The coefficients of inertial force for an elliptical cylinder of axis ratio 2:1 placed in oscillatory flow of nonviscous fluid are equal 1.5 and 3 for oscillations aligned with major and minor axis, respectively (see, Kochin et al.[7]). For sharp pycnocline ![]() the coefficient Cx fairly well agrees with the above-mentioned theoretical estimate in a wide range of
the coefficient Cx fairly well agrees with the above-mentioned theoretical estimate in a wide range of ![]() It seems likely that the increase of Cx with
It seems likely that the increase of Cx with ![]() is associated with the effect kindred to flow contraction as the increase of pycnocline thickness decreases the upper layer of constant density. It should be noted that Cx did not depend on
is associated with the effect kindred to flow contraction as the increase of pycnocline thickness decreases the upper layer of constant density. It should be noted that Cx did not depend on ![]() under experimental conditions, to within the experimental error.
under experimental conditions, to within the experimental error.
The coefficient of vertical force Cy shows complicated behavior depending on the test parameters. Generally, Cy decreases with ![]() and increases with
and increases with ![]() at low
at low ![]() However, at high
However, at high ![]() the
the
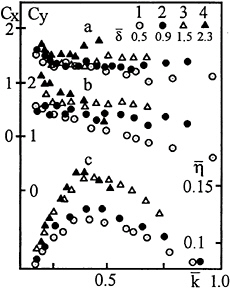
Fig. 2.
behaviour of Cy changes (points 4 shown in Fig. 2b). Moreover, at fixed ![]() and
and ![]() depends on
depends on ![]() . Because of this, the set of
. Because of this, the set of ![]() dependencies is supplemented with the set of corresponding
dependencies is supplemented with the set of corresponding ![]() versus
versus![]() data shown in Fig.2c.
data shown in Fig.2c.
The dependence of Cy on wave amplitudes was studied at low ![]() The range of amplitude variation was quite narrow. The upper limit was imposed by the onset of wave breaking. The specific limitations of the wave maker design imposed the lower limit of studied amplitudes. In the region covered by experiments, Cy decreases by 28% when the wave amplitude is doubled at constant
The range of amplitude variation was quite narrow. The upper limit was imposed by the onset of wave breaking. The specific limitations of the wave maker design imposed the lower limit of studied amplitudes. In the region covered by experiments, Cy decreases by 28% when the wave amplitude is doubled at constant ![]() and
and ![]() This effect presumably corresponds to the non-linear reduction of inertial loads as reported by Chaplin [6].
This effect presumably corresponds to the non-linear reduction of inertial loads as reported by Chaplin [6].
The phase lags between the loads acting on the cylinder and oscillations of the pycnocline are 105°±1.5° and 201°±2° for horizontal and vertical force, respectively. The measurements have not revealed any clear dependence of these phase lags on the parameters of the problem.
For the cylinder located close to the pycno
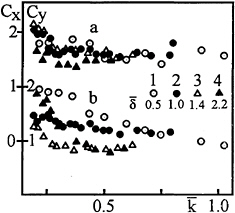
Fig. 3.
cline, the phase lags were not measured and the amplitude of waves was recorded at the distance of 12cm from the center of the cylinder.
As the cylinder approaches the pycnocline, the force coefficients Cx, Cy show increasingly stronger dependence on ![]() and
and ![]() At the same time, the measurements have shown the linear increase of loading with
At the same time, the measurements have shown the linear increase of loading with ![]() . In other words, no amplitude dependence of Cx and Cy was observed, to within the experimental error. Presumably, the presence of density gradient in the vicinity of a body inhibits separation and reduces non-linear effects. For the cylinder located in the upper layer close to pycnocline at
. In other words, no amplitude dependence of Cx and Cy was observed, to within the experimental error. Presumably, the presence of density gradient in the vicinity of a body inhibits separation and reduces non-linear effects. For the cylinder located in the upper layer close to pycnocline at ![]() the results of measurements are presented in Fig.3a,b. The comparison of Fig.3a and Fig.2a shows that the proximity of the interface increases Cx at low
the results of measurements are presented in Fig.3a,b. The comparison of Fig.3a and Fig.2a shows that the proximity of the interface increases Cx at low ![]() compared to the case of cylinder located in the middle of the upper layer. However, at large
compared to the case of cylinder located in the middle of the upper layer. However, at large ![]() when the cylinder is completely surrounded by stratified fluid, Cx drops (points 4 in Fig.3a).
when the cylinder is completely surrounded by stratified fluid, Cx drops (points 4 in Fig.3a).
The vertical wave loads decrease with the increase of ![]() Razumeenko [4] showed that the buoyancy and inertial forces may partially cancel each other. Assuming that the density distribution is not distorted by waves and may be considered as linear in the vicinity of a body, one can show that the ratio of inertial and buoyancy forces is governed by the parameter
Razumeenko [4] showed that the buoyancy and inertial forces may partially cancel each other. Assuming that the density distribution is not distorted by waves and may be considered as linear in the vicinity of a body, one can show that the ratio of inertial and buoyancy forces is governed by the parameter ![]()
![]() where
where ![]() is the buoyancy frequency or Brunt-Vaisala frequency. The parameter α has the physical sense of Froude number. Buoyancy force is major at α<1 while inertial loads dominate at α>1.
is the buoyancy frequency or Brunt-Vaisala frequency. The parameter α has the physical sense of Froude number. Buoyancy force is major at α<1 while inertial loads dominate at α>1.
The case of the cylinder located in the lower layer close to the pycnocline at ![]() is illustrated in Fig.4a,b. For all the wave numbers studied, the lower layer may be considered as infinitely deep (k(H–h1)>3). At low
is illustrated in Fig.4a,b. For all the wave numbers studied, the lower layer may be considered as infinitely deep (k(H–h1)>3). At low ![]() the vertical and horizontal loads exerted by waves in this case are lower compared to the case of the cylinder located right above the pycnocline
the vertical and horizontal loads exerted by waves in this case are lower compared to the case of the cylinder located right above the pycnocline ![]() (see Figs.3,4). The increase of loading is observed at
(see Figs.3,4). The increase of loading is observed at ![]() when the upper portion of the cylinder is immersed in the pycnocline (points 2 in Fig.4a,b). The further increase of
when the upper portion of the cylinder is immersed in the pycnocline (points 2 in Fig.4a,b). The further increase of ![]() decreases the values of Cx and Cy markedly. However, complete cancellation of buoyancy and inertial forces was not observed though the parameter α varied in the range 0.1<α<∞. Apparently, the increase of
decreases the values of Cx and Cy markedly. However, complete cancellation of buoyancy and inertial forces was not observed though the parameter α varied in the range 0.1<α<∞. Apparently, the increase of ![]() gives rise to additional diffraction loads.
gives rise to additional diffraction loads.
The godographs of the summary force vector shown in Fig.5 provide a vivid illustration to the change of the force pattern with the increase of ![]() The godographs shown in Fig.5 correspond to the case of the cylinder placed at
The godographs shown in Fig.5 correspond to the case of the cylinder placed at ![]() The length of the summary force vector
The length of the summary force vector ![]() is normalized by the maximum amplitude of its horizontal component. At low
is normalized by the maximum amplitude of its horizontal component. At low ![]() the godographs plotted at any
the godographs plotted at any ![]() closely approach elliptic curves. The curve 1 corresponds to the following parameters:
closely approach elliptic curves. The curve 1 corresponds to the following parameters: ![]() At large
At large ![]() one can see an apparent direction along which the loading is maximal. The amplitude of forces acting normally to this direction is 5–6 times less. This effect is illustrated by the curve 2 obtained at
one can see an apparent direction along which the loading is maximal. The amplitude of forces acting normally to this direction is 5–6 times less. This effect is illustrated by the curve 2 obtained at ![]() The shape of curve 2 imply almost in phase oscillation of horizontal and vertical loads. For both the figures the arrows indicate the sequence of time.
The shape of curve 2 imply almost in phase oscillation of horizontal and vertical loads. For both the figures the arrows indicate the sequence of time.
It is interesting to note that the angle Θ between the horizontal direction and the direction
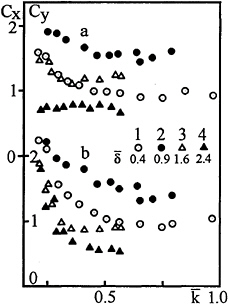
Fig. 4.
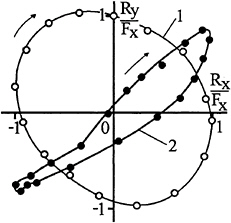
Fig. 5.
of maximum loading agrees with the relation Θ= arcsin (ω/Nm), where Nm is the maximum of the Brunt-Vaisala frequency N(y). The sign of the angle depends on the direction of orbital motion of fluid particles so that the variants of a body placed above and bellow the interface give mirror image patterns.
The direction of rotation of the summary force vector coincides with the direction of orbital motion of fluid particles at any studied ![]() as exemplified by curves 1,2 (see Fig.5) recorded under conditions of inertia- and buoyancy dominated vertical loading, respectively.
as exemplified by curves 1,2 (see Fig.5) recorded under conditions of inertia- and buoyancy dominated vertical loading, respectively.
3.
THEORETICAL ANALYSIS
It is assumed that the inviscid incompressible fluid occupies the region –∞<x<∞, –∞< y<0 and there are three layers: homogeneous upper and lower ones and a linearly stratified middle one. Thus, density stratification in an undisturbed state ρ(y) takes the form
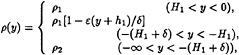
where H1=h1–δ/2 is the depth of upper layer. This three-layer fluid is the model of a smooth pycnocline and approximates the density distribution (1). Contrary to the experimental conditions, it is assumed that the depth of the lower layer is infinite.
The stable stratification of fluids, corresponding to an increasing density in the direction of the gravity force, allows the existence of internal waves. Small amplitude waves are described by the linear theory of internal waves presented in detail, for example, by Phillips [1], Miropolsky [2]. For a horizontally homogeneous fluid at rest there exists a countable number of free harmonic wave modes when a continuous density variation occurs only in a finite interval of depth. To each wave mode there corresponds a dispersion dependence of the wave frequency on the wave number.
We investigate the scattering of an internal wave of the first mode, incident on a solid horizontal elliptic cylinder. As the cylinder axis is
parallel to the front of the incident wave, the 2-D problem is considered. It is assumed that the upper layer is bounded by a rigid lid. This approximation allows to 'filter off' the surface waves without distorting significantly the internal ones. The disturbed oscillating motion of the fluid is assumed to be steady and the flow inside upper and lower layers is potential.
In the upper and lower homogeneous layers the total velocity potentials ![]() 1,3(x,y,t) satisfy the equations
1,3(x,y,t) satisfy the equations
Δ![]() 1=0(–H1<y<0),
1=0(–H1<y<0),
Δ![]() 3=0 (–∞<y<–(H1+δ)),
3=0 (–∞<y<–(H1+δ)),
where the subscripts 1 and 3 refer to the upper and lower layers, respectively.
The internal wave equations for the vertical velocity v2(x,y,t) in the middle layer are described within the Boussinesq approximation
∂2Δv2/∂t2+N2∂2v2/∂x2=0
(–(H1+δ)<y<–H1),
where ![]() is constant, g1=εg/(2+ε). The boundary conditions are the following
is constant, g1=εg/(2+ε). The boundary conditions are the following
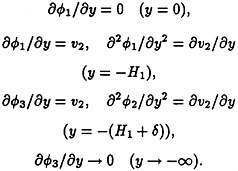
From the theory of linear internal waves it follows that in such a fluid the existence of free internal waves is possible only with ω<N. Let the wave incident from the right be an arbitrary internal mode with a vertical velocity
v(x,y,t)=η0Re{V(y) exp[i(kx+ωt)]}. (6)
The wave number k satisfies the dispersion relation
tan µδ=kµ(1+tanh kH1)/(µ2 tanh kH1–k2), (7)
where ![]() There exists a countable number of values kj(k1<k2<…), satisfying the given dispersion relation. The eigenfunctions V(y) of the wave modes are represented as
There exists a countable number of values kj(k1<k2<…), satisfying the given dispersion relation. The eigenfunctions V(y) of the wave modes are represented as
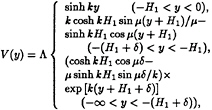
(8)
where
Λ=–iωμ2δ/[kcosh kH1(1–cos μδ)+ μ sinh kH1 sin μδ].
It is supposed, that the incoming internal wave is represented only by the first mode with wave number k1. The feature of this mode is that its eigenfunction, determined in (8), has a constant sign over a depth of fluid. By analogy with Sect. 2 let us define the amplitude of this internal wave as the average value of the vertical displacements of fluid particles over the thickness of a stratified layer. The vertical displacement of fluid particle in internal wave η(x,y,t) is determined from ∂η/∂t=v. Similarly to (6) it is possible to express
η(x,y,t)=η0Re{E(y) exp[i(kx+ωt)]},
where E=–iV/ω. Normalizing multiplier Λ is introduced into (8) so that
In this case η0 is the dimensional value of internal wave amplitude.
When the cylinder is fully submerged in the upper or lower homogeneous layer, the solution of diffraction problem can be obtained numerically with the help of the coupled finite element method (CFEM). The velocity potential is represented by finite element method in a narrow
region surrounding a body and by the boundary integral equation in the outer region. This method is highly efficient and universal and can be used for complex-shaped bodies and for a system of bodies both in 2-D and 3-D flows. The examples of the solution of diffraction problem for two-layer fluid are given by Sturova [8]. To use CFEM, it is necessary to determine the Green function.
For a body located in the upper layer one should derive the Green function describing the field of a point source of pulsating strength which is placed at the fixed point (ξ,ζ) of the upper layer. In this case the Green function in the upper layer takes the form G1(x,y,ξ,ζ):
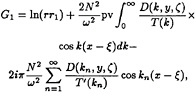
(9)
where r=[(x–ξ)2+(y–ζ)2]1/2,
r1=[(x–ξ)2+(y+ζ)2]1/2,
D(k,y,ζ)=k exp (–kH1) cosh kζ cosh ky× tan µδ/cosh kH1,
T(k)=kμ(1+tanh kH1)– tan μδ(μ2 tanh kH1–k2),
the symbol pv indicates the principal-value integration and the prime denotes differentiation with respect to k.
The Green function for the source in the lower layer was obtained previously by Sturova [9] and in the lower layer has the form
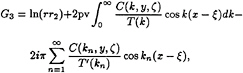
(10)
where r3=[(x–ξ)2+(y+ζ+2(H1+δ))2]1/2,
C(k,y,ζ)=(k tan µδ+µ tanh kH1)× exp[k(y+ζ+2(H1+δ))].
The expressions (9),(10) are somewhat simplified in the case of infinite thickness of the upper layer. Introducing the substitution y1=y+H1+δ/2,
ζ1=ζ+H1+δ/2 and assuming H1 → ∞, we shall obtain
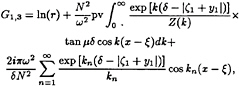
(11)
where Z(k)=2µ+k(2–N2/ω2) tan µδ.
In this case the explicit dependence of wave number on frequency may be derived from the dispersion relation (7)
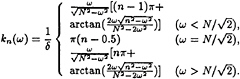
The exciting forces on the body may be obtained by integration of pressure over the body surface. Omitting the hydrostatic term, the pressure p(x,y,t) satisfies the relation
∂2p/∂x2=ρ0∂2v/∂t∂y.
It is assumed that
p=η0Re[(P0+P)eiωt],
where the pressure due to the incident wave P0(x,y) is equal to
and the diffraction pressure P(x,y) should be determined having regard to the boundary condition on a cylinder surface.
When the body is fully submerged in a layer of constant density, in which the flow is irrotational, the total velocity potential ![]() (x,y,t) can be written as
(x,y,t) can be written as
![]() =η0Re[Φ0+Φ)eiωt],
=η0Re[Φ0+Φ)eiωt],
where the incident potential Φ0(x,y) and the diffraction potential Φ(x,y) are
For the potential flow the boundary condition at cylinder surface L has the form
where ![]() is the inward normal to the cylinder surface. In addition, the scattered wave portion of the potential should satisfy the Sommerfeld radiation condition at infinity for outgoing waves.
is the inward normal to the cylinder surface. In addition, the scattered wave portion of the potential should satisfy the Sommerfeld radiation condition at infinity for outgoing waves.
The exciting forces Fx, Fy and the moment M are determined as
where for the sake of convenience we introduce the notation F1=Fx, F2=Fy, F3=M, n1= nx, n2=ny, ![]() x0 and y0 are the coordinates of the point about which the moment of exciting forces is determined.
x0 and y0 are the coordinates of the point about which the moment of exciting forces is determined.
In the considered problem it is of interest to investigate the influence of pycnocline thickness on the loads acting on the body entirely located in the upper or lower layer. Numerical results for exciting forces on elliptic cylinder submerged under the interface of two-layer fluid are presented by Sturova [8]. In this case the upper layer can be both infinite and bounded by a rigid lid or free surface. Here, we use only the results [8] for infinite two-layer fluid. In this fluid there is only one wave mode, for which ω2=g1k. The numerical results of CFEM for horizontal force Fx, vertical force Fy and moment M of exciting forces relative to the axis of the cylinder are shown in Fig. 6. The cross-section of the cylinder represented the ellipse with a horizontal major axis and the aspect ratio 2:1, the distance from the cylinder axis to the middle of the stratified layer is equal to a minor axis of ellipse b, relative difference of density between layers is ε=0.03. Number of finite elements accounted by CFEM is equal 18.
In numerical realization, the main difference between two-layer fluid and smooth pycnocline is that, in the latter case, the Green function has infinite number of simple poles in integral term and infinite number of items in a sum, what corresponds to the existence of countable number of free internal wave modes for pycnocline stratification. However, as the influence of high modes is very small, only finite number of modes was taken into account. This number increases with pycnocline thickness and can be more than 100.
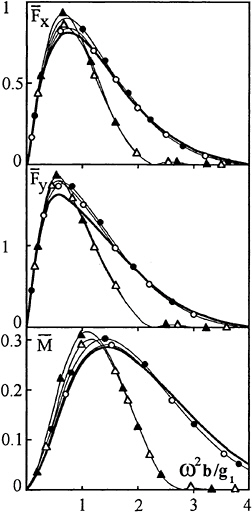
Fig. 6.
The following designations are used in Fig.6
The solid lines show the results of Sturova [8] for two-layer fluid, the light and dark points correspond to the pycnocline thickness ![]() the light and dark triangles correspond to
the light and dark triangles correspond to ![]() The light (dark) points and triangles represent the results for the body submerged in the upper (lower) layer.
The light (dark) points and triangles represent the results for the body submerged in the upper (lower) layer.
It is evident, that the effect of pycnocline thickness is essential at ω2b/g1>1. At fixed wave frequency, the greater pycnocline thickness corresponds to shorter incident internal wave, with a consequent drop of diffraction loads.
In parallel with above-mentioned algorithm, the diffraction loads are determined approximately using the Green function
G=ln r. (12)
This Green function describes a field of point source in unbounded homogeneous fluid. This approximate solution for two-layer fluid (or its particular case of homogeneous fluid with free surface) closely approaches the fully consistent solution for a body located far away from the interface (see, Sturova [8]).
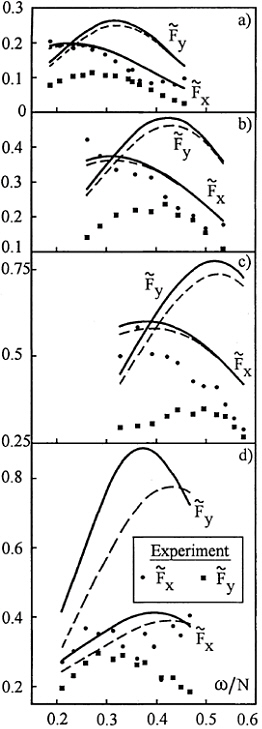
The comparison of theoretical and experimental results for exciting forces is shown in Fig.7a–d. The experimental conditions are given in Table 1.
The elliptic cylinder was fully submerged in the upper layer well away from the pycnocline. Fig.7a–c corresponds to the fixed depth of submergence and increasing thickness of pycnocline. The results for the body located close to the pycnocline are presented in Fig.7d. The solid lines in Fig.7 show the numerical results with the Green function (9), the dash lines show the approximate solutions with the Green function (12). The following designations are used
The dark points (squares) represent the experimental values for ![]()
Table 1. Experimental conditions
|
Fig. No. |
h1(cm) |
h(cm) |
δ(cm) |
|
|
Fig.7 |
a |
14 |
6.1 |
1.4 |
|
b |
14.3 |
6.1 |
2.7 |
|
|
c |
14.5 |
6.1 |
4.4 |
|
|
d |
13.9 |
10.8 |
1.5 |
|
|
a |
12.7 |
15 |
2.6 |
|
|
b |
15.2 |
10.8 |
6.6 |
|
There is a qualitative agreement between theory and experiment, in particular, the theory predicts well the position of maximal forces. For the horizontal force Fx, a good quantitative agreement is observed. The measured values of vertical force Fy are appreciably smaller than the theoretical results. This fact has not yet a coherent explanation. The reported comparisons of measured and calculated loads exerted by surface waves on a cylinder submerged in homogeneous fluid are restricted to the case of circular cylinder. In this case, the estimates of both components of wave-induced forces obtained within the framework of linear theory are in good agreement with the experimental values measured at low Keulegan-Carpenter numbers for the waves of small steepness (see, for example, Chaplin [6]). It seems likely that the non-uniform direction-dependent departure between the measured and calculated loads observed in the present study is conditioned by non-linear effects. The manifestations of flow separation are different depending on orientation of the elliptic cylinder in the flow.
The comparison of diffraction forces calculated by the exact and approximate algorithms shows that these solutions closely fit each other at large distances from sharp pycnocline; otherwise there exists an essential discrepancy.
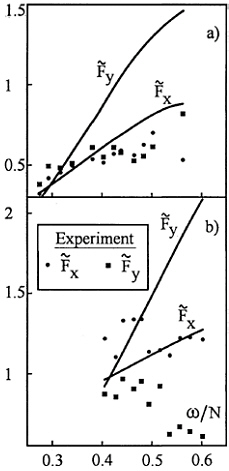
The results obtained for the body partially submerged in pycnocline are shown in Fig.8. The calculations are performed based on the approximate algorithm. In this case, the body experiences the action of periodic buoyancy force in addition to inertial loading. The buoyancy force
was derived from the parameters of the incident wave. The results of approximate solution are shown in Fig.8 by solid lines, the experimental values are denoted analogously to Fig.7. The experimental conditions are given in Table 1.
The agreement between the predicted and measured loads is better for the horizontal component as compared to the vertical component what is especially notable at high wave frequencies. In general, the results of this series of computations give better fit to the experimental data at low frequency (large length) of incident waves what is consistent with the physical assumptions used in the formulation of the approximate solution.
4.
CONCLUSIONS
This study is among the first attempts to determine the diffraction loads induced by internal waves on restricted horizontal elliptic cylinder in the case of continuous pycnocline stratification. It is shown that the presence of a finite layer of variable density changes the character of wave loading compared to the case of two-layer fluid with a step change in density.
The comparison between the experimental data and the computations reveals that the vertical force is essentially overestimated by the linear theory. There are reasons to believe that this departure results from non-linear effects. The elliptic shape of cross-section implies different conditions for separation depending on orientation of the cylinder in the flow.
In future, it would be desirable to continue the investigation of internal wave scattering with the study on role of the shape of cylinder cross-section and refined account of effects conditioned by continuous stratification.
ACKNOWLEDGMENT
This work was made possible in part by Grant No. JHX 100 from International Science Foundation and Russian Government.
REFERENCES
1. Phillips, O.M., ”The Dynamics of the Upper Ocean,” 2nd ed. Cambridge Univ.Press, Cambridge e.a., 1977.
2. Miropolsky, Yu.Z., ”Dynamics of Internal Gravity Waves in the Ocean,” Gidrometeoizdat, Leningrad, 1981 (in Russian).
3. Ermanyuk, E. & Sturova, I., ”Effects of Regular Waves on the Body Submerged in a Stratified Fluid, ” 20th Symposium on Naval Hydrodynamics, Santa Barbara, Calif., USA, Aug. 1994, pp.232–246.
4. Razumeenko, Y.V., ”Changeability of Hydro-physic Ocean Fields; Problems of Manoeuvrability of Submerged Objects in Real Ocean,” International Symposium on Ship Hydrodynamics, St.-Petersburg, Russia, 1995, pp. 275–288 (in Russian).
5. Sarpkaya, T.,” Forces on a Circular Cylinder in Viscous Oscillatory Flow at Low Keulegan-Carpenter Numbers,” Journal of Fluid Mechanics, Vol. 165, Apr. 1986, pp.61–77.
6. Chaplin, J.R., ”Wave Forces on a Horizontal Cylinder Beneath Waves,” Journal of Fluid Mechanics, Vol. 147, Oct. 1984, pp. 449–464.
7. Kochin, N.E., Kibel, I.A., Rose N.V. ”Theoretical Hydromechanics”, Fizmatgiz, Moskva, P. 1, 1963 (in Russian).
8. Sturova, I.V., ”Scattering of Surface and Internal Waves on Submerged Body,” Computational Technology, Novosibirsk, Vol. 2, No. 4, 1993, pp.30–45 (in Russian).
9. Sturova, I.V., ”Effect of Anomalous Dispersion Dependences on Scattering and Generation to Internal Waves,” Journal of Applied Mechanics and Technical Physics, Vol. 35, No. 3, Nov. 1994, pp.366–372.