Velocity and Turbulence in the Near-Field Region of Tip Vortices from Elliptical Wings: Its Impact on Cavitation
A.Pauchet (Ecole Nationale Supérieure de Techniques Avancées, France)
ABSTRACT
The tip vortex flow has been the subject of numerous experimental and numerical works, but the peculiarity of this very confine flow makes it one of the most difficult to describe by any measurement or computational means. This fact is obvious if we admit that the various problems that are engendered in aero and hydrodynamic are still partially solved and other literature continue to appear, presenting steps forward in advancing the understanding of the roll-up process at the vicinity of a wing. Most of the time, the subject of the research being the consequence of the vortical flow, drag increase, cavitation, wake perturbations, etc., some other secondary problems appearing within the context of these researches are not analysed. For example, the connection of the vortical flow and the axial flow that are coexisting, but also the turbulence that rests in the tip vortex core. The present work reviews the different papers dealing with the experimental description of the organisation of the tip vortex flow without any consideration of the main subject that has motivated the work. In order to keep this review to reasonable proportions, we confined ourselves to the literature presenting results on both axial and tangential velocities and the associated fluctuations in the near field of the wings. For a variety of flow conditions, foil planforms, cross sections, and locations of measurement along the vortex path, will found that the axial velocity in the vortex centre can be greater or smaller than the free stream velocity but this will not allow to conclude concerning the organisation of the axial flow with respect to the rotating flow. Using the data collected within the context of the Action Concertee Cavitation research program on tip vortex cavitation, some of these results are presented in a way so that some trends are set out. For identical planforms foils the increase of Reynolds number seams to favoured the jet-like behaviour, but the increase of the axial velocity is not as high as it should be to balance the pressure drop governed by the rotating flow. The pressure loss corresponding to the difference between the maximum axial velocity that should occur due to the minimum pressure and the maximum axial velocity measured is for reasonable lift coefficients in order of magnitude, once the dynamic pressure and increases highly, up to six times the dynamic pressure as the lift coefficient increases. The same trend is noticed but not so markedly when the foil shape is sweep backward.
Concerning the fluctuations measured in the vortex core using various means (hot wire, holography, Laser Doppler Velocimetry, etc.) the literature often reports a high level of fluctuations in the vortex core on both components, attributed to the spatial modification of position of the vortex trajectory, or the velocity gradients encountered when passing through the vortex core. This particular problem is analysed concerning LDV measurements of axial and tangential velocity profiles measured close and far from an elliptical wing tip. It is shone that in the very near region to the foil tip where no fluctuation of position are measurable the axial fluctuations are important but they are decreasing for more distant positions downstream the tip for which the wandering is noticeable. The statistical analysis of the tangential instantaneous velocities for five positions of measurements performed as the measuring volume is crossing the vortex core very near the foil tip demonstrates that positive and negative velocities are both measured at the same time. The estimation of the standard deviation is then not well adapted in the case of histograms having two peaks and thus over estimates the maximum fluctuation level.
A simple and more appropriate method is applied by computing separately the deviations associated to the velocities of identical signs, in order to make a more realistic estimation of the standard deviation, inferior by a factor four to the classical computation. By this mean, the bias induced by the finite dimension of the measuring volume with respect to size of the vortex core is eliminated. In the case of superimposed fluctuation of positions, the method is not efficient but an other method is proposed.
In conclusion, the effect on the critical cavitation conditions of both the axial flow and the turbulence in the vortex core are found to be negligible.
NOMENCLATURE
|
a |
tip vortex core radius |
|
Cl |
lift coefficient |
|
cpmin |
minimum pressure coefficient on the vortex axis |
|
cmax |
maximum foil chord |
|
k* |
non dimensional velocity fluctuations ((u'2+v'2)/U∞2)0.5 |
|
p∞ |
static reference pressure |
|
r* |
non dimensional distance to the vortex centre (r/cmax) |
|
U∞ |
free stream velocity |
|
U* |
non dimensional mean axial velocity (U/U∞) |
|
Uo* |
non dimensional mean axial velocity at the tip vortex centre (Uo/U∞) |
|
u* |
non dimensional instantaneous axial velocity (u/U∞) |
|
u'* |
non dimensional axial velocity fluctuation |
|
V* |
non dimensional mean tangential velocity (V/U∞) |
|
v* |
non dimensional tangential instantaneous velocity (v/U∞) |
|
v'* |
non dimensional tangential velocity fluctuation |
|
x* |
non dimensional distance to the wing tip in the free stream direction (x/cmax) |
|
δ |
turbulent boundary layer thickness for a flat plate of length cmax and U∞ without pressure gradient |
|
ΔV* |
non dimensional maximum tangential velocity magnitude (Vmax–Vmin)/U∞ |
|
δV* |
non dimensional difference between the maximum tangential velocity and the absolute value of the minimum tangential velocity (Vmax–|Vmin|)/U∞ |
|
Γ0 |
foil bound circulation at mid span |
|
Γ* |
non dimensional local tip vortex intensity Γ/Γ0 |
|
σd |
desinent cavitation number |
INTRODUCTION
Because of the possible interaction of the tip vortices of large aircrafts on following smaller planes, considerable attention has been given to the evolution of the tangential and axial velocities and the turbulence intensity in the far field region (more than 10 foil chords) (Spreiter and Sacks (1951), Staufenbiel and Vitting, (1990), Chow et al. (1991) Chigier and Cosiglia (1972), Orloff and Grant (1973), Baker and Saffman (1974), Cliffone and Orloff (1974), Singh and Uberoi (1976), McAlister and Takahashi (1991)). In this region, the roll-up of the vortices is fully achieved and the predominant effect is the diffusion of the tip vortex due to viscosity. Because tip vortex cavitation occurs at short distances from the wing tip, most recent works have been concerned on the very near region (less than a chord), Stinebring et al. (1991), Fruman et al. (1992a, 1992b, 1993, 1994, 1995a, b, c, 1996) and Pauchet et al. (1994, 1996), and the intermediate region (comprised between one and ten chords), Arndt and Keller (1991), Arndt et al (1991), Green and Acosta (1991).
In the very near region, the roll-up of the vortex is initiated and a rapid change of its local intensity (circulation) occurs. Moreover, it is in this same region that the boundary layer over the surface of the foil develops into the vortex viscous core. In this region the vortex is not axisymmetric as shown by flow visualization (Francis et Katz (1988), Chow et al. (1991), Pascal (1993), Liang et al. (1991)), Particle Image Velocimetry (PIV) (Green and Acosta (1991), Pogozelski et al. (1993), Shekarriz et al. (1993)) and Laser Doppler Velocimetry measurements (Baker et al. (1974), Accardo et al. (1984), Higuchi et al. (1987), Stinebring et al. (1991), Arndt and Keller (1991), Falçao de Campos (1989, 1992), Fruman, et al. (1992b)). Because of this lack of symmetry and uncompletion of the roll-up it is difficult to obtain, from a characteristic tangential velocity profile, informations on the tip vortex characteristics: vortex intensity and vortex core radius.
It should be pointed out that defining the vortex intensity in the near region is a subject of much debate. Indeed, let us assume that the velocity field is fully known in a plane normal to the vortex axis. The circulation of the velocity vector can be computed then over any closed path around the vortex. If the path encloses the whole wake of the wing, the tip vortex and a reasonable outboard surface, the circulation will be equal to the mid span bound circulation of the foil. If the path is now reduced in size, part of the circulation carried out by the wake will be ignored and the circulation around this path will decrease accordingly. If the viscous core region is reached by reducing the
dimension of the path, the circulation will be further reduced. In the limiting case of a very small close path around the vortex axis, the circulation will vanish. Because Stinebring et al. (1991) have determined, by conducing three component LDV surveys of the tip vortex issued from a trapezoidal wing in the very near region, that the contribution of the radial components was negligible in the outboard region of the wing along a line parallel to the span centred on the vortex axis, Fruman and coworkers have systematically measured the tangential velocities outboard of the wing and along a direction parallel to the span in tip vortices issued from elliptical wings for numerous positions comprised between the tip and one chord downstream and a variety of experimental conditions. These velocity profiles are characterized by an inner region where the velocities increase linearly as for a solid body rotation, an outer region where they decrease as for a potential vortex, and an intermediate region which assures a smooth transition between the previous ones. The viscous core radius is taken as the radial distance between the vortex axis and the position where the maximum tangential velocity occurs. The local intensity of the vortex is estimated by determining the asymptotic value of the angular momentum per unit mass, product of the local tangential velocity and its distance to the vortex axis, far from the vortex axis. Even if the absolute value of the vortex intensity so estimated is not the intrinsic one, it gives, if the procedure is systematically applied, a very good idea of the roll-up process along the vortex path.
Using such a procedure, the effects of the wing Reynolds number, the cross section, the tripping of the laminar to turbulent boundary layer transition, the water and polymer solution mass flow ejection, the background turbulence, etc., on tip vortex roll-up in the very near region have been investigated for foils having an elliptical distribution of the chord along the span. It has been possible to show that at the tip of the wing the vortex intensity has already a finite value which, for the same flow conditions, increases when the foil tip moves from an upstream to a downstream position (Fruman et al. 1995a). The local circulation increases with increasing lift coefficient and distance to the foil tip, and reaches, for large enough distances, the mid-span bound circulation of the foil. The vortex core radius is, at the tip of the foil, of about half of the thickness of the turbulent boundary layer, computed as for a flat plate of length equal to the maximum chord, decreases to a minimum at a distance comprised between one and two tenths of the maximum chord and then steadily increases because of diffusion. The evolution of the local vortex intensity and core radius remains nearly the same even if the flow conditions are modified by changing the foil cross section, by tripping the laminar to turbulent boundary layer transition or by increasing the background turbulence. A considerable amount of information was also obtained on the fluctuations of the tangential velocities and detailed analysis of the effect of the finite dimension of the measuring volume and vortex wandering were conducted by Fruman et al. (1994) and Fruman “and Billard (1996). Measurements of the velocity fluctuations have also demonstrated quite conclusively that they result from the contribution of vortex wandering and “true” turbulence. If due account is taken of the wandering effect (Orloff and Grant (1973), Baker et al. (1974), Green and Acosta (1991), Green (1991), Fruman et al. (1994)), the “true” turbulence is seen to increases considerably, as compared to the background values, in the inner, solid body rotation, region.
The interpretation of the measurements of the axial velocity profiles is not straightforward. Data available show that both a jet-like (Chigier and Corsiglia (1972), Orloff and Grant (1973), Accardo et al. (1984), Staufenbiel and Vitting, (1990), McAlister and Takahashi (1991) Arndt and Keller (1991), Chow et al. (1991), Green and Acosta (1991), Fruman et al. (1992a,)) or a wake-like (Orloff and Grant (1973), Baker et al. (1974), Accardo et al. (1984), Staufenbiel and Vitting, (1990), McAlister and Takahashi (1991), Stinebring et al. (1991), Green and Acosta (1991), Fruman et al. (1992a, 1993)) behaviour can be present depending on a multitude of parameters: foil planform and tip geometry, incidence angle (lift coefficient), Reynolds number, surface roughness, etc. Because the pressure in the vortex core decreases as a result of the rotation, the axial velocity on the vortex axis has to increase to satisfy Bernoulli's equation without head losses and a jet-like behaviour should therefore result. The wake-like behaviour near the tip can be interpreted schematically by considering that the vortex core consist essentially of liquid which has transited within the boundary layer and thus has velocities much reduced as compared to the free stream velocity.
Using the tangential velocities measured outboard of the wing along a direction parallel to the span and the simplified radial momentum equation, assuming that the radial velocity component can be neglected, Stinebring et al. (1991) have estimated the pressure coefficient at a position where cavitation first occur. Comparison with the desinent cavitation number (with sign changed) was very favorable. Fruman et al. (1992a, 1992b), Pauchet et al. (1993) have extended this procedure and shown that the minimum pressure on
the vortex axis occurs at a distance of the tip of the order of one tenth of the maximum chord for elliptical planform foils. The minimum pressure coefficient (with sign changed) compares remarkable well with the desinent cavitation numbers for a variety of foil planform, cross section and Reynolds numbers. This satisfactory agreement seems to indicate that the peculiarities of the axial velocity profiles in the core region as well as the turbulent velocity fluctuations do not participate in the equilibrium conditions of the nuclei captured by the vortex and, therefore, in the onset of cavitation. The purpose of this paper is to revisit these questions and to shed some light of the reasons leading to both jet- and wake-like behaviour of the axial velocities but also to find some explanation to the high level of turbulence that prevails in the vortex core.
BASIC EQUATIONS
Following Batchelor (1964) let us write Bernoulli's equation along a stream line leading to the axis of the tip vortex,
[1]
where p∞ and U∞ are the pressure and the velocity of the free stream flow, ρ is the liquid density, Ur=0 is the velocity of the vortex axis and Δp is the head loss by viscosity along the streamline. Assuming that the radial velocities do not contribute to the radial equilibrium, we can write,
[2]
where V is the tangential component of the velocity and r is the distance to the vortex axis. Integration of equation [2] and substitution in to equation [1] gives,
[3]
U(r=0) is the axial velocity on the vortex axis since the radial and tangential components vanish. A jet-and a wake-like behaviour of the axial velocity corresponds respectively to a positive or negative value of the term between brackets. The pressure drop associated with the dissipation due to viscosity must thus exceed the gain brought by setting the fluid in rotation in order to achieve a wake-like effect. If expression [3] is computed for the position downstream of the tip where the minimum pressure coefficient occurs, x=xmin, we have, taking into account that it has been rather conclusively demonstrated that,
σd=–Cpmin [4]
where Cpmin is the minimum of the pressure coefficient on the axis of the vortex,
[5]
Since σd can be expressed (Billet and Holl (1979)) as a function of the lift coefficient, Cl and the wing Reynolds number, Re, by,
σd=k Re0.4 Cl2 [6]
the expression giving the pressure loss is,
[7]
where k is a constant whose value depends on the planform and the cross section of the foil, Fruman et al. (1992b), Pauchet et al. (1993).
If the planform and the cross section of the foil are kept constant, the term between brackets will be only a function of Re and C1. Our next objective is to try to determine, using the very large data base acquired during the Action Concertée Cavitation (ACC) program (Fruman (1995)), the trend followed by the non dimensional axial velocity at the vortex centreline.
EXPERIMENTAL
Experiments were performed in the ENSTA Cavitation Tunnel (ECT), the Ecole Navale Cavitation Tunnel (ENCT) and the Grand Tunnel Hydrodynamique (GTH) of the Bassin d'Essais des Carènes. They essentially consisted in determining the cavitation conditions and tangential and axial velocity profiles along the path of tip vortices issued from wings of elliptical planform and NACA 16020 and 0020 cross sections. Table 1 gives a summary of the height, H, and width, W, of each test section, the semi-span, s, and maximum chord, cmax, of each of the foils tested, the range of Reynolds numbers relative to the maximum chord, Re, reached in the tests sections and the length of the measuring volume of the LDV arrangement, Lmv, employed for measuring the velocities, non dimensionalized by the thickness, δ, of the
boundary layer which will develop over a flat plate, of length cmax, without pressure gradient in the fully turbulent regime.
Table 1: Dimensions of the tests sections and of the foils, range of Reynolds numbers and non dimensional length of the measuring volume of the LDV arrangement.
|
H×W (mm2) |
S×cmax (mm2) |
Re (×10–6) |
Lmv/δ |
|
|
ECT |
80×150 |
60×40 |
0.1–0.5 |
1.6 |
|
ENCT |
192×192 |
120×80 |
0.5–1.2 |
2.8 |
|
GTH |
1114×1114 |
713×475 |
2.5–8.0 |
1.7 |
Let be x the direction of the free stream velocity, y the direction of the wing span, z the direction normal to the xy plane and select the tip of the wing as the origin of x and the centre of the vortex as the origin of y and z. Velocities in the x (axial, U) and z (tangential, V) directions were measured in the ECT and the ENCT along the y axis while in the GTH x and y (tangential) components were measured along the z axis. Dantec LDV systems were operated in the back scattering mode in the ECT and ENCT and in the forward scattering mode in the GTH.
Prior to measuring the velocity profiles, the centre of the vortex at each axial position was determined as described by Fruman et al. (1992b), by: letting the measuring volume coincide with the bubbles within the vortex core at cavitation inception conditions; displacing the measuring volume in the outboard direction (ECT and ENCT tunnels) or in the suction side direction (in the GTH tunnels) up to reaching a maximum tangential velocity; measuring over a short distance on either side of this position the z component (ECT and ENCT) or the y component (GTH) and determining the position of the largest “tangential ” component. At this position, the y and z axis are supposed to cross the centre of the vortex and the whole velocity profiles are then measured.
In the ECT and ENCT the measuring directions of the LDV are made to coincide with the x and z directions. In the GTH they are rotated 45° with respect to the x and y directions. This later arrangements allows to reduce the statistical bias between the two velocity components.
RESULTS AND DISCUSSION
Velocities
It is by now well substantiated (Fruman et al (1992a and b, 1993, 1995)) that: a) the tangential velocity profiles can be described, whatever the generating conditions, by three zones, the viscous region (0<r<0.8a) where V is increasing with the distance from the centre proportionally to the angular velocity, ω=Γ/2π, a potential region (2a <r <∞) where V is decreasing as the inverse of the radius, and a transition zone between these two regions, b) the maximum tangential velocity is reached at a distance a from the vortex centre corresponding to around 50 percent of the boundary layer thickness computed as for a flat plate of length equal to the maximum chord, c) the roll-up process is already initiated at the foil tip and the local vortex intensity is a fraction of the mid span bound circulation, d) the maximum tangential velocity reaches an absolute maximum along the vortex path at about one tenth of the maximum chord from the tip, corresponding to the position where the local vortex core radius is a minimum.
A large amount of information available on axial velocity distribution in tip vortices show that both a jet or a wake behaviour can exist depending on a multitude of parameters: foil planform and tip geometry, incidence angle (lift coefficient), Reynolds number, surface roughness, etc. This can be clearly seen in Figure 1, where the non dimensional axial velocity on the vortex axis at varied stations along the vortex path within a distance of up to ten chords from the tip, given by the references listed in Table 2, has been plotted as a function of the Reynolds number, comprised between 0.15 to 4.75×106. Some general trends can be described: i) the extreme values (excess or deficit) of the axial velocity are reached at the centre of the viscous core, ii) for a given incidence angle and free stream velocity, when an excess (or a deficit) is present in the core, its maximum (minimum) occurs very close to the foil tip, iii) downstream the tip, the velocity excess (deficit) decreases gradually, iv) when the incidence is increased, it tends to accentuate the jet-like (wake-like) behaviour at a given position down from the tip.
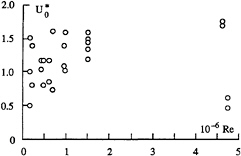
Figure 1: Maximum axial velocity, non dimensionalized with the free stream velocity, as a function of the Reynolds numbers, sources listed in Table 2.
Table 2: Extreme values of the reduced axial velocity measured in the tip vortex for distances less than ten chords from the tip of various foil planforms and cross sections for Reynolds numbers comprised between 0.15 to 4.75×106.
|
Uo* |
Re (×10–6) |
x* |
Incid. Angle |
Cross. Sect/Planf. |
|
|
Singh |
1,52 |
0,15 |
0,80 |
- |
NACA64 618 |
|
(1976) |
1,00 |
0,15 |
2,40 |
- |
Rectangular |
|
0,50 |
0,15 |
5,00 |
- |
||
|
Green |
1,62 |
0,68 |
2,00 |
10° |
NACA 66 209 |
|
(1991) |
0,74 |
0,68 |
10,00 |
10° |
Rectangular |
|
Green et al. |
1,17 |
0,41 |
2,00 |
NACA 66 209 |
|
|
(1991) |
1,04 |
0,41 |
0,96 |
- |
|
|
0,96 |
0,41 |
15,00 |
|||
|
Stinebring et al. |
0,47 |
4,75 |
0,07 |
- |
- |
|
(1991) |
0,63 |
4,75 |
0,67 |
- |
Trapezoidal |
|
Chow et al. |
1,77 |
4,60 |
0,74 |
10° |
NACA 0012 |
|
(1991) |
1,69 |
4,60 |
1,42 |
10° |
Rectangular |
|
Chigier et al. |
1,40 |
0,95 |
close |
12° |
NACA 0015 |
|
(1972) |
1,10 |
0,95 |
far |
12° |
Rectangular |
|
Arndt et al. |
1,60 |
0,97 |
2,35 |
12° |
NACA 66 415 |
|
(1991) |
1,03 |
0,97 |
2,35 |
4° |
Elliptical |
|
Staufenbiel et al |
1,40 |
0,15 |
0,20 |
13° |
CLARK Y |
|
(1990) |
0,80 |
4,00 |
0,20 |
13° |
Rectangular |
|
Orloff et al. |
0,85 |
0,60 |
2,00 |
8° |
NACA 0015 |
|
(1993) |
1,18 |
0,60 |
2,00 |
12° |
Rectangular |
|
MacAlister et al. |
1,60 |
1,50 |
0,10 |
NACA 0015 |
|
|
(1991) |
1,35 |
1,50 |
1,00 |
Rectangular |
|
|
1,20 |
1,50 |
4,00 |
|||
|
1,50 |
1,50 |
0,10 |
|||
|
1,45 |
1,50 |
0,10 |
|||
|
1,20 |
1,50 |
0,10 |
|||
|
Accardo et al. |
1,17 |
0,48 |
0,09 |
10° |
NACA 0014 |
|
(1984) |
0,80 |
0,48 |
0,70 |
10° |
Rectangular |
Recently, very systematic investigations of the axial and tangential velocity evolution with distance to the tip have been conducted for elliptical chord distributions along the span. Particular attention has been given to the very near region comprised within one chord from the tip. For an elliptical planform foil of cross section NACA 16020 at 10° incidence and equal lift coefficient, Figures 2 shows the non dimensional axial velocity at the vortex axis as a function of the distance to the tip. For the three Reynolds numbers tested, a jet behaviour occurs and it is amplified when the Reynolds number increases. The maximum of the axial velocity seems to move downstream from the tip when the Reynolds number increases, but remains in all cases confined to a distance of less than 20 percent of the maximum chord. After reaching the maximum, the jet effect decays all the more so that the Reynolds number is smaller. This behaviour can be paralleled with that of the maximum tangential velocity as shown in Figure 3 for the same flow conditions. Indeed, a maximum occurs at a distance of about ten percent of the maximum chord whatever the Reynolds numbers and decays downstream.
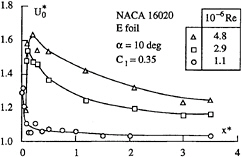
Figure 2: Non dimensional maximum axial velocity as a function of the non dimensional distance to the foil tip.
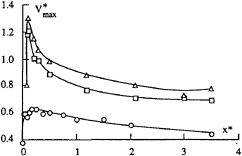
Figure 3: Non dimensional maximum tangential velocity as a function of the non dimensional distance to the foil tip (same conditions as in Figure 2).
The effect of modifying the foil planform, but keeping the same spanwise elliptical chord distribution, on axial velocities is illustrated in Figure 4 (Fruman et al. (1993, 1995)) for an equal incidence angle, position downstream and Reynolds number. For a Straight Leading Edge (SLE) planform, there is a clear indication of a jet behaviour. When the tip of the wing is moved downstream and the planform becomes Elliptical (E), the jet behaviour is practically eliminated. With a Strait Trailing Edge (STE), the farthest downstream position of the tip, a strong wake-like behaviour develops. The jet and wake behaviour can be somehow correlated with the size of the viscous core as shown in Figure 5 where the radial distribution of the tangential velocity has been plotted. It is clear that the downstream displacement of the tip induces an increase of the viscous core size, a modification of the angular velocity in the viscous core and a modification of the local tip vortex intensity. The augmentation of the viscous core radius and reduction of the angular velocity can only be related to the process of roll-up initiation along the leading edge of the foil and the wrapping of the boundary layer. In the STE foil case, a larger amount of low momentum fluid participates in the core formation and, because of the short distance between the measuring station and the tip, neither the outside, nearly unperturbed, axial flow nor the axial pressure gradient are capable of achieving the acceleration of the core stream. It seems very much clear that momentum transfer by shear between the retarded or accelerated core flow and the outside flow is very much reduced in this rotating flow configuration if compared to what it can be expected in a usual jet or wake shear layer.
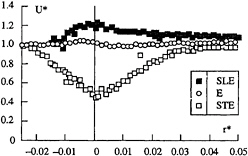
Figure 4: Radial distribution of the axial velocity measured at x*=0.12 and a Reynolds number of 1.1×106 for foil having three different planforms.
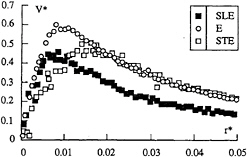
Figure 5: Radial distribution of the axial velocity measured at x*=0.12 and a Reynolds number of 1.1×106 for foil having three different planforms.
It has to be recalled here that the measurements of the axial and tangential velocities conducted in the GTH, in a direction normal to the plane defined by the free stream velocity and the foil span, shows very clearly the three dimensional character of the flow in the near region. The difference between the absolute values of the maximum and minimum of the tangential velocity, δV, have been plotted in Figure 6 for three flow situations and the same Reynolds number. It shows clearly that the three dimensionality is confined to a distance of about one chord downstream the tip (the near region) and that it is independent of the foil and incidence (lift coefficient). In this region, a good estimate of the azimuthal gradient of the tangential velocity can be obtained by dividing δV* by the viscous core radius and π. The order of magnitude of this velocity gradient is, taking a core radius of 2.5 mm, of 1300 reciprocal seconds at the first measuring station and at least one order of magnitude less one chord from the tip. By continuity, this velocity gradient has to be compensated by the axial gradient of the axial velocity and the radial gradient of the radial velocity. Figure 7 shows, for the flow conditions of Figure 6, the non dimensional axial velocity on the vortex axis as a function of the distance to the tip. The axial gradient, evaluated between the tip and the station where the maximum occurs, is at the most only one tenth of the value estimated above in the very vicinity of the tip (130 s–1). Therefore, the contribution of the radial gradient of the radial component should be preponderant in this region, as Stinebring et al. (1991) have shown and the evolution of the axial velocity do not respond to the need of satisfying the continuity equation.
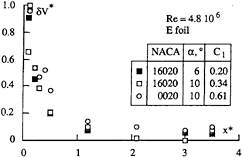
Figure 6: Non dimensional difference between the two extreme values of tangential velocity profile as a function of the non dimensional distance to the foil tip.
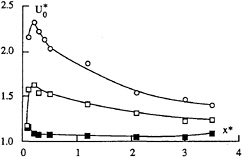
Figure 7: Non dimensional maximum axial velocity as a function of the non dimensional distance to the foil tip.
The non dimensional pressure loss computed using expression [7] has been plotted in Figure 8 as a function of the Reynolds number ranging from 0.5 to 5×106. In spite of the limited data available, it seems that the pressure loss either remains nearly constant or decreases slightly when the Reynolds number increases. Also, it increases when the lift coefficient increases whatever the cross section of the elliptical foil and the manipulation undergone by the boundary layer, Figure 9. The pressure is less than the unperturbed dynamic pressure for the lowest lift coefficients and increases to more than six times the dynamic pressure for the largest lift coefficients. The latter can be related to the breakdown of the vortex occurring at the highest values of the incidence angle (>12 deg). In these flow conditions, a peculiar radial distribution of the axial velocity was observed, Figure 10. As shown, a kind of annular jet-like region surrounds a central region where the velocities drop rather sharply and reach a minimum. This central region corresponds to a wake behaviour. The axial velocity profile modification can be correlated with observations made during tip vortex cavitation and showing, Figure 11, that a continuous vapour tube extends from the tip to a distance corresponding to the position of the minimum pressure (x*=0.2), thereafter the vortex is only feed by tiny bubbles escaping from the rear of the tube. Finally, the effect of modifying the planform of the foil, keeping constant the chord distribution, is illustrated in Table 3 for the NACA 16020 cross section and two incidence angles. When the tip is moved downstream, going from the SLE to the STE position, the non dimensional pressure loss increases in agreement with the already mentioned change of the axial velocity behaviour (see Figure 4). It is interesting to see that the non dimensional pressure loss can be as low as 0.2 in the case of the SLE and 6° incidence. The pressure loss can therefore be related to the viscous dissipation over the foil surface during vortex initiation along the foil leading edge.
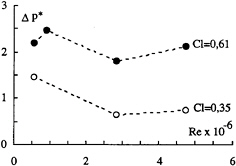
Figure 8: Evolution of the pressure loss non dimensionalized by the dynamic pressure based on the upstream velocity as a function of the Reynolds number for the NACA 16020 E foil at 6 and 10 deg incidence.
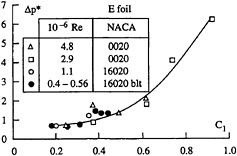
Figure 9: Evolution of the pressure loss non dimensionalized by the dynamic pressure based on the upstream velocity as a function of the lift coefficient.
Table 3: Pressure loss non dimensionalized by the dynamic pressure based on the upstream velocity for three different foils at 6 and 10 deg incidence
|
10 deg Re=1.1×106 |
6 deg Re=1.2×106 |
||
|
ΔP* |
SLE |
1.1 |
0.2 |
|
E |
1.5 |
1.0 |
|
|
STE |
2.3 |
1.6 |
|
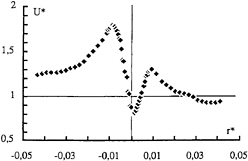
Figure 10: Radial distribution of the axial velocity measured at x*=0.3 from the NACA 0020 E foil tip at 15 deg incidence and 6 m/s (GTH).

Figure 11: Tip vortex cavitation developing at the NACA 0020 foil extremity at 17.7 deg for σ=16.4 and Re=3×106 (GTH).
Velocity fluctuations
Numerous measurements have demonstrated that velocity fluctuations increase considerably, as compared to the background levels, in the viscous core of the vortex. Fluctuations as high as 60 percent and 55 percent for the tangential and axial components respectively on the vortex axis have been reported (Fruman et al. (1992b)). These fluctuations decay radially quite rapidly and reach the background level at a distance corresponding to the theoretical limit of the region where viscous effects predominates; i.e. twice the viscous core radius.
Figures 12a and b, show the maximum of the axial and tangential fluctuations as a function of the distance to the tip for the NACA 16020 elliptical foil at 10° incidence and three Reynolds numbers, 1.1, 2.8 and 4.8 ×106. The maximum of the axial fluctuations vary little with distance and increase with increasing Reynolds numbers Figure 12a. This upward trend is directly proportional to the Reynolds number, the ratio u'*/Rex10–6 is varying between 0.1 and 0.15 for distance larger than x*=0.1. The maximum value occurs near the foil tip (0.1<x*<0.2) and slowly decreases to reach an asymptotic value behind x*=2.0.
The evolution of the maximum tangential velocity fluctuations along the vortex path do not seams to be modified by the Reynolds number augmentation Figure 12b. The absolute maximum tangential velocity fluctuation occurs very near the tip of the foil at x*<0.2, corresponding to the position of maximum axial velocity peak, it's also the position where the difference between the minimum and the maximum tangential velocity reaches an extremum and also, where the minimum pressure coefficient occurs, Fruman et al. (1992b). Then following downstream the vortex centre line, the maximum tangential fluctuations markedly decreases down to x*=1 and then reaches a constant value equal to 0.4.
Figure 13a and b, shows the dependence of the maximum axial and tangential fluctuations with the distance to the tip of the NACA 16020 elliptical foil for three different values of the lift coefficient at equal Reynolds number, 4.8×106. In the very near region to the tip x*<0.3, the maximum axial fluctuation is increasing with increasing lift coefficient Figure 13a, downstream this trend is not so clear. The rise of the maximum tangential velocity fluctuations is controlled by the lift coefficient increase Figure 13b, in each condition the extreme value occurs in the proximity of the foil tip and then v'* slowly fall with downstream distance.
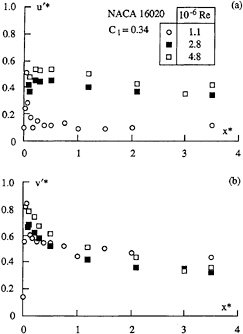
Figure 12: Fluctuations associated to the axial (a) and tangential (b) velocities as a function of the non dimensionalized distance from the NACA 16020 Elliptical foil at 10 deg incidence.
Figure 14 shows the evolution of both the maximum tangential and axial velocity fluctuations with the vortex angular velocity measured at x*=0.2 for the elliptical foils having a NACA 0020 at 4, 6, 8, 10 deg for Re=4.8×106 and a NACA 16020 cross section at 6, 10 deg for Re=4.8×106 and 10 deg for Re=2.8×106. The tangential velocity fluctuations are in both cases much greater than the axial ones, in accordance with the results presented in the previous Figures 12 and 13 a,b. The fluctuations associated with the two components vary linearly with the angular velocity, the slope of the tangential velocity being slightly greater than the axial one. In the case of an elliptical planform, Pauchet et al. (1996) have conducted experiments to analyze the effect of the turbulence on the TVC and they have found that the trajectory of the vortex emitted from of an elliptical foil is very stable in the near region of the tip (x*<0.2) even when the upstream turbulence is homogeneously increased from 1.5 percent to 3.5 percent. We can then consider that the major part of
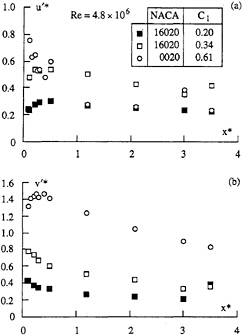
Figure 13: Fluctuations associated to the axial (a) and tangential (b) velocities as a function of the non dimensionalized distance from Elliptical foils for three different lift coefficient.
the tangential velocity fluctuations increase shone in the Figure 14 can be directly related to the increase of the tangential velocity gradient encountered when the measuring volume coincides with the vortex centre, without any contribution of the vortex wandering, Fruman et al. (1994). In order to reinforce this fact, the mean velocity fluctuation k* divided by the maximum amplitude ΔV* has been plotted as a function of the distance x* in Figure 15 for various incidence angles, two different cross sections, and Reynolds numbers comprised between 2.74×106 and 5.70×106. Close to the foil tip the mean value is 0.6, with a scattering of ±8 percent and decreases downstream to reach a value of 0.45 with a scattering of ±20 percent. It must be reminded that far downstream the vortex wandering can not be neglected Fruman et al. (1994), Pauchet et al. (1996), and must be accounted for the scatter increase of the measured velocities.
In order to have a better idea of how the tangential velocity gradient contributes in the estimated fluctuations when the measuring volume is close to
the vortex centre, we have analysed the statistical distribution of the data for both components. Figures 16a and b are respectively showing the mean axial and tangential velocity profiles measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106. Associated to five positions of measurements within the vortex core, the non dimentionalized instantaneous velocity distributions for a sample of 600 measurements are shown. Figure 16a, a nearly gaussien distributions is observed regardless of the position. The central position of each of the five distribution is exactly corresponding to the maximum mean axial velocity Uo*=2.3. The deviation is giving a good estimate of the maximum fluctuation u'*=0.58. For the five positions the tangential instantaneous velocites are distributed around two values of opposite signs which describes an histogram with two nearly gaussiens Figure 16b. The gap between the two peaks is greater than the difference between the maximum and the minimum mean values (ΔV*) of the tangential velocity profile. Depending on the position of the measuring volume with respect to the vortex centre, the area under the left peak is decreasing as the area of the second peak is increasing. This reveals two important facts: i) when the measuring volume is crossing the vortex centre, both positive and negative tangential velocities are measured; the calculation of the standard deviation is absurd for the present statistical distribution, being not gaussien, v'*=1.40, ii) the instantaneous tangential velocities can reach values as large as 1.5 time the maximum (or minimum) mean value.
In order to make a more realistic estimation of the fluctuations, it is possible to separate the computation of the standard deviation for each histogram peak. This is obtained by first the separation of the negative and the positive instantaneous velocities and secondly by the separate calculation of the mean and the deviation associated of the two samples corresponding to the negative and the positive velocities. The mean tangential velocity profile is then not modified by the summation of each separate mean values, negative and positive. If the same operation is applied to the deviations corresponding to each sample, the maximum fluctuations is decreased by a factor of 4, Figure 17. This treatment is cutting down the maximum deviation by approximately the difference between the two extreme mean values of the tangential velocity profile, v'*(corrected)=0.28. By this method, in the case of LDV measurements in a vortical flow spatially stable (without wandering), the bias due to the finite dimension of the measuring volume on the standard deviation can be eliminated.
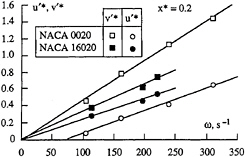
Figure 14: Axial and tangential velocity fluctuations as a function of the vortex angular velocity.
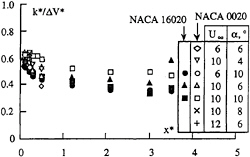
Figure 15: Evolution of the mean velocity fluctuation k* divided by the maximum amplitude Δv* as a function of the distance x*.
The next step will be to applied the same procedure to a case where the errors due to the measuring volume dimension and the spatial fluctuations of the vortex centre are superimposed. This particular condition can be achieved when moving downstream along the vortex path for the same flow conditions as previously. At x*=3.5, the amplitude of the vortex wandering was estimated to be 5 mm Fruman et al. (1992) by positioning the LDV measuring volume on the two extreme locations taken by the vapour tube for conditions just below the critical cavitation conditions. This amplitude is closely the same as the vortex core extension “a” as well as the same order of magnitude of the measuring volume length (4.7 mm). Figures 18a and b are respectively showing the mean axial and tangential velocity profiles measured at x*=3.5, with the non dimentionalized instantaneous velocity distributions to five positions in the vortex core.
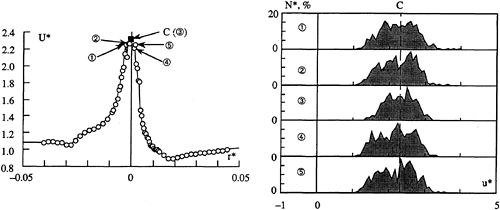
Figure 16 a: Radial distribution of the mean axial velocity measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106. The non dimentionalized instantaneous velocity distributions (sample of 600 measurements) associated to five positions of measurement in the vortex core are described.
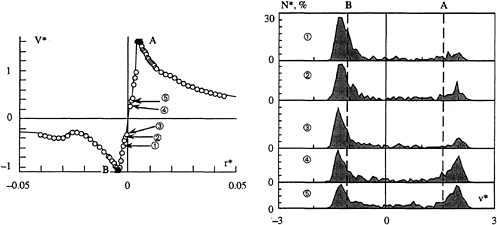
Figure 16 b: Radial distribution of the mean tangential velocity measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106. The non dimentionalized instantaneous velocity distributions (sample of 600 measurements) associated to five positions of measurement in the vortex core are described.
The sampling being unchanged, probably not sufficient for these conditions, the scattering noticed on both components in the region corresponding to the core extension clearly indicates the effect induced by the modification of the position of the vortex trajectory during the measurement process. Surprisingly enough, the instantaneous axial velocity distribution is restricted around the maximum mean value that leads to a much smaller velocity fluctuation level (u'*=0.25) compared to the relatively scattered distribution measured to the position close to the foil tip where the wandering is negligible. The double peak histogram is still present in the instantaneous tangential velocity distributions Figures 18b. The two peaks are at equal distance from the zero velocity as a result of the symmetry of tangential velocity profile and closer as the angular velocity is decreasing. The position of each peak is still “outside” the two extreme mean values of the tangential velocity profile indicating that at the position corresponding to a mean velocity close to zero, the instantaneous velocities are much greater or smaller than respectively the maximum and the minimum mean tangential velocity. An important scatter of the tangential velocity distributions is observed between the two main peaks. This particular characteristic can be attributed to the fluctuation induced by the “wandering”. But in spite of that, the classical estimation of the deviation (applying the standard computation of the deviation to the total sample without any corrections) is entirely governed by the velocity amplitude corresponding to the distance between the two peaks of the statistical distribution because the scattering that appears between the two peaks due to the spatial fluctuations has in fact a very low influence on the variance computation. This fact has been confirmed by Pauchet et al. (1996). In the previous case, when the tangential velocity profile is measured close to the foil tip where no wandering is measurable, the simple statistical treatment applied is efficient enough in first order to filter out the bias induced by the dimension of the measuring volume with respect to the velocity gradient encountered. But this procedure do not seams appropriated to be directly applied to the statistical distribution shown Figure 18b. It appears difficult to find a perfect double peak histogram in the statistical distributions shown Figure 18b, no1 and 5 for examples, compared to the ones in Figure 16b. Then, an other statistical procedure must be found to separate the bias induced by the wandering and the dimension of the measuring volume. One solution can be obtained by applying a Pearson low, derived from the Gaussien low. It will allow to distinguish the wandering effect on the statistical distribution from the pure geometrical bias by qualifying the dissymetry on each side of the distribution. This method is actually in is development phase and will be presented later.
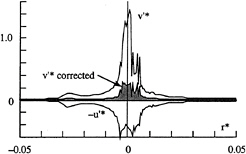
Figure 17: Radial distribution of the tangential velocity fluctuations corrected and non corrected, and the opposite value of the axial velocity fluctuations measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106.
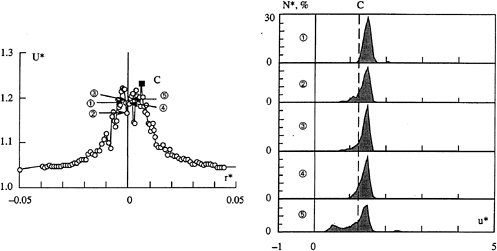
Figure 18 a: Radial distribution of the mean axial velocity measured at x*=3.5 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106. The non dimentionalized instantaneous velocity distributions (sample of 600 measurements) associated to five positions of measurement in the vortex core are described.
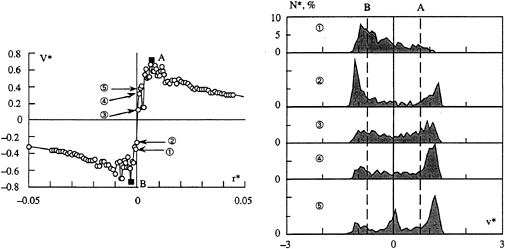
Figure 18 b: Radial distribution of the mean tangential velocity measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106. The non dimentionalized instantaneous velocity distributions (sample of 600 measurements) associated to five positions of measurement in the vortex core are described.
CONCLUSION
The three dimensionality of the tip vortex flow is confined to a distance of about one chord downstream the tip and in that region, the azimuthal gradient of the tangential velocity is not compensated by the axial gradient of the axial velocity. Therefore, the contribution of the radial gradient of the radial component should be preponderant in this region. It seems very much clear that momentum transfer by shear between the retarded or accelerated core flow and the outside flow is very much reduced in this rotating flow configuration if compared to what it can be expected in a usual jet or wake shear layer. The increase of Reynolds number seams to favoured the jet-like behaviour, but the increase of the axial velocity is not as high as it should be to balance the pressure drop governed by the rotating flow. The pressure loss corresponding to the difference between the maximum axial velocity that should occur due to the minimum pressure and the maximum axial velocity measured is for reasonable lift coefficients in order of magnitude, once the dynamic pressure. The pressure loss increases up to six times the dynamic pressure as the lift coefficient increases. For identical flow conditions, the pressure loss is very low in the case of the SLE foil and increases moderately when the foil shape is sweep backward.
The statistical analysis conducted on LDV data obtained for positions of measurements crossing the vortex centre demonstrates that the maximum velocity fluctuation estimated is completely determined by the velocity gradient encountered when passing through the vortex core and the wandering has, in that case, a very poor effect on the fluctuations measured. Concerning the axial velocity fluctuations, it appears that near the foil tip, the jet present in the core is very turbulent, far downstream the maximum axial velocity has decreased as well as the fluctuations. The wandering do not seams to significantly influence the axial fluctuations measured.
A method is applied to correct the standard deviation value associated to the tangential velocity. The configuration of the flow field into the vortex core induces the measurements of both positive and negative instantaneous velocities at the same time. Thus the distribution of the velocity is not gaussien as it would be normally found but distributed according a double peak histogram. Without fluctuations of the vortex position, the instantaneous velocity distribution is concentrated on two gaussien peaks, each one corresponding to positive and negative velocities, respectively larger than the maximum mean tangential velocity and smaller than the minimum mean tangential velocity.
This statistical phenomenon is induced by a measuring volume dimension in the same order of magnitude of the vortex core dimension. The consequence is an important over estimation of the tangential fluctuations based on the classical estimation of the standard deviation during the measurements performed inside the solid body rotation core region. In that case the axial fluctuations are less important than the tangential ones as shone in Figure 19. If an appropriate statistical method is applied the tangential fluctuations are drastically reduced and finally are found to be 50 percent lower than the axial fluctuations Figure 19. It is therefore obvious that the fluctuations in the vortex close to its initiation but already detached from the foil surface is not isotropic. The tangential fluctuations are in order of magnitude close to the boundary layer fluctuations (20 percent) that develops over the foil tip while the axial ones are at an extremely high level, the highest being located precisely where minimum value of the pressure coefficient along the vortex axis occurs but also where the tip vortex cavitation is initiated. Consequently we must admit that these highly turbulent properties of the axial flow do not modifies the minimum pressure coefficient. There are still some objections that can be suggest. First, the bias due to the axial velocity gradient is not corrected at all and may be also an important parameter to a certain over estimation of the axial fluctuations especially where the jet behaviour is the most important, some work still needs to be done on the subject, but we can imagine that the corrections brought will go in the same way as the reduction of fluctuations found for the tangential component. Secondly the bias induced on both the axial and tangential mean velocity profiles are not corrected in spite of the fact that they might be important, in particular for the tangential velocity profiles. In spite of all these uncertainties, the essential point is in fact that even if these errors have been left unresolved because of time, they can be qualified as systematic errors. Thus, if we admit that these errors are determined by the ratio shone in the Table 1, the length of the measuring volume of the LDV arrangement, Lmv, non dimensionalized by the thickness, δ, of the boundary layer which will develop over a flat plate, of length cmax, without pressure gradient in the fully turbulent regime. This crucial point fully confirms the validity of all the results and the analysis conducted within the context of the ACC research program because of its systematic approach adopted by all the members of the ACC, for the description of the tip vortex velocity field. Our knowledge of the tip vortex flow organisation very close to the foil extremity has progressed, in spite of the fact that the absolute values of the flow field is not perfectly described.
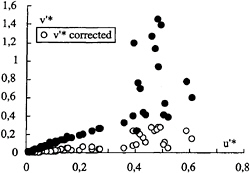
Figure 19: Radial distribution of the tangential velocity fluctuations corrected and non corrected as a function of the axial velocity fluctuations measured at x*=0.2 from the tip of the NACA 0020 elliptical foil at 10 deg incidence and a Reynolds number of 5.7×106.
ACKNOWLEDGEMENTS
This work has been sponsored by the Direction des Recherches, Etudes et Techniques (DRET) of the Ministry of Défense, France, and is part of the Action Concertée Cavitation program. I wish to acknowledge Dr. D.H.Fruman for reviewing the manuscript and helpful discussion.
REFERENCES
Accardo, L., Cenedese, A., Cioffi, F., ( 1984). “Experimental analysis of tip vortex by Laser Doppler anamometry”. Symposuim on application of Laser Anemometry in Fluid Mechanics—II, Lisbon, Portugal.
Arndt, R.E.A., Arakeri, V.H., Higuchi, H., ( 1991), “Some observations of tip-vortex cavitation”. J. Fluid Mech, vol 229, pp 269–289.
Arndt, R.E.A., Keller, A.P., ( 1991). “Water quality effects on cavitation inception in a trailing vortex. ” Cavitation '91, ASME FED 116, pp 1–8 and (1992). Journal of Fluids Engineering, 114, pp. 430–438.
Bacheleor G.K. ( 1964). “Axial flow in trailing line vortices”. J Fluid Mech, vol 20, pp 645–658.
Baker, G.R., Barker, S.J., Bofah, K.K., Saffman, P. G., ( 1974). “Laser anemometer measurements of trailing vorticies in water”. J. of Fluid Mech., Vol 65, part 2, pp. 325– 336.
Billet, M.L., Holl, J.W., ( 1979), “Scale effects on various types of limited cavitation”. ASME International Symposium on cavitation inception, NY, USA.
Cliffone, D.L., Orloff, K.L., ( 1974). “Axial flow flow measurements in trailing vorticies”. AIAA Journal, Vol. 12, No. 8, p. 1154.
Chigier and Cosiglia ( 1972). “Tip vortices— velocity distributions”. AIAA Journal paper No 72–41.
Chow J.S., Zigliac G.G., Bradshaw P. ( 1991). “Initial roll-up of a wing tip vortex”. Federal Aviation Administration International Wake Vortex Symposium , Washington DC, october.
Falçao de Campos, J.A.C., George, M.F., Mackay, M., ( 1989). “Experimental investigation of tip vorticies“. Cavitation and Multiphase Flow Forum, ASME FED 79, pp. 25–30.
Falçao de Campos, J.A.C., ( 1992). “Laser Doppler Velocity measurements on tip vorticies in non cavitating and cavitating conditions“. Cavitation and Multiphase Flow Forum, ASME FED 135.
Francis, T.B., Katz, J., ( 1988). “Observation on the development of a vortex on a rectangular hydrofoil ”. ASME Fluids Engineering, Vol. 110, pp. 208–215.
Fruman, D.H., Dugué, C. and Cerrutti, P., ( 1992a). Enroulement et cavitation de tourbillon marginal. Revue Scientifique et Technique de la Défense, pp. 133–141.
Fruman, D.H., Dugué, C., Pauchet, A., Cerrutti, P., Briançon-Marjollet, L., ( 1992b). “Tip vortex roll-up and cavitation”. Nineteenth Symposium on Naval Hydrodynamics, August 24–28, Seoul..
Fruman, D.H., Cerrutti, P., Pichon, T., Dupont, P., ( 1993). “Effect of hydrofoil planform on tip vortex roll-up and cavitation ”. 4th International Symposium on Cavitation Inception, New Orleans, ASME FED-Vol. 177, pp. 113–124 and ( 1995a), transaction of the ASME FED-Vol 177, pp. 162–169, and Journal of fluids engineering 117, March.
Fruman D.H., Castro, F., Pauchet, A., Pichon, T., ( 1994). “On tip vortex turbulence, wandering and cavitation occurrence.” Second International Symposium on Cavitation, Tokyo, Japan, Proceedings, H.Kato ed., pp. 151–157.
Fruman, D.H., Cerrutti, P., Pichon, T. and Dupont, P., ( 1995a), “Effect of hydrofoil planform on tip vortex roll-up and cavitation ”. Journal of
Fluids Engineering, 117, pp. 113–124, March.
Fruman, D.H., Pichon, T., Cerrutti, P., ( 1995b), “Effect of drag-reducing polymer solution ejection on tip vortex cavitation ”. Journal of marine science and technology, Tokyo, Japan .
Fruman D.H., ( 1995c). The “Action Concertée Cavitation” research program and accomplishments. International symposium on cavitation, Deauville, France.
Fruman D.H., Billard, J.Y., ( 1996). “The tip vortex : effect of drag reducing agent on confined turbulence ”. ASME Fluids Engineering Division Summer Meeting, San Diego, California, USA.
Green, S.I., ( 1991). “Correlating single phase flow measurements with observations of trailing vortex cavitation”. Journal of Fluids Engineering, 113, pp. 125–129.
Green, S.I. and Acosta, A.J., ( 1991). “Unsteady flow in trailing vortices”. J. Fluid Mechanics, 227, PP. 107–134.
Higushi, H., Quadrelli, J.C., Farell C., ( 1987). Vortex roll-up from a elliptic wing. AIAA Journal, Vol. 25, No. 12, pp. 1537–1542.
Liang, X., Ramaprian B.R. ( 1991). “Visualisation of the Wing-Tip Vortex in Temporal and Spatial Pressure gradients”. Journal of Fluids Engineering, Vol. 113, pp. 511–515.
McAlister K.W., Takahashi R.K. ( 1991). “NACA 0015 wing pressure and trailing vortex measurements”. NASA Technical Paper 3151, AVSCOM Technical Report 91-A-003.
Orloff K.L. and Grant G.R. ( 1973). “The application of scanning laser doppler velocimeter to trailing vortex definition and alleviation”. AIAA Journal, paper No. 73– 680.
Pascal, Ph., ( 1993). “Etude experimentale de l'évolution d'un écoulement tourbillonnaire”. Rech. Aérosp., no 1993–6, Novembre— Décembre, p. 27–44.
Pauchet, A., Briançon Marjollet L., Fruman, D.H., ( 1993). “Recent results on the effect of cross section on hydraufoil tip vortex cavitation occurence at hight Reynolds numbers” Cavitation and Multiphase Flow Forum, ASME-Vol. 153, pp. 81–86, Washington D.C., June.
Pauchet, A., Briançon Marjollet L., Gowing, S., Cerrutti, P, Pichon, T., ( 1994). “Effect of foil size and shape on tip vortex cavitation occurence”. Second International Symposium on Cavitation, Tokyo, H.Kato ed. pp 133–139.
Pauchet, A., Viot, X., Fruman, D.H.F., ( 1996). “Effect of turbulence on Tip Vortex Cavitation” . ASME Fluids Engineering Division Summer Meeting, San Diego, California, USA.
Pogozelski, E.M., Shekarriz, A., Katz, J. and Huang, T.T., ( 1993). “Three dimensional near field behaviour of a tip vortex developing on an elliptic foil”. 31st Aerospace Sciences Meeting and Exhibit, Reno, NV, January.
Shekarriz, A., Fu, T.C., Katz, J. and Huang, T.T., ( 1993). “Near field behavior of a tip vortex”. AIAA Journal, 31, 1, pp. 112–118.
Singh, P.I., Uberoi M.S., ( 1976). “Experiment on vortex stability”. The Physics of Fluids, Vol. 19, No. 12, December.
Spreiter J.R., Sacks, A.H., ( 1951), “The rolling up of the trailing vortex sheet and its effect on the downwash behind wings”. Journal of the aeronautical sciences 18, pp. 21–32 et 72.
Staufenbiel R., Vitting T., ( 1990). Formation of vorticies and vortex wake alleviation by tip vortices . ICAS-90–3.2.2.
Stinebring, D.R., Farrell, K.J., Billet, M.L., ( 1991), “The structure of three-dimensional tip vortex at hight reynolds numbers ”. Journal of fluids engineering, September, Vol 113 pp. 496–503.

















