3
Symmetries, Forces, and Particles
INTRODUCTION
Several decades of experiments in high-energy physics have produced an extremely rich and detailed set of data on elementary particles, the most important of which are summarized in the 700-page Particle Data Book (Physical Review D, vol. 50, no. 3, part 1, August 1994: Web site at http://pdg.lbl.gov/pdg.html). For example, the particle known as the K meson is unstable and has about 70 ways in which it can disintegrate into a set of lighter particles. For each decay mode, many measurements have been made-for example, the nature. speeds, and directions of the particles produced. How can one make sense out of this wealth of data? Theoretical particle physics aims to uncover the regularities hidden in the data and to formulate rules and laws that provide an understanding of the data in as simple and precise a way as possible.
The most useful tool in this enterprise is symmetry, which is described below. Symmetries have allowed an extremely compact synthesis to be made of all of the knowledge of particle physics: the Standard Model. There are now many very precise tests of this synthesis. A description of how the strong, weak, and electromagnetic forces arise as a consequence of three symmetries can be found below; indeed, the symmetries dictate precisely the form of these three interactions.
Note: This chapter presents a picture of the rich theoretical underpinnings to the field of elementary-particle physics. Although it attempts to do so without a great deal of technical language, some readers may find parts of this chapter more challenging than the rest of the report.
However, these symmetries lead to an astonishing-and obviously wrong prediction: All of the elementary particles should be massless. To reconcile this puzzle, the symmetries must be "broken," which implies that there must be new forces that have not yet been discovered. In the Standard Model, these new forces are related to a hypothetical particle called the Higgs boson. Interaction of the Higgs boson with other particles generates particle masses but does not provide real understanding of the observed pattern of masses. Also, one might expect such a theory to generate particle masses that are much heavier than observed. The masses of elementary particles are a crucial clue in deciphering the ultimate theory of nature, and much detective work lies ahead.
With all of its successes in giving order to the wealth of data from high-energy particle collisions, the Standard Model brings a whole new set of questions into sharp focus. What determines the particles, symmetries, and mass scales of this theory? Could they have been very different, completely changing the nature of the world in which we live? Physicists are able to describe the physical universe with astonishing simplicity and precision but have very little understanding as to why it is this way. Several theoretical proposals are discussed later that extend the Standard Model to address, particularly, the question of particle masses. There are other issues that even these theories do not begin to address, such as the role of gravity. Superstring theory, which offers the hope of a complete, all-encompassing theory of the origin of particles-together with all of their symmetries and interactions-is discussed at the end of this chapter.
SYMMETRIES
Symmetry arguments have a long and honorable history in physics, but only in recent times have they come to dominate our understanding of fundamental physics. The power and beauty of such arguments became fully apparent only when expressed in mathematical form. The committee hopes, however, to convey the spirit of this subject by discussing some of its central physical concepts.
What precisely do we mean when we say that physical laws display symmetry? A square is symmetric when rotated through 90 degrees around its center. This operation produces an orientation identical to the initial one-we say that a symmetry operation leaves an object invariant. A circle is left unchanged (invariant) by a rotation through any angle. Since it allows more symmetry operations, it possesses a larger symmetry. More generally, an object is said to be symmetrical when there are operations on the object that could have changed its appearance but in fact do not.
Similarly, physical laws also have symmetry. One of the basic principles of physics is that the laws of physics at one location are the same as at another, and at one time, the same as at another. This principle is equivalent to a symmetry: The laws of physics are invariant when we change our viewpoint-either from one location to another or from one time to another.
Rotations provide another familiar example of a symmetry. Imagine a laboratory as a windowless spaceship in free-fall, isolated from electric and magnetic forces, in which an experimentalist has some apparatus to determine a certain law of physics. Suppose that the experimentalist makes a measurement, the spaceship is rotated, and the same measurement is made again. The results of the two measurements are always found to be the same: When writing the laws of physics, there is no need to specify the orientation of the laboratory. Much less familiar, and more far reaching, it is not necessary to specify the speed of the laboratory—the laws of physics do not change if the experiment is done, for example, on an airplane. This last symmetry principle was the crucial one that led Einstein to develop special relativity. All of the astonishing results of special relativity—such as the equivalence of mass and energy and the inability to travel faster than light—follow from the requirement that physics be symmetrical under the operations discussed.
Symmetries and Particle Physics
How are these symmetries of space and time—which are called space-time symmetries—relevant to particles and their interactions? First, there is a direct consequence for the very nature of elementary particles themselves. Rotational symmetry leads to elementary particles' possessing a new attribute, called spin. For example, electrons come in two varieties: left-handed and right-handed. The difference can be pictured in terms of the view of a football's spin as seen by the quarterback who threw the pass. The football spins clockwise if thrown by a right-hander and counterclockwise if thrown by a left-hander. Photons also come in the same two varieties of spin, but other particles have three spin orientations, and still others are spinless.
The symmetries of space and time also constrain the rules by which all particles interact. One should not forget why it is so important to understand these interactions. The explanation of every physical process, from the growth of plants to space shuttle lift-off, has its fundamental origin in these interactions. The properties of materials, from concrete to quicksand, ultimately depend on the properties of elementary particles.
Consider a collision between two electrons, shown in Figure 3.1. The two electrons labeled 1 and 2 approach each other, collide, and then leave as the two electrons labeled 3 and 4. Quantum mechanics says that there is no unique outcome: Sometimes the electrons are deflected by large angles, sometimes by small angles. In this quantum world the laws of physics can be phrased in terms of probabilities. If the laws determine the probabilities for all possible outcomes, then the description is complete. The problem is that the probabilities depend on the speeds, directions, and spins of each of the four electrons for which there are an infinite number of possible values. The importance of symmetry can now be appreciated: Probabilities depend on the speeds, directions,
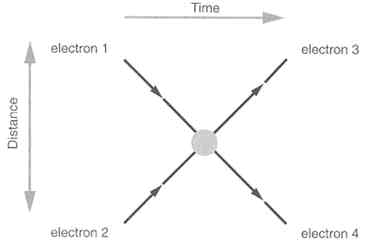
FIGURE 3.1 Collision of two incoming electrons, 1 and 2, into two outgoing electrons. 3 and 4.
and spins of particles in a way that is determined by symmetries. In general. symmetries, place powerful restrictions on the nature of interactions between elementary particles. Probabilities can be expressed in terms of just a few numbers (called parameters), even though there are many possible initial and final configurations.
As physicists discovered more elementary particles, they found that patterns in their properties could be understood in terms of mathematical symmetries. These newer symmetries often act in more abstract, so-called internal spaces. For example, early experiments on protons and neutrons revealed that although their electric charges differ, these particles are fundamentally similar and their strongest interactions are identical. This close similarity inspired the concept of a two-dimensional "internal" space, in which protons and neutrons correspond to different directions. The similarity of their behavior becomes the statement that physics is unchanged as one rotates in this imaginary internal space.
If the laws of physics are not changed by such a rotation, this operation is said to be an internal symmetry. The fruitfulness of this way of thinking was revealed as additional particles were discovered. Each had to be located in internal space. Apparent asymmetries in the distribution of known particles within internal space would appear if one had only part of the picture. In this way the existence of particles necessary to complete the symmetric pattern, and some of their properties, could be predicted. An early example of this was provided by discovery of the omega-minus (Ω) particle, which was predicted ahead of time to fill a gap in the symmetrical pattern shown in Figure 3.2. The
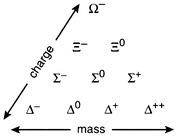
FIGURE 3.2 Pattern of particles that allowed prediction of the Ω- particle. Particles in the same row have similar masses: particles with the same electric charge (shown by superscripts) also lie on straight lines.
most recent example is the discovery of the t quark, which completed the particles listed in Table 2.1.
Local or Gauge Symmetries
The most profound and powerful symmetries of physical law established at present are so-called local or gauge symmetries. Such symmetries underlie both Einstein's theory of gravity (also called general relativity) and the Standard Model of strong, weak, and electromagnetic interactions. Most of the matter on Earth is made up of just two quarks, the so-called up and down quarks, denoted by u and d. (A glossary to describe many of these terms is included in the Appendix at the end of this report.) Because of internal symmetries, each of these quarks comes in three varieties, which are labeled by colors: ur, ug, and ub, represent the red, green, and blue up quarks. Physical laws are invariant if quark colors are interchanged, for example, if ur, and ug are switched. In fact, a local symmetry means that physical laws are unchanged even when different interchanges are made at different locations in space. For example, one might switch ur with ug in one part of the laboratory and ur with ub in another part. There are an infinite number of such local operations, and requiring the laws to be unchanged under any of them is extremely constraining.
Local internal symmetries actually require the existence of particles (called force carriers) whose interactions are the origin of the forces. The local symmetry that acts on the three colors leads to the strong force that binds quarks into nuclei. Insight into this basis for the understanding of forces can be gained by returning to the example of the collision of two electrons in Figure 3.1. The circular blob represents the actual interaction between particles and is highly constrained if it arises in a theory with a local internal symmetry. If one could look inside this blob at high magnification, such a theory would dictate that the interaction results from exchange of a force particle, which for an electromagnetic interaction is called the photon, as illustrated in Figure 3.3. Furthermore, the interaction of a photon with two electrons is itself greatly constrained by local symmetry. No matter what the speeds, directions, and spins of the par-
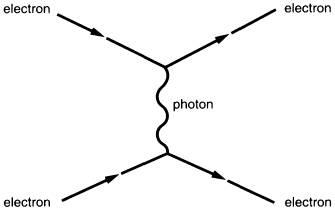
FIGURE 3.3 Collision of two electrons resulting from exchange of a photon.

FIGURE 3.4 Electromagnetic vertex of an electron: The electron emits a photon with a probability, in emissions per second, proportional to the electron's charge.
ticles, only a single parameter—the electric charge of the electron—is needed to describe this interaction. This is the same single parameter that enters all electromagnetic interactions of the electron, for example, the bending of the path of an electron in a magnetic field and the electron's binding to an atomic nucleus. The electromagnetic interaction is represented diagramatically in Figure 3.4 as a vertex at which the three particles come together. (In these figures, straight lines represent matter particles and wavy lines represent force particles.) Local symmetries are also called gauge symmetries, and the resulting force particles, such as the photon, are known as gauge bosons.
It is startling to realize that the apparent infinite variety of chemical properties and reactions of atoms and molecules all result fundamentally from this single electromagnetic vertex. The very existence of the photon, as well as the
form of the electric and magnetic interactions, is a consequence of the local electromagnetic symmetry.
It is clear that symmetries are the most powerful tool physicists have for understanding the properties and interactions of particles, yet only by careful experimentation can we learn which symmetries nature possesses. Many symmetries have been proposed, but measurements provide the only sure guide. Future experiments will continue the quest to uncover more of nature's symmetries, and theoretical physics will struggle further to understand why nature has chosen these symmetries.
THE STANDARD MODEL
A major development in theoretical physics this century was the construction of what are called quantum field theories—theories of particles and their interactions that incorporate the probabilistic laws of quantum mechanics, special relativity, and the symmetries discussed above. This enterprise began soon after the discovery of quantum mechanics in the late 1920s. The quantum field theory of electromagnetism, describing the electron and the photon, reached its final form in the late 1940s, but theories involving larger local internal symmetries were not fully understood until the early 1970s. Quantum field theories are the basic tool for theoretical particle physicists. There are many such theories, and the great variety of phenomena they can describe is the subject of continuing research.
The Standard Model is a quantum field theory that provides a concise and accurate description of all known particle phenomena. This discussion relies on the ideas of symmetry and interaction vertices introduced in the previous section.
Three local internal symmetries have been discovered in nature: They are called strong, weak, and electromagnetic, after the three forces to which they give rise.
Strong symmetry leads to force particles of the strong interactions—the gluons, g. The matter particles that feel this force are called up and down quarks, u and d, and come in red, green and blue varieties. The gluon vertex for the up quark is illustrated in Figure 3.5. A quark of one color goes into the interaction and comes out as a quark of a different color, but its other properties are not changed. The mathematical theory of quarks and gluons that underlies this vertex is called ''quantum chromodynamics," or QCD for short. The strength of the gluon interaction is called g3. It is large, making this QCD interaction strong. The matter particles that do not feel this strong force are leptons: the electron, e, and its neutrino, ve, as well as their second- and third-generation counterparts, the muon and tau, and their respective neutrinos.
The force particles of the weak interaction, the W and Z bosons. are very massive, which results in a force with a very short range—much less than the
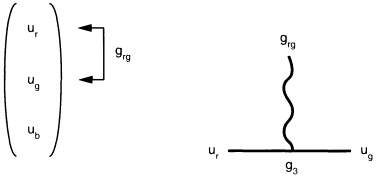
FIGURE 3.5 Quark triplets and the gluon vertex.
diameter of a proton. The electromagnetic interaction, on the other hand, has a massless force particle, the photon, with a corresponding range of interaction that is infinite, allowing us to see to the edge of the universe. A single parameter g2 describes the strength of the weak interactions (see Figure 3.6), whereas g1 gives the strength of the electromagnetic interaction.
The weak symmetry has a very peculiar property. Only counterclockwise spinning (left-handed) quarks and leptons feel the weak force. The reason nature treats left-handed and right-handed objects differently is one of the many questions about the nature of forces for which we have as yet no adequate answers.
As indicated earlier, symmetries dictate both the forces and the so-called multiplet structure of particles that feel these forces. Table 3.1 summarizes this information about how the three forces that arise from local internal symmetries relate to the four basic types of matter particle (u, d, e, Ve,). For strong and weak forces, the entries represent the size of the multiplet of particles that interacts with the corresponding force particles. The strong force acts among triplets of quarks (three colors), changing one into the other; the weak force acts between quark and lepton doublets, again changing one into the other. An entry "I" implies that there is no interaction, since there is nothing to change into. Electromagnetic force acts on all particles except neutrinos (not changing their nature), and the entry in Table 3.1 gives the electric charges of particles.
Table 3.1 represents the limit reached at present in the quest for a simple understanding of particle interactions. There are several questions that this knowledge raises, questions that are not answered by the Standard Model: Why is it that some particles feel the strong force and some do not? Why are the weak interactions left-handed? Why are there not multiplets having more than three components? In short, why are the matter particles what they are, and why do they interact with force particles in the way shown in Table 3.1? This table offers a mystifying array of numbers—how can it be understood?
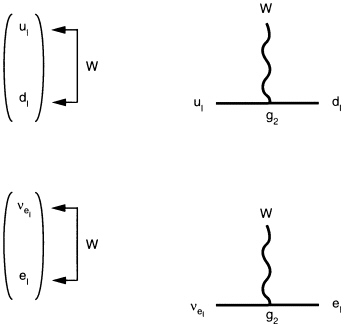
FIGURE 3.6 Left-handed doublets and the weak vertices.
TABLE 3.1 The Aperiodic Table
|
Force/Particle |
(u1,d1) |
ur |
dr |
(Ve1, e1) |
er |
|
Strong |
3 |
3 |
3 |
1 |
1 |
|
Weak |
2 |
1 |
1 |
2 |
1 |
|
Electromagnetic |
2/3, −1/3 |
2/3 |
−1/3 |
0, −1 |
−1 |
The four matter particles discussed so far (u,d, e, ve) are the members of the first family, or generation, of particles. Three such generations of particles have been found, as shown in Table 2.1. The only known difference between the three generations is their mass-in particular, the force particle vertices of the heavier generations are identical to those of Figures 3.4, 3.5, and 3.6 for the lightest generation. This replication of particles suggests to some that there is a new internal symmetry to be discovered that is responsible for the different generations. Physicists believe that some deeper understanding of the three
rows, or periods, of Table 2.1 will eventually be found, in the same way that the revolution of quantum mechanics led to an understanding of the periodic table of the elements. In contrast, the particles of a single generation cannot be grouped into subgroups or periods of particles with similar properties-Table 3.1 does not have a periodic structure.
Spontaneous Symmetry Breaking
Whereas interactions of the force particles are restricted by the three local symmetries, the observed masses of the quarks are restricted by the strong symmetry. For example, although ur, ug, and ub have the same mass, members of weak doublets, such as ve and e, do not. The nonzero masses of elementary particles are said to break electroweak symmetries (i.e., if the electroweak symmetry was unbroken, the masses would all be zero). This seems unsatisfactory—surely all aspects of a theory should have the same symmetry. In fact, physicists believe that the equations of the theory do initially possess electroweak symmetries but that something within the theory causes the solutions to the equations to break the symmetry. This important phenomenon of spontaneous symmetry breaking can be illustrated by the examples of the square and circle mentioned earlier. Recall that these shapes are symmetrical when rotated about their centers, by 90 degrees for the square and any angle for the circle. If a square and a circle are drawn on an elastic sheet and the sheet is stretched in one direction so that these shapes are elongated into a rectangle and an oval, we have broken the symmetry. Now, if the rectangle is rotated by 90 degrees, it does not match the shape corresponding to its original position. This stretching is a simple analogy for the spontaneous symmetry breaking that occurs in theories of particle physics. The first step is to infer from data what stretching is occurring which is understood quite well—and the next step is to understand what is causing the stretching. Here there are ideas, but the correct answer is not yet known.
When the sheet is stretched, the symmetries of the square and circle are not completely broken: The resulting rectangle and oval are both symmetric with respect to rotations about their centers by an angle of 180 degrees. Similarly, not all of the electroweak symmetries are broken—the local electromagnetic symmetry discussed in the last section is unbroken. An important consequence of an exact local symmetry is that it requires the mass of the corresponding force particle to vanish. This explains why gluons and photons are massless. On the other hand, W and Z particles, which correspond to the broken parts of the electroweak symmetry, are not constrained to be massless. In fact, they are so heavy that only in the 1980s did accelerators attain sufficient energies to produce them.
Higgs Boson
The origin of electroweak symmetry breaking, which leads to masses for W and Z particles as well as for quarks and leptons, is a crucial problem of particle physics. What is doing the stretching? The stretching must be generated by some new interactions of the theory-the known interactions illustrated in Figures 3.4, 3.5, and 3.6 are not able to do the job. In the Standard Model, a hypothetical particle, called the Higgs boson, is introduced and given interactions, which allow the elementary particles to become heavy. The Higgs boson is quite unlike either a matter or a force particle. When physicists say that the Standard Model has been verified in thousands of experiments, they are referring to all the processes that result from the force particle vertices of Figures 3.4 through 3.6. The Higgs boson is still a matter of speculation, lacking solid experimental support. Nevertheless, something must generate particle masses, and physicists know that this physics is inextricably linked to the mass scale of the W and Z particles.
Generation-Changing Interactions
The interactions that generate the quark and lepton masses play a role in a small but very significant property of the weak force. This is an interaction that causes the generation of a particle to change, as illustrated in Figure 3.7. The
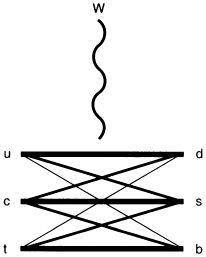
FIGURE 3.7 Generation structure of the weak force.
TABLE 3.2 The 18 Parameters of the Standard Model
|
Quantities |
Number of Parameters |
|
Fundamental electroweak mass scale |
1 |
|
Strengths of the three forces |
3 |
|
Masses of electron, muon, and tau |
3 |
|
Masses of u, c, and t quark |
3 |
|
Masses of d, s, and b quark |
3 |
|
Strengths of flavor-changing weak force |
3 |
|
Magnitude of CP symmetry breaking |
1 |
|
Higgs boson mass |
1 |
dark lines represent the strongest part of the weak force, which does not change generation. The regular and faint lines represent smaller pieces of the weak force, which are called flavor-changing interactions and are described by three parameters. Experiments have not uncovered any flavor-changing interactions of leptons.
Are the laws of physics invariant under the interchange of particles and antiparticles? If so, there would be a new symmetry of nature, known as CP. The masses and interactions of the particles are nearly identical to those of the antiparticles, but there is a small difference-CP is not an exact symmetry of nature. Breaking of the CP symmetry has been observed as a very small difference in neutral K meson decay probabilities. Within the Standard Model, it is the interactions of the Higgs boson that break CP symmetry, an origin for CP breaking that must be viewed as speculative. This breaking is described by a single extra parameter that enters the flavor-changing vertices of weak interactions. The parameter is capable of describing all of the CP violation observed to date. New experiments studying K and B mesons will soon test whether the generation-changing parts of the weak interaction, illustrated in Figure 3.7, really do provide the answer to the puzzle of the origin of CP violation.
A good theory allows calculations that predict many phenomena in terms of just a few free parameters, which must be measured. The Standard Model has been used to calculate thousands of phenomena in terms of the 18 independent parameters listed in Table 3.2. These are the few quantities that cannot be calculated within the Standard Model.
There is a limit to the accuracy of predictions resulting from calculations in the Standard Model. Frequently this is just because high-accuracy calculations are lengthy. In these cases, great effort can produce extraordinarily precise predictions. For example, the motion of electrons in magnetic fields has been successfully predicted to one part in a trillion. (The measurement is also a great effort!) Calculations of processes induced by the weak force have been com-
puted to better than one part in a thousand and have been verified at experiments carried out at Fermilab, CERN (the European Laboratory for Particle Physics), and the Stanford Linear Accelerator Center (SLAC) over the past 5 years.
For the strong force, calculations are more difficult. Over the last decade, the rapid increase in the speed of computers has allowed remarkable progress; for example, the masses of the proton and rho meson have been computed to an accuracy of about 10%. As yet, these calculations are far from yielding a quantitative understanding of more complex phenomena such as the detailed structure of the proton, but many important calculations are under way.
The Standard Model represents an astonishing synthesis of our understanding of the properties and interactions of elementary particles. The next two sections describe how physicists, inspired by its success, are attempting to understand fundamental laws at a deeper level, with greater conviction than ever before that new symmetries remain to be discovered.
BEYOND THE STANDARD MODEL
Two questions are paramount in furthering an understanding of particles and their interactions, and both of these involve the masses of the particles.
The first question involves the masses of force carriers. The massless photon can be understood in terms of the electromagnetic symmetry, and the mass of the proton follows from the dynamics generated by the strong symmetry. Hence. it is only the mass scale of weak interactions, which leads to heavy W and Z particles, that is not constrained by a symmetry principle. Without such a symmetry, it is not just that the mass scale of weak interactions cannot be determined by theory; rather, the theory naturally makes the mass scale huge, many orders of magnitude larger than observed in nature. The theory can be made to agree with observation only if several large contributions to the weak mass scale are made to cancel, which is an unnatural fine-tuning.
The second question involves the pattern of masses and interactions of the matter particles, shown in Tables 2.1 and 3.1, together with the 18 parameters indicated in Table 3.2. What determines this structure and the values of these parameters? Could a larger symmetry be responsible for grouping the particle in generations, and could such a symmetry provide an understanding of the pattern of interaction strengths and particle masses'?
Symmetry Breaking and Supersymmetry
The first question, which is about how symmetries break, is considered now. Physicists are sure that there are new forces responsible for symmetry breaking, and these new forces should themselves be governed by a new symmetry. One possibility is an extension of space-time symmetry, known as supersymmetry. A second is another local internal symmetry, which physicists call technicolor sym-
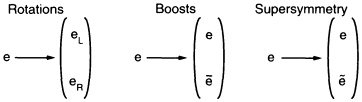
FIGURE 3.8 Space-time properties of the electron. Rotation symmetry leads to electrons with both left- and right-handed spin. Symmetry under velocity changes leads to a further doubling of the particles, with the electron partnered with its antiparticle. Supersymmetry would lead to still one more doubling: The electron would be partnered with its superpartner.
metry in analogy with the strong color symmetry. Another possibility is that it could be some new scheme that has yet to be invented.
Supersymmetry adds new dimensions to space-time with coordinates that are not ordinary numbers but have a quantum mechanical character. The breaking of such a symmetry could provide an origin for the weak scale. As indicated, as space-time symmetries get larger, the number of states associated with a particle, such as an electron, also increases. It is therefore no surprise that the further extension of space-time symmetries to include supersymmetry leads to a further doubling of the kinds of particles, as illustrated in Figure 3.8. For example, the electron has a superpartner, called the selectron. Moreover, Higgs particles are required.
Technicolor, if it exists, would be a new strong force-similar in many ways to the known strong, or color, force. In the same way that the strong force is responsible for the masses of the proton and other hadrons, so the strong technicolor force could provide masses for the W and Z particles.
As elementary-particle physicists look beyond the Standard Model, they expect to discover a new force. The symmetries for the new forces differ greatly in their predictions: For example, supersymmetry incorporates the Higgs particle of the Standard Model as the origin for quark and lepton masses, whereas in technicolor theories there is no Higgs particle. Theoretical difficulties in constructing complete technicolor theories of nature have led many physicists to see supersymmetry as the most likely option. If supersymmetry does provide the key to the weak scale, then the early decades of the twenty-first century will be a time of great discoveries for particle physics: many new particles, the superpartners of particles, and observations of many new effects in rare processes. The most exciting prospect is that measurements of the masses and interactions of the new superpartner particles will shed light on another great puzzle—the pattern of quark and lepton masses. If technicolor forces are discovered, the future will be even more interesting. As well as a whole new hadron spectroscopy, additional new forces of nature must be present to generate masses for
quarks and leptons. As experiments reach toward the answer to the great question of how the weak symmetry is broken, physicists anticipate the possibility of dramatic developments in the future direction of the field.
Grand Unification
The second question introduced at the beginning of this section concerns the origin of the multiplicity of particles, forces, and masses. Progress can be made by a conceptually straightforward extension of the use of local internal symmetries.
If a generation is considered in more detail, including the colors of the quarks, one finds that it has 15 particle components. The three local symmetries of the Standard Model distinguish between these components: Some feel strong and weak forces, whereas others do not, so it is natural to arrange these components into five groups (see Table 3.1). Is it possible that the local symmetries of the Standard Model are just fragments of a much larger, grand unified symmetry? Remarkably, there is such a symmetry that treats all 15 particles of a generation as components of a single fundamental object. The most remarkable aspect is that the properties of this symmetry lead precisely to each and every number in Table 3.1. Grand unified symmetries provide an understanding of the patterns of particles.
If there is a single large local symmetry treating all members of a generation in an equivalent symmetrical way, why does one not observe a single force acting identically on equal-mass particles u, d, e, and ve? The grand unified symmetry must break at an energy scale that is larger than has been probed by accelerators. In the same way that the electromagnetic force is the low-energy relic from the breaking of electroweak forces, so the three forces of the Standard Model could be the low-energy remnant of a force based on a larger broken symmetry at higher energies. However, as physicists try to understand nature by introducing larger symmetries, the issue of how these symmetries are broken becomes even more important.
In gauge theories, the force between two particles, governed by the interaction strength g, depends slightly on the energy at which the particles collide. At very high energies the grand unified symmetry is unbroken and relates the three interaction strengths, in fact making them equal, g1 = g2 = g3, as the three forces become a single force. However, at lower energies, where today's experiments are performed, the grand unified symmetry is broken and the three interaction strengths have different dependencies on particle energy, as shown in Figure 3.9. A combination of g1 and g2 (measured at the energy scale of weak interactions) is predicted to be in the range 0.230 to 0.236 if the theory is supersymmetric and in the range 0.212 to 0.218 if it is not. Thus, grand unified theories can precisely predict this quantity, which in the Standard Model could take any value in the range 0 to 1. It has been measured at CERN and SLAC to be 0.231, providing
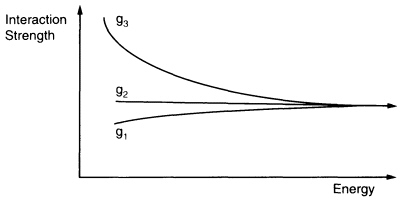
FIGURE 3.9 Unification of strong, weak, and electromagnetic forces. The strengths of the three forces g1, g2, and g3 depend on the energy at which measurements are made. This dependence has been observed experimentally and can be calculated theoretically. Values for g1, g2, and g3, measured at the energy scale of weak interactions, can be extrapolated theoretically to high energies where, if the theory is supersymmetric, they are found to meet, providing a visual picture of the unification of the three forces.
evidence for both grand unification and supersymmetry. Perhaps the most dramatic prediction of grand unification is that protons—a fundamental building block of all matter—are not stable, but decay into lighter particles. The simplest nonsupersymmetric theories have been excluded by experiments that searched for, but did not find, proton decay. The supersymmetric theory predicts a longer life for the proton—only a few in a hundred thousand tons of matter (equivalent to a large battleship) will decay each year. Other phenomena could also probe the structure of these supersymmetric grand unified theories: Neutrinos may have mass, and muons may be converted to electrons when they are close to an atomic nucleus.
Why Are There Three Generations?
The muon and tau are identical to the electron, except that they are much heavier. Why should these heavy copies of the electron exist? Why are there three generations of matter as shown in Table 2.1 ? Physicists once again look to symmetries for the answer. Consider an equilateral triangle drawn on an elastic sheet. This is an analogy for a symmetric world in which there are three identical charged leptons, with one side of the triangle representing each lepton. The symmetry of the triangle under a rotation of 120 degrees shows that the three leptons are identical. If the triangle is stretched, the three sides are no longer equal, analogous to our world where the electron, muon, and tau have very different masses. As discussed earlier, physicists believe that a symmetrical
theory lies behind nature, but that this symmetry is broken by the stretching that produces the familiar world in which we live. The symmetry is not manifest directly, but its presence is inferred from the stretched forms that have broken the symmetry. To understand why nature looks the way we find it, we have to understand broken symmetries. Even if we are able to uncover these broken symmetries of nature, physicists ask why the symmetry was there in the first place: Why start with an equilateral triangle? Why not a square or something else? The next section describes work of the past decade that has grappled with such questions.
PHYSICS OF THE PLANCK SCALE
The energy scale at which the strengths of the three forces are predicted (by assuming supersymmetry) to become equal, as shown in Figure 3.9, is very high, about 1014 times larger than the energy scale of weak interactions. Above this energy scale, the symmetry becomes so encompassing that quarks and leptons become unified; this is called grand unification. This energy scale is intriguingly close to the famous Planck energy scale, which is about a hundred times larger. Unfortunately, this energy is so high that it can be reached only by theoretical speculation.
The Planck scale of energy is where the gravitational force becomes strong. At low energies, gravity is an incredibly weak force, noticeable only in the influence of large objects such as planets and stars. The gravitational force depends on a particle's mass when at rest, but on its energy when in motion, so that it increases with increasing energy and at the Planck scale is competitive with the other forces of nature. The Planck scale is determined by the three fundamental units of nature: the maximum speed (that of light, c), the quantum of action (Planck's constant, h), and the gravitational coupling constant (Newton's gravitational constant, G). A mathematical combination of these three constants to yield a term whose units are those of energy results in the Planck energy scale. With other combinations, a Planck length, a Planck time, and a Planck mass can be constructed-any fundamental physical quantity that is not described by a pure dimensionless number such as 2 or π. Given the fundamental nature of these constants it is reasonable to suppose that the Planck scale is the fundamental scale of physics. It is remarkable that these quantities, the Planck of 10−43 proton masses, are so disparate, not only from macroscopic length of 10−33 cm, the Planck time of 10−43 s, and the Planck mass quantities but also from the basic scale of the Standard Model. Indeed there is a disparity of 17 orders of magnitude between these scales. This disparity gives rise to the question: Why is the weak scale, which determines the overall scale for the masses of observed particles, 10−43 times smaller than the Planck scale? Not only is a new symmetry needed to govern the weak scale, but the question arises as to why the energy associated with this new symmetry is so low.
If the purported unification scale is so close to the Planck length, then gravity must be treated on an equal footing with the other forces of nature. This is a long-outstanding problem of theoretical physics. Einstein's theory of gravity is remarkably successful at low energies, yet it gives rise to deep problems and inconsistencies at high-energy. These problems suggest that it must be replaced by a more fundamental theory, reinforcing the view that new physics will appear close to the Planck length that might unify all the forces of nature, including gravity. Fortunately, there exists a theory that appears to have the potential of achieving these goals—string theory.
String Theory
What is string theory? String theory says that if we could look at a quark with a microscope that can resolve distances of 10−33 cm, we would not see smaller subobjects, but rather a quark would look to us like a little closed string.
String theory is a natural generalization of previous theories of particles but represents a radical departure from the tradition initiated by Thales of Miletus. In uncovering string theory about 25 years ago, physicists set out on a path whose end we can still barely conceive, one that has led to a trail of theoretical surprises—including supersymmetry—without obvious historical parallel.
String theory not only eliminates the contradiction between gravity and quantum mechanics but in a sense explains why just this combination exists in nature. String theory also automatically generates all of the ingredients that seem to be needed as building blocks of the Standard Model. In these and other ways, string theory provides potential answers to many of the puzzles posed by the Standard Model.
Two major revolutions in physics have already occurred in this century: relativity and quantum mechanics. These were associated with two of the three really basic parameters of physics: the velocity of light and Planck's quantum of action. Both revolutions involved major conceptual changes in the framework of physical thought. In each case, the new theory was totally different from the old in its basic tools and concepts, but it reduced approximately to the old one when the appropriate parameter could be considered small.
The last parameter of this sort is Newton's gravitational constant. A third revolution appears to be likely, and string theory—which reduces to more familiar theories at large distances—may be the key. Perhaps this third revolution will lead to a final theory or perhaps only to a next theory that will lead to new questions.
The present state of theoretical physics is reminiscent of the days of confusion that preceded the birth of quantum theory in the mid-1920s, when it was clear that a new theory was coming but not at all clear what this theory was. In the present case, a whole host of theoretical insights clearly point toward a basic
change in all of the concepts of space and time. One should not underestimate the likely scope of this change.
String theory is now in the midst of intense theoretical development. Although it appears to have the potential of reproducing the Standard Model and explaining its structure and parameters, the understanding is too primitive to be able to make complete predictions about details of the Standard Model; however, the main qualitative properties of the Standard Model have been derived from string theory in a strikingly elegant way. Moreover, string theory requires the existence of both quantum mechanics and gravity, whereas previous theories in physics make it impossible to have both together; other general predictions of string theory are gauge invariance, which has been seen to be the bread and butter of the Standard Model, and supersymmetry, which is one of the main targets in the worldwide enterprise of particle physics. Many deep problems remain to be solved before the theory can be compared directly with experiment. Nonetheless string theory is testable by experiment. It would be easy for new experimental discoveries that did not fit into a straightforward extrapolation of the Standard Model to provide evidence that string theory is the wrong theory to follow. Conversely, the discovery of supersymmetry would be an important validation for string theory. In addition, this discovery would provide invaluable clues as to the mechanism of supersymmetry breaking that could help in unraveling the predictions of string theory.
Thus, we have the beginnings of a new theory of fundamental physics—string theory—whose full elucidation could be as revolutionary as the discovery of quantum mechanics or relativity.



















