3
Flood Frequency Estimates for the American River
Introduction
Effective planning and design of flood risk management projects require accurate estimates of flood risk. Such estimates allow a quantitative balancing of flood control efforts and the resultant benefits, and also enhance the credibility of floodplain development restrictions. They allow determination of the design flows from specified exceedance probabilities, as well as the expected benefits associated with alternative flood risk management proposals. These considerations are critical for the American River, where billions of dollars of property are at risk from flooding.
Fitting a continuous mathematical distribution to data sets yields a compact and smoothed representation of the flood frequency distribution revealed by the available data, and a systematic procedure for extrapolation to flood discharges larger than those historically observed. While the American River flood record at Fair Oaks is almost 100 years in length, there is a goal of providing flood projection for at least the flood that has a chance of 1 in 200 of being exceeded in any year. This requires extrapolation beyond the data, as well as smoothing of the empirical frequency curve to obtain a more consistent and reliable estimate of the 100-year flood.
A variety of distribution functions and estimation methods are available for estimating a flood frequency distribution. The guidelines for frequency analysis presented in Bulletin 17-B (IACWD, 1982) were established to provide consistency in the federal flood risk management process. In estimating a flood frequency distribution for the American River, the committee believed it was desirable to follow the spirit of these guidelines, although not necessarily the exact letter. The committee based its estimation on the log-Pearson type III distribution, as specified in Bulletin 17-B. With only a traditional systematic gaged record, we employed the conventional log-space method of moments recommended by Bulletin 17-B. When additional historical flood information is included or some peaks are censored, the Expected Moments Algorithm is used as the generalization of the conventional log space method of moments method. The Expected Moments Algorithm, developed well after the publication of Bulletin 17-B, makes more effective use of historical and paleoflood information than does the weighted moments method recommended by Bulletin 17-B for use with historical information.
This chapter is organized as follows. An overview of the basic approach of Bulletin 17-B is followed by a discussion of recent innovations in flood frequency analysis that post-date Bulletin 17-B but are nevertheless consistent with its
approach. Estimates of flood frequency distributions for the American River using various combinations of systematic, historical, and paleodata are presented along with a recommended distribution. Finally, evidence suggesting that the recommended distribution should not be extrapolated beyond a return period of 200 years is presented.
Bulletin 17-B
Recommended procedures for flood frequency analyses by federal agencies are described in Bulletin 17-B (IACWD, 1982). Thomas (1985) describes the history of the development of these procedures. The recommended technique is based on fitting a Pearson type III distribution to the base-10 logarithms of the peak discharges. The flood flow Q associated with cumulative probability p is then
where ![]() and S are the sample mean and standard deviation of the base-10 logarithms Xi, and Kp is a frequency factor that depends on the skew coefficient and selected exceedance probability. The mean, standard deviation, and skew coefficient of station data are computed using
and S are the sample mean and standard deviation of the base-10 logarithms Xi, and Kp is a frequency factor that depends on the skew coefficient and selected exceedance probability. The mean, standard deviation, and skew coefficient of station data are computed using
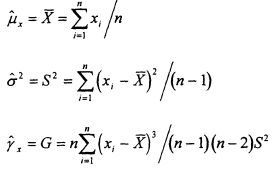
Estimation of the Skew Parameter
Because of the variability of at-site sample skew coefficients, Bulletin 17-B recommends using a weighted average of the station skew coefficient and a generalized skew coefficient, a regional estimate of the log space skewness. In the absence of detailed studies, the generalized skew coefficient Gg for sites in the United States can be read from Plate I in the Bulletin. Assuming that the generalized skew coefficient is unbiased and independent of station skew coefficient, the mean square error (MSE) of the weighted estimate is minimized by weighting the station and generalized skew coefficients inversely proportional to their individual mean square errors:
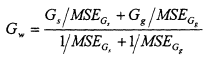
Here Gw is the weighted skew coefficient, Gs is the station skew coefficient, and Gg is the generalized regional estimate of the skew coefficient; MSE[•] is the mean square error of the indicated variable. McCuen (1979) and Stedinger and Tasker (1986a,b) discuss the development of skew coefficient maps and regression estimators of Gg and MSE[Gg].
Outliers
Unusual high or low annual floods are normally called outliers. Bulletin 17-B defines outliers as "data points that depart significantly from the trend of the remaining data." High outliers are retained unless historical information is identified showing that such floods are the largest in a period longer than the systematic record. Low outliers pose a problem. Due to the log transformation, one or more unusual low flow values can distort the entire fitted frequency curve. To avoid this problem Bulletin 17-B recommends a test of whether a low outlier is statistically significant (IACWD, 1981; Stedinger et al., 1993). Flood peaks identified as low outliers are omitted from the computation of ![]() , S, and G, and a conditional probability adjustment is applied to account for the omission. In practice the low outlier test rarely leads to the identification of any more than a few outlying observations.
, S, and G, and a conditional probability adjustment is applied to account for the omission. In practice the low outlier test rarely leads to the identification of any more than a few outlying observations.
Historical and Paleoflood Information
Bulletin 17-B recommends a historical flood moment adjustment to account for knowledge that a given number of events exceeded some discharge threshold (Qh) in a period of known duration prior to the systematic flood record. This adjustment, in effect, "fills in the ungaged portion of the historic period with an appropriate number of replicates of the below-Qh portion of the systematic record" (Kirby, 1981, p. c-47). Although the Bulletin 17-B historical adjustment was intended primarily for use with historical data, it can also be applied to paleoflood data.
Alternative Treatments of Outliers and Historical and Paleoflood Information
Both outliers and historical and paleoflood data can be handled in the framework of censored data. The influence of low outliers can be eliminated by censoring below a low threshold. Historical and paleoflood data can be treated as observations above a high threshold. Research subsequent to the publication of Bulletin 17-B has identified efficient statistical methods for treating censored data.
Censoring
Censoring below a threshold can be an effective way to account for the fact that commonly assumed parametric distributions (such as the log-Pearson type III distribution) may be inadequate to fit the "true" distribution at a given site. At the very low end, the fact that use of annual flood data (i.e., the largest peak flow in a year) can result in inclusion in the data set peak flows that are clearly not associated with floods. Floods associated with distinctly different hydrometeorological processes, such as hurricanes, convective storms, and rain-on-snow, can lead to complex distributional shapes. In some cases, it is clear that certain mechanisms do not produce large floods, and peak discharges associated with these mechanisms can be separated in the analysis. (In the case of the American River, peak discharges at late spring or early summer snowmelt events are excluded from the analysis.) It is also possible to use mixture models in the analysis or highly parameterized distributions (such as the Wake by) that have complex shapes. These techniques suffer from estimation problems caused by the large number of parameters. It may be preferable to resort instead to methods for censoring the data set below some threshold. Although censoring reduces the quantity of sample data, Monte Carlo results indicate that censoring can actually improve estimation efficiency (Wang, 1997). The practice of low censoring effectively allows the analyst to place the estimation focus where it belongs, on the upper tail of the distribution (NRC, 1988).
There are several approaches that can be used in estimation with data censored below a given threshold. Non-parametric approaches avoid the assumption of a specific distribution function. Parametric approaches are based on an assumed distribution either for the entire population or for exceedances of a specified threshold.
Non-parametric estimation methods, which typically use kernel-based estimators of the density or quantile function, can be applied to estimation of the upper tail of a distribution (Moon and Lall, 1994). Particularly appropriate is the use of kernel functions with bounded support, as only the data values falling within a finite range of an estimated quantile have a bearing on the resulting estimate. Breiman and Stone (1985) give a non-parametric method for tail modeling, which essentially involves fitting a quadratic model to the upper part of the data. Non-parametric methods in general, and especially kernel-based methods, are often criticized when they are used for extrapolation beyond the range of the data; but extrapolation beyond the data poses problems for all methods of estimation. The committee did not explore the application of non-parametric methods to the American River data because such an approach would diverge significantly from the Bulletin 17-B guidelines.
There are several estimation methods that can be applied to fit a chosen distribution, such as the log-Pearson type III, to values exceeding a given threshold. The method of maximum likelihood is efficient for many distributions (Leese, 1973; Stedinger and Cohn, 1986), but it often has convergence problems for the log-Pearson type III. Alternative methods include distributional truncation (see Durrans, 1996); partial probability weighted moments (Wang, 1990,1996; Kroll and Stedinger, 1996); probability plot regression (Kroll and Stedinger, 1996); LH moments (Wang, 1997); and the Expected Moments Algorithm (Cohn et al., 1997). The last method
was developed explicitly for use with the log-Pearson type III distribution.
An approach sometimes applied to estimation with data censored at relatively high levels is to choose a distribution appropriate for the upper tail of the data. In some cases, there is theoretical support for the choice of distribution. For example, if a random variable has a generalized extreme value distribution, then the distribution of exceedances of a sufficiently high threshold is of the generalized Pareto type (Pickands, 1975; Smith, 1985). Smith (1987, 1989), Hosking and Wallis (1987), and Rosjberg et al. (1992) have applied this result to flood frequency analysis.
A fundamental question in censoring, for which there is little guidance, is the choice of the censoring threshold. Several investigators have considered this issue (Pickands, 1975; Hill, 1975; Hall, 1982; Hall and Welsh, 1985), with the general conclusion that the threshold level should depend on unknown population properties of the tail. Thus, these theoretical results are of limited usefulness for small samples. The use of LH moments (Wang, 1997) renders unnecessary the choice of a censoring threshold, but introduces in its place the need to choose the order of the LH moments used. Kernel-based non-parametric estimators also eliminate the need to explicitly choose a censoring threshold, but one is implicitly established based on the bandwidth estimate. Further, one can argue that the bandwidth estimate should depend on the quantile being estimated (Tomic et al., 1996), and this gives rise to a non-unique censoring threshold when multiple quantiles are of interest. The net effect of all this is that it is difficult to give any definitive guidance on the selection of a censoring threshold. An investigator must use professional judgment to a significant degree, though it is possible to obtain some guidance and insight through investigations of physical causes of flooding at a site, studies to assess the sensitivities of quantile estimates to the choice of censoring threshold, and comparisons with nearby hydrologically similar sites.
Historical and Paleoflood Data
As discussed in Chapter 2, historical and paleoflood information represents a censored sample because only the largest floods are recorded. The use and value of such information in flood frequency analyses has been explored in several studies (Leese, 1973; Condie and Lee, 1982; Hosking and Wallis, 1986; Hirsch and Stedinger, 1987; Salas et al., 1994; Cohn et al., 1997). Research has confirmed the value of historical and paleoflood information when properly employed (Jin and Stedinger 1989). In particular, Stedinger and Cohn (1986) and Cohn and Stedinger (1987) have considered a wide range of cases using the effective record length and average gain to describe the value of historical information. In general, the weighted moments estimator included in Bulletin 17-B is not particularly effective at utilizing historical information (Stedinger and Cohn, 1986; Lane, 1987).
Maximum Likelihood Estimation (MLE) procedures can be used to integrate systematic, historical, and paleoflood information (Stedinger et al., 1993). Ostenaa et al. (1996) use a Bayesian approach to extend standard MLE procedures. This extension better represents the uncertainty in the various sources of information. The previously mentioned Expected Moments Algorithm of Cohn et al. (1997) can also
be used with historical and paleoflood information. The Expected Moments Algorithm is as efficient as standard maximum likelihood approaches and works well with the log-Pearson type III distribution.
Expected Probability
Flood frequency analysis often focuses on estimation of the flood quantile x1-q, the quantile that will be exceeded with probability q = 1/T. However, different statistical estimators of x1-q have different properties (Stedinger, 1997; Beard, 1997). Most estimators provide an almost unbiased estimator of x1-q:
However, interest may be in a value that in the future will be exceeded with probability q, so that
when both X and X1-q are viewed as random variables. If a very long record is available, these two criteria would lead to almost the same design value. With short records, they lead to different estimates because of the effect of the uncertainty in the estimated parameters.
Beard (1978) developed the expected probability correction to ensure that the second criterion is met. However, this correction generally increases the bias in estimated damages calculated for dwellings and economic activities located at fixed locations in a basin (Stedinger, 1997). This paradox arises because the estimated T-year flood is a (random) level computed by the hydrologist based on the fitted frequency distribution, whereas the expected damages are calculated for human and economic activities at fixed flood levels. Recently NRC (1995) concluded that, for the economic evaluation of projects, an expected probability adjustment should not be made because of the upward bias it introduces. Beard (1997, 1998) disagreed with that conclusion. Although a correction for expected probability may be appropriate in some decision-making frameworks, the committee decided not to apply such a correction to its recommended American River frequency distribution.
Summary Of Committee Approach
In estimating the probability distribution of three-day rain flood discharges for the American River at Folsom, the committee decided to adopt an overall approach that was consistent with the philosophy of Bulletin 17-B guidelines. This includes the assumption of the log-Pearson type III distribution and estimation based on preserving log-space moments. Estimation was based on traditional method of moments and the Expected Moments Algorithm. The latter method was chosen over maximum likelihood and other methods because it (1) can be applied readily to the
log-Pearson type III distribution; (2) has been shown to be relatively efficient; and (3) is consistent in principle with Bulletin 17-B. It was also decided to use EMA to explore various low censoring limits.
Analysis Of American River Data
The committee used the following data to explore estimation of the probability distribution of three-day rain floods on the American River at Folsom Dam (although not all of the data were used to estimate its recommended distribution):
- annual maximum average three-day rain flood discharges for the period 1905-1997, as reconstructed by the USACE;
- the estimated peak of the 1862 flood (265,000 cfs), assumed to be the largest instantaneous peak flood discharge since 1848;
- paleoflood information from the U.S. Bureau of Reclamation (i.e., non-exceedance of 300,000-400,000 cfs during the last 1,500-3,500 years).
- the skew map from Bulletin 17-B;
- estimated log skews for maximum annual three-day rain flood discharges from the Feather River at Oreville, Yuba River at Maryville, Mokelumne River, Stanislaus River, Tuolumne River, and Merced River; and
- two PMF estimates for the American River at Folsom Dam (three-day average flows of 401,000 cfs and 485,000 cfs).
Estimation of Average Three-Day Flows from Instantaneous Peak Flows
Use of the historical and paleoflood data required that a relationship be developed between instantaneous peak discharge and maximum three-day average discharge. This relationship was derived from a log-log linear regression with the observed three-day maximum as the dependent and the instantaneous peaks as the independent variables.
The instantaneous peak flows corresponding to Fair Oaks (below Folsom) were obtained from the USACE, Sacramento District. For the period water years (WY) 1905-1955 these are, with certain exceptions, identical to USGS annual peaks at Fair Oaks. The exceptions occur in years for which the USGS peak of record is either unknown (WY 1918), a snowmelt, as distinct from a rainfall event (1910, 1912, 1913, 1929 and 1933); or when the maximum three-day discharge is associated with an event other than that which produced the instantaneous maximum (1908, 1914, 1915, 1916, 1937, 1941, 1946). In the period since 1956, estimates of unregulated instantaneous maxima are generally not available, although the USACE and others have estimated peak flows for 1956-86, and for 1997. It must be assumed that the magnitudes of reconstructed peak flows are known with less precision than are gaged flows.
A log-log ordinary least squares (OLS) regression was first estimated using the 38 measured, rainfall-generated instantaneous peaks (Qp) and corresponding
mean three-day discharges (Q3) from the 1905-1955 (unregulated) period. This equation, expressed in real (cfs) terms, is:
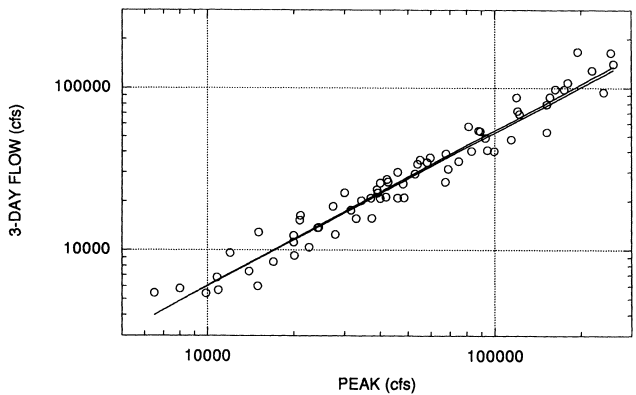
Although the log-space fit appears satisfactory, the use of this equation to predict volumes for events significantly larger than those used in estimating the equation would involve considerable extrapolation, with attending increases in confidence bounds, since the largest peak observed in this period was 180,000 cfs (WY 1951). Several larger events occurred in the latter period (1956-1997), and a second equation was estimated that included these (reconstructed) data. This equation, based on 68 observations (low flows in 1964 and 1977 were excluded) is:
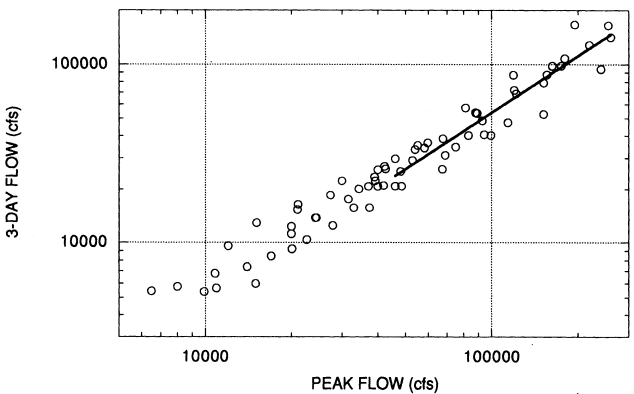
The second model differs very little from the model based on measured data only, suggesting that USACE procedures are not seriously biased (Figure 3.1). Since it appeared reasonable to assume an adequate degree of homogeneity between earlier and later records, a third equation was fitted to the upper 50% of the data in order to minimize the influence of low observations, and to further reduce the error bounds on predicted volumes. This final equation, based on 35 observations (half measured, half reconstructed) was estimated as: (Figure 3.2)
This equation was used to predict both the magnitude and the 95% confidence bounds of the three-day flow associated with the 1862 floods and the paleoflood threshold, as summarized in Table 3.1.
Generalized Skew Coefficient
A critical parameter in the development of a frequency curve in the Bulletin 17-B framework is the generalized skew coefficient. While on average the logarithms of annual peaks at U.S. gages have a skew near zero, floods in particular regions are thought to have skewness coefficients that can be greater or less than that value. Unfortunately, sample estimates of the coefficient of skewness are very unstable, even with long records. For example, even with a 90-year record, such as that available for the American River, the standard error of estimate of the sample skewness coefficient is 0.25.
To help get around this large error and to stabilize estimates of flood exceedance probabilities and quantiles, Bulletin 17-B provides a skew map that can be used to compute a generalized skew. That map is based on 2,972 stations across the United States that had at least 25 years of record as of WY 1973. Efforts were employed to reject low outliers, but no effort was made to use historical information.
The American River basin is in an area where map skew values change rapidly with location; hence the map skews are likely to be less reliable. For the location of the American River gage at Fair Oaks, the map value is about 0.0.
Given the age of the Bulletin 17-B skew map and a concern with three-day volumes rather than annual peaks, the committee chose to estimate an alternative regional ("map") skew. This regional skew estimate is based on log skews computed from maximum annual three-day rain flood data from seven large west slope Sierra rivers (USACE, 1998). For each of these discharge series there are about 25 more years of data than were used to construct the Bulletin 17-B skew map. The estimated log skews are given in Table 3.2. (Note that the skew for the Merced was adjusted to account for a low outlier. Bulletin 17-B procedures were used to detect and correct for the low outlier.) Averaging these values yields a regional skewness coefficient -0.1 for three-day flows.
Estimating the standard error of our alternative regional skew estimate is complicated by the highly cross-correlated the flood data from the seven rivers. (The average pairwise correlation between the flood series is 0.89.) A Monte Carlo experiment was conducted to determine the sampling error of the average skewness coefficient for seven stations with n = 100 years of record when the correlation among concurrent flows was 0.89. While a single station had a standard error of 0.25 (variance 0.063), the standard error of the sample average of seven stations decreased by only 5%, to 0.21. (This result is consistent with a formula provided in Stedinger [1983].) We are in the unfortunate position of being unable to resolve with any precision the value of the sample skewness coefficient for the American River. More stations could be included in the analysis, but there are no other large basins in the northern and central Sierra Nevada that are like the American River.
The two estimates of regional skew, 0.0 and -0.1, bracket the at-site skew of -0.06. The latter regional skew was derived specifically for three-day maxima and for large basins in the Sierra Nevada, like the American River, it would appear to be the more relevant of the two. Moreover, the former, based on the Bulletin 17-B skew map, is also limited in its precision by the high correlation among floods in the same year, and is based on shorter records for annual maxima.
TABLE 3.1 Estimated Three-Day Discharge Magnitudes and 95% Confidence Limits
|
|
1862 Event |
Paleo Lower |
Paleo Upper |
|
Est. peak (cfs) |
265,000 |
300,000 |
400,000 |
|
Est. three-Day Q (cfs mean) |
147,000 |
167,000 |
224,000 |
|
Ratio Q3/Qp |
0.55 |
0.56 |
0.56 |
|
Lower 95% conf. bound |
95,000 |
108,000 |
143,000 |
|
Ratio to Qp |
0.36 |
0.36 |
0.36 |
|
Upper 95% conf. bound |
226,000 |
258,000 |
352,000 |
|
Ratio to Qp |
0.85 |
0.86 |
0.88 |
TABLE 3.2 Sample Log(10) Skews for West Slope Central Sierra Basins
|
Basin |
Area |
Period |
1-Day Q |
3-Day Q |
7-Day Q |
|
Feather |
3,624 |
1902-1997 |
-0.258 |
-0.230 |
-0.252 |
|
Yuba |
1,339 |
1904-1997 |
-0.389 |
-0.332 |
-0.412 |
|
American |
1,888 |
1905-1997 |
-0.187 |
-0.062 |
-0.159 |
|
Mokelumne |
627 |
1905-1997 |
0.067 |
0.067 |
0.008 |
|
Stanislaus |
904 |
1916-1997 |
-0.056 |
0.000 |
0.016 |
|
Toulumne |
1,533 |
1897-1997 |
-0.190 |
-0.132 |
-0.180 |
|
Merceda |
1,037 |
1902-1997 |
-0.086 |
0.014 |
0.015 |
|
Mean |
|
|
-0.157 |
-0.096 |
-0.138 |
|
Std. Dev. |
|
|
0.148 |
0.144 |
0.163 |
|
Calculations by HEC-FFA v3.0 (1992)a low outlier (1977) removed according to Bulletin 17-B procedures. SOURCE: USACE, Sacramento District. |
|||||
If either 0.0 or -0.1 is combined in a weighted average with the sample skew of -0.06 using the Bulletin 17-B weights, and the result is rounded to the nearest tenth, the result is -0.1. Unfortunately, the Bulletin 17-B weights are not optimal in this case because an unbiased estimate of the precision of the regional skewness estimators has not been employed (Tasker and Stedinger, 1986). That consideration would result in more weight on the regional estimate of -0.1. In addition, the error in the regional estimates is almost surely highly correlated with the error in the at-site estimator, and this would further change the optimal weights. The committee recommends that the regional skew value of -0.1 be adopted as the weighted skew coefficient for the logarithms of the three-day rain flood discharges for the American River.
The choice of the skew coefficient can be considered a critical decision and Bulletin 17-B encourages hydrologists to perform site-specific studies to improve estimates of the skewness coefficient. The Bulletin 17-B skew map was developed almost 25 years ago and has a very steep gradient in the region of the Fair Oaks gage making its precision questionable in this area. USACE (1998) incorrectly read the Bulletin 17-B skew map as +0.1 by using the centroid of the basin rather than the location of the gage, which yields 0.0 for a weighted skewness coefficient. When a map skew of 0.0 is combined with the station skew of -0.067 and rounded a value of -0.10 is obtained. Table 3.2 provides estimates of skewness coefficients for the American River and six other rivers for three durations: 1-day, 3-day, and 7-day using the available records up through 1997. The skews of the American River for those three durations equal -0.187, -0.06, and -0.159, which average to -0.136. If one looks regionally over the seven sites in the table, then the computed skewness
coefficients for 1-day, 3-day, and 7-day are -0.157, -0.096, and -0.138, which average to -0.130. After rounding to two-decimal digits, skew values for all three durations support choice of -0.10 as the skewness coefficient for three-day volumes on the American River.
Alternative Frequency Estimates for the American River Data
The committee chose five cases (with subcases) to explore alternate estimates of the probability distribution of three-day average rain flood discharges on the American River at Fair Oaks. The first case duplicates the USACE analysis (USACE, 1998). The remaining four cases vary with respect to the skew estimate and the use of historical and paleoflood data. All cases are consistent with the spirit of Bulletin 17-B.
Case 1: Systematic Record with Zero Skew (Sys. w/Zero Skew)
This is a duplication of the USACE approach (without the expected probability correction), using the conventional method of moments, as specified in Bulletin 17-B.
Case 2: Systematic Record with Weighted Skew (Sys. w/Skew -0.1)
This case is based on the committee's estimate of weighted skew equal to -0.1, using the conventional method of moments, as specified in Bulletin 17-B.
Case 3: Systematic Record and Historical Data with Weighted Skew (Sys. & Hist. w/ Skew -0.1)
Historical information is added in this case, through the use of the expected moments algorithm (EMA). Three subcases are run.
Case 3a: Three-day discharge for 1862 flood between the 95% confidence limits of 95,000 cfs and 226,000 cfs; all other floods in period 1848-1904 between 0 and 95,000 cfs.
Case 3b: Three-day discharge for 1862 flood between 95,000 cfs and 226,000 cfs; all other floods in period 1848-1904 between 0 and 226,000 cfs.
Case 3c: Three-day discharge for 1862 flood equal to 147,000 cfs; all other floods in period 1848-1904 between 0 and 147,000 cfs.
Note that Cases 3a and 3b are intended to bracket the results of using the historical data with a fixed skew, while 3c gives a best estimate.
Case 4: Systematic Record and Historical Data with Skew Estimated by EMA (Sys. & Hist. w/EMA Skew)
The EMA is applied to the systematic record and the historical information without specifying the skew; hence the skew is estimated by the EMA. This case has three subcases.
Case 4a: Three-day discharge for 1862 flood between 95,000 cfs and 226,000 cfs; all other events in period 1848-1904 between 0 and 95,000 cfs.
Case 4b: Three-day discharge for 1862 flood between 95,000 cfs and 226,000 cfs; all other floods in period 1848-1904 between 0 and 226,000 cfs.
Case 4c: Three-day discharge for 1862 flood equal to 147,000 cfs; all other floods in period 1848-1904 between 0 and 147,000 cfs.
Note that Cases 4a and 4b are intended to bracket the results of using the historical data with a skew estimated by EMA, while Case 4c gives a best estimate.
Case 5: Systematic Record and Historical and Paleoflood Information with Skew Estimated by EMA (Sys. & Hist. & Paleo. w/EMA Skew)
The EMA is applied to the systematic record and the historical and paleoflood information without specifying the skew. This case has three subcases.
Case 5a: Three-day discharge for 1862 flood between 95,000 cfs and 226,000 cfs; all other floods in period 1848-1904 between 0 and 95,000 cfs. All floods in the 3,350 year period from approximately 1,500 B.C. through 1847 A.D. are less than 108,000 cfs (the lower 95% confidence limit of the lower paleoflood non-exceedance threshold).
Case 5b: Three-day discharge for 1862 flood between 95,000 cfs and 226,000 cfs; all other floods in period 1848-1904 between 0 and 226,000 cfs. All floods in last 1,350 year period (prior to 1848) less than 352,000 cfs (the upper 95% confidence limit of the upper paleoflood non-exceedance threshold).
Case 5c: Three-day discharge for 1862 flood equal to 147,000 cfs; all other floods in period 1848-1904 between 0 and 147,000 cfs. All floods in last 2,350 year period (prior to 1848) less than 197,000 cfs (the median estimate of the three-day flow associated with the average of the upper and lower paleoflood non-exceedance limits).
Note that Cases 5a and 5b are intended to bracket the results of using the historical and paleoflood data with a skew estimated by EMA, while Case 5c gives a best estimate.
Results
Table 3.3 displays the results of the flood frequency analysis; Cases 1, 3c, and 5c are plotted in Figure 3.3. Estimates of Q100, the discharge with annual exceedance probability of 1 in 100, range from about 87,000 cfs for the case with the lowest paleoflood exceedance threshold (Case 5a), to 205,000 cfs for the case duplicating the 1998 USACE estimate (Case 1). Excluding case 1, which the committee believes is based on too high a log-skew, and the cases using paleoflood data, the range of estimates of Q100 is much smaller, from 169,000 cfs to 191,000 cfs. Note that our best estimated distribution using the paleoflood information (Case 5c) falls well below the data (Figure 3.3). The recommended distribution of three-day flows for the American River at Fair Oaks is derived from Case 3c, which is based on the use of a weighted log skew of -0.1 and the median estimator of the three-day flow associated with the 1862 flood. The estimate of Q100 for this case is 185,000 cfs. There is little difference between case 3c and 4c, where for case 4c the skew was estimated with the systematic and historical data.
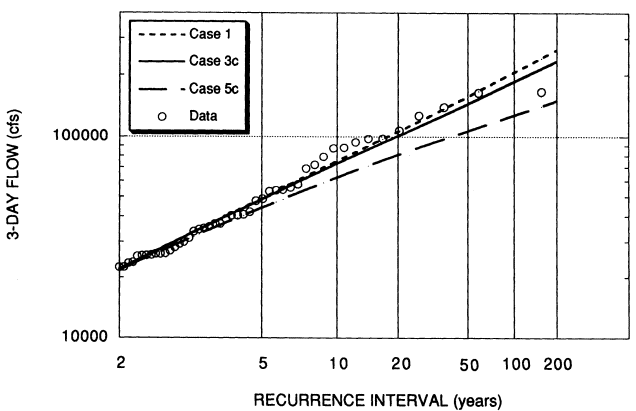
Figure 3.3
Estimated flood frequency distributions for annual maximum unregulated three-day rain flood flows, American River at Fair Oaks, Cases 1, 3c, and 5c. Case 1 is the 1998 USACE distribution, Case 3c is the distribution recommended by the committee, and Case 5c incorporates the USBR paleoflood data. Only the upper half of the distributions is shown. Plotting position is from Cunnane (1978).
TABLE 3.3 Final Results of Flood Frequency Analysis for Case Studies
|
|
Sys. w/ Zero Skew |
Sys. w/ Skew -0.1 |
Sys. & Hist. w/ Skew -0.1 |
Sys. & Hist. w/ EMA Skew |
Sys. & Hist. & Paleo w/ EMA Skew |
||||||
|
Case |
1 |
2 |
3a |
3b |
3c |
4a |
4b |
4c |
5a |
5b |
5c |
|
Case description |
|||||||||||
|
Nsa |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
|
Nhb |
0 |
0 |
56 |
56 |
56 |
56 |
56 |
56 |
56 |
56 |
56 |
|
UB on Hc |
0 |
0 |
95,000 |
226,000 |
147,000 |
95,000 |
226,000 |
147,000 |
95,000 |
226,000 |
147,000 |
|
Q1862 LBd |
0 |
0 |
95.000 |
95,000 |
147,000 |
95,000 |
95,000 |
147,000 |
95,000 |
95,000 |
147,000 |
|
Q1862 UBe |
0 |
0 |
226,000 |
226,000 |
147,000 |
226,000 |
226,000 |
147,000 |
226,000 |
226,000 |
147,000 |
|
Npf |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3,350 |
1,350 |
2,350 |
|
UB on Pg |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
108,000 |
352,000 |
197,000 |
|
Estimated parameter values |
|||||||||||
|
Ln-mean |
9.9830 |
|
9.9438 |
9.9923 |
9.9769 |
9.9447 |
9.9923 |
9.9774 |
9.7883 |
9.9775 |
9.9243 |
|
Ln-StDev |
0.9656 |
0.9656 |
0.9349 |
0.9667 |
0.9552 |
0.9359 |
0.9666 |
0.9558 |
0.8105 |
0.9451 |
0.8967 |
|
Skew |
0.0000 |
-0.1000 |
-0.1000 |
-0.1000 |
-0.1000 |
-0.1254 |
-0.0974 |
-0.1141 |
-0.4895 |
-0.221 |
-0.379 |
|
Log10-mean |
4.3355 |
4.3355 |
4.3186 |
4.3396 |
4.3329 |
4.3189 |
4.3396 |
4.3331 |
4.2510 |
4.3332 |
4.3101 |
|
Log10-StDev |
0.4193 |
0.4193 |
0.4060 |
0.4198 |
0.4149 |
0.4065 |
0.4198 |
0.4151 |
0.3520 |
0.4104 |
0.3894 |
A guideline for the analysis was that the exceedance probability for the PMF values should be less than 0.001. This expectation is met for Cases 2, 3a,b,c and 4a,b,c for both PMF values, though not by much. In particular, among those 7 alternatives, the exceedance probability of the lower PMF of 401,000 cfs was always between 1-in-1,300 and 1-in-2,700. For Case 1 with a skewness coefficient of 0, the exceedance probability of the lower PMF was only 1-in-800, which seems too low; for the higher PMF value of 485,000 cfs, the probability decreased to 1-in-1600, and for Cases 2, 3c and 4c was about 1-in-3,000.
As is the case here, flood frequency analysis is generally faced with significant data limitations and as a result estimated flood quantiles are of limited accuracy. To estimate the 100-year or 200-year flood with the 93 years of systematic data available for the American River is to stretch the limits of the data set. Use of the historical information back to the middle of the 19th century helps, but the precision of the 100- and 200-year events is still far less than desirable.
Two sources of errors should be considered. The first is errors that result from use of a probability distribution that fails to describe the character of the true distribution of floods. Here the log-Pearson type III distribution has been employed as recommended in Bulletin 17-B. As suggested later in this report, it seems that the log-Pearson type III distribution has trouble describing the distribution from which the flood record is drawn without overestimating the magnitude of quantiles with return periods greater than 200 years. The committee does not try to quantify this model error. A second source of error is the sampling error that results from using limited-size data sets to estimate the parameters of the log-Pearson type III distribution. The magnitudes of the floods observed in any year vary widely, and if a different set of floods had occurred during the period of record, different parameters would have been computed. This parameter estimation error or sampling error can be quantified in several ways.
A simple measure of the precision of a quantile estimator ![]() of a quantile Qp is the estimator's variance Var[
of a quantile Qp is the estimator's variance Var[![]() ], or its standard error, SE, where
], or its standard error, SE, where
The variance and the standard error are descriptions of the average distance between the estimator and the quantile Qp from one possible sample to another.
Confidence intervals are another description of precision. For the committee's analysis of the American River, 90% confidence intervals were constructed for different quantile estimators. In log space, the endpoints of each confidence log interval equal the quantile estimator plus or minus 1.645 times the estimated standard error of the estimator. The real-space endpoints equal the exponential log space endpoints. In repeated sampling, intervals constructed in this way should contain the true quantiles approximately 90 percent of the time. This asymptotic normal formula for quantile estimators is widely used (Kite, 1988; Stedinger et al., 1993, section 18.4.1). Monte Carlo simulations were conducted to estimate the standard errors of the calculated formulas for Cases 2-4, and the results were checked against those calculated with maximum likelihood estimators.
The Monte Carlo results, as well as formulas provided in Stedinger (1983) and Chowdhury and Stedinger (1991), provide the standard errors of estimators as a function of the parameter values, which parameters are estimated and the length of the data set. The confidence intervals reported below for Cases 1 and 2 assume that the skewness coefficient is known, and only the location and scale parameters of the log-Pearson type III distribution were estimated. Such a computation is recommended by Bulletin 17-B. Unfortunately, these confidence intervals are too narrow, because they ignore the error in the estimated coefficient of skewness (Chowdhury and Stedinger, 1991). Case 3 also assumes that the coefficient of skewness is known. In estimating confidence intervals for Case 3c, our recommended case, the committee chose to use the confidence intervals obtained for Case 4c, which employed the at-site skewness estimator.
The confidence intervals for Cases 1, 2 and 4c are in Table 3.4. The confidence intervals for Case 4c provide a good description of the uncertainty for Cases 3 and 4 because both are based on an estimated skewness coefficient and use of historical information. This is particularly important for the more extreme quantiles. Confidence intervals for Cases 1 and 2 should be wider than those computed for Case 4, because the frequency analyses in Cases 1 and 2 did not use historical information.
For the most part, the committee's recommendations do not deviate significantly from the USACE results. There is really relatively little difference between the estimated quantiles for Case 1 as proposed by the USACE and Case 3c recommended by the committee. The difference is that Case 3c uses a refined and slightly different site-specific regional skewness coefficient with the available historical flood information for the American River. When the differences between the quantiles are viewed with the perspective provided by the 90 percent confidence intervals, they are quite close at the 200-year and even the 500-year return period event. Beyond, the frequency curves begin to diverge.
The important message provided by confidence intervals for Case 4c is that the uncertainty in the estimated quantiles is very large (see Figure 3.3). The confidence intervals for Cases 1 and 2, computed assuming the skewness coefficients are known (and ignoring historical information), are not much better. Based on the likely variability in quantile estimators from sample to sample—even with historical information back until the middle of the 19th century, a 90 percent confidence interval for the true 100-year flood for Case 4c is from 131,000 cfs to 257,000 cfs. This is also a good description of the uncertainty in the 100-year flood estimate for the recommended Case 3c. Given the available record for the American River and the attempts to develop an improved regional estimate of the skewness coefficient, this is as well as the 100-year flood can be estimated. For the most part, this sampling uncertainty is substantially larger than the differences in quantile estimates obtained by the different assumptions adopted in Cases 1-4. Thus, the major source of error in the determination of flood quantiles for the American River and flood risk for Sacramento appears to be the hydrologic record limited to 150 years of
TABLE 3.4 Confidence Intervals for Cases 1,2, and 4ca
|
Return Period |
Low End Point |
Quantile Estimator |
Upper End Point |
|
90% Confidence Intervals for Case 1b |
|
|
|
|
10 |
60,000 |
75,000 |
93,000 |
|
20 |
82,000 |
106,000 |
136,000 |
|
50 |
118,000 |
157,000 |
210,000 |
|
100 |
149,000 |
205,000 |
281,000 |
|
200 |
185,000 |
260,000 |
367,000 |
|
500 |
240,000 |
349,000 |
507,000 |
|
1,000 |
288,000 |
428,000 |
636,000 |
|
90% Confidence Intervals for Case 2b |
|
|
|
|
10 |
59,000 |
74,000 |
92,000 |
|
20 |
81,000 |
103,000 |
132,000 |
|
50 |
113,000 |
149,000 |
197,000 |
|
100 |
140,000 |
191,000 |
258,000 |
|
200 |
171,000 |
238,000 |
330,000 |
|
500 |
217,000 |
310,000 |
443,000 |
|
1,000 |
256,000 |
373,000 |
543,000 |
|
90% Confidence Intervals for Case 4cc |
|
|
|
|
10 |
60,000 |
72,000 |
88,000 |
|
20 |
81,000 |
100,000 |
126,000 |
|
50 |
109,000 |
145,000 |
192,000 |
|
100 |
131,000 |
184,000 |
257,000 |
|
200 |
154,000 |
228,000 |
338,000 |
|
500 |
184,000 |
295,000 |
475,000 |
|
1,000 |
206,000 |
354,000 |
607,000 |
|
a Intervals for case 4c assumed to apply to Case 3c b Computed assuming specified skewness coefficient is correct. c Describes the uncertainty in Case 3c recommended by the committee. |
|||
experience, coupled with the variability of the magnitudes of floods from year to year.
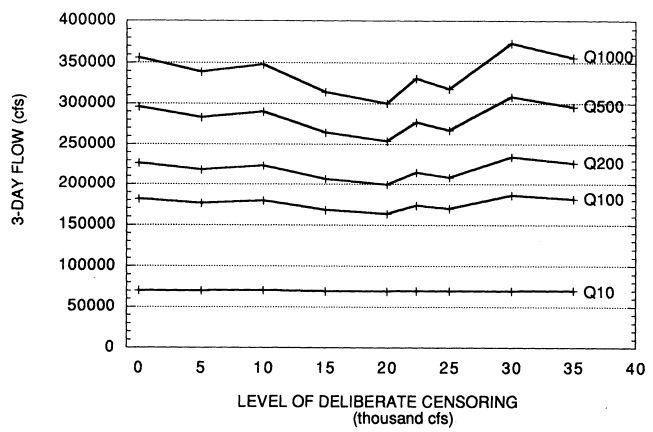
Low Censoring
Application of the Bulletin 17-B low outlier test to the American River average three-day rain flood discharge series does not indicate any low outliers, although the 1977 data point is noticeably lower than the rest of the data. Nonetheless, the committee decided to use the EMA to evaluate the effect of censoring the data. The conditions of Case 3c (our preferred case) were used; the censoring threshold was varied 5,000 cfs to 35,000 cfs, in increments of 5,000 cfs. (The median three-day flow is 22,340 cfs; 35,000 cfs has an estimated exceedance
probability of about 0.3.) Figure 3.4 gives the results. As can be seen, censoring up to 35,000 cfs does not have a significant effect on the estimated distribution.
Beyond Bulletin 17-B
The log-Pearson type III distribution was selected as a national standard because it provided a reasonably good fit to empirical flood distributions from a wide range of U.S. watersheds. There is no reason, however, to believe for any watershed that the log-Pearson type III or any relatively simple distribution will fit the distribution of annual floods over the entire possible range of flows. For this reason, various researchers have suggested the use of mixture models, highly parameterized distributions, non-parametric estimation methods, and estimation methods based on censoring below a high threshold. These methods have not been commonly adopted in practice, in part because their use sometimes results in relatively high estimation variances.
While our preferred estimate of the frequency distribution of three-day flows on the American River is consistent with the systematic and historical data, there is no assurance that it can be extrapolated for very high recurrence intervals. Consider, for example, the two recent PMF estimates. Based on our preferred distribution, the estimated exceedance probabilities for these PMF estimates are about 3 x 10-4 and 6 x 10-4. While these are lower than our proposed absolute minimum standard of 1 x 10-3, they are not much lower. The paleoflood information also calls into question the wisdom of extrapolating our preferred distribution for very large recurrence intervals. Note, however, it was decided not to use the USBR paleoflood information to extrapolate the frequency distribution of three-day rain flood flows because of concerns about the validity of the assumption that floods are independent and identically distributed during the period represented by this information.
To explore the extrapolation issue, the committee conducted some simple analyses using the precipitation data that it assembled for the American River basin. The object of these analyses was to gain insight into the possible shape of the upper tail of the American River flood frequency distribution, not to provide an alternative distribution estimate.
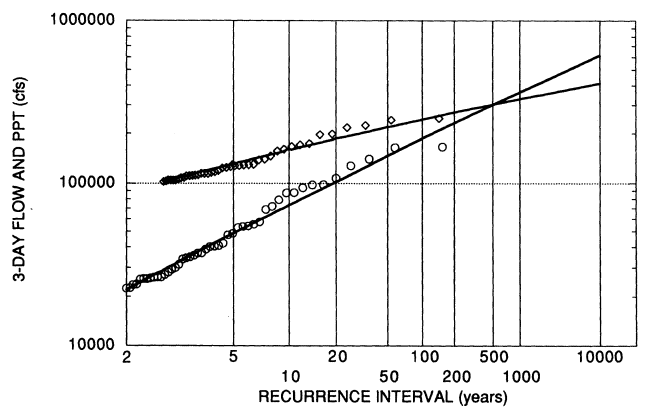
Based on the weights given in Table 2.1, the committee developed a partial duration series of three-day basin average precipitation for the period 1906-1998 using daily data from the Represa, Auburn, Placerville, Nevada City, Lake Spaulding, and Tahoe City gages (refer to Chapter 2 for a discussion of these data). A threshold of 6 inches was used, yielding an average of about one event every two years. To these data we fitted a shifted exponential distribution by the method of moments applied to the threshold exceedance data. Figure 3.5 shows the empirical and fitted distribution of the precipitation data. The probabilities for the precipitation data have been adjusted to account for the data from a partial duration series (Langbein, 1948). Judging from the plot, the fit is adequate. Also shown in Figure 3.5 is the empirical three-day discharge distribution and the committee's preferred estimated flood frequency distribution.
The most notable feature of Figure 3.5 is the crossing of the estimated
precipitation and discharge distributions. This crossing of distribution curves provides compelling evidence that the log-Pearson type III distribution that in the committee's opinion "best" fits the systematic and historical data does not fit the distribution of significantly larger flows. What is most important is the large difference in the slopes (standard deviations) of the two distributions. This difference appears to be too great to be due to errors in our basin average precipitation series. It is also difficult to believe that the "correct" distribution of basin average precipitation would abruptly bend upward for larger than observed precipitation amounts. It seems more likely that the distribution of three-day flood discharge bends downward for larger than observed discharges.
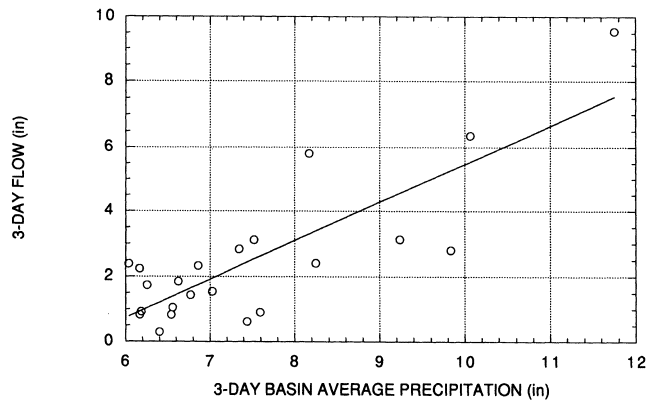
Based on the precipitation data and a simple rainfall-runoff model it is possible to suggest how the discharge distribution might deviate from the log-Pearson type III distribution for large discharges. In developing a simple rainfall runoff model it would be desirable to have for each event in the three-day partial duration precipitation series a corresponding three-day average flow. Such flows are readily available for the period prior to the closure of Folsom Dam in 1955. For flows after 1955, corrections for upstream storage in Folsom and subsequent reservoirs were generally made only for the annual flood. Use of those flows might result in a biased rainfall runoff model since they are not random. This left the committee with data from 22 out of the total of 42 partial duration precipitation events. Using these 22 pairs of precipitation and flow volumes, the committee estimated a linear regression for predicting discharge. The regression equation and associated statistics are given by:
where Q is the three-day flow volume (inches) and P is the three-day basin average precipitation (inches). (For precipitation amounts exceeding 36 inches, runoff depth predicted by this relationship exceeds the precipitation depth. Based on the estimated exponential model, the probability of a three-day precipitation amount exceeding 36 inches is less than 5 x 10-7.)
The coefficient of determination for the regression is 0.65 and the standard error of regression or standard derivation of residuals is 1.3 inches. Figure 3.6 shows the data and the estimated regression. There is very large scatter in the plot of three-day runoff versus three-day precipitation. This is due to the critical role of antecedent conditions (soil moisture and snowpack) in determining runoff-volumes.
Based on the distribution fitted to the partial duration precipitation series, the estimated regression, and an assumed distribution of regression residuals, it is possible to estimate the probability distribution of the upper tail of the three-day flood discharges. The committee assumed that three-day precipitation amounts larger than 6 inches were exponentially distributed (as illustrated in Figure 3.5). Using the regression equation with normally distributed errors as a simple statistical rainfall runoff model, the committee computed by numerical integration the probability distribution of three-day runoff. The resulting distribution was corrected for the simulated discharges that constituted a partial duration flood series (Langbein, 1948).
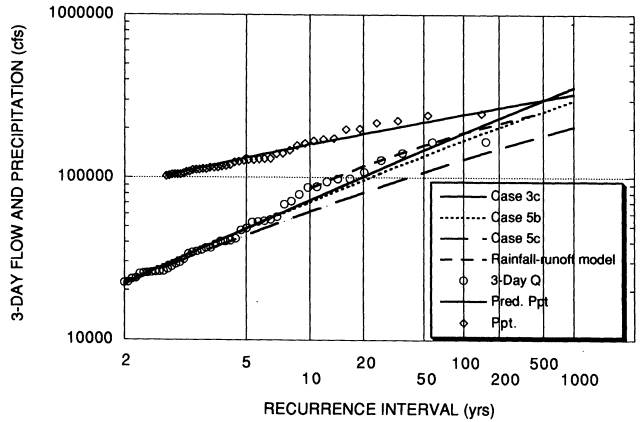
Figure 3.7 shows the distribution based on the rainfall-runoff modeling, along with the empirical and fitted distributions of precipitation and discharge. The estimated quantiles fit the discharge data very well. They cross the estimated log-Pearson type III distribution at about the 100-year discharge and asymptotically approach the precipitation distribution. One inch of discharge as indicated in this figure is equivalent to an average three-day streamflow of 16,922 cfs.
Also shown in Figure 3.7 is the distribution resulting from Case 5c based on the paleoflood information. Case 5c is based on the median estimate of the three-day flow associated with the average of the upper and lower non-exceedance limits. Hence the "best" estimated distribution based on the paleoflood information is well below the distribution based on rainfall-runoff modeling.
The committee does not claimed that its rainfall-runoff estimate of the three-day flood distribution is correct, although it believes that beyond the 1-in-500-year discharge, it better represents the "true" distribution than does the committee's "best" log-Pearson type III distribution. The analysis can and should be improved as follows:
- Unregulated three-day flows should be estimated for all major storms for which there is systematic precipitation data.
- A more thorough effort should be made to develop a series of basin average precipitation for the major storms in the systematic record.
- Frequency analysis of the basin average precipitation series should be based on a regional precipitation analysis and should consider distributions other than the shifted exponential (i.e., the generalized Pareto).
- Using the extended precipitation and discharge series, alternative rainfall-runoff models should be explored.
- An error analysis should be conducted to determine the uncertainties in the estimated probability distributions.
The results of such an analysis would provide useful information about the upper tail of the probability distribution of three-day flows on the American River.
Summary
Following the spirit of Bulletin 17-B, the committee estimated the probability distribution of average three-day flood discharges for the American River at Fair Oaks using various combinations of systematic, historical, and paleoflood data. Results based on the systematic and paleoflood data are consistent, implying a log skew (to the nearest tenth) of -0.1. Averaging station skews at comparable Sierra Nevada rivers gives a similar result. Use of the paleoflood data implies that the log skew is much more negative, and as a result when the paleoflood data is used with the systematic and historical data, the resulting fitted log-Pearson type III distribution does not provide an adequate description of the flood flow frequency relationships for floods with exceedance probabilities from 0.5 up to and beyond 0.002. Frequency analysis based on a series of basin average precipitation data supports the latter possibility.
The committee's recommended flood frequency distribution for three-day rain flood flows on the American River is based on the application of the Expected Moments Algorithm to systematic data and historical data with an assumed log skew of -0.1. Approximate confidence intervals were obtained by Monte Carlo simulation. The committee believes that this approach meets the spirit of Bulletin 17-B guidelines. Based on the evidence that the "true" distribution flattens for very large floods, the committee is hesitant to recommend the use of its selected distribution for annual exceedance probabilities less than 1 in 200. If it is necessary to extrapolate the distribution for smaller exceedance probabilities, the recommended distribution provides a basis that is consistent with Bulletin 17-B guidelines, however, other estimation approaches should be investigated, including the rainfall-runoff approach explored by the committee.