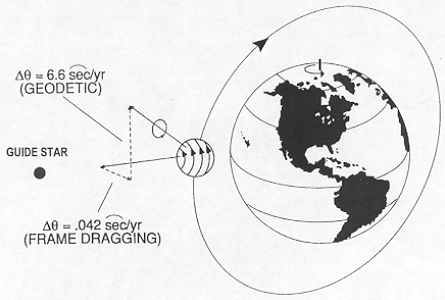
SIGNIFICANCE OF FRAME DRAGGING
Geometrical Viewpoint
Rotation and the Foundations of Physics. Rotation
has played a central, if problematic, role in the
foundations of mechanics and dynamics. Although natural
philosophers from Galileo to Newton had a clear
understanding of the invariance of physical law in
reference frames in relative rectilinear motion, the same
could not be said with respect to rotational motion.
Newton's famous "bucket" thought experiment illustrates the
problem. Water co-rotating with a bucket climbs the wall of
the bucket. Is this caused by rotation relative to absolute
space, or relative to distant matter? If the bucket did not
rotate, while distant matter rotated around it, would the
same behavior result? Newton's gravitational theory was
incapable of answering this question.
Despite the success of Newtonian dynamics in accounting
quantitatively for the details of planetary motion, the
tides, and local gravity, this conceptual issue remained
unresolved. Interestingly, Foucault's 1851 demonstration
that the plane of swing of a pendulum maintained a relation
to the fixed stars while the Earth rotated underneath it
caused a public sensation, and Foucault pendula quickly
appeared throughout Europe and the United States. And while
few physics textbooks today discuss the success of
Newtonian gravity in explaining such phenomena as the
advance of the lunar perigee, they do tend to discuss
Foucault's pendulum.
The conceptual relation between local dynamics and
distant matter was a central theme of Ernst Mach's
formulation of a natural philosophy. In 1872, in
History and Root of the Principle of the Conservation
of Energy, he wrote:
If we think of the Earth at rest and the other
celestial bodies revolving around it, there is no
flattening of the Earth, no Foucault's experiment, and
so on—at least according to our usual conception of the
law of inertia. Now one can solve the difficulty in two
ways; either all motion is absolute, or our law of
inertia is wrongly
expressed . . . . I [prefer] the
second. The law of inertia must be so conceived that
exactly the same thing results from the second
supposition as from the first.
Mach's thinking influenced Einstein's development of
general relativity. Although he later grew disillusioned
with Mach, Einstein's conception of the law of inertia was
meant to embody the loose collection of ideas now called
Mach's principle. The resulting theory, general relativity,
was not completely successful in that regard, yet it did
ultimately succeed in resolving the issue of Newton's
bucket. Ironically, that fact was not demonstrated until
1966, as discussed below.
Geometry and Frame Dragging. General relativity
describes gravitation as synonymous with the effects of
curved space-time. A "test" body (an electrically neutral
body small enough to be unaffected by tidal forces) moves
on a geodesic, the straightest possible trajectory, in the
space-time around a gravitating body. Thus a satellite in
orbit around the Earth (assumed non-rotating for the
moment) describes a helical path in space-time (a circle in
space, while moving forward in time) that for a single
orbit is, say, 7000 km in radius, and 1.5 light-hours or
1.8 billion km long in the "time direction." Any portion of
that space-time curve can be regarded as straight to high
approximation.
However, if the gravitating body also rotates, an
additional geometrical effect, called frame dragging,
should be present. There are a number of manifestations of
this predicted effect. A particle released from infinity on
the equatorial plane of a rotating body, moving initially
in a radial direction (i.e., with zero angular momentum),
will have it trajectory deflected away from a radial line
so that it orbits the rotation of the body, all the while
maintaining zero angular momentum. The period of a
co-rotating body is longer than the period of a
counter-rotating particle orbiting at the same radius.
Light rays sent around the equatorial plane of rotating
body (e.g., by the use of a ring of mirrors) take less time
to return to a fixed point when they propagate with the
sense of rotation of the body than when they propagate in
the opposite direction. Finally, a gyroscope at rest
outside a rotating body will precess relative to fixed
objects at great distance. Since gyroscope axes define a
local sense of non-rotation, local reference frames whose
orientation is defined by gyroscopes rotate relative to
frames fixed by distant object.
Because geometry underlies all gravitational dynamics in
GR, one can think of the effect just described as a
"dragging" of the space-time geometry around the rotating
body, much as a rotating cylinder causes a viscous fluid in
which it is immersed to be dragged around in a
whirlpool-like fashion. It is important to emphasize that
this geometric effect associated with rotation is
conceptually different from the static space-time curvature
produced by a non-rotating body. The latter effect imprints
itself on the external, far field of the source via the
mass M, a scalar quantity (as in the limiting
gravitational acceleration at large distances, given by
GM/R2). By contrast, frame
dragging imprints itself via the angular momentum of the
source, a pseudo-vector quantity J.
Frame Dragging and Newton's Bucket. The existence
of the frame-dragging effect suggests that rotation is not
strictly absolute, but can be relational, that is, defined
relative to other masses, just as is rectilinear motion.
Although approximate solutions of the equations of general
relativity for rotating bodies were obtained as early as
1918 (by Lense and Thirring, whence the alternative
terminology "Lense-Thirring effect" for frame dragging), it
was not until 1966 that an indication of this relational
property of rotation was found. This result came from a
theoretical analysis of the space-time in the interior of a
slowly rotating, approximately spherical shell of matter. A
hypothetical gyroscope at the center of the shell was shown
to precess, and in the limit that the shell's gravitational
radius 2GM/c2 tends to its
physical radius (a condition corresponding loosely to
cosmological values), the precession angular velocity tends
to that of the shell itself. In other words, in that limit,
gyroscope axes are locked to the distant matter
constituting the shell. In 1985, further extensions of this
work showed that, at the center of the shell, the requisite
centrifugal forces would be induced by frame dragging,
sufficient to cause water to climb the side of a
"non-rotating" bucket, exactly in accord with Mach's stated
preference. Consequently, within GR, rotation really is a
relational concept, defines with reference to distant
matter.
Thus frame dragging within general relativity has
significant conceptual and philosophical implications
concerning the relationship between local physics and the
distant cosmos and the possibility of "absolute" space.
Gravitomagnetic Viewpoint
Another viewpoint on frame dragging exploits a
similarity, in the weak-field, slow-motion limit, between
general relativity and electrodynamics. Specifically, the
space-time metric component g00 ≈
- 1 - 2 Φ/c2 +. . ., which
contains the Newtonian gravitational potential Φ, is
analogous to the scalar potential V of
electromagnetism. The component
g0i, which has no
correspondence in Newtonian gravitation, is analogous to
the vector potential Ai (i
varies over the spatial dimension). Associated with these
potentials are a "gravitoelectric" field
Eg, a "gravitomagnetic" field
Bg, and equations of motion that
approximately parallel the corresponding Maxwell equations
and Lorentz force equation of electrodynamics. The spatial
part of the metric gif, which relates
to spatial curvature, has no counterpart in
electromagnetism. It affects some of the equations but
plays no direct role in frame dragging. This viewpoint also
arises from treating general relativity at lowest order as
a tensor (spin-2) field theory, analogously to treating
electromagnetism as a vestor (spin-1) theory.
In this approach, static matter generates a
gravitoelectric potential g00 and space
curvature gif, while moving matter
generates in addition a gravitomagnetic potential
g0i. A rotating mass generates a
gravitomagnetic dipole field, analogous to the magnetic
dipole field of a rotating charge (apart from a numerical
factor), and a rotating matter current (a gyroscope)
external to the source experiences a torque ("spin-spin"
interaction) analogous to that of a current loop in a
magnetic field (apart from a sign change that reflects the
attractive nature of gravity).
Gravitomagnetism and Lorentz Invariance. In
electrodynamics there is an intimate connection between
electric and magnetic fields, resulting from Lorentz
invariance. What appears to be pure electric field in one
reference frame can be combined electric and magnetic field
as seen in a reference frame moving relative to the first.
General relativity is compatible with Lorentz invariance at
its foundational level, and thus there should be analogous
connections between gravitoelectric and gravitomagnetic
effects. the field of a mass moving with uniform velocity
v relative to an observer should be equivalent to
that of a static mass as seen by an observer moving with
velocity -v. The field of the moving mass contains
a gravitomagnetic field generated by its mass current
(g0i =
-4viGM/Rc3). The
field of the static mass contains only the gravitoelectric
field g00, and the spatial curvature
gij ≡
gsδij. Under a Lorentz
transformation to the frame of an observer with velocity
-v, there results, to first in
v/c, g0i =
-vi(g00 +
gs)/c =
-4viGM/Rc3. Thus,
gravitomagnetism can be said to be related to
gravitoelectrostatics through Lorentz invariance.
On the other hand, the gravitomagnetic field of a
rotating mass cannot be obtained from the static
field of a non-rotating mass by a simple rotation of
coordinates, first, because such a rotating frame contains
centrifugal and coriolis pseudoforces that distinguish it
from a non-rotating coordinate system cannot be defined
globally, indeed can be defined only out to a radius at
which the rotational velocity equals the speed of light.
Thus, although some aspects of gravitomagnetism can be
related directly to static gravity, frame dragging cannot
be related to it so simply.
This result is consistent with the idea that frame
dragging imprints the angular momentum J of the
source on the distant space-time. A linearly moving source
imprints both its mass M and its linear momentum
p on the distant space-time; however, the latter can
always be eliminated by a global Lorentz transformation to
a frame in which the body is at rest (p = 0). On the
other hand, the angular momentum, like the mass, cannot be
changed or eliminated by a global transformation.
Gravitomagnetism and Astrophysical Processes. The
precession and forces associated with frame dragging have
found important applications in astrophysical processes.
Models for relativistic jets of matter ejected from the
cores of quasars and active galactic nuclei invoke such
frame-dragging forces acting on the matter and magnetic
fields associated with accretion disks around rapidly
rotating, supermassive black holes.
Frame-dragging effects also play an important role in
the late-time evolution (the final few minutes) of
in-spiraling binary systems of compact stars (neutron stars
or black holes). That role includes precessions of the
spins of the objects and of the orbital plane and
contributions to the emitted gravitational radiation and
the evolution of the orbital phase. These effects are
potentially detectable in gravitational wave signals
received in the worldwide array of laser inferferometric
gravitational wave observatories currently under
construction, including LIGO in the United States and a
similar project called VIRGO in Europe.
SIGNIFICANCE OF GEODETIC
PRECESSION
Geometrical
Viewpoint
The geodetic effect is most simply viewed as a
combination of a precession resulting from
gravitoelectrostatics, and a precession related to curved
space-time. A gyroscope in motion in the gravitoelectric
field of a body experiences a precession that is described
by the interaction of special relativistic corrections to
the basic equations of motion with the external
gravitoelectrostatic field, completely analogous to the
effect in electrodynamics. This piece amounts to one-third
of the total effect.
The remaining two-thirds of the effect comes from the
curvature of space around the source. It can be understood
by a two-dimensional analogy: on the surface of the Earth,
transport a vector (a stick with an arrowhead lying on the
surface) locally parallel to itself (i.e., not moving to
the right or to the left) around a closed curve. If, for
example, the curve consists of following the 0° line of
longitude from the equator to the North Pole, following the
90° line of longitude from the Pole to the equator, and
then following the equator back tot he starting point, the
vector will be found to have rotated by 90° relative to its
initial orientation. This failure of a parallel-transported
vector to return to its initial state on completing a
closed path is the hallmark of curvature (indeed, this
process is used in differential geometry to define the
Riemann curvature tensor). thus a gyroscope, whose axis can
be shown to undergo parallel transport (provided that the
gyroscope is in free fall), will undergo a change in its
spin direction on completing each orbit in the curved
space-time around the Earth. The precise amount turns out
to be twice that of the gravitoelectric precession.
Gravitomagnetic Viewpoint
An alternative, purely gravitomagnetic, viewpoint works
in the co-moving frame of the gyroscope, in which there is
an apparent gravitomagnetic field of the source in linear
motion
(-4viGM/Rc3),
resulting in a precession analogous to that of a spin in a
magnetic field. However, the net effect is reduced by 25
percent by the Thomas precession, which results from the
fact that the co-moving frame of the gyroscope is actually
a sequence of Lorentz frames with different instantaneous
directions of the velocity, and whose axes therefore are
rotated relative to each other. (The relative effect of
Thomas precession here is smaller than in the
electromagnetic case because of the factor of 4 that
appears in the gravitomagnetic potential.)
GP-B AND OTHER TESTS OF GENERAL
RELATIVITY
Experimental Gravity and General
Relativity
Prior to 1960, the empirical basis of general relativity
consisted the Eötvös experiment, which verified the
underlying equivalence principle, and two experiments that
checked the theory itself: the deflection of light and
Mercury's perihelion advance. The latter two experiments
were regarded as being good only to 20 to 50 percent, and
10 percent, respectively.
Since 1960, however, significant progress has been made,
both in improving the precision of existing tests and in
performing new high-precision tests. This progress was
enabled by the rapidly evolving technology of
high-precision, high-stability, quantum-governed measuring
tools, such as atomic clocks, lasers, and radio telescopes,
together with progress in space exploration.
Improved tests were made of the Einstein equivalence
principle, the foundation for the geometric viewpoint of
gravitational theory. This principle is satisfied by
general relativity and by all theories called "metric
theories." these tests included improved tests of the
composition-independence of free fall (Eötvös experiment:
null tests to 10-12), tests of spatial isotropy
(local Lorentz invariance of non-gravitational
interactions: null tests to 10-22), and tests of
the gravitational redshift (to 10-4). It is
worth noting that a satellite test of the equivalence
principle (STEP) has been proposed that could improve the
test of composition-independence of free fall to the level
of 10-17.
The "classic tests" of general relativity were
substantially improved: light defection (using Very Long
Baseline Interferometry, or VLBI) to 0.1 percent, and
Mercury's perihelion advance to 0.1 percent. New tests were
performed: Shapiro time delay in signal propagation (using
Viking spacecraft tracking) to 0.1 percent equality of
acceleration of Earth and Moon toward the Sun (Nordtvedt
effect) to 10-12 (translated to a
10-2 null test of relevant theoretical
parameters). the Hulse-Taylor binary pulsar provided a test
of the existence of gravitational waves in agreement with
general relativity to 0.4 percent. Because the system
contains neutron stars with strongly relativistic,
nonlinear internal gravitational fields, the observations
also provided indirect support for the theory in
strong-gravitational-field regimes, through its prediction
that such internal structure is effaced in the orbital and
gravitational wave dynamics (by contrast with most
alternative theories).
No previous experimental tests of general relativity
directly probe the effect of frame dragging. Some effects
of gravitomagnetism associated with translational motion of
matter are present in such tests as the Nordtvedt effect,
and in the orbital dynamics and gravitational wave emission
of the binary pulsar, and some authorities have argued that
the gravitomagnetic field has already been confirmed by
indirect measurements. However, the gravitomagnetic effects
in question occur in complicated combination with other
effects, and so the gravitomagnetic contributions cannot be
cleanly separated. No gravitomagnetic effects associated
with rotation have ever been detected directly, in
isolation from other relativistic gravitational
effects.
Alternative Metric Theories of Gravity
Within a restricted class of alternative theories of
gravity called metric theories, a useful framework has been
developed, called the parameterized post-Newtonian (PPN)
framework. It characterizes the weak-field, post-Newtonian
limit of substantial, though not complete, range of metric
theories by a set of 10 parameters, γ, β, ξ,
α1,
α2, . . . , whose
values vary from theory to theory. Such theories generally
contain, in addition to the basic space-time metric,
auxiliary fields (scalar, vector, tensor, and so on) that
mediate the gravitational interaction. The Jordan-Fierz
Brans-Dicke scalar-tensor theory is the most famous
example; recently, extensions of that theory have become
popular in inflationary cosmological model building and in
superstring-inspired gravitational theories.
In general relativity, γ = β = 1, while the
other parameters vanish. Observations of the Shapiro time
delay and of light deflection place the bound |γ - 1|
< 2 x 10-3, and measurements of Mercury's
perihelion advance combined with measurements of γ
yield | β - 1| < 3 x 10-3.
Non-zero values for either of the parameters
α1 or α2 signal the
presence of auxiliary fields whose coupling to the distant
universe produces local gravitational effects dependent on
the local velocity relative to a preferred universal frame.
Such effects appear as violations of local Lorentz
invariance in gravitational interactions, and they produce
anomalies in geophysics (Earth tides) and in orbital
dynamics. Assuming that the solar system moves relative to
the cosmos with the velocity 350 km/s, as determined from
the dipole anisotropy of the cosmic background radiation,
several bounds have been placed on the α parameters,
specifically |α1| < 4 x
10-4.
In the PPN framework, the frame-dragging effect depends
on the combination 1 + γ + α1/4. The 1
+ γ part comes from the connection between
gravitomagnetism and gravitoelectrostatics via Lorentz
transformations (in the PPN framework,
g00 + gs = 2(1 +
γ) GM/Rc2; see the
section "Gravitomagnetic
Viewpoint," pp. 6-8), and the α1
indicates a possible violation of that local Lorentz
invariance. Thus from this point of view, frame dragging
tests the local Lorentz invariance of gravity. The bounds
that have been placed on γ and α1 are
tighter in their implications for frame dragging than those
GP-B can hope to achieve. It should be noted, however, that
those bounds come from experiments whose conceptual basis
is completely different from that of frame dragging and
rely on an assumption about the relevant velocity that
controls preferred frame effects. GP-B measures frame
dragging directly.
The geodetic effect depends on the combination 1 +
2γ. the first term corresponds to the gravitoelectric
precession, the second term to the effect of spatial
curvature; equivalently, 2 + 2γ comes from
gravitomagnetic precession viewed from the gyroscope's
frame, with a reduction of -1 from Thomas precession
(despite the use of Lorentz transformations in this latter
argument, α1 does not appear). With a
projected accuracy of 75 ppm in its measurement of the
geodetic effect, GP-B offers a factor-of-20 improvement in
the accuracy of the measurement of γ, from 2 x
10-3 to 10-4. This is at the level
where deviations from the exact unity value of GR could
occur in a class of well-motivated, cosmologically
important scalar-tensor alternative theories
(generalizations of the Brans-Dicke theory), in which
cosmological evolution following inflation naturally drives
such theories toward but not all the way to equivalence
with GR. Depending on the specific model, deviations from
γ = 1 could lie between 10-3 and
10-7. A bound from GP-B could constrain such
models.
Wider Classes of Gravitational Theory
Metric theories of gravity whose post-Newtonian limits
fit within PPN framework represent only a portion of the
"space" of alternative theories. This space includes metric
theories that do not fit the PPN model, and the relatively
poorly explored class of non-metric theories of gravity. It
is fair to say that, should a breakdown of general
relativity at the classical (non-quantum) level occur, it
is likely to involve non-metric gravity and would lead to a
radical conceptual revision of our view of gravity.
There is strong reason to suspect, from a number of
different quarters, that non-metric revisions of GR at some
level will be necessary. Unlike the other
fundamental interactions, GR has a dimensional coupling
constant and is not renormalizable in quantum field theory.
The theory stands as a major stumbling block in the way of
the unification of the interactions. In other words,
physicists devoted to unification believe that GR must
break down at some level. This is one of the greatest
challenges of modern theoretical physics. It is generally
assumed, though not proven, that the failure of GR will
occur at the level of quantum gravity, far from the regime
of observable effects that can be tested by local
experiments. On the other hand, examples exist of
unification-induced modifications of GR (in
superstring-inspired theories, for instance), in which
residual effects do occur at the classical, detectable
level of cosmology.
Non-metric modification of GR could still be viable,
provided they are compatible with the high-precision
experiments that check the Einstein equivalence principle
underlying metric gravity. (One motivation for proposing
experiments such as STEP is to provide dramatically
improved tests of this principle and thereby to test for
the effects of such modifications.) Within this broader
class of theories, no conclusion can be drawn about prior
bounds on frame-dragging effects from other experiments
such as light deflection, time delay, or tests of local
Lorentz invariance. On the other hand, there are currently
no examples of non-metric theories that agree with all
local observations and yet predict a detectably different
frame dragging.
OTHER TESTS OF FRAME DRAGGING
OR GEODETIC PRECESSION
There has been no prior, direct test of general
relativistic frame dragging. Apart from GP-B, the leading
current proposal for a possible future test is LAGEOS III,
a third laser-ranged geodynamics satellite launched into an
orbit whose inclination is supplementary to that of LAGEOS
I or II. The frame dragging induced by the rotation of the
Earth causes a precession of the orbital planes of both
satellites (the orbits are in effect gyroscopes); the use
of two satellites with accurately supplementary
inclinations permits the cancellation of the 107
times larger, but equal and opposite precessions induced by
the Earth's Newtonian multipole moments. At best, this
proposed experiment would yield a 10 percent test of frame
dragging. It has not been approved for launch by any space
agency at present.
Other less promising or less fully developed proposals
include detecting the gravitomagnetic contribution to
gravity gradients, as measured by orbiting superconducting
gravity gradiometers; measuring the precession of the plane
of a Foucault pendulum erected at the South Pole; and
measuring the precession of orbiting non-cryogenic
gyroscopes by optical means. A recently published proposal
(B. Lange, Phys. Rev. Lett. 74, 1904 (1995)) based on the
latter idea would use an autocollimator to sense the
orientation of an unsupported gyro, thus giving it the
working name AC-USG. The design of such a project is still
at the conceptual stage, but it is claimed that it could be
much more accurate than the present GP-B design. The
natural angular sensitivity of an optical autocollimator is
far better than that of a readout based on the
superconducting London moment; the single gyro in AC-USG
would be in a drag-free environment, with a much larger
spacing between gyro and housing than in GP-B; the
spacecraft would roll around the gyro axis rather than
around the direction to the reference star, thereby
minimizing a certain class of spurious torques; and two
counter-orbiting satellites could be used to largely cancel
some other kinds of errors. Despite these apparent
advantages, it is too soon to say whether the AC-USG could
work as claimed. The error analysis of the GP-B is the
result of decades of work, many Ph.D. theses, and detailed
engineering designs, and a similarly thorough and cautious
approach would be needed for AC-USG. Consequently, the task
group could not assess its claims quantitatively or discuss
the budget for such a project; but if future scientific
developments require a better measurement of gyro
precession, this approach could be a promising one.
One test of geodetic precession has been reported,
namely that of the lunar orbit (viewed as a gyroscope) in
the field of the Sun, measured using lunar laser ranging
combined with VLBI data (see B. Bertotti, I. Cinfolini, and
P.L. Bender, Phys. Rev. Lett. 58, 1062 (1987) and I.I.
Shapiro et al., Phys. Rev. Lett. 61, 2843 (1988)). The
result agrees with general relativity to about 2 percent.
In the Hulse-Taylor binary pulsar, the effect of frame
dragging of the pulsar's spin axis caused by the spin of
its companion is too small to be detected. There is,
however, a potential precession of the pulsar's spin caused
by a combination of the gravitomagnetic field generated by
the companion's orbital motion (relative to the center of
mass), together with the companion's gravitoelectric field
and the resulting space curvature, through which the pulsar
moves. Although a very significant secular change in the
radio pulse shape has been observed (an effect not observed
in other pulsars), given the uncertainties in the structure
of the emitting region of pulsars, it seems unlikely that
such measurements will ever yield results better than the
results of the lunar test of the geodetic effect, much less
those of GP-B.
Geodetic precession is sensitive to the value of the PPN
parameter γ. VLBI measurements of the deflection of
light are unlikely to reach below the GP-B level of
10-4 in (1 - γ). No planned or proposed
interplanetary probes will have the requisite tracking
capability to measure the Shapiro time delay to higher
accuracy than has been done. Planning for orbiting optical
interferometers with microarc-second accuracy and the
capability to improve light deflection measurements by 2 or
more orders of magnitude appears to have halted. The
European Space Agency has plans for a successor to the
Hipparchos mission, the Global Astrometric Interferometer
for Astrophysics (GAIA), with 20-microarc-sec accuracy,
which could measure light deflection and γ to
10-4. Although this accuracy would be comparable
to that of GP-B, this mission is unlikely to fly before
2006. Thus on the 1999 to 2000 time frame of GP-B, there is
unlikely to be a competitive measurement of space curvature
via the parameter γ.