Numerical Simulation of Turbulent Flows Around Hydrofoil
C.C.S.Song and C.Chen
(University of Minnesota, USA)
Abstract
The numerical solution to the unsteady compressible flows at small Mach number has always run into trouble due to the disparity between the sound speed and convective speed. The equation of unsteady incompressible flows are even more difficult to solve numerically than that of compressible flows. More importantly, the incompressible flow equations contain no physical information related to pressure waves which is an essential mechanism of rapidly accelerating flow such as hydraulic transients and acoustics. The compressible hydrodynamic equations have been developed to remedy the mathematical and physical shortcomings of the incompressible flow approach. The large eddy simulation approach based on the compressible hydrodynamic equations has been applied to flow around a two dimensional hydrofoil and tip vortex flow around a three dimensional hydrofoil. The simulated mean flow, as well as the turbulent correlations in the two dimensional case have been compared with experimental data. The tip vortex trajectory and the structure of tip vortex core have been studied.
Nomenclature
|
A+ |
constant |
|
As |
projected surface area |
|
a0 |
sound speed |
|
Cl |
lift coefficient |
|
C0 |
base chord length |
|
Cs |
Smagorinsky constant |
|
D |
damping coefficient |
|
L |
lift |
|
M |
Mach number |
|
n |
normal coordinate of wall |
|
p |
pressure |
|
p0 |
reference pressure |
|
Rc |
radius of curvature |
|
Re |
Reynolds number |
|
Rex |
Reynolds number based on x |
|
Rθ |
Reynolds number based on momentum thickness |
|
r |
radius in polar coordinate |
|
rc |
core radius |
|
Sij |
strain rate tensor |
|
St |
Strouhal number |
|
t |
time |
|
U |
reference velocity |
|
u |
resolved velocity components |
|
ue |
velocity at outer flow |
|
|
unresolved velocity components |
|
ut |
tangential velocity |
|
|
shear velocity |
|
Vt |
mean tangential velocity |
|
x,y,z |
coordinates |
|
yw |
distance from the wall |
|
Δ, Δi |
length scales |
|
Г |
circulation |
|
ν |
molecular viscosity |
|
νt |
turbulent viscosity |
|
ω |
mean vorticity |
|
ωm |
local maximum mean vorticity |
|
ρ |
density |
|
ρ0 |
reference density |
|
θ |
momentum thickness |
1. INTRODUCTION
The compressible hydrodynamics concept has been commonly used to treat hydrodynamic transient. However, in most cases, only one-dimensional situations have been considered. For three dimensional flow phenomena, the commonly used equations are either compressible Navier-Stokes equation for relatively high Mach number flows, or incompressible Navier-Stokes equations for hydrodynamic flows. The incompressible hydrodynamic equations have been
widely used in treating fluid mechanics problems with water as the flow medium. But the incompressible assumption changes the nature of the governing equations from that of hyperbolic type to that of elliptic type. Hence, the traditional numerical method for solving hyperbolic equations cannot be applied. Many difficulties have been encountered in solving the incompressible equations.
In order to obtain the hyperbolic property of the incompressible equation, Chorin [1] has proposed an artificial compressibility method. With this method, one can obtain the steady state solution of incompressible flow in the same way as one solves the compressible Navier-Stokes equations. However, for unsteady hydrodynamic problems, this method does not capture the essential effect of compressibility on fluctuating pressure or flow noise. In most unsteady flows, the weak compressibility of the fluid can contribute a great deal to the pressure field, hence the whole flow phenomena.
The three dimensional compressible hydrodynamic equations, which previously were called the weakly compressible model, has been established by Song and Yuan [2]. This set of equations not only retains the hyperbolic property, but also preserves the hydrodynamic compressibility effect in the equations. By using the property of the small change in density in the case of low Mach number flows, the dynamic part of the flow field is decoupled from the energy equation. But the compressibility effect on the pressure field still remains. Compressible hydrodynamic equations have been successfully used in solving various unsteady, low Mach number flow problems [3, 4].
Flow around foils is a class of common and important phenomena in fluid mechanics. Its significance in engineering practice is evident. Tip vortex as one of the flow pattern in three dimensional cases has not been understood fully; however, its effects on the foil performance is essential. It is theoretically interesting and practically important to understand the principle, origin, and development process of tip vortex.
It is extremely difficult to fully resolve large Reynolds number flows because they contain a very large range of different size eddies. The large eddies simulation (LES) approach, by which large eddies are resolved and small eddies are modeled, has been rapidly developed. The current paper presents numerical simulations of turbulent flows around a two dimensional and a three dimensional hydrofoil by solving the compressible hydrodynamic equations with the large eddy simulation method. The tip vortex flow phenomena will be analyzed as well.
2. GOVERNING EQUATIONS FOR LES
2.1 Compressible Hydrodynamic Equations
To implement the large eddy simulation, one needs to apply the cell volume integration over the governing equations, namely, the conservation of mass and momentum equations. A simple volume average method, by which the resolved quantity is treated as a constant over each finite volume, has been used. This is similar to the method introduced by Deardorff [5] and later extended by Schumann [6]. The volume averaged conservation equations have the similar form as the Reynolds average equations. One extra term ![]() is generated from the nonlinear term of the momentum equation. It has been referred as the sub-grid scale Reynolds stress which is analogous to the time averaged Reynolds stress.
is generated from the nonlinear term of the momentum equation. It has been referred as the sub-grid scale Reynolds stress which is analogous to the time averaged Reynolds stress.
Customarily, the sub-grid scale Reynolds stresses are decomposed into the sum of a tracefree tensor and a diagonal tensor. The diagonal tensor part is brought out in a similar way as the dynamic pressure p from the viscosity stress tensor. It is usually combined with pressure as a modified pressure, because they have similar properties, except one is from the molecular viscosity stress tensor, the other is from the unresolved turbulent stress tensor. The modified pressure properly represents the resolved pressure field. The trace-free part of the sub-grid scale Reynolds stress tensor need to be modeled in order to close the set of equations. The model will be discussed in more detail later.
The essential point for deriving compressible hydrodynamic equations is to use the equation of state appropriate to liquids or small Mach number, for which density change in the flow is small. Consider a barotropic flow with low Mach number, one can approximate the equation of state as:
(1)
Where p0 and ρ0 are reference pressure and density. a0 is the sound speed, which can be considered as constant. This expression has been widely used in hydraulic transient analysis.
From the above equation, one can solve for
ρ and substitute it into the averaged conservation equation of mass and hence get:
(2)
By dimensional analysis, one can show that the second term is of order M2 while the first term is of order M2St. In the case of small Mach number flows, the second term can be ignored. But since the first term is related to the Strouhal number, this term cannot be neglected, especially, when flow is highly time dependent and the Strouhal number is large. It is essential to retain the first term in the continuity equation for flows involving rapid acceleration such as hydraulic transient and hydroacoustics. It also keeps the whole equation set to be of the hyperbolic type. It should also be pointed out that the third term in Eq. (2) is the noise production term.
Similarly, one can substitute the equation of state into the conservation equation of momentum. By considering the density change to be small, one can get the final equation set as following:
(3)
where ![]() is stress tensor,
is stress tensor,
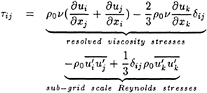
Eq. (2) and (3) are called compressible hydrodynamic equations. There are four unknowns and four equations. Obviously, this set of equation is closed except that the sub-grid scale turbulent stress need to be modeled. The energy equation has been decoupled. And the equation set has the hyperbolic property and it retains the compressibility effect to the flow field through the continuity equation, Eq.(2).
2.2 SGS Model
The Smagorinsky model is a simple and widely used model for modeling the unresolved sub-grid scale Reynolds stresses. In analogy to the definition for viscosity stresses, the sub-grid scale Reynolds stresses are assumed to be proportional to strain rate of the resolved flow field [7], i.e.
(4)
where νt is the unresolved turbulent viscosity, or the sub-grid scale diffusivity. νt depends on the length scale of the cell and the strain of the resolved flow field in the following way:
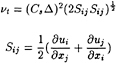
(5)
Where Δ represents the filter width, which is taken to be the length scale of the finite volume. There are several ways to decide Δ. According to Bardina et al. [8], a better choice might be:
whereΔi is the three dimensions of the finite volume.
Cs is the Smagorinsky constant. Many different values for different flow situations have been used. For homogeneous isotropic turbulence, Lilly [9] determined that Cs≈0.23. Deardorff [5] used Cs=0.1 for his simulation of turbulent channel flow. And several simulations [10, 11] have used values between 0.1 and 0.23. It is supposed this constant is a universal constant and independent of grid size. But this seems not the case. The simulations that have been carried out by the authors suggested that this constant needs to be adjusted somehow for different mesh systems and flow situations. For the two dimensional simulation to be presented herein, better results have been obtained by using Cs=0.14. And for the primary tip vortex simulation, the tip vortex trajectory is insensitive to this constant.
For turbulence near a solid wall, Eq. (5) has been modified in a similar way as proposed by Moin and Kim [12].
(6)
Where D is a non-dimensional damping factor. Van Driet exponential damping function has been used,
D=1−exp(−y+/A+)
It is easy to see, this damping factor will only modify the turbulent viscosity near the solid wall.
3. COMPUTATIONAL CONSIDERATIONS
The size of the largest eddies and the size of the smallest eddies are extremely far apart in turbulent flows. And their difference increases with increasing Reynolds number of the flow. It is very difficult to solve the equations governing the turbulent flows, especially in the case of large Reynolds number flows. In order to gain maximum accuracy with available computer resources, nonuniform mesh system and multi-mesh system has been used.
As the boundary layer on the foil surface and the wake behind the foil are the primary objects in the simulation of flow around two dimensional foil, the computational domain is deliberately divided into two regions. The fine mesh region encloses the foil and covers the wake behind the foil where the gradients are relatively large. The coarse mesh region covers the rest of the computational domain from the lower channel wall to upper channel wall. For the simulation of flow around three dimensional foil, tip vortex is the major objective at this stage of the research. Hence fine mesh has been arranged to resolve the tip part of the foil and the tip vortex behind it. This multi-mesh system has been very beneficial in a sense of using the computer time and memory efficiently.
The artificial interface condition between the fine mesh region and the coarse mesh region is given special attention. For boundary points of the coarse mesh, the primary variables are directly taken from the the corresponding fine mesh region. For boundary points of the fine mesh region, the velocity values and the pressure gradients have been matched to the coarse mesh region. Matching pressure gradient instead of matching pressure itself has enabled the unsteady pressure waves generated by the foil to propagate outward properly. Otherwise, a pressure wave will reflect back and accumulate large errors in the inner zone and hence cause the computation to be broken down.
Wall boundary conditions are very important for the computation. Special attention should be paid to high Reynolds number flows, since the mesh size usually is not fine enough to resolve the details of the boundary layer. Appropriate partial slip boundary conditions have to be used. Many [3, 6, 13] have used the wall function as a medium to obtain the approximation for the phantom point velocity values. However, the associated assumption of fully developed turbulent boundary layer has limited its usage. Especially it cannot be applied for flow that has laminar boundary layer, transition, as well as turbulent boundary layer. A new way to impose the partial slip condition has been developed for the present simulation in the case of two dimensional flow. By assuming the boundary layer is quasi-steady during a certain time period, say, the time interval of the outer flow calculation increment, one can use the steady boundary layer equations by ignoring the local acceleration term, ![]() .
.
In the current simulation, Crank-Nicolson's fully implicit second order scheme is used to solve the boundary layer equations. The outer flow conditions are obtained by inputting the pressure field near the wall from the outer flow computation. In the leading part of the foil, the laminar boundary layer is assumed. The transition starting point is determined by laminar boundary layer separation or according to the following criteria [14],
where
θ is the momentum thickness of the boundary layer.
Starting from whichever comes first, the turbulent boundary layer equation will be applied. For turbulent boundary layer calculation, Prandtl's mixing length model is used.
After the boundary layer separation, non-slip velocity boundary condition has been used, since after separation, the boundary layer is fairly thick, and the velocity gradient normal to the wall has become much smaller compared with the boundary layer before the separation. Hence, the non-slip boundary condition will be appropriate.
The quasi-steady boundary layer calculation provided the information for imposing the partial slip boundary conditions in the outer flow. It is a novel combination of boundary layer computation and outer flow simulation. For unsteady
large eddy simulation, it certainly can improve the accuracy in reflecting the boundary layer effect to the outer flow and flow in the wake.
The pressure condition on the solid walls has been specified in the following way,
(7)
Where Rc is the radius of curvature of the wall. This is obvious, since the curved wall will generate a centrifugal force, which will result in a pressure gradient normal to the wall.
Boundary layers along the channel walls are not so interesting for present study; in addition, these boundary layers will not affect the foil wall boundary layer and the wake region. The channel wall has been simply treated with full slip velocity and zero gradient pressure conditions.
The well-known MacCormack predictor-corrector numerical scheme has been used in solving the compressible hydrodynamic equations for large eddy simulation. The scheme is of second order accuracy in time and space.
4. NUMERICAL RESULTS AND DISCUSSIONS
4.1 Flow Around 2-D Foil
A two dimensional foil that has been tested in a water channel by Huang [15] at National Taiwan University has been simulated. The Reynolds number of the flow is 1.6×106. And the angle of attack is −5.9.
Fig. 1 shows two instantaneous vorticity fields near the trailing edge of the foil and in the wake. One may note that at pressure side of the foil, a very thin boundary layer is formed, and the vorticity in this layer has a positive sign. On the other hand a relatively thick boundary layer exists at the suction side of the foil. The vorticity is negative in this layer. Apparently, there is no visible separation for the simulated flow. However, the vorticity with opposite sign from two sides of the foil meet at the trailing edge and form a vortex sheet, which is very unstable. Vortices roll-up and negative and positive vortices alternatively shed downstream. A more vivid picture of the
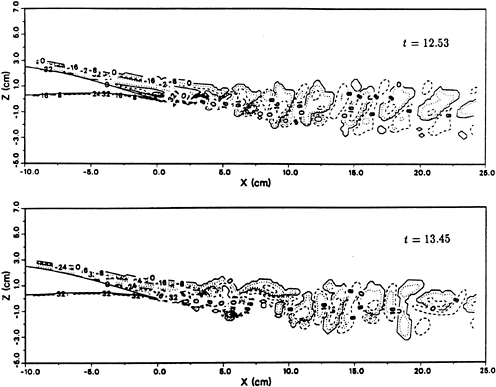
Fig. 1 Instantaneous Vorticity Contours
vortex shedding can be seen through animations of color coded pressure and vorticity fields.
The mean flow field around the foil body is shown in Fig. 2. The calculated values are compared with the experimental data. It can be seen they agree very well. The mean flow profiles in the boundary layer are plotted against the experimental measurement in Fig. 3. Again, fairly good agreement has been reached. Mean flow velocity
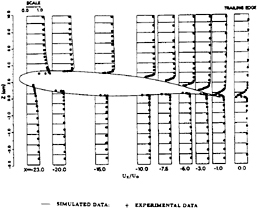
Fig. 2 Simulated and Measured Mean Flow Ux around the Foil
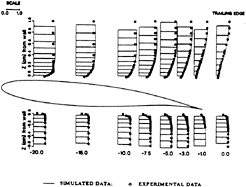
Fig. 3 Simulated and Measured Mean Boundary Layer Profiles
vectors are shown in Figs. 4 and 5 for simulated values and experiment values respectively. The agreement between simulated values and experimental data is quite good. It can be concluded that the mean velocity field can be reproduced by the numerical simulations very well.
As discussed above, the turbulence has been divided into the resolved large scale part and the unresolved sub-grid scale part. The former is simulated while the latter is modeled through the resolved flow field. Figs.6(a) and (b) provide the
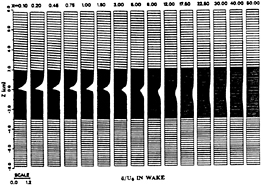
Fig. 4 Simulated Velocity Vectors in the Wake

Fig. 5 Measured Velocity Vectors in the Wake
turbulent intensity ![]() for these two parts in several stations in the wake. And the sum of the two parts is plotted in Fig. 6(c). It is interesting to note that in the wake region near the trailing edge, the main contribution is from the modeled part, while in the wake region far from the trailing edge, the main contribution is from the resolved large eddies. This is consistent with the general understanding that eddies are larger in the far field but they are smaller near the trailing edge. The pattern that eddy sizes change from small to large as flow goes downstream can be easily seen on Fig. 1. In Fig. 6(d), the measured turbulent intensity
for these two parts in several stations in the wake. And the sum of the two parts is plotted in Fig. 6(c). It is interesting to note that in the wake region near the trailing edge, the main contribution is from the modeled part, while in the wake region far from the trailing edge, the main contribution is from the resolved large eddies. This is consistent with the general understanding that eddies are larger in the far field but they are smaller near the trailing edge. The pattern that eddy sizes change from small to large as flow goes downstream can be easily seen on Fig. 1. In Fig. 6(d), the measured turbulent intensity ![]() is shown. Comparing Fig.6(c) and Fig. 6(d), one can see that the shape is quite similar, mainly in the far wake region. But in the near wake region, the sharp peak right after the trailing edge as shown in Fig./, 6(d) is lost in the simulation. Evidently a very thin shear layer after
is shown. Comparing Fig.6(c) and Fig. 6(d), one can see that the shape is quite similar, mainly in the far wake region. But in the near wake region, the sharp peak right after the trailing edge as shown in Fig./, 6(d) is lost in the simulation. Evidently a very thin shear layer after
the trailing edge produces the strong and fine turbulent eddies. Relatively poor agreement in the near field may be due to the three dimensionality of small scale and insufficient grid refinement.
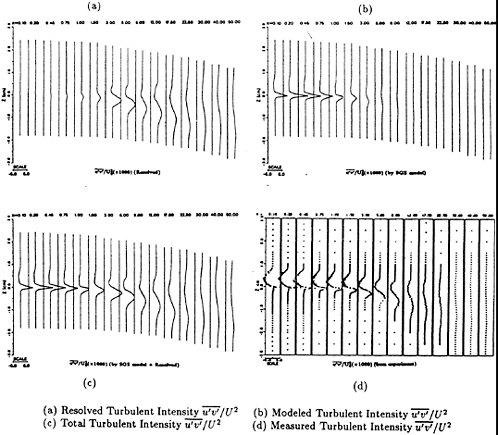
Fig. 6 Comparison of Turbulent Intensity in the Wake
4.2. Tip Vortex Flow
A three dimensional foil with a modified NACA 4215 section and an elliptic planform has been studied. Extensive experimental research for tip vortex cavitation with this foil has been conducted [16, 17]. Tip vortex is the focus in the present numerical simulation. The coordinate axes are so chosen that x is along the main flow direction, y is normal to the plane of the foil, positive pointing from pressure side to suction side, and z is in the span-wise direction from the foil base to the tip of the foil. The effective angle of attack is about 14º. And the Reynolds number of the simulation is 7.0×105. However, since the mesh size are not fine enough and the boundary layer on the foil surface is not resolved well in the current three dimensional simulation.
The lift coefficient is defined as Cl= ![]() , where L is the total lift; As is the projected area of the foil. Calculated lift coefficient is 0.72, which is very close to the experimental result, 0.72∼0.73 [ 17].
, where L is the total lift; As is the projected area of the foil. Calculated lift coefficient is 0.72, which is very close to the experimental result, 0.72∼0.73 [ 17].
Fig. 7 shows the velocity vectors projected on a cross-section normal to the flow direction. The swirl around the tip vortex is quite apparent. The interaction between wake and tip vortex can be observed by noting the sudden changing of flow direction below the swirl. The corresponding vorticity distribution (x-component) is
shown in Fig. 8. The vorticity contour lines form nearly concentric circles indicating the intensity
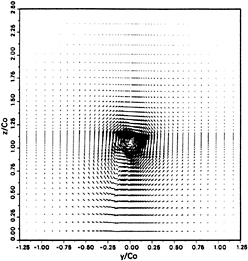
Fig. 7: Projected Velocity Vectors at x/C0= 1.06 Cross-Section
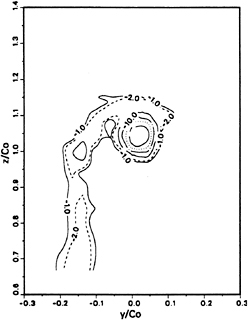
Fig. 8 Vorticity Contours of x-Component at x/C0=1.06 Cross-Section
increases towards the vortex core. Vorticity contours on a surface parallel to the x-z plane and through the axis of the tip vortex are shown in Fig. 9.
The simulated tip vortex trajectory
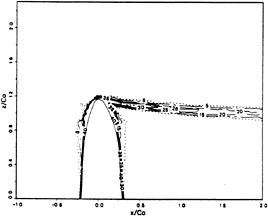
Fig. 9 Vorticity Magnitude at y/C0=0.0 Cross-Section
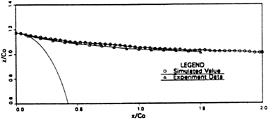
Fig. 10 Tip Vortex Trajectory
is plotted and compared with the measurement in Fig. 10. The agreement is very good. It is worth pointing out that the current simulation has not tried to resolve the boundary layers on the foil surface. It is believed that the boundary layer on the foil surface germinates the tip vortex, but the above result seems to imply that the tip vortex trajectory is independent of the boundary layer. This result agrees with the measurement [16] that the tip vortex trajectory is insensitive to the Reynolds number and the angle of attack.
The pressure coefficient in the tip vortex core as a function of x is plotted in Fig. 11. It can be seen that the pressure reaches the lowest point at the tip where the tip vortex originates. The pressure increases in the downstream direction. This is understandable because the tip vortex core is very small at the beginning and grows in the downstream direction due to diffusion. Increasing core size means weakening vorticity and increasing pressure.
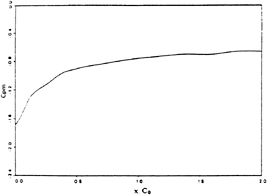
Fig. 11 Minimum Pressure Coefficient at Tip Vortex Core
It is a difficult task to measure the full details of the structure of tip vortex. On the other hand theoretical analysis of tip vortex has always required an assumption that the tip vortex is a Rankine vortex. The Rankine vortex model ignores two aspects of the real fluid flow phenomena. Firstly, according to the Rankine vortex model, the vorticity field should be axis symmetric about the vortex core. However, the wake behind the foil always disturbs this symmetry. The region affected by the wake becomes larger as the wake spreads wider along the streamwise direction. Measurements engaging the assumption of symmetric vorticity field could lead to errors in their data since the tangential velocity profiles around the tip vortex core are quite different depending on how the wake affects them. Secondly, the Rankine vortex model assumes that, the flow field around tip vortex is divided into rotational core region and irrotational outer region. And the vorticity is concentrated inside the core region. This cannot be true for the real flow situation because of the diffusivity of the fluid and turbulence. Again the wake plays an important role in distributing the vorticity in the flow field.
Numerical diffusion can distort the results of numerical simulations. But numerical simulations can provide at least a qualitative structure of the real tip vortex. Since the tip vortex is not symmetric and the vorticity is not just concentrated inside the core region, the traditional definition for core radius needs to be reconsidered. In the present study, the circulation Г about the core is calculated first as following,
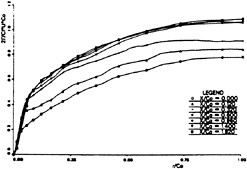
Fig. 12 Nondimensional Circulation around Tip Vortex Core
The variations of Г as function of radius from the core at several stations along streamwise direction have been plotted in Fig. 12. Note that Г is nondimensionalized by taking theoretical value of ![]() as the reference value so that, in the ideal case, all curves in Fig. 12 would approach 1 asymptotically. The asymptotic values for the last four curves is about 1.05. This slight difference from 1 could be caused by the fact that the flow simulated here is bounded by the walls. By comparing the curves for different stations, one could see that the asymptotic value starts with about 0.75 at the tip and gradually increases to the maximum value of 1.05 at about x/C0=0.5. This means that the vorticity in the z-direction is gradually changing the direction into the vorticity in the x-direction, i.e., the tip vortex. In other word, the circulation contributed to the lift is gradually converting into the circulation of tip vortex. This process finishes at about x/C0=0.5 position. The steep gradient near the core shows that the vorticity is very strong near the core, and becomes weak as it goes far from the core.
as the reference value so that, in the ideal case, all curves in Fig. 12 would approach 1 asymptotically. The asymptotic values for the last four curves is about 1.05. This slight difference from 1 could be caused by the fact that the flow simulated here is bounded by the walls. By comparing the curves for different stations, one could see that the asymptotic value starts with about 0.75 at the tip and gradually increases to the maximum value of 1.05 at about x/C0=0.5. This means that the vorticity in the z-direction is gradually changing the direction into the vorticity in the x-direction, i.e., the tip vortex. In other word, the circulation contributed to the lift is gradually converting into the circulation of tip vortex. This process finishes at about x/C0=0.5 position. The steep gradient near the core shows that the vorticity is very strong near the core, and becomes weak as it goes far from the core.
The mean tangential velocity can be calculated based on the circulation calculated above. The mean tangential velocity at one of the x-station has been shown in Fig. 13. The corresponding tangential velocity profile of the Rankine vortex is compared in the same figure. As can be seen, in the core region, the two are quite close. But outside the core, they are very different. No-
tice that the former is rotational outside the core while the latter is irrotational. From this comparison, one could see that it is appropriate to define the tip vortex core radius as the distance from the core center to the maximum mean tangential velocity point.
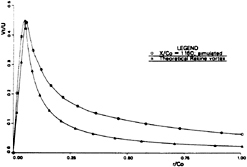
Fig. 13 Mean Tangential Velocity around Tip Vortex Core
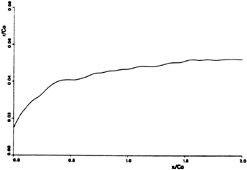
Fig. 14 Radius of Tip Vortex Core
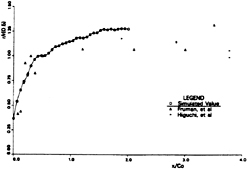
Fig. 15 Nondimensional Radius of Tip Vortex Core
The core radius calculated according to the above definition has been shown in Fig. 14. Obviously, the core radius increases in downstream direction. The diffusion of the vorticity in the core could be the reason for it. There have been some experimental measurements on the core radius of tip vortex [18], where the radius is nondimensionalized by the radius at half of the base chord position, namely, rc(0.5). In Fig. 15, the calculated core radius is compared with the experimental results based on the nondimensional
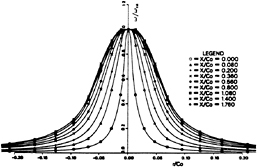
Fig. 16 Mean Vorticity around Tip Vortex Core
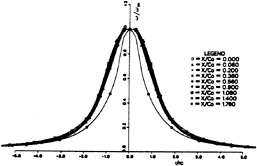
Fig. 17 Mean Vorticity around Tip Vortex Core
radius as described above. It can be seen that the agreement is fairly good.
In spite of the non-symmetric vorticity field around the tip vortex core, one could get a mean vorticity by means of the circulation, i.e.,
The profiles of mean vorticity calculated in this way have been nondimensionalized by its local maximum value and shown in Fig. 16. The
diffusion property of tip vortex core is quite obvious. When the radius is nondimensionalized by the local vortex core radius, one can obtain a very interesting result as shown in Fig. 17. All the mean vorticity curves have almost collapsed to one curve except the one at x/C0=0. This could mean that the vorticity diffusion around the vortex core obeys a similarity rule.
5. SUMMARY
The numerical simulations of flows around the two dimensional foil and the three dimensional foil based on the compressible hydrodynamic equations have been studied. Compressible hydrodynamics has drawn more and more attention for solving various hydrodynamic flow problems. It has been proved that this set of equations has two major advantages over the incompressible equations. The parabolic property of the equations makes the numerical solution more convenient. And, by including the effect of compressibility enables the set of equations to correctly model the flows involving rapid accelerations, such as pressure waves generated by hydraulic transients and acoustics. It is very important to note that the incompressible flow equations does not retain such physical information. The large eddy simulation by utilizing the compressible hydrodynamic equations has the potential to treat various low Mach number flows and correctly simulate pressure fluctuations. In addition, multi-mesh system can serve as a useful tool to use the available computer resources effectively.
The simulation of two dimensional foil has shown that the mean flow field is quite accurately simulated by the present large eddy simulation method. The large eddies in the far downstream of the wake can be captured fairly accurately in terms of the turbulent intensity in that region, where large scale eddies contribute the most part to the turbulent intensity. However, in the near wake region, the small turbulent eddies are dominant, hence, the large eddy simulation method cannot resolve them well. The turbulence structure right after the trailing edge is so complicated that this simple strain rate model such as Smagorinsky SGS model cannot handle it well.
The numerical study of tip vortex flow has provided much knowledge on its structure. The independence of the tip vortex trajectory on the Reynolds number, boundary layer where the tip vortex originated, has been observed again from the numerical solution. The simulated tip vortex shows that the ideal Rankine vortex assumption for such case is inapplicable. Two major effects have spoiled the assumption. One is the effect from the wake behind the foil, which destroys the symmetry of the vortex. The other is the effect of diffusivity because of which the vorticity does not exist only inside the core. The vorticity is strong inside the core, but there is no clear margin for the edge of the core. Instead, the vorticity is smoothly distributed by diffusion with the highest value at the core. The wake behind the foil also contributes to the re-distribution of the vorticity. Although the vortex is not symmetric, the core radius can be defined through the profile of the mean tangential velocity around the vortex core. By defining the maximum mean tangential velocity point as the edge of the vortex core, one could see that inside the core, the tangential velocity profile is quite close to the case of the Rankine vortex; while outside the core, it is very different from that of irrotational flow. By analyzing the circulation along the streamwise direction, one can see that the circulation contributed to the lift has completely converted into the circulation of the tip vortex up to the point of about half base chord length. The core radius as defined above has a similar trend as the experimental results. The mean vorticity profiles calculated from the circulation have suggested that the diffusion of the vorticity could follow the similarity rule when the radius is nondimensionalized with the core radius of the vortex.
Acknowledgment
This research has been supported by the Office of Naval Research under the contract N/N00014–91-J-1239. And the grant from the Minnesota Supercomputer Institute has made the numerical simulations possible. The authors are grateful to these supporters. The authors would also thank Dr. Arndt for the valuable discussions.
REFERENCES
1. Chorin, A.J., “A Numerical Method for Solving Incompressible Viscous Flow Problem, ” Journal of Computational Physics, vol. 2, 1967, pp. 12–26.
2. Song, C.C.S., and Yuan, M., “A Weakly Compressible Flow Model and Rapid Convergence Methods,” Journal of Fluids Engineering, vol. 110, 1988, pp. 441–445.
3. Song, C.C.S., and Yuan, M., “Simulation of Vortex-Shedding Flow about a Cylinder at High Reynolds Number,” Journal of Fluids Engineering, vol. 112, 1990, pp. 155–163.
4. Song, C.C.S., He, J., Chen, C., and Chen, X., “Computation of Turbulent Flow for Hydraulic Machinery: Hydrofoil, Francis Turbine, and Draft Tube,” International Research Center on Hydraulic Machinery (Beijing), Nov. 20–23., 1991
5. Deardorff, J.W., “A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Number,” Journal of Fluid Mechanics, vol. 41, 1970, pp. 452–480.
6. Schumann, U., “Sub-grid—Scale Model for Finite Difference Simulations of Turbulent Flows in Plane Channels and Annuli,” Journal of Computational Physics, vol. 18, 1975, pp. 376– 404.
7. Smagorinsky, J., “General Circulation Experiments with the Primitive Equations,” Monthly Weather Review, vol. 91, No.3, 1963, pp. 99–164.
8. Bardina, J., Ferziger, J., and Reynolds, W.C. , “Improved Sub-Grid Scale Models for Large Eddy Simulation,” AIAA paper, 80–1357, 1980.
9. Lilly, D.K., “On the Application of the Eddy Viscosity Concept in the Inertial Subrange of Turbulence,”, NCAR Manuscript, No.123, 1966.
10. Mason, P.J., and Callen, N.S., “On the Magnitude of the Subgrid-Scale Eddy Coefficient in Large-Eddy Simulations of Turbulent Channel Flow.” Journal of Fluid Mechanics, vol. 162, 1986, p.439.
11. Piomelli, U., Moin, P., and Ferziger, J.H., “Model Consistency in Large Eddy Simulation of Turbulent Channel Flows, ” Physics of Fluids, Vol.31, 1988, p.1884.
12. Moin, P., and Kim, J., “Numerical Investigation of Turbulent Channel Flow,” Journal of Fluid Mechanics, vol. 118, 1982, pp. 341–377.
13. Ghose, S., and Kline, S.J., “The Computation of Optimum Pressure Recovery in Two-Dimensional Diffuser, ” Journal of Fluids Engineering, vol. 100, 1987, pp. 419–426.
14. Cebeci, T., and Bradshaw, P., Momentum Transfer in Boundary Layers, Hemisphere Publishing Corporation , 1977.
15. Huang, J.L., “Personal Communications,” 1991.
16. Arndt, R.E.A., Arakeri, V.H., and Higuchi, H., “Some Observations of Tip Vortex Cavitation,” Journal of Fluid Mechanics, vol. 229, 1991, pp. 269–289.
17. Arndt, R.E.A., and Christian Dugue, “Recent Advances in Tip Vortex Cavitation Research,” Proc. Intl. Symp. on Propulsors and Cavitation, Hamburg, Germany, June, 1992.
18. Maines, B.H., and Arndt, R.E.A., “Bubble Dynamics of Cavitation Inception in a Wing Tip Vortex,” Cavitation and Multiphase Flow Forum, ASME Fluids Engineering Conference, Washington D.C., June 21–24, 1993.
DISCUSSION
by Professor Roger Arndt, University of Minnesota
The numerical results in this paper complement a companion experimental study of tip vortex cavitation (Maines and Arndt, 1993a, b). Although quantitative comparisons are not yet possible, there is a wealth of qualitative information that has provided guidance in our studies of cavitation inception. The authors have noted the lack of viscous effects on vortex trajectory which is in agreement with our experiments. They have also found that the minimum pressure in the vortex is very close to the tip in a region where the vortex structure is highly complex and cannot be modeled by axisymmetric analogs, such as the Rankine or Lamb vortex. Visual observations of cavitation as reported by many authors in the past gave the impression that the minimum pressure in the vortex is located about one-half chord length downstream where the vortex is fully rolled-up. However, careful observation of the inception process using high speed cinematography indicates that the minimum pressure is very close to the tip, x/co∼0.15. This is in agreement with detailed velocity measurements by Fruman et al. (1992).
As pointed out by the authors, numerical diffusion can distort the results of numerical simulations. The Reynolds number corresponding to the calculations in Figure 11 has not been stated. However, it is interesting to note that our experimental observations for a series of foils of identical planform, but with different cross sections and different boundary layer characteristics, indicate that an almost universal cavitation scaling law exists:
where 0.045<k<0.073 and Re is Reynolds number based on maximum chord length. Our initial thought was that the appropriate viscous scaling parameter is a Reynolds number based on circulation, Г / ν , where the variation in k represents the dependence of the initial development of the vortex on the details of the boundary layer flow in the tip region. If one uses a value of k= 0.065 for the modified NACA 4215 hydrofoil studied in this paper, the equivalent Reynolds number for the calculation in Figure 11 would only be 18,000 which is well below the range of our experimental data in which 600, 000<Re< 1,700,000. This warrants further discussion.
In summary, this paper provides substantial insight into the vortex roll-up process. The interaction between the wake and the tip vortex is an important consideration which is fully substantiated by our experimental observations. Unfortunately, detailed comparisons between our cavitation experiments and the numerical results cannot be made until the flow at higher Reynolds number can be simulated.
Fruman, D.H., Dugue, C., Pauchet, A., Cerrutti, P. and Briancon-Marjolet, L. ( 1992), “Tip vortex roll-up and cavitation,” Nineteenth Symposium on Naval Hydrodynamics, Seoul, Korea.
Maines, B.H. and Arndt, R.E.A. ( 1993a), “Bubble dynamics of cavitation inception in a wing tip vortex,” Proceedings of the ASME Cavitation and Multiphase Flow Forum, FED Vol. 153, pp. 93–95.
Maines, B.H. and Arndt, R.E.A. ( 1993b), “Viscous effects on tip vortex cavitation,” 4th International Symposium on Cavitation Inception. ASME Winter Annual Meeting, New Orleans.
Author's Reply: See common response for the above at the end of this section.
DISCUSSION
by Dr. Thomas T.Huang, David Taylor Model Basin
Could the authors provide the grid resolution requirements around the hydrofoil and tip vortex in order to reach grid-independent numerical solution. The discussor provided an estimate of grid resolution requirements as function of Reynolds number in their paper presented in this conference (paper 7.2). The solutions of Cp, Cτ,CD, and CL for wide range of grids must be presented. The computed Cp in the core of tip vortex must be compared with the measured cavitation inception number σi. We know for sure that the measured value of σi. depends strongly on Reynolds number. The method presented by the authors will become much more useful if the requirements of grid-dependent solution are known a priori.
Author's Reply: See common response for the above at the end of this section.
DISCUSSION
by Dr. P.M.Gresho, LLNL
I appreciate your concern re: difficulty of unsteady incompressible flow. But:
Q1. Do your presented computational results differ in any significant way from those of incompressible flows?
Q2: Have you done any simulations in which the compressibility (“noise” term in mass conservation equ) is significant/
important?
Author's Reply: See common response for the above at the end of this section.
Author's Reply to Drs. Arndt, Huang, and Gresho
The authors appreciate additional insights on the quantitative characteristics of tip vortex and tip vortex cavitation provides by Professor R. Arndt's experimental results. It appears that the primary structure of a tip vortex is not sensitive to the Reynolds number. Because our computation did not fully resolve the boundary layer, it is not possible to give the precise Reynolds number to the flow simulated. But it is quite clear the computation represents a very large Reynolds number case: certainly much greater than 18,000 quoted by Professor Arndt. The reason Figure 11 may appear to indicate relatively small Reynolds number is inadequate resolution of the core of the vortex where very sharp gradient exists. Indeed later calculation with finer grids in the core region results in lower pressure on the axis of the vortex while flow elsewhere is unaffected.
To answer Dr. P.M.Gresho's questions we would like to first point out that the effect of compressibility, no matter how small the compressibility may be, is significant when flow changes rapidly with time. For very small Mach number flow, the time averaged quantities simulated by this method are identical to that of incompressible flows. But even in a very small Mach number case, this method simulates flow noise directly while an incompressible flow model will not yield flow noise. Indeed we have simulated flow noise due to boundary layer separation and vortex shedding.
The main idea behind the Large Eddy Simulation (LES) method is to resolve only the large structure of the flow while the effect of small scale turbulence is modeled by a Subgrid Scale Turbulence Model. Therefore, it is not possible to attain a grid size independent condition unless the Direct Simulation method is used and all scale turbulence are resolved. Even in that case it will only be grid size independent in statistical sense. With LES method, the small the grid size the finer scale structure of the flow can be resolved. The grid size independence stated by Dr. T.T.Huang can be meaningful only when the long time averaged quantities are concerned. As it was stated previously, the flow near the core of the tip vortex for a very large Reynolds number case has very sharp gradient and we did not achieve the grid size independent condition. But the overall flow, except for a small region in the core and in the boundary layer, is fairly well simulated.
Numerical Calculations of Transitional Flow over Flat Plate in Turbulent Non-uniform Flows
S.H.Kang, M.R.Choi, and W.P.Jeon
(Seoul National University, Korea)
ABSTRACT
The behavior of the boundary layer over a flat plate in a non-uniform incoming flow was simulated using low Reynolds number k-ε models of Launder and Sharma and Chien and a transition model. Mean velocity profiles and skin-frictions on the flat plate were also measured in the wake generated by a circular cylinder at the upstream. The Computational Preston Method (CPM) proposed by Nitsche et al. was used to measure the skin-friction coefficients in the present study.
The Launder and Sharma model predicts earlier start and short transition length than the PTM model does and Chien's model shows also earlier start of transition and damped variation. These trends are generally the same with those of the uniform flow. The PTM transition model based on the low Reynolds number k-ε of Launder and Sharma does reasonably predict skin-frictions on a flat plate during transition. However more extensive calibrations of the PTM transition model is needed. The CPM method is verified as an useful tool to investigate skin-friction over the transitional boundary layer with reasonable accuracy. The simple construction and instrumentation for the technique are appreciated. Measured skin-friction coefficient gradually changes from the leading edge to the downstream. Transition length was considerably longer than in the uniform flow.
INTRODUCTION
Reliable and accurate prediction of turbulent flows over air and hydrofoils and through turbomachinery over wide range of flow condition is important for the design and performance prediction. A rotor of compressor or turbine rotates in the highly three-dimensional turbulent wake of stator, and a propeller operates in the stern wake. Therefore the incoming flow relative to a rotor as well as a propeller is unsteady. An efficient method is required that correctly simulates complex flows containing viscous effects; transition, leading edge separation, reattachment, non-equilibrium turbulent shear flow, boundary layer separation. Various numerical methods have been developed for the two or three dimensional, compressible or incompressible, steady or unsteady viscous passage flows. The CFD techniques for turbomachinery have reached a high level of maturity, however there is still need of more validation of the codes even for the two-dimensional steady turbulent flow over wing section.
Even without a recirculation or cavitation bubble on a blade, transition is a complex phenomena which has been studied but is still not well understood. A transition region usually extends over significant fraction of the blade. The importance of steady and unsteady transition in the flows of turbomachinery was summarized by Mayle[1]. Since the blade of turbomachinery operates in the highly turbulent and non-uniform flow field, many factors affect the boundary layer transition, i.e. the incoming flow condition, pressure gradient, curvature of blades, roughness and surface vibration, acoustic disturbances etc.. A model for the correct prediction of transition point on the blade does not yet available. The transition occurs under small disturbance cirumstances by Tollmien-Schlichting process in a low-turbulence environment. Under high free stream turbulence conditions, non-linear bypass transition becomes dominant, which is poorly understood yet. Several researches were done to investigate the effects of free-stream turbulence intensity and length scale on the transition and heat transfer on a blade of turbomachinery as well as on a flat plate (cf. Abu-Ghanam and Shaw [2], Sohn and Reshotko[3], etc.).
In the transitional flow, the turbulence models have been less successful than in fully turbulent flow, mainly due to the intermittency and three-dimensionality of the flow. Techniques of DNS (direct numerical simulation), LES (large eddy simulation) or higher-order turbulence models can be used to simulate the transitional flow, however they still require too much computing time to be used for the practical engineering purposes. Two-equation
turbulence models, i.e. low Reynolds number k-ε model, as well as algebraic models, i.e. eddy viscosity model, have been widely used. The algebraic models of Cebeci-Smith and Baldwin-Lomax are difficult to be extended and modified for complex flow conditions. Low Reynolds number k-ε models were developed to treat the near wall damping effects and were applied to the calculation of flow in pipes, channels, and external boundary layers. Such a built-in function of the models makes them attractive as potential predictive tools for transitional boundary layers. Various efforts related to k-ε models were made to simulate transition during last two decades. Recent work by Schmidt and Patankar[4] was extensive and attractive. They evaluated the numerical characteristics of the Lam and Bremhorst[5] and Launder and Sharma[6] two-equation models. A modification was proposed that limits the production term in the turbulent kinetic energy eqaution and was based on a simple criterion and correlated to the free-stream turbulence level. This model was termed a production term modification model or PTM model. The model reasonably simulates skin-friction coefficient and Stanton number of zero-pressure and low accelerating flows on the flat plate. However the model is not fully confirmed for various conditions of flow.
Recently Stephens and Crawford [7] investigated the numerical prediction of boundary layer transition using the PTM model based on the model of Chien [8]. The model is one of the most widly used model for passage flow calculation of turbomachinery. They examined a new model for the case of Blair and Werle [9]. It was noted that the model does not reproduce the experimental Stanton number distribution as well as expected. The numerical predictions appeared to damp the transition of a boundary layer. They conducted a comparison between the transition results of the K.Y.Chien[8] and Launder and Sharma [6] and showed that the Chien's model predicts an earlier start of transition and damped distribution of skin-friction. The main reason of the problem was that the damping function fμ of the model is a function of y+ and for fully turbulent boundary layer. They concluded that the Chien model is not adequate for the transition study.
A numerical investigation [10] of the incompressible viscous flow through the controlled diffusion cascade blade of a compressor was carried out using the PTM model based on the low Reynolds number k-ε model of Launder and Sharma[6]. The development of the shear layer along the pressure and suction sides was generally well estimated However, there was still a considerable discrepancy in the predicted profiles of mean velocity and turbulent kinetic energy. Taking into account the uncertainty in the measurement, the transport of turbulence in the shear layer, especially through the region of transition, was reported to be one of reasons. For more detailed assessment of the numerical method, boundary layer measurements on the airfoil including the shear stress on the wall are needed not only with various free stream turbulent intensities but also in non-uniform incoming velocity profiles.
Noting that most of the transition model were studied using the measured data on the flat plate in a uniform flow with different level of turbulence intensity, their characteristics of predicting the transition shear layer of general profile were not investigated yet. More specifically, the behavior of the boundary layer over a flat plate in a non-uniform incoming flow is of practical interest, however there are not measured sets of data for the prediction method to be validated. When a flat plate is placed in a turbulent non-uniform shear layer, a new internal layer will be developed on the plate in the existing profiles of velocity, turbulent kinetic energy, and its rate of dissipation and production. The behavior of transition boundary layer was simulated using the low Reynolds number k-ε models of Launder and Sharma [6] and its PTM model and of Chien[8], and results were discussed in the present study.
Mean velocity profiles and skin-frictions on the flat plate were measured in the wake generated by the circular cylinder at the upstream. The data can be used to verify the various turbulence models of transition. Whether the flow over the leading edge is laminar-like or fully turbulent, skin-friction is sensitive parameter of importance and strongly related to heat transfer. Direct measurement of wall friction is not easy job, and almost all the methods need delicate instrumentations and advanced techniques. The simple preston tube method is known inadequate for such a developing layer. The Computational Preston Method (CPM) proposed by Nitsche et al.[11] was used to measure the skin-friction coefficients in the present study. An experimental study was performed to investigate the skin friction distributions on a flat plate with sudden change in roughness (from rough to smooth surface) under zero pressure gradient condition using the CPM method[12]. The growth of internal viscous layer was compared with measured data of Antonia and Luxton [13] as well as estimated ones using empirical correlations. The experience of CPM method is extended to transition flow in the present study.
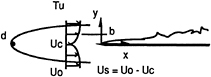
Fig. 1. Configuration of the flat plate and coordinate system.
NUMERICAL CALCULATION
Governing equations and turbulence models
For an incompressible steady turbulent flow, the continuity and Reynolds-averaged Navier-Stokes equations are the governing equations. The eddy viscosity μt is obtained by the low-Reynolds-number k-ε model. The transport equations for k and ε are written as
(1)
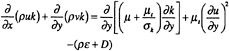
(2)
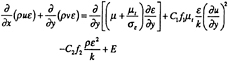
(3)
ε+D actually denotes the nonisotropic dissipation rate, possessing a finite wall value; ε is the isotropic dissipation rate, that is zero at the wall; D is the low Reynolds number term. The functions and model constants are summarized as follows:
Launder and Sharma [6] Model
(4)
Cμ=0.09, C1=1.44, C2=1.92, σk=1.0, σε=1.3 (5)
(6)
Chien [8] Model
(7)
Cμ=0.09, C1=1.35, C2=1.8, σk=1.0, σε=1.3 (8)
(9)
where
(10)
Schmidt and Patankar [4] modified the value of function, fμ, and limit the production rate of turbulent kinetic energy as follows:
(11)
(12)
(13)
where Reθ is Reynolds number based on momentum thickness. The coefficients A and B are functions of the free-stream turbulence intensity. These were calibrated considering the empirical correlations of the starting and ending locations of transition on a flat plate in uniform flow by Abu-Ghannam and Shaw [2]. The position of the free stream is not defined not only in the passage flow of blades but also over a flat plate in the wake. The actual free stream is the external flow of the wake, however turbulence of the free stream may not have direct affect on the boundary layer over the wall. As the wake flows over the plate, the internal layer will be developed from the leading edge. Therefore the value of turbulence intensity at the edge of the internal layer has strong affects on the shear layer over the surface, and the external flow has indirect influence upon growing and transition of the internal layer. Two cases were considered in the present study. The free stream value of turbulence intensity was used for PTMe, and the value at the edge of internal layer δi for PTMi csase. The location of δi was determined considering the slope of the wall layer and external wake profile.
Boundary conditions
The flow and equations are parabolic type and the calculation are carried out from the leading edge using marching procedure (Fig.1). At the inlet boundary x=0, mean velocity profiles, kinetic energy and rate of dissipation profiles are estimated using the similarity solution of the plane wake described in the text [14].
(14)
(15)
(16)
where ![]()
They are uniformly distributed from the centerline to the location of their maximum value. The dissipation rate along the free stream assumed very small for the specified value of k at the leading edge to remain to the downstream. On the plate, the no-slip condition is enforced. Since the low-Reynolds-number k-ε model is used, the boundary
conditions k=0 and ε=0 are imposed on the surfaces. The static pressure is assumed constant in the whole flow domain.
Numerical method
The discretized equations are obtained following a finite volume method. A staggered grid arrangement is used in which the scalar variables are located at the geometric center of a control volume, while the velocity components are located on the midpoints of the control faces. The unwind scheme is employed to evaluate the convection flux on the control surfaces. A pressure is constant and the integration of the continuity equation gives us the vertical component of velocity. A TDMA is used to obtain a numerical solution of the discretized equation.
EXPERIMENT AND DATA REDUCTION
Experimental apparatus and instrumentation
The experiments were performed in the 900mm x 900mm square section closed loop wind tunnel. The uniformity of mean flow is about 1% and the freestream turbulence level is around 0.3% at the speed of 30 m/s. Boundary layer measurements were earned out on a smooth flat plate of 10mm thick and 1.6 m long flat plate, which was installed on a hinge at the center of the tunnel. The two-dimensionality and uniformity of the flow was adjusted by monitoring the static pressure on the plate. A circular cylinder of 5 mm diameter was mounted on the adjustable strut ahead of the plate. Mean velocity was measured using a total head tube of 0.6 mm diameter and kinetic energies were measured using a two components hot wire system of Kanomax Co..
Numerical Preston tube method (CPM)
The Preston tube method is one of the most widely used shear stress measuring techniques due to its simple construction. The correlation curve between the dynamic head of a wall Pitot tube, q and the corresponding wall shear stress, τ is usually represented by a calibration curve based on the law of the wall.
(17)
where d is diameter of the Preston tube. If the effective distance from the wall corresponding to the tube diameter and the dynamic head is obtained from the law of the wall, the calibration curve can be obtained from direct calculation.
Nitsche et al. [11] reported an empirical curve of displacement factor ![]() as a function of
as a function of ![]() . Since the law of the wall is not generally known, he used the velocity profile of three parameters, as proposed by Szablewski [15].
. Since the law of the wall is not generally known, he used the velocity profile of three parameters, as proposed by Szablewski [15].
(18)
where K1 formally corresponds to the von Karman constant, K2 to Van Driest damping factor, and K3 to the dimensionless pressure parameter. For K=1.3, K1=0.4, K2=26, K3=0, the empirical calibration curve according to Preston method is obtained and used for the fully developed turbulent boundary layer. The unknown parameters, K1, K2, K3 (one of the parameters is fixed in some cases) and the value of wall shear stress are obtained analyzing the measured values of dynamic head using Preston tubes of different size. The procedure of the CPM is summarized as follows[11]:
-
Measure dynamic heads using Preston tubes of different size.
-
Assume the value of wall shear stress.
-
Determine yeff for each tube.
-
Compare the calculated and measured dynamic heads.
-
Go back to step (3), adjust shear stress and repeat step (4).
-
Compare the converged wall shear stresses of each tube. If they are different each other, adjust parameters in the eq.(2). Go back to step (2) and repeat the same procedure until the converged stress is obtained.
The probe diameters should be small and not thicker than 20% of the boundary layer. The probe diameter ratio should be more than 1.5 to get significant differences in the basic shear stress[11].
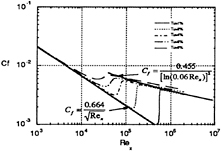
Fig.2 Skin-friction distributions on a flat plate in a uniform flow using LS model.
RESULTS AND DISCUSSION
Calculated results
The boundary layer on a flat plate in a uniform flow with free-stream turbulence intensity was simulated using Launder-Sharma(LS), Chien, and PTM models. Various grid spacing in the longitudinal and transverse directions and the initial profiles of turbulent kinetic energy and dissipation rate are tested for accurate and consistent prediction. Predicted distributions of skin-friction, ![]() for various turbulence intensities are presented in Figs.2, 3, and 4. The LS natural transition model predicts earlier start and short transition length than the PTM model does. Chien's model shows also earlier start of transition and dampe d variation as discussed by Stephens and Crawford[7]. The PTM transition model successfully simulates the transition in Fig.5, since it was calibrated using measured data of Abu-Ghannam and Shaw [2]. The boundary layer over the leading edge is a laminar-like flow with high turbulence intensity, which is early diffused into the flow near the wall due to the turbulence in the external flow. These results confirm the discussed aspects in the previous studies of the uniform flow of high turbulence intensity [4, 7, 10].
for various turbulence intensities are presented in Figs.2, 3, and 4. The LS natural transition model predicts earlier start and short transition length than the PTM model does. Chien's model shows also earlier start of transition and dampe d variation as discussed by Stephens and Crawford[7]. The PTM transition model successfully simulates the transition in Fig.5, since it was calibrated using measured data of Abu-Ghannam and Shaw [2]. The boundary layer over the leading edge is a laminar-like flow with high turbulence intensity, which is early diffused into the flow near the wall due to the turbulence in the external flow. These results confirm the discussed aspects in the previous studies of the uniform flow of high turbulence intensity [4, 7, 10].
Shear layer development on a flat plate in a turbulent wake was simulated using four turbulence model, i.e. Launder-Sharma (LS), Chien, PTM e and PTMi models. The values of free stream velocity, U o, turbulence intensity, Tu, maximum velocity defect, Us and half width of the wake, b are free parameters of the incoming flow. The values used in calculation are:
free stream velocity, Uo: 10, 20 m/s
maximum velocity defect Us: 0.5,1,2,4 m/s
half width of the wake, b: 0.005,0.01,0.02,0.04m
free stream turbulence intensity, Tu: 1, 2%
The bold faced values are the standard values of each quantity when the others are changed. Kinetic viscosity, v is fixed as 1.25×10−5 m2/s.
Before going into parametric study, the shear layer was simulated for the above standard values of wake. Simulated distributions of skin friction coefficient presented in Fig. 6 shows that the LS natural transition models predicts earlier start and short transition length than the PTM model does. Chien's model shows also earlier start of transition and damped variation. These trends are generally the same with those of the uniform flow. PTM e and PTMi models show considerably different distributions from each other. PTMi model using the value of turbulence intensity at the edge of internal layer has stronger physical meaning, however there are not enough data to investigate their validity. Limited discussion will be given later in the present paper. The trend of Cf
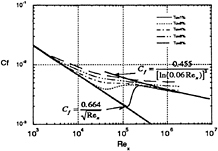
Fig. 3 Skin-friction distributions on a flat plate in a uniform flow using Chien model.
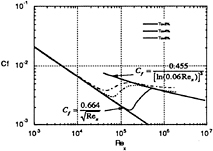
Fig.4 Skin-friction distributions on a flat plate in a uniform flow using PTM model.
distribution is not changed in Fig. 7 for larger value of Us=2m/s.
The values of free stream velocity, Uo and maximum velocity defect, Us may mainly contribute to development and transition of the internal layer. For the free stream velocity, Uo of 10 and 20 m/s, Us was changed 1, 2, 4 m/s. The maximum value of turbulence intensity in the wake, which is dependent of only Us/Uo, are 3.5, 7.0, 13.9 percent respectively at the leading edge. The variation of skin-friction distribution using the PTMi model are presented in Fig. 8. The value of skin-friction coefficient along the plate is nearly the same for the same value of Us/Uo, which means transition is strongly dependent upon turbulence intensity. The growth of internal layer is shown in Fig. 9. The magnitude of δi were thicker than that in the uniform flow due to existing shear stress of the external flow, however growing rate is nearly same with the Blasius solution and increases more during transition. The effect of half width of the wake and free-stream
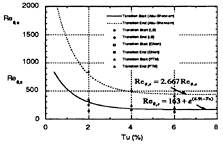
Fig. 5 Comparison of starting and ending locations of transition on a flat plate in a uniform flow.
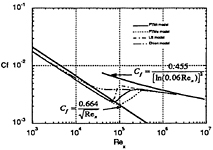
Fig.6 Skin-friction distributions on a flat plate in a wake for Us=1 m/s and Uo=10 m/s.
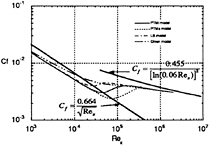
Fig.7 Skin-friction distributions on a flat plate in a wake for Us=2 m/s and Uo=10 m/s.
turbulence on the skin-friction distribution was very small, however the internal layer grows faster as the wake becomes thicker and free stream turbulence increases (not shown here). A wake profile in a strong turbulence intensity was not tried here, since the turbulence structure is not known yet.
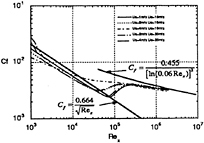
Fig.8 Skin-friction distributions on a flat plate in a wake using PTMi model.
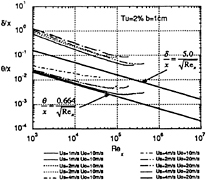
Fig.9 Predicted thickness of internal layer on a flat plate in a wake using PTMi model.
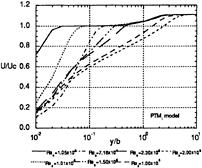
Fig.10 Predicted profiles of velocity on a flat plate in a standard wake using PTMi model.
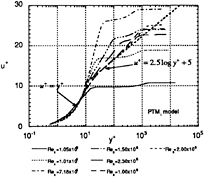
Fig.11 Predicted profiles of velocity on a flat plate in a standard wake using PTMi model.
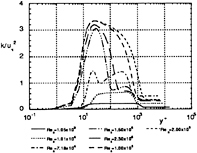
Fig.12 Predicted profiles of turbulent kinetic energy on a flat plate in a standard wake using PTMi model.
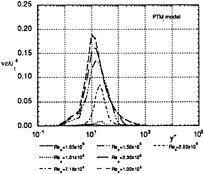
Fig. 13 Predicted profiles of dissipation on a flat plate in a standard wake using PTMi model.
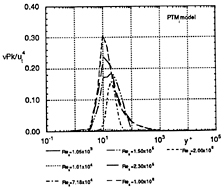
Fig.14 Predicted profiles of kinetic energy production on a flat plate in a standard wake using PTMi model
Simulated profiles of non-dimensionalized velocity presented in Figs. 10 and 11. show how the internal layer develops from the Blasius to the logarithmic law profiles near the wall. The turbulent kinetic energy distributions are presented in Fig. 12. The incoming turbulent kinetic energy in the wake rapidly decreases at the leading edge due to the zero boundary condition, however turbulence is self-generated and has its maximum value near the wall in the transition region. At the end of transition turbulent kinetic energy duffuses to the external flow and finally the profile approaches to the typical one of the equilibrium turbulent boundary layer. It is observed that the maximum value of kinetic energy during transition is larger than the peak value in the fully developed turbulent boundary layer at the downstream. The dissipation rate and production are presented in Figs. 13 and 14 respectively. The rates rapidly increase near the wall (y+=10−20) during the transition process, and show typical profiles of the equilibrium layer at the downstream, too. Turbulent kinetic energy production and its dissipation rate becomes nearly identical at the end of transition. The evolution of turbulence during transition seems to be reasonably simulated with the PTMi model, however it should be confirmed by measurement.
The PTM transition model based on the low Reynolds number k-ε of Launder and Sharma does reasonably predict skin-frictions on a flat plate during transition. However need of extensive calibrations using various transition data is shown by the present numerical investigations.
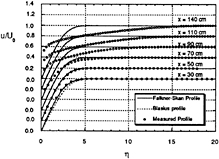
Fig. 15. Mean velocity profiles on the flat plate in the uniform free stream.
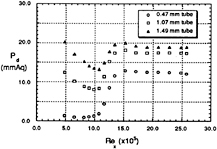
Fig. 16. Measured values of total pressure by three Preston tubes of different size.
Measurement of boundary layer in uniform flow
Measurement was carried out at the uniform speed of 25 m/s. Typical three regimes of flow, i.e. laminar, transitional, and turbulent, appear at this speed over the 1.5 m long flat plate in the present study. Mean velocity profiles at several stations of laminar, transitional and turbulent flows are shown in Fig. 15. Since the plate was slightly inclined to keep parallel flow over the leading edge, the external flow was accelerated a little (dUo/dx=0.096 1/s). The measured profiles over the leading edge nicely coincide with the Falkner-Skan flow with weak favorable pressure gradient. The flow changes near the wall and transfer to the external flow, then becomes fully turbulent boundary layer profile at the downstream. The transition starts at Rex=8×105( Reθ=550) and ends at Rex=1.4×106 (Reθ=1400). The value of shape factor slowly changes from 2.5 to 1.3. These results coincides with measured values of Sohn and Reshotko[ 3].
The measured values of total pressure by three Preston tubes of different diameter, i.e. 0.47, 1.07 and 1.49 mm, are presented in Fig. 16. The total head decreases first along the plate with the boundary
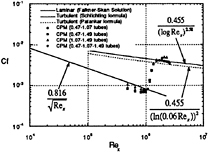
Fig. 17. Variation of skin-friction on the plate measured by CPM technique in the uniform flow.
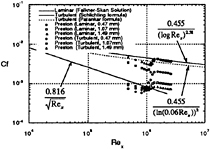
Fig. 18. Variation of skin-friction on the plate measured by Preston tube method in the uniform flow.
layer thickness, then increases in the transition region, and decreases again over the turbulent region. The parameter K1 was only adjusted to obtain skin-friction by CPM technique as was suggested in the previous study[7]. K2 was fixed as 26 and K3 as 0. Except the tube set of 1.07–1.49 mm (the diameter ratio is larger than 1.5), the estimated skin-friction coefficients show consistant values each other in Fig. 17. They are in coincidence with values from turbulent empirical correlations, however smaller than the Falkner-Skan solution. This deviation may attribute to the inaccuracy of the effective distance in case of laminar flow in the CPM procedure. As expected, the conventional Preston tube method can not be used for the transitional boundary layer as shown in Fig. 18. The variation of parameter K1 is shown in Fig. 19. It changes from 0.0 to 0.42 over the transition region. Due to the CPM profile adopted in the present study, the law of the wall in the limitted region of Preston tube diameter can be expressed as families of function of variable von-Karman constant. Non-dimensionalized velocity profiles using the measured shear velocity are plotted in Fig. 20. The profile over the leading edge shows typical laminar flow characteristic (cf. however the turbulence level may be quite different from the laminar flow [3]) and
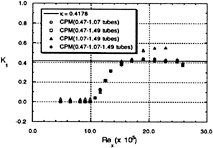
Fig. 19. Variation of K1 along the plate in the uniform flow.
becomes typical logarithmic profiles of the fully developed turbulent boundary layer at the far downstream location.
From this fundamental test in the uniform flow, the CPM technique is verified to be a useful tool to investigate the skin-friction of the transitional boundary layer with reasonable accuracy. The simple construction and instrumentation for the technique should be appreciated.
Measurement of boundary layer in the wake
The velocity distributions generated using a circular cylinder of 5 mm diameter ahead of the plate confirm the similarity solution[ 14] between x/D=10 and 30. When the wake center is adjusted to be located at the leading edge, the measured incoming velocity just ahead of the plate still coincides with the similarity profiles in Fig. 21. The cylinder was located at 0.6 m upstream. The maximum value of velocity deficit Us was 3.53 m/s and the half width of the wake, b was 0.0136 m at the position of the leading edge.
The thickness of the internal layer, which is estimated by comparing the velocity profile with the similarity profile of wake. The variation of thickness is compared with calculated values in Fig. 22. Raw data of the dynamic pressure measured by Preston tubes are shown in Fig. 23. The skin-friction coefficient gradually changes from the leading edge to the downstream in Fig. 24. Transition length shows very long, i.e. it starts at Rex=8×104 and ends at Rex=2.0×106. This is partially due to the high level of turbulence intensity (5%) at the center of the incoming wake. However the length is longer than that of the uniform flow with the free stream intensity of 5%. Effects of the non-zero values of Reynolds stresses in the wake on the development of the internal layer are beyond the scope of the present study. The values of skin-friction using the conventional Preston tube method show that it is not
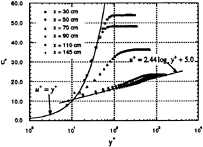
Fig. 20. Non Dimensional velocity profiles on the flat plate in the uniform flow.
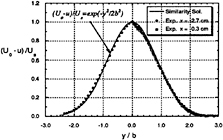
Fig. 21. Velocity profiles in the incoming wake ahead of the flat plate.
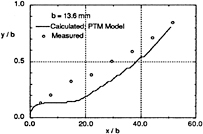
Fig. 22. Variation of the internal layer along the plate.
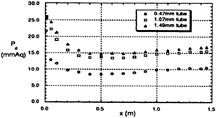
Fig 23. Measured values of total pressure by Preston tubes of three different size.
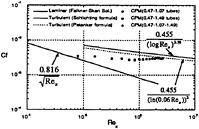
Fig. 24. Variation of skin-friction on the plate in the non-uniform incoming flow.
valid for this case, too. The value of K1 at the first point is already large, i.e. 0.2, then monotonically increases to the von Karman constant, 0.42 in Fig. 25. Considering these aspects of the flow, the boundary layer over the leading edge can be a laminar-like flow with high turbulence intensity, of which energy is diffused into the flow near the wall due to the natural turbulence production in the external flow. Further investigation is needed for turbulence characteristics here. Finally the non-dimensional velocity profiles are shown in Fig. 26. Logarithmic region appears even at the first measuring point, however the profile considerably deviates from the fully developed profile.
Taking into account of small increases in the measured values over the plate due to the small acceleration of the free stream, the length of transition was shortly estimated in the both PTMe and PTMi calculations. Furthermore the transition is considerably delayed in the PTMe calculation. The accuracy of CPM measurement should be further investigaed.
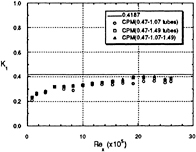
Fig. 25. Variation of K1 along the plate in the uniform flow.
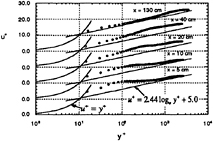
Fig.26. Non-dimensional velocity profiles on the plate in the wake.
CONCLUSION
The results of the numerical and experimental study of the transitional boundary layer over the flat plate in a non-uniform flow are summarized as follows:
-
The Launder and Sharma model predicts earlier start and short transition length than the PTM model does. Chien's model shows also earlier start of transition and damped variation. These trends are generally the same with those in the uniform flow. PTMe and PTMi models show considerably different distribution from each other.
-
The value of skin-friction coefficient along the plate is nearly identical for the same value of Us/Uo, which means transition is strongly dependent upon turbulence intensity within the internal layer.
-
The PTM transition model based on the low Reynolds number k-ε of Launder and Sharma does reasonably predict skin-frictions on a flat plate during transition. However more extensive calibrations is needed.
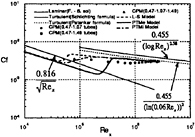
Fig. 27. Calculated and measured skin-friction coefficients on the flat plate in the non-uniform flow.
-
The variation of skin-friction was obtained using the CPM technique. The method is verified as an useful tool to investigate skin-friction over the transitional boundary layer with reasonable accuracy. The simple construction and instrumentation for the technique are appreciated.
-
The skin-friction coefficient gradually changes from the leading edge to the downstream. Transition length was considerably longer than in the uniform flow.
ACKNOWLEDGEMENT
The authors would like to extend our appreciation to the Turbo and Power Machinery Research Center and the Korean Science and Engineering Foundation for supporting the present work.
REFERENCES
1. Mayle, R.E., “The Role of Laminar—Turbulent Transition in Gas Turbine Engines, The 1991 IGTI Scholar Lecture”, J. of Turbomachinery, Trans. of ASME, Vol.113, pp. 509–537, 1991.
2. B.J.Abu-Ghannam and R.Shaw, “Natural Transition Boundary Layer—The Effects of Turbulence, Pressure Gradient, and Flow History”, J. of Mech. Eng. Science, Vol.22, No.5, pp. 213–228, 1980.
3. K.H.Sohn and E.Reshotko, “Experimental Study of Boundary Layer Transition With Elevated Free stream Turbulence on a Heated Flat Plate,” NASA CR 187068, 1991.
4. R.C Schmidt and S.V.Patankar, “Simulating Boundary Layer Transition With Low-Reynolds Number k-Ɛ Turbulence Models: Part 2 - An Approach to Improving the Predictions, ” J. of Turbomachinery, Vol.113, 1991.
5. C.K.G.Lam and K.Bremhorst, “A Modified Form of the k-ε Model for Predicting Wall Turbulence,” J. of Fluids Eng., Vol.103, pp. 456– 460, 1981.
6. B.E.Launder and B.I.Sharma, “Application of the Energy-Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc”, Letters in Heat and Mass Transfer, Vol. 1, p. 131, 1974.
7. C.A.Stephens and M.E.Crawford, “An Investigation into the Numerical Prediction of Boundary Layer Transition Using the K.YChien Turbulence Model,” NASA CR 185252, 1990.
8. K.Y.Chien, “Predictions of Channel and Boundary Layer Flows with a Low Reynolds Number Turbulence Model,” AIAA J., Vol.20, pp. 33–38, 1982.
9. W.Szablewski, “Turbulence Drenzschichten in Ablosenahe. Z.”, Angrew. Math. Mech. 49, pp. 215, 1969.
10. S.H.Kang, J.S.Lee, Y.H.Kim and K.Y.Kim,” Numerical Calculations of the Turbulent Flow through a Controlled Diffusion Compressor Blade in Cascade”, (submitted to J. of Turbomachinery), 1992.
11. W.Nitsche et al., “A Computational Preston tube Method,” Turbulent Shear Flows, Vol. 4, 1983, pp. 261–276.
12. S.H.Kang, J.Y.Yoo, J.M.Lee, W.P.Jeon, ” Characteristics of a Turbulent Boundary Layer on the Flat Plate with Sudden Change in Surface Roughness,” Trans. of KSME, 16(12), 1992.
13. R.A.Antonia and R.E.Luxton, “The response of a turbulent boundary layer to a step change in surface roughness. Part 2. Rough to smooth,” J. of Fluid Mech., Vol. 53, 1972, pp. 737–757.
14. H.Tennekes and J.L Lumley, A First Course in Turbulence, The MIT Press, 1974.
15. M.F.Blair and M.J.Werle, “The Influence of Free Stream Turbulence on the Zero-Pressure Gradient Fully Turbulent Boundary Layer,” United Technologies Research Center, Rept. R80– 914388–12, 1980.
Computation of the Tip Vortex Flow on Three-Dimensional Foils with a Parabolized Navier-Stokes Solver
L.R.C.Eca and J.A.C.Falcao de Campos
(Instituto Superior Técnico, Portugal)
M.Hoekstra (MARIN, The Netherlands)
Abstract
A numerical method for the calculation of the incompressible viscous flow at the tip of wings is presented. The method is based on a finite-difference approximation of the Reynolds-averaged Parabolised Navier-Stokes equations for steady incompressible flow. An eddy viscosity algebraic turbulence model is used.
The method is applied to the calculation of the flow at the tip of wings with rectangular planform. The sensitivity of the numerical solution to the accuracy of the boundary conditions imposed at the viscous region boundaries is investigated by changing the location of the boundaries. The results show that the present method uses an efficient approach to the calculation of tip vortex flows. The specification of the inlet boundary conditions is also investigated and the use of Neumann boundary conditions is proposed to obtain a smoother solution close to the inlet boundary. A good agreement between the numerical predictions and experimental data is obtained. However, the size of the vortex core is overpredicted.
Nomenclature
|
|
- Contravariant base vectors. |
|
c |
- Wing chord. |
|
Cp |
- Pressure coefficient, |
|
gij |
- Contravariant metric tensor. |
|
|
Jacobian of the coordinate transformation. |
|
p |
- Pressure. |
|
|
Pressure dependent variable, |
|
Re |
- Reynolds number, |
|
U∞ |
- Free-stream velocity. |
|
Ui |
- Cartesian velocity components. |
|
Vi |
- Contravariant velocity components. |
|
|
- Velocity dependent variables, |
|
x,y,z |
- Cartesian coordinates. |
|
|
- Christoffel symbols of the second kind. |
|
ξ,η,ζ |
- Curvilinear coordinates. |
|
μ |
- Fluid effective viscosity. |
|
ν |
- Fluid kinematic viscosity. |
|
ρ |
- Fluid mass density. |
|
|
- Stress tensor. |
1 Introduction
Several engineering problems are associated with the generation of trailing tip vortices on lifting surfaces of finite span. The dangers created by tip vortex wakes of aircraft to following aircraft and the noise and vibrations caused by rotor blade vortex interactions on helicopters are two examples of such problems in aeronautics. In marine applications, such as hydrofoils and marine propellers, tip vortex flows are often associated with cavitation. The rotational motion around the vortex center creates a low pressure region in the tip vortex core. If the pressure is sufficiently low cavitation will occur. Tip vortex cavitation is a major source of noise generated by the propeller and in some cases is the first type of cavitation to appear. The ability to predict the inception of tip vortex cavitation remains one of the present challenges of the propeller designer.
The objective of the present work was to initiate the development of a numerical method for the calculation of steady viscous flow on propeller blade tips. The flow at the tip of wings/hydrofoils is geometrically simpler than the flow on propeller
blade tips, but the main physical features of tip vortex flows are already present. Furthermore, the effect of the detailed shape of the tip on the tip vortex characteristics can already be investigated. Therefore, the subject of the present paper is the description of a numerical method for the calculation of steady incompressible viscous flow at the tip of wings/hydrofoils.
In incompressible flow, the first approaches to the calculation of tip vortex flows were reported by Govidan et al. in [1] and [2]. Govidan et al. used the parabolised Navier-Stokes equations to calculate tip vortex flows. In Govidan's approach, streamwise diffusion is neglected and the streamwise pressure gradient is obtained from inviscid flow calculations. This means that a full parabolisation of the Navier-Stokes equations is used. The numerical solution of the conservation equations is based on a formulation proposed by Briley and McDonald in [3], that uses a primary-secondary velocity decomposition. Govidan et al. applied the method to a rectangular wing with a rounded tip with promising results, [2].
Also in the present method we adopted the Parabolised Navier-Stokes 1 (PNS) equations, because tip vortex flows have a predominant flow direction. However, in the present method only streamwise diffusion is neglected. This means that only a partial parabolisation is obtained because the elliptic character is retained in the pressure field, the streamwise pressure gradient is obtained in the solution. These equations were proposed by Rubin, [5], for flows with a predominant flow direction. As shown by Rubin in [6], these equations contain all the important terms of the Navier-Stokes equations for high Reynolds number flows. The use of the Parabolised Navier-Stokes equations allows a more efficient solution procedure than the full Navier-Stokes equations.
In the recent literature there are some examples of the application of the PNS for incompressible viscous flow calculations. A method based on these equations has been developed in the last 10 years by Hoekstra and Raven for the calculation of ship stern flows, [ 7], [8], [9] and [10], and more recently Rosenfeld et al. in [11], presented a method for the calculation of the incompressible viscous flow over slender bodies. The method of Hoekstra and Raven is embodied in the computer code PARNASSOS, and was used as the starting point for the present method, which is described in detail in [12].
The paper is organized in the following way : The mathematical formulation with the boundary conditions appropriate to this problem and the turbulence model are presented in section 2. The solution procedure is described in section 3. The results of the application of the method to the calculation of the flow at the tip of rectangular wings are presented and discussed in section 4. The conclusions of this paper are summarized in section 5.
2 Governing Equations
The Navier-Stokes equations can be written in several different forms. The strong conservation form of the equations in general boundary-fitted curvilinear coordinate systems has been derived by several authors, [13], [14], [15], and is generally accepted as the more suitable for numerical purposes, [14]. For steady incompressible flow these equations can be written as :
![]() ,
,
(1)
![]() ,
,
(2)
with
![]() .
.
(3)
The tensorial summation convention applies; p is the pressure, ρ the fluid mass density, μ the fluid effective viscosity2, Vi are the contravariant velocity components, (x1,x2,x3)=(x,y,z) are the coordinates of a cartesian coordinate system, (ξ1, ξ2,ξ3)=(ξ,η,ζ) are the curvilinear coordinates, ![]() is the Jacobian of the transformation between the two systems and gij is the contravariant metric tensor.
is the Jacobian of the transformation between the two systems and gij is the contravariant metric tensor.
Equations (1) and (2) are written in divergence form and so a finite-volume discretization of these equations may satisfy a discrete analogue of the divergence theorem, [16], which means that a conservative discretization of the equations is possible. However, in the Parabolised Navier-Stokes3 equations diffusion is neglected in the streamwise
|
1 |
In [4] Rubin et al. refer to these equations as the Reduced Navier-Stokes equations when diffusion terms in the η momentum equation are neglected. |
|
2 |
The fluid effective viscosity, μ, is obtained with an isotropic eddy-viscosity algebraic turbulence model, see section 2.1 |
|
3 |
The Parabolised Navier-Stokes equations will be denoted by PNS. |
direction and the strong conservation form of the momentum equations, (2), expresses conservation of momentum in the coordinate directions of a cartesian coordinate system, (x,y,z), [16]. In general, the x,y,z directions of a cartesian coordinate system are not flow conforming and so the strong conservation form of the momentum equations may not be compatible with the physical approximations assumed in the PNS equations.
The contravariant form is a more attractive way to write these equations. This form of the equations expresses conservation of mass and momentum along the ξ,η,ζ directions of a boundary-fitted curvilinear grid, which may also be a flow conforming coordinate system. The Reynolds-averaged momentum equations in contravariant form on a boundary-fitted curvilinear grid (ξ,η,ζ) can be written in the following form for a stationary incompressible flow :
![]() ,
,
(4)
where
![]() .
.
The tensorial summation convention applies, ξ is a streamwise coordinate, η a coordinate normal to the wall and ζ a transverse coordinate and ![]() are Christoffel symbols of the second kind. A partial parabolisation is obtained by neglecting the streamwise diffusion in the momentum equations, i. e. the terms with j=1 in the viscous terms of equations (4). The elliptic character of the equations is retained in the pressure field.
are Christoffel symbols of the second kind. A partial parabolisation is obtained by neglecting the streamwise diffusion in the momentum equations, i. e. the terms with j=1 in the viscous terms of equations (4). The elliptic character of the equations is retained in the pressure field.
Equations (4) are written in weak conservation form and so their numerical discretization may originate unphysical source terms in the discretized equations, [17]. Mynett et al., [18], used a different formulation of equations (4) to obtain an invariant finite-volume discretization of the equations. However, their formulation is also in weak conservation form. A finite-volume discretization of Mynett's formulation was applied by Segal et al. in 2-D calculations, [19]. One of the criteria proposed by Segal et al., [19], to evaluate the quality of the numerical discretization is that the discretized form of the conservation equations should be satisfied in a uniform flow. The discretization given by Segal et al., [19], satisfies this property in 2-D cases, but there is no proof that it will do so as well in 3-D, due to the presence of the Christoffel symbols of the second kind in the equations, [17].
An alternative way to write equations (1) and (4) is to use the cartesian velocity components, Ui, as the dependent variables. The contravariant velocity components, Vi, are related to the cartesian components, Ui, by the following equation :
![]() ,
,
(5)
where ![]() is the velocity vector in cartesian components,
is the velocity vector in cartesian components,
![]() ,
,
and ![]() are the contravariant base vectors,
are the contravariant base vectors,
![]() .
.
Substituting (5) in (1), (3) and (4) and with the help of the following metric relation, see for example [20],
![]() ,
,
(6)
the equations of conservation of mass and momentum along the ξ,η,ζ directions become :
![]() ,
,
(7)
![]() ,
,
(8)
with
![]() ,
,
(9)
and
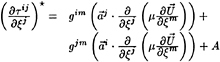 ,
,
(10)
(11)
Streamwise diffusion is neglected, i. e. the terms with j=1 in the viscous terms of equation (8) are dropped.
In the PNS equations written with cartesian components, Ui, as dependent variables only the diffusion terms include derivatives of contravariant base vectors, term A of equation (10). Furthermore, there are no implicit geometrical identities in the equations. In the same equations
written with the contravariant velocity components, Vi, as the dependent variables, (4), the identity (6) is implicitly satisfied. This means that in a certain sense, equations (8) allow a more conservative discretization than equations (4), because the identity (6) has to be respected numerically in the discretization of equations (4) to avoid unphysical source terms in the discretized equations. A simple example is given by the calculation of a uniform flow with a discretized form of the PNS equations, [17]. In a uniform flow, the discretized momentum equations (8) are satisfied independently of the grid metric properties and of the discretization scheme because all the terms are identically zero. We note that equations (8) are not in divergence form and so the use of a finite-volume discretization technique, that would ensure the satisfaction of a discrete analogue of the divergence theorem, is not possible.
As mentioned before, the use of parabolised equations for the flow simulation implies that a physical meaning is attached to the grid, since diffusion is neglected in the streamwise direction. This means that if the ξ,η,ζ system is roughly flow conforming, the use of contravariant velocity components as dependent variables is much more attractive than the use of cartesian components, because it enables the possibility of using the physical characteristics of the flow in the solution procedure.
Taking into account these considerations, the PNS equations written with the cartesian components, Ui as the dependent variables are used to obtain the discretized equations, but the dependent variables used in the calculation are the contravariant velocity components. This means that the relations between cartesian components and contravariant components,
![]() , (12)
, (12)
are used to obtain the final form of the discretized equations after the discretization of the equations (7) and (8). With this procedure, we exploit of the numerical advantages of discretizing the contravariant PNS equations with Ui as velocity dependent variables, and keep the flow-conforming contravariant velocity components as the dependent variables of the discretized equations. We note that substituting (12) in (7) and (8) we obtain the PNS equations written with Vi as dependent variables, equations (1) and (4). However, in the present formulation the substitution of (12) is made after the discretization of equations (7) and (8), which means that the discretization of the metric terms of the contravariant PNS equations with Vi as the dependent variables does not need to be dealt with explicitly.
Due to the existence of grid singularities the velocity variables chosen are not the contravariant velocity components, V1,V2 and V3, [10], but these components multiplied by the Jacobian of the transformation, ![]() . At present, we also multiply the pressure by the Jacobian of the transformation to obtain the pressure dependent variable, for numerical reasons :
. At present, we also multiply the pressure by the Jacobian of the transformation to obtain the pressure dependent variable, for numerical reasons :
(13)
The flow solution is obtained by solving the continuity and momentum equations with the appropriate boundary conditions. The velocity component in the normal direction, V2, is obtained by solving the continuity equation and the three momentum equations are used to obtain the remaining two components of the velocity and the pressure. The diffusion terms in the η momentum equation are dropped. As mentioned by Rubin et al. in [4] if the η coordinates are locally normal to ξ—at least near boundaries—all the diffusion terms in the momentum equation in the normal direction, η, may be dropped. This means that normal pressure variations, ![]() , are essentially inviscid in origin and so the present set of equations represents an extension of interacting boundary layer theory.
, are essentially inviscid in origin and so the present set of equations represents an extension of interacting boundary layer theory.
2.1 Boundary Conditions
The flow around the tip of a wing has six boundaries. A schematic view of these boundaries in the physical and computational domain is given in figure 1. The six boundaries of the flow domain are denoted as follows : The inlet4ABCD and the outlet EFGH. The external boundary BFGC, the wing surface and the inner5 boundaries ABFE and CDHG, which constitute the inlet and outlet of the cross-flow.
The inlet boundary is placed downstream of the stagnation region, because in the present method a downstream calculation procedure is used. Furthermore, a zonal approach is adopted in the present method and so the stagnation region may
|
4 |
In figure 1 the inlet boundary is a spanwise section of the wing. |
|
5 |
In figure 1 the inner boundary is a chordwise section of the wing. |
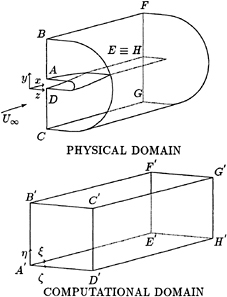
Figure 1: Illustration of the boundaries of the calculation of the flow at the tip of wings in the physical and computational domains.
be predicted with a boundary-layer method. The inlet boundary is not a natural boundary of the flow and so the choice between Dirichlet and Neumann boundary conditions is not clear, because in both cases some approximations will be required to specify the boundary conditions. From the implementation point of view, a straightforward option is to specify the three velocity components at the inlet boundary. However, it may be difficult to obtain a good estimate of the inlet velocity profiles and this may produce a non-smooth behaviour of the solution near the inlet boundary.
To improve the smoothness of the solution near the inlet boundary, Hoekstra in [10] suggests the use of a Neumann boundary condition for the normal velocity component, V2. In the present work a different approach was tested. Neumann boundary conditions are applied to the three velocity components. A good estimate of the streamwise velocity gradient at the inlet boundary may be even more difficult than the estimate of the velocity profiles, but since the specification of streamwise velocity gradient is a weaker type of boundary condition, a less accurate prediction of its value should be less damaging to the solution than the use of a poor estimate of the velocity profiles.
In the present paper the two types of boundary conditions are compared, respectively the specification of velocity profiles and the specification of stream wise velocity gradient. In both cases the specified values are obtained with the help of a potential flow calculation, [21], and standard boundary layer profiles, [22].
At the outlet boundary a pressure boundary condition is required. The use of Dirichlet boundary conditions is not a good choice. A good approximation of the pressure field at the outlet boundary will be hard to obtain, due to the presence of the tip vortex and its influence on the pressure field. This leads us to choose a Neumann boundary condition. In the present calculations the streamwise pressure gradient was set equal to zero.
The typical cross-sections of the wing and of the wake in the physical space and in the computational domain are illustrated in figure 2.
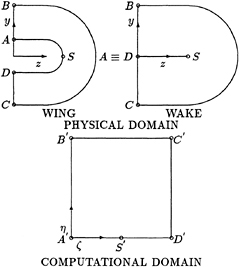
Figure 2: Illustration of the typical cross-section on the wing and wake and of the computational domain.
Boundary BC is the external boundary (surface BFGC of figure 1), where the tangential components of the velocity and the pressure are prescribed by a potential flow calculation, [21]. Boundaries AB and DC are the inlet and outlet of the cross-flow (surfaces ABFE & CDHG of figure 1). Exact boundary conditions are available if the inner boundary is placed at the symmetry plane of the wing. For a given number of grid nodes, a finer discretization of the tip vortex region can be obtained if the inner boundary
is placed close to the tip. However, we will no longer have exact boundary conditions at the inner boundary and so approximate boundary conditions will have to be used. In the present applications the cross-stream derivatives ![]() of the cartesian velocity components and of the pressure were set equal to zero. We note that it is not safe to impose zero cross-stream derivatives directly to the dependent variables, since they are a function of the grid properties.
of the cartesian velocity components and of the pressure were set equal to zero. We note that it is not safe to impose zero cross-stream derivatives directly to the dependent variables, since they are a function of the grid properties.
Boundary AD has different properties in the cross-sections located on the wing and on the wake. On a cross-section of the wing it coincides with the wing surface, where the no-slip condition applies. The three velocity components are set equal to zero and the flow is calculated down to the wing, without wall functions. At the wake section, boundary AD is a fictitious boundary in the physical space. All the variables have to be calculated along this ‘boundary', since the boundary nodes of the computational domain are field nodes in the physical space. A special treatment has to be included for point S where the transformation is singular, ![]() .
.
2.2 Turbulence Model
There is a wide range of turbulence models available in the literature varying from the simple eddy-viscosity turbulence models, which can be algebraic or solve one or two transport equations, to the more complex second moment closures, which solve transport equations for each of the Reynolds stresses appearing in the momentum equations. The computer time required by the several models available is very different and according to Launder, [23], the use of a second moment closure can increase the computational time by 50 to 500% in comparison with an eddyviscosity model. Although Launder suggests that the second moment closure is the more reliable for complex flows, [23], the time penalty is still very high compared with eddy-viscosity turbulence models. Bearing in mind that the more popular two-equation eddy-viscosity models have well known shortcomings, like for example the poor performance of the k–∈ model in adverse pressure gradient, [24], we have adopted at this stage of the development the simple algebraic isotropic eddyviscosity model of Cebeci & Smith, [25], which was already incorporated in PARNASSOS, [9].
The present implementation of the Cebeci & Smith turbulence model follows an approach similar to the one given by Cebeci et al. in [26]. A detailed description can be found in [12].
3 Numerical Solution
3.1 Discretized Equations
The continuity and contravariant momentum equations written for the cartesian velocity components, (7) and (8), are discretized in a single block regular grid by a finite-difference approximation. The discretization procedure is similar to the one used in PARNASSOS. All the variables are defined on the grid nodes, (i,j,k)6 since grid staggering is not used and Newton linearization is applied to the convective terms. The momentum equation in the ξ and ζ directions are discretized at the nodal points (i,j,k). The momentum equation in the normal direction, η, is discretized at ![]() and the continuity equation at
and the continuity equation at ![]() . A description of the different schemes used in the discretization process can be found in references [7] to [10] or [12]. With a careful discretization of the diffusion terms, [17], the present discretization technique only requires first derivatives of the grid coordinates.
. A description of the different schemes used in the discretization process can be found in references [7] to [10] or [12]. With a careful discretization of the diffusion terms, [17], the present discretization technique only requires first derivatives of the grid coordinates.
The contribution to the discretized equations of the cartesian components of the velocity and pressure at the singularity is dealt with explicitly. The cartesian velocity components and pressure are taken from a previous iteration7 and substituted in the discretized equations. This explicit treatment requires that the cartesian velocity components and pressure at the singularity have to be updated in the iterative procedure used to solve the discretized equations. The present approach is to obtain the cartesian velocity components and the pressure at the singularity in every iteration by the arithmetic mean of the surrounding nodes.
3.2 Solution Procedure
The solution procedure is based on the one used in the code PARNASSOS, [7], [8], [9] and [10]. Here we will only describe the major features of the procedure. A more detailed description can
|
6 |
The indices refer to the ξ,η and ζ direction, respectively. |
|
7 |
The solution procedure has to be iterative due to the non-linearity of the equations. |
be found in [12]. The solution is obtained iteratively by a space-marching process. Two iteration cycles can be distinguished : the local and the global iteration process.
The local iteration process refers to the solution of the flow at a streamwise station where all the grid nodes have the same main-stream coordinate, ξ. The solution is obtained simultaneously for all the variables with a Coupled Strongly Implicit Procedure (CSIP), [5]. Iteration is required by the non-linearity of the differential equations and by the incomplete factorization of the CSIP.
The discretization of the continuity equation at ![]() imposes that the normal velocity dependent variable,
imposes that the normal velocity dependent variable, ![]() , has to be specified at the boundary η=0 (Boundary AD of figure 2). On the wing surface
, has to be specified at the boundary η=0 (Boundary AD of figure 2). On the wing surface ![]() is known from the no-slip condition but in the wake its value has to be determined as part of the solution. The discretization of the η momentum equation at
is known from the no-slip condition but in the wake its value has to be determined as part of the solution. The discretization of the η momentum equation at ![]() gives two algebraic equations per node for the determination of
gives two algebraic equations per node for the determination of ![]() at the ‘boundary' η=0, because each grid node of the physical domain is transformed into two in the computational domain8. One of the two equations can be used to obtain an equation for
at the ‘boundary' η=0, because each grid node of the physical domain is transformed into two in the computational domain8. One of the two equations can be used to obtain an equation for ![]() along the fictitious boundary. However, it is not clear which equation should be used and large overshoots of
along the fictitious boundary. However, it is not clear which equation should be used and large overshoots of ![]() can be obtained at the fictitious boundary with this approach. In the present method
can be obtained at the fictitious boundary with this approach. In the present method ![]() is calculated to ensure continuity of the pressure on the fictitious boundary for every iteration of the CSIP.
is calculated to ensure continuity of the pressure on the fictitious boundary for every iteration of the CSIP.
The discretized momentum equations at a streamwise station where all the grid nodes have the same main-stream coordinate, ξ, include the pressure field at the downstream station. This implies that in order to obtain the solution by a space-marching process in the main-stream direction, the pressure field at the downstream stations has to be taken from a previous sweep. The downstream marching process has to be repeated until the pressure field does not change between consecutive sweeps of the domain. This iterative procedure constitutes the global iteration process. To increase the convergence rate of this process each downstream sweep is followed by an upstream sweep to update the pressure field, [10]. The two sweeps form a predictor-corrector method for the pressure, which is constructed adding a quasitime derivative of the pressure to the ξ momenturn equation, [10]. Another improvement in the pressure field convergence can be obtained by using a multiple stepsize in the first sweeps to allow a rapid approach of the correct pressure level, [9]. This means that the grid is initially coarse in the main-stream direction and is subsequently refined in two or three stages.
4 Results and Discussion
A rectangular wing of aspect ratio 4 with a NACA 0015 airfoil section was used to investigate several numerical and physical aspects of the calculation of tip vortex flows with the present method. These aspects include the sensitivity to the extent of the computation domain. Namely, the location of the outlet boundary, inner boundary and external boundary. Numerical studies were also performed to evaluate the influence of the type of boundary conditions at the inlet. The latter studies were carried for two tip geometries. The different aspects investigated were analysed by comparing different numerical solutions with a reference case to be described below in section 4.1.
The calculations were all performed on a CRAY YMP. The code does not use parallelization, but the use of vectorization proved to be efficient in reducing the CPU time required. On the CRAY YMP the code runs typically at 70 MFlops with vectorization and at 8 MFlops without it.
In all the calculations, the global iteration process was stopped when the maximum pressure difference between consecutive sweeps, (ΔCp)max, was less than 5.0×10−3. The convergence criteria of the CSIP were differences between consecutive iterations of less than 1.0×10−3U∞ in the physical components of the velocity and 2.0×10−4 in Cp.
4.1 Reference Test Case
The reference case in the present comparisons is a rectangular wing of aspect ratio 4 with a NACA 0015 airfoil section and a rounded tip, obtained by rotating the wing section at the tip around its chord. The angle of attack is 6.5 degrees and the Reynolds number based on the chord length is 8.5×105.
The boundaries of the viscous flow region for the reference case were placed at the following locations :
|
8 |
The discretization of the ξ and ζ momentum equations is centered at (i,j,k) and so the two algebraic equations are equal. |
-
The inlet boundary is 10% of the chord downstream of the leading edge.
-
The inner boundary, inlet and outlet of the cross-flow, is placed at a distance of 40% of the chord length inboard of the tip of the wing.
-
The distance between the external boundary and the wing is 30% of the chord length at the station of maximum thickness of the wing.
-
The outlet boundary is 1.82 chords downstream of the trailing edge.
The discretization of the viscous flow region was performed with 145 streamwise stations, including 81 on the wing and 64 in the wake. In the transverse sections of each streamwise station a 51×47 2-D grid was generated with an algebraic interpolation technique described in [12]. An illustration of the grid is given in figure 3. To obtain a clearer visualization of the grid the plots of the grid at the boundaries do not include all the grid lines.
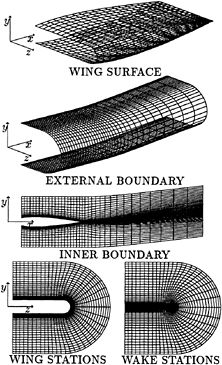
Figure 3: Illustration of the grid used in the reference case.
The convergence criteria were satisfied after 29 sweeps and the CPU time spent in this calculation was 38 minutes and 48 seconds.
4.2 Sensitivity to the Choice of the Size of the Computation Domain
In the present zonal approach to the calculation of tip vortex flows, some of the boundaries of the viscous region are artificial boundaries and so the specification of the boundary conditions will include approximations of the local flow. Examples of these boundaries are the inlet and outlet planes, the external boundary and the inner boundary. This excludes only the wing surface where we have a natural boundary of the flow. This section is dedicated to the evaluation of the sensitivity of the solution to the specification of the boundary conditions at the artificial boundaries of the viscous flow region, by changing their location. The inlet boundary is excluded from this investigation because the procedure used to estimate the inlet boundary conditions is based on simple approximations and so the comparison between solutions with inlet stations at different locations is not very conclusive.
The differences between the various calculations will be illustrated by comparing the solutions in two different streamwise stations. The two selected stations are located in the region of formation of the tip vortex, ![]() , and in the near wake,
, and in the near wake, ![]() .
.
4.2.1 Outlet Boundary
At the outlet boundary a streamwise pressure boundary condition is required. In the present calculations the streamwise pressure gradient was set equal to zero, which is only true for an outlet station sufficiently far downstream of the wing. To evaluate the influence of this approximate boundary condition three different calculations were performed with outlet boundaries at ![]() = 1.741,
= 1.741, ![]() (reference case), and
(reference case), and ![]() . The three grids differ only in the location of the outlet boundary.
. The three grids differ only in the location of the outlet boundary.
The differences between the dimensionless pressure and cartesian velocity components9 calculated with outlet boundaries at ![]() and
and ![]() are smaller than 1.0×10−3 for all the streamwise stations, with the exception of the station at
are smaller than 1.0×10−3 for all the streamwise stations, with the exception of the station at ![]() , where a maximum Cp difference of 5.0×10−3 occurs. This means that
, where a maximum Cp difference of 5.0×10−3 occurs. This means that
|
9 |
The cartesian velocity components are divided by the undisturbed velocity, U∞, to obtain dimensionless components. |
the imposition of zero streamwise pressure gradient at , has a neglible ![]() effect on the solution.
effect on the solution.
The differences between the solutions with outlet stations at ![]() and
and ![]() are larger than in the previous comparison. Downstream of
are larger than in the previous comparison. Downstream of ![]() the Cp differences between the two solutions become larger than 5.0×10−3 and at
the Cp differences between the two solutions become larger than 5.0×10−3 and at ![]() the maximum Cp difference is 0.01. Upstream of the outlet boundary the differences decrease rapidly and at
the maximum Cp difference is 0.01. Upstream of the outlet boundary the differences decrease rapidly and at ![]() the maximum differences are smaller than 5.0×10−3.
the maximum differences are smaller than 5.0×10−3.
4.2.2 Inner Boundary
A simple approach was adopted for the specification of the boundary conditions at the inner boundary. The cross-stream derivatives of the pressure and of the cartesian velocity components are set equal to zero. The influence of these approximate boundary conditions was investigated by comparing the solutions of two calculations with inner boundaries at different locations.
One of the calculations is the reference case, where the inner boundary is located at 80% of the half-span, ![]() . The other calculation was performed on a grid with the inner boundary located at approximately 70% of the half-span,
. The other calculation was performed on a grid with the inner boundary located at approximately 70% of the half-span, ![]() . This grid was constructed by adding extra grid lines at the inner boundary on each streamwise station of the grid used in the reference case. This is illustrated in figure 4 for a wing station.
. This grid was constructed by adding extra grid lines at the inner boundary on each streamwise station of the grid used in the reference case. This is illustrated in figure 4 for a wing station.
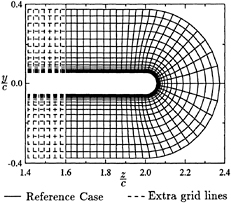
Figure 4: Comparison between the grid of the reference case and the grid with the inner boundary moved 20% of the chord inboard of the tip.
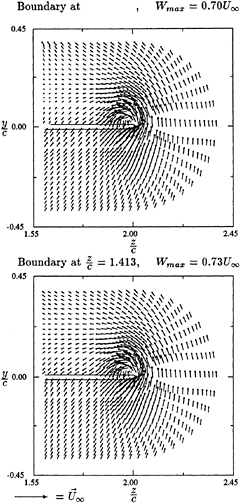
Figure 5: Comparison of the transverse velocity fields at ![]() for solutions obtained with different locations of the inner boundary.
for solutions obtained with different locations of the inner boundary.
The comparison of the two solutions in their common region is presented in figures 5 and 6, where Wmax stands for maximum transverse velocity component. In the wing station at ![]() the imposition of zero cross-stream derivatives at
the imposition of zero cross-stream derivatives at ![]() instead of 1.413 reduces the cross-flow velocity components. This reduction of cross-flow at
instead of 1.413 reduces the cross-flow velocity components. This reduction of cross-flow at ![]() , caused by the imposed boundary conditions, produces a non smooth behaviour of the transverse velocity field close to the external boundary on the upper surface. We recall that at the external boundary the tangential velocity components are imposed. A smooth so-
, caused by the imposed boundary conditions, produces a non smooth behaviour of the transverse velocity field close to the external boundary on the upper surface. We recall that at the external boundary the tangential velocity components are imposed. A smooth so-
lution is obtained at the same location with the inner boundary moved inboard, which indicates that the perturbation in the transverse velocity field is caused by the imposition of zero cross-stream derivatives at the boundary and not by the imposed tangential velocity component at the external boundary. In the tip vortex region the two solutions are similar. However, the larger crossflow velocities, obtained with the inner boundary moved inboard, produce a reduction in Cp minimum at the lower surface of the tip of 0.04. In the near-wake station, ![]() , the comparison between the cross-flow velocities of the two solutions is similar to the one described for the wing station.
, the comparison between the cross-flow velocities of the two solutions is similar to the one described for the wing station.
The results obtained with the approximate boundary conditions suggest that the present approach is more efficient in the calculation of the tip vortex, than placing the inner boundary at the symmetry plane of the wing to obtain exact boundary conditions.
4.2.3 External Boundary
At the external boundary the tangential velocity components and the pressure are prescribed by a potential flow solution. The circulation imposed in the potential flow calculation to satisfy the Kutta condition at the wing's trailing edge does not include the viscous effects and so it is different from the circulation of the flow external to the viscous domain that would match the viscous solution. This means that the interaction between the viscous and inviscid solutions must be included in the solution procedure to obtain the exact boundary conditions at the external boundary. Since we do not perform viscous/inviscid interaction, the present boundary conditions are approximate boundary conditions. As a result of these approximate boundary conditions a pressure discontinuity is obtained at the trailing edge. We note that the circulation imposed in the potential flow calculation is independent of the location of the external boundary, but the tangential velocity components and pressure imposed at the external boundary are approximate values and so the location of the external boundary may influence the solution of the viscous region of the flow. To investigate the effect of the specification of the boundary conditions at the external boundary the solutions of two calculations with external boundaries at different locations are compared.
The two calculations were performed on grids with the external boundary located at a distance
Figure 6: Comparison of the pressure fields at two different stations for solutions obtained with different locations of the inner boundary.
of 30% (reference case) and 42.5% of the chord length at the station of maximum thickness of the wing. The calculation performed with the external boundary closer to the wing is the reference case. The grid of the other calculation was constructed by adding extra grid lines10 at the external boundary in each streamwise station of
|
10 |
The procedure is equivalent to the one illustrated in figure 4. |
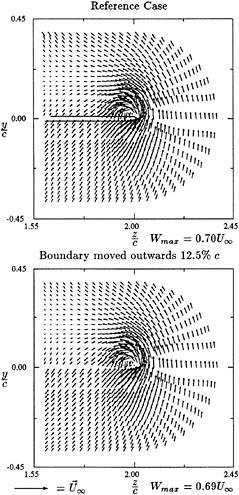
Figure 7: Comparison of the transverse velocity fields at ![]() for solutions obtained with different locations of the external boundary.
for solutions obtained with different locations of the external boundary.
the grid used in the reference case.
The comparison of the two solutions in their common region is presented in figures 7 and 8.
In the wing station at ![]() there are no significant differences between the transverse velocity fields of the two calculations. The non-smooth behaviour of the transverse velocity field close to the external boundary on the upper surface is not present in the solution obtained with the external boundary moved outwards, because in the wider computation domain the local crossflow components are determined by the boundary condition at the inner boundary without a conflict with the conditions imposed on the external boundary
there are no significant differences between the transverse velocity fields of the two calculations. The non-smooth behaviour of the transverse velocity field close to the external boundary on the upper surface is not present in the solution obtained with the external boundary moved outwards, because in the wider computation domain the local crossflow components are determined by the boundary condition at the inner boundary without a conflict with the conditions imposed on the external boundary
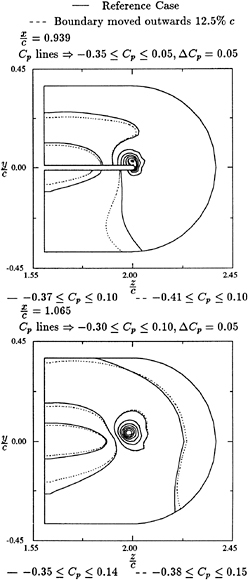
Figure 8: Comparison of the pressure fields at two different stations for solutions obtained with different locations of the external boundary.
(compare the earlier discussion in section 4.2.2). The pressure fields of the two solutions have clear differences close to the external boundary of the reference case, which in the lower surface also affect the surface pressure distribution. However, in the tip vortex region the effect of moving the external boundary outwards is not significant.
In the near wake station, ![]() , the comparison between the cross-flow velocities of the two solutions is similar to the one described for the wing station. The differences of the two solutions close to the external boundary of the reference case are larger than in the wing station, but the effect in the tip vortex region is still very small.
, the comparison between the cross-flow velocities of the two solutions is similar to the one described for the wing station. The differences of the two solutions close to the external boundary of the reference case are larger than in the wing station, but the effect in the tip vortex region is still very small.
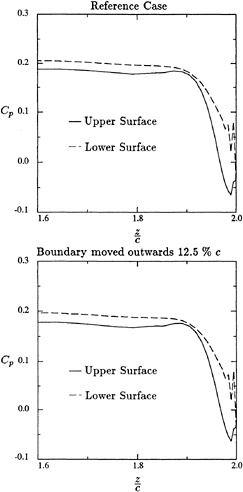
Figure 9: Pressure distribution at the trailing edge computed from the upper and lower surfaces of the wing for solutions obtained with different locations of the external boundary.
The pressure discontinuity at the trailing edge is illustrated in figure 9 for the calculations with the two different locations of the external boundary. The larger pressure discontinuities are obtained in the tip vortex region, where a small pressure oscillation is obtained on the lower surface for both solutions. A small difference between the pressure level of the two solutions is obtained, but the pressure discontinuity is the same in the two calculations. These results indicate that the pressure discontinuity is mainly determined by the difference in circulation of the outer flow in the potential and viscous flow calculations, which is not affected by the change in the location of the external boundary.
The comparison of the results of the calculations performed with different locations of the external boundary showed that the influence of the approximate boundary conditions imposed at the external boundary on the solution in the tip vortex region are small. These results suggest that the present zonal approach is acceptable for tip vortex calculations, because it reduces substantially the size of the region to be discretized, compared with an alternative external boundary at a location where undisturbed flow conditions could be imposed. Further investigations will be required to address the influence of the viscous/inviscid interaction.
4.3 Specification of the initial velocity profiles
At the inlet station two types of boundary conditions were tested : prescribed velocity profiles and prescribed streamwise velocity gradients. It should be mentioned the the Neumann condition was applied as a Dirichlet condition, updated in the course of the solution process. So in the case of prescribed streamwise velocity gradient the velocity profiles at the inlet boundary are obtained iteratively. This makes the convergence usually slower than in the case of prescribed velocity profiles. However, the specification of velocity profiles at the inlet station may be difficult and a poor approximation of the initial velocity profiles can cause divergence of the solution close to the inlet station.
Our approach to the specification of the initial velocity profiles is based on simple assumptions. The velocity profiles are derived from standard boundary layer profiles, [22], defined by the local momentum thickness, θ, and skin friction coefficient, Cf. The values of θ and Cf at the inner boundary are obtained from a 2-D calculation, [27], and the spanwise variation of θ and Cf is obtained by a Hermite interpolation of the predicted 2-D values on the upper and lower sur-
faces at the inner boundary. In the potential flow region the velocity profiles are obtained from a potential flow solution, [21]. Due to numerical difficulties with the source-based panel method, it is not possible to calculate the potential flow solution at very small distances to the wing surface and so we have calculated the velocity components along a line η=constant at a sufficient distance from the wing surface. In the region between this line and the viscous region thickness, determined by the specified θ and Cf, we assume that the potential flow velocity components do not change in the η direction.
The streamwise velocity gradient is specified applying the procedure described above to the first two stations of the grid and using a first order approximation to the derivatives. With this weaker boundary condition of the Neumann type, the velocity profiles at the inlet boundary are allowed to adjust to the local flow characteristics. As mentioned before, the streamwise velocity gradient is not specified implicitly in the calculation. The velocity profiles at the inlet boundary are updated in the course of the iteration process to obtain the specified streamwise velocity gradient. This makes the convergence rate of the solution lower and highly time consuming because the initial profiles change between consecutive sweeps. In the present solution the inlet velocity profiles were updated only when the maximum pressure difference between consecutive sweeps at the second streamwise station was ΔCp>2.0×10−2.
The flow of the reference case was calculated with both types of inlet conditions. The results obtained with specified velocity profiles at the inlet boundary exhibit a rapid change of the pressure field in the initial streamwise stations. A clear visualization of the disturbances caused by the specification of the inlet velocity profiles is presented in figure 10, where the pressure field at the first calculated station, ![]() , of the two solutions is compared. The pressure field obtained with specified inlet velocity profiles is clearly disturbed by the specification of the initial velocity profiles. With specified streamwise velocity gradient a smooth pressure field is obtained at
, of the two solutions is compared. The pressure field obtained with specified inlet velocity profiles is clearly disturbed by the specification of the initial velocity profiles. With specified streamwise velocity gradient a smooth pressure field is obtained at ![]() .
.
We found that the disturbances in the solution obtained with specified velocity profiles are restricted to the three initial stations and so it is important to know the effect of the inlet boundary conditions in the generation and development of the tip vortex. The calculated pressure fields of the two solutions are compared in figure 11,
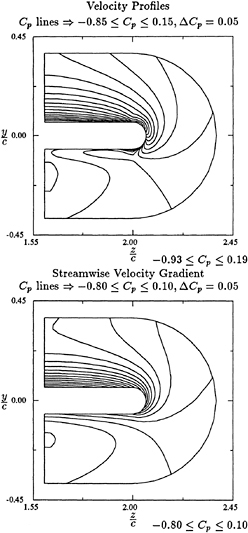
Figure 10: Comparison of the pressure fields at the first streamwise station for solutions obtained with different inlet boundary conditions.
for the streamwise stations at ![]() and
and ![]() .
.
In the wing station, ![]() , the minimum pressure coefficient is 0.05 lower in the solution obtained with Neumann boundary conditions at the inlet station. The differences are smaller than the ones obtained at the inlet stations, but the effect of the different inlet boundary conditions is still visible in this region. However, the vortex location is virtually the same in the two calculations. In the wake stations,
, the minimum pressure coefficient is 0.05 lower in the solution obtained with Neumann boundary conditions at the inlet station. The differences are smaller than the ones obtained at the inlet stations, but the effect of the different inlet boundary conditions is still visible in this region. However, the vortex location is virtually the same in the two calculations. In the wake stations, ![]() in figure
in figure
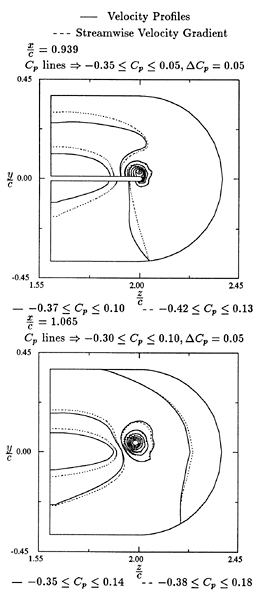
Figure 11: Comparison of the pressure fields at two different streamwise stations for solutions obtained with different inlet boundary conditions.
11, the comparison of the two solutions is similar to the one described above for the wing station. The differences between the two solutions have become smaller than in the wing station; the tip vortex location is again hardly affected.
4.3.1 Effect of the Tip Geometry
It is interesting to know whether the behaviour of the solution process for the two types of inlet boundary conditions is the same for other tip geometries. Therefore the flow at the tip of a rectangular wing with a squared tip was also calculated. The wing aspect ratio (4) and airfoil section (NACA 0015) are the same as in the reference case. The same angle of attack and Reynolds number were used, respectively 6.5 degrees and 8.5×105. In the previous test cases the tip geometry is smooth. In a wing with a squared tip the geometry has two discontinuities in the tangential derivatives. The local features of the flow close to the geometry discontinuities make the specification of the inlet velocity profiles more difficult in this case. In the present specification of inlet velocity profiles no special treatment was included to account for the geometry discontinuities, the simple procedure described before was applied without any modifications and so the inlet conditions will locally be highly inaccurate. The grid used in these calculations is similar to the grid of the reference case illustrated in figure 3. The location of the boundaries and the streamwise stepsize are equal to the ones used in the reference case.
In the calculation performed with specified velocity profiles at the inlet boundary the pressure field did not converge in the initial stations of the grid. The pressure field showed a non-smooth behaviour in these initial stations and several jumps in (ΔCp)max are obtained in the first streamwise station downstream of the inlet plane. Nevertheless in the last sweeps performed, the pressure differences between consecutive sweeps downstream of the initial streamwise stations are three orders of magnitude smaller than the pressure differences close to the inlet boundary.
The same flow was calculated with specified streamwise velocity gradient at the inlet boundary. In this solution the inlet velocity profiles were updated only when the maximum pressure difference between consecutive sweeps at the second streamwise station was ΔCp>2.0×10−2. With this type of boundary conditions it is possible to obtain a converged pressure field in the whole computation domain. The imposition of a weaker boundary condition at the inlet boundary removed the jumps of (ΔCp)max at the inlet boundary obtained with specified velocity profiles.
The pressure field at the first calculated sta-
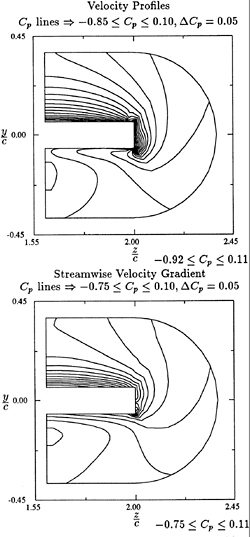
Figure 12: Comparison of the pressure fields at the first streamwise station for solutions obtained with different inlet boundary conditions.
tion, ![]() , of the two solutions is compared in figure 12. The disturbances in the pressure field close to the inlet boundary are evident and a particularly non-smooth solution is obtained close to the geometry discontinuities. A smoother solution is obtained at
, of the two solutions is compared in figure 12. The disturbances in the pressure field close to the inlet boundary are evident and a particularly non-smooth solution is obtained close to the geometry discontinuities. A smoother solution is obtained at ![]() with specified streamwise velocity gradient.
with specified streamwise velocity gradient.
The effect of the different inlet boundary conditions on the tip vortex generation and development is similar to the one obtained on a wing with a rounded tip.
These results show that the specification of inaccurate velocity profiles at the inlet boundary can deteriorate the convergence of the method close to the inlet boundary. The results obtained with streamwise velocity gradient at the inlet boundaries did not reveal any convergence difficulties of the method and the use of weaker boundary conditions enabled the adjustment of the solution to the local flow characteristics. This suggests that innaccuracies in the specification of the streamwise velocity gradient are less damaging to the solution process than inaccuracies in the specification of inlet velocity profiles. However, with Neumann boundary conditions at the inlet boundary the method becomes more time consuming than with specified velocity profiles.
4.4 Comparison with Experimental Results
The results obtained with the present method are compared with experimental results available in the literature, and with the results of the method of Govidan et al., [2], to evaluate its performance. The test cases include two wings of rectangular planform with a squared and a rounded tip.
4.4.1 Wing with Rounded Tip
The first test case is a rectangular wing of aspect ratio 6 with a NACA 0012 airfoil section and a rounded tip. The purpose of this test case is to compare the results of the present method with the results of the method of Govidan et al., [2]. The latter also uses a space-marching process to obtain the solution, but with a single sweep through the computational domain in the streamwise direction, because a full parabolisation of the Navier-Stokes equations is used, the streamwise pressure gradient is obtained from an inviscid flow solution. Although a different solution method is adopted by Govidan et al., the physical approximations assumed in the governing equations are the same as the ones used in the present method with the exception of the streamwise pressure gradient. The comparison of the results of the two methods enables the evaluation of the streamwise pressure gradient influence on tip vortex calculations. The calculations were performed for the conditions given in [2] : Angle of attack of 6.18 degrees and Reynolds number based on the chord length of 7.52×105.
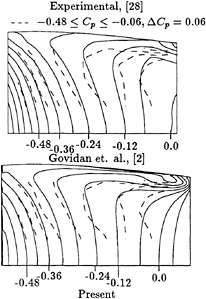
Figure 13: Comparison between the predicted pressure distribution on the wing surface and experimental results for the flow at the tip of a rectangular wing, with an angle of attack of 6.18 degrees and a Reynolds number of 7.52×105.
The location of the boundaries of the computation domain were identical to the ones used by Govidan et al. in [2], with the exception of the outlet boundary. The results presented in [2] include only the wing region, the outlet station is 6% of the chord upstream of the trailing edge. In the method of Govidan et al., the flow solution at a transverse plane depends only on upstream occurrences and so there are no streamwise boundary conditions required at the outlet plane. In the present method, the elliptic character of the equations is retained in the pressure field and so a downstream pressure boundary condition is required at the outlet station. Close to the trailing edge of the wing, it is not possible to impose a physically acceptable boundary condition and so the outlet station has to be moved into the far wake. In the present grid, the outlet station is located three chords downstream of the trailing edge. The inlet boundary is 15% of the chord downstream of the leading edge. Like in the calculations of Govidan et al., the inlet boundary conditions of the present calculations consist of specified velocity profiles. The inner boundary, inlet and outlet of the cross-flow, is placed at a distance of 40% of the chord length inboard of the tip of the wing. The distance between the external boundary and the wing is 30% of the chord length at the station of maximum thickness of the wing.
A number of 161 streamwise stations was used, including 81 on the wing and 80 on the wake. A 40×47 2-D grid was generated on each streamwise station11.
In figure 13 the calculated pressure distribution on the wing surface is compared with the predictions of Govidan et al., [2], and the experimental results of Gray et al. [28], given in [2]. The present results show better agreement with the experimental results than the predictions of Govidan et al. Notice the mismatch of predicted and experimental isobars close to the leading edge in the results of Govidan et al. A significant improvement is obtained in the prediction of the pressure distribution close to the tip. We note that Govidan et al., [2], used a 120×40×47 grid to discretize the viscous region between 15% and 94% of the chord, while the present results were obtained with an equal number of nodes in the transverse sections but with only 81 stations between 15% of the chord and the trailing edge.
4.5 Wing with Squared Tip
Experimental results including mean velocity LDV measurements have been reported recently by Falcão de Campos et al., [29], for a rectangular wing of aspect ratio 4 with a NACA 0015 airfoil section and a squared tip. The experimental investigations included flows at three different angles of attack, 4.5, 6.5 and 8.5 degrees at a Reynolds number of 8.5×105. These flows have been numerically simulated with the present method.
The boundaries of the viscous flow region were placed in the same locations as in the reference case of section 4. The grid has 145 streamwise stations, including 81 on the wing and 64 on the wake. In the transverse sections of each streamwise station a 51×47 2-D grid was generated. The calculations were performed with Neumann boundary conditions at the inlet station, i.e. the streamwise velocity gradient is specified.
The experimental measurements were performed on planes perpendicular to the undisturbed flow and the measuring plane does not coincide with a grid plane. To compare the present
|
11 |
The grid is similar to the one used in the reference test case illustrated in figure 3. |
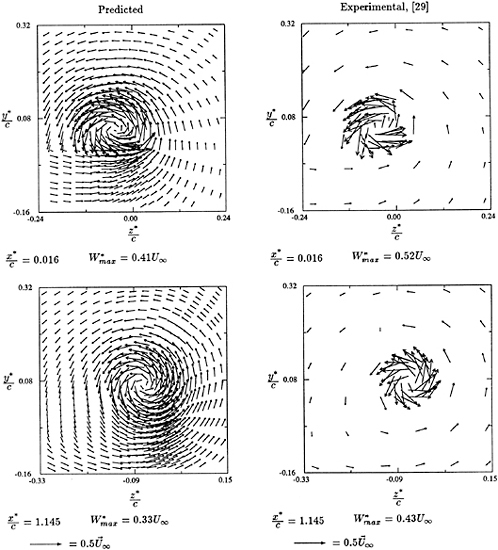
Figure 14: Comparison between the present predictions and the experimental results for the flow at the tip of a rectangular wing with a squared tip. Angle of attack 6.5 degrees and Reynolds number of 8.5×105.
results with the experimental data the velocity components at the experimental measuring plane are obtained from the values at the grid nodes using linear interpolation along the ξ lines. Furthermore, the comparisons are performed in the cartesian coordinate system of the experimental investigations, which has the x* direction aligned with the undisturbed flow, U∞. In the present comparisons the origin of the coordinate system (x*,y*,z*), is placed at the tip of the trailing edge, (x*=0, y*=0, z*=0) ≡ (x=1.0,y= 0.0,z=2.0).
The numerical predictions of the transverse velocity fields at ![]() and
and ![]() are compared with the experimental results in figure 14, for the flow with an angle of attack of 6.5 degrees. An excellent correlation of the tip vortex location is obtained in both planes, but in both cases the maximum transverse velocities are underpredicted in the calculations. Upon inspection it may be seen that a more diffused vortex is obtained in the calculations. This is particularly evident at the plane
are compared with the experimental results in figure 14, for the flow with an angle of attack of 6.5 degrees. An excellent correlation of the tip vortex location is obtained in both planes, but in both cases the maximum transverse velocities are underpredicted in the calculations. Upon inspection it may be seen that a more diffused vortex is obtained in the calculations. This is particularly evident at the plane ![]() , where a nearly axisymmetric flowfield is obtained in the vicinity of the vortex core. However, the asymmetry of the vortex close to the trailing edge is well predicted and the flowfield away from the vortex center shows a very good correlation with the experimental results. The location of the vortical wake in the station close to the trailing edge,
, where a nearly axisymmetric flowfield is obtained in the vicinity of the vortex core. However, the asymmetry of the vortex close to the trailing edge is well predicted and the flowfield away from the vortex center shows a very good correlation with the experimental results. The location of the vortical wake in the station close to the trailing edge, ![]() , is also well predicted. Furthermore, although the maximum values of the tranverse velocity components are larger in the experimental results, the downstream decrease of
, is also well predicted. Furthermore, although the maximum values of the tranverse velocity components are larger in the experimental results, the downstream decrease of ![]() in the predictions is very close to the experimental one.
in the predictions is very close to the experimental one.
The turbulence model used in this method does not account for streamline curvature effects. It is well documented in the literature that in the vortex core the turbulent diffusion should be negligible, see for example [30]. In the present turbulence model the eddy viscosity is related to the displacement thickness, which is determined along the grid η lines. The streamwise velocity defect in the tip vortex region causes an increase of the local displacement thickness and consequently of the eddy viscosity. This means that with the present model the eddy viscosity exhibits a maximum at the tip vortex region, which is in total contradiction with the physical characteristics of the flow. It is thought that the large values of the eddy viscosity in the vortex core may be reponsible for the overprediction of the vortex core size in the present calculations.
The overprediction of the vortex core size has a large effect on the calculated pressure in the vortex core. The minimum pressure coefficient in the vortex core is approximately proportional to the square of the inverse of the core size, which means that an accurate prediction of the core size is essential for a good prediction of the pressure field.
The comparison between predictions and experimental results for the flows with angles of attack of 4.5 and 8.5 degrees is similar to the one obtained with an angle of attack of 6.5 degrees, [12]. The correlation between the vortex location of the predictions and experimental results is still excellent, but the vortex core size is again overpredicted. The location of the vortical wake close to the trailing edge is in good agreement with the experimental results for both angles of attack and the flowfield away from the vortex center is in excellent agreement with the experimental results.
5 Conclusions
A numerical method for the calculation of the steady, incompressible, viscous flow at the tip of wings was developed. The effect of the choice of the extent of the computation domain on the solution of tip vortex flows has been investigated by changing the location of the boundaries. The results showed that the present zonal approach to the calculation of tip vortex flows is efficient, because a large part of the flow field does not need to be discretized and a finer discretization can be obtained in the tip vortex region for a given number of grid nodes. However, the imposition of potential flow conditions at the external boundary implies that the viscous/inviscid interaction has to be incorporated in the solution procedure to account for the difference in the external flow circulation associated with the viscous and inviscid solutions respectively. In the present calculations the viscous/inviscid interaction is neglected and so a pressure discontinuity is obtained at the trailing edge.
The specification of appropriate inlet boundary conditions may be difficult. When initial velocity profiles are specified convergence problems in the initial stations may result if a poor estimate of the initial velocity profiles is used. An improved solution can be obtained by specifying the streamwise velocity gradient at the inlet boundary. However, this type of boundary condition reduces the convergence rate of the method, making it more time consuming. The comparison between the solutions obtained with the two types of boundary conditions suggests that the influence of small inaccuracies in the inlet velocity profiles is restricted to a small region close to the inlet boundary.
The present calculations showed that the streamwise pressure gradient of the inviscid flow solution is not a good approximation to the streamwise pressure gradient of the viscous flow in the tip vortex region. This was revealed in the comparison with experimental results, [28], of the present method and the method of Govidan et al.,
[2], which imposes the streamwise pressure gradient from inviscid flow calculations.
A good correlation between numerical predictions and experimental results was obtained for the calculation of the flow at the tip of a rectangular wing with a squared tip. However, the size of the tip vortex core is overpredicted in the present calculations. The turbulence model is likely to be responsible for the excess of diffusion in the tip vortex core, because the physical characteristics of the local flow are not well reproduced in the present model. The overprediction of the vortex core size still precludes an accurate prediction of the suction peak in the vortex core.
Acknowledgement
The work was carried out while the first author was on leave from Institute Superior Técnico and supported by grants of the Comissão Permanente INVOTAN of the Junta Nacional de Investigação Cientifica and of the SCIENCE PLAN of the EUROPEAN COMMUNITIES which are gratefully acknowledged. The support of the Stichting Nationale Computer Faciliteiten in the present calculations is also gratefully acknowledged.
References
[1] Govidan T.R., Levy R., Shamroth S.J. — Computation of The Tip Vortex Generation Process for Ship Propeller Blades—4th International Conference on Ship Hydrodynamics, Washington D.C., 1985.
[2] Govidan T.R., Jong F.J., Levy R., Shamroth S.J. —Validation of a Forward Marching Procedure to Compute The Tip Vortex Generation for Ship Propeller Blades— 17th Symposium on Naval Hydrodynamics, August-September 1988, The Hague, The Netherlands.
[3] Briley W.R., McDonald H. —Three-Dimensional Viscous Flow with Large Secondary Velocity. —Journal of Fluid Mechanics, Vol. 144, 1984, pp. 47–77.
[4] Rubin S.G., Tannehill J.C. —Parabolized/Reduced Navier-Stokes Computational Techniques. —Annual Review of Fluid Mechanics, Vol. 24, 1992, pp. 117– 144.
[5] Rubin S.G. —Incompressible Navier-Stokes and Parabolised Navier-Stokes Formulations and Computational Techniques . — Computational Methods in Viscous Flows, Vol. 3 in the series Recent Advances in Numerical Methods in Fluids (ed. Habashi) Pineridge Press, 1984.
[6] Rubin S.G. —Global Relaxation Procedure for a Reduced Form of the Navier-Stokes Equations. —Proceedings of the 9th—International Conference on Numerical Methods in Fluid Dynamics, Lecture Notes in Physics, Vol. 218, Springer-Verlag, 1985, pp. 62–71.
[7] Raven H.C., Hoekstra M. —A Parabolised Navier-Stokes Solution Method for Ship Stern Flow Calculations. —2th International Symposium on Ship Viscous Resistance, Goteborg Sweden, March 1985.
[8] Hoekstra M., Raven H.C. —Application of a Parabolised Navier-Stokes Solution System to Ship Stern Flow Computation . —Osaka International Colloquium on Ship Viscous Flow, Osaka Japan, October 1985.
[9] Hoekstra M., Raven H.C. —Ship Boundary Layer and Wake Calculation with a Parabolised Navier-Stokes Solution System. —4th International Conference on Numerical Ship Hydrodynamics”, Washington D.C., 1985.
[10] Hoekstra M. -Recent Developments in a Ship Stern Flow Prediction Code. —5th International Conference on Numerical Ship Hydrodynamics, Hiroshima, September 1989.
[11] Rosenfeld M., Israeli M., Wolfshtein M. — A Method for Solving Three-Dimensional Viscous Incompressible Flows over Slender Bodies—Journal of Computational Physics, Vol. 88, 1990, pp. 255–283.
[12] Eça L. —Numerical Solution of the Parabolised Navier-Stokes Equations for Incompressible Tip Vortex Flows —PhD Thesis, Institute Superior Técnico, Lisbon, March 1993.
[13] Vinokur M. —Conservation Equations of Gasdynamics in Curvilinear Coordinate Systems. —Journal of Computational Physics, Vol. 14 , 1974, pp 105–125.
[14] Warsi Z.U.A. —Conservation Form of the Navier-Stokes Equations in General Nonsteady Coordinates. —AIAA Journal, Vol. 19, February 1981, pp 240–242.
[15] Zhang H., Camarero R., Kahawita R. — Conservation Form of the Equations of Fluid Dynamics in General Nonsteady Coordinates. —AIAA Journal, Vol. 23, November 1985, pp 1819–1820.
[16] Hoekstra M. —Some Fundamental Aspects of the Computation of Incompressible Flows. —Second Osaka International Colloquium on Ship Viscous Flow, September 1991. Osaka Japan.
[17] Eça L., Hoekstra M. —Discretization of the Parabolised Navier-Stokes Equations. — First European Computational Fluid Dynamics Conference, Brussels, September 1992.
[18] Mynett A.E., Wesseling P., Segal A., Kassels C.G.M. —The ISNaS Incompressible Navier-Stokes Solver: Invariant Discretization. —Applied Scientific Research, Vol. 48, 1991, pp. 175–191.
[19] Segal A., Wesseling P., Van Kan J., Oosterlee C.W., Kassels K. —Invariant Discretization of the Incompressible Navier-Stokes Equations in Boundary-Fitted Coordinates. —International Journal of Numerical Methods in Fluids, Vol. 15, 1992, pp. 411–426.
[20] Sokolnikoff I.S. —Tensor Analysis. —John Wiley & Sons Inc., 1951.
[21] Raven H.C. —Berekening van de potentiaalstroming rond draagvlakken met het programma DAWSON, (in Dutch) ”Calculation of Potential Flow on Lifting Surfaces with the Program Dawson, (Engl. Transl.) —MARIN Report No 50501–1-RD, May 1985.
[22] Hoekstra M. —Generation of Initial Velocity Profiles for Boundary Layer Calculations. — Marin Report No 50028–1-SR, March 1980.
[23] Launder B. —On the Modelling of Turbulent Industrial Flows. —First European Computational Fluid Dynamics Conference, Brussels, September 1992.
[24] Rodi W., Scheuerer G. —Scrutinizing the k–∈ Model Under Adverse Pressure Gradient Conditions. —Journal of Fluids Engineering, Transactions of the ASME, Vol. 108 , June 1986, pp. 174–179.
[25] Cebeci T., Smith A.M.O. —Analysis of Turbulent Boundary Layers. —Academic Press, November 1984.
[26] Cebeci T., Clark R.W., Chang K.C., Halsey N.D., Lee K. —Airfoils with Separations and the Resulting Wakes. —Journal of Fluid Mechanics, Vol. 163, 1986, pp. 323–347.
[27] Eça L.R.C., Falcão de Campos J.A.C. — Analysis of Two-Dimensional Foils Using a Viscous-Inviscid Interaction Method. — International Shipbuilding Progress, (accepted for publication).
[28] Gray R.B., McMahon H.M., Shenoy K.R., Hammer M.L. —Surface Pressure Measurements at Two Tips of a Model Helicopter Rotor in Hover—NASA CR-3281, 1980.
[29] Falcão de Campos J.A.C., George M.F., Mackay M. —Velocity Measurements of the Tip Vortex Flow in the Near- Wake of Hydrofoils. — 1993, Submitted for publication to the Journal of Fluids Engineering.
[30] Bradshaw P. —Effects of Streamline Curvature on Turbulent Flow—AGARDograph 169, AD—768316, 1973.
DISCUSSION
by Dr. Spyros A.Kinnas
MIT
The authors presented a very interesting approach in solving the tip vortex simulation problem. I would like to ask two questions:
-
They match a potential flow solution in the inner part of the span to a viscous representation of the outer part. How sensitive are the results on the cut-off location?
-
In the case of a rectangular planform wing with round geometry in the spanwise direction, were they able to capture a similar vortex roll-up structure along the chord to that of a body of revolution at an angle?
Author's Reply
Our reply to the questions asked by Dr. Kinnas is:
-
In our present approach, see section 2.1, the boundary conditions in the inner part of the span
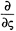 , imply that cross-stream derivatives, , of the cartesian velocity components and of the pressure are set equal to zero. A potential flow solution is used to specify boundary conditions at the external boundary, without viscous-inviscid interaction. This means that approximate boundary conditions are used on both boundaries. The comparisons between results obtained with different locations of the inner and external boundaries presented in sections 4.2.3 and 4.2.4 show a small influence of the boundaries location on the solution in the tip vortex region.
, imply that cross-stream derivatives, , of the cartesian velocity components and of the pressure are set equal to zero. A potential flow solution is used to specify boundary conditions at the external boundary, without viscous-inviscid interaction. This means that approximate boundary conditions are used on both boundaries. The comparisons between results obtained with different locations of the inner and external boundaries presented in sections 4.2.3 and 4.2.4 show a small influence of the boundaries location on the solution in the tip vortex region. -
In this study we did not make any visualization of the limiting streamlines and so we have not yet performed a detailed analysis of the separation pattern at the tip of the wing. The vortex roll-up structure in the case of a round-nosed body of revolution at an angle of attack is strongly dependent on the angle of attack and can be rather complex, as shown for instance in Tobak and Peak, [1]. However, from the analysis of the cross-flow velocities close to the tip, [2], there may be some similarity between the rounded tip wing and the body of revolution at an intermediate angle of attack, where a single dominant vortical structure exists. Such structure has been captured with a similar method in the calculations of Rosenfeld et al., [3], for a prolate spheroid at 10º of incidence.
[1] Tobak, M. and Peake, D.J. Topology of Three-Dimensional Separated Flows— Annual Review of Fluid Mechanics, 1982, Vol. 15, pp. 61–85.
[2] Eca, L. Numerical Solution of the Parabolized Navier-Stokes Equations for Incompressible Tip Vortex Flows, PhD Thesis, Instituto Superior Técnico, Lisbon, March 1993.
[3] Rosenfeld, M., Israeli, M. and Wolfshtein, M. A Method for Solving Three-Dimensional Viscous Incompressible Flows Over Slender Bodies, Journal of Computational Physics, 1990, Vol. 88, pp. 255–283.


















































