Chapter 2: A Model for Assessment Development: Achieving Balance
The Curriculum and Evaluation Standards for School Mathematics (NCTM, 1989), indicated a clear need for new mathematics assessments that would embrace mathematical goals that had not been considered in traditional norm-referenced tests. Because it is tempting, in any process of change, to concentrate solely on aspects that were previously ignored, the main theme of this chapter is achieving balance in assessing various aspects of mathematical knowledge, including skills that were adequately assessed by traditional tests as well as newer goals such as problem solving and mathematical communication. Chapter 1 describes many of the differences between traditional norm-referenced tests and standards-based assessments, but such descriptions are not sufficient for building a balanced assessment, and they provide too little guidance for evaluating the extent to which an assessment fits with a set of standards. There are a variety of ways to achieve balance. This chapter presents one way that is based upon on a distinction among mathematical skills, conceptual understanding, and problem solving, but that remains quite flexible in its interpretation and use. The chapter begins by describing several different formulations of assessment principles that collectively frame the construction of a "model for balance" to guide assessment development work. The chapter continues with descriptions of several types of assessment, according to their origin and use, followed by a detailed description of the model. The chapter closes with recommendations for using the model to evaluate the balance of an assessment system.
Conceptual frameworks for mathematics assessment
Encouraged by the publication of the NCTM Standards, several groups began defining principles that could guide the development of balanced pictures of mathematical accomplishment.
In Measuring What Counts, the MSEB put forward three fundamental assessment principles that would support effective learning of mathematics (NRC, 1993b):
-
The Content Principle—assessment should reflect the mathematics that is most important for students to learn.
-
The Learning Principle—assessment should enhance mathematics learning and support good instructional practice.
-
The Equity Principle—assessment should support every student's opportunity to learn important mathematics.
At the same time, the New Standards and Balanced Assessment organizations produced a framework for balance, based on NCTM's Standards. The seven principal dimensions of the resulting framework are outlined below (Schoenfeld, Burkhardt, Daro, & Stanley, 1993):
-
Content—assessment should reflect content in a broad sense and include concepts, senses, procedures and techniques, representations, and connections.
-
Thinking processes—assessment should engage students in a wide range of thinking processes that include conjecturing, organizing, explaining, investigating, formulating, and planning.
-
Student products—assessment should require a variety of student products that include models, plans, and reports.
-
Mathematical point of view—assessment should present mathematics as an interconnected body of knowledge, by engaging students in mathematics that is connected to realistic, illustrative, and pure contexts.
-
Diversity—assessment should be sensitive to issues of access.
-
Circumstances of performance—assessment should vary according to time allocated, whether it is performed individually, in pairs, or in groups, and whether there is opportunity for feedback and revision.
-
Pedagogics and aesthetics—assessment tasks should be engaging, believable, and understandable, and should not disenfranchise the common sense of the student.
Two years later, the NCTM Assessment Standards for School Mathematics (1995) produced a set of standards for assessment
that incorporated MSEB's assessment principles. NCTM's six standards for assessment are listed below:
-
Mathematics—assessment should reflect the mathematics that all students need to know and be able to do. The content of assessment must be shaped by important mathematics that is broad and balanced.
-
Learning—assessment should enhance mathematics learning. Assessment tasks should offer students an opportunity to learn important mathematics.
-
Equity—assessment should promote equity. All students should have the opportunity to learn the mathematics that is to be assessed. And all students should have an equal opportunity to show what they know and can do on assessments.
-
Openness—assessment should be an open process. Students should either be able to do what the standards are asking them to do or know how far they are from meeting the standards and understand what they need to do to close the gap.
-
Inferences—assessment should promote valid inferences. Assessment allows us to make more or less valid inferences about what students know and can do. It is more difficult to make valid inferences about those aspects that students do not appear to know.
-
Coherence—assessment should be a coherent process. The cohesion of assessments should reflect the cohesion of instruction and teaching.
The frameworks produced by these organizations are complementary rather than competing, and so there is a great deal of overlap among the three. The linkages between the details of the three frameworks are illustrated by the diagram in Table 1.
Together, these three conceptual frameworks suggest the development of a broad and balanced approach to assessment. The challenge for task designers, therefore, becomes that of translating what is being advanced by these conceptual frameworks into worthwhile assessment opportunities for all students.
Types of assessment
An assessment that carries out these visions for balance must take a broad view of assessment, encompassing various types of student products and circumstances of performance. For the purposes of this document, school mathematics assessment will be described by two types: on-demand assessment and classroom-embedded assessment.
Table 1. Comparison of Principles
|
MSEB Principles |
BA/NS Dimensions |
NCTM Standards |
|
Content |
Content |
Mathematics |
|
Learning |
Thinking processes Student products Mathematical point of view Pedagogics and aesthetics |
Learning |
|
Equity |
Diversity Circumstances of performance |
Equity Openness Inferences Coherence |
On-demand assessment refers to testing that is completed in time-limited conditions. Some on-demand assessments are standardized in order to see how different students perform under the same conditions. A truly standardized test, however, is impossible to create—there will always be aspects of a test that will advantage or disadvantage some but not all students. On-demand norm-referenced tests are used for the purpose of sorting or ranking students, but on-demand assessments can be standardized and used to serve other purposes. For example, standards-based on-demand examinations can be standardized (as far as possible) and used to determine whether students meet a set of standards.
On-demand assessments also are constructed by teachers to assess the taught curriculum. A teacher-constructed examination can be standards-based. In this case, the standards to which the examination is referenced are the standards of the individual teacher (or group of teachers teaching the same course). These individual standards may or may not coincide with publicly negotiated standards.
Classroom-embedded assessment refers to assessment that teachers use in their daily work to assess what students know and can do. This type of assessment is useful in enabling teachers to understand how students are progressing and to design or adjust on-going instructional strategies. Embedded assessment also can be used as a component of portfolio assessment. In Vermont, for example, embedded assessments are used to compile student portfolios, and these contribute to the statewide assessments in mathematics. One of the strengths of embedded assessment is that it can bridge the gap between instruction and assessment.
In this document the assessment issues that are discussed are applicable to each of these assessment arenas. Chapter 3 concentrates on task design issues that have been identified as part of the
task development efforts conducted by Balanced Assessment and New Standards. The rest of this chapter examines the conditions that need to be present for an assessment system, test, or examination to be balanced. What follows here is an overall model for mathematics assessment.
A model for a balanced assessment in mathematics
The first question that must be asked of an assessment system is, ''What mathematics do we want to assess?" The answer will depend on the mathematics that is specified in a state's or district's standards. But this question also needs to be answered in a way that is specific enough to enable teachers to provide opportunities for students to learn the mathematics that is to be assessed. The document Every Child Mathematically Proficient: An Action Plan provides an outline of what students should be able to do by the end of the ninth grade (Learning First Alliance, 1998, p. 11-12). Many other outlines also are feasible, but this one provides a useful starting point for developing the content specifications of an examination.
The next question that must be asked of an assessment system is, "What do we want students to be able to do with the mathematics described in the content specifications?" The New Standards Performance Standards ask students to show that they have a repertoire of mathematical skills, that they understand mathematical concepts, that they can use mathematics to solve problems, and that they can put mathematics to work by completing extended projects. In the New Standards Reference Examinations, tasks are designed with the following categories in mind:
-
Mathematical Skills
-
Conceptual Understanding
-
Mathematical Problem Solving
These three categories are comparable to the mathematical abilities categories used by the National Assessment of Educational Progress [NAEP] in their assessment of mathematics: procedural knowledge, conceptual understanding, and problem solving (National Assessment Governing Board, 1995).
Because many tasks require a combination of skills, concepts, and problem-solving strategies, classification under these headings often requires identification of the task hurdle: the primary mathematical skill, concept, or strategy that the student must employ in order to demonstrate some success on the task. Still, the boundaries that separate these categories are not well defined (nor do they need to be). The utility of these categories lies not in their precision, but in their role in developing a balanced view of
mathematics assessment. Important here is the realization that to de-emphasize one of these aspects of assessment would be to promote a distorted and impoverished view of school mathematics. The domain need not be organized in this precise way, but these three categories do provide a useful model.
Mathematical skills as an assessment target
When the assessment target is mathematical skills, tasks that assess students' knowledge of important facts, routines, or algorithms are needed. Usually, mathematical skills tasks can be solved by recalling an important idea or well-practiced routine.
The task Right Triangle is designed to assess whether students can find the length of the hypotenuse of a right triangle. The hurdle in Right Triangle is procedural. Students will typically use the Pythagorean Theorem to find the length of the hypotenuse in a right triangle, a procedure that all students who have been taught the Pythagorean Theorem will have learned. The choice of numbers and the absence of an elaborate context helps ensure that the conceptual demand of the task is kept to a minimum.
The task Find the Volume is also a straight-forward task that measures skills. To find the volume, the student must know (or know how to find) and use the formula for the volume of a rectangular prism. The task is not designed to reveal what the student understands about volume. A student solving this task might know little about volume, beyond the formula.
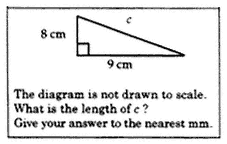
Figure 1. Right Triangle
Figure 2. Find the Volume
Measurements taken from a box give the length, width, and height to be 36, 14 and 16 inches.
Find the volume of the box.
Figures 1 and 2 reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
Mathematical skill tasks make little or no conceptual or strategic demands on students. This approach allows assessment of students' factual and procedural capabilities without confounding them with other capabilities.
Conceptual understanding as an assessment target
When tasks focus on conceptual understanding, they require students to use an idea, reformulate it and express it in their own terms. Tasks that call only for students to apply well-practiced routines or algorithms are not sufficient for the purpose of assessing conceptual understanding. Conceptual understanding tasks require that students represent, use, or explain a concept.
Good conceptual understanding tasks should not be solvable from an understanding of mathematics that is inherently fragile and composed of decontextualized or fragmented slivers of mathematical knowledge-no matter how well learned and remembered.
Figure 3. Almost Right
The sides of a triangle have lengths 8, 9, and 12. One of the angles in this triangle is either a right angle or close to it.
Decide if this angle is exactly a right angle, a little larger, or a little smaller.
Give reasons to support your decision.
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
The task Almost Right is presented as an assessment of conceptual understanding. In responding to Almost Right, students are to decide whether an angle that is very close to 90 degrees is right, obtuse, or acute. In our trials, the majority of students used the converse of the Pythagorean Theorem to reason that the triangle is not a right triangle because 64 + 81 > 144. Then, in order to decide whether the angle is obtuse or acute, students use the fact that 64 + 81 > 144, and some make the correct inference that the angle is acute. Clearly, no procedural use of the Pythagorean Theorem will facilitate this level of fluency with the concepts; as a consequence, Almost Right is classified as an assessment of conceptual understanding.
The task Gutter (Figure 4) also assesses conceptual understanding. The conceptual hurdle to be navigated here is that of expressing the radius of the semi-circular base in terms of W. This can be accomplished by setting up the equation πr = W and then solving for r. This task is not wholly free of procedure. To arrive at the solution, a student must manipulate this equation correctly and then carry out the required substitutions. Nevertheless, the symbolic representation required far outweighs the symbolic manipulation that is required. And it is negotiating the hurdles posed by representation and re-expression in this task that indicates fluency in understanding of the relationship between radius and circumference. Clearly, this is a task that cannot be solved through algorithmic manipulations, but it may be solved by students who have had the opportunity to work with and reflect on the relationships between diameter and circumference and between the area of the base and the volume of a solid that has regular cross-sections.
Conceptual understanding tasks make little or no procedural or strategic demands on students. This approach allows assessment of students' conceptual understandings without confounding them with other capabilities.
Problem solving as an assessment target
When mathematical problem solving is to be assessed, tasks must make these requirements of students:
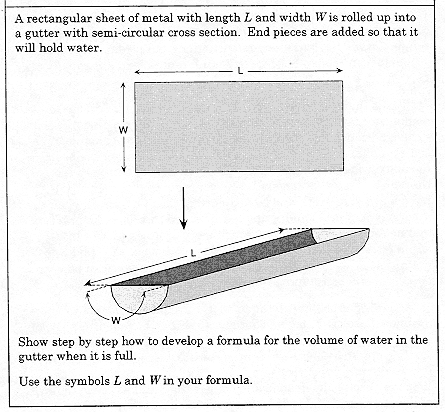
Figure 4. Gutter
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
-
formulate an approach to a problem;
-
select the mathematical procedures, concepts, and strategies necessary, and then deploy these when implementing a solution; and
-
draw a conclusion.
If students are to formulate an approach, the task should not provide too much structure or directive instruction (either explicitly or implicitly). This is because if a task contains a large amount of structure, this structure will provide an approach for the students. Chapter 3 provides examples of tasks whose structure dictates a particular approach to the task, even though the problem may be solved in a variety of ways.
If students are to be required to select procedures, facts, and concepts, and then use these to solve a problem, care must be taken to ensure that the skills and concepts that students are asked to use are ones that they have already fully absorbed. When a task
requires students to try to make high-level use of unassimilated skills and concepts, they are often unable to make any headway. This is usually because the strategic use of unabsorbed skills and concepts causes the total cognitive demand of the task to be unreasonably high. Such assessment situations can be demoralizing for students, can lead to false-negative inferences, and are usually a waste of assessment time.
Tasks that work well to assess problem solving in an on-demand situation are ones that ask students to bring together skills and concepts that they understand well. For example, when the examination is to be designed for the tenth grade, the best tasks to use to contribute to the problem-solving score are those that draw largely on the skills and concepts that students will have learned in ninth and even eighth grade. Of course, when the assessment of problem solving is embedded in classroom practice and not strictly time-limited, much more complex tasks can be administered. In classroom situations (and when the stakes are not high), these more complex problem-solving tasks can be used to help students learn and assimilate skills and concepts.
Choosing problem-solving tasks that require students to make high-level use of skills and concepts that they have learned one or even two years previously does not mean that standards are necessarily going to be lowered. On the contrary, grade-level appropriate assessment of skills and concepts can be assessed by tasks that are specifically designed to do just that, and so the standards of technical skill and conceptual understanding can be protected.
The next task, Snark Soda (Figure 5), is an example of a longer task that assesses problem solving. This problem-solving task contains few or no directive steps. Also in Snark Soda, the skills and concepts that the student is to draw on are likely to be well understood by high school students. Snark Soda exemplifies well what we mean by high level use of well-assimilated concepts, facts, and skills.
To be successful on Snark Soda, the student must be able to identify and manage these three main components:
-
fitting shapes of solid geometry such as cylinders and hemispheres to the different parts of the given bottle;
-
measuring the diagram (described as an accurate and full-size drawing) to find values for parameters such as the radius and height for these shapes;
-
computing the volume of these shapes, using the measured values.

Figure 5. Snark Soda
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
Problem-solving tasks should make medium-level procedural and conceptual demands on students. Worthwhile problem-solving tasks can assess the way in which students use skills and concepts that they have fully absorbed.
Why develop different types of task?
One type of task is not enough to give a broad and balanced vision of mathematics. Until recently, the only widely available tests were various norm-referenced tests that were characterized by short, closed, multiple-choice items that assessed procedural skills, at the expense of any assessment of conceptual understanding or problem solving. Early attempts to address this
imbalance were characterized by the development of assessment tasks that emphasized contextual and mathematical connections or that reflected the richness, elegance, and beauty of mathematics. Once again, a single task type emerged. These assessment tasks were often complex constructed-response tasks that focused simultaneously on aspects of conceptual, procedural, and strategic knowledge. As will be explained further in Chapter 3, however, when skills and concepts are assessed through problem-solving tasks, there is the risk of making false-negative errors about students' procedural and conceptual knowledge. Frequently, students' responses to problem-solving tasks can lead to the inference that they lack proficiency in basic skills and concepts, even though further analysis will reveal that students understand the concepts. Apparently, students are often unable to use procedures and concepts in situations where the strategic demands of the task are high.
Separate procedural, conceptual, and problem-solving tasks provide a balanced yet unconfounded assessment of these important capabilities. The balance of an assessment is therefore found in the assessment as a whole and not in the individual tasks that make up the assessment.
One content area, three different tasks
The tasks Find the Volume, Gutter, and Snark Soda are presented here to illustrate assessment tasks that measure mathematical skill, conceptual understanding, and mathematical problem solving, respectively. They also illustrate how differently structured tasks that all focus on the same content area can be used to measure procedural, conceptual, and strategic aspects of mathematical learning.
If a test or classroom practice confines itself to just one or two of these aspects of mathematical learning, then the test or classroom practice will not be sufficiently balanced because it will not give students the opportunity to show what they can do across all three; and all three are important. Phil Daro, Executive Director of New Standards, makes this point by using a three-legged stool as a metaphor for the curriculum (personal communication, March, 1999). One leg represents skills, a second conceptual understanding, and a third problem solving. If one of the legs were missing, the stool would clearly fall in the direction of the missing leg. Analogously, if one of these three critical curricular dimensions is missing, then the curriculum will fall in the direction of the missing dimension.
If, however, the test or classroom practice ensures that all three aspects are addressed in a way that is accessible to students
and enables students to show what they can do across all three, then that test or classroom practice has gone a substantial way toward balance.
The same task might measure different aspects of mathematics
Thus far the discussion has been about balance as a property of a test and about task categorization—as problem solving, conceptual understanding, or skills—based on properties of the task. But as pointed out earlier, the boundaries between these categories are not precise. Furthermore, the classification depends on the mathematics level of the students. In other words, what a task is assessing must be evaluated in relation to the group for whom the task is intended (Wilson, Fernandez, & Hadaway, 1993; Schoenfeld, 1985). Problem-solving tasks, for example, are often identified as tasks that are non-routine. But what is non-routine to one student might be routine for another. The same holds for the classification of tasks that are designed to assess conceptual understanding. For example, the task Almost Right was designed to assess conceptual understanding. If this task were administered to a group of students who were accustomed to using tasks of this type in class to practice applying the Cosine Law, then it would assess skills rather than conceptual understanding.
Maintaining skills while achieving depth and balance
Many traditional mathematical skills remain essential and need to be maintained, rather than ignored, in any effort to promote conceptual understanding and problem solving. Using different tasks for each of these assessment objectives makes it possible to report separate scores for mathematical skills, conceptual understanding, and mathematical problem solving. Such a score report makes visible the importance of each of these capabilities in a broad and balanced assessment. In addition, this visible balance reassures the public that skills remain critical and, as Massell, Kirst, and Hoppe (1997) argue, aids in gaining public support for the current attempt to encourage a broader view of mathematics education than that which is associated with the traditional curriculum.
Curriculum development benefits are also afforded by reporting separate scores for separate learning objectives. When an examination is designed to report scores for important aspects of mathematical learning according to well-chosen categories, the information that teachers, supervisors, and administrators receive is far more specific than the information that might be gained from a single mathematics score. For example, when states or districts use the New Standards Reference Examination, the information that is provided in the individual, class, school, district, and state
score reports is organized according to three reporting categories: Mathematical Skills, Conceptual Understanding, and Mathematical Problem Solving. This means that a teacher or other interested party can use these sub-scores to determine how extra support might best be allocated. For example, if students' mathematical skills scores indicate that a large proportion of students has met the standards, while mathematical problem-solving scores indicate that a large proportion of students has not met the problem-solving standards, this would indicate that additional classroom instructional efforts may need to be directed at creating opportunities for the students to develop greater problem-solving capabilities.
The whole is greater than the sum of its parts
It is important to stress that procedural, conceptual, and problem-solving knowledge are not mutually exclusive constructs. For example, mathematical problem-solving tasks should not be constructed so that they are devoid of mathematical skills and concepts. Problem-solving tasks meriting placement in a balanced mathematics assessment will incorporate skills and concepts, but these skills and concepts should not constitute a major hurdle of the task. By the same token, neither skills nor conceptual understanding tasks will totally lack a formulation component: Every task, even those that are simply cast, will require some amount of figuring out what to do. Nonetheless, when the desired measurement target is either skills or conceptual understanding, strategy formulation should not constitute a significant hurdle.
On the basis of the model that is described so far, we would not wish to advance a model of assessment that is in the form of a two-dimensional array—with mathematical skills, conceptual understanding, and mathematical problem solving along one axis and topics such as number, measurement, geometry, algebra, statistics, and probability along the other. To do so would be to neglect at least two other dimensions: mathematical connections and mathematical communication, both of which are of critical importance because they are both strong indicators of mathematical power.
Assessing mathematical connections
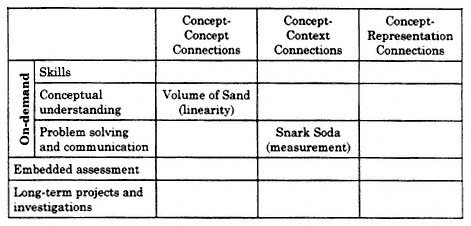
A balanced assessment must provide evidence about whether students are able to use mathematical skills and concepts as they are connected within mathematics or to some real-world context. There are three important kinds of mathematical connections:
-
Concept-concept connections
-
Concept-context connections
-
Concept-representation connections
Concept-concept connections are often referred to as connections within mathematics. For a student to make concept-concept connections, the student will need to experience and to understand the rich interplay among mathematical ideas, and to begin to see mathematics as an integrated whole. An emphasis on concept-concept connections through instruction is important in enabling students to learn concepts and to learn about the interconnectedness of mathematics as a discipline. Certainly, an instructional emphasis on concept-concept connections between and within grades is a prerequisite for success on the kinds of problem-solving tasks that require students to make high-level use of concepts and skills that they have learned in previous grades. Achieving success on such problem-solving tasks will help students to absorb prior knowledge more fully, strengthen their understandings, and help them to accommodate new ideas.
Examples of types of tasks that capture the spirit of the concept-concept connections are provided in the Core Assignments developed recently by the National Center on Education and the Economy (NCEE). In the task Volume of Sand in a Rectangular Prism (adapted from NCEE's Core Assignment: Volume, 1998) students are given three congruent rectangular prisms that are filled to various heights with sand and are asked to plot the volume of sand in the container as a function of the height of the sand. Next, students are asked to address the following questions or discussion points:
![]() What kind of a function is it? Say why!
What kind of a function is it? Say why!
![]() What is the slope of the line?
What is the slope of the line?
![]() How can the slope be interpreted in terms of the sand in the containers?
How can the slope be interpreted in terms of the sand in the containers?
![]() What is the equation of the line?
What is the equation of the line?
![]() How does this equation relate to the volume formula of rectangular prisms?
How does this equation relate to the volume formula of rectangular prisms?
![]() Suppose the container were turned so that one of its sides became the base, how would the graph of the function change?
Suppose the container were turned so that one of its sides became the base, how would the graph of the function change?
In this task, conceptual understanding about rectangular prisms and their volume is connected to concepts of linear function and slope. Students must graph volume as a function of the changing height of sand in a rectangular prism. Then they must find and interpret the slope of the graph in terms of the area of the base of a rectangular prism.
Students and teachers alike have found this task quite difficult. Although both students and teachers had previously demonstrated that they could find the slope of a straight line, many were initially unsuccessful doing so in the context of this task. Once they had
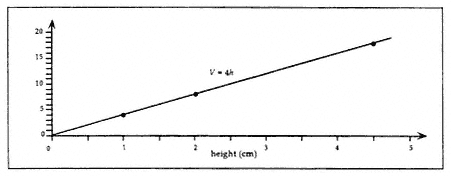
Figure 6. Volume versus height in a rectangular prism
calculated the slope of the line, some had difficulty attaching meaning to it. According to some teachers, their difficulties with this task reflected their lack of experience working with the concepts of linear function and volume at the same time.
As a worthwhile learning opportunity for students, teachers could present a graph representing the volume of sand in a container as a function of height. Figure 6 serves as an example for such an approach.
Students can see that the graph is a straight line with equation V = 4h, and they are asked to use the graph to address the following questions:
![]() What can be said about the shape of the container that holds the sand?
What can be said about the shape of the container that holds the sand?
![]() What can be said about the shape of the base?
What can be said about the shape of the base?
![]() What can be said about the size of the base?
What can be said about the size of the base?
![]() What can be said about the shape of the container?
What can be said about the shape of the container?
Instead of using mathematical connections in working from the physical structure to its mathematical representation, students are asked in this exercise to use the mathematical representation to make inferences about the physical structure. Both teachers and students have reported that this approach has helped them to better understand how the slope of the graph is related to the area of the base of the container.
Concept-context connections are made when mathematics is extracted from a context outside of mathematics. Such contexts can deepen students' understanding of important mathematics (NCTM, 1989; NRC, 1993b, 1998). When students are given the opportunity to use conceptual and procedural knowledge in contexts outside of mathematics, they also are given the opportunity to strengthen their existing understandings and hone their mathematical power.
Measuring Up (NRC, 1993a) and High School Mathematics at Work (NRC, 1998) are good sources for high-quality, complex tasks that are mathematically rich and contextually relevant and that can be used as either instructional or assessment tasks. (If used for an assessment however, most of these extended tasks are more appropriate for assessment that is spread out over several days rather than examinations that are time-limited.) Snark Soda is one example of a task that makes use of contexts outside mathematics and that could be used in an on-demand assessment. Chapter 3 contains several tasks in which the essential mathematics is contextualized: Students must model shopping carts or paper cups, extract mathematics from a forester's diameter tape, deal with physical constraints, or grapple with issues of percent increase and decrease. Each of these tasks presents enormous challenges for large numbers of students in middle and high school. Many teachers are surprised by the lack of mathematical power that is evident when students attempt to use basic mathematics to solve problems set in a context. These inadequacies cannot be addressed if students are not encouraged to connect mathematics to the world around them.
Concept-representation connections are those that give students the opportunity to translate among different representations, such as between a formula and a graph. Research suggests that forms of representations need not be taught as ends in themselves but can be useful both for achieving understanding and for communicating that understanding (Greeno & Hall, 1997).
The crucial role that mathematical connections play in instruction and learning does not, however, mean that every assessment task should make connections either within or outside mathematics. What is necessary is for the entire set of tasks in an assessment package or test to be balanced with respect to mathematical connections. Certainly, if a test were devoid of mathematical connections, there would be less incentive for teachers to make mathematical connections a part of their regular classroom practice. Traditional norm-referenced tests generally do not make use of mathematical connections in the way that we are advocating here. As a consequence, traditional mathematics curricula also have failed to place much emphasis on mathematical connections. If assessment practice continues to ignore mathematical connections, important opportunities to enhance mathematics learning and to support good instructional practice will be lost (NRC, 1993b).
Assessing mathematical communication
In contrast to mathematical connections, all assessment tasks require at least some communication. In the case of selected-
response or short, closed, procedural tasks, communication is frequently trivial. As tasks become more complex, the communication requirements become more significant.
In the world beyond school, it is often important to communicate to an outside audience, such as a boss, a client, a politician, or a friend. Thus, students should be able to communicate about mathematical ideas by describing mathematical concepts and explaining reasoning and results. When developing mathematical communication, students should use the language of mathematics, its symbols, notation, graphs, and expressions, to communicate through reading, writing, speaking, and listening. The power of mathematical communication lies in its capacity to foster deeper understanding of mathematics (Cobb & Lampert, 1998; NCTM, 1998; Zucker & Esty, 1993). It is incumbent upon assessments, therefore, to incorporate a broad and balanced concept of mathematical communication. Similarly, it is important that classroom instruction provide the opportunity for students to communicate mathematical ideas. If students do not communicate mathematical ideas regularly, it is unlikely that they will know what to do when this is required in an assessment.
Circumstances of performance
The dimensions of balance that are described here cannot be addressed adequately in an examination or test—where students are expected to work individually, with few if any resources, and in a strictly time-limited situation. On-demand examinations and tests simply cannot assess problem solving, mathematical connections, or mathematical communication adequately (Arcavi, Kessel, Meira, & Smith, 1998). Also, on-demand examinations cannot assess students' capabilities in problem-posing, careful revision of argument, extended work, presentation, or organization of material from outside sources. For these reasons, it will almost always be necessary to vary the circumstances under which assessments are performed if the goal is to assess everything that is specified in the standards (Webb, 1997). These variations in circumstances can include:
-
On-demand tests or examinations created by the teacher or by an external body.
-
Classroom-embedded assessment that is completed by the student as part of the day-to-day requirements of a mathematics course. Some components of this can be completed in collaboration with peers, and other portions should be completed individually.
-
Long-term projects and investigations, with opportunity for feedback and revision. Such projects provide opportunity for
-
students to put mathematics to work in an extended way, where they have opportunity to use resources around them, and where problem solving is more like problem solving in the real world.
These variations in circumstances of performance will yield a variety of student products, including open-ended constructed-response items. The variety can be greater with the realization that constructed responses do not need to be written, especially for long-term projects. For example, a constructed response might be spoken or built. The product could even be a video or part of a group assessment.
Recommendations for evaluating the balance of an assessment system
Many different schemes can be used to organize and evaluate an assessment program. One model is to construct charts as templates that might be used by an assessment specialist when evaluating the balance of a school, district, or state assessment system. Although in some schemes, such charts might focus on aspects of learning such as thinking processes, the charts that follow build from the ideas presented earlier in the chapter on circumstances of performance, on-demand assessment, and mathematical connections.
Chart 1 helps develop an overview of the balance of the key aspects of the standards or learning expectations that are represented in the assessment system. It is important to work from expectations to assessments, rather than from assessments to expectations, because this will help to ensure that assessment does not rely solely on those aspects that are easy to assess and neglect those desirable aspects that are intrinsically more difficult to assess.
The NCTM's 9-12 standard on functions, for example, lists expectations that students can
![]() model real-world phenomena with a variety of functions;
model real-world phenomena with a variety of functions;
![]() represent and analyze relationships using tables, verbal rules, equations, and graphs;
represent and analyze relationships using tables, verbal rules, equations, and graphs;
![]() translate among tabular, symbolic, and graphical representations of functions;
translate among tabular, symbolic, and graphical representations of functions;
![]() recognize that a variety of problem situations can be modeled by the same type of function;
recognize that a variety of problem situations can be modeled by the same type of function;
![]() analyze the effects of parameter changes on the graphs of functions. (NCTM, 1989, p. 154)
analyze the effects of parameter changes on the graphs of functions. (NCTM, 1989, p. 154)
Chart 1. Circumstances of Performance
|
|
On-demand Assessment |
Embedded Assessment |
Long-term projects and investigations |
|
Skills |
Translate . . . Represent . . . |
Translate . . . |
|
|
Conceptual understanding |
Analyze . . . |
Recognize . . . |
|
|
Problem solving and communication |
Model . . . |
|
Model . . . |
|
Mathematical connections |
|
Translate . . . |
|
The teacher or assessment coordinator might decide to distribute these as shown in Chart 1. Note that some expectations appear more than once in the chart. It is critical, of course, that all expectations appear at least once.
This chart gives the assessment coordinator the opportunity to flag those critical dimensions that cannot be assessed in an examination. For example, Chart 1 provides the opportunity to map content expectations onto the assessment system, allowing some of those expectations to be developed through extended work with feedback and revision, oral presentations, and the construction of responses that are not necessarily written.
Chart 2 is to be used for focusing on the on-demand components of an assessment system. Illustrative entries are chosen from among the tasks discussed in this chapter. The column headings in Chart 2 might be general content strands, such as geometry or algebra or specific topics within a standard, depending on the scope of the assessment. It is very difficult to do justice to the assessment of problem solving in a test or examination. However, problem solving should not be dropped altogether from tests or examinations. Although examinations may be a far from perfect place to measure problem solving, putting problem solving in the assessment increases the likelihood that it will be addressed in the classroom (Webb, 1997).
The amount of time needed for a specific on-demand assessment is largely controlled by the amount of time needed to assess each of the different learning expectations. Groups of tasks that take about two to five minutes each to complete can provide a good assessment of procedural or conceptual knowledge. Assessment of problem solving requires the use of tasks that take considerably longer to complete. The minimum amount of time that can reasonably be allocated to a problem-solving task is about ten
Chart 2. On-Demand Assessment Components
|
|
Geometry |
Other topics or content strands . . . |
||
|
Skills |
Find the Volume |
|
|
|
|
Conceptual understanding |
Almost Right |
|
|
|
|
Problem solving and communication |
Gutter |
|
|
|
minutes. But fifteen-minute tasks are long enough to give students the opportunity to show how they can carry their work through to a solution, and yet short enough to ensure that not too much assessment time is wasted if the student is unable to formulate any approach to a particular task. The smallest number of tasks that might contribute to a reliable problem-solving score is about six. Therefore, it is reasonable to allot 90 minutes to an on-demand assessment of problem solving. The minimum amount of time that might be spent assessing procedural and conceptual knowledge in an on-demand context is approximately 75 minutes. The New Standards Reference Examination accomplishes this in three sittings of about 55 minutes each.
On-demand examinations scores do not need to be based upon data obtained from traditional closed-book responses, prepared by students without access to any external resources that might be useful for solving mathematical problems. Examination scores could, as an alternative, be made up of two scores—one that is derived from the on-demand component, and one that is derived from coursework; that is, work that is generated as a course requirement, and could include a range of responses that are written, oral, video, or built.
Chart 3 can be used to trace the path of mathematical connections throughout the entire assessment system. The emphasis given to each cell would depend on the mathematical connections that are emphasized in the learning expectations. The development of mathematical connections is vital to an enhanced understanding of mathematics. Absent the development of such connections, mathematics remains fragmented, cluttered, and decontextualized.
The recommendations in this chapter can be used to address the development of a single test or a complete assessment program. Chapter 3, addresses specific task development issues. The research and experience presented in Chapter 3 will provide additional support for the assessment model and recommendations presented in this chapter.