Chapter 3: Assessment and Opportunity to Perform
This chapter focuses on issues that arose during the New Standards' task development process, undertaken to build balanced assessments. The research and task development experience discussed here also offers additional insight about the foundations of the model for assessment that is presented in Chapter 2. The target audience for the assessments included both students who have encountered a standards-based curriculum as well as students in classrooms with a traditional curriculum. As part of the development process, information about instructional experiences was gathered so that results could be interpreted meaningfully and defensibly for both groups of students. In presenting several task development case studies, including analysis of some notable failures as well as successes, more information is provided to help the reader see why the model for a balanced assessment is defined as it is. Although the examples in this chapter are drawn from work with high school students, the ideas apply across grade levels.
One of the most striking aspects of task development is just how hard students find many tasks that are designed to assess conceptual understanding or problem solving. Time and again when tasks were piloted in classrooms—tasks that appeared to provide students the opportunity to show what they know—The tasks were for some reason inaccessible for most students. One explanation for this result is that many of the tasks may not closely resemble those that students are accustomed to completing in class.
In light of the evidence generated in the classroom, we had to make choices about how to proceed. One option, for example, was to declare that such tasks are too ambitious and to abandon them in favor of assessment tasks similar to those that students are accustomed to completing in class and for homework. Because the goal of the project was to produce tasks and assessments that would enhance instruction and student learning, we decided instead to advance the craft of task development sufficiently to provide students access to what had been previously inaccessible tasks.
Meeting that challenge required looking closely at the students' performances and attempting to determine what was making the tasks so difficult. Two broad themes emerged. First, students are sometimes not given sufficient opportunity to perform, by which we mean some aspects of a task prevent students from showing what they have learned. Opportunity to perform is a primary focus of this chapter. Second, students are sometimes not given sufficient opportunity to learn, by which we mean the students' classroom experiences have not left them well equipped to succeed on certain kinds of tasks. Opportunity-to-learn issues are addressed in Chapter 4.
Of course, opportunity-to-perform and opportunity-to-learn issues are inextricably linked. If students have not had the opportunity to learn, then it will be difficult to identify task characteristics that could prevent students from showing what they know and can do. Nonetheless, it is important to try to separate these issues and to recognize where the responsibility for each lies. Responsibility for opportunity to perform lies with the task and the task developer, and opportunity to learn is primarily the responsibility of administrators, teachers, parents, and students.
In our work, opportunity-to-perform issues emerged as a recasting of the time-honored concept of task validity—whether a task measures what it is intended to measure—because unless students are given sufficient opportunity to perform it is not possible to make valid inferences about what the students know and can do. Thus, when draft versions of a task failed to produce expected results in field trials, we questioned the task's face validity and asked what the task did measure. The challenge was to determine the source of the difficulty and then to revise the task in ways that maintain the important mathematical ideas the task was intended to assess.
This chapter briefly describes the task development process and then illustrates several key concepts that emerged while attempting to construct tasks that provide students with opportunities to perform. In particular, some tasks create cognitive overload by attempting to assess skills, conceptual understanding,
and problem solving simultaneously. When tasks seem inaccessible, there are ways to create access while maintaining task integrity. One such way is to provide carefully constructed scaffolding. When placing tasks in contexts, the context sometimes obscures the mathematics. Another issue is over-zealous assessment—the temptation to assess everything that is possible from a given context. When many students gave incorrect responses, sometimes the source was a task miscue—an element of the task presentation that leads students to give an incorrect response. Some tasks are stated in such a way that an incorrect solution is obvious and enticing. Without thinking the problem through, most students will respond with that solution. Such task presentations contained what can be called elephant traps. The chapter closes with a list of recommendations for avoiding these obstacles. This list might serve as a starting point for those readers who wish to develop assessment tasks that maximize students' opportunities to perform.
The development process
The New Standards task development process is designed to produce candidate assessment tasks for a series of standards-based examination that are referenced to the New Standards Performance Standards. The following outline briefly describes the high school task development process that evolved in the course of this work:
Task kernels are solicited from teachers and professional assessment developers in the U.S., Europe, and Australia, and also from U.S. curriculum development projects; for example, The Interactive Mathematics Project, Core Plus, Modeling Our World, College Preparatory Mathematics, Connected Mathematics, and Mathematics in Context.
Task kernels are tried out in a small number of classrooms under the observation of a task designer who makes rudimentary judgments about the tasks' measurement targets.
The preliminary tasks are sent to an expert review panel, together with the initial judgments about their measurement targets. The review panel is composed of a curriculum developer, a mathematician, a grade level appropriate mathematics teacher, and a mathematics educator who has a special interest and expertise in identifying and addressing equity issues.
Following this initial review, the tasks are organized into balanced packages comprising roughly 45 minutes worth of assessment and are sent to three teachers who live and work in different educational environments in the U.S. These ''co-developers" then administer the candidate task packages to their own students or observe their colleagues administering the tasks to appropriate groups of students.
At a task development meeting the co-developers work with New Standards staff and members of the expert review panel to revise the tasks in the light of the classroom trials, to identify or verify the tasks' measurement targets, and to create rudimentary scoring rubrics for each task.
The tasks that survive the task development meeting are sent to a second set of co-developers for further classroom trials. At a second task development meeting, the tasks, their measurement targets, and their rubrics are again revised as necessary.
Finally, a balanced and robust set of tasks is selected and used to create a version of the New Standards Reference Examination. These examinations are field tested in a stratified sample of schools.
Once the data from the field-test is available, the examination tasks are returned to the expert panel for final review and any necessary final revisions.
The final examinations are compiled and put before an equity review panel prior to being published.
As can be seen from this description, the task development process provides many opportunities for learning.
When cognitive overload stymies opportunity to perform
The task Hang Glider (Figure 7) simultaneously requires mathematical skill, conceptual understanding, and mathematical problem solving. As such, it is a good example of cognitive overload.
Question 1 is relatively straightforward, requiring only some fairly primitive modeling. Students must realize that to estimate the area of sail needed, they must multiply their body weight by 1 square foot per pound of body weight and add the weight of the frame. (A more complex task emerges if the weight of the sail itself is considered, but no student in our sample took this direction.)
In Question 2, the complexity of the task soars. The diagram in Figure 8 illustrates one possible approach to solving for the total sail area. The left-hand side of the hang glider is decomposed into two triangles that are rotated and reflected in order to reconstitute the right hand side into a rectangle of length l and width w / 2, where l and w are the length and width of the hang glider. In this question, both the conceptual and the strategic hurdles are quite high.
Question 3 adds another dimension. One route towards success is to recognize and then solve equations relating l and w. For example, if the answer to Question 1 was 130 square feet, the formula from Question 2 gives 130 = 1/2 wl.
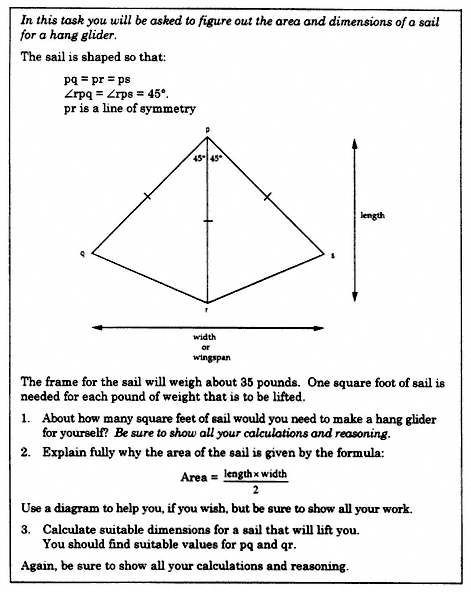
Figure 7. Hang Glider
Reprinted with permission from the Balanced Assessment project, University of California, Berkely.
Finding a second equation relating l and w is much more difficult. One way to do this is to use the diagram to find a relationship between w and l:
pq2 + ps2 = qs2, pq = ps = l, and qs = w.
So, l2 + l2 = w2.
Then w = ![]() 2l.
2l.
Finally, w = ![]() 2l can be substituted into the equation wl/2 = 130, giving 260 =
2l can be substituted into the equation wl/2 = 130, giving 260 = ![]() 2l2. Solving this gives l
2l2. Solving this gives l ![]() 13.5. Clearly, the solution to this portion of the task involves highly non-trivial conceptual and manipulative demands.
13.5. Clearly, the solution to this portion of the task involves highly non-trivial conceptual and manipulative demands.
The length of qr still needs to be determined. This can be done using the law of sines:
sin 45°/qr = sin 67.5°/13.5.
But the student has no chance of reaching this point without sufficient success on Question 1 and Question 2, to be able to draw upon those solutions to set up the equation that acts as the springboard to Question 3.
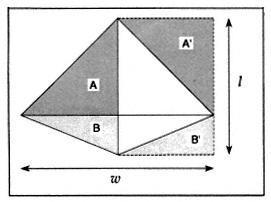
Figure 8. Hang Glider solution
This task was piloted with 184 high school students. Using a four-point scoring rubric that defines a score of '1' as little or no success, just 17 students in the entire pilot group were able to achieve a score of '2' or higher. Not a single student was able to fully accomplish the task, and just one was able provide a response that could be marked as "ready for revision."
It is difficult to make reasonable inferences about the specific nature of the obstacles that stand between the students and success on this difficult task. Is the obstacle that the students were unable to formulate successful approaches to the problem? Or was it that the students were unable to handle the total skill and concept demands? As it was given, Hang Glider indicated neither what students know and can do nor what students do not know and cannot do.
Hang Glider demands that students make very high-level use of mathematical ideas. The data suggest that only the most talented of students will have enough experience to access these concepts and to use them in the sophisticated way that Hang Glider demands. In other words, Hang Glider is a task that asks students to make strategic use of concepts that are, for the majority of tenth grade students, not fully integrated into the students' existing conceptual frameworks (Hiebert & Carpenter, 1992).
Our developmental experience shows that when students work simultaneously at the cutting edge of both their strategic domain
and their conceptual domain, the result is cognitive overload, and only the most talented can demonstrate success. Because all students can and should benefit from studying to prepare for standards-based assessments, the assessments should be designed so that students may be successful not only through special insight but also through hard work. This is not to say that the concepts entailed in Hang Glider will never be fair game in an assessment. Concepts such as these are fair game, but care must be taken to ensure that they are assessed in an arena that does not have confounding strategic hurdles. Tasks entailing a high strategic hurdle often provide a false negative assessment of what students understand about underlying concepts.
Creating access while preserving task integrity
One of the design challenges associated with developing almost any non-routine task is that of creating access without radically altering the intended measurement target. Responses to the challenge can be caricatured as follows:
A task that seems appropriate for a specified cohort of students turns out to be almost totally inaccessible. Initial classroom trials reveal that almost no students can make any sensible headway on the task. As a result, the task is subjected to a series of creative revisions. In subsequent classroom trials, the task produces a distribution of responses that is considerably more palatable. All involved are happy.
That is, all involved are happy until someone asks, What is still being assessed by the revised task? Does it still exemplify the kind of challenging and non-routine task that students should be able to do? Or, have the task revisions taken away the most interesting and mathematically challenging parts of the task? Often, creative task revisions introduced to promote access actually produce a less challenging and significantly more routine task that measures something quite different from the originally intended assessment target.
One example of a seemingly inaccessible task emerged in early trials of the now successful and relatively accessible1 task Snark Soda (Figure 5, p. 19). Initial pilots of this task produced virtually no success among large numbers of high school students. The following complaint typified the response of almost all students who attempted the original version of this task:
“There are no numbers, and without numbers you cannot find the volume of anything.”
Apparently, students did not think to measure the drawing of the soda bottle, even though the drawing was described as being full size and accurate. Clearly, if this were the only thing that Snark Soda was going to tell us about students' thinking, then it was not going to emerge as an informative assessment task.
The design challenge was to create a version of the task that would lead students to recognize the measurements they needed to make without destroying the core ideas behind the task. Initial suggestions identified ways that the diagram of the bottle could be labeled with judiciously selected measurements. One argument supporting this particular revision was that using rulers to measure diagrams can be quite alien to the culture of many American high school mathematics classes. Some teachers reported that they caution their students not to use rulers to measure diagrams in traditional geometry classes. The problem with this particular direction for task revision, however, was that it would completely carry out the primary modeling component of the task. In other words, to provide measurements for the bottle (including deciding which measurements would need to be made) would have been tantamount to doing the most interesting and challenging part of the task for the students. This change would have radically altered the assessment target of Snark Soda, shifting it from problem solving to skills.
To preserve the integrity of the task as a problem-solving one—where students would decide where to take measurements on the bottle and how to decompose it into familiar geometric shapes—it was decided that measurements should not be supplied. Instead, the task was more subtly modified, by adding the words use a ruler to measure the bottle . With this revision, students could be directed to find the necessary measurements, but the heart of the task was not altered.
One might ask why this simple solution was not suggested as the initial "fix" for Snark Soda. Perhaps the reluctance results from the long tradition of creating assessments composed entirely of bite-sized tasks and parceling out bite-sized assignments for students to do in their mathematics classes. Classrooms need to become places where students are given the opportunity to learn and then practice how to formulate and implement their own approaches to challenging, non-routine tasks. Assessments need to provide opportunities for students to showcase their mathematical understanding in ways that are challenging and non-routine.
Scaffolding—guidelines and some case studies
Scaffolding is a technique that is used frequently in task development to regulate the accessibility of tasks. Snark Soda (as presented on page 19) is an example of a relatively unscaffolded task. It could be turned into a highly scaffolded task by offering, for example, the following instructions to the student:
-
Divide the drawing of the bottle into good approximations of regular geometric shapes. Sketch the geometric shapes you have chosen.
-
Measure the drawing of the bottle and mark the dimensions on your sketches.
-
Use your sketches, measurements, and formula sheet to find a good approximation of the volume of liquid in the bottle.
If this more-scaffolded version of the task were administered to students, the challenge for the student would probably be radically different from the challenge offered by the less-scaffolded version of Snark Soda. The scaffolding suggested here would shift the assessment target of the task away from problem solving and toward mathematical skills.
Several small-scale research studies have been conducted to investigate systematically the influence of scaffolding on students' performance on problem-solving tasks. In these studies, two different versions of the same task were administered to several different classes of students. The tasks were identical in all aspects except the amount of scaffolding.
In the first study (Shannon & Zawojewski, 1995), students were presented with two versions of a task involving shopping carts. The relatively unscaffolded version was called Supermarket Carts (Figure 9). The scaffolded version was called Shopping Carts, and it was identical to Supermarket Carts except that Questions 1 and 2 were replaced by the following questions:
-
What is the length in centimeters of one full size shopping cart?
-
When they are "stacked," by how much distance does each shopping cart stick out beyond the next one in the line? Show in a rough sketch of nested carts what this distance refers to.
-
What would be the total length of a row of 20 nested carts?
-
How many nested carts could fit in a space 10 meters long?
-
Create a formula that will tell you the length S of storage space needed for carts when you know the number N of shopping carts to be "stacked." You will need to show HOW you built your rule; that is, we will need to know what information you drew upon and how you used it.
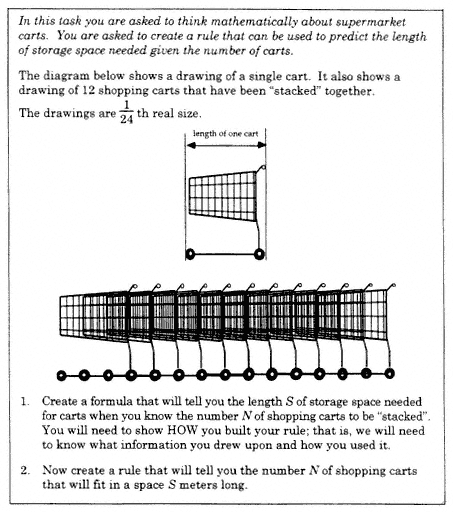
Figure 9. Supermarket Carts
Later versions of these tasks appear in Balanced Assessment for the Mathematics Curriculum: Middle Grades Assessment Package 2 and High School Package 1, © 1999, The Regents of the University of California. All rights reserved. Published by Dale Seymour Publications, an imprint of Pearson Learning. Used by permission. Further information on these packages can be obtained from the publisher or the project Web site, www.educ.msu.edu/MARS.
-
Now create a formula that will tell you the number N of shopping carts that will fit in a space S meters long.
Teachers divided their classes into two comparable groups. One version of the task was administered to each group within the same classroom. Students worked on the task individually under the impression that only one task was being administered.
In response to the scaffolded Shopping Carts, almost all students managed to develop an appropriate linear function to model the nested carts, but in response to the unscaffolded Supermarket Carts,
few students were able to do so. It seems reasonable to speculate that had the students who attempted Supermarket Carts been given the opportunity to attempt Shopping Carts, they would have shown a similar level of competence in developing an appropriate linear function.
The results of this study illustrate the role scaffolding plays in altering both the assessment target and the challenge of tasks. Shopping Carts is a scaffolded task. Implicitly, an approach to the task is outlined by the directive questions that target specific skills and concepts. Supermarket Carts is a less-scaffolded task. No auxiliary questions suggest or direct an approach. Students are told what to produce, but they are not told how to produce it. Supermarket Carts does not ensure that specific skills and concepts will be targeted. The less-scaffolded nature of Supermarket Carts provides the opportunity for exploration of the general strategies that students deploy in developing their approach to a non-routine task that calls for a mathematical model of a physical structure. In recognition of its substantial strategic hurdle, Supermarket Carts would be primarily a problem-solving task. The carefully constructed questions that direct an approach in Shopping Carts, on the other hand, reduce the strategic hurdle considerably, so that it would be categorized as an assessment of conceptual understanding.
Investigations of these and other tasks suggest that using student responses to less-scaffolded tasks to make judgments about students' basic competencies is to run the risk of making false negative judgments. Tasks such as the unscaffolded Supermarket Carts that seem to be good means of assessing general problem-solving strategies will probably underestimate students' proficiency in dealing with underlying skills and concepts. For example, when teachers were asked to administer only Supermarket Carts to their students, they expressed little doubt about its appropriateness in assessing what their students had learned about linear functions. In fact, those who had recently completed work in linear functions with their students fully expected that most of their students would be able to rise to the demands of this task. When it emerged instead that few students were able to model successfully the length of the stack as a linear function of the number of carts in the stack, the teachers expressed disappointment and feared that perhaps their students had learned little if anything about linear functions. However, the research suggests that these students probably did learn about linear functions but simply were not yet able to select and deploy this knowledge in a non-routine task with a high strategic hurdle.
Investigations of the role of scaffolding also suggest that giving students the opportunity to practice solving scaffolded tasks such
as Shopping Carts does not breed success on unscaffolded tasks such as Supermarket Carts. Furthermore, if tasks are often scaffolded to make them more accessible for students, students also must be given the opportunity to practice solving other tasks that are unscaffolded, non-routine, and challenging. Scaffolding, if too widely used, will thwart efforts to implement a broad and balanced system of mathematics instruction and assessment.
Contextual challenge and barriers to performance
The small-scale study described in the previous section concentrated on the role of scaffolding in altering the structure of a task and thus regulating task challenge. Another series of small-scale studies was designed to investigate the role of context in altering the challenge of a task. The surprising results of these studies indicate the importance of determining empirically (rather than through professional judgment) how the context can inhibit opportunity to perform. Scaffolded and unscaffolded versions of the task Storage Containers were produced by replacing the carts in each of Shopping Carts and Supermarket Carts with stackable storage containers. This pair of tasks (scaffolded and unscaffolded) involving Storage Containers was of the same form as Shopping Carts and Supermarket Carts, differing only in minor contextual features. The effect of replacing carts with containers was explored by comparing student performance on unscaffolded containers with unscaffolded carts and scaffolded containers with scaffolded carts. In each of these paired sets of tasks, Storage Containers emerged as significantly less challenging than its counterpart involving carts. When student performance on the unscaffolded containers tasks was compared with performance on the scaffolded version of carts, the containers task again emerged as less challenging. From a performance standpoint, these two pairs of tasks are clearly not of the same form, and so there must be additional differences that could explain the relative performance hurdles.
The following is a list of some of the subtle differences in the tasks:
-
The drawings of the storage container that are provided are much less complicated geometrically than the drawings of the shopping carts.
-
In carts, the stack is horizontal and as each new cart is added the length of the stack increases horizontally. In storage containers, the stack is vertical, and as each new container is added the height of the stack increases vertically.
-
In carts the scale factor is 1/24; in containers the scale factor is 1/10.
Careful attention to students completing the cart- and container-based tasks revealed that it was easier for the students to take measurements from the stack of containers than from the stack of carts. Physical characteristics of the carts, such as the wheels and handles, seem to add unnecessary complication and confusion to the task of measuring the carts.
Students would physically mime the growth of the containers as they grappled with its representation but did not use any similar action with respect to carts. The vertical increases of the stack of containers seemed to be easier for students to visualize than the horizontal increases of the stack of carts. One speculation, therefore, is that the greater ease in visualizing the vertical growth of the containers helps students construct the corresponding symbolic representation. In some part, this may account for the superior performance of students on the tasks involving containers.
In addition, the choice of scale factor, 1/24 in the drawings of the carts and 1/10 in the drawings of the containers, emerged as a strong influencing characteristic (Shannon & Zawojewski, 1995). The scale factor of 1/24 provided a greater hurdle in the unscaffolded Supermarket Carts than in the scaffolded Shopping Carts. However, the scale factor of 1/10 did not emerge as a significant hurdle in either version of Storage Containers.
This series of comparisons of tasks involving shopping containers and carts demonstrates how contextual issues can be used (advertently or inadvertently) to alter the challenge of a task without altering its general structure or lowering its strategic hurdle. These contextual issues relate to opportunity to perform.
To continue investigation of these issues, the parallel task Paper Cups was produced by replacing the storage containers with paper cups. The paper cups were drawn to 1/2 actual size. The challenge of Paper Cups did not seem as great as the challenge of Storage Containers . So, as before, scaffolded Paper Cups was compared with scaffolded Storage Containers, and unscaffolded Paper Cups with unscaffolded Storage Containers.
Both versions of Paper Cups emerged as more accessible than the corresponding Storage Containers tasks, and this relative ease also can be explained in terms of contextual characteristics.
When many students attempted Storage Containers, they measured the size of one container (2 centimeters scaled up to give the actual size of a container as 20) and then measured the amount that each additional container stuck out above the one below (0.5 centimeters scaled up to give the actual size of a stick out as 5). Then they tried to represent the height of the stack in terms of the height of one container plus the height of x-1 stick outs; algebraically,
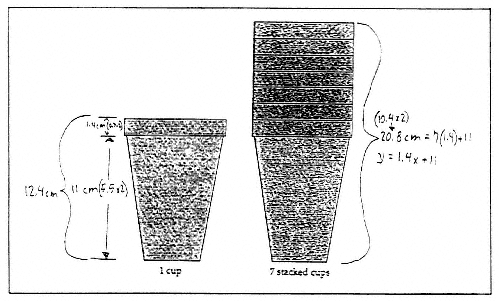
Figure 10. Student solution to Paper Cups
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
as H = 20 + 5(x-1), where H represented the total height of the task, and x represented the number of containers in the stack.
When students produce a formula of this type, it is clear that they have successfully navigated what we refer to as the x-1 aspect of this family of tasks. This is an aspect of Shopping Carts that very few students manage to process correctly. The mistake that occurs when students do not successfully navigate the x-1 aspect of Storage Containers is usually expressed as follows:
H = 20 + 5x, where H represents the total height of the task, and x represents the number of containers in the stack.
In contrast to both Shopping Carts and Storage Containers, however, many students working on Paper Cups will immediately decompose the cup into the following two parts, which they sometimes label as the body and the brim, as illustrated in the student solution in Figure 10. This decomposition enables many students to create the required formula directly in terms of the height of body of one cup plus the height of x brims, as illustrated in the remainder of this student's response (Figure 11).
Clearly, the structure of the cup lends itself to this decomposition, which enables students to finesse the x-1 aspect of the task. The specific features of the cup reduce the conceptual demands of the problem. We say this because the specific features of the cup enable students to deal with x lips rather than x-1 cups, and dealing with
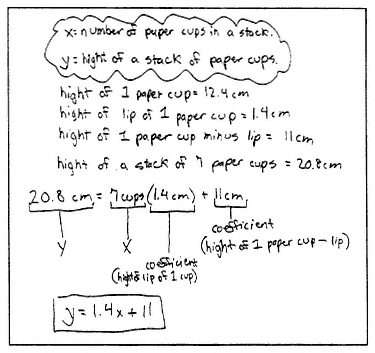
Figure 11. Student solution (cont.)
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
x is less sophisticated than dealing with x-1. Put in another way, the contextual factors associated with the cup provide greater opportunity for students to perform.
Paper Cups emerges, therefore, as a task that has a relatively high strategic hurdle, is appropriately challenging, and yet can be presented without relying on any directive questioning. It is a type of task that can he quite beneficial to use with students who are not accustomed to solving context-based problems. It also is a good introduction to non-routine tasks because it may be solved with lower levels of tenacity, it encourages perseverance, and it enables students to show what they can do rather than what they cannot do.
These findings have important implications for the model of assessment that is advanced in Chapter 2, which recommends separating assessment of mathematical skills, conceptual understanding, and problem solving. In this family of problem-solving tasks that involved stacks, students showed the most success when the conceptual demand of the task was reduced. Therefore, task developers should take care that the conceptual demands of a problem-solving task do not prevent students from showcasing their problem-solving capabilities.
These findings also demonstrate one way to increase access to a task without using scaffolding to structure or dictate an approach to the task, thereby reducing its strategic demands. Access may be improved by reducing the conceptual demand of the task while keeping the strategic demand of the task intact. Of course this does not mean that assessment of conceptual understanding is to be sacrificed in the interest of assessing problem solving. Remember, the model advanced in Chapter 2 recommends creating specific tasks to assess conceptual understanding. In these specially designed tasks, the conceptual demands will need to be as deep and as far ranging as the conceptual demands of the standards on which the assessment is based.
The implications of contextual challenge on opportunity to learn
Considerable attention has been invested in examining both the obvious and the more subtle differences among the cart, container, and cup tasks. Given current recommendations to situate some mathematical learning and assessment activities in realistic contexts (e.g., NRC 1993b; NCTM, 1995), it is worthwhile to explore in detail the ways in which specific contexts outside of mathematics can facilitate or challenge mathematical thinking. In assessment, particularly when the stakes are high, it is imperative to discern the ways in which the contexts affect opportunity to perform and consequently issues such as equity and fairness. Because any context will be more familiar to some students than others, some bias is inevitable, but bias can be reduced through continual review and input from equity experts who can detect biases not apparent to the task designer.
Some connections with the world outside of mathematics are recommended for learning as well as for assessment (e.g., NCTM, 1989, 1995; NRC, 1993b). In view of this recommendation, the research into the relative effects of replacing carts with containers and then containers with cups leads to questions about the relative effects of the specifics of linear function tasks that rely on contexts such as car rental charges, phone call charges, and electricity charges. When each of these involves an initial value in the form of a fixed charge and a constant increase in the form of a fixed charge per day, or fixed charge per minute of call, or fixed cost per kilowatt-hour of electricity, each of these situations can be modeled by y = kx + b. These types of problems are now commonly used in schools to teach linear functions. The issue is how the specifics of these situations might count for or against student learning. A comparison of student performance on this type of task relative to student performance on Paper Cups or other stacking applications would probably lead to interesting insights. At this stage, it seems that the context of the tasks involving stacking would make the underlying concepts more accessible to students. This is because
the quantities that are to be related to each other in Paper Cups (number and height) seem to be much more tangible for students than the quantities to be related in tasks situated in contexts involving rental car, phone call, or electricity charges.
In addition, examples of stacking enable the students to trace the structure of the stack in different representations (i.e., verbal, table, and diagram) and this makes it possible to use the structure to demystify the translation to more abstract representations (i.e., graph, formula). And it is this attribute of these structures that suggests their use in the initial teaching of concepts such as linear functions. The variables that need to be represented in physical structures comprised of cups or books are more concrete and more visible for students than are the quantities such as cost and time in tasks involving rental cars and telephones or quantities such as cost and kilowatt-hours in tasks involving utility bills. If students are taught about linear functions using contexts they can visualize in a concrete tangible way, it is hoped that they will be able to apply the ideas they have learned to less obvious situations. A related point is that the call for connections with the world outside mathematics has led to frequent use of contexts such as rental cars, phone calls, and utility bills, and our assessment development experience suggests that these contexts probably differ greatly in their abstractness and in their ability to serve as learning tools. Explorations should be carried out into the effectiveness of frequently used contexts, to determine whether these contexts are truly suitable for initial learning purposes.
Over-zealous assessment
Sometimes task designers, in their eagerness to create worthwhile tasks, try to assess everything that it is possible to assess in a given situation. This phenomenon can be called over-zealous assessment . The problem of this affliction is most apparent in assessment opportunities where less might actually mean more.
Through scaffolding, for example, task designers sometimes try to wrench every possible detail out of a given context or scenario. Overuse of scaffolding generally dictates a solution path for the student, and serves to control what the student uses in the assessment. One advantage of tightly controlled assessments is that they tend to have better measurement characteristics. For example, if the intention is to build a large-scale assessment that can be standardized, then the scores will be more reliable and generalizable when the test comprises many tightly controlled items rather than smaller numbers of less well-specified problems. The disadvantage of tightly controlled assessments is that the task designer effectively specifies the mathematics, and all that remains for the student is to be led through a series of steps dictating the solution
to a task that might once have been interesting and challenging. If tests comprise only tightly controlled tasks, then the assessment will not include the full range of tasks that is necessary for a balanced assessment. Highly scaffolded tests greatly restrict the opportunity to assess strategy formulation, tenacity, high-level use of skills and concepts, communication and mathematical connections. Overuse of scaffolding, therefore, decreases the capability of assessments to improve the ways in which the teaching, learning, and assessment of mathematics is enacted (as envisioned by NCTM, 1989, 1991, 1995; NRC, 1989, 1990, 1993b).
Scaffolding is not the only means of assessing everything in a given situation. It is sometimes tempting to pose a problem-solving task with a substantial strategic hurdle, then go on to load the task down with additional mathematically important ideas. Question 2 in Supermarket Carts (p. 40), for example, asks students to manipulate the function they were asked to create in Question 1. Undoubtedly this sort of skill is important and does not deserve to be embedded in a larger problem. The equity issues are obvious—it is unlikely that students stymied by Question 1 will be able to even attempt Question 2. In such cases, it would be unreasonable to make inferences about the students' ability to manipulate symbolic expressions. This is not to say that short closed questions such as these have no place in an assessment. On the contrary, important skills such as these should have their own place in an assessment—but not tucked away at the bottom of a larger assessment of strategic use of mathematics. Indeed, their place is in assessment tasks designed specifically to assess mathematical skills and concepts, and these assessment tasks might well be those that use scaffolding intentionally to target specified aspects of mathematics.
Turning task miscues into opportunity to perform
The effort that is put into developing assessment tasks and identifying their assessment targets will be wasted if similar effort is not paid to the interpretation of student work. Hiebert and Carpenter have noted that the assessment of understanding relies heavily on indirect inference from student responses to a task (Hiebert & Carpenter, 1992). Our own work in the development of assessments has shown that great care must be taken before inferring causal linkages between student understanding and students' responses to a given task; for example, it might not be reasonable to infer from a completely incorrect solution that the student does not understand the underlying concept.
There is a large amount of evidence illustrating how task characteristics can miscue students, leading them to provide an incorrect response. Miscues manifest themselves in a whole range of aspects, including graphics that mislead, sentence structure
that miscommunicates, and assumptions that are not shared between task-doers and task-makers. Miscues also can be a source of bias when different groups of students have differential familiarity with some aspect of the task presentation. Although some bias is inevitable, task designers should make every effort to detect and reduce it whenever possible.
One example of a miscue is provided by a recent attempt to assess probability. Students were asked to analyze a game that was presented as having been devised to raise money for the school library. The designer's intent was to ask students to estimate how much money the game would raise and to say how the game should be changed to raise more money for the library. An unfortunate choice of question, How could they raise more money for the library?, stimulated a whole host of creative money raising suggestions, but few of these dealt with the intended mathematical activity of changing the odds of the game. The problem here was the task's miscue rather than students' conceptions or misconceptions about probability.
Examples of miscue founded on unshared assumptions were provided by attempts to use the context of a forester's Diameter at Breast Height (DBH) tape to explore student understanding of the relationship between diameter and circumference. A DBH tape is used to provide a direct reading of the measure of the diameter of a tree. The tape is wrapped around the circumference, and the measure of the tree's diameter is read directly from the tape (based on appropriately scaled markings).
An initial version of the assessment task asked students to explain how they would create such a tape. This prompted students to provide a plethora of explanations including: the tape would need to be long because trees can be incredibly large, the material would need to be flexible so that it could be wrapped around a tree, and marks would need to be put on at least one end so that the measurements could be read. Here was a classic case of task miscue, which had more to say about task presentation than about students' understanding of the relationship between the diameter and circumference of a circle. Ultimately, a useful version of this task removed the miscues by providing students with a diagram showing part of a tape that was calibrated in centimeters and part of a special tape that was blank. Students calibrated the special tape so that it could be used to measure the diameter of trees directly.
Examples of graphics that miscue abound in task development work. Many of the students who respond to the tasks speak English only as a second language, and so graphics can be a useful way of reducing the reading challenge of a task. Such graphics are of two main types:
-
those that are essential for communicating the mathematics intrinsic to the task; cups, carts, and containers, for example, are intrinsic graphics because these represent the physical structures to be modeled; and
-
those that are used for cosmetic purposes or with the intent of reducing the reading challenge of the task.
In a task that asked students to design a circular ice-skating rink, according to a set of given constraints, a graphic depicting a skater on a circular ice-rink was inserted to reduce the reading challenge of the task. Yet early trials of the task produced large numbers of student responses based on a rink that was square rather than circular. These responses led us to notice that the graphic showing the circular ice-rink was framed by a dark square border. This border may have been the most perceptually salient feature of the graphic, and as a consequence it had unintentionally miscued the students.
Another interesting example of miscue by graphic occurred with the task Shoelaces. A large one-half scale drawing of a shoe was provided to serve an equity purpose; in early trials of the task, some students were able to use the lace holes on their own shoes as props when they were working on the task. For equity purposes, therefore, it seemed important that all students have access to a realistic drawing of a shoe with lace-holes and laces. This graphic caused no difficulty and is intrinsic to the task. The difficulties centered on a smaller cosmetic graphic. The most perceptually salient characteristic of this graphic, for many students, turned out to be its right-angular heel. This aspect served as an invitation for an unexpectedly large number of students to try applying the Pythagorean Theorem to this task. When the square root of the square of the height of the shoe plus the square of the length of the shoe did not seem to produce a reasonable final result, many students then multiplied this by the number of lace holes. When the graphic was adjusted so that it no longer had the appearance of a right triangle, no further applications of the Pythagorean Theorem to this linear function task emerged. More important, once students were freed from the unintended task miscue, they were able to show what they did know or could figure out about modeling the length of the lace needed as a function of the number of lace holes.
Once miscues have been identified, they serve to remind task developers that task development is a humbling experience. These episodes stress the importance of trying out different versions of a new task with small groups of students and peers, and of taking seriously those responses that appear odd or inexplicable, regardless of how few of them occur.
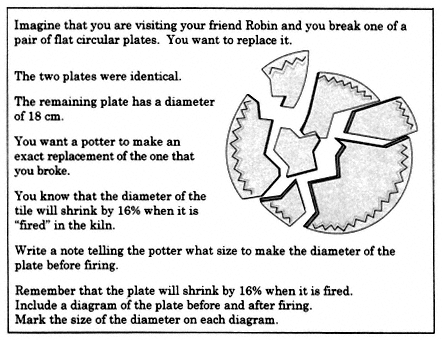
Figure 12. Broken Plate (version 1)
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
Turning elephant traps into learning opportunities
With regard to assessment, the term elephant trap refers to an unintended task hurdle or a task hurdle that provides no information other than the observation that large numbers of students consistently arrive at a common incorrect response. The task Broken Plate (Figure 12) provides an example of this phenomenon.
When this task was administered to a stratified sample of high school students, there was a remarkable convergence among the student responses. Students invariably decided that the diameter of the plate before firing should be 20.88 centimeters, because 16% of 18 is 2.88, and 18 + 2.88 = 20.88. Students had obviously fallen into the trap of thinking that an x% increase followed by an x% decrease will get you back where you started. This task does not encourage students to demonstrate what they know, but instead traps them into showing what they do not know.
Perhaps the most useful characteristic of the task Broken Plate is that it highlights aspects of percentage increase and decrease as problematic and identifies an area of instructional need. A second version of Broken Plate (Figure 13) was piloted with another sample of students. This version incorporates an incorrect response that

Figure 13. Broken Plate (version 2)
Reprinted with permission from New StandardsTM. For more information contact National Center on Education and the Economy, 202-783-3668 or www.ncee.org.
typified student performance on the initial version. The response to this later version was remarkable:
-
students' responses spanned a range of answers rather than conforming to a single type,
-
the majority of students' responses to Question 2 were correct, and
-
students were able to use the typical incorrect response to develop a correct one.
We would argue that this technique of incorporating an incorrect response and identifying it as such can frequently be
used to enable a task to function as a learning opportunity. The juxtaposition of the incorrect response and the student's misconception will create cognitive conflict for the student. The student is given the opportunity to reflect on an incorrect response, resolve the conflict, and produce the correct response.
The technique of giving students a wrong answer and asking them to supply a correct one is recommended in a recent publication commissioned by the NAEP Validity Studies (Jakwerth, Stancavage, & Reed, 1999). This technique was used with considerable success in the development of the Key Stage 3 mathematics tests that were developed to assess the National Curriculum for Mathematics in England and Wales (Close, 1996). The technique of situating common misconceptions in assessments is one that provides a direct opportunity for assessment to enhance learning and so heed the call that is expressed in The Learning Principle (NRC, 1993b) and the Learning Standard (NCTM, 1995).
Not every student will successfully resolve the conflict posed by such an approach. Indeed, some refuse the opportunity by asserting that the student response labeled as incorrect is in fact not wrong! What reason do students give for this? Often, they simply assert that the incorrect response is correct because it coincides with what they would have done or that it coincides with what they believe to be true. Nonetheless, what we have identified here is how cognitive conflict can be used to convert an elephant trap into an opportunity to learn. The constructive use of mathematical errors and misconception corroborates previous research in using student misconception as a learning tool (Bell, 1993; Bell, Swan, Onslow, Pratt, & Purdy, 1985; Borasi, 1996; Graeber & Campbell, 1993).
Recommendations for task development
What follows is a list of recommendations for those who are interested in creating assessments or evaluating the quality of assessments. This list includes those recommendations from the NAEP Validity Studies (Jakwerth, Stancavage, & Reed, 1999) that appear appropriate to mathematics assessment. The NAEP Validity Studies investigation was conducted by interviewing students immediately after they had completed the eighth-grade 1998 national NAEP assessments in reading and civics about their test-taking behaviors and their reasons for omitting questions. Many students find constructed-response tasks difficult in general, and particularly difficult when they are asked to complete such tasks under time-limited conditions. The NAEP Validity Studies report that in the 1996 NAEP mathematics assessment, omission rates at grade eight were as high as 25 percent on some questions, with the highest omission rates on the extended-response questions items. There is a need to create extended-response mathematics tasks
that are as accessible as possible. Recommendations for task development are as follows:
-
Select contexts that create rather than restrict access. Do not assume that a realistic context will facilitate access. It is possible to explore the accessibility of a particular context by trying out the same mathematical idea in a range of different contexts.
-
Keep the reading challenge of the task low. Use diagrams to communicate the demands of the task. Test out the graphics: they should not include irrelevant variables that might miscue the student.
-
Use clear and unambiguous vocabulary.
-
Avoid esoteric abbreviations or idioms that might not be familiar to all students.
-
Use scaffolding to create access but evaluate the effect on the assessment target.
-
Beware of over-zealous assessment where there is the temptation to load a task down with too many parts. If students have been unsuccessful on the first or second part of a task, they are unlikely to attempt parts that come later.
-
Beware of cognitive overload. Try tasks out with students to make sure that the cognitive demands of the tasks are aligned with the expectations laid out in the standards and that the demand is appropriate with the circumstances of performance that are required. More can be expected in a situation where the circumstances of performance are characterized as research-feedback-and-revision than on a timed situation.
-
Locate talented task designers. In addition to developing its own tasks, New Standards sought kernel tasks from many sources, including The Balanced Assessment Project, mathematics teachers from across the U.S., curriculum developers, and task developers in Australia and England.
Perhaps the most sound practical advice is that all revisions to high-stakes assessments should be tried out with students to explore the effect of these revisions on opportunity to perform. No one can guess reliably how students will respond to a particular version of a task.
























