Charles Roy Henderson
April 1, 1911–March 14, 1989
BY L. DALE VAN VLECK
TWO MEN, BOTH born in the farming community of Page County, Iowa, had more impact on modern animal production in the United States and the world than any other pair of scientists since the rediscovery of Mendel's laws. Both men specialized in the area of agricultural sciences known as animal breeding and genetics. The first, born near Shambaugh, Iowa, on January 3, 1896, was Jay Laurence Lush. The second, born near Coin, Iowa, on April 1, 1911, was Charles Roy Henderson, who became a graduate student under Lush at Iowa State College in 1946. Lush also preceded Henderson as a member of the National Academy of Sciences.
Lush, and later Henderson, led the profession for nearly all of the twentieth century. Lush outlined the basic principles and methods for genetic improvement. Henderson followed by developing methods first to estimate the genetic parameters needed for the application of those principles and then to predict most accurately the genetic values of animals available for selection. Henderson's methods have been since the 1950s—and will be for the foreseeable future—the basis for genetic evaluations for every breed of every class of livestock in every country of the world. Millions of beef cattle, dairy cattle, pigs, sheep, and other
species are evaluated annually with what are called ''Henderson's mixed model equations." These equations are also applied to statistical analyses in many other disciplines. The impact of Henderson's discoveries is perhaps incalculable. The discoveries, however, can be documented.
Personal History
Farm Boy, Athlete, Scholar
Charles Roy Henderson was the first of four sons of Arthur James and Maud McMichael Henderson. One sister died at an early age. Charles Roy was born on the Henderson farm in Morton Township in Page County near Coin in southwest Iowa. He was forever proud of Page County and of growing up on a diversified farm with dairy cows and pigs, and with horses used for farm operations. Henderson was active both in 4-H and Future Farmers of America, which honored him as Iowa's Farmer of the Year during his final year in high school. He was probably even better known in Page County for his athletic achievements, which began at an early age. At one Page County Farm Bureau picnic he entered and won three consecutive races: for twelve and under, fourteen and under, and sixteen and under. The rules were changed the next year to be races for ages ten to twelve, thirteen to fourteen, and fifteen to sixteen! In addition to being the main member of the Coin High School track team, he was also the center of the basketball team when basketball still required a center jump after each score.
His track career flourished at Iowa State College (now Iowa State University) on both the indoor and outdoor teams. Highlights included a world indoor record for a relay (4 by 220 yards) of 1:31.8 in 1932; an Iowa State field house record for the indoor 440-yard run of 51.7 seconds
in 1933, which stood for thirty years; and an outdoor personal best of 48.6 seconds in 1933, when the world record was 47.4 seconds.
While running track in both the indoor and outdoor seasons, he also was a member of the college livestock judging team and worked his way through college at numerous jobs, including waiting on tables at the dining room of the women's dormitory. The remainder of his time (or the other way around) was devoted to full time study. He graduated in four years and in the final year was taking courses for a graduate program in animal nutrition. Henderson's academic record at graduation was the best in his division, surpassed in the whole college by only one engineering student. His grades in chemistry included 96, 98, and 95 by quarter in his freshman year. Of his seven courses in mathematics the lowest grade was 98.
Sports And Music
The athlete from Iowa retained his interest in sports throughout his life. As a faculty member at Cornell, he was a faithful fan of most of the sports teams. His attendance at track, basketball, and football events was particularly regular while his sons were growing up. His interest in the Drake relays held in Des Moines was obvious. Although he could not attend with the regularity of one of his younger brothers, who was said to have attended 48 of 50 consecutive Drake relays, Henderson attended several times in connection with speaking trips in the Midwest.
Among his sports heroes were two near-contemporaries, Glen Cunningham of Kansas, who had overcome near fatal burns to become a premier miler, and naturally, the Olympian sprinter from Ohio, Jesse Owen. No doubt Henderson admired others as well, but an unlikely sport for an Iowan, ice hockey, furnished others. His loyalty to
the Cornell hockey team, which rose from a new, usually soundly defeated team to become two-time national champions under Coach Ned Harkness, was nearly an addiction. Harkness, a rather unimposing person, was a motivator who could turn good athletes into superior team players, including a national championship team with a 29–0 record. What impressed Henderson even more was Harkness's off-the-rink interest in his players' success as students. Another hockey hero was an imposing athlete and scholar, Ken Dryden—varsity baseball shortstop, dean's list student, Nader's raider, and perhaps one of the best hockey goalies ever. For example, when he returned to hockey after a year of studying for his law degree, he joined the Montreal Canadians just before the play-offs and led them to a Stanley Cup. From the time Dryden signed with the then elite team of hockey, Henderson was a fan of "Les Habitants."
Henderson attributed his strong interest in music to its relationship to mathematics. When I asked his wife where or when that interest began (which was somewhat unusual for a boy from a country school in Iowa), she told me that the county school superintendent, later state school superintendent, had visited his grade school one day with a portable phonograph. Since Henderson most likely would have told that story many years later, my conclusion is that the superintendent's windup phonograph and the music, which he remembered as the William Tell Overture, must have made a strong impression. His radio at work and, I'm sure, at home was usually tuned to a classical music FM station—often WHCU in Ithaca, which coincidentally also carried all Cornell basketball, football, and hockey games. The dial did not need to be changed. My impression was that his favorite composer was Johannes Sebastian Bach. His wife told me she thought his favorite selection was Bach's Air for the G String. At his memorial service four
pieces by Bach were featured, including Air for the G String at the interlude.
Nutrition, Extension, And Marriage
On graduation with a B.S. in the midst of the depression years of the 1930s, Henderson continued as an M.S. student in animal nutrition. His grades of A for ten hours of statistics and of B for eighteen hours of nutrition research suggest his early liking for statistics. The background in nutrition and obvious excellence in statistics eventually led him back to Iowa State to study with Lush, followed by an eminent statistical career in animal breeding and genetics at Cornell University.
In 1935 with an M.S. in animal nutrition, Henderson accepted a position as county agent in a county bordering Page County. In 1939 he was asked to become a district land use planning specialist. To prepare for this he enrolled for eight hours of economics at the Iowa State summer session. A fellow county agent one county closer to Ames asked if his daughter (who was working on her M.S. in education) could ride with Henderson to Ames that summer. Less than eighteen months later, on December 21, 1940, that daughter, Marian Mae Martin, married Charles R. Henderson in Chariton, Iowa. In January 1941 they moved to Ohio University in Athens, where Henderson taught animal husbandry and managed livestock enterprises on the university farm for nearly two years. Their first son, Charles, Jr., was born in Athens. Later children were James M. and Elizabeth Ann, both born in Ithaca, New York.
In late 1942 Henderson volunteered for and was accepted with a commission as a first lieutenant in the Medical Department's Nutrition Division of the U.S. Army. He served nearly four years and finished as commanding officer of
the Army Medical Nutrition Laboratory in Chicago with the rank of major. He thought of his army experience as being particularly fortunate because nearly all of it involved research in nutrition and statistics. He was responsible for all aspects of data recording and statistical analyses. His enjoyment of that experience must have contributed to his decision to return to Iowa State as a Ph.D. student in animal breeding with Jay Lush. He had a joint major in animal breeding and genetics and a minor in statistics. His minor was much more than the usual one. In the two years at Iowa State his program included 18 hours in statistics, all with grades of A. This was begun at age thirty-five with a family, including his son Charles, Jr.
Academic Heroes
The person most influencing his professional career was undoubtedly Jay Lush, a true hero in Henderson's eyes. Although Lush accepted him for graduate work and signed course registration material for the first year, the official chair of his graduate committee was Lanoy N. Hazel, who joined the Iowa State faculty soon after Henderson arrived. Alexander Mood, representing statistics, was an original member of Henderson's graduate committee. When Mood left Iowa State, Oscar Kempthorne was his replacement. The other important committee member was John Gowen for genetics.
Other than Lush, Henderson's most significant role model was Sewall Wright, whose work with path coefficients influenced Lush's teaching of animal breeding. Despite the great regard of Henderson for Lush and Wright, Henderson took a completely different approach to the teaching of correlation and causation—the approach of mixed linear models, which was infinitely more understandable (at least to his students) than path coefficients. In addition to the
basic foundation Lush and Wright had built for animal breeding and genetics, another basis for Henderson's admiration of Lush and Wright was that both continued their work long after formal retirement, Wright into his nineties and Lush into his eighties. Henderson was determined to follow that model, which he did until the week he died, two weeks before his seventy-eighth birthday shortly after preparing slides for a scientific meeting to be held a week later. A colleague presented his paper, using notes prepared by Henderson. He died after a brief illness on March 14, 1989, in Urbana, where for several years he had held a full time, half-year visiting professor appointment at the University of Illinois. He had been elected to the National Academy of Sciences in 1985 at age seventy-four (Lush had been elected at age seventy-one in 1967) as one of only a few animal scientists to receive that honor.
Professional History
The Mixed Linear Model Problem
Careers in science usually do not begin at age thirty-seven and continue for more than forty years, as did Henderson's. After four years in the Medical Division of the U.S. Army, Henderson returned to Iowa State to work with Lush and Hazel for a Ph.D. Within two years he had accepted a position as associate professor at Cornell University with a thesis to be completed that fall while at Cornell. At that time animal breeders relied on the techniques of Wright and Lush based on path coefficient methods which led to a later formalization called selection index. This method is used to predict unobservable breeding values assumed to be jointly distributed with observations that have been adjusted for all fixed environmental influences. Animal breeders also utilized least squares procedures
based on work of Fisher and Yates in England to estimate the adjustment factors from what is now called "messy" data, using fixed effects linear models. The adjective "messy" refers to unbalanced data with many, if not most, subclasses having no observations. The selection index approach also requires estimates of components of variance for the random effects influencing the records, such as uncorrelated environmental effects and the nonobservable breeding values. And here was the problem of how to estimate these variance components from messy data. Prior to 1946, methods to do this had not been developed except for nested (not cross-classified) designs. These were problems that Henderson solved. Henderson almost single-handedly merged the selection index methods of Wright and Lush with the fixed linear model approach of Fisher and Yates into a single method to solve the mixed (fixed and random effects) linear model problem. The solution was what animal breeders and others now call Henderson's mixed model equations. Henderson credited the development of these equations to a homework question in a mathematical statistics course taught by Alexander Mood, a member of his graduate committee. That historic question (Mood, p. 164) is as follows:
Suppose intelligence quotients for students in a particular age group are normally distributed about a mean of 100 with standard deviation 15. The I.Q., say x1, of a particular student is to be estimated by a test on which he scores 130. It is further given that test scores are normally distributed about the true I.Q. as a mean with standard deviation 5. What is the maximum-likelihood estimate of the student's I.Q.? (The answer is not 130).
Ph.D. Thesis
The Wright-Lush and Fisher-Yates approaches were the starting points for Henderson as he began his thesis research.
His thesis topic was on estimation of variances due to general, specific, and maternal combining abilities from single crosses among inbred lines of swine. The model for such data would require a linear model with many fixed environmental and many random genetic factors with many missing subclasses. No methods existed to estimate variance components from such data. The challenge of his thesis data led Henderson to develop two methods to estimate variance components, later known as Henderson's Methods 1 and 3. Method 3 was particularly powerful as it allowed unbiased estimation of variance components in the presence of confounding with fixed environmental factors. Method 2 was developed somewhat later and was widely used by animal breeders for many years as it was computationally much less demanding than Method 3. In 1951 he presented these methods at a conference in North Carolina where he met Fisher, who encouraged him to publish the methods. The full paper was published in Biometrics in 1953 and quickly became the standard reference for estimation of variance components. The paper was later selected by the Institute for Scientific Information as a most frequently cited scientific publication—"a citation classic." This work led to his being named a fellow of the American Statistical Association.
As part of his Ph.D. thesis research, Henderson invented a method to minimize the bias caused by interaction effects in estimates of fixed model effects in missing subclass cases. Many techniques for linear models were presented in detail in the appendix of his thesis. These techniques were incorporated into the most widely used statistical package of the 1960s, a package written by Walter Harvey, still used around the world by animal breeders. The thesis was also used for many years by animal breeders
as a reference, especially the large number of students and visitors who studied with Lush and Hazel at Iowa State.
For his thesis Henderson also developed an ingenious method to evaluate merits of random inbred lines from large sets of data with many missing subclasses. He estimated breeding values by least squares as if they were fixed effects and then used those estimates as random data with selection index methods. This method was known as regressed least squares. He never, however, published his thesis material, even though it was used by many researchers. He had no joint papers with thesis advisors Lush and Hazel. The only published connection with his thesis is an abstract at the 1949 annual meeting of the American Society of Animal Science with the same title as his thesis.
Combining Least Squares And Selection Index
What seems to have happened is that soon after his arrival at Cornell he discovered the solution to the problem of mixed linear models that completed the combining of least squares procedures with selection index. An abstract for the 1949 annual meeting of the American Dairy Science Association indicates the birth of Henderson's mixed model equations. Rather than publish outdated although original contributions, he had simply moved on to a more correct approach. Although he was quite confident of his invention, proofs of the optimal properties would not be obtained until more than ten years later.
A colleague Henderson met as a Senior Fulbright Research Fellow to New Zealand in 1955 was Shayle R. Searle, who worked as a statistician for the New Zealand Dairy Board. Searle introduced Henderson to matrix algebra. Searle later obtained his Ph.D. with Henderson. After returning to New Zealand for two years, Searle accepted a position in biometry at Cornell and became again a colleague
of Henderson. Searle helped considerably as a student and as a colleague with the matrix proofs of the desirable properties of Henderson's mixed model equations, which, parenthetically, were for years incorrectly called maximum likelihood equations.
Matrix algebra can be used to describe the power of Henderson's mixed model equations, which have been and will be used extensively by animal breeders and are now and will continue in the future to be the basis for linear mixed model analyses. Let y be a vector of observations of order n. The general linear model for the observations can be written as:
y = Xβ + ∊
where
β is a vector of fixed effects,
X is the matrix that associates the fixed effects with the observations in y, and ∈ is a vector of random effects.
The mean vector of y is E [y] = Xβ and the variance of the observation vector, y, is V(y) = V(∊) = V of order n X n.
With correlations among elements of ∊ the structure of V is not the identity matrix. The generalized least squares solution for β has been known for sixty years to be obtained from the generalized least squares equations:
(X'V-1X) ![]() = X'V-1y
= X'V-1y
The problem is that V-1 must be calculated. Computational time to obtain inverses of matrices such as V-1 is proportional to n3. Thus, even with faster and faster computers (in 1948 few of any power were available) when, depending on the decade, the number of observations reached a few hundred, then thousands, later tens of thousands,
and still later a few million, obtaining the inverse was impossible. If X'V-1X could be calculated, iterative methods can be used to obtain solutions to the equations but obtaining V-1 for all except trivial problems may still be impossible. The generalized least squares equations do define solutions for the fixed effects, β. Such solutions denoted as ![]() yield X
yield X![]() , which are best linear unbiased estimators (BLUE) of Xβ. But, what animal breeders and other people needed were predictors of random effects such as breeding values. These are included in ∊ as in the mixed linear model:
, which are best linear unbiased estimators (BLUE) of Xβ. But, what animal breeders and other people needed were predictors of random effects such as breeding values. These are included in ∊ as in the mixed linear model:
∊ = Zu + e
where u is the vector of random effects to be predicted (e.g., breeding values), Z is the matrix associating effects in u with y, and e is a vector of random effects uncorrelated with u.
Predictors of elements of u which have the properties of BLUP, best linear unbiased predictors, can be obtained as E[u1/2y] with the restriction that E[û] = E[u]. One way to obtain û is
û = GZ'V-1(y - X![]() )
)
where GZ' = cov (u,y'). The corresponding selection index predictor (also called best linear predictor) is:
u = GZ'V-1y - Xβ)
where β, the vector of fixed effects, is assumed known exactly instead of using ![]() the BLUE of β. To adjust for fixed effects to obtain BLUP, not only must V-1 be calculated,
the BLUE of β. To adjust for fixed effects to obtain BLUP, not only must V-1 be calculated, ![]()
must be obtained from solving the generalized least squares equations.
The Mixed Model Equations
This then is the problem Henderson saw and solved. How could ![]() and û be obtained without inverting V? His solution, and also the approach of Wright and Lush later formalized by Hazel and Fairfield-Smith as selection index, require knowledge of variance components making up V. That was the stimulus for his development of methods to estimate variance components for which he first became well known, not only in the field of animal breeding and genetics but also in the field of statistics. His goal in developing methods to estimate variance components (he developed various procedures during the next thirty-six years) was not a mathematical-statistical exercise. His reason was to obtain the best possible predictions of breeding values to use for optimizing selection of breeding animals.
and û be obtained without inverting V? His solution, and also the approach of Wright and Lush later formalized by Hazel and Fairfield-Smith as selection index, require knowledge of variance components making up V. That was the stimulus for his development of methods to estimate variance components for which he first became well known, not only in the field of animal breeding and genetics but also in the field of statistics. His goal in developing methods to estimate variance components (he developed various procedures during the next thirty-six years) was not a mathematical-statistical exercise. His reason was to obtain the best possible predictions of breeding values to use for optimizing selection of breeding animals.
In passing, it can be noted that a 1979 conference honored Henderson for his contributions to the estimation of variance components and to the application of those techniques. All the conference papers (by leading researchers) were published, including Henderson's closing paper entitled ''Using Estimates of Variances in Predictions of Breeding Values Under a Selection Model." More on that later.
Even with the assumption that good estimates of variance components represented in V are available, the problem was how to obtain V-1. Henderson's solution was intuitive and did not involve calculation of V-1. He very likely did try to find efficient ways to do that, but he was unsuccessful. What he did do was this. If elements of u are assumed to be fixed effects, then for the linear model
y = Xβ + Zu + e
the weighted least squares equations to solve when assuming both β and u are fixed are:
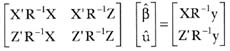
where R = V (e), which usually has a simple structure: diagonal and homogeneous for single traits or block diagonal or multiple-traits, so that R-1 is easily obtained. Henderson's first formulation involved single trait equations multiplied through by σ2, the homogeneous variance of R = Iσ2. In that case, the equations are what are called ordinary least squares equations
In the general formulation, what he did was add G-1 where G = V(u) to the Z'R-1Z block of the least squares equations:
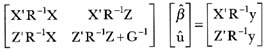
What he thought and what he proved several years later was that the solutions to these "modified" least squares equations were, in fact, BLUE for β and BLUP for u (i.e., were identical to ![]() and û presented earlier). Because R-1 is usually easily obtained and in many cases the structure of G is such that G-1 is also easily obtained, then simple iteration can be used to obtain
and û presented earlier). Because R-1 is usually easily obtained and in many cases the structure of G is such that G-1 is also easily obtained, then simple iteration can be used to obtain ![]() and û from the mixed model equations, known to most animal breeders and statisticians as "Henderson's mixed model equations." The importance of this discovery cannot be overemphasized. These equations
and û from the mixed model equations, known to most animal breeders and statisticians as "Henderson's mixed model equations." The importance of this discovery cannot be overemphasized. These equations
are easily constructed and relatively easily solved even for millions of equations such as is now the case for genetic evaluations in many countries for most classes of livestock. These equations are the foundation for nearly all applications of analyses for mixed linear models. In fact, they are also the basis for rather sophisticated methods of variance component estimation using principles of maximum likelihood and restricted (residual) maximum likelihood. It seems likely that these equations will be used for decades if not longer for analyses of mixed linear models (and, in fact, in further modified form also for nonlinear or generalized linear models).
The proofs that solutions from mixed model equations are the BLUE of β and BLUP of u are in papers in 1959 and 1963. The proofs are based on an identity for V-1 with V = ZGZ' + R due to Henderson's colleague-student-colleague, Shayle R. Searle.
Improved methods of estimating variance components have been developed, many with the stimulus and prodding of Henderson. No doubt Methods 1, 2, and 3 for estimation of variance components would have been developed without Henderson, only later, but it seems unlikely that anyone would have discovered "Henderson's" mixed model equations.
Inverting a Special Matrix
What Henderson considered his second most important discovery was a way to obtain G-1 for a special case important to geneticists. Related animals have genetic material in common. Wright worked out a measure of this genetic relationship between pairs of animals called the numerator relationship. A numerator relationship matrix contains the relationships among any number of animals. Having a fraction of genes in common is like a fractional replication of
genetic effects for related animals. In fact, for a simple model G = Aσ2 where A is the numerator relationship matrix and σ2 is the genetic variance (variance of breeding values). Animal and plant breeders typically want to make use of this partial genetic replication through Aσ2 to obtain more accurate predictions of breeding values or to predict breeding values for animals without records. In animal models typically used in animal breeding the number of animals may range from thousands to millions. However, to apply Henderson's mixed model equations G-1 rather than G is needed. Thus, for G = A![]() what is needed is A-1(G-1 = A-1
what is needed is A-1(G-1 = A-1![]() . Again the n3 problem, even if A can be calculated by known n2 rules. This discovery took longer. Henderson's first attempts were in New Zealand during his Fulbright leave with Searle in 1955. Not until 1975 did he publish a simple set of rules to obtain elements of A-1 without having to calculate A. All that is needed is a list of animals with each animal's sire and dam. These calculations take time in order of n2 (and much less in the absence of inbreeding) and enable calculation of A-1 for applications such as the 13 million animals involved in genetic evaluations of the Holstein breed in the United States. What this discovery allows is use of information on all relatives of an animal (all partial replications of genetic effects) rather than only records of selected close relatives as with selection index procedures. An added advantage is that use of A through A-1 automatically corrects evaluations for one parent for the genetic merit of the other parent (the mate). This way of obtaining A-1 also results in sparseness of the mixed model equations which facilitates solution by iteration.
. Again the n3 problem, even if A can be calculated by known n2 rules. This discovery took longer. Henderson's first attempts were in New Zealand during his Fulbright leave with Searle in 1955. Not until 1975 did he publish a simple set of rules to obtain elements of A-1 without having to calculate A. All that is needed is a list of animals with each animal's sire and dam. These calculations take time in order of n2 (and much less in the absence of inbreeding) and enable calculation of A-1 for applications such as the 13 million animals involved in genetic evaluations of the Holstein breed in the United States. What this discovery allows is use of information on all relatives of an animal (all partial replications of genetic effects) rather than only records of selected close relatives as with selection index procedures. An added advantage is that use of A through A-1 automatically corrects evaluations for one parent for the genetic merit of the other parent (the mate). This way of obtaining A-1 also results in sparseness of the mixed model equations which facilitates solution by iteration.
This discovery, and discovery is the correct word, was accomplished by looking at small examples with pencil and paper, an approach Henderson regularly followed. These examples would have involved inverting small matrices "by
hand," a procedure Henderson was exceedingly proficient at doing. He finally was able to determine the pattern as well as the numerical elements of the inverse; these elements generally involved repeating fractions such as 4/3 or -2/3. It may have been fortunate that Henderson did not have a personal computer with a matrix inverter, as the patterns with 4/3 and -2/3 are much easier to see than 1.33333333 and -.66666667.
A potential disadvantage of this method of calculating A-1 is in application to the mixed model equations. The A-1 matrix computed by Henderson's rules is of the order of the number of unique animals, including sires and dams, some of which may not have records. Thus, equations need to be included for animals that do not have records. Usually least squares equations will involve only the model for the available records. What Henderson knew but did not publish until later was that the mixed model equations can be augmented to include equations for the animals without records. These equations are tied to the equations for animals with records with the ![]() part of the mixed model equations. Solutions for animals without records are basically selection index predictions using relationships to relatives with records and their predicted breeding values. This method is particularly valuable for multiple trait models and for models with both direct and maternal effects when all animals do not have measurements for all traits or do not all become mothers of progeny with records.
part of the mixed model equations. Solutions for animals without records are basically selection index predictions using relationships to relatives with records and their predicted breeding values. This method is particularly valuable for multiple trait models and for models with both direct and maternal effects when all animals do not have measurements for all traits or do not all become mothers of progeny with records.
The sum of the discoveries of 1) the modification of the least squares equations to form mixed model equations with solutions that have BLUE and BLUP properties, 2) the easy calculation of A-1, and 3) the augmentation of the mixed model equations to include equations for animals without records (for all or some traits) has provided animal breeders
worldwide with the best possible tools for genetic selection.
Henderson consolidated knowledge of the properties of selection index as an extension of the work of Wright and Lush. He also showed that the BLUP properties of solutions to the mixed model equations have the same properties as selection index. These properties are widely used in constructing standard errors of the predictors of breeding values and even for designing optimum selection plans.
The Selection Bias Problem
A problem with real breeding data is that selection of potential parents occurs based on their records. Selection violates the usual assumptions of random sampling needed to obtain unbiased predictors of breeding values. Henderson showed in a classic paper, which also clearly set out the properties of the mixed model equations, that under many selection methods and intensities of selection his mixed model equations provide estimators and predictors unbiased by selection if the data on which selection was based were included in the mixed model equations. Neither least squares nor selection index has this property.
Various simulation studies have shown even for other types of selection that the mixed model equations account for most if not all bias. Of particular importance is the finding that using the mixed model equations as a basis for REML estimation of genetic and environmental variance components provides estimates for the population as if selection had not occurred.
Many other examples of Henderson's contributions to the understanding of linear models, variance component estimation, and genetic evaluations could be described. However, a major contribution of a different nature should be listed.
Young Sire Testing Programs
Artificial insemination of dairy cattle was becoming important in New York State and throughout the United States when Henderson came to Cornell in 1948. He soon found that genetic evaluations of sires used in artificial insemination based on records from the originating herds were essentially worthless. He developed methods to account for the herd of origin effects which were widely adopted. More importantly, he and colleagues at Cornell early in the 1950s persuaded the New York artificial insemination organization to begin a program of using semen of young bulls randomly in many herds to produce samples of daughters having records in several herds. The New York group, although originally widely criticized and worse, continued the program. The group of sampled bulls totaled twenty in the first year. Other artificial insemination organizations gradually began similar programs after seeing the success of the rather limited New York program. By the 1980s, more than 1,200 young bulls were being sampled annually in the United States.
The synergistic effects of young sire sampling exploited through artificial insemination, records available through cooperative recording associations, and genetic evaluations (the BLUPs) have resulted in the greatest success story in applied animal breeding. The rate of genetic progress in dairy cattle has reached levels approaching theoretical limits. Henderson can be correctly credited with being the prime force in developing two of the three necessary bases for that success: young sire sampling and best possible genetic evaluations of those sires, potential parents of new young sires, and cows to produce replacement heifers. This was his practical contribution to one major industry, the dairy cattle industry.
Similarly, his mixed model equations with relationships of all animals included and augmented for animals without records are used nearly universally around the world and for all livestock species. A safe prediction is that no better methods will be found—perhaps better models, but not better methods. Henderson's mixed model equations have also allowed the proliferation of statistical packages that now handle messy unbalanced data with models including fixed and random effects. The generality of his discoveries and his perseverance in developing and proving the properties seems likely to result in Henderson's mixed model equations being used for many decades. New uses of the equations such as improved algorithms for estimating variance components seem to be found regularly. The contributions of an academic career that started at thirty-seven years of age and was carried forward eagerly with enthusiasm, patience, and insight for forty years will continue to be utilized and will not soon be forgotten by animal breeders and statisticians. Although his name eventually may become disconnected with the discoveries, the discoveries will continue to enrich the scientific community.
Many of his students and colleagues not only admired Henderson as a brilliant scientist but also as a person. We were certain his ideas came easily despite the evidence of twenty years to develop rules for A-1. His wife, to whom he was a devoted partner, insisted to me that her husband felt his successes were not easily achieved and were due mostly to much hard work and perseverance. His work ethics contributed greatly to his success and also inspired by example his students. He listed some of these on a handwritten transparency he prepared by request at his farewell lecture at Kyoto University, where he was teaching as a Distinguished Visiting Professor in 1985:
Some Advice to Young Scientists:
- Study methods of your predecessors.
- Work hard.
- Do not fear to try new ideas.
- Discuss your ideas with others freely.
- Be quick to admit errors. Progress comes by correcting mistakes.
- Always be optimistic. Nature is benign.
- Enjoy your scientific work. It can be a great joy.
C. R. Henderson
Kyoto University
December 16, 1985
MOST OF THE MATERIAL in this memoir was taken from papers presented at a symposium, The Legacy of C. R. Henderson, at the 1990 annual meeting of the American Dairy Science Association by five of Henderson's thirty-two Ph.D. and seventeen M.S. students and from a brief biography I prepared for the Journal of Animal Science (accepted, but not yet published). Much of the personal information was provided by his wife Marian or other family members and by the Department of Animal Science at Cornell University for my presentation at the 1990 symposium. Some material is the result of memories from having been one of Henderson's students and as a fellow faculty member in an adjoining office over a period of thirty one years.
Honors and Distinctions
|
1955 |
Senior Fulbright Research Scholar (New Zealand) |
|
1964 |
Borden Award (highest award of American Dairy Science Association) Animal Breeding and Genetics Award, American Society of Animal Science |
|
1968 |
Award of Merit, Eastern Artificial Insemination Cooperative |
|
1969 |
Fellow, American Statistical Association |
|
1971 |
Morrison Award (highest award of American Society of Animal Science) |
|
1977 |
National Association of Animal Breeders Award, American Dairy Science Association |
|
1980 |
Massey University Fellow (New Zealand) |
|
1981 |
Sesnon endowed professorship, University of California, Davis Fellow, American Society of Animal Science Hermann von Nathusius Medal, German Society of Animal Production |
|
1982 |
Jay L. Lush Animal Breeding and Genetics Award, American Dairy Science Association |
|
1984 |
Henry A. Wallace Award for Service to Agriculture, Iowa State University |
|
1985 |
Alumni Research Award, Iowa State University Distinguished Visiting Professor, University of Kyoto, Japan Member, National Academy of Science |
References
Freeman, A. E. 1991. C. R. Henderson: Contributions to the dairy industry. J. Dairy Sci. 74:4045–51.
Kennedy, B. W. 1991. C. R. Henderson: The unfinished legacy. J. Dairy Sci. 74:4067–81.
Mood, A. M. 1950. Introduction to the Theory of Statistics. New York: McGraw-Hill.
Schaeffer, L. R. 1991. C. R. Henderson: Contributions to predicting genetic merit. J. Dairy Sci. 74:4052–66.
Searle, S. R. 1991. C. R. Henderson, the statistician; and his contributions to variance components estimation. J. Dairy Sci. 74:4035–44.
Van Vleck, L. D. 1991. C. R. Henderson: Farm boy, athlete, and scientist. J. Dairy Sci. 74:4082–96.
Van Vleck, L. D. 1997. Charles Roy Henderson, 1911–1989: A brief biography. J. Anim. Sci. (accepted).
Van Vleck, L. D. and S. R. Searle, eds. 1979. Variance components and animal breeding: Proceedings of a conference in honor of C. R. Henderson. Cornell University, Ithaca, NY.
Selected Bibliography
1952 Specific and general combining ability. In Heterosis, ed. J. W. Gowen, pp. 352–70. Ames: Iowa State College Press.
1953 Estimation of variance and covariance components. Biometrics 9:226–52.
1954 Selecting and sampling young bulls. In Proceedings of the 7th Annual Convention of the National Association of Animal Breeders, p 93. Columbia, Md.: National Association of Animal Breeders.
1959 With O. Kempthorne, S. R. Searle, and C. M. von Krosigk. The estimation of environmental and genetic trends from records subject to culling. Biometrics 15:192–218.
1963 Selection index and expected genetic advance. In Statistical Genetics and Plant Breeding, ed. W. D. Hanson and H. F. Robinson, pp. 141–63. Washington, D.C.: National Academy of Sciences-National Research Council.
1965 A sire evaluation method which accounts for unknown genetic and environmental trends, herd differences, season, age effects, and differential culling. In Proceedings of the Symposium on Estimating Breeding Values of Dairy Sires and Cows, pp. 172–204. Washington, D.C.: USDA-ARS.
1968 With E. P. Cunningham. An iterative procedure for estimating fixed effects and variance components in mixed model situations. Biometrics 24:13–25.
1969 Design and analysis of animal science experiments. In Techniques and Procedures in Animal Science Research, pp. 1–35. Albany, N.Y.: Am. Soc. Am. Sci.
1970 A new sire evaluation method. In Proceedings of the 23rd Annual Convention of the National Association of Animal Breeders, pp. 31–35. Columbia, Md.: National Association of Animal Breeders.
1973 Sire evaluation and genetic trends. In Proceedings of the Animal Breeding and Genetics Symposium in Honor of Dr. Jay L. Lush, pp. 10–43. Champaign, Ill.: ASAS and ADSA.
With N. S. Urquhart and D. L. Weeks. Estimation associated with linear models. A revisitation. Commun. Stat. 1:303–30.
1974 General flexibility of linear model techniques for sire evaluation. J. Dairy Sci. 57:963–72.
1975 Best linear unbiased estimation and prediction under a selection model. Biometrics 31 (2):423–47.
A rapid method for computing the inverse of a relationship matrix. J. Dairy Sci. 58:1727–30.
Comparison of alternative sire evaluation methods. J Anim. Sci. 41:760–70.
1976 A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics 32:69–83.
Multiple trait evaluation using relatives' records. J. Anim. Sci. 43:1188–97.
1977 Best linear unbiased prediction of breeding values not in the model for records. J. Dairy Sci. 60:783–87.
Prediction of merits of single crosses. Theor. Appl. Genet. 49:273–82.
Prediction of future records. In Proceedings of the International Conference on Quantitative Genetics, pp. 615–38. Ames: Iowa State University Press.
1979 With C. R. Henderson, Jr. Analysis of covariance in mixed models with unequal subclass numbers. Commun. Stat. Theor. Meth. A8(8):751–87.
1984 Applications of Linear Models in Animal Breeding. Guelph, Ontario: University of Guelph.
ANOVA, MIVQUE, REML, and ML algorithms for estimation of variances and covariances. In Proceedings of the 50th Anniversary of the Iowa State University Statistics Lab, pp. 257–80. Ames: Iowa State University Press.
1985 MIVQUE and REML estimation of additive and nonadditive genetic variances. J. Anim. Sci. 61:113–21.
Equivalent linear models to reduce computations. J. Dairy Sci. 68:2267–77.



























