EXECUTIVE SUMMARY
Mathematics is one of humanity’s great achievements. By enhancing the capabilities of the human mind, mathematics has facilitated the development of science, technology, engineering, business, and government. Mathematics is also an intellectual achievement of great sophistication and beauty that epitomizes the power of deductive reasoning. For people to participate fully in society, they must know basic mathematics. Citizens who cannot reason mathematically are cut off from whole realms of human endeavor. Innumeracy deprives them not only of opportunity but also of competence in everyday tasks.
The mathematics students need to learn today is not the same mathematics that their parents and grandparents needed to learn. When today’s students become adults, they will face new demands for mathematical proficiency that school mathematics should attempt to anticipate. Moreover, mathematics is a realm no longer restricted to a select few. All young Americans must learn to think mathematically, and they must think mathematically to learn.
All young Americans must learn to think mathematically, and they must think mathematically to learn.
Adding It Up: Helping Children Learn Mathematics is about school mathematics from pre-kindergarten to eighth grade. It addresses the concerns expressed by many Americans, from prominent politicians to the people next door, that too few students in our elementary and middle schools are successfully acquiring the mathematical knowledge, the skill, and the confidence they need to use the mathematics they have learned. Moreover, certain segments of the U.S. population are not well represented among those who do succeed in school mathematics.
The mathematics curriculum during the preschool, elementary school, and middle school years has many components. But at the heart of mathematics in those years are concepts of number and operations with numbers— the mathematical domain of number. In this report, much of our attention is given to issues associated with teaching and learning about number in pre-kindergarten through eighth-grade mathematics. Many controversies over the teaching of mathematics center on the understanding and use of numbers. The learning of concepts associated with number also has been more thoroughly investigated than the learning of other parts of the mathematics curriculum. And much of the rest of the mathematics curriculum, some of which we do address, is intertwined with number concepts.
Number is a rich, many-sided domain whose simplest forms are comprehended by very young children and whose far reaches are still being explored by mathematicians. Proficiency with numbers and numerical operations is an important foundation for further education in mathematics and in fields that use mathematics. Because much of this report attends to the learning and teaching of number, it is important to emphasize that our perspective is considerably broader than just computation. First, numbers and operations are abstractions—ideas based on experience but independent of any particular experience. Communication about numbers, therefore, requires some form of external representation, such as a graph or a system of notation. The usefulness of numerical ideas is enhanced when students encounter and use multiple representations for the same concept. Second, the numbers and operations of school mathematics are organized as number systems, such as the whole numbers, and the regularities of each system can help students learn with understanding. Third, numerical computations require algorithms—step-by-step procedures for performing the computations. An algorithm can be more or less useful to students depending on how it works and how well it is understood. And finally, the domain of number both supports and is supported by other branches of mathematics, including algebra, measure, space, data, and chance. Our decision to address the domain of number was a pragmatic one; in no way does it imply that the elementary and middle school curriculum should be limited to arithmetic.
Our decision to address the domain of number was a pragmatic one; in no way does it imply that the elementary and middle school curriculum should be limited to arithmetic.
About This Report
The Committee on Mathematics Learning was established by the National Research Council at the end of 1998. It was formed at the request of the Division of Elementary, Secondary, and Informal Education in the
National Science Foundation’s Directorate for Education and Human Resources and the U.S. Department of Education’s Office of Educational Research and Improvement. The sponsors were concerned about the shortage of reliable information on the learning of mathematics by schoolchildren that could be used to guide best practice in the early years of schooling. More specifically, the committee was given the following charge:
-
To synthesize the rich and diverse research on pre-kindergarten through eighth-grade mathematics learning.
-
To provide research-based recommendations for teaching, teacher education, and curriculum for improving student learning and to identify areas where research is needed.
-
To give advice and guidance to educators, researchers, publishers, policy makers, and parents.
We based our conclusions in this report on a careful review of the research literature on mathematics teaching and learning. Many educational questions, however, cannot be answered by research. Choices about the mathematics curriculum and the methods used to bring about that curriculum depend in part on what society wants educated adults to know and be able to do. Research can inform these decisions—for example, by demonstrating what knowledge, skills, and abilities employees need in the workplace. But ideas about what children need to know also depend on value judgments based on previous experience and convictions, and these judgments often fall outside the domain of research.
Once the learning objectives for mathematics education have been established, research can guide decisions about how to achieve these objectives. In preparing this report, we sought research that is relevant to important educational issues, sound in shedding light on the questions it sets out to answer, and generalizable in that it can be applied to circumstances beyond those of the study itself. We also looked for multiple lines of research that converge on a particular point and fit well within a larger network of evidence. Because studies that touch on a key question and yield unequivocal findings are rare in educational research, we have sought to point out when we have used professional judgment and reasoned argument to make connections, note patterns, and fill in gaps. In the final chapter of the report, we have also called for additional research in areas where it could improve educational practice.
The State of School Mathematics in the United States
One area in which the research evidence is consistent and compelling concerns weaknesses in the mathematical performance of U.S. students. State, national, and international assessments conducted over the past 30 years indicate that, although U.S. students may not fare badly when asked to perform straightforward computational procedures, they tend to have a limited understanding of basic mathematical concepts. They are also notably deficient in their ability to apply mathematical skills to solve even simple problems. Although performance in mathematics is generally low, there are signs from national assessments that it has been improving over the past decade. In a number of schools and states, students’ mathematical performance is among the best in the world. The evidence suggests, however, that many students are still not being given the educational opportunities they need to achieve at high levels.
Most students in grades pre-K to 8 encounter a rather shallow curriculum.
In comparison with the curricula of countries achieving well on international comparisons, the U.S. elementary and middle school mathematics curriculum has been characterized as shallow, undemanding, and diffuse in content coverage. U.S. mathematics textbooks cover more topics, but more superficially, than their counterparts in other countries do. Despite efforts over the last half-century to set higher learning goals for U.S. school mathematics and to provide new instructional materials and better assessments, most students in grades pre-K to 8 encounter a rather shallow curriculum. The instruction they are given continues to emphasize the execution of paper-and-pencil skills in arithmetic through demonstrations of procedures followed by repeated practice.
To ensure that students are meeting standards, states and districts have, during the past decade or so, mandated a variety of assessments in mathematics, many with serious consequences for students, teachers, and schools. Although intended to ensure that all students have an opportunity to learn mathematics, some of these assessments are not well aligned with the curriculum. Those that were originally designed to rank order students, schools, and districts seldom provide information that can be used to improve instruction.
The preparation of U.S. preschool to middle school teachers often falls far short of equipping them with the knowledge they need for helping students develop mathematical proficiency. Many students in grades pre-K to 8 continue to be taught by teachers who may not have appropriate certification at that grade and who have at best a shaky grasp of mathematics.
Mathematical Proficiency
Our analyses of the mathematics to be learned, our reading of the research in cognitive psychology and mathematics education, our experience as learners and teachers of mathematics, and our judgment as to the mathematical knowledge, understanding, and skill people need today have led us to adopt a composite, comprehensive view of successful mathematics learning. Recognizing that no term captures completely all aspects of expertise, competence, knowledge, and facility in mathematics, we have chosen mathematical proficiency to capture what we think it means for anyone to learn mathematics successfully. Mathematical proficiency, as we see it, has five strands:
-
conceptual understanding—comprehension of mathematical concepts, operations, and relations
-
procedural fluency—skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
-
strategic competence—ability to formulate, represent, and solve mathematical problems
-
adaptive reasoning—capacity for logical thought, reflection, explanation, and justification
-
productive disposition—habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.
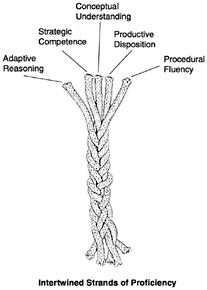
The most important observation we make about these five strands is that they are interwoven and interdependent. This observation has implications for how students acquire mathematical proficiency, how teachers develop that proficiency in their students, and how teachers are educated to achieve that goal.
The Mathematical Knowledge Children Bring to School
Children begin learning mathematics well before they enter elementary school. Starting from infancy and continuing throughout the preschool period, they develop a base of skills, concepts, and misconceptions. At all ages, students encounter quantitative situations outside of school from which they learn a variety of things about number. Their experiences include, for example, noticing that a sister received more candies, counting the stairs
between the first and second floors of an apartment, dividing a cake so everyone gets the same amount, and figuring out how far it is to the bus stop.
By the time children reach kindergarten, many of them can use their counting skills to solve simple problems that call for adding, subtracting, multiplying, or dividing. It is only when they move beyond what they understand informally—to the base-10 system for teens and larger numbers, for example—that their fluency and strategic competencies falter. Young children also show a remarkable ability to formulate, represent, and solve simple mathematical problems and to reason and explain their mathematical activities. They are positively disposed to do and to understand mathematics when they first encounter it. For the preschool child, the strands of mathematical proficiency are especially closely knit.
Although most U.S. children enter school with a basic understanding of number, their knowledge is limited to small whole numbers and heavily influenced by the context in which the numbers appear. Furthermore, not all children enter school with the informal understanding of number assumed by the elementary school curriculum.
Developing Proficiency with Whole Numbers
Whole numbers are the easiest numbers to understand and use. In the early grades, children begin by solving numerical problems using methods that are intuitive and concrete. They then proceed to methods that are more problem independent, mathematically sophisticated, and reliant on standard symbolic notation. Some form of this progression is seen in each operation for both single-digit and multidigit numbers.
For most of a century, learning single-digit arithmetic—the sums and products of single-digit numbers and their companion differences and quotients (e.g., 5+7=12, 12–5=7, 12–7=5 and 5×7=35, 35÷5=7, 35÷7=5) — has been characterized in the United States as “learning basic facts,” and the emphasis has been on memorizing those facts. Acquiring proficiency in single-digit arithmetic, however, involves much more than memorizing. Even in the early grades, students choose adaptively among different procedures, depending on the numbers involved and the context. We use the term basic number combinations to highlight the relational character of this knowledge.
For addition and subtraction, many children follow a well-documented progression of procedures. Counting becomes abbreviated and rapid, and students begin to use properties of arithmetic to simplify their computation. Basic multiplication and division combinations are more of a challenge. Learning these combinations seems to require much specific pattern-based
knowledge that needs to be orchestrated into accessible and rapid-enough procedures. When given instruction that emphasizes thinking strategies, children are able to develop the strands of proficiency in a unified manner.
When given instruction that emphasizes thinking strategies, children are able to develop the strands of proficiency in a unified manner.
Learning to use algorithms for computation with multidigit numbers is an important part of developing mathematical proficiency. Algorithms are procedures that can be executed in the same way to solve a variety of problems arising from different situations and involving different numbers. Children can and do devise algorithms for carrying out multidigit arithmetic, using reasoning to justify their inventions and developing confidence in the process. A variety of instructional approaches (using physical materials, special counting activities, and mental computation) are effective in helping students learn multidigit arithmetic by focusing on the base-ten structure and encouraging students to use algorithms that they understand. Physical materials are not automatically meaningful to students, however, and need to be connected to the situations being modeled. Because of its conciseness, the base-ten place-value system takes time to master. Full understanding of the system, however, is not required before students begin to learn multidigit algorithms— the two can be developed in tandem. The learning of whole number arithmetic demands that attention be given to developing all strands of proficiency in concert, emphasizing no strand at the expense of the others.
Developing Proficiency with Rational Numbers
In grades pre-K to 8, the rational numbers present a major challenge, in part because rational numbers are represented in several ways (e.g., common fractions and decimal fractions) and used in many ways (e.g., as parts of regions and sets, as ratios, as quotients). There are numerous properties for students to learn, including the significant fact that the two numbers that compose a common fraction (numerator and denominator) are related through multiplication and division, not addition.
Students’ informal notions of partitioning, sharing, and measuring provide a starting point for building the concept of rational number. Young children appreciate the idea of “fair shares,” and they can use that understanding to partition quantities into equal parts. In some ways, sharing can play the role for rational numbers that counting does for whole numbers.
As with whole numbers, the written notations and spoken words used for decimal and common fractions contribute to—or at least do not help correct— the many kinds of errors students make with them. Furthermore, many students do not understand the meanings of and connections between the various symbols for rational numbers when they are asked to compute with
them, which creates barriers to developing the strands of proficiency in an integrated fashion.
Proportions are statements that two ratios are equal. Understanding and working with the relationships in a situation involving proportions is called proportional reasoning and has been described as the capstone of elementary school arithmetic. Proportional reasoning is sophisticated and complex; it needs to develop over many years. Students need to have a solid understanding of proportional situations and be able to reason about them informally before formal procedures are introduced.
Developing Proficiency Beyond Number
Many students have difficulties making the transition from school arithmetic to school algebra—with its symbolism, equation solving, and emphasis on relationships among quantities. Recent calls of “algebra for all” have increased the number of students making the transition and therefore the number encountering obstacles. Over the past two decades, much has been learned about the nature of students’ difficulties in algebra. Various innovative approaches to beginning algebra, many using computational tools, have been investigated. At the same time, modifications of elementary school mathematics have been developed and studied that are aimed at introducing the notions of algebra earlier. These new approaches offer considerable promise for avoiding the difficulties many students now experience.
Just as the elementary and middle school mathematics curriculum should prepare students for the study of algebra, so it should also include attention to other domains of mathematics. Students need to learn to make and interpret measurements and to engage in geometric reasoning. They also need to gather, describe, analyze, and interpret data and to use elementary concepts from probability. Instruction that emphasizes more than a single strand of proficiency has been shown to enhance students’ learning about space and measure and shows considerable promise for helping students learn about data and chance.
Teaching for Mathematical Proficiency
Effective teaching—teaching that fosters the development of mathematical proficiency over time—can take a variety of forms, each with its own possibilities and risks. All forms of instruction can best be examined from the perspective of how teachers, students, and content interact in contexts to produce teaching and learning. The effectiveness of mathematics teaching
and learning is a function of teachers’ knowledge and use of mathematical content, of teachers’ attention to and work with students, and of students’ engagement in and use of mathematical tasks. Effectiveness depends on enactment, on the mutual and interdependent interaction of the three elements—mathematical content, teacher, students—as instruction unfolds. The quality of instruction depends, for example, on whether teachers select cognitively demanding tasks, plan the lesson by elaborating the mathematics that the students are to learn through those tasks, and allocate sufficient time for the students to engage in and spend time on the tasks. Effective teachers have high expectations for their students, motivate them to value learning activities, can interact with students with different abilities and backgrounds, and can establish communities of learners. A teacher’s expectations about students and the mathematics they are able to learn can powerfully influence the tasks the teacher poses for the students, the questions they are asked, the time they have to respond, and the encouragement they are given—in other words, their opportunities and motivation for learning. How the students respond to the opportunities the teacher offers then shapes how the teacher sees their capacity and progress, as well as the tasks they are subsequently given.
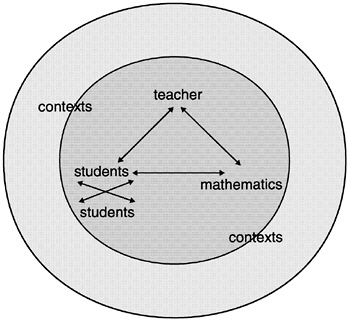
The quality of instruction also depends on how students engage with learning tasks. Students must link their informal knowledge and experience to mathematical abstractions. Manipulatives (physical objects used to represent mathematical ideas), when used well, can provide such links. The use of calculators can enhance students’ conceptual understanding, and practice can help them make automatic those procedures they understand. Although much is known about characteristics of effective instruction, research on teaching has often been restricted to describing isolated fragments of teaching and learning rather than examining continued interactions among the teacher, the students, and the mathematical content.
Developing Proficiency in Teaching Mathematics
Proficiency in teaching mathematics is related to effectiveness: consistently helping students learn worthwhile mathematical content. It also entails versatility: being able to work effectively with a wide variety of students in different environments and across a range of mathematical content. Despite the common myth that teaching is little more than common sense or that some people are just born teachers, effective teaching practice can be learned. Just as mathematical proficiency itself involves interwoven strands, teaching for mathematical proficiency requires similarly interrelated components: conceptual understanding of the core knowledge of mathematics, students, and instructional practices needed for teaching; procedural fluency in carrying out basic instructional routines; strategic competence in planning effective instruction and solving problems that arise while teaching; adaptive reasoning in justifying and explaining one’s practices and in reflecting on those practices; and a productive disposition toward mathematics, teaching, learning, and the improvement of practice.
Effective programs of teacher preparation and professional development help teachers understand the mathematics they teach, how their students learn that mathematics, and how to facilitate that learning. In these programs, teachers are not given prescriptions for practice or readymade solutions to teaching problems. Instead, they adapt what they are learning to deal with problems that arise in their own teaching.
Recommendations
As a goal of instruction, mathematical proficiency provides a better way to think about mathematics learning than narrower views that leave out key features of what it means to know and be able to do mathematics. It takes time for proficiency to develop fully, but in every grade in school, students can demonstrate mathematical proficiency in some form. The overriding premise of our work is that throughout the grades from pre-K through 8 all students can and should be mathematically proficient.
The overriding premise of our work is that throughout the grades from pre-K through 8 all students can and should be mathematically proficient.
School mathematics in the United States does not now enable most students to develop the strands of mathematical proficiency in a sound fashion. Proficiency for all demands that fundamental changes be made concurrently in curriculum, instructional materials, assessments, classroom practice, teacher preparation, and professional development. These changes will require continuing, coordinated action on the part of policy makers, teacher educators,
teachers, and parents. Although some readers may feel that substantial advances are already being made in reforming mathematics teaching and learning, we find real progress toward mathematical proficiency to be woefully inadequate.
These observations lead us to five principal recommendations regarding mathematical proficiency that reflect our vision for school mathematics. The full report augments these five with specific recommendations that detail policies and practices needed if all children are to become mathematically proficient.
-
The integrated and balanced development of all five strands of mathematical proficiency (conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition) should guide the teaching and learning of school mathematics. Instruction should not be based on extreme positions that students learn, on one hand, solely by internalizing what a teacher or book says or, on the other hand, solely by inventing mathematics on their own.
One of the most serious and persistent problems facing school mathematics in the United States is the tendency to concentrate on one strand of proficiency to the exclusion of the rest. For too long, students have been the victims of crosscurrents in mathematics instruction, as advocates of one learning goal or another have attempted to control the mathematics to be taught and tested. We believe that this narrow and unstable treatment of mathematics is, in part, responsible for the inadequate performance that U.S. students display on national and international assessments. Our first recommendation is that these crosscurrents be resolved into an integrated, balanced treatment of all strands of mathematical proficiency at every point in teaching and learning.
Although we endorse no single approach, we contend that instruction needs to configure the relations among teachers, students, and mathematics in ways that promote the development of mathematical proficiency. Under this view, significant instructional time is devoted to developing concepts and methods, and carefully directed practice, with feedback, is used to support learning. Discussions build on students’ thinking. They attend to relationships between problems and solutions and to the nature of justification and mathematical argument. All strands of proficiency can grow in a coordinated, interactive fashion.
-
Teachers’ professional development should be high quality, sustained, and systematically designed and deployed to help all students develop mathematical proficiency. Schools should support, as a central part of teachers’ work, engagement in sustained efforts to improve their mathematics instruction. This support requires the provision of time and resources.
Improving students’ learning depends on the capabilities of classroom teachers. Although children bring important mathematical knowledge with them to class, most of the mathematics they know is learned in school and depends on those who teach it to them. Teachers cannot automatically know how to teach more effectively. Learning to teach well cannot be accomplished once and for all in a preservice program; it is a career-long challenge.
As we have indicated, proficiency in mathematics teaching has parallels to proficiency in mathematics. Unfortunately, just as students’ opportunities to learn mathematics effectively have been insufficient, so have teachers’ opportunities to learn more about mathematics, students’ learning and thinking, and their teaching practice. Regular time needs to be provided for teachers to continue their professional development, conferring with one another about common problems and working together to develop their teaching proficiency. They need access to resources and expertise that will assist them in improving their instruction, including access to mathematics specialists in every elementary school. If the United States is serious about improving students’ mathematics learning, it has no choice but to invest in more effective and sustained opportunities for teachers to learn.
-
The coordination of curriculum, instructional materials, assessment, instruction, professional development, and school organization around the development of mathematical proficiency should drive school improvement efforts.
Piecemeal efforts aimed at narrow learning goals have failed to improve U.S. students’ learning. The development of mathematical proficiency provides a broad, compelling goal around which all parts of the educational community can rally. If even one sector of that community lags behind, it can thwart the development of mathematical proficiency.
The school mathematics curriculum needs to be organized within and across grades to support, in a coordinated fashion, all strands of mathematical proficiency. Programs at all grades should build on the informal knowledge
children bring to school. An integrated approach should be taken to the development of proficiency with whole numbers, integers, and rational numbers to ensure that all students in grades pre-K to 8 can use the numbers fluently and flexibly to solve challenging but accessible problems. Students should also understand and be able to translate within and across the various common representations for numbers.
A major focus of the study of number should be the conceptual bases for the operations and how they relate to real situations. For each operation, all students should understand and be able to carry out an algorithm that is general and efficient. Before they get to the formal study of algebra, they already should have had numerous experiences in representing, abstracting, and generalizing relationships among numbers and operations with numbers. They should be introduced to these algebraic ways of thinking well before they are expected to be proficient in manipulating algebraic symbols. They also need to learn concepts of space, measure, data, and chance in ways that link these domains to that of number.
Materials for instruction need to develop the core content of school mathematics in depth and with continuity. In addition to helping students learn, these materials should also support teachers’ understanding of mathematical concepts, of students’ thinking, and of effective pedagogical techniques. Mathematics assessments need to enable and not just gauge the development of proficiency. All elements of curriculum, instruction, materials, and assessment should be aligned toward common learning goals.
Every school should be organized so that the teachers are just as much learners as the students are. The professional development activities in which teachers of mathematics are engaged need to be focused on mathematical proficiency. Just as mathematical proficiency demands the integrated, coordinated development of all strands, so the enhancement of each student’s opportunities to become proficient requires the integrated, coordinated efforts of all parts of the educational community.
-
Efforts to improve students’ mathematics learning should be informed by scientific evidence, and their effectiveness should be evaluated systematically. Such efforts should be coordinated, continual, and cumulative.
Steady and continuing improvements in students’ mathematics learning can be made only if decisions about instruction are based on the best available information. As new, systematically collected information becomes available,
better decisions can be made, and mathematics instruction should gradually but steadily become more effective. Unfortunately, too many new programs are tried but then abandoned before their effectiveness has been well tested, and lessons learned from program evaluations are often lost. Without high-quality, cumulative information, the system of school mathematics cannot learn.
-
Additional research should be undertaken on the nature, development, and assessment of mathematical proficiency.
We are convinced that the goal of mathematical proficiency for all students is the right goal. Not surprisingly, however, much of the research on mathematics teaching and learning has been conducted to address narrower learning goals, since shifting, relatively narrow goals have been the norm. Although we have interpreted much of that research for this report, extensive work remains to refine and elaborate our portrayal of mathematical proficiency. In many places, our conclusions are tentative, awaiting better evidence.
We urge researchers concerned with school mathematics to frame their questions with a view to the goal of developing mathematical proficiency for all students. Evidence from such research, together with information from evaluations of current and future programs of curriculum and professional development, will enable the United States to make the genuine, lasting improvements in school mathematics learning that have eluded it to date.
Conclusion
The goal of mathematical proficiency is an extremely ambitious one. In fact, in no country—not even those performing highest on international surveys of mathematics achievement—do all students display mathematical proficiency as we have defined it in this report. The United States will never reach this goal by continuing to tinker with the controls of educational policy, pushing one button at a time. Instead, systematic modifications will need to be made in how the teaching and learning of mathematics commonly proceed, and new kinds of support will be required. At all levels of the U.S. educational system, the formulation and implementation of policies demands sustained, focused attention to school mathematics. We hope this report will be the basis for innovative, comprehensive, long-term policies that can enable every student to become mathematically proficient.














