3
The Critical Importance of Well-Prepared Teachers for Student Learning and Achievement
Nearly everyone now accepts the premise that teachers make a difference in the lives of their students. One report (Coleman et al., 1966) briefly cast doubt on the direct importance of teachers in student achievement. This report seemed to indicate that the impact of teachers and the quality of teaching were less important to student learning and achievement than other factors, such as students’ socioeconomic status. However, subsequent research in classrooms has demonstrated that teachers do make a tangible difference in student achievement. For example, variation in student achievement has been systematically related to variation in the classroom behaviors of teachers (as summarized in a review of the literature by Good et al., 1975).
Reflecting these findings, King and Newman (2000) state, “Since teachers have the most direct, sustained contact with students and considerable control over what is taught and the climate for learning, improving teachers’ knowledge, skills and dispositions through professional development is a critical step in improving student achievement.” The National Commission on Teaching and America’s Future (NCTAF, 1996) and other national groups, such as the Education Trust (1998), earlier reached similar conclusions based on research that tracked the academic achievement of individual students over long time periods (see, for example, Sanders and Rivers, 1996). Further, all of these organizations have shown that well-qualified teachers and high-quality teaching can close the achievement gap between economically disadvantaged students and their more affluent peers.
The public also recognizes the importance of well-prepared teachers. In a large survey, Haselkorn and Harris (1998) reported that “roughly nine out of ten Americans believe the best way to
|
Public opinion overwhelmingly favors “ensuring a well-qualified teacher in every classroom” as the top education priority. Indeed, teachers—once viewed as central to the problem of student underachievement—are now being recognized as the solution. In teacher preparation there is a “multiplier effect” that can span generations. While a sound undergraduate science education is essential for producing the next generation of scientists, it is equally critical for future teachers of science. The refrain, “You can’t teach what you don’t know,” surely applies. National Science Board, 1999 |
lift student achievement is to ensure a qualified teacher in every classroom.” This survey revealed, in addition, a strong belief by the public that prospective teachers need special training and skills, not simply a good general education.
It is important to examine the veracity of the conclusion that well-prepared teachers and high-quality teaching matter. It also is important to document and understand what specific characteristics of teachers, and the school settings in which they work, contribute to successful student outcomes. This information can then be used to help determine how better to educate and support successful teachers. If high-quality teaching is essential to success in student learning and if the academic success and achievement of students can be linked to specific characteristics of teaching—such information might be used to argue against a recent trend in many districts toward dilution of requirements for teacher education and certification in response to teacher shortages, class-size reductions, and growing K-12 student populations.
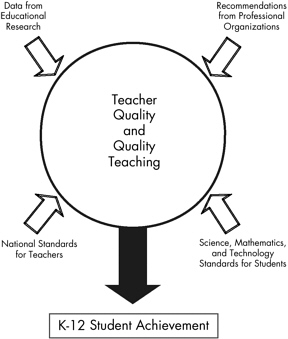
Figure 3-1 provides an overview of how research data, recommendations of professional organizations and their reports, national standards for teachers of science and mathematics, and extant standards for K-12 students in science and mathematics can influence the quality of K-12 teachers, teaching, and student achievement.
THE EVIDENCE THAT HIGH-QUALITY TEACHING MATTERS
Before discussing further the various aspects of teacher quality, the study committee wishes to acknowledge and to emphasize that there are countless thousands of science and mathematics teachers who do excellent jobs in helping their students learn and achieve, often in very difficult circumstances and at
FIGURE 3-1 Factors that influence teacher quality and quality teaching and their effects on student achievement. Depicted are four areas examined in this report and describing what is known about preparing quality teachers and their impact on K-12 student achievement in mathematics and science.
relatively low pay. The committee’s list of concerns and recommendations for addressing those concerns are not intended to paint all teachers with the same brush. Indeed, most of the concerns expressed in this report can be attributed to preparation and continuing professional development that are now either out-of-date or inadequate to meet the demands of new approaches to teaching and learning of science and mathematics. However, everyone who is concerned about the quality of education should consider carefully adopting policies and practices that encourage the most qualified individuals to prepare for, enter, and remain in science and mathematics teaching and revamping or jettisoning those practices that dissuade or impede them from doing so.
In the last few years, a number of large-scale studies of teaching have elucidated how teacher quality makes a difference in the achievement of students. Three of these studies and their conclusions are summarized below. An examination of studies that focus more specifically on science and mathematics teaching and K-12 student achievement follows.
TEACHER QUALITY AND GENERAL STUDENT ACHIEVEMENT: THREE STUDIES
Later reports frequently cite studies by Sanders and colleagues (see below), Ferguson (1991), and Ferguson and Ladd (1996) as evidence that the qualifications of teachers not only matter in student achievement but also are major variables in improving student learning and achievement.
For over 15 years, Sanders and his colleagues associated with the Tennessee Value-Added Assessment System (TVAAS) have analyzed data from annual tests in mathematics, science, reading, language, and social studies given to grade 3-8 students in Tennessee. Utilizing a database now in excess of 5 million records, Sanders and his colleagues have tracked individual students over time and studied each child’s academic achievement year by year. In this way, they have been able to identify a year when a child makes average progress, exceeds average progress, or achieves no gain.
In a study intended to gauge the cumulative and residual effects of teacher qualifications on student achievement, Sanders and Rivers (1996) gathered test or achievement data for a cohort of students from the time they were second-graders to the time they had completed fifth grade. By disaggregating the data, the researchers were able to see the impact of quality teaching on each child over time (Sanders and Rivers, 1996).1 Sanders and Rivers reported that student achievement at each grade level correlated positively with the quality of the teachers who taught those students. Also of interest was the researchers’ discovery of residual effects; that is, they found that the individual children they studied tended not to recover after a school
year’s worth of classroom experience with an ineffective teacher. Conversely, a child who spent one year with a highly effective teacher tended to experience academic benefits even two years later. In this and other studies, Sanders and his colleagues have shown that placing students in classrooms with high-quality teaching does matter. Variables such as the racial and/or ethnic composition of schools, students’ socioeconomic levels, and the mean achievement of an entire school correlated far less with student achievement when compared to the variable of teacher quality.
In a large-scale study of younger children in grades 3-5, Sanders and colleagues Wright and Horn found that “teacher effects are dominant factors affecting student academic gain,” especially in mathematics but also, noticeably, in science (Wright et al., 1997).
In a 1991 study, Ferguson examined student scores on standardized tests in reading and mathematics, teacher qualifications, and class size in 900 out of 1,000 school districts in Texas. The teacher qualifications examined in each district included teacher performance on the Texas state teacher examinations, years of teaching experience, and teachers’ acquisition of advanced (master’s) degrees. Ferguson (1991) found that the following teacher qualifications, listed in order from most to least important, had statistically significant effects on student scores: teacher language scores on the state examination, class size, years of teaching experience, and the earning of an advanced degree. According to a review of the study conducted by the National Center for Education Statistics (cited in Sparks and Hirsh, 2000), teacher expertise, as Ferguson had defined it, explained 40 percent of the variance in the students’ achievement in reading and mathematics.
Later, in 1996, Ferguson and Ladd used Sanders’ statistical approach to study nearly 30,000 Alabama fourth graders during the 1990-91 school year. They found that students’ test scores in mathematics and reading were positively affected by two teacher variables: higher than average scores on the American College Testing program’s college entrance examination and completion of one or more master’s degrees.
|
Since teachers have the most direct, sustained contact with students and considerable control over what is taught and the climate for learning, improving teachers’ knowledge, skill and dispositions through professional development is a critical step in improving student achievement. King and Newman, 2000 |
TEACHER QUALITY AND STUDENT ACHIEVEMENT IN SCIENCE AND MATHEMATICS
Research that attempted to investigate the relationship between teacher quality and student achievement began in earnest in the 1960s and 1970s. In a meta-analysis of previous work, Druva and Anderson (1983) uncovered a number of important and statistically significant positive correlations that shed light on the variable of teacher quality in science instruction. Teaching background, teacher behavior in the classroom, and student outcomes were examined. Findings included that teachers with greater content knowledge in a given subject and those with more teaching experience were more likely to ask higher level, cognitively based questions. Teachers with more content knowledge also had a greater orientation toward seeking information from students through questioning and discussion in their teaching compared to teachers with less content knowledge. This was particularly significant in the case of biology teachers. Students’ ability to understand the essentials of the scientific method was positively correlated with the number of science courses (both in biology and in other science disciplines) that their teachers had taken. The degree to which students reported that they “liked science” correlated positively with the number of science courses taken by the teachers.
In 1989, McDiarmid et al. concluded, on the basis of research extant at the time, that teachers’ subject matter understanding and their pedagogical orientations and decisions critically influence the quality of their teaching. “Teachers’ capacity to pose questions, select tasks, evaluate their pupil’s understanding, and to make curricular decisions all depend on how they themselves understand the subject matter.” And in 1995, Chaney demonstrated a relationship between middle-school science and mathematics teachers’ professional preparation and student performance.
These consistently positive correlations appear to support the importance of high levels of preparation for teachers in both content and pedagogy. This preparation and subsequent teaching experience also appear to enhance student achievement.
THE IMPORTANCE OF TEACHER CERTIFICATION
Hawk et al. (1985) conducted a specific study of the relationship between teachers’ certification in mathematics and their teaching effectiveness. Two groups, each of 18 teachers
who had taught at least one course in mathematics in grades 6-12, participated in the seven-month study. One group consisted of teachers who held either subject area certification or endorsement in mathematics (“in-field teachers”), and the other group consisted of teachers who lacked these credentials (“out-of-field teachers”). Both groups of teachers taught the same mathematics course in the same school to students of the same general ability. Pretest scores of students across the different groups did not differ significantly from each other. Researchers proceeded to examine comparative teacher effectiveness by looking at student achievement,2 teacher professional skills,3 and teacher knowledge of the subject field.4
Students taught by in-field teachers scored significantly higher on general mathematics (p< .001) and algebra (p<.01) tests than did students taught by out-of-field teachers. In-field teachers scored significantly higher (p<.001 ) on the test of teachers’ subject matter knowledge than did out-of-field teachers. In-field teachers also scored significantly higher (p<. 001) on the Carolina Teacher Performance Assessment System than did their out-of-field counterparts. No significant differences were observed between the two groups based on years of teaching experience, years of experience teaching mathematics, or level of degree earned. Overall, in-field mathematics teachers knew more mathematics and showed evidence of using more effective teaching practices than did their out-of-field counterparts. Hawk et al. (1985) concluded that certification requirements are an effective mechanism to assure higher student achievement in mathematics.
Also important to this discussion are Ingersoll’s (1999) findings that, nationwide, approximately one third of all secondary school teachers of mathematics have neither a major nor a minor in mathematics, mathematics education, or in such related disciplines as engineering or physics. Similarly, about 20 percent of science teachers lack even a minor in science or science education, and “over half of teachers teaching physical sciences classes (chemistry,
physics, earth science, or space science) are without an academic major or minor in any one of the physical sciences” (Ingersoll, 1999).5,6 As one might expect, the situation was worse in high-poverty schools. The fact that significant numbers of the more than 314,000 current secondary school science and mathematics teachers are teaching without full certification in these subjects should cause significant concern about the science and mathematics instruction children may or may not be receiving.
These concerns are reinforced by Fetler (1999), who investigated the relationship between measures of a teacher’s experience with mathematics and educational level and student achievement in mathematics. Fetler used scores from the administration of the Stanford Achievement Test (Stanford 9) to 1.3 million students in grades 9 through 11 in 785 California high schools. The test’s content is oriented toward basic skills and its publisher claims that it is based on NCTM standards in mathematics (NCTM, 1989). Fetler found that three variables related to teacher preparation correlated with student test scores: the number of teachers in those high schools with emergency teaching permits, teaching experience as measured by years of service (excluding substitute experience), and teachers’ educational level. Specifically, (1) student test results correlated positively with amount of teaching experience, (2) lower average student test scores in a school corre-
lated with higher numbers of teachers with emergency permits in that school, and (3) higher average student scores in a school correlated higher levels of education among the teachers in that school. After controlling for socioeconomic status, Fetler concluded that student achievement in mathematics significantly correlated with teacher experience and preparation.
As a result of his study, Fetler (1999), commented, “After controlling for poverty, teacher experience and preparation significantly predict test scores” and “Schools with higher percentages of teachers on emergency permits tended to have lower achieving students in mathematics.”
In light of the positive impact of infield teaching on student achievement, why is out-of-field teaching so prevalent and what might be done to curtail the practice? This report examines that issue more fully in a subsequent section on recruiting teachers and staffing schools (see Chapter 6 “Other Benefits of Partnerships for Teacher Education in Science and Mathematics”).
DATA FROM NATIONAL AND INTERNATIONAL TESTS
Studies of the National Assessment of Educational Progress (NAEP)7 also point to the importance of teachers’ levels of content preparation. Although the NAEP is designed primarily to determine how U.S. students are doing in various subjects at grades 4, 8, and 12, recent NAEPs also have collected some data about the teachers whose students took these examinations (e.g., Hawkins et al., 1998). The 1996 data show a statistically significant correlation coefficient of 0.26 between the percentage of students whose teachers have a college major in mathematics and the average mathematics scores of those students (Hawkins et al., 1998). Hence, there is some evidence to suggest the position that the more well versed a teacher is in the subject, the better his/ her students do on this type of standardized examination. Hawkins et al. (1998) concluded that, “At the eighth-grade level, students who were taught by teachers with teaching certificates in mathematics outperformed students
whose teachers had teaching certificates in education or an ‘other’ field.”
The Third International Mathematics and Science Study (TIMSS) collected information in the mid-1990s on student performance in these subjects around the world and also gathered information about teachers. In mathematics, fourth-grade students in the United States scored slightly above average on the TIMSS examination, but eighth- and twelfth-grade students performed below and well below average, respectively. The findings from the science component of TIMSS indicate that fourth and eighth graders scored above the international average in science. However, U.S. twelfth graders performed below the international average in science, and the United States ranked among the lowest of 21 nations in the TIMSS end-of-secondary school assessment of science general knowledge. Overall, the “international standing of U.S. students was stronger at the eighth-grade level than at the twelfth-grade level in both mathematics and science among the countries that participated in the assessments at both grade levels” (U.S. Department of Education, 1997b; Harmon et al., 1997). These findings suggest that a study of the characteristics of teachers in U.S. middle schools might possibly point to ways to change teacher preparation in mathematics (National Science Board, 1999; NRC, 1999c).
Another component of TIMSS with direct bearing on issues in mathematics teacher preparation is Stigler and Hiebert’s (1997) comparative analysis of TIMSS videotapes of grade 8 mathematics classes in Germany, Japan, and the United States.8 The comparison shows some startling differences in the instructional practices of mathematics teachers among the three countries (U. S. Department of Education, 1996; NRC, 1999c), such as
-
Japanese teachers widely practice what the U.S. mathematics reform effort has recommended, while U.S. teachers do so less frequently.
-
An emphasis on cultivating student understanding is evident in the steps typical of Japanese grade 8 mathematics lessons. In contrast, an emphasis on skill acquisition is evident in the steps
-
common to most U.S. and German mathematics lessons.
-
The U.S. and German emphasis on skills rather than understanding also carries over into the type of mathematics work that students are assigned to do at their desks during class.
-
U.S. teachers rarely develop mathematical concepts, in contrast to German and Japanese teachers.
It is important to recognize that directly relating the NAEP and TIMSS data about teacher training or practices and approaches to student performance is difficult at best. For example, more experienced teachers with better mathematics backgrounds may be assigned to teach classes composed of more motivated or more well-prepared students (U.S. Department of Education, 1996). It also is important to understand that student performance on these kinds of standardized examinations reflects the curriculum studied up to the time students take a particular examination, a state or a nation’s cultural emphasis on and support for education, and many other variables. Some of these factors are likely to have at least as much influence on test performance, if not more so, than teachers. Despite these other interacting variables, however, it is revealing that nearly 40 percent of grade 8 students in the United States learn mathematics from teachers who do not have college majors in either mathematics or mathematics education (Hawkins et al., 1998).
Nonetheless, in terms of certification, many eighth-grade teachers have sufficient backgrounds in mathematics to be certified in mathematics in many states. For example, 15 units in mathematics (with some specified variety of courses) were cited as satisfactory preparation for junior high-school mathematics teachers in the last recommendations of the Mathematical Association of America (1991)9 (although some states do require additional units in the subject). Yet, the TIMSS videos and test results suggest that even those teachers with certification in the discipline are teaching only a limited array of mathematical concepts and skills and doing so in ways that may be ineffective for long-term learning and mastery. The TIMSS video data also suggest that, unlike their counterparts in other countries such as Japan, many U.S. mathematics teachers present mathematical manipulations and algorithms to their students without first making certain that the students understand how and why such procedures are used.
|
9 |
An updated version of these recommendations from the Conference Board on the Mathematical Sciences will call for 21 hours in mathematics for all middle-school mathematics teachers. Additional information is available at <http://www.maa.org/cbms/metdraft/index.htm>. |
These differences in approach and emphasis may account for the lower performance of U.S. students on the kinds of questions that were asked on the TIMSS examination. It is telling that the eighth grade students whose teachers were most knowledgeable about the NCTM standards extant at that time performed better on the NAEP than did students whose teachers knew little or nothing about those standards (Hawkins et al., 1998).
Taken together, the TIMSS data on student achievement in mathematics and the NAEP data on teachers’ mathematics backgrounds lend support to the proposition that students perform better when they are able to learn from teachers who know their subject matter well and who are well informed about improved ways to teach.
CONTENT PREPARATION IS CRITICAL FOR HIGH-QUALITY TEACHING IN SCIENCE AND MATHEMATICS
What level and type of subject-matter knowledge (content knowledge) do K-12 teachers of science or mathematics need? Teacher educators and subject matter specialists have been trying to address this question for many years. One straightforward answer comes from examining the national standards in science and mathematics for grades K-12. The national standards for K-12 science and mathematics do not dictate the level of knowledge required of K-12 teachers. Some find it reasonable to suggest, however, that, at a bare minimum, teachers should possess knowledge and deep understanding of the subject matter recommended for students at the level of their teaching and, preferably, one grade level category above their particular teaching level.10 Thus, the science knowledge set forth in the National Science Education Standards for middle-level students would be the minimum level of science knowledge required of teachers for the elementary grades.11 The mathematics knowledge set forth in the National Council of Teachers of Mathematics standards for middle-level students would be the minimum level of mathematics knowledge required of teachers for the elementary grades. High-school
teachers of science and mathematics would have deep understanding of what is taught through first-year courses in their subject areas at colleges and universities. It should be noted that acquiring the desirable depth of understanding at any level usually will require advanced study of the pertinent subject matter. The content suggested for each major grade level category in the National Science Education Standards (NRC, 1996a) and by the Principles and Standards for School Mathematics (NCTM, 2000) are provided in Appendix B. A forthcoming publication from the Conference Board of the Mathematical Sciences (see footnote 9) also will address issues of teacher education for prospective teachers of mathematics.
However, despite the seemingly straightforward guidance reviewed above, the question of what content teachers need is deceptively multifaceted and complex. Level of content knowledge typically has been defined by the specific number of hours of science content or mathematics content coursework that must be a part of prospective teachers’ preparation. At the elementary school level, this might be one to three courses, which, depending on the teacher education program or specific state requirements may or may not be tailored to prospective teachers at this grade level. At the secondary level, a teacher who teaches biology might be required to complete courses or demonstrate competency in genetics, ecology, physiology, microbiology, and conservation principles. That teacher also needs to acquire some breadth of knowledge in the other sciences, as well as in mathematics. Some states require a major or at least a minor in the appropriate field but may not articulate the details of specific subjects a teacher is expected to have studied nor the minimum hours of coursework required. To push more prospective teachers toward adequate content preparation, some states have limited the number of hours a candidate can take in education as part of the bachelor degree. For example, in 1999, the Colorado state legislature adopted the following conditions for teacher licensure, including at the elementary grades:
-
a teacher preparation option must be available to students to complete as undergraduates;
-
the bachelor’s degree shall consist of no more than 120 semester hours; all candidates must complete an academic/ subject matter major and other general education requirements; and
-
the program shall include a minimum of 800 hours of organized and supervised school-based experiences.
Currently, in Texas, the teacher preparation component of a student’s
baccalaureate program (excluding student teaching) can account for no more than 18 semester hours. Other states, such as New York, have moved to a required five-year program, thereby ensuring that candidates have strong preparation in a major followed by a coherent teacher preparation program. In addition, a recent report from the American Federation of Teachers (2000) recommended that education for prospective teachers be organized as a five-year process at a minimum. Clearly, some policymakers believe that teachers’ knowledge of content in a subject area is important to successful teaching and to successful student learning, although how this is put into practice and interpreted varies widely among the states.
It is important to keep in mind that when one examines the evidence of what it takes to teach science or mathematics well, increasing the teaching of content alone, without regard to how and in what context that content is taught, is insufficient. For example, the knowledge base in many fields of science, mathematics, and technology is growing and changing so rapidly that specific content that a student learns during preparation for teaching may be out-of-date or may need to be revised substantially by the time that person begins teaching. Teaching prospective teachers content knowledge without helping them also to understand how to keep abreast of developments in their subject area cannot lead to effective teaching of these disciplines.
Science and mathematics educators agree that strong content preparation is necessary but also look at the way that content is taught. The National Science Education Standards (NRC, 1996a) state
Teachers of science will be the representatives of the science community in their classrooms, and they form much of their image of science through the science courses they take in college. If that image is to reflect the nature of science as presented in the standards, prospective and practicing teachers must take science courses in which they learn science through inquiry, having the same opportunities as their students will have to develop understanding.
The recently released content or “core” standards from the Interstate New Teacher Assessment and Support Consortium (INTASC, 1999) reinforce this recommendation by specifying that teachers of science and mathematics need to understand content as well as know how to apply that content in problem-solving and inquiry-based situations in the classroom. The principles from INTASC’s Core Standards state further that all beginning teachers in science should have more laboratory experience than they can acquire through the lab-oriented courses currently offered to prospective teachers at many colleges and universities as shown in Table 3-1.
TABLE 3-1 INTASC Core Principle #1 on Expectations of Teachers’ Content Knowledge
|
Principle Number 1: |
|
The teacher understands the central concepts, tools of inquiry, and structures of the discipline(s) he or she teaches and can create learning experiences that make these aspects of subject matter meaningful for students. |
|
Knowledge |
|
The teacher understands major concepts, assumptions, debates, processes of inquiry, and ways of knowing that are central to the discipline(s) s/he teaches. The teacher understands how students’ conceptual frameworks and their misconceptions for an area of knowledge can influence their learning. The teacher can relate his/her disciplinary knowledge to other subject areas. |
|
Dispositions |
|
The teacher realizes that subject matter knowledge is not a fixed body of facts but is complex and ever evolving. S/he seeks to keep abreast of new ideas and understandings in the field. The teacher appreciates multiple perspectives and conveys to learners how knowledge is developed from the vantage point of the knower. The teacher has enthusiasm for the discipline(s) s/he teaches and sees connections to everyday life. The teacher is committed to continuous learning and engages in professional discourse about subject matter knowledge and children’s learning of the discipline. |
|
Performances |
|
The teacher effectively uses multiple representations and explanations of disciplinary concepts that capture key ideas and link them to students’ prior understandings. The teacher can represent and use differing viewpoints, theories, “ways of knowing,” and methods of inquiry in his/her teaching of subject matter concepts. The teacher can evaluate teaching resources and curriculum materials for their comprehensiveness, accuracy, and usefulness for representing particular ideas and concepts. The teacher engages students in generating knowledge and testing hypotheses according to the methods of inquiry and standards of evidence used in the discipline. The teacher develops and uses curricula that encourage students to see, question, and interpret ideas from diverse perspectives. The teacher can create interdisciplinary learning experiences that allow students to integrate knowledge, skills, and methods of inquiry from several subject areas. |
|
Source: INTASC Core Standards, Council of Chief State School Officers. Available at <http://www.ccsso.org/intascst.html>. |
The recently released Inquiry and the National Science Education Standards (National Research Council, 2000a) puts it another way: “Programs are needed that explicitly attend to inquiry—both as a learning outcome for teachers and as a way for teachers to learn science subject matter.”
But what research exists to support this recent emphasis upon knowing, understanding, and being able to do science and mathematics? Ball (1998) contended that, to teach mathematics effectively, a teacher must have knowledge of mathematics and a conceptual understanding of the principles underlying its topics, rules, and definitions. Ball (1990) and then Cooney (1994) also stated that content knowledge must be a central focus and an integral part of a mathematics teacher’s preparation program. Similarly, after an extensive review of science education, Coble and Koballa (1996) concluded that science content must be the centerpiece of the preparation of science teachers. The major ideas of science “should form the core of the science content knowledge of all teachers, with depth of understanding reflected in the teacher’s chosen level of teaching.”
THE NATURE AND IMPORTANCE OF CONTENT KNOWLEDGE IN THE EDUCATION OF TEACHERS OF SCIENCE AND MATHEMATICS
What science or mathematics should a teacher know to be an effective teacher in these disciplines and subject areas? According to Shulman and Grossman (1988), content knowledge consists of an understanding of key facts, concepts, principles, and the frameworks of a discipline, as well as the rules of evidence and proof that are part of that discipline.
In an extensive review of the literature on the education of science teachers, Anderson and Mitchener (1994) noted that most preparation in subject matter occurs outside of schools of education. Prospective secondary science and mathematics teachers devote a large portion of their studies to their particular disciplines, but little is known about what students really learn in their subject area courses. This lack of knowledge about the real value of courses is particularly interesting in light of the fact that students in teacher education spend the majority of their academic time taking courses in the arts and sciences departments.
Ball (1990) and Borko et al. (1993) contended that teachers do not develop a deep understanding of mathematics during their own K-12 education or even
in their undergraduate coursework. Even today, college coursework in mathematics may not stress conceptual understanding of content. Rather, the emphasis is on performing mathematical manipulations in a lecture format. Science coursework often is similar. Arons (1990) pointed out that college science courses, particularly introductory survey courses, focus on the major achievements in an area of science. Then, when prospective teachers of science go on in science coursework—most often some of the same coursework engaged in by science majors—they are exposed to science as a body of facts, not, as Coble and Koballa found more recently (1996), as a way of knowing the natural world through inquiry.12
Until recently, many teacher educators have taken it for granted that teacher candidates would be knowledgeable about subject matter in the discipline(s) in which they elected to major. Beyond reports that noted the number of courses taken at the college level by candidates, Cooney (1994) and Manouchehri (1997) could find no studies on the kinds or levels of secondary teachers’ knowledge of mathematics. Moreover, research on the relationships between teachers’ actual content knowledge (vs. amount of pedagogical training and experience) and the amount of student learning that occurs usually has been inconclusive.
Some recent studies do, however, point to a relationship between teachers’ content background and the quality of their instruction. Reviews of the research on this subject (Fennema and Franke, 1992; Manouchehri, 1997) indicate that the importance of teachers’ actual knowledge of content in mathematics and their conceptual understanding of mathematics in particular is coming under focused study. As early as 1985, Steinberg et al. found that teachers with deeper conceptual understanding also engaged students in active problem solving, and helped students see relationships inside and outside of mathematics. These authors suggested that there is a relationship between the quality of secondary teachers’ knowledge of mathematics and the quality of their classroom instruction. More recent studies have confirmed the strong positive relationship between a teacher’s conceptual understanding of mathematics and the choices he or she
|
12 |
Undergraduate science, mathematics, and engineering education has begun to change during the past decade in ways that are consistent with the reforms being espoused for grades K-12. Rothman and Narum (1999) provide an overview of these changes in undergraduate education and predict the kinds of change that is likely over the next 10 years. Additional information about this report is available at <http://www.pkal.org/news/thennow100.html>. |
makes in his or her instruction.
Brown and Borko (1992) concluded that teaching mathematics from a conceptual perspective is very unlikely to occur unless a teacher has deep conceptual understanding of the mathematics subject matter at hand. Later, Manouchehri (1997) stated flatly that the research literature supports the notion that “in the absence of conceptual understanding of content, effective teaching is highly improbable.”
Few parallel studies exist for science education. Carlsen (1988) found that teachers with deeper conceptual understanding of science allowed their students to engage in discourse more often than teachers with weaker conceptual backgrounds. Carlsen also noted that teachers with greater understanding of content asked students a greater number of high-level questions, whereas teachers who did not know the material tended to dominate the classroom discussion.
Hashweh (1987) studied the effects of teachers’ knowledge of subject matter in biology and physics on teachers’ abilities to teach these subjects. He found that teachers with higher levels of content knowledge integrated pieces of that knowledge more often into their teaching. These teachers also recognized higher order principles in the discipline, and their instructional strategies reflected this depth of knowledge. Within their specialty, teachers with greater content knowledge wrote examination questions that focused less on recall and more on students being able to apply and transfer information. However, when they were teaching outside of their specialty, these teachers followed textbook chapters more closely and were less likely to recognize or address student misconceptions. Hashweh concluded that knowledge of subject matter contributed greatly to these teachers’ ability to translate a written curriculum into an active curriculum in biology and physics.
As was noted earlier in this report, some policymakers and teacher educators believe that prospective teachers should emphasize their preparation in subject matter at the expense of preparation in education. Do teachers who were majors in science or mathematics understand the subjects they teach better than teachers who were education majors? Ball and Wilson (1990) conducted a study at Michigan State University that examined this question with prospective elementary teachers before and after they had completed their teacher preparation programs. They looked at two groups, one composed of prospective teachers who had been prepared in a traditional preparation program, and the other composed of prospective teachers who had been prepared in an alternative program.
Their focus was the influence of these programs on the prospective teachers’ teaching of mathematics. Ball and Wilson found that both groups of teacher candidates lacked understanding of the underlying relationships of mathematics. At the beginning of their teacher preparation programs, 60 percent of these prospective teachers could not generate a real-world example that would demonstrate to their students an application for the division of fractions. Moreover, they still could not generate an appropriate representation of division of fractions after they had graduated from their respective preparation programs. Ball and Wilson (1990) concluded that neither group was prepared to teach mathematics for understanding or to teach mathematics in ways that differ from “telling and drilling algorithms into students.”
What else, then, needs to take place in teacher education programs to support candidates adequately in the effective teaching of science and/or mathematics? Several possible answers were revealed in a study of teachers’ understanding of mathematics conducted recently by Ma (1999). Ma studied groups of elementary school teachers in China and the United States. Despite China’s more limited teacher preparation program, Ma found that the Chinese teachers had a more profound understanding13 of the mathematics they were teaching. This deeper understanding both of mathematics content and its application allowed Chinese teachers to promote mathematical learning and inquiry more effectively than their counterparts in the United States, especially when students raised novel ideas or claims that were outside the scope of the lesson being presented in class.
Ma’s study provides some insights that might guide an upgrading of teacher knowledge in the United States. Specifically, most of the Chinese teachers only taught mathematics, up to three or four classes per day. Much of the rest of their day was unencumbered, allowing for reflection on their teaching and, perhaps more importantly, for shared study and conversation with fellow teachers about content and how to teach it. Their teaching assignments also permitted them to gain over time a better grasp of the entire elementary
school curriculum for mathematics. None of these features—specialist teachers in elementary schools, time for learning collaboratively with other teachers, and experience at a variety of grade levels—is common to U.S. elementary schools.
The kind and quality of teachers’ inservice education can make a difference in how their students achieve. Cohen and Hill (1998) reported on a large-scale study of mathematics teachers in California who participated in a sustained program of professional development. Although this study actually focused on the effects of educational policy, it revealed important information about the opportunities that teachers need both to learn and to teach new state-required mathematics content as a means of enhancing student achievement. Using data from a 1994 survey of California elementary school teachers and student scores from the 1994 California Learning Assessment System (CLAS), this study examined whether students who are taught by teachers with more extensive opportunities for inservice education would perform better than students whose teachers had less extensive opportunities for inservice. “More extensive” was defined as ongoing opportunities to learn subject matter deeply, adopt new curriculum, and learn about appropriate and aligned assessments of student learning and achievement. “Less extensive” was defined as participation in special topic workshops. Cohen and Hill (1998) found that the more time teachers spent in curriculum workshops, including those with opportunities to examine new curriculum with other teachers, the more reform-oriented and less conventional was their teaching practice. In fact, the difference was nearly 0.75 standard deviation higher, a statistically significant difference.
These results also appeared to be associated with student achievement. After taking student characteristics and school conditions into account, there was a modest positive correlation between the degree to which teachers reported that their classroom practice was oriented to California’s state Mathematics Framework and average student scores on the CLAS. Cohen and Hill (1998) noted in particular the fact of the teachers’ involvement with such work as writing topic units potentially to substitute for or elaborate on less indepth textbook treatments. In addition, these teachers were involved in the construction of rubrics for assessing student responses to open-ended kinds of problems. No similar relationship was found for these two variables in schools where teachers engaged in a high degree of conventional practice.
Other studies have produced similar results. For example, another study of
student achievement in California demonstrated that when teachers had experienced extended inservice opportunities to learn about mathematics curriculum and instruction, their students’ achievement increased (Wiley and Yoon, 1995). Also, a study of mathematics reform, Quantitative Understanding: Amplifying Student Achievement and Reasoning (QUASAR), program found higher achievement among students whose teachers were involved in a sustained program of curriculum development, in this case, a program that emphasized enhancing teachers’ understanding of strategies, having teachers implement new strategies, and encouraging teachers to reflect on instructional outcomes (Brown et al., 1995).14
In addition, Grouws and Schultz (1996) summarized a series of studies designed to gauge the impact of the University of Wisconsin’s Cognitively Guided Instruction (CGI) research program for mathematics teacher effectiveness. According to Grouws and Schultz, the studies found that providing teachers with knowledge of how students think and opportunities to develop strategies in specific content domains changed teaching behaviors and improved student learning. In one study of first- and second-grade teachers, the CGI group provided teachers with knowledge of young children’s thinking and with strategies for teaching addition and subtraction. Subsequently, these teachers spent more time in their mathematics instruction on problem solving and assessing student thinking than a control group of teachers who received equivalent hours of inservice training. The students of CGI teachers also performed better in some math assessments—higher in problem solving, comparably on computational tasks.
In their review, Grouws and Schultz specifically note a certain type of teacher knowledge, called pedagogical content knowledge (Shulman, 1986). They state, “In mathematics, pedagogical content knowledge includes, but is not limited to, useful representations, unifying ideas, clarifying examples and counterexamples, helpful analogies, important relationships, and connections among ideas. Thus, pedagogical content knowledge is a subset of content knowledge that has particular utility for planning and conducting lessons that facilitate student learning.”
All of the studies cited in this chapter, as well as those cited earlier (e.g., Fetler, 1999), lend strong support to the idea that when teachers receive high-
|
14 |
Information about the QUASAR program is available at <http://www.ed.gov/pubs/math/part6.html>. |
quality preparation and engage in rich professional development, their understanding of education reform and the strategies underlying that reform is enhanced. However, it is clear that even the best teachers by themselves will be unable to make the kinds of inroads in improving student learning and academic achievement that are being expected across the United States. Their efforts must be supported by school and policy infrastructure, policies, and priorities that offer to teachers opportunities for continuing professional development and growth and that provide the facilities and resources necessary to encourage teaching and learning. Teachers also need good working conditions in order to thrive as professionals. The next chapter discusses the kinds of recommendations that professional organizations for teaching and in the various science and mathematics disciplines have issued for improving teacher education.






















