3
Current SAIPE Models
USER OVERVIEW
The Census Bureau's Small Area Income and Poverty Estimates (SAIPE) Program produces income and poverty estimates for states and counties, including estimates of median household income, total poor, poor under age 5 (states only), poor aged 5-17 in families, and poor under age 18. These estimates, which are updated every year for states and every 2 years for counties, are termed “indirect estimates.” They are indirect because they are developed from statistical models that use data from other areas and time periods, unlike “ direct estimates,” which are based solely on a survey's sample cases in the given area and period.1 The use of indirect estimation for producing updated state and county income and poverty estimates is necessary because there is currently no survey or administrative record data source that can provide the required estimates with sufficient reliability for intercensal years. Indirect estimates of poor school-age children for school districts are derived by using decennial census data to allocate the updated county estimates among districts.
The March Current Population Survey (CPS) collects the detailed in-
|
1 |
Other terms are also used in the research literature for these concepts: for example, direct estimates are sometimes called “sample-based” estimates, and indirect estimates are sometimes called “synthetic,” “model-based,” or “model-dependent” estimates (see U.S. Office of Management and Budget, 1993). |
formation on income needed to produce the required income and poverty estimates. However, the sample is too small to produce sufficiently reliable direct estimates for states, let alone counties. Indeed, most counties have no CPS sample. Therefore, state and county income and poverty estimates are obtained from statistical regression models, and the SAIPE estimates are produced by using weighted averages of the regression predictions and the direct CPS estimates, when the latter are available. The weighted average approach for combining the model predictions and the direct estimates is advantageous in that it strikes an effective tradeoff of the model error of the model predictions and the sampling error of the direct estimates.
The state-level model predictions are obtained from regression models in which a state's direct CPS estimate for the reference year is the dependent variable and the predictor variables are obtained from such sources as Internal Revenue Service (IRS) tax returns, food stamp records, population estimates from the Census Bureau's demographic estimates program, and the previous census. The SAIPE estimate for a state is then a weighted average of the model prediction and the direct estimate for the state.
The same general approach is used for the SAIPE county estimates, with the same sources of data for the predictor variables in the regression models. One difference is that 3 years of March CPS information are combined to form the dependent variables in the regression models and to calculate the direct estimates. For the poverty models, another difference is that the county models estimate numbers of poor (in logarithms), while the state models estimate the proportions of poor. For the one-third of counties that have households in the CPS sample, the model predictions are combined with the direct estimates, as is done for the state models. For the other two-thirds of counties, the model predictions are taken to be the estimates. As a last step in developing the SAIPE county poverty estimates, each of the county estimates in a state is multiplied by a constant factor that makes the sum of the adjusted county estimates equal the SAIPE state estimate.
For school districts, no administrative data are currently available from which to form predictor variables for use in poverty models. IRS and food stamp data are not available at the school district level. Counts of students approved to receive free school lunches are a potential source for all districts, but they are not now nationally available, and there are serious concerns about the comparability of the counts across all districts. Hence, the Census Bureau produces estimates for districts using a “shares” approach. This approach assumes that each school district in a county has the same proportion (share) of that county's poor school-age children in the estimation, or reference, year as it did in the 1990 census.
Then the 1990 census shares of poor school-age children for school districts within counties are applied to the updated SAIPE county estimates to produce the SAIPE school district estimates for the reference year.
The production of indirect estimates like those from the SAIPE program is a complex operation that needs to be fully evaluated. The evaluation should check on the input data from the multiple sources, it should examine the adequacy of the models used to produce the model predictions, and it should carefully assess the resulting estimates. Since flaws in any aspect of the estimation process can distort indirect estimates, an evaluation scheme of this form should be a standard component of a small-area estimation program. Moreover, the evaluation should be done every time that estimates are produced.
The panel and the Census Bureau performed detailed evaluations of the SAIPE state and county estimates of poor school-age children, which are described in the companion volume to this report (National Research Council, 2000c). These evaluations include internal assessment of the structure and functioning of the regression models, external comparisons with census data, and, for counties, external comparisons with aggregate CPS estimates. Census and CPS aggregate data are not ideal for evaluation purposes. Yet they can help answer the key question of whether the model estimates show any strong, persistent biases for areas with specific attributes (e.g., areas with large or small populations, high or low poverty rates, rapid or slow changes in poverty rates) that could have adverse consequences when the estimates are used for fund allocation or other program purposes.
SAIPE county estimates of poor school-age children have also been evaluated by consulting state demographers and others with local knowledge. Since estimates are always subject to error, whether they are produced by a model or from local (or other) information sources, one should not be overly concerned by discrepancies between individual estimates and local sources. However, local assessment may indicate persistent patterns of marked discrepancies for areas with common attributes that should be investigated.
The internal and external evaluations of the 1993 and 1995 state and county estimates led the panel to conclude that the models are working reasonably well and that these estimates are preferable to 1990 census estimates as a basis for Title I allocations (National Research Council, 1998, 1999). According to Census Bureau calculations, the SAIPE estimates, on average, have more variability due to sampling error and prediction error than the census estimates. However, the out-of-date census estimates have considerably more bias. For example, estimates produced for 1989 using the modeling approach differed much less from the 1990 census estimates than did estimates from the 1980 census.
Although the evaluations of the SAIPE state and county estimates have supported their use for fund allocation, they have identified aspects of the models that require additional research and development. Some priorities for SAIPE model development are presented later in this chapter (see also National Research Council, 2000c). In addition to research to improve the existing models, research is needed to examine how data from new sources, such as the 2000 census and the proposed American Community Survey, may contribute to the production of the SAIPE estimates. (The potential uses of these sources in the SAIPE program are discussed in Chapter 4.)
As noted above, the lack of administrative data at the school district level led the Census Bureau to use a simple shares approach based on 1990 census data for allocating the updated SAIPE county estimates of poor school-age children among school districts. Only limited evaluations of the school district estimates are possible, but it is clear that the estimates are not very reliable for most school districts. Nevertheless, the evaluations led the panel to conclude that the 1995 school district estimates were the best available for Title I allocations–for example, as good as or superior to 1990 census estimates or estimates based on school lunch counts. Marked improvement of the SAIPE poverty estimates for school districts and other subcounty areas will require investment in new or modified data sources that can provide the basis for improved models for these areas. (Chapter 5 identifies possible new administrative data sources that would likely improve SAIPE subcounty estimates.)
The next few sections of this chapter present a technical overview of the SAIPE models for estimates of poor school-age children for states, counties, and school districts, including a description of the Census Bureau's methods for estimating variability in the state and county estimates, and a summary of the evaluations conducted to date. The chapter then briefly summarizes the other SAIPE models (e.g., median household income and poverty for other age groups) and the Census Bureau's methods for producing small-area population estimates and their evaluation. (Population estimates are used both in the SAIPE poverty models and in Title I and other fund allocation programs.) The last section of the chapter provides recommendations to the Census Bureau for research and development to improve the current SAIPE models.
MODELS FOR POOR SCHOOL-AGE CHILDREN
State and County Models
The Census Bureau constructs separate regression models for estimating the numbers of poor school-age children at the state and county
levels.2 In the state model, the dependent variable is an estimate of the proportion of school-age children who are poor; in the county model, it is the logarithm of the number of poor school-age children. In both cases, the dependent variable is constructed from CPS data. For both models, the deviations from the regression are assumed to follow a variance components model with two components. One component represents sampling error in the dependent variable. The other component represents the deviations in the model predictions from the true values that would occur in a model in which the dependent variable is not subject to sampling error; the Census Bureau, as is commonly done, refers to this component as model error. The state and county estimates are weighted averages of the direct CPS estimates (where available) and the regression predictions, where the weights are functions of the variance components. School district estimates are derived from county estimates under the assumption that the relative proportion (share) of the poor school-age children in a county who are in a particular school district in the reference year is the same as it was in the 1990 census.
Input Data
Both the state and county models of poor school-age children use input data from five sources: the March CPS; the previous census; the Census Bureau's population estimates program; food stamp administrative records; and IRS individual income tax returns. The dependent variable in the state regression model is formed from data from the March CPS for the reference year. The dependent variable in the county model is created as a weighted average of estimates calculated from 3 years of March CPS data, centered on the reference year, in order to improve the precision of the CPS estimates. The other four sources are used to form predictor variables for the regression models.
After examining a variety of administrative records, the Census Bureau chose food stamp and tax return data as sources of predictor variables. These sources were chosen because they contain data from which variables related to poverty can be constructed, because they are available for all states and counties, and because they are, as far as possible, constructed using the same definitions and procedures nationwide (see National Research Council, 2000c, for details of how these data are obtained). The Census Bureau receives an extract of information on tax returns each fall that were filed in April for the preceding year (the extract omits some
|
2 |
More precisely, the Census Bureau's estimates pertain to related children aged 5-17 in poor families, termed “poor school-age children” in this report; see Chapter 1:fn 2. |
returns, such as those filed late). The Census Bureau receives monthly counts of food stamp recipients from the U.S. Department of Agriculture for states. For most counties, the Bureau receives food stamp counts that pertain to July 1 of the reference year; for some counties the counts are an average of the monthly counts for the year. A concern with using food stamp recipient data in the state and county models is that participation rates (recipients as a proportion of people who are eligible to apply) differ across areas. These differences may have become larger due to the effects of the 1996 legislation that changed several social welfare programs (see Chapter 5).
State Model
As noted above, the state model for the proportion of school-age children who are poor is estimated for the year of interest—the reference year—using CPS data for that year (the year subscript is suppressed below). The state model is
yj = α0 + α1x1j + α2x2j + α3x3j + α4x4j + uj + ej, (3.1)
where:
|
yj |
= |
estimated proportion of school-age children in state j who are in poverty based on the March CPS that collects income data pertaining to the reference year, |
|
x1j |
= |
proportion of child exemptions reported by families in poverty on tax returns in state j, |
|
x2j |
= |
proportion of people receiving food stamps in state j, |
|
x3j |
= |
proportion of people under age 65 not included on an income tax return in state j, |
|
x4j |
= |
residual for state j from a regression of the proportion of poor school-age children estimated from the prior decennial census on the three predictor variables, (x1j, x2j,x3j), for the census reporting period, |
|
uj |
= |
model error for state j, and |
|
ej |
= |
sampling error of the dependent variable for state j. |
The uj are independent of ej for all j and i. Also, it is assumed that uj ~ NI(0, ![]() ) and that ej ~ NI(0,
) and that ej ~ NI(0, ![]() ), where ~NI(µ, σ2) is read “distributed normally and independently with mean µ and variance σ2.” The
), where ~NI(µ, σ2) is read “distributed normally and independently with mean µ and variance σ2.” The ![]() are estimated from CPS data using a generalized variance function (GVF) procedure documented in Otto and Bell (1995).
are estimated from CPS data using a generalized variance function (GVF) procedure documented in Otto and Bell (1995).
The coefficients for model (3.1) and the model error variance (![]() ) are
) are
estimated by maximum likelihood, treating the estimated ![]() as known. The SAIPE estimate of the proportion of school-age children living in poverty in a state is a weighted average of the model-based estimate (ŷj) and the CPS-based direct estimate for the state (yj), where the weights are proportional to the estimated precision of the two components. The SAIPE estimate for the proportion of school-age children in poverty in state j is
as known. The SAIPE estimate of the proportion of school-age children living in poverty in a state is a weighted average of the model-based estimate (ŷj) and the CPS-based direct estimate for the state (yj), where the weights are proportional to the estimated precision of the two components. The SAIPE estimate for the proportion of school-age children in poverty in state j is 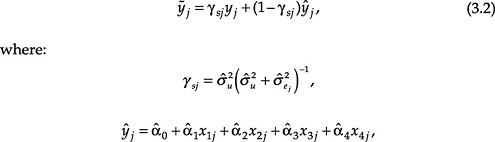
![]() is the maximum likelihood estimate of
is the maximum likelihood estimate of ![]() , (
, (![]() ) is the maximum likelihood estimate of (α0, α1, α2, α3, α4) and
) is the maximum likelihood estimate of (α0, α1, α2, α3, α4) and ![]() is the estimate of the variance of the CPS estimate yj, based on CPS data. (Both “estimator” and “predictor” are used in the literature to describe
is the estimate of the variance of the CPS estimate yj, based on CPS data. (Both “estimator” and “predictor” are used in the literature to describe ![]() .)
.)
An initial estimate of the number of poor school-age children for a state is obtained by multiplying the estimated proportion poor (![]() ) by the estimated total number of noninstitutionalized school-age children in the state, which is obtained from the Census Bureau' s program of population estimates.
) by the estimated total number of noninstitutionalized school-age children in the state, which is obtained from the Census Bureau' s program of population estimates.
The initial state-level estimates of the number of poor school-age children are then ratio adjusted to sum to the CPS national estimate of poor school-age children. Thus, the final estimate of the number of poor school-age children in state is![]()
where ![]() is the CPS estimate of the number of poor school-age children in state j,
is the CPS estimate of the number of poor school-age children in state j, ![]() j is the estimated number of noninstitutionalized school-age children in state j from the Census Bureau population estimates, and the summation is over all states. Historically, the ratio adjustment in (3.3) has changed the estimates by less than 1 percent.
j is the estimated number of noninstitutionalized school-age children in state j from the Census Bureau population estimates, and the summation is over all states. Historically, the ratio adjustment in (3.3) has changed the estimates by less than 1 percent.
County Model
The state model uses proportion poor as the dependent variable and proportions as explanatory variables. The county model is slightly different in that it uses the logarithm of number poor as the dependent variable and is a model linear in logarithms. The county model is ![]()
where:
|
zji |
= |
log (3-year weighted average of number of poor school-age children in county i of state j based on 3 years of March CPS data),3 |
|
w1ji |
= |
log (number of child exemptions reported by families in poverty on tax returns in county i of state j), |
|
w2ji |
= |
log (number of people receiving food stamps in county i of state j), |
|
w3ji |
= |
log (estimated population under age 18 in county i of state j), |
|
w4ji |
= |
log (number of child exemptions on tax returns in county i of state j), |
|
w5ji |
= |
log (number of poor school-age children in county i of state j in the previous census), |
|
vji |
= |
model error for county i of state j, and |
|
aji |
= |
sampling error of the dependent variable for county i of state j. |
It is assumed that vji ~ NI(0, ![]() ), that vji is independent of vkm for all ji and km, and that aji ~ NI(0, nji−1
), that vji is independent of vkm for all ji and km, and that aji ~ NI(0, nji−1![]() ), where nji is the CPS sample size for county i of state j.4 Although the variables carry a state identification, there are no state effects in the model.
), where nji is the CPS sample size for county i of state j.4 Although the variables carry a state identification, there are no state effects in the model.
The between-county variance component, ![]() , is estimated using data from the 1990 census. A model, analogous to (3.4), is constructed in which the dependent variable is obtained from the 1990 census long form and the predictor variables are for the census reporting year. In this model, the census sampling variance (corresponding to nji−1
, is estimated using data from the 1990 census. A model, analogous to (3.4), is constructed in which the dependent variable is obtained from the 1990 census long form and the predictor variables are for the census reporting year. In this model, the census sampling variance (corresponding to nji−1![]() ) is estimated using a generalized variance function and is then treated as fixed
) is estimated using a generalized variance function and is then treated as fixed
|
3 |
The number of poor school-age children is the product of the weighted 3-year average CPS poverty rate for related children aged 5-17 and the weighted 3-year average CPS number of related children aged 5-17; see National Research Council (2000c:Ch.4) for derivation of the weights. |
|
4 |
The assumption that the variance of aji is simply inversely proportional to sample size is only an approximation, given the clustered CPS sample design. A different formulation may be preferable; see the discussion below of improved estimation of variance components. |
in fitting the model by maximum likelihood. The maximum likelihood parameter estimates obtained from the census data are estimated census regression coefficients and the estimated model error variance, ![]() . The assumption is made that the model error variance in the census regression and the county model regression (3.4) are the same. Documentation of the estimation approach is provided by Fisher (1997); see also National Research Council (2000c:Ch.4).
. The assumption is made that the model error variance in the census regression and the county model regression (3.4) are the same. Documentation of the estimation approach is provided by Fisher (1997); see also National Research Council (2000c:Ch.4).
Data from the CPS and ![]() from the census regression are used to estimate
from the census regression are used to estimate ![]() and the vector (β0, β1, β2, β3, β4) of equation (3.4). The estimate
and the vector (β0, β1, β2, β3, β4) of equation (3.4). The estimate ![]() is treated as fixed in the final estimation. Counties that are in the CPS sample and that have one or more poor school-age sampled children are included in the estimation data set for the county model, and those with no poor school-age sampled children are omitted.
is treated as fixed in the final estimation. Counties that are in the CPS sample and that have one or more poor school-age sampled children are included in the estimation data set for the county model, and those with no poor school-age sampled children are omitted.
The predictor of the logarithm of the number of poor school-age children in county i of state j is 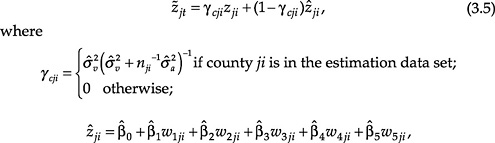
and (![]() ) is the maximum likelihood estimator of the regression vector. An initial predictor of the number of poor school-age children for county ji is obtained by transforming back to the initial scale:
) is the maximum likelihood estimator of the regression vector. An initial predictor of the number of poor school-age children for county ji is obtained by transforming back to the initial scale:![]()
where ![]() ji adjusts for the bias introduced by exponentiation, which is a nonlinear transformation. This bias adjustment is derived from the expression for the mean of the lognormal distribution (see Fisher, 1997).5
ji adjusts for the bias introduced by exponentiation, which is a nonlinear transformation. This bias adjustment is derived from the expression for the mean of the lognormal distribution (see Fisher, 1997).5
The final county estimates for a state are ratio adjusted so that the sum of the county estimates in a state is equal to the estimated state total obtained from the state model. Thus, the estimate for county ji is
|
5 |
Another possibility would be to use the procedure in Duan (1983). |
![]()
where the summation is over the counties in state j, and ![]() is the state estimate defined in equation (3.3). Unlike the ratio adjustment for the state estimates, these adjustments are often large and highly variable across states. For the final county estimates of poor school-age children in 1993, the average state ratio adjustment –the SAIPE state estimate divided by the sum of the initial county estimates, known as the state raking factor–was 1.07; two-thirds of the factors were between 0.98 and 1.16. For 1995, the average state raking factor was 0.97; two-thirds of the factors were between 0.88 and 1.06. The correlation between raking factors for states in 1993 and 1995 is low, which implies that there was little systematic variation by state across these years.
is the state estimate defined in equation (3.3). Unlike the ratio adjustment for the state estimates, these adjustments are often large and highly variable across states. For the final county estimates of poor school-age children in 1993, the average state ratio adjustment –the SAIPE state estimate divided by the sum of the initial county estimates, known as the state raking factor–was 1.07; two-thirds of the factors were between 0.98 and 1.16. For 1995, the average state raking factor was 0.97; two-thirds of the factors were between 0.88 and 1.06. The correlation between raking factors for states in 1993 and 1995 is low, which implies that there was little systematic variation by state across these years.
School District Procedure
Because of the lack of administrative data at the school district level for constructing predictor variables, the school district estimates of poor school-age children are produced by a shares approach rather than by regression modeling. This shares approach allocates the updated county estimates among school districts in the same proportions that poor school-age children were distributed across the districts in the 1990 census. Although the general approach is simple, a number of complications arise in its application (see National Research Council, 2000c:Ch.7, for further details).
First, school district boundaries change over time. To address this problem, the Census Bureau conducts a survey every 2 years in which officials in every state are asked to update the boundaries for the districts in their state. Using these boundaries, the 1990 census blocks are allocated to school districts, and the census counts of poor school-age children are summed for the blocks in each district. When school district boundaries cut through blocks, the block counts are proportionately allocated.
Second, some school districts cross county boundaries. These districts are divided into parts by county, and the shares approach is applied to school district parts within each county. The estimate for a school district is then obtained by adding together the estimates for its parts.
Third, some school districts cover only selected grades (e.g., kindergarten through grade 8), with the result that some blocks are in more than one school district. This problem is addressed by allocating the poor children in the appropriate age range to each district.
Fourth, for many districts the census estimates of poor school-age children are subject to substantial levels of sampling error because they are derived from data collected from the census long-form sample. To reduce this sampling error, the estimates for the district parts are ratio adjusted to make the total number of school-age children from the long-form sample conform to the number of school-age children from the complete census.
The estimated number of poor school-age children in school district part d in county i in state j for the reference year is given by![]()
where Rjid is the ratio-adjusted estimate of the proportion of poor school-agechildren in that district part in the 1990 census, and ![]() ji is the updated county estimate given by (3.7). The ratio-adjustedestimate Rjid is given by Rjid = CjidA′jidAjid−1, where in district part d in county i in state j, Cjidis the estimated number of poor school-age children from the long-form sample, A′jid is the number of school-age children from the complete census, and Ajid is the estimated number of school-age children from the long-form sample.
ji is the updated county estimate given by (3.7). The ratio-adjustedestimate Rjid is given by Rjid = CjidA′jidAjid−1, where in district part d in county i in state j, Cjidis the estimated number of poor school-age children from the long-form sample, A′jid is the number of school-age children from the complete census, and Ajid is the estimated number of school-age children from the long-form sample.
Evaluations
As recommended by the National Research Council panel, the Census Bureau conducted an extensive set of evaluations of the SAIPE estimates of poor school-age children for states and counties. Due to data constraints, more limited evaluations were conducted of the estimates of poor school-age children for school districts. The companion technical documentation volume to this report describes the methods and results of the state, county, and school district evaluations in detail (National Research Council, 2000c:Ch.6, Ch.7). Below we summarize the principal evaluation methods under two headings—internal evaluation and external evaluation—and highlight key results.
Internal Evaluations of State and County Models
For each year for which the state and county models were estimated, an internal evaluation was conducted of the underlying assumptions and features of the models. Internal evaluations were also conducted of alternative forms of the county model. Such evaluations, which principally involved examination of the residuals from the regression before taking
the weighted average of the regression estimates with the direct estimates or raking to control totals, are necessary to establish that a model is performing well in terms of its assumptions.6
Six assumptions were examined for the state and county models, most often by reviewing a variety of graphical plots:
-
linearity of the relationships between the dependent variable and the predictor variables;
-
constancy of the assumed linear relationship over time (evaluated by comparing the regression coefficients across years);
-
absence of systematic patterns in the standardized residuals across categories of states or counties (e.g., counties categorized by population size), where nonrandom patterns could indicate bias and the need for additional predictor variables in the regression model;7
-
normality (primarily, symmetry and moderate tail length) of the distribution of the standardized residuals;
-
homogeneity of the variances of the standardized residuals (typically examined with respect to the values of the predictor variables); and
-
absence of outliers for the dependent and predictor variables.
The evaluation also examined t-statistics to determine the significance of the predictor variables and whether one or more of them should be excluded from a model.
State Model Results of the internal evaluations of the state model (estimated for each of the years 1989 to 1993, 1995, and 1996) largely supported the model's assumptions.8 There was no evidence of non-linearity in the relation between the dependent variable and each predictor variable; the regression coefficients were generally similar across years; only one regression coefficient was not statistically significant (at the 5% level), and it failed to achieve significance in only 1 of the 7 years; there was no evidence of outliers or heterogenous variance; and there was only a small degree of skewness of the standardized residuals. The only evidence of possible bias is that the state model fairly consistently underpredicted the proportion of school-age children who were poor in some Western states and fairly consistently overpredicted this proportion in other Western states.
|
6 |
Such evaluations are often referred to as “regression diagnostics.” |
|
7 |
See National Research Council (2000c:Ch.6) for the calculation of the standardized residuals and the categories of states and counties examined. |
|
8 |
The state model was not estimated for 1994 because a redesign of the CPS sample after the 1990 census was partly but not completely phased in for the March 1995 CPS. |
A review of the estimated model error variances in the state model turned up an anomalous result in that the variances were estimated to be zero in every year but 1993. This outcome implies (absent sampling variability) that the model predicts state poverty rates for school-age children perfectly. As a consequence, the direct estimates receive zero weight in the weighted averages of the model estimates and the direct estimates, even when they are quite precise. While differences between the model estimates and the direct estimates are neither unusually large nor strongly persistent, it is not plausible to assume that the model has perfect predictive power. The problem may be that the procedure used by the Census Bureau tends to overestimate the sampling variances. These variances are estimated from the CPS data using a generalized variance function. They are then used in the maximum likelihood procedure that estimates the model error variance in the state model regression. With this procedure, if the estimates of sampling error variances are too large, the estimate of model error variance will be too small.
County Model Internal evaluations were conducted for alternative county models, which were estimated for 1989 and 1993,9 and for the current county model, which was estimated for 1989, 1993, and 1995. Analysis of the alternative county models largely supported the model assumptions, the analysis did not strongly support one model over another. Some problems were identified: most models tended to overpredict the number of poor school-age children in larger urban counties, especially those with large percentages of Hispanics; all models showed some variance heterogeneity, particularly with respect to CPS sample size and often with respect to the predicted value (number or proportion poor of school-age children); and some models exhibited more problems with outliers and skewness than others. None of the other models was clearly superior to the current SAIPE county model.
Analysis of the current model for 1989, 1993, and 1995 found fairly similar regression coefficients for the predictor variables w1, w2, and w5 in equation (3.4) for all 3 estimation years. The sum of the coefficients for w3 and w4 within the regression equation was similar and close to zero in each year. The sum of all coefficients in the regression model was close to
|
9 |
The 13 alternative models varied on three dimensions: treatment of information from the previous census (whether the model included a census-based predictor variable in a single equation or estimated both census and CPS numbers of poor school-age children in a bivariate system of equations); the form of the variables (whether poverty rates or numbers, transformed or not transformed to logarithms); and whether the model included fixed state effects (see National Research Council, 2000c:Ch.5). |
1 for all 3 estimation years. (If this sum were 1, the model is expressible as a model with the poverty rate as the dependent variable and rates as predictor variables.) The current model consistently slightly overpredicted the number of poor school-age children in counties with smaller population sizes and in counties in metropolitan areas that are not the central county of the areas.10 It also exhibited variance heterogeneity with respect to CPS sample size and the predicted value of the number of poor school-age children. The variance heterogeneity with respect to CPS sample size could be a result of a problem in the procedure used to estimate sampling error variances, a problem in the procedure used to estimate model error variance, or, possibly, heterogeneity in the model error variance.
External Evaluations of State and County Models
External evaluations involve comparisons of the estimates from a model with target or “true” values that were not used to develop the model. Such evaluations are important but difficult to carry out. Two sources of comparison values have been used for external evaluations of the SAIPE state and county models for poor school-age children–the previous census and weighted aggregates of CPS direct estimates–but neither source is ideal for this purpose. The census estimates can provide an evaluation for only one year, 1989. Also, they are not true values: they are affected by sampling variability and population undercount. Furthermore, the census measurement of poverty differs from the CPS measurement in ways that are not fully understood (see Chapter 4). The weighted CPS direct estimates can be produced for multiple years, but the sample sizes for CPS estimates, even when the sample is aggregated for 3 years for the county model evaluations, are small for many categories of counties, thus making comparisons with them much less reliable than comparisons with census estimates. Nonetheless, both sources can indicate patterns of differences that suggest possible persistent biases in the model estimates.
In addition to the comparisons with census and CPS estimates, reviewed below, another external evaluation of the 1993 county model estimates of poor school-age children was based on local knowledge. The analysis for this evaluation first identified groups of counties (e.g., large central city counties) for which the 1993 estimates seemed unusually high or low in relation to prior levels and trends (e.g., from 1980 to 1990) in the
|
10 |
A central county is the county in a metropolitan area that contains the central city of the area. |
.
number and proportion poor of school-age children and known socioeconomic trends. Then knowledgeable local people, such as state demographers and state data center staff, were contacted about the counties in these groups. These people questioned the statistical reliability of the 1993 estimates in general and the estimates for specific counties, but they did not identify categories of counties for which the apparent trends in school-age poverty seemed unreasonable.
State Model Comparisons of 1990 census estimates of poor school-age children in 1989 with state model estimates for 1989, 1980 census estimates, and March 1990 CPS direct estimates supported the use of the model estimates. Differences between the 1989 state model estimates and 1990 census estimates were much smaller than the differences between the March 1990 CPS direct estimates and the 1990 census estimates and considerably smaller than the differences between the 1980 census and 1990 census estimates. (Comparable evaluations were not performed for alternative models or for categories of states.)
County Model Estimates of poor school-age children in 1989 from the SAIPE county model and several alternative models and four simpler procedures were compared to 1990 census estimates for all counties and for categories of counties (see National Research Council, 2000c:Ch.6). Overall, the SAIPE model and alternative models performed better than the simpler procedures.11 For example, the average absolute difference between the 1989 estimates from the SAIPE county model and the 1990 census estimates was 11 percent of the average number of poor school-age children. In contrast, the average absolute difference was 23 percent for the simplest procedure –the stable shares procedure, which assumed no change from 1979 to 1989 in county shares of the national number of poor school-age children. 12
The SAIPE and alternative models also performed better than the simpler procedures in terms of algebraic differences from census esti
|
11 |
The four simpler procedures assumed (1) no change from 1979 to 1989 in the county shares of the national number of poor school-age children; (2) no change in the county shares within each state; (3) no change in the county proportions poor of school-age children within each state; and (4) that the 1989 values could be estimated by an average of 1980 census estimates and estimates from one of the county models. |
|
12 |
The formula for the average absolute difference, where there are n counties (i), and γ is the estimated number of poor school-age children from a model or the census, is |
|
13 |
The formula for the category algebraic difference for counties (i) in each category (j) is |
mates for categories of counties.13 A large algebraic difference for a particular category of counties suggests that the estimation procedure is producing biased estimates for the counties in that category. Analysis showed that for most of the categories of counties investigated, the model estimates had smaller algebraic differences and fewer obvious patterns of differences across categories than did the estimates from the simpler procedures. On balance, the current SAIPE county model performed somewhat better than the other models that were evaluated, including a model that was initially selected to serve as the basis for the county estimates. 14 The only potential biases evident with the current model were that it tended to overpredict (underpredict) the number of poor school-age children in counties with the greatest decreases (increases) in school-age poverty rates from 1980 to 1990 and to overpredict the number of poor school-age children in counties with large percentages of Hispanics and counties in the Mountain and Pacific divisions. The problem in the Mountain and Pacific divisions must be attributable to the state model since the county model is raked to the state model, and census divisions are combinations of states. In general, no model can be expected to perform well in predicting for counties that experience very large changes in poverty rates.
Comparisons of algebraic differences for categories of counties between estimates from the county model and weighted 3-year CPS direct estimates centered on 1989, 1993, and 1995 found large model-CPS differences, due mainly to the small sample sizes of the CPS direct estimates. A few differences were both large and in the same direction (plus or minus) for all 3 years, suggesting a possible bias. The model tended to underpredict the number of poor school-age children in counties with large percentages of Hispanics and, to a lesser extent, in counties with large percentages of blacks. The model estimates also differed consistently from weighted CPS estimates for some categories of rural counties classified by economic type.
Evaluations of the School District Model
Evaluations of the school district estimates of poor school-age children in 1995 were constrained by lack of comparison data. An internal evaluation assessed the sampling variability of the 1990 census estimates,
|
14 |
The current SAIPE model uses the population under age 18 as predictor variable w3; the previous candidate model used the population under age 21. The revised formulation of this predictor variable improved the performance of the model for estimates of poor school-age children for counties categorized by percentage of group-quarters residents and population size. |
used to form within-county shares of poor school-age children to apply to estimates from the county model for 1995 (see National Research Council, 2000c:Ch.7). For the census long-form estimates, the average coefficient of variation (the standard error of the estimate divided by the estimate) was 32 percent for all school districts, ranging from 64 percent for the one-sixth of districts with the smallest populations to 14 percent for the one-sixth of districts with the largest populations. For ratio-adjusted estimates, in which the long-form estimates of the proportions poor of school-age children were applied to short-form estimates of total school-age children, the average coefficient of variation was 30 percent for all school districts, a modest reduction from that for the long-form estimates. Even after ratio adjustment, the very high level of sampling variability in the census estimates for many small districts introduces a potentially high degree of error in the updated estimates for these districts. However, it is important to remember that small districts account for a small proportion of the nation's poor school-age children.
An external evaluation compared estimates of poor school-age children in 1989 from several shares models with 1990 census estimates.15 All of the methods evaluated exhibited large differences from the census estimates–much larger than the differences of the SAIPE county model estimates from the 1990 census estimates (see National Research Council, 2000c:Ch.7). However, the shares method that was analogous to the Census Bureau's procedure for the 1995 school district estimates (which applied 1980 census school district shares of poor school-age children within counties to 1989 county model estimates) performed better than a method that assumed no change from 1980 to 1990 in the nationwide relative shares for school districts. The average absolute difference, relative to the average number of poor school-age children per district, was 22 percent for the school district estimates from the SAIPE county shares method, compared with 29 percent for the estimates from the stable shares method. The SAIPE county shares method also performed better than a shares method based on states instead of counties.
By population size, the SAIPE shares method performed reasonably well for districts with 40,000 or more people in 1990, which were 8 percent of districts and included 55 percent of poor children aged 5-17. It performed poorly for districts with 5,000 or fewer people in 1990, which were 47 percent of districts and included 8 percent of poor children aged 5-17. The greater sampling error in the 1990 census estimates for smaller dis-
|
15 |
The evaluation file was restricted to school districts that were not coterminous with a county, that covered all grades, and that were the same between 1980 and 1990: 9,243 of the 15,226 districts in the 1990 census. |
tricts accounted in part for the larger differences between the SAIPE shares method and the 1990 census estimates for small districts relative to large districts.
For New York and Indiana, a similar evaluation was conducted with the addition of two methods that formed within-county shares of poor school-age children for school districts in 1989 from (1) counts of students approved to receive free school lunches in 1990 and (2) counts of students approved to receive free or reduced-price school lunches in 1990. By comparison with 1990 census estimates for these states, the two methods that used contemporaneous school lunch data as the basis for within-county shares performed about the same as a method that used 1980 census within-county shares, with the shares in each case applied to 1990 census county estimates (see National Research Council, 2000c:App. D; Betson, 1999b).
Variance Estimation
The Census Bureau produces variance estimates for the numbers of poor school-age children for states and counties that are estimated from the state and county models. Essentially the same variance estimation procedure is used for the two sets of estimates. Table 3-1 shows illustrative state and county estimates (for Maryland) of poor school-age children, the associated 90 percent confidence intervals that are derived from the variance estimates, and the coefficients of variation. Note that the coefficients of variation for county estimates are similar across counties of all population sizes.
Both the state and county numbers of poor school-age children are estimated from weighted averages of model predictions and direct estimates (see equations (3.2) and (3.5). For the state estimates, the weighted average is an estimate of the proportion poor of school-age children; for the county estimates, it is an estimate of the logarithm of the number of poor school age-children. In both cases the variance of the model prediction component of the weighted average is estimated from the regression model using maximum likelihood estimation. The variances of the state direct estimates are estimated from a generalized variance function that reflects the CPS sample design. The variances of the county direct estimates (for counties in the estimation data set) are estimated from the partition of the sampling variance estimated from the regression analysis (as described above, “County Model”).
The estimated variances of the state and county weighted averages are then computed as a weighted combination of the estimated variances of the model predictions and of the direct estimates, where the weights are the squared values of the weights used in forming the averages. Since
TABLE 3-1 Illustrative SAIPE Estimates of Poor School-Age Children: 1995 State and County Estimates for the State of Maryland
|
Area |
Estimate |
90 Percent Confidence Interval |
Coefficient of Variation (in percent) |
|
|
Maryland |
107,724 |
97,793- |
117,655 |
5.6 |
|
Baltimore City |
40,170 |
31,489- |
48,851 |
13.1 |
|
Prince George's County |
12,735 |
9,978- |
15,492 |
13.1 |
|
Baltimore County |
9,657 |
7,600- |
11,714 |
12.9 |
|
Montgomery County |
9,249 |
7,263- |
11,235 |
13.1 |
|
Anne Arundel County |
5,571 |
4,363- |
6,779 |
13.2 |
|
Harford County |
2,984 |
2,328- |
3,640 |
13.4 |
|
Washington County |
2,916 |
2,288- |
3,544 |
13.1 |
|
Allegany County |
2,788 |
2,165- |
3,411 |
13.6 |
|
Frederick County |
2,303 |
1,794- |
2,812 |
13.4 |
|
Wicomico County |
2,456 |
1,923- |
2,989 |
13.2 |
|
St. Mary's County |
2,091 |
1,616- |
2,566 |
13.8 |
|
Charles County |
2,025 |
1,556- |
2,494 |
14.1 |
|
Howard County |
1,894 |
1,460- |
2,328 |
13.9 |
|
Cecil County |
1,743 |
1,355- |
2,131 |
13.6 |
|
Carroll County |
1,360 |
1,050- |
1,670 |
13.3 |
|
Garrett County |
1,256 |
970- |
1,542 |
13.9 |
|
Dorchester County |
1,096 |
850- |
1,342 |
13.6 |
|
Worcester County |
1,071 |
833- |
1,309 |
13.5 |
|
Calvert County |
1,025 |
795- |
1,255 |
13.6 |
|
Somerset County |
839 |
636- |
1,042 |
14.7 |
|
Caroline County |
810 |
630- |
990 |
13.5 |
|
Queen Anne's County |
697 |
533- |
861 |
14.3 |
|
Talbot County |
639 |
496- |
782 |
13.6 |
|
Kent County |
349 |
267- |
431 |
14.3 |
|
NOTE: The 90 percent confidence interval is derived from the variance estimates developed by the Census Bureau as described in the text. It is the estimate of poor school-age children plus or minus 1.645 times the standard error (the square root of the variance estimate). The coefficient of variation is the standard error as a percent of the estimate. SOURCE: Census Bureau's web site: http://www.census.gov/hhes/www/saipe.html. |
||||
the weights used in forming the averages are themselves sample estimates, the variances of the state and county weighted averages should also reflect the effect of the sampling error in the estimated weights. The methodology of Prasad and Rao (1990) could be applied for this purpose. However, in practice the weights for the state direct estimates are zero for all but one of the estimation years because the model error variance was estimated to be zero, and they are mostly zero for the county direct estimates because most counties had no CPS sample. The Census Bureau
found the effect on the variance estimates resulting from the sampling error of the estimated weights to be negligible for the state averages and judged it to be also negligible for the county averages. Thus, no allowance was made for the sampling error in the estimated weights in estimating the variances of the state and county weighted averages.
The number of poor school-age children in a state is obtained by multiplying the weighted average of the proportion poor of school-age children in the state by the population estimate of the number of school-age children in the state. The state population estimates are subject to error, but this fact is ignored in calculating variance estimates for the state estimates of numbers of poor school-age children. Also, the state estimates of the numbers of poor school-age children are controlled to the national direct estimate of the number of poor school-age children from the CPS. The effect on the variances of the state estimates due to this adjustment was also determined to be negligible, and so was ignored.
The county weighted averages are logarithms of the numbers of poor school-age children. They are then transformed to estimated numbers using equation (3.6). The variances of the estimated numbers are obtained by assuming that the estimated logarithms of the numbers are normally distributed and then using the known relationship between the variance of the logarithms and the variance of the original observations in this situation. After the transformation to the numbers scale, the county estimates are controlled to state estimates of poor school-age children. The effect of this final step on the variance is complicated by the correlations between the county estimates and the state estimates. The linearization (Taylor-Series) method used to account for the effect of these state-level controls on the variances of the county estimates currently incorporates the state variances but ignores the correlation between a county estimate and the corresponding state estimate.
Estimation of the variances of the state and county estimates of poor school-age children depends heavily on the estimates of the model and sampling error variance components in the regression models. As discussed elsewhere in this chapter, these variance components are currently not well estimated for either the state or county model. Improvement in the estimation of these variance components is needed to improve the variance estimates of the state and county estimates.
OTHER SAIPE MODELS
This section describes other models in the SAIPE Program. However, unlike the models described above, the panel did not review these other models.
State-Level Models
In addition to the Title I estimates for poor children aged 5-17 who are related to and living in families (referred to as “poor school-age children” in this report), the Census Bureau develops state-level estimates for four population groups: (1) poor children under age 5; (2) all poor children aged 5-17 (a slightly larger population than poor related children aged 5-17);16 (3) poor people aged 18-64; and (4) poor people aged 65 and over. The estimates for these four population groups are produced by using models that are similar to the state model for poor related children aged 5-17. The Census Bureau publishes state-level estimates for poor children under age 5; poor related children aged 5-17; poor people under age 18 (the sum of the estimates for groups (1) and (2) above); and total poor people (the sum of the estimates for groups (1)-(4) above). Estimates for poor people aged 18-64 are not published because users have not expressed a need for them. There is interest in state estimates for poor people aged 65 and over, but the SAIPE estimates are not published because Census Bureau evaluations showed that they were not markedly better than census estimates.
All of the state-level poverty models are of the same form as that described above for poor related children aged 5-17. In each case, the dependent variable is a poverty rate for the specified age range, and the regression model is of the form displayed in equation (3.1). As can be seen in Table 3-2, predictor variables for the models for poor under age 5, poor aged 5-17, and poor aged 18-64 are broadly similar, differing only in the age ranges included, but the model for poor aged 65 and over has some different predictors. The models are used to produce model predictions (ŷj) for each of the states, and these predictions are then combined with the state direct estimates (yj) by means of a weighted average as given in equation (3.2). The resulting weighted estimates are then converted from poverty rates to numbers of poor and ratio adjusted to national CPS estimates by applying equation (3.3) for the specified age group.
The Census Bureau also produces indirect state estimates of median household income. In this case, the regression model uses the state 's March CPS median household income for the reference year as the dependent variable and has two predictor variables: median household income from the most recent decennial census and an estimate of median house-
|
16 |
The models for poor related children aged 5-17 and all poor children aged 5-17 differ only in the dependent variable. The reason for the model for poor related children aged 5-17 is to satisfy the requirements of the Title I legislation: it is this model that is described above and that the panel has reviewed (see Ch. 1:fn.2 for a definition of related children). |
hold income for the reference year derived from census and tax return data. The estimate of median household income for the reference year is obtained by computing the ratio of a state's median household income in the reference year to that in the census year from tax return data, then applying this ratio to the state's median household income estimate from the census. The regression equation is used to produce a regression prediction of median household income for each state; the final state estimate is produced as a weighted average of its regression prediction and its direct estimate.17
County-Level Models
The SAIPE Program produces indirect county-level estimates for poor people under age 18, poor (related) children aged 5-17, and total poor. The methodology for producing the estimates for poor people under age 18 and total poor is essentially the same as that described earlier for poor children aged 5-17. In each case the dependent variable is the logarithm of a 3-year average of county-level observations, and the predictor variables are obtained from census, food stamp, and IRS data and also placed on the logarithmic scale. The predictor variables for the three models differ only in the age ranges covered, as displayed in Table 3-3. The regression model for each age range, given by equation (3.4), is fitted by maximum likelihood estimation. A regression prediction of the logarithm of the number poor is produced from the regression equation, and a weighted average of this prediction and the direct estimate of the logarithm of the number poor (if available) is computed with weights given by equation (3.5). Finally, the logarithms are transformed back to the numbers of poor using equation (3.6), and the county estimates of numbers of poor are ratio adjusted to sum to the state estimates using equation (3.7).
The SAIPE Program also produces estimates of median household income at the county level. The regression model uses the 3-year average of median household income from the March CPS (not transformed to logarithms) as the dependent variable and six predictor variables: median adjusted gross income from tax returns; the ratio of the number of dependent tax returns to the total number of returns; the logarithm of the proportion of the Bureau of Economic Analysis (BEA) estimate of total personal income derived from government transfers; the previous census estimate of median household income; the ratio of the BEA estimated per
|
17 |
See the Census Bureau's web site for information on the state poverty and median household income models: http://www.census.gov/hhes/www/saipe.html. |
TABLE 3-2 Predictor Variables for SAIPE State Models of Poor People of Various Ages
|
Dependent Variable (from 1 year of March CPS) |
||||
|
Predictor Variable |
Poor Under Age 5 |
Poor Aged 5-17 |
Poor Aged 18-64 |
Poor Aged 65 and Over |
|
x1 |
Proportion of exemptions under age 65 reported by families in poverty on tax returns |
Proportion of child exemptions reported by families in poverty on tax returns |
Same as under age 5 |
Proportion of exemptions aged 65 and over reported by families in poverty on tax returns |
|
x2 |
Proportion of people receiving food stamps |
Same as under age 5 |
Same as under age 5 |
Proportion of people receiving Supplemental Security Income benefits |
|
x3 |
Proportion of people under age 65 who were not included on an income tax return |
Same as under age 5 |
Same as under age 5 |
Proportion of people aged 65 and over who were not included on an income tax return |
|
x4 |
Residual from a regression of the proportion of poor children under age 5 from the most recent decennial census on the other three predictor variables for the census income year |
Residual from a regression of the proportion of poor children aged 5-17 from the most recent decennial census on the other three predictor variables for the census income year |
Residual from a regression of the proportion of poor people aged 18-64 from the most recent decennial census on the other three predictor variables for the census income year |
Proportion poor of people aged 65 and over from the most recent decennial census |
|
NOTE: All variables are at the state level. |
||||
capita total personal income for the reference year to the BEA estimate corresponding to the time period covered by the previous census; and the product of the two previous predictor variables (census-based median household income and the BEA ratio). The final county estimate of median household income is produced as a weighted average of the regression prediction and the direct estimate.18
POPULATION ESTIMATES
The SAIPE Program uses total population estimates and estimates for particular age groups as predictor variables in the state and county models. Such estimates are also needed to accompany the SAIPE poverty
|
18 |
See the Census Bureau's web site for information on the county poverty and median household income models: http://www.census.gov/hhes/www/saipe.html. |
estimates for use in fund allocation programs. For example, Title I requires estimates of the total number of school-age children to convert SAIPE estimates of the numbers of poor school-age children for counties and school districts to poverty rates.
The Census Bureau has an extensive and long-standing program to produce small-area population estimates by using the previous census updated with administrative records. The extent of geographic and demographic detail provided by the estimates program has expanded since it first began producing U.S. population estimates in the early 1900s and state population estimates in the 1940s. The Bureau currently produces estimates of total population by single years of age, sex, race, and Hispanic origin, monthly for the United States and annually for states and counties. Every 2 years, the Bureau also produces estimates of total population for incorporated places and, in selected states, county subdivisions. The Bureau also recently began producing biennial estimates of total population and children aged 5-17 for school districts.
TABLE 3-3 Predictor Variables for SAIPE County Models of Poor People of Various Ages
|
Dependent Variable (from 3-Year Average of March CPS) |
|||
|
Predictor Variables |
Poor Under Age 18 |
Poor Aged 5-17 |
All Poor People |
|
w1 |
Log number of child exemptions reported by families in poverty on tax returns |
Same as poor under age 18 |
Log number of exemptions of all ages reported by families in poverty on tax returns |
|
w2 |
Log number of people receiving food stamps |
Same as poor under age 18 |
Same as poor under age 18 |
|
w3 |
Log estimated population under age 18 |
Same as poor under age 18 |
Log estimated total population |
|
w4 |
Log number of child exemptions on tax returns |
Same as poor under age 18 |
Log number of exemptions of all ages on tax returns |
|
w5 |
Log number of poor under age 18 in previous census |
Log number of poor related children aged 5-17 in previous census |
Log total number of poor in previous census |
Over the years, the Census Bureau has made advances in estimation methods and in gaining access to and incorporating new sources of administrative records data that relate to population change. The currently used methods for estimating total population and population by age are briefly summarized below (for more detail, see National Research Council, 2000c:Ch. 8; see also U.S. Census Bureau, 1995; Long, 1993; Sink, 1996).
Methodology
Total Population
Total population estimates for the United States are developed by the component method of demographic analysis, in which the population from the previous census is updated by adding births and international immigration and subtracting deaths and emigration.19 State estimates of total population are the sum of independently developed county estimates that are constrained to sum to the national estimate.
The county estimates of total population are also developed by the component method: the numbers of births and deaths are based on reported birth and death statistics for each county; reports of the Immigration and Naturalization Service are used to estimate net legal immigration from abroad; reports of the Department of Defense and Office of Personnel Management are used to estimate net movement of federal personnel in and out of the country; and administrative records are used to estimate net migration among counties. Net migration of people under age 65 is estimated for each county from a year-to-year match of IRS federal income tax returns; for people aged 65 and over, net migration is estimated for each county from the change in Medicare enrollment. Estimates are developed separately for household and group quarters populations. Each of the various administrative record sources used for county population estimates requires processing and editing, often based on assumptions, to allocate the data to counties as accurately as possible.
For school districts, total population estimates are currently developed by a shares method. In this approach, 1990 census within-county
|
19 |
The methodology for national-level population estimates includes an “inflation-deflation” procedure in which census estimates for age groups are adjusted for net undercount as estimated from demographic analysis. The adjusted estimates are then updated for births, deaths, immigration, and emigration. As a last step, the estimates are readjusted to match the census-based age distribution. |
shares of the county population for school districts (or component parts) are applied to the updated county total population estimates. The shares method necessarily assumes that each school district in a county added (or lost) population following the census in the same proportion as the county as a whole.
Population by Age
State estimates for single years of age, controlled to state total population estimates, are developed by a cohort-component method in which migration rates for the school-age population are derived from school enrollment data. In turn, these rates are used to estimate migration rates for other age groups under age 65.
Recently, the Census Bureau developed experimental state estimates of the population by age, sex, race, and Hispanic origin by a cohort-component method in which federal income tax return data are used to estimate net migration on the basis of estimates of gross inmigration and gross outmigration.20 This procedure for estimating migration is applied to taxfilers and their dependents when the primary taxfiler's social security number matches to a 20-percent sample of the Social Security Administration 's Numident file. The demographic characteristics of the primary taxfiler are obtained from the Numident file, the spouse and dependents are assigned the same race and Hispanic origin as the primary taxfiler, and age is assigned by a set of rules (e.g., all child dependents are assumed to be under age 20). For this experimental method, the resulting state age-sex-race-Hispanic origin estimates are controlled to the state age-sex population estimates developed as first described.
County estimates for single years of age are developed from a raking-ratio adjustment of the estimates from the previous census. The initial matrix of counts for each county by age, sex, race, and Hispanic origin from the previous census is adjusted to match simultaneously the postcensal estimate of the total county population and the postcensal estimates for the applicable state by age, sex, race, and Hispanic origin. This ratio-raking procedure is applied separately for people in group quarters and people not in group quarters under the assumption that the age distribution of each county within a state changes in the same manner as that state's age distribution.
School district estimates for children aged 5-17 are developed from a shares approach, similar to that described for total population estimates
|
20 |
See the Census Bureau's web site: http://www.census.gov/population/estimates/state.html. |
for school districts. Because school district boundaries change, it is necessary in estimating numbers of school-age children (and total population) for school districts to obtain updated boundaries for the reference year and to retabulate the 1990 census within-county shares according to the new boundaries.
Evaluations
Repeated evaluations of the accuracy of the population estimates, conducted by comparing estimates developed from the previous census to counts from the current census, show several patterns. The proportional differences of the estimates in comparison with the census are larger on average for small areas than for large ones; the proportional differences tend to be larger for areas in which the population is changing rapidly than for areas that are more stable; and the proportional differences for age groups tend to be higher than those for the total population. Furthermore, estimates produced by using components of population change are usually more accurate than those produced by such methods as the raking-ratio adjustment (used for county age estimates) or the shares method (used to produce school district estimates).
Evaluations of 1990 population estimates for counties and school districts show that, for the total population, the average absolute difference between the 1990 population estimates based on updating the 1980 census values and the 1990 census counts was 2.3 percent of the average population for counties and 9.6 percent of the average population for school districts. For all children aged 5-17, the average absolute difference between the 1990 population estimates and the 1990 census counts was 4.9 percent of the average number of school-age children for counties and 12.0 percent of the average number of school-age children for school districts. These differences are much smaller than the average absolute difference for poor children aged 5-17, which was 10.7 percent of the average number of poor school-age children for counties and 22.2 percent of the average number of poor school-age children for school districts (National Research Council, 2000c:Ch.7; see fn. 12 above for the average absolute difference formula).21 It will be important to repeat these evaluations using 2000 census data.
|
21 |
A difference between the comparisons of population estimates and those of poverty estimates is that the census comparison estimates for poor school-age children are from the long-form sample and, hence, are subject to error from sampling variability. This error results in an overestimate of the difference between the SAIPE poverty estimates and the census poverty numbers that would be obtained from a complete enumeration. |
An additional evaluation found that use of population estimates instead of census counts had only a modest effect on the accuracy of the estimated numbers of poor school-age children for counties. The analysis compared 1990 census estimates of poor school-age children in 1989 with 1989 estimates from two variants of the SAIPE county model. Each variant predicted the log poverty rate for school-age children; one variant converted estimated poverty rates to estimated numbers of poor school-age children by using 1980 census-based population estimates for school-age children for 1990; the other variant converted rates to numbers by using 1990 census population counts. The average absolute difference between the model-based estimates of poor school-age children and the 1990 census estimates was only slightly higher for the first variant than for the second variant (see National Research Council, 2000c:App.C).
PRIORITIES FOR SAIPE MODEL DEVELOPMENT
Evaluations of the SAIPE estimates indicate that, although the estimates are generally better than the available alternatives for states and counties and at least as good as the available alternatives for school districts, they are subject to appreciable levels of error, particularly for small counties and school districts. Thus, efforts to improve the accuracy of the estimates for such purposes as fund allocations are well warranted. In addition, since there is currently a 3- to 4-year lag between the production of the estimates and the year to which they relate, it is highly desirable to seek ways to improve the timeliness of the estimates. This section describes some research priorities for improving the accuracy and timeliness of the state, county, and school district estimates, which the panel believes could be implemented in the next estimation cycle.
Research and development for the population estimates is heavily dependent on enhancements to administrative records. Possible improvements to these estimates are discussed in Chapter 5, which deals with such enhancements.
Research Priorities for the State and County Models
The focus of this discussion is on research activities that should be undertaken in an attempt to improve the SAIPE state and county estimates in the near term. The following areas for research and development are discussed below: the incorporation of state random effects in the county model; the incorporation of counties with CPS households but with no sampled poor school-age children in the county modeling; the possible use of time-series and multivariate models; and improved
estimation of the components of variance in both the state and county models.
However, before turning to those activities, the panel offers a broader perspective on the SAIPE Program. The program produces a variety of different estimates (e.g., numbers in poverty in different age bands) at different levels (states, counties, and school districts). Currently, these estimates are produced somewhat independently of one another, and the state and county models are formulated differently in a number of respects. From a theoretical perspective, a preferred approach would be to use a single integrated hierarchical model that would produce all the estimates at both the state and county levels. This approach would not only ensure consistency for the estimates, but it would also likely improve their precision, in part because the estimates for one age band would be able to “borrow strength” from the data available for another age band through the use of a multivariate model.
A further extension of this approach would be to incorporate data for other time periods in the model. For example, sample data are available from the March CPS every year, and data from prior years can provide valuable information in predicting the values for the current year. The same will also be true for the American Community Survey after 2003, if it is implemented as currently planned.
Although such an overarching model may be attractive from a theoretical perspective, its full implementation is almost certainly impracticable, at least in the near term. Nonetheless, the panel considers that it would be useful for the Census Bureau to keep such a model in mind as it develops its longer term plans for the SAIPE program. Even if the single overall model cannot be achieved, model enhancements that move the estimation procedures closer to the ideal may be possible and should be pursued.
Incorporation of State Random Effects in the County Model
State estimates obtained from the county model by aggregating the county estimates within each state are made to conform to the state estimates from the state model by a ratio adjustment, the state raking factor. As noted above, these raking factors vary considerably across states. Several sources could contribute to this variability, including the different measurement scales used in the state and county models (proportions for the former, logarithms of numbers for the latter), the use of 3-year averages of CPS estimates as the dependent variable in the county model versus single-year estimates in the state model, sampling variability, and, possibly, individual state effects that are not captured in the county model. Preliminary work by the panel suggests that a sizable proportion of the
variation in the state raking factors is due to sampling variability. Further investigation should be carried out to better understand the causes of this variation.
In an effort to determine whether the state raking factors could reflect state effects that are missing from the county model, the Census Bureau examined a county regression model that included fixed state effects. The use of this model did not reduce the spread of the raking factors; rather, it increased it. Also, while the addition of fixed state effects reduced some nonrandom residual patterns in the regression output, a fixed state effects model estimated for 1989 did not perform better than other models in comparison with 1990 census estimates.
An alternative approach for incorporating state effects in the county model is to treat them as random rather than fixed effects. This formulation leads to a nested model in which the model error is the sum of a county-within-state random effect and a state random effect. Fuller and Goyeneche (1998) describe the model and report on a preliminary evaluation of it. Their evaluation suggests the presence of a small state random effect. The Census Bureau should conduct a thorough evaluation of this model to examine all of its properties.
Including Counties with No Poor Sampled School-Age Children
As described above, the current county model is expressed in terms of logarithmic transformations of the 3-year average numbers of poor school-age children (the dependent variable) and the values of the predictor variables. Although this form of transformation makes the distributions of the variables more symmetric, possibly makes the functional relationship between the dependent variable and the predictor variables more linear, and provides reasonably homogeneous error variances, it has the disadvantage of not accommodating zero input values. Thus, counties with some CPS-sampled households but no CPS school-age children living in poverty in the 3-year average are excluded from the estimation of the regression coefficients in the county model. A large number of CPS counties are excluded from the regression data set for this reason: 304 of 1,488 counties for the 1993 model and 262 of 1,247 counties for the 1995 model.22 Although the model estimates the numbers of poor school-age children in these excluded counties relatively well (see National Research Council, 2000c:Ch.6), dropping such a large fraction of counties dimin-
|
22 |
In addition, a small number of counties with CPS sampled households (41 for the 1993 model and 27 for the 1995 model) are excluded from the regression data set because the sampled households lacked any school-age children. |
ishes the model's face validity and produces estimates with higher variability than if these counties were included.
One solution to this problem is to shift the starting point of the logarithmic transformation (i.e., using log (z + c), c > 0) to allow inclusion of all counties that have sampled households in the CPS or to use some other form of transformation. A preferable, but less straightforward, solution is to use generalized linear modeling (see McCullagh and Nelder, 1989), an approach that has been developed to provide models for variables with a wide variety of distributional forms. In this particular case, the Poisson distribution is a natural one to consider, since data on counts–for which zero is a natural observation–are typically modeled well using this distribution. Applying the generalized linear modeling framework, all counties included in the CPS can be used to estimate the regression coefficients, and best linear unbiased predictors (BLUPs) can be used to combine the model and direct estimates.
While the application of generalized linear modeling is fairly routine in many applications, the complex sample design of the CPS must be taken into account in the estimation of the regression coefficients and in estimating the variances of the model predictions. Recent developments in generalized linear mixed models (e.g., Robinson, 1991; Zeger and Karim, 1991) provide the basis for developing approaches that can reflect the sampling design.
The Census Bureau has recently conducted research on a hierarchical Bayesian modeling approach that makes it possible to include counties in the model that have some sampled CPS households but none with poor school-age children (see Fisher and Asher, 1999b). This work should continue.
Time-Series and Multivariate Modeling
As noted above, a unified overall model that provides all the SAIPE estimates and that incorporates data from other time periods is theoretically attractive, but not practical, at least in the immediate future. However, there are possibilities for using multivariate and time-series approaches in more limited ways. The panel recommends that the Census Bureau continue and expand its research in these areas.
Fay (1987) provides an early example of a multivariate approach, applied to the estimation of median income in four-person families by state. The dependent variables in his trivariate model were the state median incomes of four-person, three-person, and five-person families. In estimating the median income for four-person families, the model borrows strength from the regressions for the other two dependent variables by allowing for a correlation of the model errors in the regressions. This
kind of approach could, for instance, be applied in SAIPE in an attempt to improve the estimates of poor children aged 5-17 by incorporating estimates for other age ranges in the state and county models.
Bell (1997a) applied a bivariate model for the county estimates of poor school-age children in which the two dependent variables were the 3-year average of CPS data for the reference year (described above) and the 1990 census estimate. The purpose of this model was to make more complete use of census data, through a correlation of the model errors for the two regressions. The panel evaluated several versions of the bivariate model for 1993 estimates, and the results were promising (National Research Council, 2000c:App.B). These models were not pursued for use at that time, primarily because it was not possible to conduct external evaluations of them. However, they have the potential to improve the county estimates, and further research on their application in SAIPE should be conducted.
The above approach could also be generalized to a time-series structure. Census Bureau staff have begun work on assessing the potential benefits of using multiple years of CPS data in the state model but have not yet completed their analyses.
Multivariate and time-series approaches will become increasingly important as data from new sources–such as data from several years of the American Community Survey–become available. The Census Bureau should pursue work on these types of models, which will need extensive development and evaluation to see if they have advantages and to ensure that they do not introduce unanticipated problems. In the longer term, it may be possible to adapt time-series approaches to develop forecasts of income and poverty in order to make the estimates more timely for program use (see “Improving Timeliness” below for approaches to improve timeliness in the near term).
Improved Estimation of Variance Components
Both the state and county models have two variance components, model error and sampling error. Model error is assumed to be independently and identically distributed across areas (states or counties). Sampling error depends on the CPS sample size and poverty rate in the area, as well as the complex stratified multistage CPS sample design. Estimates of these variance components are needed for three purposes: they are used in the maximum likelihood estimation of the regression coefficients in the models; they are used in computing the standard errors of the state and county estimates; and they are used to determine the weights for forming the weighted averages of the model estimates and direct estimates in equations (3.2) and (3.5). The last purpose is most important for
the state estimates since, unlike most counties, all states have CPS samples of sufficient size to produce direct estimates that can usefully contribute to the weighted average.
Different approaches are used to estimate the two variance components in the state and county models. In the state model, sampling error variance is estimated by using a generalized variance function (GVF) that reflects the effects of the CPS sample design, and the model error variance is then obtained through maximum likelihood estimation, essentially subtracting the total sampling error variance from the total variance. In the county model, the model error variance is equated to the model error variance in a corresponding regression model for 1990 census data; that model error variance is estimated in the manner described for the state model error variance, with the census sampling error being estimated with a GVF for the census long-form sample. The total sampling error variance in the county model is then obtained by maximum-likelihood estimation and partitioned among counties in inverse proportion to CPS sample size. Both of these approaches are problematic, and further research is needed for both models.
In the case of the state model, the maximum-likelihood estimation has led to zero estimates of model error variance in 6 of the 7 years for which the state model was estimated, with the consequence that the direct estimates are assigned zero weight in the weighted averages. The untenable result of a zero model error variance likely derives from a misspecification of the GVF for the CPS that results in overestimation of the sampling error variance.
Research is needed to improve the estimation of the sampling error variance for the state model. The use of a Bayesian model to account for the uncertainty in the estimates of the model error variance is another approach that should be pursued. Bell (1999) has explored such a model, which yields positive estimates of model error variance that could be useful for producing the state model estimates. Pending the outcome of these two areas of research, some simple adjustments should be examined and applied as appropriate. For example, minimum weights that are a function of the CPS sample size in each state could be assigned to the direct estimates for each state.
For the estimation of the variance components in the county model, reliance on the assumption that the model error variance for the CPS equation is the same as that for the 1990 census equation is questionable. An alternative approach is that used with the state model, that is, estimating the sampling error variance from a GVF and obtaining the model error variance by maximum likelihood estimation. The Census Bureau has examined an empirically based GVF in which sampling error variance of the county direct estimates is inversely proportional to the square
root of CPS sample size. This approach improves upon the current method (see Fisher and Asher, 1999a), but more research is needed. An alternative approach that should also be explored is to estimate a withincounty design effect based on counties with reasonable numbers of CPS sample segments. This design effect could then be used to develop a GVF from which sampling errors could be estimated for all counties with some CPS sample.
A complication that arises in modeling GVFs for the direct county estimates is that the sampling errors of these estimates are affected not only by the clustered CPS sample within counties, but also by the poverty rates in those counties, rates that can be estimated only imprecisely. Future research should consider alternative methods of estimating county poverty rates for use in the GVFs, including smoothing the estimates in some manner.
Reducing the Variability in the 1990 Census School District Estimates
Essentially, the school district model distributes the updated county estimate of the number of poor school-age children between the school districts (or parts of school districts) in the county in proportion to the estimated shares that the districts (or parts) had of the county's poor school-age children at the last census (see “School District Procedure” above). The census numbers of poor school-age children in the school districts are estimated from the census long form. Since these estimated numbers are based on small long-form sample sizes for many school districts, they are subject to substantial sampling error (see National Research Council, 2000c:Ch.7).
To improve the precision of census long-form estimates, the Census Bureau builds in adjustments as part of regular census data processing to make long-form totals conform to short-form totals for key short-form items for weighting areas (subcounty areas or sometimes entire counties that have a specified minimum number of sample persons). For the purpose of estimating school district shares, the Census Bureau extended this approach by forcing the long-form estimate of the number of school-age children in each school district to conform to the short-form number of such children. In essence, the procedure estimated the proportion poor of school-age children in a district from the long form and then applied that proportion to the short-form number of school-age children in the district.
This adjustment improved the precision of the school district census estimates of poor school-age children by a small, but important, amount. Further improvements might be obtained by extending the adjustment to forcing long- and short-form totals to agree on characteristics that are related to poverty, such as race, ethnicity, home tenure (owner, renter),
family type, and type of residential area (central city, urban, rural), at the school district level. Although only a modest improvement in the school district census estimates may be achieved with these further adjustments, any improvement would be helpful.
Another approach for improving the census school district estimates is to use a smoothing procedure to reduce the sampling errors in the long-form estimates of the proportions poor of school-age children. These smoothed proportions would then be multiplied by the short-form numbers of school-age children to produce the census estimates of numbers of poor school-age children. Thus, for example, a school district's proportion poor could be estimated by a weighted average of its estimated proportion poor from the long form and the overall proportion poor for the county in which it is located, with the weight given to the long-form estimate depending on the school district 's long-form sample size. This procedure, which reduces sampling error at the cost of potentially introducing some bias, is likely to be effective for school districts (or parts of districts) that have small long-form samples.
Improving Timeliness
The Census Bureau currently produces income and poverty estimates from the SAIPE Program with a lag of about 3 years. So the school district estimates of school-age children in 1996 who were in poverty in 1995 were released in early 1999 for use in Title I allocations for the 1999-2000 and 2000-2001 school years. Although these estimates are considerably more current than estimates based on the 1990 census, they are still out of date by 3 or 4 years. Since there can be substantial changes in income and poverty in short time periods (see National Research Council, 2000c:Ch.3), it is important to explore methods for reducing this time lag.
One reason for the time lag for SAIPE poverty estimates is the length of time it takes to obtain population estimates for use in the state and county models. The population estimates are not available until more than 2 years after the income reference year.23 A different approach would be to use the population estimates for July of the income reference year rather than the population estimates for July of the following year. This approach would have the advantage of reducing the time lag of the poverty estimates. Alternatively, population estimates could perhaps be developed for January of the year following the income reference year, which would be more timely than the estimates for July of the following
|
23 |
preliminary estimates are available a year earlier (e.g., spring 1999 for July 1998 estimates), but evaluation has shown that they may differ from the second round of estimates by as much as 3 percent for state estimates and more than 5 percent for county estimates. |
year and yet would reflect the CPS concept of measuring poverty for the previous calendar year.
Another source of delay for the SAIPE poverty estimates is the lag in obtaining the food stamp data used in the county model. Monthly food stamp counts for states are available with little delay from the U.S. Department of Agriculture, so the state model uses a 12-month average of food stamp data, centered on January 1 following the income reference year, as a predictor variable. The delay results from the construction of the food stamp predictor for the county model. That predictor makes use of county-level food stamp counts for July of the income reference year (for some counties, the data are the average of the monthly counts for the year), which take much longer to obtain than the state totals. In some instances, the counts must be collected from individual states, and the complete data set is not usually available until 2 years after its reference date. The food stamp predictor in the county model is then formed by raking the county counts to the slightly more current state numbers used in the state model.
In the interest of timeliness, a study should be carried out to investigate the effects of basing the food stamp predictor in the county model on counts from an earlier period, such as data for July of the year prior to the income reference year. Even though the county-level data for July are raked to the state food stamp numbers for the reference year, the use of earlier data for counties may affect the performance of the food stamp predictor variable in the county model. The recommended study should evaluate the extent of any such effects.
Yet another issue that should be examined is the year of the state estimates to which the county estimates are raked. The current practice is to rake the county estimates to state estimates for the middle year of the 3 years of CPS data that are used for the dependent variable in the county model. An alternative approach would be to rake the county estimates to state estimates for the most recent of the 3 years. In effect, such raking would update the county, and hence the school district, estimates by 1 year under a modeling assumption about the uniformity of the distribution of the temporal changes in poverty across counties within states. This assumption only has to be approximately correct for this procedure to provide a benefit. Another possible approach–that could be combined with raking the state estimates to the latest year–would be to construct the dependent variable in the county model as a weighted average of the 3-year CPS estimates that gives more weight to the most recent year.
CONCLUSION
The panel commends the Census Bureau for investigating several of the research topics the panel identified for the current SAIPE state and county models. Work on technical aspects of the models and on the timeliness of the estimates is important in the near term. Also important is work on the role that new data sources could play in improving the state and county income and poverty estimates and the estimates of poor school-age children for school districts. We discuss data sources in the next two chapters.






































