5
Case Studies
This chapter illustrates the Corps of Engineers's application of risk analysis by reviewing two Corps flood damage reduction projects: Beargrass Creek in Louisville, Kentucky, and the Red River of the North in East Grand Forks, Minnesota, and Grand Forks, North Dakota. The Beargrass Creek case study describes the entire procedure of risk-based engineering and economic analysis applied to a typical Corps flood damage reduction project. The Red River of the North case study focuses on the reliability of the levee system in Grand Forks, which suffered a devastating failure in April 1997 that resulted in more than $1 billion in flood damages and related emergency services.
The Corps of Engineers has used risk analysis methods in several flood damage reduction studies across the nation, any of which could have been chosen for detailed investigation. Given the limits of the committee's time and resources, the committee chose to focus upon the Beargrass Creek and Red River case studies for the following reasons: committee member proximity to Corps offices, a high level of interest in these two studies, and the availability of documentation from the Corps that adequately described their risk analysis applications.
Differences in approaches taken at Beargrass Creek and along the Red River of the North to reducing flood damages are reflected in these studies. At Beargrass Creek, the primary flood damage reduction measures were detention basins; at the Red River of the North, the primary measures were levees. The Corps uses rainfall-runoff models in nearly all of its flood damage reduction studies to simulate streamflows needed for flood-frequency analysis, and a rainfall-runoff model was employed in the Beargrass Creek study. In the Red River study, however, the goal
was to design a system that would, with a reasonable degree of reliability, contain a flood of the magnitude of 1997's devastating flood. The Corps focused on traditional flood–frequency analysis and manipulated the frequency curve at a gage location to derive frequency curves at other locations (vs. using a rainfall-runoff model to derive those curves).
BEARGRASS CREEK
In 1997 the Corps held a workshop (USACE, 1997b) at which experience accumulated since 1991 in risk analysis for flood damage reduction studies was reviewed. O'Leary (1997) described how the new procedures had been applied in the Corps's Louisville, Kentucky, district office. In particular, O'Leary described an application to a flood damage reduction project for Beargrass Creek, economic analyses for which were done both under the old procedures without risk and uncertainty analysis and under the new procedures that include those factors. Conclusions of the Beargrass Creek study are summarized in two volumes of project reports (USACE, 1997c,d). These documents, plus a site visit to the Louisville district by a member of this committee, form the basis of this discussion of the Beargrass Creek study. The Beargrass Creek data are distributed with the Corps's Hydrologic Engineering Center Flood Damage Assessment (HEC-FDA) computer program for risk analysis as an example data set. The Beargrass Creek study is also used for illustration in the HEC-FDA program manual and in the Corps 's Risk Training course manual. Although there are variations from study to study in the application of risk analysis, Beargrass Creek is a reasonably representative case with which to examine the methodology.
As shown Figure 5.1, Beargrass Creek flows through the city of Louisville, Kentucky, and into the Ohio River on its south bank. The Beargrass Creek basin has a drainage area of 61 square miles, which encompasses about half of Louisville. The basin currently (year 2000) has a population of about 200,000. This flood damage reduction study's focal point is the lower portion of the basin shown in Figure 5.1 —the South Fork of Beargrass Creek and Buechel Branch, a tributary of the South Fork.
Locally intense rainstorms (rather than regional storms) cause flooding in Beargrass Creek. A 2-year return period storm causes the creek to overflow its banks and produces some flood damage. Under existing conditions, the Corps estimates that a 10-year flood will impact

FIGURE 5.1 The Beargrass Creek basin in Louisville, Kentucky. SOURCE: USACE (1997a) (Figure II-1).
about 300 buildings and cause about $7 million in flood damages, while a 100-year flood will impact about 750 buildings and cause about $45 million in flood damages (USACE, 1997c). The expected annual flood damage under existing conditions is approximately $3 million per year.
Flood Damage Reduction Measures
Beargrass Creek has several flood damage reduction structures, the most notable of which is a very large levee at its outlet on the Ohio River (Figure 5.2a). This levee was built following a disastrous flood on the Ohio in January 1937, and the levee crest is an elevation of 3 feet above the 1937 flood level on the Ohio River. During the 1937 flood it was reported that “at the Public Library, the flood waters reached a height such that a Statue of Lincoln appeared to be walking on water!” (USACE, 1997b, p. III-2). Near the mouth of Beargrass Creek, a set of
gates can be closed to prevent water from the Ohio River from flowing back up into Louisville. In the event of such a flood, a massive pump station with a capacity of 7,800 cubic feet per second (cfs) is activated to discharge the flow of Beargrass Creek over the levee and into the Ohio River.
Between 1906 and 1943, a traditional channel improvement project was constructed on the lower reaches of the South Fork of Beargrass Creek. It consists of a concrete lined rectangular channel with vertical sides, with a small low-flow channel down the center (Figure 5.2b). The channel's flood conveyance capacity is perhaps twice that of the natural channel it replaced, but the concrete channel is a distinctive type of landscape feature that environmental concerns will no longer permit. Other structures have been added since then, including a dry bed reservoir completed in 1980, which functions as an in-stream detention basin during floods.
The proposed flood damage reduction measures for Beargrass Creek form an interesting contrast to traditional approaches. The emphasis of the proposed measures is on altering the natural channel as little as possible and detaining the floodwaters with detention basins. These basins are either located on the creek itself or more often in flood pool areas adjacent to the creek into which excessive waters can drain, be held for a few hours until the main flood has passed, and then gradually return to the creek. Figure 5.2c shows a grassed detention pond area with a concrete weir (in the center of the picture) adjacent to the creek. Figure 5.2d shows Beargrass Creek at this location (a discharge pipe from the pond is visible on the right side of the photograph). Water flows from the creek into the pond over the weir and discharges back into the creek through the pipe. The National Economic Development flood damage reduction alternative on Beargrass Creek called for a total of eight detention basins, one flood wall or levee, and one section of modified channel. Other alternatives such as flood-proofing, flood warning systems, and enlargement of bridge openings were considered but were not included in the final plan.
The evolution of flood damage reduction on Beargrass Creek represents an interesting mixture of the old and the new—massive levees and control structures on the Ohio River, traditional approaches (the concrete-lined channel) in the lower part of the basin, more modern instream and off-channel detention basins in the upstream areas, and local channel modifications and floodwalls. Maintenance and improvement of stormwater drainage facilities in Beargrass Creek are the responsibility of the Jefferson County Metropolitan Sewer District, which is the principal local partner working with the Corps to plan and develop flood damage reduction measures.
In some locations, development has been prohibited in the floodway; but in other places, buildings are located adjacent to the creek. The Corps's feasibility report includes the following comments: “Urbanization continues to alter the character of the watershed as open land is converted to residential, commercial and industrial uses. The quest for open area residential settings in the late 1960s and early 1970s caused a tremendous increase in urbanization of the entire basin. Several developers have utilized the aesthetic beauty of the streambanks as sites for residential as well as commercial developments. This has resulted in increased runoff throughout the drainage area as development has occasionally encroached on the floodplain and, less frequently, the floodway” (USACE, 1997b, p. II-2).
Damage Reaches
To conduct the flood damage assessment, the two main creeks— South Fork of Beargrass Creek and Buechel Branch—are divided into damage reaches. Flood damage and risk assessment results are summarized for each damage reach, and the expected annual damage for the project as a whole is found by summing the expected annual damages for each reach. As shown in Figure 5.3, the South Fork was divided into 15 damage reaches and the Buechel Branch into 5 reaches (a sixth damage reach on Buechel Branch is not shown in this figure). Approximately 12 miles of Beargrass Creek, and 2.2 miles of Buechel Branch are covered by the these damage reaches. The average length of a damage reach is thus 0.8 miles for the South Fork of the Beargrass Creek, and the average length for Buechel Branch is 0.4 miles. The shorter reaches on Buechel Branch are adjacent to similarly short, upstream reaches in Beargrass Creek where most flood damage occurs. Longer damage reaches are used downstream on Beargrass Creek where less damage occurs.
The highest expected annual flood damage is on Reach SF-9 on the upper portion of the South Fork of Beargrass Creek. Results from this damage reach are used for illustrative purposes at various points in this chapter.
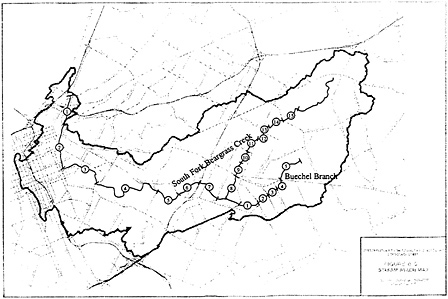
FIGURE 5.3 Damage reaches on the South Fork of Beargrass Creek and Buechel Branch. SOURCE: USACE (1997a) (Figure III-3).
Flood Hydrology
Most of the flood damage reduction measures being considered are detention basins, which diminish flood discharge by temporarily storing floodwater. It follows that the study's flood hydrology component has to be conducted using a time-varying rainfall–runoff model because this allows for the routing of storage water through detention basins. In this case, the HEC-1 rainfall–runoff model from the Corps's Hydrologic Engineering Center (HEC) was used to quantify the flood discharges. The Hydrologic Engineering Center has subsequently released a successor rainfall-runoff model to HEC-1, called HEC-HMS (Hydrologic Modeling System), which can also be used for this type of study (HEC, 1998b).
In each damage reach, and for each alternative plan considered, the risk analysis procedure for flood damage assessment requires a flood – frequency curve defining the annual maximum flood discharge at that location which is equaled or exceeded in any given year with a given probability. In this study all these flood–frequency curves were produced through rainfall–runoff modeling. In other words, a storm of a given
return period was used as input to the HEC-1 model, the water was routed through the basin, and the magnitude of the discharge at the top end of each damage reach was determined (Corps hydrologists have assumed, based on experience in the basin, that storms of given return periods produce floods of the equivalent return period). By repeating this exercise for each of the annual storm frequencies to be considered, a flood–frequency curve was produced for each damage reach. There are eight standard annual exceedance probabilities normally used to define this frequency curve: p = 0.5, 0.2, 0.1, 0.04, 0.02, 0.01, 0.004, and 0.002, corresponding to return periods of 2, 5, 10, 25, 50, 100, 250, and 500 years, respectively. In this study, because even small floods cause damage, a 1-year return period event was included in the analysis and assigned an exceedance probability of 0.999.
Considering that there are 21 damage reaches in the study area and 8 annual frequencies to be considered, each alternative plan considered requires the development of 21 flood–frequency curves involving 168 discharge estimates. During project planning, as dozens of alternative components and plans were considered, the sheer magnitude of the tasks of hydrologic simulation and data assembly becomes apparent.
The hydrologic analysis is further complicated by the fact that the design of detention basins is not simply a cut-and-dried matter. A basin designed to capture a 100-year flood requires a high–capacity outlet structure. Such a basin will have little impact on smaller floods because the outlet structure is so large that smaller events pass through almost unimpeded. If smaller floods are to be captured, a more confined outlet structure is needed, which in turn increases the required storage volume for larger floods. This situation was resolved in the Beargrass Creek study by settling on a 10-year flood as the nominal design event for sizing flood ponds and outlet works. The structures designed in this manner were then subjected to the whole range of floods required for the economic analysis.
Rainfall–Runoff Model
The HEC-1 model was validated by using historical rainfall and runoff data for four floods (March 1964, April 1970, July 1973, February 1990). Modeling results were within 5 percent to 10 percent of observed flows at two U.S. Geological Survey (USGS) streamflow gaging stations: South Fork of Beargrass Creek at Trevallian Way and Middle Fork
of Beargrass Creek at Old Cannons Lane, which have flow records beginning in 1940 and 1944, respectively, and continuing to the present. A total of 42 subbasins were used in the HEC-1 model, and runoff was computed using the U.S. Soil Conservation Service (renamed the Natural Resources Conservation Service in 1994) curve number loss rates and unit hydrographs. The Soil Conservation Service curve numbers were adjusted to allow the matching of observed and modeled flows for the historical events. A 6-hour design storm was used, which is about twice the time of concentration of the basin. The design storm duration chosen is longer than the time of concentration of the basin so that the flood hydrograph has time to rise and reach its peak outflow at the basin outlet while the storm is still continuing. If the design storm is shorter than the time of concentration, rainfall could have ceased in part of the basin before the outflow peaks at the basin outlet. The storm rainfall hydrograph was based on National Weather Service 1961 Technical Paper 40 (NWS, 1961) and on a Soil Conservation Service storm hydrograph, and a 5-minute time interval of computation was used for determining the design discharges.
There is a long flood record of 56 years of data (1940–1996) available in the study area (USGS gage on the South Fork of Beargrass Creek at Trevallian Way). A comparison was made of observed flood frequencies at this site with those simulated by HEC-1, with some adjustment of the older flood data to allow for later development. Traditional flood frequency analysis of observed flow data had little impact in the study. This may have been the case because there was only one gage available within the study area, or because the basin has changed so much over time that the flood record there does not represent homogeneous conditions. Furthermore, the alternatives mostly involve flood storage, which requires computation of the entire flood hydrograph, not just the peak discharge.
Uncertainty in Flood Discharge
Uncertainty in flood hydrology is represented by a range in the estimated flood–frequency curve at each damage reach. In the HEC-FDA program, there are two options for specifying this uncertainty: an analytical method based on the log-Pearson distribution and a more approximate graphical method. The log-Pearson distribution is a mathematical function used for flood–frequency analysis, the parameters of which are determined from the mean, standard deviation, and coefficient
of skewness of the logarithms of the annual maximum discharge data. The graphical method is a flood frequency analysis performed directly on the annual maximum discharge data without fitting them with a mathematical function. In this case the graphical method was used with an equivalent record length of 56 years of data, the length of the flood record of the USGS gage station at Trevallian Way at the time of the study. Figure 5.4 shows the flood–frequency curve for damage reach SF-9 on the South Fork of Beargrass Creek, with corresponding confidence limits based on ± 2 standard deviations about the mean curve.
The confidence limits in this graph are symmetric about the mean when the logarithm to base 10 of the discharge is taken, rather than the discharge itself. This can be expressed mathematically as:
where Q is the discharge value at the confidence limit, logQ is the expected flood discharge, σlogQ is the standard deviation (shown in the rightmost column of Table 5.1), and K is the number of standard deviations above or below the mean that the confidence limit lies. Because these confidence limits are defined in the log space, it follows that they are not symmetric in the real flood discharge space. As Table 5.1 shows, the expected discharge for the 100-year flood (p = 0.01) is 4,310 cfs, the upper confidence limit is 6,176 cfs, and the lower limit is 3,008 cfs. The difference between the mean and the upper confidence limit is thus about 40 percent larger than the difference between the mean and the lower confidence limit. The confidence limits for graphical frequency analysis are computed using a method based on order statistics, as described in USACE (1997d). In this method, a given flood discharge estimate is considered a sample from a binomial distribution, whose parameters p and n are the nonexceedance probability of the flood and the equivalent record length of flood observations in the area, respectively. In this case, n = 56 years, since this is the record length of the Trevallian Way gage.
River Hydraulics
Water surface profiles for all events were determined using the HEC-2 river hydraulics program from the Corps's Hydrologic Engineering Center in Davis, California. Field-surveyed cross sections were obtained

FIGURE 5.4 The flood–frequency curve and its uncertainty at damage reach SF-9 on the South Fork of Beargrass Creek.
at all bridges and at some stream sections near bridges. Maps with a scale of 1 inch = 100 feet with contour intervals of 2 feet were used to define cross sections elsewhere on the stream reaches and were used for measuring the distance between cross sections on the channel and in the left and right overbank areas. Manning's n values for roughness were based on field inspection, on reproduction of known high-water marks from the March 1964 flood on Beargrass Creek, and on reproduction of the rating curve of the USGS gage at Trevallian Way. Manning's equation relates the channel velocity to the channel's shape, slope, and roughness. Manning's n is a numerical value describing the channel roughness. Manning's n values in the concrete channel ranged from 0.015 at the channel invert to 0.027 near the top of the bank. In the natural channels, Manning 's n values ranged from 0.035 to 0.050. In the overbank areas, these values ranged from 0.045 to 0.065. Where buildings blocked the flow, the cross sections were cut off at the effective
TABLE 5.1 Uncertainties in Estimated Discharge Values at Reach SF-9
|
Exceedance Probability |
Mean Discharge (cfs) |
Mean−2 Std Dev. (cfs) |
Mean+ 2 Std Dev. (cfs) |
σlogQ |
|
0.01 |
4,310 |
3,008 |
6,176 |
0.0781 |
|
0.1 |
2,620 |
2,051 |
3,346 |
0.0531 |
|
0.5 |
1,220 |
1,098 |
1,356 |
0.0229 |
flow limits. A total of 201 cross sections were used for the South Fork of Beargrass Creek, and 61 cross sections were used for Buechel Branch. The average distance between cross sections was 330 feet on the South Fork of Beargrass Creek and 245 feet on Buechel Branch. Cross sections are spaced more closely than this near bridges and more sparsely in reaches where the cross section is relatively constant.
Figure 5.5 shows the water surface profiles along Beargrass Creek for the eight flood frequencies considered, under existing conditions without any planned control measures. The horizontal axis of this graph is the distance in miles upstream from Beargrass Creek's outlet on the Ohio River. The vertical axis is the elevation of the water surface in feet above mean sea level. The bottom profile in this graph is the channel invert or channel bottom elevation. The top profile is for p = 0.002—the 500-year flood. This particular profile shows a sharp drop near the bottom end of the channel, caused by a bridge at that location that constricts the flow. The flat water surface elevation upstream of the bridge is a backwater effect produced by the inadequate capacity of the bridge opening to convey the flow that comes to it.
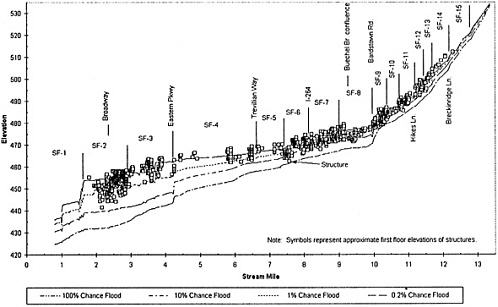
For each flood profile computed, the number of structures flooded and the degree to which they are flooded must be assessed. Figure 5.6 shows the locations of the first-floor elevations of structures affected by flooding on the South Fork of Beargrass Creek in relation to several flood water surface profiles under existing conditions. Damage reach SF-9 is located between river miles (RM) 9.960 and 10.363, near the point where there is a sharp drop in the channel bed and water surface elevation on Beargrass Creek. It can be seen that the density of development varies along the channel. Flood damage reduction measures are most effective when they are located close to damage reaches with significant numbers of structures, and they are least effective when they are distant from such reaches.
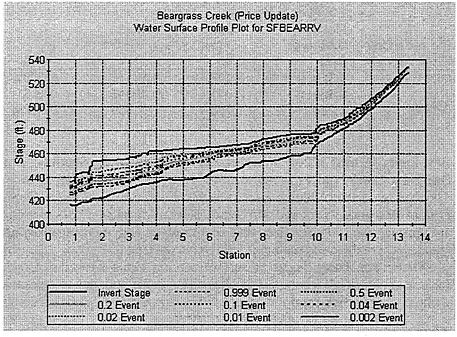
FIGURE 5.5 Water surface profiles for design floods in Beargrass Creek under existing conditions.
Each damage reach has an index location, which is an equivalent point at which all of the damages along the reach are assumed to occur. On reach SF-9, this index location is at river mile 10.124. To assess damages to structures within each reach, an equivalent elevation is found for each structure at the index location such that its depth of flooding at that location is the same as it would have been at the correct location on the flood profile, as shown in Figure 5.7.
The technique of assigning an elevation at the index location can be far more complex than Figure 5.7 implies, because allowance is made in the HEC-FDA program for the various flood profiles to be nonparallel and also to change in gradient upstream of the index location compared to downstream. In the Beargrass Creek study, a single flood profile for the p = 0.01 event was chosen, and all other profiles were assumed parallel to this one. One damage reach on Beargrass Creek was subdivided into three subreaches to make this assumption more nearly correct. A spatial distribution of buildings over the damage reach is thus converted
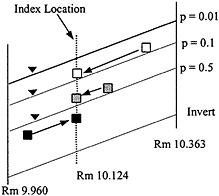
FIGURE 5.7 Assignment of structures to an index location.
into a probability distribution of buildings at the index location, where the uncertainty in flood stage is quantified.
Uncertainty in Flood Stage
The uncertainty in the water surface elevation was quantified by assuming that the standard deviation of the elevation at the index location for the 100-year discharge is 0.5 feet. The 100-year discharge at reach SF-9 is 4,310 cfs, which is the next to last set of points in Fugure 5.8. To the right of these points, between the 100-year and 500-year flood discharges, the uncertainties are assumed to be constant. For discharges lower than the 100-year return period, the uncertainties in stage height are reduced linearly in proportion to the depth of water in the channel. The various lines shown in Figure 5.8 are drawn as the expected water surface elevation ± 1 or 2 standard deviations determined in this manner.
Economic Analysis
The Corps's analysis of a flood damage reduction project's economic costs and benefits is guided by the Principles and Guidelines (Box 1.1 provides details on the P&G's application to flood damage reduction

FIGURE 5.8 Uncertainty in the flood stage for existing conditions at reach SF-9 of the South Fork of Beargrass Creek.
studies). According to the P&G, the economic analysis of damages avoided to floodplain structures because of a flood damage reduction project is restricted to existing structures (i.e., federal policy does not allow damages avoided to prospective future structures to be counted as benefits). The P&G do, however, call for the benefits of increased net income generated by floodplain activities after a project has been constructed (so-called “intensification benefits”) to be included in the economic analysis.
Economic analysis of flood damages considers various sorts of flood damage, principal among them being the damage to flooded structures. Information about the structures is quantified using a “structure inventory,” an exhaustive tabulation of every building and other kind of structure subjected to flooding in the study region. A separate computer program called Structure Inventory for Damage Analysis (SID) was used
to evaluate the number of structures flooded as a function of water surface elevation. Structures are divided into four categories: single-family residential, multifamily residential, commercial, and public. A structure is considered to be flooded if the computed flood elevation is above its first-floor elevation. The amount of damage D is a function of the depth of flooding h and the type of structure, and is expressed by a factor, r(h), which is equal to a percentage of the value of the structure ( V) and of its contents (C). This analysis can be expressed as
D=r1(h)V + r2(h)C. (5.2)
For residential structures, these damage factors were quantified in 1995 by the Federal Emergency Management Agency (FEMA) using data from flood damage claims. For example, for a one-story house without a basement flooded to a depth of 3 feet, the FEMA estimate is that the damage factors are r1= 27% of the value of the structure and r2 = 35% of the value of the contents. For the same house flooded to a depth of 6 feet, the corresponding damage factors are r1 = 40% for the structure, and r2 = 45% for the contents, respectively. The Marshall and Swift Residential Cost Handbook (Marshall and Swift, 1999) was used to estimate the value of single- and multi-family structures (it bears mentioning that the use of standard references such as the Marshall and Swift handbook may potentially represent another source of “knowledge uncertainty ”). The values of their contents were assumed to be 40 percent to 44 percent of the value of the structure. For commercial and public buildings, the values of the structures and their contents were established through personal interviews by Corps personnel. About 85 percent of the structures subject to flood damage are residential buildings.
Types of flood damages beyond those to structures were also considered. For instance, there are several automobile sales lots in the floodplain, and prospective damages to cars parked there during a flood were estimated. Nonphysical damage costs include the costs of emergency services and traffic diversion during flooding. Damage to roads and utilities were also considered.
Uncertainty in Flood Damage
The economic analysis has three sources of uncertainty:
-
the elevation of the first floor of the building,
-
the degree of damage given the depth of flooding within the building, and
-
the economic value of the structure and its contents.
For most structures in Beargrass Creek, the first-floor elevation was estimated from the ground elevation on maps with a scale of 1 inch = 100 feet and with contour intervals of 2 feet. For a sample of 195 structures (16% of the total number), the first-floor elevations were surveyed. It was found that the average difference between estimated and surveyed first-floor elevations of these structures was 0.62 feet.
Corps Engineering Manual (EM) 1110-2-1619 (USACE, 1996b) was used to estimate values for the uncertainties in economic analysis. A standard deviation of 0.2 feet was used to define the uncertainty in first-floor elevations. The uncertainty in the degree of damage given a depth of inundation was estimated by varying the percent damage factor described previously. For residential structures the value of the structure was assigned a standard deviation of 10 percent of the building value, and the ratio of the value of the contents to the structure was allowed to vary with a standard deviation of 20 percent to 25 percent.
For commercial property a separate damage estimate, based on interviews with the owners, was made for each significant property and was expressed as a triangular distribution with a minimum, expected, and maximum damage value for the property. Because every individual structure potentially affected by flooding is inventoried in the damage estimate data, the amount of work required to collect all these damage data was extensive.
The end result of these estimates at each damage reach and damage category is a damage–stage curve (such as Figure 5.9) that accumulates the damage to all multifamily structures in this damage reach for various water surface elevations at the index location, denoted by stage on the horizontal axis. This curve is prepared by first dividing the range of the stage (476–486 feet) into increments —increments of 0.5 feet in this case. For each structure, a cycle of 100 Monte Carlo simulations is carried out in which the first-floor elevation and the values of the structure and contents are randomly varied. From these simulations estimates are formed for each 0.5-foot stage height increment of what the expected damage and standard deviation of the damage to that structure would be if the flood stage were to rise to that elevation. For each stage increment, these means and standard deviations are accumulated over all structures in the
reach to form the estimate of the mean and standard deviation of the reach damage (Figure 5.9).
A similar function is prepared for each of the damage categories. At any flood stage, the sum of the damages across all categories is the total flood damage for that reach.
Project Planning
The discussion of the Beargrass Creek study reviewed the technical means by which a particular flood damage reduction plan is evaluated. A plan consists of a set of flood damage reduction measures, such as detention ponds, levees or floodwalls, and channel modifications, implemented at particular locations on the creek. The base plan against which all others are considered is the “without plan,” which means a plan that considers existing conditions in the floodplain and the development expected to occur even in the absence of a flood damage reduction plan. Such development must meet floodplain management policies and have structures elevated out of the 100-year floodplain. A base year of 1996 was chosen for the Beargrass Creek study.
In carrying out project planning, the spatial location of the principal damage reaches is important because flood damage reduction measures located just upstream of or within such reaches have greater economic impact than do flood damage reduction measures located in areas of low flood damage. Project planning also involves a great deal of interaction with local and state agencies, in this case principally the Jefferson County Metropolitan Sewer District.
The Beargrass Creek project planning team consisted primarily of three individuals in the Corps's Louisville district office: a project planner from the planning division, a hydraulic engineer from the hydrology and hydraulics design section, and an economic analyst from the economics branch. The HEC-FDA computer program with risk analysis was carried out by the economic analyst using flood–frequency curves and water surface profiles supplied by the hydrology and hydraulics section and using project alternatives defined by the project planner. The hydrology and hydraulics section was also responsible for the preliminary sizing of potential project structures being considered as plan components. The bulk of the work of implementing the risk analysis aspects of flood damage assessment thus fell within the domain of the Corps economic analyst.
The HEC-FDA program is applied during the feasibility phase of
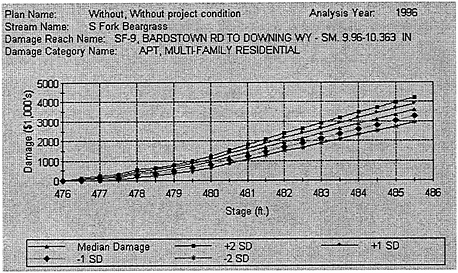
FIGURE 5.9 The damage–stage curve with uncertainty for multifamily residential property in Reach SF-9 of the South Fork of Beargrass Creek.
flood damage reduction planning. This had been preceded by a reconnaissance phase, a preliminary assessment of whether reasonable flood damage reduction planning can be done in the area. As explained in Chapter 2, the reconnaissance phase is fully funded by the federal government, but the feasibility phase must have half the costs met by a local sponsor. Assuming the feasibility phase yields an acceptable plan and additional funds are authorized, the project proceeds to a detailed design and construction phase, which also requires local cost sharing. The Beargrass Creek project is now (as of May 2000) in the detailed design phase.
Evaluation of Project Alternatives
Expected annual flood damages in Beargrass Creek under existing conditions are estimated to be $3 million. Project benefits are calculated as the difference between this figure and the lower expected annual damages that result with project components in place. Project costs are annualized values of construction costs discounted over a 50-year period using an interest rate of 7.625 percent. Project net benefits are the differ-
ence between project benefits and costs. For components to be included in the project, they must have positive net benefits.
The first step in evaluating project alternatives is to consider each component flood damage reduction measure by itself to see if it yields positive net benefits. A total of 22 components were examined individually, 11 on the South Fork of Beargrass Creek and 11 on Buechel Branch. All 11 of the South Fork components were economically justified on a stand-alone basis. Only 3 of the 11 components on Buechel Branch were justified individually: the other 8 components were thus deleted from further consideration.
The next step is to formulate the National Economic Development (NED) plan. In theory, this is supposed to proceed by selecting first the component with the largest net benefits, adding the component with the next largest net benefits, evaluating them together, and continuing to add more components until the combined set of components has the largest overall net benefits. It turned out that this idealized approach could not be used at the South Fork of Beargrass Creek because of economic and hydraulic interactions among the components. The study team commented: “Therefore, the formulation process was different and more complicated than originally anticipated. The study team could not follow the incremental analysis procedure to build up the NED plan because the process became a loop of H&H computer runs. Our component with the greatest net benefits is located near the midpoint of the stream; thus, each time we would add a component upstream it would affect all components downstream and vice versa. We could never truly optimize or identify the plan which produces the greatest net benefits” (USACE, 1997c, p. IV-62).
The problems were further complicated by the fact that there are three separate sections of the study region: the South Fork of Beargrass Creek and Buechel Branch upstream of their junction and the South Fork downstream of this junction (Figure 5.3). In the downstream region, flood damage reduction measures on the upper South Fork and Buechel Branch compete for project benefits by reducing flood damages. The result of these complications is that the plan was built up incrementally by separately considering the three sections of the region. First, the most upstream control structure in each section was selected, then structures downstream were added. At the end—when the components from the three sections had been aggregated into a single overall plan—it was determined whether the plan could be improved by omitting individual marginal components. The end result of this iterative process was a recommended plan with 10 components: 8 detention basins, 1 floodwall,
and 1 channel improvement.
Each plan has to be evaluated using the Monte Carlo simulation process. The number of simulations varies by reach, with 10,000 required for Reach SF-9 and with a range of 10,000–100,000 required for the other reaches. On a 300 MHz Pentium computer, evaluation of a single plan takes about 25 minutes of computation time.
Risk of Flooding
The HEC-FDA program also produces a set of statistics that quantify the risk of being flooded in any reach for a given plan, as shown in Table 5.2. For reach SF-9, the target elevation is 477.2 feet, which is the elevation of the overbank area in this reach. The probability estimates shown are annual exceedance probability and conditional nonexceedance probability. The annual exceedance probability refers to the risk that flooding will occur considering all possible floods in any year. The conditional nonexceedance probability describes the likelihood that flooding will not occur during a flood of defined severity, such as the 100-year (1 percent chance) flood.
There is a subtle but important distinction between these two types of risk measures. The annual exceedance probability accumulates all the uncertainties into a single estimate both from the natural variability of the unknown severity of floods and from the knowledge uncertainty in estimating methods and computational parameters. The conditional non-exceedance probability estimate divides these two uncertainties, because it is conditional on the severity of the natural event and thus represents only the knowledge uncertainty component. In this sense, the conditional nonexceedance probability corresponds most closely to the traditional idea of adding 1 foot or 3 feet on the 100-year base flood elevation, while the annual exceedance probability corresponds more closely to the goal of ensuring that the chance of being flooded is less than a given value, such as 1 percent, considering all sources of uncertainty.
The “target stage annual exceedance probability” values in Table 5.2 are the median and the expected value or mean of the chance that flooding will occur in any given year for the various reaches. Thus, for reach SF-9, there is approximately a 36 percent chance that flooding will occur beyond the target stage in any given year, while in reach SF-14 upstream, that chance is only about 9 percent. The “long term risk” values in the
TABLE 5.2 Risk of Flooding in Damage Reaches Calculated Uncertainty for 1996 at Beargrass Creek
figure refer to the chance (Rn) that there will be flooding above the target stage at least once in n years, determined by the formula
Rn = 1− (1−pe)n, (5.3)
where pe is the expected annual exceedance probability. For example, for reach SF-9, where pe = 0.3640, for n = 10 years, R10 = 1− (1 − 0.3640)10 = 0.9892, as shown in Table 5.2.
The conditional nonexceedance probability values shown on the right-hand side of Table 5.2 are conditional risk values that correspond to the reliability that particular floods can be conveyed without causing damage in this reach. Thus, in reach SF-9, a 10 percent chance event (10-year flood) has about a 0.27 percent chance of being conveyed without exceeding the target stage, while for a 1 percent chance event (100-year flood), there is essentially no chance that it will pass without exceeding the target stage. By contrast, in Reach SF-14 at the upstream end of the study area, the conditional nonexceedance probability of the reach passing the 10-year flood is about 52 percent; that of the reach passing the 100-year flood is about 100 percent. As the flood severity increases, the chance of a reach being passed without flooding diminishes.
Effect on Project Economics of Including Risk and Uncertainty
The HEC-FDA program that includes risk and uncertainty factors in project analysis became available to the Beargrass creek project team late in the study period. Before then, the team used an earlier economic analysis program (Expected Annual Damage, or EAD) which computed expected annual damages without these uncertainties. O' Leary (1997) presented the data shown in Table 5.3 to compare the two approaches. It is evident that including risk and uncertainty increases the expected annual damage both with and without flood damage reduction plans. The net effect of their inclusion on the Beargrass Creek project is to increase the annual flood damage reduction benefits from $2.078 million to $2.314 million. The study team made a comparison between the components included in the National Economic Development plan in the two computer programs and found that there was no change. Hence, although the inclusion of risk and uncertainty increased project benefits, it did not result in changing the flood damage reduction components included in the National Economic Development plan.
O'Leary (1997) also presented statistics of the project benefits derived from the HEC-FDA program for the National Economic Development plan. The expected annual benefits of the National Economic Development plan—$2.314 million—are the same in Table 5.3 and Table 5.4. The net benefits in the fourth column of Table 5.4 are found by subtracting the annual project costs from the expected annual benefits; the benefit-to-cost ratio is the ratio of the expected benefits to costs.
The 25th percentile, median (50th percentile), and 75th percentile of the expected annual benefits are also shown. The project net benefits are positive at all levels of assessment, and all benefit-to-cost ratios are greater than 1.00. It is interesting to see that the median expected annual benefits ($2.071 million) are nearly the same as the expected value of these benefits without considering uncertainty ($2.078 million). Moreover, the expected value ($2.314 million) is greater than the median, and the difference between the 75th percentile and the median is greater than the difference between the median and the 25th percentile. All these characteristics point to the fact that the distributions of flood damages and of expected annual benefits are positively skewed when uncertainties in project hydrology, hydraulics, and economics are considered. This is why the project benefits increase when these uncertainties are considered. The project benefits for the 25th percentile, 50th percentile, and 75th percentile in Table 5.4 should be read with caution because they are compiled for the project by adding together the corresponding values for all the damage reaches. The percentile value of a sum of random variables is not necessarily equal to the sum of the percentile values of each variable.
TABLE 5.3 Expected Annual Damages (EAD) With and Without Uncertainty in Damage Computations (millions of dollars per year)
|
Analysis Program |
EAD Without Plan |
EAD With NED Plan |
Expected Annual Benefits |
|
EAD Program (no uncertainty) |
3.015 |
0.937 |
2.078 |
|
HEC-FDA (considering uncertainty) |
3.998 |
1.684 |
2.314 |
|
SOURCE: O'Leary (1997). |
|||
TABLE 5.4 Statistics of project benefits under the NED plan using the HEC-FDA Program
|
Statistic |
Expected Annual Benefits |
Annual Project Costs |
Net Benefits |
Benefit to Cost Ratio |
|
Expected Mean |
2.314 |
0.810 |
1.504 |
2.86 |
|
25th Percentile |
1.365 |
0.810 |
0.555 |
1.69 |
|
Median (50%) |
2.071 |
0.810 |
1.261 |
2.56 |
|
75th Percentile |
3.054 |
0.810 |
2.244 |
3.77 |
|
SOURCE: O'Leary (1997). |
||||
RED RIVER OF THE NORTH AT EAST GRAND FORKS, MINNESOTA, AND GRAND FORKS, NORTH DAKOTA
A devastating flood occurred at East Grand Forks, Minnesota, and Grand Forks, North Dakota, in April 1997. After the flood, flood damage reduction studies previously done for the two cities were combined into a joint study, and risk analysis was performed to evaluate the reliability of the proposed alternatives and to evaluate their economic impacts. A risk analysis study performed before the flood was presented in a paper at the Corps's 1997 Pacific Grove, California, workshop (Lesher and Foley, 1997). This paper and subsequent analysis (USACE, 1998a, b, c), as well as a visit to the Corps's St. Paul district office by a member of this committee, form the basis of this discussion of the East Grand Forks–Grand Forks study.
East Grand Forks, Minnesota, and Grand Forks, North Dakota, are located on opposite banks of the Red River of the North and are approximately 300 miles above the river's mouth at Lake Winnipeg, Manitoba, Canada (Figure 5.10). The East Grand Forks–Grand Forks metropolitan area has a population of approximately 60,000 and is located about 100 miles south of the U.S.–Canadian border. The total drainage area of the East Grand Forks–Grand Forks basin is 30,100 square miles. Included in this drainage area is the Red Lake River subbasin that effectively drains about 3,700 square miles in Minnesota and joins the mainstream of the Red River at East Grand Forks. The study area of East Grand Forks–Grand Forks lies in the middle of the Red
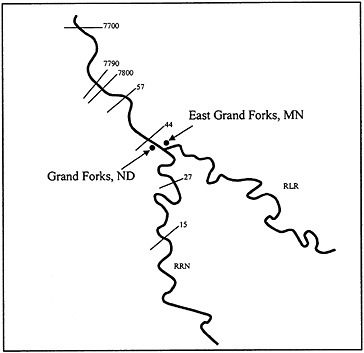
FIGURE 5.10 Schematic of the Red River of the North (RRN) and Red Lake River (RLR) at the East Grand Forks, Minnesota and Grand Forks, North Dakota study area. Numbers indicate USGS stream gages.
River Valley. The valley is exceptionally flat with a gradient that slopes 3–10 feet per mile toward the river with the north–south axis having a gradient of about three-quarters of a foot per mile. The valley extends approximately 23 miles west and 35 miles east of East Grand Forks– Grand Forks and is a former glacial lake bed.
Both cities have a long history of significant flooding from the Red River of the North and the Red Lake River. The most damaging flood of record occurred in April 1997 (see Table 5.5), when the temporary levee systems and flood-fighting efforts of both communities could not hold back the floodwaters of the Red River. The resulting damages were disastrous and affected both cities dramatically. Total damages to existing structures and contents during the 1997 flood were estimated to exceed $800 million. An additional $240 million was spent for emergency-related costs.
TABLE 5.5 Maximum Recorded Instantaneous Peak Flows; Red River of the North at Grant Forks, North Dakota
|
Order |
Date |
Discharge (cfs) |
|
1 |
April 18, 1997 |
136,900 |
|
2 |
April 10, 1897 |
85,000 |
|
3 |
April 26, 1979 |
82,000 |
|
4 |
April 18, 1882 |
75,000 |
|
5 |
April 21, 1996 |
58,400 |
|
6 |
April 4, 1966 |
55,000 |
|
7 |
April 11, 1978 |
54,200 |
|
8 |
May 12, 1950 |
54,000 |
|
9 |
April 16, 1969 |
53,500 |
|
10 |
April 24, 1893 |
53,300 |
|
SOURCE: USACE (1998a). |
||
Risk Analysis
A risk analysis for the proposed flood damage reduction project for the Red River of the North at East Grand Forks, Minnesota, and Grand Forks, North Dakota, used a Latin Hypercube analysis to sample interactions among uncertain relationships associated with flood discharge and elevation estimation. Latin Hypercube is a stratified sampling technique used in simulation modeling. Stratified sampling techniques, as opposed to Monte Carlo-type techniques, tend to force convergence of a sampled distribution in fewer samples. Because the Hydrologic Engineering Center Flood Damage Analysis program (HEC-FDA) was new at the time, and in the interest of saving time, the analysis was performed using a spreadsheet template. The flood damage reduction alternatives analyzed included levees of various heights and a diversion channel in conjunction with levees. The project reliability option in the HEC risk spreadsheet was used to determine the reliability of the alternative levee heights and of the diversion channel in conjunction with levees. The following sections discuss the sensitivity in quantifying the uncertainties and the representation of risk for the alternatives.
Discharge–Frequency Relationships
The log-Pearson Type III distribution, recommended in the Water Resource Council's Bulletin 17B (IACWD, 1981) and incorporated
within the Corps's HEC Flood Frequency Analysis (HEC-FFA) computer program, was used for frequency analysis of maximum annual streamflows, and the noncentral t distribution was used for the development of confidence limits. Discharge–frequency relationships were needed for both the levees and the diversion channel in combination with levees. An analysis (coincidental frequency) was performed to develop the discharge– frequency curves for the Red River of the North downstream and upstream of the Red Lake River for the levees only condition. A graphical method was used to develop the discharge–frequency curves for the diversion channel in combination with levees. Details of these procedures can be found in a Corps instruction manual from the St. Paul district (USACE, 1998a). A brief discussion of these procedures is provided below.
The Grand Forks USGS stream gage (XS 44) is currently located 0.4 miles downstream from the Red Lake River in Grand Forks, North Dakota (Figure 5.10). The discharge–frequency curve for this station along with the 95 percent and 5 percent confidence limits (90% confidence band) are plotted in Figure 5.11. An illustration of the noncentral t probability density function for the 1 percent event is also shown in that figure. Selected quantities of that discharge–frequency relationship are shown in column 2 of Table 5.6. The coincidental discharge–frequency relationship for the Red River just upstream of the mouth of the Red Lake River (column 3 of Table 5.6) was computed with the HEC-FFA computer program. The basic flow values were obtained by routing the 96 years of available data on Red Lake River flows from Crookston (55 miles upstream of the mouth) downstream to Grand Forks. The resulting flows were subtracted from the Red River at Grand Forks flows to obtain coincident discharges on the Red River upstream of Red Lake River. The two-station comparison method of Bulletin 17B was used to adjust the logarithmic mean and standard deviation of this short record (96 years) based on regression analysis with the long-term record at the Grand Forks station (172 years). Correlation of coincident flows for the short record with concurrent peak flows for the long record produced a correlation coefficient of 0.975.
Adjustment of the statistics yielded an equivalent record length of 165 years. The adopted coincidental discharge–frequency curve for the Red River upstream of the Red Lake River is shown in column 3 of Table 5.6 for selected annual exceedance probabilities. The coincidental discharge –frequency curve for the Red Lake River at the mouth was determined by computing the difference in Red River flows both upstream and downstream of Red Lake River (see column 4 in Table 5.6). Statistics for the adopted relationship were approximated by synthetic methods presented in Bulletin 17B (for more details, see USACE (1998a)).
TABLE 5.6 Instantaneous Annual Peak Discharges (cfs) and their Annual Exceedance Probabilities (%) — Existing Conditions
|
Instantaneous Annual Peak Discharges (cfs) |
|||
|
Annual Exceedance Probability in Percent |
Red River of the North Below Red Lake River |
Red River of the North Above Red Lake River |
Red Lake River at the Mouth [based on difference] |
|
0.2 |
169,000 |
128,000 |
41,000 |
|
0.47 |
136,900 |
102,000 |
34,900 |
|
0.5 |
134,000 |
100,000 |
34,000 |
|
1.0 |
110,000 |
81,700 |
28,300 |
|
2.0 |
89,000 |
64,900 |
24,100 |
|
5.0 |
63,900 |
45,500 |
18,400 |
|
10.0 |
47,300 |
32,900 |
14,400 |
|
20.0 |
32,600 |
21,900 |
10,700 |
|
50.0 |
15,500 |
9,590 |
5,910 |
|
80.0 |
7,150 |
3,970 |
3,180 |
|
90.0 |
4,700 |
2,450 |
2,250 |
|
95.0 |
3,290 |
1,620 |
1,670 |
|
99.0 |
1,660 |
726 |
934 |
and downstream of Red Lake River (see column 4 in Table 5.6). Statistics for the adopted relationship were approximated by synthetic methods presented in Bulletin 17B (for more details, see USACE (1998a)).
The Plan Comparison Letter Report developed in February 1998 for flood damage reduction studies for East Grand Forks, Minnesota, and Grand Forks, North Dakota, evaluated an alternative flood damage reduction plan that included a split-flow diversion channel along with permanent levees. The discharge–frequency relationships for the modified conditions, shown in Table 5.7, were developed as follows. The modified-condition discharge–frequency curve for the Red River upstream of Red Lake River was graphically developed based upon the operation of the diversion channel inlet. Red River flows are not diverted until floods start to exceed those having return periods of 5 years (20% annual exceedance probability). The channel is designed to continue to divert Red River flows at a rate that allows the design flood (0.47%) discharge of 102,000 cfs (upstream of the diversion) to be split such that 50,500 cfs is diverted and 51,500 cfs is passed through the cities. This operation is reflected in the modified discharge–frequency relationship shown in Table 5.7 for the Red River upstream of Red Lake River (columns 2 and
TABLE 5.7 Instantaneous Annual Peak Discharges (cfs) and their Annual Exceedance Probabilities (%)—Condition with Diversion Channels
|
Instantaneous Annual Peak Discharges (cfs) |
||||
|
Red River of the North Above Red Lake River |
||||
|
Annual Exceedence Probability in Percent |
Above Diversion |
Below Diversion |
Red Lake River at the Mouth |
Red River of the North Below Red Lake River |
|
0.2 |
128,000 |
55,000 |
41,000 |
96,000 |
|
0.47 |
102,000 |
51,500 |
34,900 |
86,400 |
|
0.5 |
100,000 |
51,000 |
34,000 |
85,000 |
|
1.0 |
81,700 |
47,500 |
28,300 |
75,800 |
|
2.0 |
64,900 |
43,000 |
24,100 |
67,100 |
|
5.0 |
45,500 |
36,500 |
18,400 |
54,900 |
|
10.0 |
32,900 |
30,000 |
14,400 |
44,400 |
|
20.0 |
21,900 |
21,900 |
10,700 |
32,600 |
|
50.0 |
9,590 |
9,590 |
5,910 |
15,500 |
3).Synthetic statistics (mean, standard deviation, and skewness) in accordance with methodology presented in Bulletin 17B were computed for the discharge-frequency relationships of the below-diversion flows.
The modified-condition discharge–frequency curve for the Red River downstream of Red Lake River was graphically computed based upon the operation of the diversion channel. The modified-condition Red River discharges upstream of Red River were added to the coincident flows on Red Lake River (column 4). The resulting discharges were plotted for graphical development of the modified-condition discharge– frequency relationship for the Red River downstream of Red Lake River and are summarized in Table 5.7 (column 5). Synthetic statistics for this discharge–frequency relationship were computed for use in the risk analysis.
Elevation–Discharge Relationships
The water surface elevations computed using the HEC-2 computer program are shown in Table 5.8 for three cross sections (7790, 7800, and 7922) corresponding to the previous USGS gage locations and for cross
section 44, which corresponds to the current USGS gage location (see Figure 5.10 for the cross section locations). These computed water surface elevations (CWSE) were based on the expected discharge quantities from the coincidental frequency analysis performed in June 1994 for the Grand Forks Feasibility Study. These data were used to transfer observed elevations from previous USGS gage sites to the current site (cross section 44) at river mile 297.65, and they were used in determining the elevation –discharge uncertainty. The water surface profile analysis was performed using cross-sectional data obtained from field surveys. Data were also obtained from field surveys and from USGS topographic maps. The HEC-2 model was calibrated to the USGS stream gage data and to high-water marks for the 1969, 1975, 1978, 1979 and 1989 flood events throughout the study area. Note that these water surface elevations assume the existing East Grand Forks and Grand Forks emergency levees are effective. The levees were assumed effective because through extraordinary efforts, they have generally been effective for past floods with the exception of the 1997 flood.
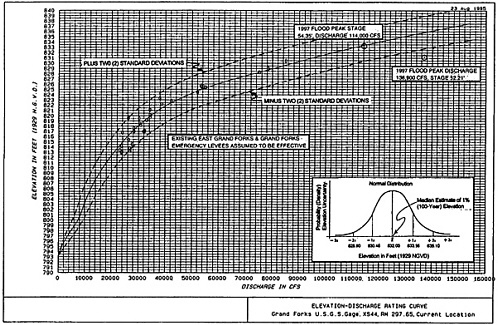
Ratings at stream gage locations provide an opportunity to directly analyze elevation–discharge uncertainty. The measured data are used to derive the “best fit” elevation-discharge rating at the stream gage location, which generally represents the most reliable information available. In this study, the adopted rating curve for computing elevation uncertainty is based on the computed water surface elevations from the calibrated HEC-2 model shown in Table 5.8.
This adopted rating curve for cross section 44 at the current USGS gage is shown in Figure 5.12. Measurements at the gage location were used directly to assess the uncertainty of the elevation–discharge relationship. The normal distribution was used to describe the distribution of error from the “best-fit” elevation–discharge rating curve. The observed gage data (for the four cross sections presented in Table 5.8) were transferred to the current gage site at river mile 297.65 based on the gage location adjustments presented in Table 5.9, which were computed from the water surface elevations in Table 5.8. These adjustments were plotted against the corresponding discharge below the Red Lake River, and curves were developed to obtain adjustments for other discharges.
The deviations of the observed elevations from the fitted curve were used to estimate the uncertainty of the elevation–discharge rating curve shown in Figure 5.11. The deviations reflect the uncertainty in data values as a result of changes in flow regime, bed form, roughness/resistance to flow, and other factors inherent to flow in natural streams. Errors also
TABLE 5.8 Computed Water Surface Elevations of the Red River of the North at Grand Forks, North Dakota (units in feet above sea level)
|
Floods |
||||||||
|
Cross Section Number |
River Mile |
Minimum Channel Bottom in Feet |
20% (5-year) |
10% (10-year) |
4% (25-year) |
2% (50-year) |
1% (100-year) |
0.2% (500-year) |
|
7790 |
295.70 |
773.15 |
817.20 |
821.70 |
825.00 |
827.30 |
829.60 |
834.80 |
|
7800 |
296.00 |
774.2 |
817.39 |
821.87 |
825.19 |
827.52 |
829.83 |
835.01 |
|
7922 |
297.55 |
774.60 |
818.26 |
822.74 |
826.27 |
828.83 |
831.58 |
837.25 |
|
44a |
297.65 |
772.40 |
818.39 |
822.91 |
826.67 |
829.18 |
831.84 |
837.59 |
|
a Current Location of USGS gage. |
||||||||
TABLE 5.9 Adjustments Used in Transferring Observed Elevations from Previous USGS Gage Sites to Current Gage Site at RM 297.65 (XS 44)
|
Expected Probability Discharge (cfs) |
Adjustment Factor (cfs) |
||||
|
Probability |
Below Red Lake River |
Above Red Lake River |
XS 7790, RM 295.70 |
XS 7800, RM 296.00 |
XS 7922, RM 297.55 |
|
38% |
20,000 |
12,500 |
1.28 |
1.06 |
0.12 |
|
27% |
25,000 |
16,100 |
1.23 |
1.02 |
0.12 |
|
20% |
30,600 |
20,300 |
1.19 |
1.00 |
0.13 |
|
10% |
43,900 |
30,300 |
1.21 |
1.04 |
0.17 |
|
4% |
63,500 |
45,800 |
1.67 |
1.48 |
0.40 |
|
2% |
81,500 |
58,800 |
1.88 |
1.66 |
0.35 |
|
1% |
101,000 |
73,500 |
2.24 |
2.02 |
0.26 |
result from field measurements or malfunctioning equipment. A minimum of 8–10 measurements is normally required for meaningful results. The measure used to define the elevation–discharge relationship uncertainty is the standard deviation:
Where X = observed elevation adjusted to current gage location (if 5.12 necessary), M = computed elevation from adopted rating curve, and N = number of measured discharge values (events).
The elevation uncertainty was computed for two different discharge ranges for this analysis. Based on the observed elevations plotted on the adopted rating curve, it appeared that there was greater uncertainty for discharges less than about 10% of annual exceedance probability event due to ice effects on flow. Therefore, the standard deviation was computed for discharges greater than between 22,000 cfs, which corresponds approximately to the zero damage elevation based on the adopted rating curve, and 44,000 cfs, which is slightly greater than the 10 percent annual exceedance probability. The standard deviation was also computed for discharges greater than 50,000 cfs. During the period of record, there were 25 events with a discharge between 22,000 and 44,000 cfs and 10 events with a discharge greater than 50,000 cfs. The standard deviation was 1.66 feet for discharges between 22,000 and 44,000 cfs and was 1.55
feet for discharges greater than 50,000 cfs. In the risk and uncertainty simulations, the standard deviation was linearly interpolated between 1.66 and 1.55 feet for discharges between 44,000 and 50,000 cfs. (See USACE (1998b) for more details.)
In an earlier risk analysis that was performed for the Grand Forks Feasibility Study, a much lower standard deviation of 0.50 feet was used for discharges greater than 50,000 cfs. However, adding the 1997 flood to the analysis resulted in a standard deviation of 1.55 feet, which is similar to that computed for discharges less than 44,000 cfs. It should be noted that the discharge and elevation used in this analysis for the 1997 flood was the peak discharge of 136,900 cfs occurring on April 18, 1997 (see Table 5.4), and an elevation of 831.21 feet (Stage 52.21). The peak elevation of 833.35 feet (Stage 54.35) occurred on April 22, 1997 at a discharge of 114,000 cfs. The elevation of 831.21 feet was almost 5 feet below the rating curve at a discharge of 136,900 cfs; however, the peak elevation of 833.35 feet at a discharge of 114,000 cfs was essentially on the adopted rating curve. Both of these points are plotted on the rating curve in Figure 5.12. Lines representing ± 2 standard deviations for the normal distribution, which encompasses approximately 95 percent of all possible outcomes, are also shown on the rating curve. An illustration of the normal distribution at the 1 percent (100-year) event for the project levee condition is also shown in Figure 5.12.
Risk and Uncertainty Analysis Results
Four index locations were selected to evaluate project performance and project sizing. These locations are cross sections 57, 44 (current USGS gage), 27, and 15 (Figure 5.10). The four locations were selected based on economic requirements for project sizing (see USACE, 1998c). The elevation–discharge rating curves (based on HEC-2 analysis) for existing and project conditions at these locations can be found in the USACE (1998b). Each of these rating curves shows three conditions, where applicable: (1) existing conditions, (2) removal of the pedestrian bridge at cross sections 7920-7922 and with project levees (“levee only”); and (3) with removal of the pedestrian bridge, with project levees, and with the diversion channel (“diversion channel”). Existing conditions means that the existing emergency levees are assumed to be effective up to and including the 5 percent (20-year) event and are ineffective for larger floods. The 5 percent (20-year) event was selected based
on comparison of water surface profiles with effective and probable failure point (PFP) levee elevations provided by the Geotechnical Design Section analysis (see USACE, 1998b, paragraph A.2.11 and Appendix B of this report). The pedestrian bridge was removed based on input from the cities of East Grand Forks and Grand Forks. The rating curves for the diversion channel alternative were based on limited information. The Red River to the North would start to divert into the diversion channel at the 20 percent (5-year) flood; therefore, up to this point the rating curve for existing conditions with levees was used.
An additional location was also selected to evaluate the performance of the levee only and diversion channel with 1 percent (100-year) levee alternatives. This location is at cross section 7700 at the downstream end of the project levees (see Figure 5.10). Cross section 7700 was selected based on hydraulic analysis as the least critical location—the location where the levees in combination with the diversion channel would first overtop from downstream backwater (see USACE, 1998b).
Project Reliability
The project reliability results are summarized in Table 5.10, Table 5.11 through Table 5.12. Table 5.9 contains the results for the levees-only alternatives. Table 5.11 contains the results for the diversion channel in combination with 1 percent (100-year) levees. Note that in Table 5.10, three different alternative top-of-levee heights are evaluated, whereas in Table 5.11, it is always the same alternative—diversion channel with 1 percent levees— but for the three different events. The top-of-levee elevations were computed based on a water surface elevation profile to ensure initial overtopping would occur at the least-critical location (here, cross section 7700). The downstream top-of-levee elevations were selected with the intent of having 90 percent probability of containing the specified flood and were based on previous risk analysis for the Grand Forks Feasibility Study preliminarily updated to include the 1997 flood. The 2 percent (50-year), 1 percent (100-year), and 0.47 percent (210-year/1997 flood) top-of-levee profiles are 3.2, 3.4, and 2.7 feet above their respective water surface profiles at the downstream end (Table 5.10).
As seen in Table 5.10, the intent of having 90 percent probability of containing the specified flood is generally realized. The 2 percent levees have a 92 percent probability of containing the 2 percent flood. The 1 percent levees have a 90 percent probability of containing the 1 percent
flood. The 0.47 percent levees have an 87 percent probability of containing the 0.47 percent flood.
TABLE 5.10 Reliability at Top of Levee for Three Top-of-Levee Heights
|
2 % (50-year) Leveea |
1% (100-year) Leveeb |
0.47% (210-year) Leveec |
||||
|
Gage Location |
Top of Levee (ft.) |
Reliability (%) |
Top of Levee (ft.) |
Reliability (%) |
Top of Levee (ft.) |
Reliability (%) |
|
XS 7700d |
830.2 |
92.5 |
832.7 |
90.7 |
834.8 |
87.7 |
|
XS 57 |
832.0 |
92.0 |
834.2 |
90.5 |
836.2 |
86.4 |
|
XS 44 |
833.2 |
93.2 |
835.6 |
91.3 |
837.5 |
86.3 |
|
XS 27 |
834.3 |
92.1 |
836.9 |
89.5 |
839.0 |
86.5 |
|
XS 15 |
835.2 |
92.7 |
837.7 |
90.0 |
839.7 |
85.5 |
|
aTop of levee for the 2% levee is computed water surface elevation plus 3.2 feet. bTop of levee for the 1% levee is computed water surface elevation plus 3.4 feet. cTop of levee for 0.47% levee is computed water surface elevation plus 2.7 feet. dDownstream end of project. |
||||||
TABLE 5.11 Project Reliability at Top of Levee for Diversion Channel with 1 Percent (100-Year) Levees for Three Different Events
|
Gage Location |
Top of Levee (ft) |
Reliability 2% (50-year) Event |
1% (100-year) Event |
0.47% (210-year) Event |
|
XS 7700a |
832.7b |
99.9 |
99.6 |
98.9 |
|
XS 57 |
834.2 |
100.0 |
99.6 |
99.2 |
|
XS 44 |
835.6 |
99.9 |
99.6 |
99.4 |
|
XS 27 |
836.9 |
99.6 |
99.5 |
99.1 |
|
XS 15 |
837.7 |
99.7 |
99.6 |
99.2 |
|
aDownstream end of project. bTop of levee is computed water surface elevation plus 3.4 feet. |
||||
Reliability results for the diversion channel with 1 percent levees are summarized in Table 5.11. Note again that the levees constructed in combination with the diversion are the same as for the 1 percent flood without the diversion channel and are the same for all three floods analyzed. As seen in the table, there is a 99 percent or greater probability of containing the flood for all three floods considered when the project includes the diversion channel.
As previously noted, the most critical location for project performance is at cross section 7700 at the downstream end of the project. Table 5.12
summarizes the results for all the alternatives considered and for numerous floods. The probability of the diversion channel in combination with 1 percent levees for the 0.2 percent event is listed in the table as greater than 95%. A more specific reliability was not cited for the 0.2 percent event for two reasons: (1) the discharge–frequency curve based on the approximate statistics starts to diverge from the graphical curve for extreme events and, (2) there was limited information available to develop the Red River to the North rating curves for the diversion alternative. These reasons are also why more extreme events were not analyzed.
TABLE 5.12 Conditional Exceedance Probability of Alternative for Various Events (based on analysis at downstream end of project—XS 7700)
|
Alternative |
||||
|
Event |
2% (50-year) Levees |
1% (100-year) Levees |
0.47% (210-year) Levees |
Diversion with 1% (100-year) Levees |
|
4 % (25-year) |
99.5 |
100.0 |
100.0 |
100.0 |
|
2% (50-year) |
92.5 |
99.1 |
99.7 |
99.9 |
|
1% (100-year) |
64.3 |
90.7 |
98.3 |
99.6 |
|
0.52% (192-year) |
29.5 |
65.6 |
89.8 |
—a |
|
0.5% (200-year) |
28.2 |
64.4 |
88.7 |
—a |
|
0.47% (210-year) |
25.3 |
61.9 |
87.7 |
98.9 |
|
0.2% (500-year) |
4.4 |
21.5 |
48.0 |
>95 |
|
0.1% (1,000-year) |
0.7 |
6.0 |
20.7 |
—b |
|
aEvent not analyzed. bEvent not analyzed because (1) the discharge–frequency curve based on the approximate statistics starts to diverge from the graphical curve for extreme events and (2) there was limited information to develop the RRN rating curves for the diversion alternative. |
||||
Table 5.13 presents the simulated conditional exceedance probabilities from the economic project sizing analysis. The without-project condition is also included in this table for comparison purposes. The without-project condition is based on a zero damage elevation of 824.5 feet, assumes credit is given to the existing levees, and assumes all properties that were substantially damaged (50% or more damage) in the 1997 flood have been removed.
Based on the above analysis of alternative plans and further economic and environmental considerations, the recommended National
TABLE 5.13 Residual Risk Comparison
|
Alternative |
Annual Performance (Expected Annual Probability of Design Being Exceeded) |
|
Without Project |
0.0918 |
|
2% (50-Year) Levees |
0.0086 |
|
1% (100-Year) Levees |
0.0036 |
|
0.47% (210-Year) Levees |
0.0010 |
|
Diversion with 1% (100-Year) Levees |
0.0002 |
Economic Development (NED) plan consists of a permanent levee and floodwall system designed to reliably contain the 210-year flood event. This equates to an 87.7 percent reliability of containing the 210-year flood event (Table 5.12) and would reliably protect against a flood of the magnitude of the 1997 flood.
The recommended plan would remove protected areas from the regulatory floodplain, increase recreational opportunities, and enhance the biological diversity in the open space created. The recommended plan anticipates the need to acquire over 250 single-family residential structures, 95 apartment or condominium units, and 16 businesses along the current levee/floodwall alignment.
The total cost of the recommended multipurpose project is $350 million including recreation features and cultural resources mitigation costs. The federal share of the project would be $176 million and the nonfederal share would be $174 million. The benefit-to-cost ratio has been calculated as 1.07 for the basic flood reduction features of the project and as 1.90 for the separable recreation features (USACE, 1998b). The recommended project has an overall benefit-to-cost ratio of 1.10.
The cities of East Grand Forks, Minnesota, and Grand Forks, North Dakota, will serve as the project's nonfederal sponsors. Through legislation, the State of Minnesota has committed to provide financial support in the form of bonds and returned sales taxes to the city of East Grand Forks. In verbal and written comments from its governor, the State of North Dakota has committed to provide financial assistance to the city of Grand Forks.