|
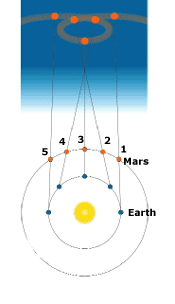
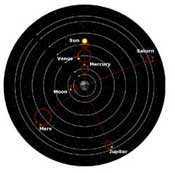
The ancients held that the Sun, Moon, and planets traveled in perfect circles around Earth and inside a sphere of fixed stars. In the second century A.D., the Greek scholar Ptolemy explained inconsistencies in planetary motion--such as the observed retrograde, or backward, motion of Mars-- by suggesting that the planets moved in small circles, or epicycles, at the same time that they revolved around Earth (right). In the early seventeenth century, the German astronomer Johannes Kepler worked out the real explanation. Because Earth orbits closer to the Sun, it moves more rapidly than does Mars (below). As a result, Mars seems to go forward as seen from Earth at positions 1 and 2, then backward when seen at positions 3 and 4, and then forward again when seen at position 5. |
 |
  |
In 1610 Galileo Galilei made meticulous notes of his observations of four wandering "stars" orbiting in a plane around Jupiter. A page from his notebooks shows that he used asterisks to represent the numbers of bodies he had discerned and that he roughly approximated their relative distances from the planet.
After tracking their movements, Galileo realized that the stars were actually moons--now known as the Galilean satellites Io, Europa, Ganymede, and Callisto. As seen in the modern photograph below, Callisto (far right) orbits about four times farther from Jupiter than does Io (near right), the nearest Galilean moon. |  |
The first law restates and clarifies Galileo's idea of inertia  . As Newton described it, an object moving in a straight line at a constant speed will continue with that exact motion until an outside force disturbs it. Since zero speed also qualifies as "traveling" at a constant speed, a corollary to the law of inertia . As Newton described it, an object moving in a straight line at a constant speed will continue with that exact motion until an outside force disturbs it. Since zero speed also qualifies as "traveling" at a constant speed, a corollary to the law of inertia  reads: A body at rest will stay that way unless another force acts upon it. We realize that all too well when we have to push a stalled car out of a crowded intersection. In that situation, inertia reads: A body at rest will stay that way unless another force acts upon it. We realize that all too well when we have to push a stalled car out of a crowded intersection. In that situation, inertia  and friction are powerful hindrances. But in the vast spaces between stars, frictional forces are nearly absent. Thus, spacecraft such asVoyager 1and Voyager 2, launched in 1977 to explore the outer planets and then escape our solar system, will sail through space for many thousands of years. They will slow down only slightly from the gravitational pull of the star they have left behind. and friction are powerful hindrances. But in the vast spaces between stars, frictional forces are nearly absent. Thus, spacecraft such asVoyager 1and Voyager 2, launched in 1977 to explore the outer planets and then escape our solar system, will sail through space for many thousands of years. They will slow down only slightly from the gravitational pull of the star they have left behind.
Newton's second law provides the mathematical recipe for how and why an object can be set into motion. If you apply force  to a mass, its velocity changes. That is, it accelerates or decelerates. As the mass of the object goes up, the resulting acceleration goes down in equal measure if the same force is applied. To picture this, imagine standing behind two people wearing roller skates. One is a 90-pound ballerina, and the other is a sumo wrestler who weighs five times as much. If you push on each person with equal force (and tact), you will accelerate the ballerina five times more quickly. That ratio holds true in space as well. Astronauts must remember it every time they grapple with objects floating around. It doesn't take much force to stop a wrench passed from one astronaut to another. But if it's a one-ton satellite, it takes just as much effort to control it in space as it does to push your car in neutral on the street. to a mass, its velocity changes. That is, it accelerates or decelerates. As the mass of the object goes up, the resulting acceleration goes down in equal measure if the same force is applied. To picture this, imagine standing behind two people wearing roller skates. One is a 90-pound ballerina, and the other is a sumo wrestler who weighs five times as much. If you push on each person with equal force (and tact), you will accelerate the ballerina five times more quickly. That ratio holds true in space as well. Astronauts must remember it every time they grapple with objects floating around. It doesn't take much force to stop a wrench passed from one astronaut to another. But if it's a one-ton satellite, it takes just as much effort to control it in space as it does to push your car in neutral on the street.
Newton's third law is justly famous. Paraphrased, we know it as follows: For every  action there exists an equal and opposite reaction. This is an easy law to see and understand. If the action is air gushing from the narrow opening of a balloon, the reaction is the balloon jetting crazily around the room. Igniting a rocket's engines propels it off the ground into space. Jumping from a canoe to a dock pushes the canoe out into the water. Even if you agree that a reaction always happens, it's a mental challenge to realize that Earth is the same as that canoe. When you jump into the air, the planet moves in the opposite direction. But because Earth is so much more massive, its response to your leap is minuscule indeed. action there exists an equal and opposite reaction. This is an easy law to see and understand. If the action is air gushing from the narrow opening of a balloon, the reaction is the balloon jetting crazily around the room. Igniting a rocket's engines propels it off the ground into space. Jumping from a canoe to a dock pushes the canoe out into the water. Even if you agree that a reaction always happens, it's a mental challenge to realize that Earth is the same as that canoe. When you jump into the air, the planet moves in the opposite direction. But because Earth is so much more massive, its response to your leap is minuscule indeed.
Newton's laws hold true for nearly every type of motion on our world as well as throughout the universe. Taken together, they express one of the most crucial physical principles that govern motion in the cosmos: the conservation of momentum  . (continued) . (continued) |

