| Newton's Thought Experiment
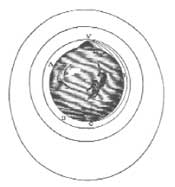
Sir Isaac Newton began his cogitation on gravity and orbits with the fact that the pull of gravity causes a thrown object to fall in a curve. In the drawing at right, he illustrated that an object hurled from a hypothetical mountain V would fall to D. If the object could be thrown harder and harder, it would fall to E, F, or G. Finally, if it could somehow be thrown hard enough from the mountaintop, or from a point in space, it would "fall" around the world (outer circles). In following his thoughts to their logical conclusion, Newton developed the theory of orbital flight. |
 |
The Eternal Free Fall of Orbits
The future of the cosmos probably was not on Isaac Newton's mind as he pondered the relation between a falling object on Earth and the Moon in orbit. He did, however, conduct a thought experiment. It went something like this: If he dropped a ball, it would descend toward Earth in free fall until it hit the ground. Launching that ball parallel to the ground from a cannon would propel it some distance, but Earth's gravity would still pull it downward in free fall. Hauling the cannon to a mountaintop would let him shoot the ball still farther. But what if he climbed the highest mountain and fired the ball fast enough--5 miles per second--so that it never touched the ground as Earth's surface curved beneath it? The ball would still fall toward Earth's center, but its fast sideways motion would keep it in a low "orbit." With this intuitive leap, Newton realized that all orbits in the solar system are never-ending free falls. Their motions are determined by the same laws that govern the flights of baseballs, the trajectories of rocks belched from a volcano, and the paths of other freely moving projectiles on Earth.
 | Unlike the tame orbits of the planets, most of which circle the Sun in paths that hug the ecliptic (Earth's orbital plane), comets such as Comet West (top) sweep through the solar system in orbits of all inclinations and orientations. |
Newton acknowledged that many predecessors had set the stage for his insights. One was the German astronomer Johannes Kepler, who worked out the correct mathematical details of planetary orbits for the first time in 1609. His painstaking calculations and the observations of his mentor, the Danish astronomer Tycho Brahe, enabled Kepler to derive three key principles. First, planets move around the Sun not in circles, as Copernicus had thought, but in oval paths called ellipses. Second, planets move faster when closer to the Sun and slower when farther away, in such a fashion that their motions sweep out equal areas of their ellipses in equal times. Third, the orbital period of a planet--its year--depends predictably upon its distance from the Sun. We can apply those laws anywhere in the universe where planetary systems revolve around other stars. We can also use them to understand other basic systems, such as two stars that orbit each other closely. But the laws are too simplistic to hold in star clusters, galaxies, and groups of galaxies, where the complexities of gravity's dances require stronger analytical tools.
Newton showed that his laws of motion and gravitation lead to other families of trajectories in the solar system besides ellipses: parabolas, hyperbolas, and, of course, circles. (Gravitational nudges from other bodies in the solar system prevent any object from orbiting the Sun in a perfect circle.) These are "conic sections"-- (continued)
|

