Nano-Opto-Mechanics: Using Light Forces in Guided-Wave Nanostructures
MATT EICHENFIELD, RYAN M. CAMACHO, JASPER CHAN, QIANG LIN, JESSIE ROSENBERG, AMIR H. SAFAVI-NAEINI, AND OSKAR PAINTER
California Institute of Technology
Pasadena, California
Kepler and Newton were the first to propose that light has momentum and can exert a mechanical force. The interaction of light with mechanical vibrations, in the form of Brillouin and Raman scattering, has been known since the 1920s and has many practical applications in the fields of spectroscopy and optoelectronics. With the advent of the laser in the 1960s, it became possible to manipulate micron-scale dielectric particles using optical “tweezers,” a technique developed by Art Ashkin (1970). This was also the beginning of the use of laser beams for trapping and manipuling gas-phase atoms, which ultimately led to the demonstration of atomic Bose-Einstein condensates.
More recently, scientists have realized that laser light, with its very low intrinsic noise, can be used to cool a macroscopic mechanical-resonant element, and perhaps reach temperatures suitable for measuring inherently quantum mechanical behavior (Schwab and Roukes, 2005). In addition to the cooling effect, optical amplification from a continuous-wave laser beam can be used to form regenerative mechanical oscillators (Kippenberg and Vahala, 2008). These developments have stimulated interest in the new field of cavity-optomechanics, and a myriad of materials, devices, and techniques are being explored.
It is now widely understood that optical gradient forces, as opposed to the scattering radiation pressure force, can be used in guided-wave nanostructures to generate very large optomechanical couplings to micro- or nano-mechanical motion (Eichenfield et al., 2009a). In contrast to the scattering radiation pressure force, which one can intuit from the reflection of momentum-carrying photons,
the gradient force, as its name suggests, results from gradients in the intensity of light, which can be substantial in the near-field.
In a recently developed nanophotonic platform for using this strong gradient optical force, light and sound are manipulated through a common nanostructure (Eichenfield et al., 2009b,c). We call these devices “optomechanical crystals” (OMCs) because of the simultaneous realization of phononic and photonic bandgap states (similar to the electronic bandgaps that form in regular crystalline materials).
OMCs enable the engineering of various integrated functionalities that are not possible in other systems. Ultimately, OMCs may be used in fully integrated planar light and sound wave circuits. In this paper, we introduce the OMC concept and describe a “photon-phonon translator,” which may have a variety of applications, from radio-frequency (RF)-over-optical communication to the study of mesoscopic quantum systems.
INTRODUCTION TO OPTOMECHANICAL CRYSTALS
Periodicity applied to the propagation of light gives rise to photonic crystals that can be used to engineer broad- and narrow-band dispersion, to confine optical modes to small volumes with high optical quality factors, and to build planar lightwave circuits (Yablonovitch, 1987). Periodicity applied to mechanical vibrations yields phononic crystals that harness mechanical vibrations the same way photonic crystals harness optical waves (Olson and El-Kady, 2008). The latter raises tantalizing possibilities, such as phononic bandgaps, nonlinear phononics, coherent sources of phonons, and planar sound wave circuits. It has been proposed that periodic structures might be used to simultaneously confine mechanical and optical modes (Maldovan and Thomas, 2006). We endeavor to take this idea one step further by using cavity-optomechanics concepts to marry mechanics and optics in ways that make both more powerful.
The dispersive interaction induced by mechanical motion (Eichenfield et al., 2009c) is responsible for coupling the photonic and phononic crystal properties of the material to yield optomechanical crystals. For the complex motion in these periodic structures, the origin of the optomechanical coupling can be subtle, and in many cases even counter-intuitive. Nonetheless, understanding the nature of the coupling is crucial, because the degree of coupling between different optical-mechanical mode pairs can vary by many orders of magnitude in the same structure. Moreover, subtle changes in the geometry can induce enormous changes in the coupling, which can be used to engineer the coupling if the system is well understood.
A perturbation theory of Maxwell’s equations with shifting material boundaries (Johnson et al., 2002) provides a simple, computationally robust method of calculating the optomechanical coupling of these complex motions. We describe below how this theory of perturbation can be used to create an intuitive, graphical
picture of the optomechanical coupling of simultaneously localized optical and mechanical modes in periodic systems.
A graphical representation illustrates methodologies for optimizing the coupling of the mechanical and optical modes. Figure 1 shows the band structure for photons and phonons (mechanical vibrations) of a quasi-1D patterned silicon nanobeam. Phonon states can be localized just as localized optical resonances can be formed in “flat-band” regions (regions of low optical dispersion in which the energy velocity of light approaches zero) close to the zone boundaries.
Because the wavelength of the optical mode and the mechanical vibration must be the same (they live on the same 1D lattice), the ratio of the frequency of optical-to-phonon modes can be given as the ratio of the speed of light to that of sound (or more generally whatever type of vibration is involved). It so happens that for the silicon nanobeam shown in Figure 1, which operates at an optical wavelength of 1.5 microns, the mechanical mode frequency is in the 1–5 gigahertz
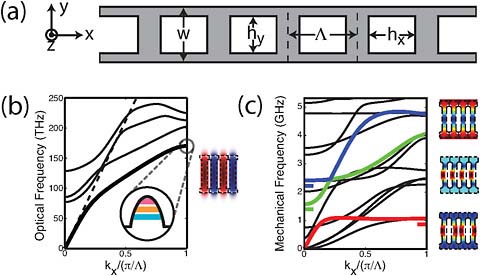
FIGURE 1 (a) General geometry of the structure projection of the periodic nanobeam (infinite structure, no defect). (b) Optical-band diagram of the nanobeam’s projection. The band from which all localized optical modes will be derived is shown in thick black, with Ey of the optical mode at the X point shown to the right of the diagram. The harmonic spatial potential created by the defect, along with the first three optical modes are shown as emanating from the X-point band-edge. (c) Mechanical band diagram of the nanobeam’s projection. The three bands that form defect modes that are discussed in this paper are colored. The bottom-most mode is from the X point of the red band; the Γ points of the green and blue bands correspond to the middle and top mechanical modes, respectively. The frequencies of the defect modes that form from the band edges are shown as short, horizontal bars. Source: Eichenfield, et al. (2009c). Reprinted with permission. Color figure available online at http://books.nap.edu/openbook.php?record_id=12821&page=59.
(GHz) range (shrinking the width of the nanobeam creates the intriguing possibility of reaching frequencies in the X-band [10–12 GHz] or even higher).
The bands in Figure 1(c) correspond to the bands that have large optomechanical coupling. By forming a “defect” in the periodic lattice through a slow reduction in the hole-to-hole pitch in the center of a patterned beam, one can form localized photon and phonon states (Figure 2). The three primary phononic localized resonances are labeled as pinch, accordion, and breathing modes (see caption).
The optomechanical coupling between mechanical and optical degrees of freedom is given to lowest order by the dispersive term, gOM = δω/δα= ωc/LOM, where ωc is the unperturbed optical cavity frequency, LOM is an effective length over which a photon’s momentum is transferred to the mechanical structure (equal to the cavity length in the case of a Fabry-Perot cavity), and α parameterizes the maximum displacement of the mechanical motion for the mode of interest. Using the perturbation theory of Maxwell’s equations with shifting material boundaries (Johnson et al., 2002), one can calculate the derivative of the resonant frequency of a structure’s optical modes, with respect to the α-parameterization of a surface deformation perpendicular to the surface of the structure.
An example of the power of the perturbative method to engineer the optomechanical coupling strength, is shown in Figure 3, in which the optomechanical coupling strength of the fundamental accordian mechanical mode at ~1.5 GHz is a function of beam width. The optomechanical coupling length approaches a minimum value close to the wavelength of light for a beam width of 700 nm, whereas it increases to more than 300 times this value for a beam only twice as wide.
THE OPTOMECHANICAL CRYSTAL “TRAVELING PHOTON-PHONON TRANSLATOR”
The OMC concept naturally lends itself to a microchip integration platform for the routing, interaction, and exchange of light and mechanics, with possible applications in photonics and RF-over-optical communication. At the heart of such applications is a device we call the “traveling photon-phonon translator.” Shown schematically in Figure 4, this device consists of two optical cavities coupled by a single phonon cavity. An input/output optical waveguide is strongly coupled to one of the optical cavities (top cavity, labeled a), as is a phononic waveguide to the phononic cavity (labeled b). The second optical cavity (bottom, labeled αp) is pumped to some large coherent state amplitude via a second optical. For the traveling photon-phonon translator to effectively convert photons to phonons, or vice-versa, several criteria relating to the input and output coupling rates of photons and phonons and internal dissipation rates must be met.
Because of the great flexibility in OMC architecture, however, fulfilling these criteria is rather simple due to the chip-scale platform in which the devices are formed, allowing many degrees of freedom for photon-phonon confinement
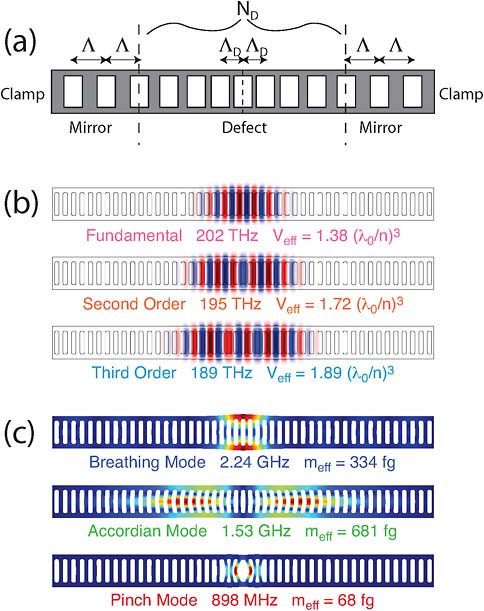
FIGURE 2 (a) Schematic illustration of actual nanobeam optomechanical crystal with defect and clamps at substrate. (b) Localized optical modes of the nanobeam OMC. The colors of the names correspond to the illustration of the inverted potential in Figure 2(b). (c) Localized, optomechanically coupled mechanical modes of the nanobeam OMC. The colors of the names correspond to the colored bands and horizontal bars showing the modal frequencies in Figure 2(c). Source: Eichenfield, et al. (2009c). Reprinted with permission. Color figure available online at http://books.nap.edu/openbook.php?record_id=12821&page=61.
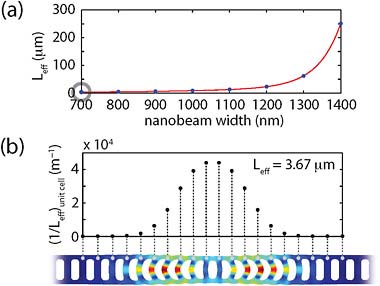
FIGURE 3 For the accordion mode with the fundamental optical mode, (a) the effective length as a function of total beam width, (b) a breakdown of individual unit cell contributions to the total optomechanical coupling for a structure with a beam width of 700 nm (circled in (a)), mode frequency of 3.97 GHz and effective motional mass of 0.334 pg, with accompanying mechanical mode plot. The narrower mechanical mode envelope results in drastically different optomechanical coupling contributions from those with the wider beam. Source: Eichenfield, et al. (2009c). Reprinted with permission.
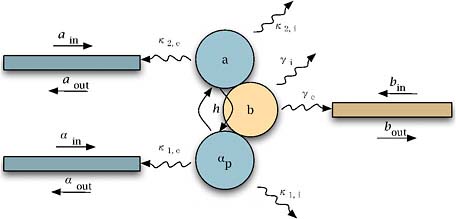
FIGURE 4 Traveling photon-phonon translator. Optical cavities and waveguides are colored blue (a and αp) while the phononic cavity and waveguide are beige (b). Color figure available online at http://books.nap.edu/openbook.php?record_id=12821&page=62.
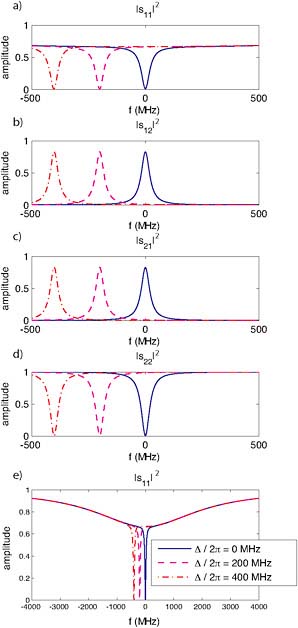
and coupling to other modes on the chip. A simulation of the scattering matrix for input and output coupled power (amplitude) for both phonons and photons is shown in Figure 5 for a structure with parameters determined from a numerical modeling of a quasi-2D OMC cavity structure. The efficiency of phonon-to-photon or photon-to-phonon transfer (the system is symmetric, and thus equal for the two conversion efficiencies) can be as high as 75 percent, limited by internal mechanical and optical loss.
These encouraging initial theoretical results indicate that the traveling photon-phonon translator concept can be used to interconvert photons and phonons with high efficiency for applications in optical delay lines (the slower phonon provides the delay), dynamic optical routing/buffering (Lin et al., 2009), and narrow-band RF/microwave filters (Hossein-Zadeh and Vahala, 2008).
Beyond classical RF-microwave photonic applications, the OMC photon-phonon translator works equally well as a quantum translator for individual quanta of phonons or photons if the phononic cavity can be coupled to a low enough bath temperature (100mK). Such a system would be very interesting as a converter of microwave to optical photons when integrated with piezoelectric materials. In the burgeoning field of circuit quantum electrodynamics (Schoelkopf and Girvin, 2008), rapid progress has been made in realizing on-chip coupled qubits via a microwave “quantum bus”; this could enable off-chip coupling via photons for long-distance quantum communication and entanglement between nodes.
REFERENCES
Ashkin, A. 1970. Acceleration and trapping of particles by radiation pressure. Physical Review Letters 24(4): 156–159.
Eichenfield, M., R. Camacho, J. Chan, K.J. Vahala, and O. Painter. 2009a. A picogram- and nanometrescale photonic crystal optomechanical cavity. Nature 459(7246): 550–555.
Eichenfield, M., J. Chan, R. Camacho, K.J. Vahala, and O. Painter. 2009b. Optomechanical crystals. Nature 462: 78–82.
Eichenfield, M., J. Chan, A.H. Safavi-Naeini, K.J. Vahala, and O. Painter. 2009c. Modeling dispersive coupling and losses of localized optical and mechanical modes in optomechanical crystals. Optics Express, 17(22): 20078–20098.
Hossein-Zadeh, M., and K.J. Vahala. 2008. Photonic RF down-converter based on optomechanical oscillation. IEEE Photonics Technology Letters 20(4): 234–236.
Johnson, S.G., M. Ibanescu, M.A. Skorobogatiy, O. Weisberg, J.D. Joannopoulos, and Y. Fink. 2002. Perturbation theory for Maxwell’s equations with shifting material boundaries. Physics Review E 65(6): 066611.
Kippenberg, T.J., and K.J. Vahala. 2008. Cavity optomechanics: back-action at the mesoscale. Science 321(5893): 1172–1176.
Lin, Q., J. Rosenberg, D. Chang, R. Camacho, M. Eichenfield, K.J. Vahala, and O. Painter. 2009. Coherent mixing of mechanical excitations in nano-optomechanical structures. http://arxiv.org/abs/0908.1128v1. Submitted to Nature Photonics.
Maldovan, M., and E.L. Thomas. 2006. Simultaneous localization of photons and phonons in two-dimensional periodic structures. Applied Physics Letters 88: 251907.
Olson, R.H. III, and I. El-Kady. 2008. Microfabricated phononic crystal devices and applications. Measurement Science and Technology 20(1): 012002.
Schoelkopf, R.J., and S.M. Girvin. 2008. Wiring up quantum systems. Nature 451(7179): 664–669.
Schwab, K.C., and M.L. Roukes. 2005. Putting mechanics into quantum mechanics. Physics Today 58(July): 36–42.
Yablonovitch, E. 1987. Inhibited spontaneous emission in solid-state physics and electronics. Physical Review Letters 58(20): 2059–2062.