1.1 OVERVIEW AND STUDY CHARTER
Advances in computing hardware and algorithms have dramatically improved the ability to simulate complex processes computationally. Today’s simulation capabilities offer the prospect of addressing questions that in the past could be addressed only by resource-intensive experimentation, if at all. However, computational results almost always depend on inputs that are uncertain, rely on approximations that introduce errors, and are based on mathematical models1 that are imperfect representations of reality. Hence, given some calculated quantity of interest (QOI) from the computational model, the corresponding true physical QOI is uncertain. If this uncertainty—the relationship between the true value of the QOI and the prediction of the computational model—cannot be quantified or bounded, then the computational results have limited value. This report recognizes the ubiquity of uncertainty in computational estimates of reality and the necessity for its quantification. In response to the observation of George Box that “all models are wrong, but some may be useful” (Box and Draper, 1987, p. 424), this report explores how to make models as useful as possible by quantifying how wrong they are.
In a typical computational science and/or engineering analysis, the physical system to be simulated is represented by a mathematical model, which often comprises a set of differential and/or integral equations. The mathematical model is approximated in some way so that the solution of the approximated model can be found by executing a set of algorithms on a computer. For example, derivatives may be approximated by finite differences, series expansions may be truncated, and so on. The computer code’s implementation of the algorithms that approximately solve the mathematical model is often called the computational model or computer model.
As computational science and engineering have matured, the process of quantifying or bounding uncertainties in a computational estimate of a physical QOI has evolved into a small set of interdependent tasks. These tasks are verification, validation, and uncertainty quantification, which are abbreviated as “VVUQ” in this report. Briefly and approximately: verification determines how well the computational model solves the math-model equations, validation determines how well the model represents the true physical system, and uncertainty quantification (UQ) plays important roles in validation and prediction.
_____________________
1 In this report, a model is defined as a representation of some portion of the world in a readily manipulatable form. A mathematical model uses the form of mathematical language and equations.
In recognition of the increasing importance of computational simulation and the increasing need to assess uncertainties in computational results, the National Research Council (NRC) was asked to study the mathematical foundations of VVUQ and to recommend steps that will ultimately lead to improved processes. The specific tasking to the Committee on Mathematical Foundations of Verification, Validation, and Uncertainty Quantification is as follows:
• A committee of the National Research Council will examine practices for VVUQ of large-scale computational simulations in several research communities.
• The committee will identify common concepts, terms, approaches, tools, and best practices of VVUQ.
• The committee will identify mathematical sciences research needed to establish a foundation for building a science of verification and validation (V&V) and for improving the practice of VVUQ.
• The committee will recommend educational changes needed in the mathematical sciences community and mathematical sciences education needed by other scientific communities to most effectively use VVUQ.
Figure 1.1 illustrates the different elements of VVUQ and their relationships to the true, physical system, the mathematical model, and the computational model. Uncertainty quantification does not appear explicitly in the figure, but it plays important roles in the processes of validation and prediction.
There is general agreement about the purposes of verification, validation, and uncertainty quantification, but different groups can differ on the details of each term’s definition. For purposes of this report the committee adopts the following definitions:
• Verification. The process of determining how accurately a computer program (“code”) correctly solves the equations of the mathematical model. This includes code verification (determining whether the code correctly implements the intended algorithms) and solution verification (determining the accuracy with which the algorithms solve the mathematical model’s equations for specified QOIs).
• Validation. The process of determining the degree to which a model is an accurate representation of the real world from the perspective of the intended uses of the model (taken from AIAA, 1998).
• Uncertainty quantification (UQ). The process of quantifying uncertainties associated with model calculations of true, physical QOIs, with the goals of accounting for all sources of uncertainty and quantifying the contributions of specific sources to the overall uncertainty.
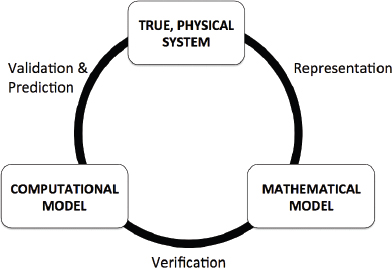
FIGURE 1.1 Verification, validation, and prediction as they relate to the true, physical system, the mathematical model, and the computational model. (Adapted from AIAA [1998].)
In this report, “quantifying uncertainty” in a prediction for a QOI means making a quantitative statement about the values that the QOI for the physical system may take, often in a new, unobserved setting. The statement could take the form of a bounding interval, a confidence interval, or a probability distribution, perhaps accompanied by an assessment of confidence in the statement. Much more is said on this topic throughout this Introduction and the rest of the report.
There is wide but not universal agreement on the terms, concepts, and definitions described above. These and other terms, many of which are potentially confusing terms of art, are discussed in the Glossary (Appendix A).
1.3.1 Focus on Prediction with Physics/Engineering Models
Mathematical models for the computational simulation of complex real-world processes are a crucial ingredient in virtually every field of science, engineering, medicine, and business. The focus of this report is on physics-based and engineering models, which often provide a strong basis for producing useful extrapolative predictions.
There is a wide range of models, but the science and engineering models on which this report focuses are most commonly composed of integral equations and partial and ordinary differential equations. Each modeling scenario has unique issues and characteristics that strongly affect the implementation of VVUQ. Relevant issues include the following:
• The level of empiricism versus physical laws encoded in the model,
• The availability and relevance of physical data to the predictions required by the scenario,
• The extent of interpolation versus extrapolation needed for the required predictions,
• The complexity of the physical system being modeled, and
• The computational demands of running the computational model.
The modeling framework assumed throughout most of this report is common in science and engineering: a complex physical process or structure is modeled using applied mathematics, typically with a mathematical model consisting of partial differential equations and/or integral equations and with a computational model that solves a numerical approximation of the mathematical model. Referring to the issues listed above, this report considers scenarios in which:
• Models are strongly governed by physical constraints and rules,
• The availability of relevant physical observations is limited,
• Predictions may be required in untested and/or unobserved physical conditions,
• The physical system being modeled may be quite complex, and
• The computational demands of the model may limit the number of simulations that can be carried out.
Of course many of these scenarios are found in other simulation and modeling applications. To this extent, the topics covered in this report are applicable to other modeling applications.
1.3.2 Focus on Mathematical and Quantitative Issues
The focus on mathematical foundations of VVUQ leads this committee to omit important concepts of model evaluation that are more qualitative in nature. The NRC report Models in Environmental Regulatory Decision Making (NRC, 2007a) considers a much broader perspective on model evaluation, including topics such as conceptual model formulation, peer review, and transparency that are not considered in this report. Behavioral Modeling and Simulation: From Individuals to Societies (NRC, 2007b) considers VVUQ for behavioral, organizational, and societal models.
This report utilizes several examples to illustrate the challenges of executing a mathematically founded VVUQ analysis. Some of these examples have broad implications, and their inclusion in this report is intended as a means to communicate VVUQ concepts and is not intended as a broader discussion of decision making with models. VVUQ activities enhance the decision-making process and are part of a larger group of decision-support tools that include modeling, simulation, and experimentation. The types of decisions discussed in this report can be grouped into two broad categories: (1) decisions that arise as part of the planning and conduct of the VVUQ activities themselves and (2) decisions made with the use of VVUQ results about an application at hand. Chapter 6 discusses the role that VVUQ plays in decision making and includes two examples of how VVUQ fits in with the decision-making process.
1.4 VVUQ PROCESSES AND PRINCIPLES
VVUQ processes must focus on a set of specified QOIs rather than on the full solution of the model. Quantitative statements about errors and uncertainties are well founded only in reference to specified QOIs. For example, there may be much more uncertainty in the estimate of maximum stress than in that of average stress in some component of some structure; thus, no single statement quantifying uncertainty would apply to both of these example QOIs. Similarly, a model may provide accurate estimates for one QOI while yielding inaccurate results for another.
Many physical systems of interest can be viewed as being composed of subsystems, which are themselves composed of sub-subsystems, and so on. Many large-scale computational models are similarly built up from a hierarchy of models, culminating in a complex integrated model. Such hierarchies are illustrated in Figure 1.2.
The advantage of such a hierarchy is that one can begin the VVUQ processes with the lowest-level subsystems, whose models are less complicated and whose data are easier and cheaper to obtain. Once this is done for the lowest-level subsystems and models, the results form a foundation for VVUQ at the next level in the hierarchy, and so on up to the full system and its QOIs.
Code verification—determining whether the code correctly executes the intended algorithms—presupposes a computer code that has been developed with software-quality engineering practices and results that are appropriate for the intended use. This report assumes that such practices are in play but does not discuss them. Code verification
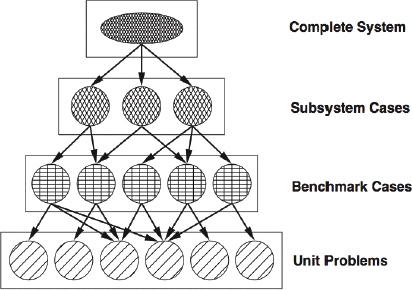
FIGURE 1.2 Validation phases suggested in AIAA (1998), based on hierarchically decomposing a physical system and the models that represent it. Levels in the validation hierarchy range from simple unit problems to benchmark cases to more integrated subsystems and eventually to the complete, integrated system. Verification and uncertainty quantification processes can fruitfully exploit a similar hierarchy.
relies on test problems for which the intended algorithm’s correct solution is known. It is challenging to develop a suite of such problems that test all of the relevant algorithms under all relevant combinations of options. Even if a typical complex science or engineering code behaves as expected for a large number of tests, one cannot prove that it has no algorithmic errors.
Solution verification—determining how accurately the numerical algorithm solves the mathematical model equations—must be carried out in terms of specified QOIs, which are usually functionals of the full computed solution. The goal of solution verification is to estimate, and control if possible, the error in each QOI for the simulation problem at hand. The error in a given QOI should not be assumed to be of the same magnitude as the error in another; rather, solution verification must be performed for each QOI individually. Further, the error in a given QOI in a given problem may differ significantly from the error in the same QOI in a slightly different problem.
As noted above, the efficiency and effectiveness of code and solution verification processes can often be enhanced by exploiting the hierarchical composition of codes and solutions, verifying first the lowest-level building blocks and moving successively to more complex levels.
The process of validation involves comparisons between QOIs computed by the model and corresponding true, physical QOIs inferred from physical observations or experiments. The intended use of the model determines how close the model’s QOIs must be to the true QOIs in order for the model to serve its purpose; that is, the intended use determines the requirements on model accuracy. Validation comparisons are conducted relative to these requirements.
In designing experiments for a validation hierarchy, the goal is to carry out a sequence of experiments efficiently, at different levels of the hierarchy, to assess quantitatively the model’s ability to predict the QOIs at the full system level. Often in science and engineering applications there are parameters within a model whose values are not known from theory or prior measurements. The best values—or a multivariate probability distribution— for these parameters for a given application must be inferred from new measurements. This inference process is calibration. When calibration is required, it is most efficiently and accurately performed at the lowest hierarchical level that provides the needed data. Higher levels introduce confounding factors that make it more difficult to draw quantitative inferences about the parameters in question.
Many factors arise in practice to complicate the validation process. Measurement and inference errors contaminate the QOIs determined from physical observations or experiments. The difference between the computational model and the mathematical model—partly caused by numerical approximations and imperfect iterative convergence—can make it difficult to infer anything about the mathematical model and difficult to determine whether a computational model is getting the “right answer for the right reason.” Validation must also take into account the effects of uncertainties in model-input parameters on computed QOIs; thus, the validation process involves UQ processes. These complications are discussed in the Chapter 5, “Model Validation and Prediction.”
Some experts distinguish model-based predictions at conditions similar to those for which physical observations exist from predictions at new, untested conditions for the physical system (AIAA, 1998; Oberkampf et al., 2004). The terms interpolative prediction and extrapolative prediction can be used to refer to the former and latter cases, respectively. Suppose that validation assessments have quantified the differences between calculated QOIs and corresponding physical QOIs that were inferred from many previous measurements. Then in the interpolative case, one may be justified in assuming a difference of similar magnitude between the predicted QOI and the true, physical QOI in the untested system. The extrapolative case is more difficult. The new conditions may introduce physical phenomena that are not well modeled, for example, causing the prediction to have greater error than the errors seen in the validation study. That is, it can be risky to assume that the validation study provides a reliable quantitative estimate of the model error for the new problem. If the validation study is assessed not to be reliable
for the new problem, it is difficult to find a rigorous basis for quantifying the uncertainty in the computationally estimated QOI.
The preceding discussion speaks of interpolative predictions as being relatively straightforward and “safe” and of extrapolative predictions as being relatively difficulty and “risky.” While this is intuitively appealing, outside of exceedingly simple settings there is no satisfactory mathematical definition of interpolative or extrapolative categories given the complex science and engineering problems that are addressed in this report. The problems of interest are characterized by large numbers of parameters, which can be viewed mathematically as forming a high-dimensional problem-domain space in which each problem corresponds to a point in the space. Given a finite set of physical observations in such a high-dimensional space, virtually any new problem will be an extrapolation beyond the portion of the domain that is “enclosed” by this set. Even if a new problem can be considered interior to the set of available physical observations, the estimated prediction uncertainty may be unreliable unless the QOI is a smooth function over this domain space. These and related issues are discussed in Chapter 5, “Model Validation and Prediction.”
1.4.4 Uncertainty Quantification
The definition adopted in this report for uncertainty quantification describes the overall task of assessing uncertainty in a computational estimate of a physical QOI. This overall task involves many smaller UQ tasks, which are briefly discussed here. This discussion does not explicitly mention exploitation of hierarchical decompositions of the problem, illustrated in Figure 1.2, but such exploitation should be considered when possible in the execution of any VVUQ process.
In the following discussion, it is assumed that preliminaries (code verification, model-parameter calibration if necessary, and validation exercises that have quantified or bounded model error) have been successfully accomplished before UQ begins for a prediction. As mentioned previously in this section, an important question that must be addressed is whether the model error inferred from validation studies is reliably relevant to the new problem being predicted.
The first UQ task is to quantify uncertainties in model inputs, often by specifying ranges or probability distributions. Model inputs include those that do not vary from problem to problem (acceleration of gravity, thermal conductivity of a given material, etc.) as well as those that are problem-dependent (such as boundary and initial conditions).
A key UQ task is to propagate input uncertainties through the calculation to quantify the effects of those uncertainties on the computed QOIs. Whether or not the computational model is an adequate representation of reality, understanding the mapping of inputs to outputs in the model is a key ingredient in the assessment of prediction uncertainty and in gaining an understanding of model behavior. It is conceptually possible to generate a large set of Monte Carlo samples of inputs, run these random input settings through the model, and collect the resulting model outputs to accomplish the forward propagation of input uncertainty. However, the computational demands of the model often preclude the possibility of carrying out a large ensemble of model runs, and the number of points required to sample a high-dimensional input-parameter space densely is prohibitively large. Also, understanding low-probability high-consequence events is difficult using standard Monte Carlo schemes because such events are rarely generated. Current research in mathematical foundations of VVUQ, described in Chapter 4, “Emulation, Reduced-Order Modeling, and Forward Propagation,” is focused on approaches for overcoming these challenges for forward propagation of uncertainties.
Another UQ task is quantification of variability in the true physical QOI, which can arise from random processes or from “hidden” variables that are absent from the model. Appropriate methods for quantification depend on the source and nature of the variability.
An important UQ task is the aggregation of uncertainties that arise from different sources. The uncertainties in the QOI that are due to uncertain inputs, true, physical variability, numerical error, and model error must be combined into a quantitative characterization of the overall uncertainty in the computational prediction of a given physical QOI. This UQ challenge and the others mentioned above are discussed in more detail in Chapter 4, “Emulation, Reduced-Order Modeling, and Forward Propagation.”
A summary of several observations regarding VVUQ follows:
• VVUQ tasks are interrelated. A solution-verification study may incorrectly characterize the accuracy of the code’s solution if code verification was inadequate. A validation assessment depends on the assessment of numerical error produced by solution verification and on the propagation of model-input uncertainties to computed QOIs.
• The processes of VVUQ should be applied in the context of an identified set of QOIs. A model may provide an excellent approximation to one QOI in a given problem while providing poor approximations to other QOIs. Thus, the questions that VVUQ must address are not well posed unless the QOIs have been defined.
• Verification and validation are not yes/no questions with yes/no answers but instead are quantitative assessments of differences. Solution verification characterizes the difference between the computational model’s solution and the underlying mathematical model’s solution. Validation involves quantitative characterization of the difference between computed QOIs and true, physical QOIs.
1.5 UNCERTAINTY AND PROBABILITY
It is unanimously agreed that statistics depends somehow on probability. But, as to what probability is and how it is connected with statistics, there has seldom been such complete disagreement and breakdown of communication since the Tower of Babel. Doubtless, much of the disagreement is merely terminological and would disappear under sufficiently sharp analysis. (Savage, 1954, p. 2)
The hopeful view expressed in the last sentence of the quotation above more than 50 years ago has not been realized. Controversy still abounds concerning the meaning and use of probability and related notions to capture uncertainty (e.g., fuzzy logic). It is not possible to address these issues comprehensively in this report, nor is it the purpose of this study. In the interest of clarity, one framework for reasoning about uncertainty was chosen (out of many possible) and is now described.
The most common method of dealing with uncertainty in VVUQ is through standard probability theory. In this approach unknowns are represented by probability distributions, and rules of probability are used to combine the probability distributions in order to assess the uncertainty in the predictions derived from computer models. This is the approach employed in this report. The approach is capable of synthesizing most, if not all, of the uncertainties that arise in VVUQ, and it offers a straightforward and readily understood means of quantifying uncertainties in model predictions of physical QOIs. This choice is not meant as a judgment that alternative frameworks are invalid or lacking but is meant to provide a single, relatively transparent framework to illuminate VVUQ issues.
Two concerns are often raised with the probabilistic approach. The first concern is the difference between epistemic and aleatoric probability and the combination of these two types of uncertainty. Aleatoric probabilities arise from actual randomness in the real system, and epistemic probabilities typically arise from a lack of knowledge.
• Example. Suppose that the manufacturing process for a weapon results in 10 percent nonfunctional weapons; then each weapon randomly has a probability of failure of 0.1 (an aleatoric probability). Alternatively, suppose that the weapon design is based partly on speculative science and the weapons cannot be physically tested. It is judged that there is a 10 percent chance that the science is wrong, in which case none of the weapons would work. Again each particular weapon has a probability of failure of 0.1 (an epistemic probability). But, obviously, the ramifications of these two 0.1 probability statements are very different.
Although a single weapon in this example has a failure probability of 0.1 under either scenario, the joint probability distributions of failure for the weapons are very different. In the aleatoric case, the weapons independently have a 0.1 probability of failure, while in the epistemic case they either all succeed or all fail together, with 0.1 probability of failure. Figure 1.3 shows the joint probability distribution of two weapons in these two different

FIGURE 1.3 The joint probability distribution for the reliability of two weapons in a stockpile. Left: Each weapon works or fails independently, with a 90 percent chance of working. Right: A common failure mode gives a 90 percent chance that both weapons work. In this case, either both weapons work or both fail.
situations. The joint distributions communicate the complete picture and clearly differentiate between the two situations. The message here is that standard probability theory does properly distinguish between the two situations, but one must take care in communicating the result. Summarizing a probabilistic description of a prediction with a single metric can be misleading. For example, the chance of failure of a weapon randomly chosen from the stockpile does not address the question of whether or not there is an appreciable chance that the entire stockpile might fail.
Many scientists are reluctant to use the same probability calculus to represent both knowledge uncertainty (epistemic probability) and true randomness (aleatoric probability). This is a centuries-old debate in science and philosophy in which this report will not engage. This report uses the standard probability calculus for both types of uncertainty to illustrate its points, while recognizing that in some applications there may be good reasons to take different approaches.
The second concern often raised with respect to standard probability theory is that it is a “precise” theory, whereas probability judgments are often imprecise. For instance, the precise statement in the above example— that there is a 10 percent chance that the science is wrong—can be questioned; might not a more accurate analysis yield 10.1 percent or 10.01 percent? Here there is less debate philosophically, in that probability judgments are indeed often imprecise. There is no agreement, however, on how to combine imprecise probability judgments into an overall assessment of the uncertainty of predictions. One option is to consider the “worst case” over all the possibilities that are not ruled out. This worst case is often so conservative that it does not provide useful information. However, when worst-case analysis is not overly conservative, it yields a powerful assessment of uncertainty.
Although open to other possibilities, the committee holds the view that currently the use of standard probability modeling is often a reasonable mechanism for producing an overall assessment of accuracy in prediction in VVUQ, and it provides a consistent framework in which this report can illustrate its points. Interval descriptions, such as 0.09 < x < 0.11, are treated in this report by conversion to standard probability distributions: for example, by treating p as being uniformly distributed over the interval (0.09, 0.11). Other treatments are possible and in some cases may be preferable.
To help clarify VVUQ concepts, the easily visualized phenomenon of dropping a ball from a tower can be used. Experiments measure the time that it takes the ball to fall from different heights. This simple example, described in Box 1.1 and discussed in this chapter and in Chapter 5, provides a ready physical example for outlining many of the main ideas of VVUQ. This section describes the physical system, posits a simple model for system behavior, and indicates how various sources of uncertainty and bias can affect the model predictions. It is also possible to explore the model in a manner that typifies many applications of physics and engineering and in a way that exposes how uncertainties arise in the resulting prediction for the QOI. These themes recur in many parts of the report.
Box 1.1
Dropping a Bowling Ball from a Tower
The time that it takes for a bowling ball to fall from a tower 100 meters (m) high will be predicted by using experimental drop times obtained from a 60-m tower (Figure 1.1.1(a)). Drop times are recorded for heights of 10, 20,…, 50 m, and a validation experiment of dropping a ball from 60 m is also conducted. The uncertainty in the measured drop times is normally distributed about the true time with a standard deviation of 0.1 seconds (s). The quantity of interest (QOI) is the drop time for the bowling ball at a height of 100 m. Since the tower is only 60 m high, a computational model is used to help make this assessment.
The conceptual model incorporates only acceleration due to gravity g, allowing the computational solution used here to be compared to an analytical solution for a verification assessment of bowling ball drop times between 10 m and 100 m.
The physical constant g is assumed to be unknown, but between 8 and 12 m/s2 (light lines). The five drop-time measurements (black dots; Figure 1.1.1(b) constrain the uncertainty about g to the probability density given by the dark line.
The drop times produced by the computational model (light lines in Figure 1.1.1(c)) are shown for 11 different values of g. The experimental data are shown with error bars of +2 standard deviations—the measurement error for the 60 m is not used. The constrained uncertainty for g results in a 95 percent prediction interval for the drop time (as a function of height) depicted by the dark region in Figure 1.1.1(b).
A validation experiment, dropping the bowling ball from 60 m, is conducted so that the prediction can be compared to the measured drop time. The drop-time measurement for 60 m (black dot in Figure 1.1.1(d)) is quite consistent with the prediction and its uncertainty.
A prediction with the uncertainty for the QOI (drop time at 100 m) is given by the light line in Figure 1.1.1(d). The uncertainty accounts for measurement error and parametric uncertainty. Numerical error and model discrepancy are not accounted for in this assessment.
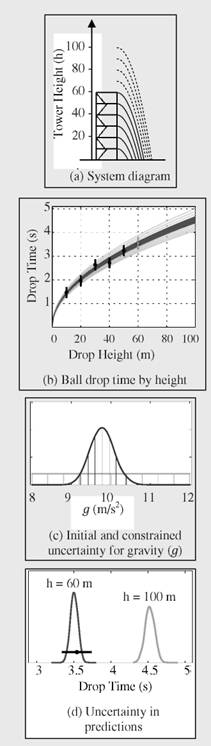
FIGURE 1.1.1
With respect to the physical system for the case study, a bowling ball is released from rest at a height h above the ground (see Figure 1.1.1(a) in Box 1.1), and the time that it takes for the ball to reach the ground is recorded. Drop heights of 10 m, 20 m,…, 60 m are available from the tower. Gravity acts on the ball, causing it to accelerate. The goal is to predict how long it takes for the bowling ball to hit the ground, starting from a height of 100 m. This drop time for a 100-m drop of a bowling ball is the QOI for this experiment. To help address this question, a computational model (described below) and a number of experimentally measured drop times from different heights will be used. But since the tower is only 60 m high, no higher drops are possible.
The simplest conceivable model for this system assumes that the bowling ball accelerates toward the ground at a constant acceleration given by the gravitational constant g (see Figure 1.1.1(b) in Box 1.1). For now, assume that the exact acceleration due to gravity is unknown—only that this acceleration is between 8 and 12 meters per second per second (m/s2). Experiments in which the bowling bowl is dropped from different heights will help to reduce this uncertainty. For now, uncertainty about g is described by a uniform prior distribution whose range is from 8 m/s2 to 12 m/s2 (see Figure 1.1.1(c), light lines, in Box 1.1).
The mathematical model is sufficiently simple and the drop time can be computed analytically for any drop height, as long as the value for g is supplied. It is far more common to solve a mathematical system using computational approaches that produce an approximate solution to the system (Morton and Mayers, 2005; Press et al., 2007). Assessing the quality of this approximation is one of the key functions of verification. Much of the work in verification focuses on quantifying or bounding the difference between computationally and mathematically derived solutions. In most applications, this quantification is challenging because the mathematical solution is not available.
A number of uncertain quantities that affect the eventual prediction uncertainty for the QOI can be identified. First and most important is the uncertain constant, g—the acceleration due to gravity. Uncertainty regarding this parameter leads to uncertainty in predictions (see Figure 1.1.1(d) in Box 1.1). In other applications, the assessed accuracy of the computational model relative to the mathematical model being solved is an important source of uncertainty (but not here because the mathematical model is relatively straightforward).
The nature, number, and accuracy of the experimental measurements also affect prediction uncertainty. Here the difference between measured and actual drop times should be within 0.2 seconds 95 percent of the time. These deviations, sometimes described as measurement “errors,” may be due to the timing process or to variations in the initial position and velocity of the bowling ball as it is released for the drops. The measurement errors are assumed to be independent, directly affecting the updated, or posterior, uncertainty for g. This would not be the case if, for instance, the stopwatch being used ran slightly fast. In that case, all the measured drop times would be systematically low. If it is known that such systematic errors may exist in the measurement process, they can be accounted for probabilistically. When such systematic effects go undetected, obtaining appropriate prediction uncertainties is more difficult.
Inadequacies in the model may also contribute uncertainty to drop-time predictions. This simple model does not account for effects due to air friction. Fortunately, a bowling ball, at the velocities obtained in these experiments, is rather insensitive to the effects of air friction. This would not be the case if a basketball was used instead. Regardless, if very high accuracy is required for the eventual prediction, then additional experiments, more accurate measurements, and/or a more accurate model may be required.
1.6.5 Propagation of Input Uncertainties
One might also like to carry out an uncertainty analysis in which a distribution on the inputs is propagated through the simulation model to give uncertainty about the outputs. This is done in Box 1.1 for both the initial and the constrained distributions for g. Such propagation analyses, which can be carried out in principle using a Monte Carlo simulation, can be very time-consuming when the model is computationally demanding. Dealing with such computational constraints when exploring how the model outputs are affected by input variations is considered in more detail in Chapter 4, “Emulation, Reduced-Order Modeling, and Forward Propagation.”
1.6.6 Validation and Prediction
At this point, the experimental observations need to be combined with the computational model in order to obtain more reliable uncertainties regarding the simulation-based prediction for the QOI—the drop time for the bowling ball at 100 m. The drop times can be used to constrain the uncertainty regarding g to give more reliable predictions and uncertainties.
In principle, this inference problem can be tackled using nonlinear regression, from either a likelihood perspective (Seber and Wild, 2003) or a Bayesian perspective (Gelman, 2004). In fact, Figure 1.1.1(c) in Box 1.1 shows the posterior distribution for g resulting from using the experimental measurements to reduce uncertainty and the posterior predictions for the drop times of the bowling ball as a function of height. Here the prediction uncertainty (given by the dark region in Figure 1.1.1(d) in Box 1.1) is due to uncertainty in g. However, this analysis has some drawbacks:
• It requires, at least in principle, many evaluations of the computational model;
• It assumes that the computational model reproduces reality when the appropriate value of g is used; and
• It does not account, in any formal way, for the increased uncertainty that one should expect in predicting the 100-m drop time when only data from heights of 60 m or less are available.
These issues highlight some of the fundamental challenges for the mathematical foundations for VVUQ. Methods for dealing with limited numbers of simulation runs have been a focus of research in VVUQ for the past few decades. However, relatively few approaches for quantifying prediction uncertainty when the computational model has deficiencies have been proposed in the research literature. Predicting the drop time for the bowling ball from 100 m is a good example of how complicated things can get, even for an example as basic as this one.
A helpful experiment—called a validation experiment—tries to assess the model’s capability for making a less drastic extrapolation. Here, experiments consisting of drop heights of 10 m,…, 50 m are used, along with the model, to make a prediction with uncertainty for a drop of 60 m. The prediction and measured results are shown in Figure 1.1.1(d) in Box 1.1, showing strong agreement between the prediction and experimental measurement. Still, the confidence that one should have in the model’s prediction for a drop of 100 m remains hard to quantify in any formal manner.
The ability to model and quantify uncertainties of this system can be used to make decisions about how knowledge of the physical system can be improved. Specifically, what actions will most effectively reduce the uncertainty in predicting the drop time for the bowling ball at 100 m? Actions might include carrying out new experiments, carrying out additional simulations, measuring initial conditions more accurately, improving the experimental timing capabilities, or improving the computational model. For example, the relative merits between extending the tower to 70 m or improving the experimental timing accuracy could be assessed quantitatively, given the available information, costs, and how the new changes are likely to improve uncertainties.
1.7 ORGANIZATION OF THIS REPORT
Following this introductory chapter is the cataloging and discussion of the elements briefly listed in it. Chapter 3 addresses code and solution verification. Chapter 4 addresses the propagation of input uncertainties through the computational model to quantify the resulting uncertainties in calculated QOIs and to carry out sensitivity analyses. Chapter 5 tackles the complex topics of validation and prediction. Chapter 6 addresses the use of computational models and VVUQ to inform important decisions. Chapter 7 discusses today’s best practices in VVUQ and identifies research that would improve mathematical foundations of VVUQ. It also discusses VVUQ-related issues in education and offers recommendations for educational changes that would enhance VVUQ capabilities among those who will need to employ them in the future.
AIAA (American Institute for Aeronautics and Astronautics). 1998. Guide for the Verification and Validation of Computational Fluid Dynamics Simulations. Reston, Va.: AIAA.
Box, G., and N. Draper. 1987. Empirical Model Building and Response Surfaces. New York: Wiley.
Gelman, Andrew. 2004. Bayesian Data Analysis. Boca Raton, Fla.: CRC Press.
Morton, K.W., and D.F. Mayers. 2005. Numerical Solution of Partial Differential Equations. Cambridge, U.K.: Cambridge University Press.
NRC (National Research Council). 2007a. Models in Environmental Regulatory Decision Making. Washington, D.C.: The National Academies Press.
NRC. 2007b. Behavioral Modeling and Simulation: From Individuals to Societies. Washington, D.C.: The National Academies Press.
Oberkampf, W.L., T.G. Trucano, and C. Hirsch. 2004. Verification, Validation, and Predictive Capability in Computational Engineering and Physics. Applied Mechanical Reviews 57:345.
Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P Flannery. 2007. Numerical Recipes: The Art of Scientific Computing, Third Edition. New York: Cambridge University Press.
Savage, L.J. 1954. The Foundations of Statistics. New York: Wiley.
Seber, G., and C.J. Wild. 2003. Nonlinear Regression. Indianapolis, Ind.: Wiley-IEEE.












