The Hog Game
|
Devise optimal strategies Explore different areas of mathematics in one problem setting Link assessment to instruction |
Suggested time allotment
A total of two or three class periods
Student social organization
Students working in pairs
Task
Assumed background: This task uses a game called Hog to pose questions that require students to use two areas of mathematics to answer. On the first day the questions concern combinatorics and reasoning about the possibility or impossibility of certain outcomes. On the second day the questions concern strategies for playing the game, based on the probabilities involved. Therefore, students should have had experience with both areas: They should be familiar with analyzing situations by enumerating all the possibilities; and they should have had experience with probabilistic situations (games in particular) that are more complex than simple coin-tossing and that require the collection

of data. The idea of formulating and communicating a strategy for playing a game should be familiar to them.
Presenting the task: The teacher should pass out the first student sheet and several number cubes (cubes numbered from 1 to 6) to each pair of students being assessed. The teacher should then read through the directions for the game and the three examples to be sure that everyone has an understanding of the rules of the game. Students should then be given the opportunity to play the game to see how it works.
Doing Part 1 (Questions 1 through 4) will be the first class period, and Part 2 (Questions 5 and 6) can be done in another one or two periods. Students should be given as much time as they need to gather a considerable amount of data as they respond to Questions 5 and 6.
Student assessment activity: See the following pages.
Names __________________ and __________________ Date ___________
This is a game called HOG. You will need number cubes, a cup, and pencil and paper. The object of the game is to get as large a score as you can.
Here are the rules:
-
Say how many number cubes you want to put in the cup.
-
Roll that many number cubes from the cup.
-
If none of the numbers you rolled is a 1, then your score is the sum of the numbers you rolled.
-
If a 1 comes up on any of your number cubes, then your score is 0.
Here are some examples:
Example: Mary said that she wanted to put 3 number cubes in the cup. Here's what she got: Since she didn't get any 1's, her score is 5 + 2 + 4, or 11.
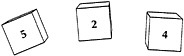
Example: Justina said that she wanted to put 7 number cubes in the cup. Here's what she got: Since she got a 1 (in fact, she got two of them), her score is 0.
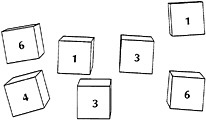
Example: José said that he wanted to put 3 number cubes in the cup. The numbers he rolled were: 5, 6, and 1. His score was 0.
You and your partner should play the game for a while to see how it works. Then answer these questions:
Names __________________ and __________________ Date ___________
Part 1
-
Tsao-lim said he wanted put 8 number cubes in the cup. He got 3, 5, 1, 4, 4, 4, 6, and 2.
What was his score? __________ Why?
-
Jeffella said she wanted to put 8 number cubes in the cup. She got 3, 5, 2, 4, 4, 4, 6, and 2.
What was her score? __________ Why?
-
Karl put 2 number cubes in the cup. His score was 7. List all of the ways he could have gotten a 7 with 2 number cubes.
-
Johann said he wanted to put 8 number cubes in the cup. It turned out that his score was 19.
-
Could all of the number cubes have been 3s? ________ Explain why or why not.
-
Could 3 of the 8 number cubes have been 3s? ________ Explain why or why not.
-
Could one of the number cubes have been a 6? ________ Explain why or why not.
Names __________________ and __________________ Date ___________
Here are some more questions about the game called HOG. Remember, the object of the game is to get as large a score as you can. Also, if any number cube you roll is a 1, then your score is 0.
Part 2
-
Estrella found a very large cup and said she wanted to put 100 number cubes in it. What do you think her score would probably be? _________ Explain why you think so.
-
Roberto says he has a strategy for playing HOG. His strategy is to put 2 number cubes in the cup every time he plays.
Quentin says he has a different strategy for playing HOG. Quentin's strategy is to put 1 number cube in the cup every time he plays.
One partner should play HOG for a while using Roberto's strategy, and the other partner should play the game for a while using Quentin's strategy. Keep track of what happens.
-
Which strategy do you think is better — Roberto's or Quentin's? ____________________ Explain your answer.
-
Suppose you want to find the best strategy for playing HOG. Each time you play it, you're going to use the same number of cubes in the cup. Remember that you are trying to get the highest total score for whatever number of times you play. How many number cubes would you choose to put in the cup? _________ Please explain how you decided on this number.
-
How sure are you that you have found the best strategy? Why do you think that?
Rationale for the mathematics education community
The Hog Game, as noted earlier, illustrates how the same underlying situation can be used as a vehicle for exploring different areas of mathematics. In this case, some of the questions about the game involve relatively simple numerical concepts, while other questions involve more sophisticated ideas from probability. Even the simplest numerical questions are non-routine, however, and are presented in a format that requires the child to explain his or her reasoning carefully.
Even though the rules of the game are straightforward (and in fact will already be familiar to some children), optimal strategies are not at all obvious. That is, students will not come to the Hog Game task with an a priori idea of what is ''supposed" to happen. (In contrast, tasks that are based on activities like flipping a fair coin and counting heads or tails often do not promote genuine exploration, and may even discourage it because children have preconceptions about what the results "should" turn out to be.)
This prototype is also another good example of an assessment task that can be linked back into instruction, through a whole-class discussion of results. One possibility is to pool the results obtained in responding to question 6, to get a more definitive idea of what strategies work best. Another is to take advantage of the computer technology that is widely available in U.S. classrooms to create a simulation of the Hog game. A very simple computer program, written in BASIC appears in an appendix to this task. (No amount of simulated play is going to be able to distinguish the strategy of putting 5 number cubes in the cup from the strategy of using 6 number cubes, because the two strategies both yield an expected score of 8, which is the best score that can be obtained. One run of a computer simulation yielded mean scores of 8.008 and 8.067 for 5 and 6 number cubes, respectively, with each strategy being used in 200,000 games.)
Task design considerations: Some students today play a game similar to this one that is known as PIG. Usually the rules state that the player declares how many times he or she is going to roll a single number cube; if the number cube shows 1 on any roll then the player's score is 0; otherwise it is the sum
of the rolls. The rules are easier to convey, however, if they are phrased in terms of rolling, once, a cup containing a pre-determined number of cubes. Unfortunately for the sake of classroom logistics, the many-cubes-in-the-cup version requires a larger supply of number cubes if all the children are going to be engaged in the task simultaneously. One way of handling this is to have only a few pairs of children working on the task at the same time.
The point of making Tsao-lim's and Jeffella's rolls in questions 1 and 2 identical — except that Jeffella got a 2 instead of Tsao-lim's 1 — is to reinforce the difference that a single number cube can make. Tsao-lim's and Jeffella's scores are not just 1 apart; Tsao-lim's 1 makes his score 0.
Note that the instructions just before the first question (as well as in questions 5 and 6) are very directive: playing the game is not left as an option. On the other hand, one of the decisions that is left up to each pair of students is how many times they should play in answering questions 5 and 6 — that is, how much data they should gather. Ultimately, of course, one would want students to view playing the game as just another tool that can be used or not used in approaching a problem, and one would want to assess the degree to which children use that tool, if it is appropriate, on their own, without explicit directions to do so.
Similarly, the instruction to "Keep track of what happens" in question 6 is deliberately vague; the students are given no guidance about how to organize their results.
Question 8 was added after the first round of pilot testing, in an attempt to tap the level of confidence that the student has in his or her results. Ideally, the student should be able to distinguish the certainty of a response to question 4c (it is impossible for Johann to get a score of 19 with 8 number cubes if one of them is a 6) from the tentative nature of a response based on a limited number of trials.
Variants and extensions:
Part 1. There are many variants of the simple numerical questions that can be posed along the lines suggested in question 4. A more substantial variant is to ask how many number
cubes a player who gets a certain score might have been using. For example, if Johann got a score of 19, what is the largest number of cubes he might have been using? What is the smallest number of cubes that he might have used? Or: Emmy rolls twice, using the same number of cubes each time. First she gets a score of 11, and then she gets a score of 23. How many cubes are in her cup?
Part 2. This task provides a good example of how the inclusion of intermediate questions can provide a "scaffolding" to help students approach the problem of deciding whether Roberto's or Quentin's strategy is better. For example, after Roberto's and Quentin's strategies are described, one might ask:
When Roberto rolls the two number cubes, what numbers could he get? List all the possible rolls with two number cubes. Then, for each one, write the score that Roberto would get for that roll. (One might even provide a 6-by-6 table to be filled out with the scores that Roberto could obtain.) Now do the same for Quentin: List all the possible rolls he could get with one number cube, and for each one write his score. Based on your findings, which strategy do you think is better — Roberto's or Quentin's? Explain your answer.
By not providing the additional questions suggested above, the task becomes more open-ended because it requires the child to supply the analytic tools (e.g. a 6-by-6 table of possible outcomes for two number cubes) that are needed.
Question 7 structures the strategy-finding task by specifying that the cup must contain the same number of cubes on every roll. An alternative would be to relax that condition. In a less structured version of the task, one child said that she would start with one cube, and increase that by one cube on every roll until she got a score of zero. Then on the next roll she would remove one cube (unless there were only one cube in the cup). This is the sort of variant that could be explored after the assessment is finished.
Protorubric
The fact that the Hog Game assessment task is divided into two parts, involving different mathematical ideas and to be done on different days, highlights the issue of the scope of the scoring rubric. Essentially there are two options in this instance: to treat the two parts separately, with a scoring rubric for each, or to lump them together under a single scoring rubric. The second alternative simply exacerbates the problem of making unambiguous judgments, since it is possible that many children will do better on one part of the task than on the other. Hence two protorubrics are provided below, one for each component of the task.
Part 1
Characteristics of the high response:

The responses to questions 1 and 2 are correct (0 and 30, respectively) with justifications that assert that (a) Tsao-Lim got a 1, and so his score is 0; and (b) Jeffella did not get any 1s, and so her score is the sum of the numbers showing.
In question 3, the pairs 5 and 2, and 4 and 3 are listed. (Listing the pairs 2 and 5, and 3 and 4 as well is perfectly acceptable, but not necessary, since the context does not require 2 and 5 to be considered as being different from 5 and 2.)
The answers to questions 4a, b, and c are correct (No, Yes, and No, respectively), and the justifications are clear and accurate. In question 4c, for instance, the justification amounts to the following argument: Since his score was 19, he didn't get any 1's. But if one of his rolls had been a 6, then even if all of Johann's other rolls were 2's, his score would be at least 20. So he couldn't have had a 6.
Characteristics of the medium response:

The justifications given for the answers to questions 1 and 2 are not completely accurate, even though the scores given are correct.
The pair 1 and 6 is given as a possibility in question 3, forgetting that the 1 would result in a score of 0.
The reasons cited for one or more of questions 4a, b, and c are not complete. For example, the response to 4c is something like: No, because 6 would be too big.
Characteristics of the low response:

There is evidence in questions 1 and 2 that the student forgets or ignores the fundamental rule of the Hog Game. As an example, the answer to question 1 might be 29 (the sum of the rolls, forgetting that the 1 makes the score zero).
In question 2, there is a mistake in the arithmetic by at most 1, resulting in a score of 29 or 31.
In question 3, numbers may be offered that are not even on the number cubes (e.g., 0 and 7).
The responses to questions 4a, b, and c show pervasive misunderstandings. For example, the response to 4a might be: Yes, because 8 × 3 = 24.
Part 2
Characteristics of the high response:

The student says that Estrella's score would probably be 0, because it is very likely that at least one of the 100 number cubes will show a 1. (If her score isn't 0, it could be anything from 200 to 600, but that information is not required.)
One highest-level response to question 6 is an analysis that shows all of Roberto's possible outcomes in a 6-by-6 table. The sum of the scores of the 36 equally likely games is 200, and hence the average score per game using Roberto's strategy is 200/36. Quentin's strategy, on the other hand, allows 6 possible games, all equally likely; the average score is 20/6. Hence Roberto's strategy is better.
A somewhat lower-level response (but perfectly satisfactory for this age level) would be to play the game perhaps 20 times with each strategy, and then compute an average score for each.
On the low end of the high category is the response that Quentin's strategy is better because Roberto has a greater chance of throwing a 1, and therefore a better chance of getting a score of 0.
For question 7, the response should describe a process of trying various candidates for the number of cubes to put in the cup. The student should take into account the results obtained so far — that is, that rolling two cubes is better than rolling only one, and that rolling 100 cubes is not good. One good approach to finding an optimal number is one of successive approximation: Try putting 10 cubes in the cup and see what happens. Then try 5 cubes, etc.
For each candidate strategy, the students should play about 20 (or more) trial games, computing an average score for each. The final strategy chosen should be based on the empirical evidence gathered. No fourth-grade child should be expected to choose a strategy on any basis more sophisticated than the successive approximation method outlined above. (The best strategy is to put either 5 or 6 number cubes in the cup.)
The response to question 8 should admit a degree of uncertainty that is appropriate for the strategy chosen and the justification provided. If the successive approximation technique is used, the high-level response would be something like: "I'm not very sure that this is the best strategy. Maybe if I tried it lots more times I would find that some other number of cubes would be better to put in the cup."
Characteristics of the medium response:
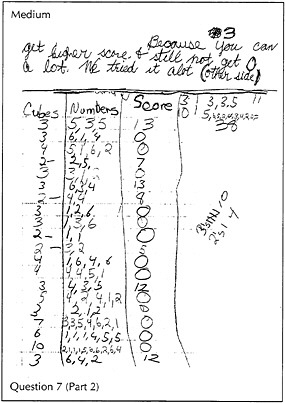
In general, either the explanations are incomplete or else there is some partial forgetting of the rules of the game. In question 5, for instance, the response is 0, with no explanation, or something around 300 or 400, with an explanation that claims there are 100 rolls and each one is going to be around a 3 or a 4.
In question 6, the response is empirically based on playing the game repeatedly, but using a small number of trials, or based on trials that are not clearly organized. Or the claim is that Roberto's strategy is better because he rolls more and hence has more of a chance to get more points (i.e., not taking into account that Roberto also has a bigger chance of rolling a 1, and thus getting a score of 0).
The answer to question 7 is based on a limited number of trials with just a few different numbers of cubes in the cup. A conclusion of "put 5 cubes in the cup", for example, might be reached without an explicit exploration of 4 and 6 cubes.
Characteristics of the low response:
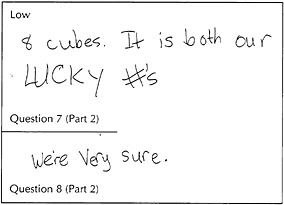
The responses to questions 6 and 7 are not at all based on any systematic, empirical investigation of the situation. Instead, the child plays the game just a few times (if at all) and records results in a way that does not convey any sense of keeping track of what is happening. The student leaps to a conclusion about Roberto and Quentin (or about opti
mal strategies in general) without justification, even though he or she may give the "correct answer" that Roberto's strategy is better.
Even an accurate answer to question 8 (such as: "I'm not sure I found the best strategy, because all I did was to guess") would not lift the response out of the low category.
Appendix
The following is a program written in Applesoft BASIC to simulate the playing of HOG. It calls for the number of number cubes to be put in the cup and for the number of rolls to be made. It then prints out the average score obtained.
|
10 |
INPUT "HOW MANY NUMBER CUBES DO YOU WANT TO PUT IN THE CUP?"; D |
|
20 |
INPUT "HOW MANY GAMES DO YOU WANT TO PLAY?"; G |
|
30 |
T = 0: REM THIS COUNTS TOTAL SCORE |
|
40 |
FOR I = 1 TO G |
|
50 |
S = 0: REM THIS IS THE SCORE WITHIN A SINGLE GAME |
|
60 |
FOR J = 1 TO D: REM LOOK AT EACH CUBE |
|
70 |
R = INT(6 * RND(1))+1: REM THIS IS A RANDOM WHOLE NUMBER BETWEEN 1 AND 6 |
|
80 |
IF R = 1 THEN GOTO 200: REM THE PROCESS IS SHORT-CIRCUITED AS SOON AS A 1 APPEARS |
|
90 |
S = S + R: REM THE CUBE ISN'T 1, SO ADD IT TO THE SCORE |
|
100 |
NEXT J |
|
110 |
T = T + S |
|
120 |
NEXT I |
|
130 |
PRINT "THE AVERAGE SCORE, PLAYING ";G;" GAMES, WITH ";D;" NUMBER CUBES, WAS '';T/G;"." |
|
140 |
PRINT: PRINT "DO YOU WANT TO PLAY AGAIN? (Y/N)" |
|
150 |
GET Q$ |
|
160 |
IF Q$ = "Y" THEN GOTO 10 |
|
170 |
END |
|
200 |
S = 0: J = D: GOTO 100 |
















