Point of View
|
Broaden the view of mathematics appropriate for 4th grade Visualize objects from other viewpoints Deduce information from a map Communicate results to others |
Suggested time allotment
One class period
Student social organization
Students working individually
Task
Assumed background: This task assumes that starting as early as kindergarten, children have had a variety of experiences with visualization, particularly imagining how something will appear from different points of view. Those experiences will include moving a small number of distinctive objects around on a horizontal surface, observing them from different viewpoints, and describing the relationships among them.

Presenting the task: The teacher should spend a brief period of time in an activity that involves imagining objects from different points of view. Three students (A, B, and C) should stand in the middle of the classroom, while the other children stand around the edges of the room. A, B, and C should be separated from each other by a few feet. Some of the children on the outside then should be asked to describe the order in which they see the three children, from left to right. Mary, for example, might see them as B, A, C, while Altoria, on the opposite side of the room, might see them as C, A, and B. Then everyone (including A, B, and C) should be asked to describe what Manuel, another child on the outside, sees. The teacher can conclude with questions like, ''Who are the children who see C in the middle?", "Who sees B directly in front of C?", etc.
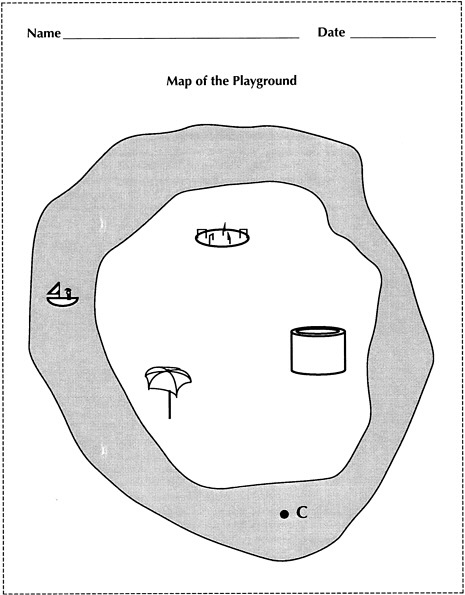
Student assessment activity: The teacher should distribute the questions along with the playground map, which is on a separate page. He or she should read the story on the students' sheet as the students read it, being sure that everyone realizes that the story refers to the map. The students will record responses both on the map and on the instruction sheet, so both pieces of paper should be collected at the end.
Name _________________________________________ Date ______________
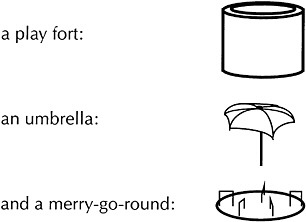
James has rented a rowboat to row in the pond around the playground. On the playground there are three pieces of equipment:
Look at the map. Find James in his boat. Imagine how the playground looks to James. From where James was, the playground looked like this:
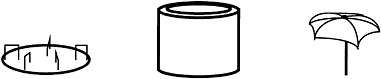
The merry-go-round was on the left, the umbrella was on the right, and the fort was in the middle.
|
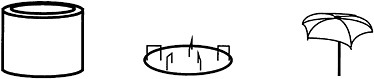
1. James rowed in the pond for a while. When he looked at the playground a second time, this is what it looked like: |
|
|
 |
|
|
Figure out where James was when he saw the playground this way. Draw a dot there and label it A. |
|
2. Then James rowed some more. He came to another spot, and stopped. When he looked at the playground from this spot, it looked different. From here, the playground looked like this: |
|
|
 |
|
|
Where was James now? Please draw another dot on the map to show where James was and label it B. |
|
|
3. James really enjoyed rowing, so he rowed some more and explored some more. After a while he was at the spot marked C. Please draw the fort, the umbrella, and the merry-go-round in the space below, to show the way the playground looked to James when he looked at it from the spot marked C. |
|
|
4. It was a warm, pleasant day, and James thought that maybe he would keep on rowing all afternoon. He rowed to a new spot on the pond. When he looked toward the playground, he was suddenly surprised. He could no longer see the umbrella! All he could see was the fort on the left, and the merry-go-round on the right. Please draw a dot on the map to show where James was when he discovered that he could not see the umbrella. Label it D. |
|
|
5. Do you think that James could row to a spot on the pond where he sees the fort on his left and the umbrella on his right, but he can't see the merry-go-round? _____ Please explain how you know. |
Rationale for the mathematics education community
Studies of the relation of visualization ability to mathematical ability are numerous. At least three issues appear to emerge from these studies. First, there seems to be a rather strong correlation between being good at visualizing and being good at mathematics. (And, of course, in addition to this general correlation, for many mathematics problems visualization is a direct requirement). Second, it appears to be true that improving one's visualization ability after about age 8 or 10 is very difficult, if not impossible. From this it would appear that developing good visualization ability while young is a matter of real importance. Finally, there is evidence that children whose greatest strengths lie in the area of visualization are often poorly served by schools, because these children seldom have any opportunity to make use of this very important skill.
Recognizing the importance of early visualization experiences, other nations (e.g., the Netherlands) include appropriate instruction early in the curriculum. One purpose of including this assessment task in the collection is to encourage such visualization experiences in the curriculum in the first four grades in the U.S.
Task design considerations: Several issues connected with the presentation of this task merit discussion.
First, the task deals only with the relative positions of the three objects — their order from left to right — not the appearance of each individual object. Thus the playground equipment has been chosen so that each piece looks almost the same regardless of the side from which it is viewed. The fort, for example, is a simple cylinder, with no door or other external features that would necessitate taking into account the object's differing appearances when viewed from different directions. In other words, the fort, taken by itself, will look the same to James no matter where he is on the pond. Other standard pieces of playground equipment (a slide, swing set, even a tetherball pole) would look very different to James as he rows around them.
Moreover, the drawings are deliberately simple and stylized, to make them easy enough for fourth graders to copy.
Each piece of equipment is shown in the same size, regardless of James' distance from it.
The pictures of the three objects, as they are drawn on the map, look as if the point of view is somewhere above and to the front of the island, from the reader's perspective. That is, one sees some of the top and some of the side of each. But the pictures of the objects on the student pages are from that same point of view, even though James would not see them that way from his place on the lake. In a sense, then, the representations of the merry-go-round, fort, and umbrella are symbols for the objects, rather than realistic pictures of them. (Note, however, that their relative sizes are reasonable.)
This is a standard convention in drawing maps, but it may place a greater burden on some students because they must infer for themselves what these pictures mean. Although James will never see the fort exactly as it is shown in question 1, he will see the three objects in the order shown, and that is what the task is all about.
Why not use very small three-dimensional objects to place on a playground map instead of the symbolic drawings used here? Although the use of such manipulative materials are called for in the Standards, there are several advantages to the symbolic drawings. First, the purpose of the assessment is to determine how well children can imagine what James' views from particular points on the lake are, in the absence of real objects. Second, the "difficulty" in using symbols for the objects would remain, because the small models are themselves symbols, albeit three-dimensional ones. And third, using three-dimensional models of equipment puts more of a premium on the child's drawing abilities; no longer can he or she simply copy an already-drawn picture or symbol of the object.
Nonetheless, it is worth reiterating that many concrete experiences that involve moving around to get different views of real objects are an essential part of developing visualization abilities. The assumption is that the early years of elementary school will provide many such experiences with small scale objects before students are asked to move to symbolic representations.
Variants and extensions: By adding more pieces of playground equipment or changing their relative positions, many variants of the task can be derived.
Another set of tasks can be created by asking the students to locate pieces of equipment on the playground so that certain views are possible. The teacher would say to the students, "As James rows around on the lake, he can see these views of the playground. Show where the fort, umbrella, merry-go-round, and tree might be so that these views would be possible."
An extension suggested by the discussion of task design considerations above would be to put some identifying marks on the playground equipment so that one or more of the pieces would look different from different directions. For instance, one could put a single access door on the base of the fort.
Protorubric
The pictures below show where the dots for A, B, and D could be placed. See the following pages for additional details.
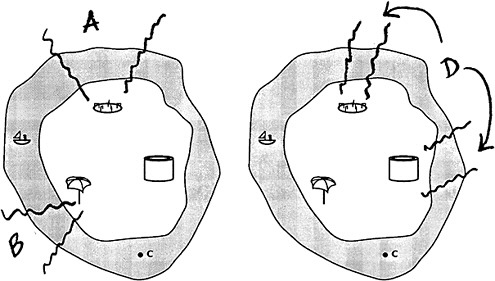
Characteristics of the high response:

The response shows that there is a firm connection between the playground map representation of the situation and the pictures from James' viewpoint.
The dots are all labeled within the limits indicated in the answer key above. (Note that a location for D in which the fort blocks the umbrella is preferable to one in which the merry-go-round blocks the umbrella, because it looks as if the merry-go-round is not tall enough.) The pictures in question 3 are drawn in the correct order, although the individual drawings can be just good enough to be recognizable.
The explanation for question 5 is well reasoned. Ordinarily, in a high response, the child says "No," and explains that if the fort is on the left and the umbrella on the right, then the merry-go-round has to be in front of both of them.
Other high responses will be more inventive: "If the boat is where the view of the merry-go-round is blocked by the fort, then James will see the fort on his left and the umbrella on his right if he stands on his head." An unanticipated response like this shows a mature ability to visualize!
Characteristics of the medium response:
The response shows an overall grasp of the situation; at most, one of the responses to questions 1 through 4 is incorrect.
The response to question 5 is correct, (No), but the explanation is inadequate. For example, "I couldn't find a place where that would happen."
Characteristics of the low response:

There is some understanding of the relationship between the playground map and the views that James sees from various places on the lake, but it is tenuous.
At least one of the answers to questions 1, 2, and 4 are within the bounds specified at the beginning of the protorubric.
References
Clements, Douglas H. and Battista, Michael T. (1992). "Geometry and spatial reasoning" in Grouws, Douglas A (ed.) Handbook of research on mathematics teaching and learning. New York: Macmillan.
deLange, Jan (1987). Mathematics, insight, and meaning. Utrecht: Rijksuniversiteit Utrecht.
Freudenthal, Hans (1983). Didactical phenomenology of mathematical structures. Dordrecht: Reidel.
Paiget, Jean, Inhelder, Barbel, and Szeminska, Alina (1960). The child's conception of geometry. New York: Basic Books.