Bridges
|
Use manipulatives in problem-solving Find patterns to organize information Use computation in the service of broader goals |
Suggested time allotment
Two class periods
Student social organization
Students working alone
Task
Assumed background: It is assumed that the students have had prior experience with using standard colored centimeter rods (or the equivalent). The task also assumes that the children have had experience with "rules" (functions) that describe a general numerical situation.
Presenting the task: Students are given an assortment of colored rods and a copy of the student pages. As always, calculators should be available. The teacher should present the task essentially as the "script" below specifies.

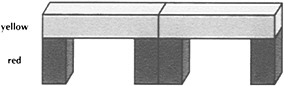
"You are an engineer who wants to build different kinds of bridges. The bridges will be made of colored rods. The first bridge you are to build is a 1-span bridge made with one yellow rod and two red rods." (Build the bridge illustrated below, with the students copying.) "The yellow rod is called a span, and the red rods are called supports . Since the yellow rod is 5 cm long, the length of the bridge is 5 cm."

"The second bridge you are to build is a 2-span bridge made with two yellow rods and four red rods (as shown below). Note that this bridge is 10 cm long."

"As you build bridges in the following activities, think of a way to keep track of the number of rods of different colors you use. Your goal is to find out how many rods of each color you would need to build a bridge of any size."
Student assessment activity: Distribute the activity sheet and read through question 1 to be sure that the children understand the basic problem. Note: the bridges have been scaled to fit the 7" × 10" page of this volume. The teacher may choose to redraw the bridges to scale when they are reproduced on standard size paper
Name _________________________________________ Date _____________
Part 1
All of the bridges in Part 1 are built with yellow rods for spans and red rods for supports, like the one shown here. This is a 2-span bridge like the one you just built. Note that the yellow rods are 5 cm long.
-
Now, build a 3-span bridge.
-
How many yellow rods did you use? _______
-
How long is your bridge? _______
-
How many red rods did you use? _______
-
How many rods did you use altogether? _______
-
-
Try to answer these questions without building a 5-span bridge. If you want, build a 5-span bridge to check your answers.
-
How many yellow rods would you need for a 5-span bridge? _______
-
How long would your bridge be? _______
-
How many red rods would you need? _______
-
How many rods would you need altogether? _______
-
-
Without building a 12-span bridge, answer the following questions.
-
How many yellow rods would you need for a 12-span bridge? _______
-
How long would your bridge be? _______
-
How many red rods would you need? _______
-
How many rods would you need altogether? _______
-
-
How many yellow rods and red rods would you need to build a 28-span bridge? _____ yellow rods and _____ red rods. Explain your answer.
-
Write a rule for figuring out the total number of rods you would need to build a bridge if you knew how many spans the bridge had.
-
How many yellow rods and red rods would you need to build a bridge that is 185 cm long? _____ yellow rods and _____ red rods. Explain your answer.
Name________________________________________ Date _____________
Part 2
The bridges for this part are built like this 2-span bridge:

The black rods are 7 cm long, and the light green rods are 3 cm long. Notice that the supports are shared between spans, except at the ends.
-
Build a 3-span bridge of this same kind, with black and light green.
-
How many black rods did you use? _____
-
How long is your bridge? _____
-
How many light green rods did you use? _____
-
How many rods did you use altogether? _____
-
-
Try to answer these questions without building a 5-span bridge. If you want to, build a 5-span bridge to check your answers.
-
How many black rods would you need for a 5-span bridge? _____
-
How long would your bridge be? _____
-
How many light green rods would you need? _____
-
How many rods would you need altogether? _____
-
-
Without building a 13-span bridge, answer the following questions.
-
How many black rods would you need for a 13-span bridge? _____
-
How long would your bridge be? _____
-
How many light green rods would you need? _____
-
How many rods would you need altogether? _____
-
-
How many black rods and light green rods would you need to build a 56-span bridge? _____ black rods and _____ light green rods. Explain your answer.
-
Write a rule for figuring out how many rods you would need to build a bridge if you knew how many spans the bridge had.
-
How many black rods and light green rods would you need to build a bridge that is at least 429 cm long? _____ black rods and _____ light green rods. Explain your answer.
Rationale for the mathematics education community
The Bridges task illustrates how manipulative materials can be used as an integral part of an assessment task. Such tasks may encourage and support the use of concrete materials in day-to-day instruction, as called for in the NCTM Standards.
The task also focuses on the generation and identification of patterns in a numerical setting, and especially on organizing information — "keeping track" — to find patterns. The child might create a table showing, for example, that 1 span requires 3 rods; 2 spans require 5 rods; and so forth. Then the child might generalize to 13, or 56, or N spans. Thus there is a progression from building a simple structure, to predicting what a more complex structure would look like, and then to generalizing to an arbitrary case.
Furthermore, it is significant that arithmetic computation — rather than being an end in and of itself — is used in the service of answering questions about the bridges. The task is designed so that a variety of approaches to the computation are feasible — calculator, mental, or traditional paper-and-pencil algorithms. More important than the computation itself, however, are the students' decisions about what computations are appropriate, and the connection between the computation and the dimensions of the bridges.
Task design considerations: The directions are phrased so as to encourage the child to use the physical materials as needed to understand the situation, and then to move beyond them. As always, the aim is to encourage self-monitoring: children should be able to decide for themselves what they need to do to understand the situation. Thus sentences are worded like, "If you want, build a 5-span bridge to check your answers."
Note that the picture in Part 2 shows the light green rod on each end of the bridge displaced so that one half centimeter just out beyond the black rods. This is done to be sure the student realizes that even in a longer bridge each light green rod except the ones on the end supports two black rods. (If the light green rods were moved in a half centimeter, so that they were flush with the ends of the black rods, the student might think that the entire configuration shown in the picture is to be
repeated.) As a result, one should be alert for the child who interprets the length of the bridge to be one centimeter more than the sum of the lengths of the black rods; for example, the bridge shown could be thought of as being 15 cm long. Such an interpretation would be completely reasonable.
The size of the numbers in question 6 of Part 1 and Part 2 were chosen carefully. Although 185 (in Part 1) may seem too large, it may be easier than a smaller number. The reason is that fourth graders may tend to rely on familiar addition and subtraction techniques. The students will approach question 6 of Part 1 by writing a long column of "5"s, appending more and more "5"s until the sum reaches 185. The smaller the target number, the more likely it is that this technique will be used, (and the more likely it is to be successful). While there is nothing mathematically "wrong" with this approach, educators want students to move beyond it. So one motivation for using a number as large as 185 is to encourage the child to think of an easier, more efficient, way to tackle the problem. By using the larger number, the assessor can get a richer picture of what the student can do. Similar comments can be made about the numbers in question 4 of both Parts.
Question 6 of Part 2 is different from the others in its use of "at least" and in the fact that 429 is not a multiple of 7. The number was chosen because the division is fairly easy to do mentally (420 divided by 7 is 60, and then two more black rods are needed to get beyond 429, for a total of 62 black rods). Of course students who do not see a way to perform the calculations mentally are free to use a calculator — although they will have to deal with the resulting decimal!
The amount of time that this kind of task requires is very much dependent on the students' prior experiences. Children who are very familiar with using centimeter rods to model situations like building bridges, or who have extensive experience in abstracting general "rules" may need significantly less time to do this task than children whose mathematical backgrounds are not as rich. For some classes, then, one full period may be sufficient time.
Variants and extensions: One straightforward set of variants can be obtained by varying the numbers in the task, or the
rod sizes used, or the way in which an individual span is constructed. For example, each span might have three upright support rods, and each horizontal piece might consist of two rods of the same color, one on top of the other. This is a setting in which children can invent their own styles of bridges and their own questions about them.
More generally, bridge-building with centimeter rods can be used to explore other mathematical topics — for example, in the area of primes and factors: "Can you build a bridge that is exactly 101 cm long, using spans of the same length?" or "Can you build two parallel bridges of the same length, one using 6-cm rods and the other using 8-cm rods; if so, how long might the bridges be?"
Protorubric
Characteristics of the high response:
The high response shows that the child can make a transition between the physical materials and the more abstract arithmetical ideas.
All questions are answered correctly. The rules described in question 5 of Parts 1 and 2 clearly describe a general case, that is, how one would find the total number of rods for any number of spans. This can be done through words or through symbols, or a combination of both. Some children may not explicitly mention the spans; for example, they might simply write "multiply by 3" for question 5 of Part 1.

The justifications in question 6 in both parts are detailed. For example, in Part 1, the explanation indicates that 185 was divided by 5, and that there are twice as many red rods as yellow rods. If a calculator is used in question 6 of Part 2, the decimal result is interpreted correctly.
Characteristics of the medium response:
Questions 1 through 4 of Parts 1 and 2 are answered satisfactorily — that is, a pattern has been noted and extended to the bridges that are too long to construct with the available rods.

Questions 5 and 6, however, are not answered appropriately; the general rule may be unclear or not universally applicable.
In Part 2, if the division of 429/7 is done using a calculator (or with pencil and paper), the resulting decimal is reported without rounding up to the next whole number.
Characteristics of the low response:
Questions 1 and 2 of Parts 1 and 2 are answered satisfactorily, although the child may have to build the 5-span bridges and count the rods before responding.
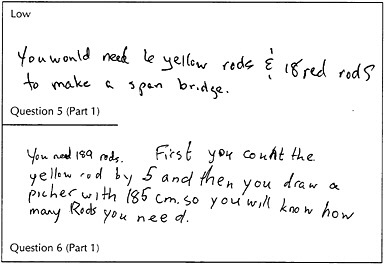
More generally, though, the low response indicates an incomplete grasp of the relationships among (a) the length of each span rod, (b) the number of spans, and (c) the total length of the bridge.










