Simulation of Strongly Nonlinear Wave Generation and Wave-Body Interactions Using a 3-D MEL Model
P.Ferrant (SIREHNA, France)
ABSTRACT
In this paper we give an overview of some of the possible applications of fully nonlinear wave simulation in three dimensions, through a report on our continuing research in this field. We describe the formulation, numerical implementation and practical applications of two different versions of the time domain Rankine panel code ANSWAVE.
The first one is based on a semi-Lagrangian formulation and is primarily applied to radiation and diffraction problems in waves of moderate steepness. The availability of an explicit model for the nonlinear incident wave allows the splitting of the total flow into incident and perturbation contributions. This “potential-splitting” formulation offers substantial savings of CPU time and memory. Applications presented hereafter include the nonlinear diffraction of long waves by a bottom-mounted vertical cylinder, the diffraction of a solitary wave by a three-dimensional obstacle, as well as the free motion of a floating body induced by a nonlinear regular wave.
In the secund version, a fully Lagrangian description of the free surface is adopted, which allows the model to simulate the propagation of steep waves, possibly up to overturning, as well as their interaction with material boundaries. The behaviour of this model will be illustrated here by the simulation of large amplitude three dimensional standing waves in a rectangular tank.
INTRODUCTION
Among the different solution methods available for nonlinear free surface problems, in the frame of potential theory, the most popular is by far the mixed Euler-Lagrange method. This approach consists in a two-step procedure in which at a given time t a boundary-value problem is first solved for the normal velocities on the free surface Sf and the potential on material boundaries Sb, Φ on Sf and Φn on Sb being given. Then the kinematic and dynamic boundary conditions, treated as ODE 's for Φ and M(x,y,z,t) on Sf, are integrated in time to obtain the new positions and potential values of points on the free surface at t+Δt. The process may then be repeated to advance the solution in time.
The MEL approach was first applied in two dimensions to the simulation of steep and overturning waves by Longuet-Higgins & Cokelet (1976), and by Faltinsen (1977), who considered the interaction of waves with a floating body. Following these pioneering works, many research groups then implemented their own version of the 2D MEL method, including Vinje & Brevig (1981), and many others ([6], [7], [8], [9], [10], [18], [29]).
Its relatively moderate computational cost (compared to recent workstations power), and the easy implementation of sophisticated numerical schemes such as higher order boundary element methods, high accuracy Taylor series expansions for the time stepping, digital filtering, spline interpolations, etc…, give the 2D MEL method the
status of a mature and reliable model, which has been validated by cross-comparisons between different numerical codes (Nestegard 1994) or by comparison with experiments (Dommermuth et al 1988). In these conditions, it now offers a valuable power of insight into a wide variety of free surface problems, ranging from wave deformation and breaking (Dommermuth et al, 1988) to nonlinear wave body interactions (Cointe et al, 1990), coastal engineering (Grilli et al, 1993), long distance propagation of wave groups (Tulin et al, 1993), or computation of waves impacting on structures (Tanizawa & Yue 1992).
The implementation of the MEL method in three dimensions is much more difficult, and not only because of the larger number of unknowns. Of course, the typical size of the linear algebraic systems to be solved is one order of magnitude larger than in corresponding 2D applications, and the resulting memory and CPU requirements are a major issue, but other difficulties resulting from the three dimensionality of the domain must not be underestimated. This includes the accurate evaluation of the velocity components on moving surfaces, but also the implementation in three dimensions of numerical methods for the tracking of moving intersections lines between Dirichlet and Neumann boundaries, the possible regridding and/or smoothing techniques to be applied during the simulation and which are much more complicated than in two dimensions, where meshes are naturally structured and thus easy to manipulate.
These specific difficulties explain why, despite the continuous improvement of computer power and numerical methods, available results from three dimensional applications of the MEL method are still rare.
Some early publications directly tackled the problem of the diffraction of a nonlinear wave on a surface piercing body (Zhou & Gu 1990, Yang & Ertekin 1992, Chan & Calisal 1993). However, low order boundary element methods were used, with approximate treatment of free surface-body intersections and coarse discretizations, so that corresponding numerical results were merely qualitative.
At the same time, more refined numerical models were developed, based on higher order panel methods, and with special attention given to the specific difficulties of the three dimensional MEL scheme, such as the accurate computation of free surface velocities and gemetry, extrapolation techniques at the intersection lines, etc… In this category, first published results mainly concerned academic problems on simplified geometries. Kang & Gong (1990) computed waves produced by the forced motion of a submerged sphere, using a spline-based panel method with Adams-Bashforth-Moulton predictor-corrector scheme for the time stepping. Romate (1989), followed by Broeze (1993) developed a nonlinear simulation model for the propagation of waves explicitly given by a stream function theory. The interaction of these waves with bottom deformations was described in Broeze (1993). Their model is based on a second order panel method, with a fourth order Runge-Kutta scheme for the time stepping. The problem of the computation of overturning waves in three dimensions was successfully solved by Xü & Yue (1992). They used a boundary element method with bi-quadratic isoparametric curvilinear elements, under the assumption of double periodicity in horizontal directions, and without accounting for wave-body interactions, the overturning being induced by the imposition of non-zero pressure patches on parts of the free surface. More recently, Boo et al (1994) simulated the propagation of nonlinear irregular waves of moderate steepness, using an Eulerian scheme applied to a rectangular domain.
On the specific aspects of the three dimensional nonlinear radiation problem, recent advances have been reported by Beck et al (1993, 1994), using the so-called ‘desingularized' method. A variety of applications were described, including the computation of added mass and damping on a modified Wigley hull at forward speed, and showed satisfactory agreement with experimental results. However, no incoming waves were accounted for in the computations.
In this paper, we describe some of the recent advances of our own approach of the solution of fully nonlinear wave-body interaction problems in hree dimensions. This research started in Sirehna in 1989 and has since been mainly sponsored by the French Ministry of Defense (DRET), through successive research contracts. Unsteady linearized flows were first addressed, with the development and validation of a linearized numerical wave tank named ANSWAVE, including wave-body motion coupling and absorbing conditions, and based on a boundary element method (Ferrant 1991–1993). Nonlinear free
surface and body boundary conditions have then been introduced in the model, with applications related to radiation and diffraction problems for submerged bodies, using a fully Lagrangian description of the free surface (Ferrant 1994). A further step in the development of the nonlinear model was achieved with the treatment of surface-piercing bodies, involving bi-cubic spline interpolations at the free surface and extrapolation techniques at the waterline (Ferrant 1995).
We describe significant results of two versions of the code differing in the formulation of the free surface motion. The first version is based on a semi-Lagrangian formulation with an explicit treatment of the incident wave through a stream function model. This model is primarily dedicated to radiation and diffraction problems in waves of moderate steepness, without overturning. Two different applications of this version are presented. First we describe the nonlinear simulation of the diffraction of long waves by a surface-piercing vertical cylinder. Higher order loads and free surface motions are computed and compared with results from the third order frequency domain model of Malenica & Molin (1995). Thenafter, the simulation of the nonlinear free motion of a floating circular dock in a regular wave is presented.
The second version of the code uses a fully Lagrangian description of the free surface and material boundaries, which potentially allows the simulation of the generation of steep three dimensional waves up to overturning, as well as their interaction with material boundaries. It is applied here to the simulation of large amplitude standing waves in a three dimensional tank. This Lagrangian version is under development and we hope to be able to present results on the generation of steep three dimensional in a wave tank in a very near future.
FORMULATION OF THE PROBLEM
Boundary Value Problem
The fluid is heavy, inviscid and incompressible. The problem is started either form rest or from prescribed initial conditions so that the flow remains irrotational in the fluid domain D. The constant atmospheric pressure at the free surface Sf is taken as the pressure of reference. The fluid velocity derives from a scalar potential ![]() satisfying Laplace equation in the fluid domain:
satisfying Laplace equation in the fluid domain:
(1) ![]()
(2) Δ![]() (M,t)=0
(M,t)=0
An initial boundary value problem for ![]() is obtained by applying suitable boundary conditions on the surfaces limiting the fluid domain: the free surface Sf, the body surface Sb, and the external surface Se which may include a bottom at finite but not necessarily constant depth.
is obtained by applying suitable boundary conditions on the surfaces limiting the fluid domain: the free surface Sf, the body surface Sb, and the external surface Se which may include a bottom at finite but not necessarily constant depth.
On the body and bottom surfaces, Neumann conditions are applied:
(3) ![]()
(4) ![]()
where n is the unit normal vector exterior to the fluid and Vb is the local velocity of the body surface, relative to the fixed coordinate system Oxyz with z pointing upwards and z=0 on the calm water level. In the case of infinite depth, the bottom condition is replaced by:
(5) ![]()
![]() --> 0 for z -->–∞
--> 0 for z -->–∞
Computations presented in this paper concern problems with a flat bottom at constant depth. The bottom condition is thus not explicitly satisfied, but is accounted for by an additional symmetry. The general case of a non uniform bottom may be treated without difficulty at the cost of additional unknowns.
On the free surface both kinematic and dynamic conditions must be satisfied. The kinematic condition states that the mass flux through the free surface is zero, and writes, in Lagrangian form:
(6) ![]()
Surface tension being ignored, the dynamic
condition accounts for the continuity of pressure accross the free surface, and is obtained by applying Bernoulli's equation:
(7) ![]()
where D/Dt stands for the material derivative.
The formulation as described above supposes a fully Lagrangian description of the free surface, with free surface markers identified as material particles. In the present paper, this formulation will be used for the simulation of large amplitude standing waves.
In some situations, it is more convenient to prescribe the horizontal motion of markers at the free surface. In particular, the simulation of diffraction and diffraction-radiation problems described in this paper rely on a semi-Lagrangian formulation in which the horizontal motion of free surface markers is inhibited. In such a formulation, the free surface vertical coordinate becomes implicitly single-valued and may be written as:
(8) z=η(x,y,t)
Introducing this notation in (6) and (7) and after some manipulations, we obtain new forms of the kinematic and dynamic free surface conditions, in which a fixed location of free surface markers in the x-y plane is implied:
(9) ![]()
(10) ![]()
Compared to the fully Lagrangian formulation (6)–(7), there is an additional difficulty due to the necessary computation of the gradient of the free surface elevation in (9). A bi-cubic spline interpolation scheme, described in a following section, has been implemented for the accurate evaluation of this term together with the velocity potential and normal vectors at the free surface.
Applying Green's formula in the domain D to the velocity potential ![]() and the free space Green function (Rankine source):
and the free space Green function (Rankine source):
(11) ![]()
the following integral representation for the velocity potential is obtained, where W is the solid angle at point M:
(12) 
In combination with the boundary conditions, the integral representation leads to a second kind Fredholm integral equation for points M on surfaces where a Neumann condition is applied and to a first kind integral equation for M on the free surface, where a Dirichlet condition is enforced.
The mixed Euler-Lagrange method consists in a time stepping procedure in which the boundary value problem is solved at each time step. At a given time t, the velocity potential on the free surface (Dirichlet condition) and its normal derivative on the other boundaries (Neumann conditions) are supposed to be given. With this mixed set of boundary conditions, the boundary value problem is solved for the normal velocity on the free surface and the potential on the other boundaries. This gives access to the right-hand sides of the free surface conditions. During a second step these equations are integrated numerically form t to t+Δt to obtain the new position and velocity potential of markers at the free surface. In most cases, the normal velocity on other surfaces is prescribed and the process can be repeated to advance the solution in time. In the case of free body motions, the procedure is modified as described in the next section
Coupling with Body Motions
When dealing with free motions of a floating body, the main additional difficulty comes out from the necessity to solve simultaneously the dynamic equations of the body motion and the fluid problem. This requires the hydrodynamic force on the body to
be known at the current time step. The problem is with the time derivative of the potential which appear in the pressure. One solution would be to compute this term by backward differentiation from previous time steps, but it is known to lead to instabilities. Here we adopted a tchnique already applied for example by Vinje & Brevig (1981) or Cointe et al (1990), which consists in solving an auxiliary boundary value problem for Φt. Φt satisfies Laplace equation in the fluid domain, its current value on the free surface is easily deduced from Bernoulli's equation, and its normal derivative on the body surface may be expressed in terms of the velocity and acceleration of the body. Thus Φt is solution of an integral equation of the same form as the one that we solve for Φ. The kernel of the discretized problem is the same, the difference between the two problems lying in the right-hand sides. The acceleration terms in the Neumann condition for Φt on the body are factorized out in a manner similar to that exposed by Kang & Gong (1990) or Wu & Eatock-Taylor (1996), separating a memory term with an homogeneous Neumann condition on the body, and impulsive terms corresponding to unit accelerations on each of the degrees of freedom of the body. In the more general case of three dimensional motions, this results at each time step in the necessity to solve seven additional boundary value problems.
Accounting for Nonlinear Incoming Waves
The overall simulation strategy is the same as in the fully Lagrangian version (Ferrant 1994). The incident wave is given by the stream function theory of Rienecker & Fenton (1981). This steady wave solution is used to prescribe the initial conditions, as well as the time dependent boundary conditions on the outer surface of the computational domain. At time t=0, the potential and wave elevation given by the incident wave model are imposed on the whole boundary of the computational domain. The Neumann condition on the body is then progressively introduced, with a ramp over half a wave period. During the simulation, Neumann conditions given by the wave model are maintained on the vertical outer boundary. On the free surface surrounding the body, the original conditions are applied, while on the other part, up to the outer Neumann boundary an absorbing layer is introduced, in which the damping is applied only to the perturbation of the incident wave, resulting in the following modified free surface conditions:
(14) ![]()
(15) ![]()
The coefficient υ is zero except in the damping zone which is an annular portion of the free surface of radius R=λ.
In this zone, υ is a cubic function varying from zero for R=Rd–λ to its maximum value at the intersection with the vertical closing surface, for R=Rd. This allows a smooth transition between the numerical solution at the free surface and the incident wave model imposed on the outer boundary. This application of the absorbing layer method has some similarity with the approach of Cointe et al (1990) for the solution of 2D nonlinear diffraction-radiation problems.
Splitting the Incident Wave Contribution
When the incident wave is given by an explicit model, a further modification of equations (14) and (15) allows to derive a modified problem formulated in term of the perturbation induced to the incident flow by the influence of the body. A comparable procedure was exposed by Lalli et al (1995), and applied to the pure diffraction problem.
The perturbation (ΦD, ηD) is defined by:
(16) Φ=Φe+ΦD
(17) η=ηe+ηD
where the subscript e indicates the potential or wave elevation of the incident wave, without perturbation. Plugging (16) and (17) into (14) and (15), we obtain the kinematic and dynamic free surface conditions for the perturbation flow:
(18) 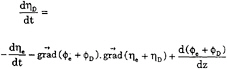
(19) 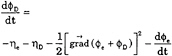
where terms from the incident flow at the right-hand side can be evaluated exactly from the stream function wave model, without influence from time or space discretization, The problem being fully non linear, equations (18) and (19) must be satisfied on the instantaneous free surface position, and thus the incident potential may possibly be evaluated above the undisturbed incident wave. This is possible here because of the continuous prolongation of the incident potential above the incident wave. One of the advantages of this formulation is that the incident wave is treated explicitly, so that it is not altered during its travel from the external surface of the computational domain to the body. The free surface mesh only has to accomodate the perturbation flow, which is mainly composed of waves travelling in radial directions from the body. This allows us to adopt relatively coarse meshes meshes ar from the body, resulting in considerable savings of memory and CPU time, without noticeable loss of accuracy. Of course, the formulation described above is not universal and depends on the availability of an explicit model for the incident wave.
NUMERICAL METHODS
Boundary Element Method
A boundary element method is used for the solution of the boundary integral equation formulation of the problem. The method is based on isoparametric triangular elements distributed over the different boundaries. A piecewise linear, continuous variation of the solution over the boundary is thus assumed, and collocation points are placed at panel vertices. Meshes are made of an assembly of different patches, with the assumption of continuous normal on each of them. On intersection lines between two patches, two collocation points are kept at the same geometrical position, and the boundary conditions corresponding to the two surfaces are both satisfied. At the intersection between two solid patches, two Neumann conditions for the two different normals are enforced, whereas at the intersection between solid boundaries and the free surface, both a Neumann (N) condition on the solid surface and a Dirichlet (D) condition on the free surface are satisfied. At corners of the domains, triple points and triple conditions, either of NNN or NND type. This discretization scheme reduces the integral formulation to a linear algebraic system to be solved for the normal velocity on Dirichlet boundaries (free surface) and the potential on Neumann boundaries. This system is made of the influence coefficients of linearly varying distribution of sources on boundary elements. Analytical formulas for the near field, and different approximate formulas for the intermediate and far field of the different panels are implemented. These coefficients are factorized with respect to sources or dipoles density at panel vertices, which are selected as control points. This scheme results in square systems of equations for the singularity distribution on the boundaries of the computational domain.
Solution of Linear Systems of Equations
For a moderate number of unknowns, the O(N2) task of evaluating the influence coefficients completely dominates CPU times, so that the majority of 2D mixed Euler-Lagrange formulations solve the linear system using direct O(N3) methods such as LU or Gauss elimination. Such a choice may also be convenient in linearized 3D formulations, where the time invariant kernel may be inverted once for all (Ferrant 1991, Nakos 1993).
However, in 3D nonlinear applications large systems of equations have to be solved at each time step, and any O(N3) solution algorithm must be rejected. In the present formulation, the linear systems to be solved are full and non-symmetric. Furthermore, due to mixed Dirichlet-Neumann conditions at the boundary, condition numbers are sensibly larger than for pure Neumann conditions.
Among the different existing iterative solution methods for nonsymmetric systems that have been implemented and tested in our boundary integral equation solver, we selected the GMRES scheme (Saad & Schultz 1983).
Applied to test cases with existing analytical solutions available for comparison, this scheme exhibited the better behaviour with a regular and monotonic convergence, and the lower overall CPU
cost for a given residual at convergence. The method is used with diagonal preconditioning, which reduces the necessary number of iterations by a factor of 2, at no additional cost. Further reductions of the number of iterations may be observed with more elaborate preconditioning techniques (Xü & Yue 1992), but the cost of such preconditionings applied to full matrices is no longer negligeable and may annihilate the advantage of the lower iteration number. The monotonic convergence of GMRES also allows a further reduction of the necessary number of iterations, by exploiting an initial guess of the solution obtained by polynomial extrapolation from previous time steps.
Interpolations and Smoothing at the Free Surface
The quality of free surface geometry and velocity computations is essential to the stability and accuracy of mixed Euler-lagrange simulations. In two-dimensional applications of the method, free surface grids are naturally structured, which allows a straightforward implementation of higher order finite difference or interpolation schemes for the computation of normal vectors and velocities at the free surface, in terms of the location and potential values at free surface nodes. When necessary, smoothing procedures for the removal of saw-tooth instabilities are also easily introduced.
In three dimensions, the extensions of such numerical schemes requires the mapping of each part of the boundary by a set of two parameters. In Broeze (1993), each part of the domain boundary is transformed into a standard rectangular domain on which bivariate interpolation schemes are applied. In Xü & Yue (1992), the interpolation schemes are directly applied in the physical domain. In both cases, each subsurface is described by a bi-parameter array of grid points.
The discretization scheme used in the present method is based on unstructured triangulations of domain boundaries. This allows the representation of arbitrary surfaces but requires the implementation of special schemes for the computation of normal vectors and velocities at the free surface. In the general case, local polynomial fitting procedures are applied at each node of the free surface, based on the position and potential of the neighbouring nodes (Ferrant 1994).
In the applications based on the semi Lagrangian formulation, the projection of surface nodes on the x-y plane is invariant and axisymmetric, and the mesh is structured in the circumferential direction, that is nodes are distributed on circles surrounding the body, with a regular spacing on each circle. This situation has allowed us to implement a bi-cubic spline interpolation scheme for both the potential and the vertical coordinate at the free surface. These quantities are first interpolated at each radial station as functions of the azimuthal angle θ. Then, interpolating splines are computed in the radial direction, at each free surface node. At the end of the interpolation procedure, the C1 representations for ![]() and η at the free surface allows an easily evaluation of the normal vector and velocity component, by direct differentiation of the interpolating splines. This procedure has been found to be more accurate than the local polynomial fitting. However, its extension to arbitrary geometries is not trivial.
and η at the free surface allows an easily evaluation of the normal vector and velocity component, by direct differentiation of the interpolating splines. This procedure has been found to be more accurate than the local polynomial fitting. However, its extension to arbitrary geometries is not trivial.
In the Lagrangian simulations presented hereafter, the free surface is also bi-parameterized, but the potential and the three coordinates at free surface points are interpolated with respect to each parameter, directly using nodal values. This removes the restriction to a single-valued free surface
The particular structure of the mesh for the present applications also permits the implementation of smoothing formulas for the removal of possible saw-tooth instabilities at the free surface. In two dimensional MEL methods, smoothing formulas based on Chebyshev polynomials, given by Longuet-Higgins & Cokelet (1976) and revisited by Dold (1992) are most often used. Here we use five points formulas which are applied successively in each isoparametric directions.
Time Marching Scheme
After the solution of the boundary value problem and the computation of fluid velocities at the free surface, free surface conditions considered as ODE's for f and h are integrated in time, which is the second step for the MEL method. A fourth order Runge-Kutta method is used for that purpose, requiring four solutions of the boundary value problem per time step. A dynamic time step control is applied, based on a Courant condition:
(20) ![]()
where Δl is the minimum panel size and C the maximum fluid velocity, at the free surface. Cn is a predetermined Courant number, with o<Cn<l. In the present computations, a basic time step Dto is chosen, and the time step is set to min (Δto, Δtc) during the simulation, with Cn=0.6.
Due to the very large CPU times required by 3D MEL simulations, some of the results presented in this paper were obtained using the Runge-Kutta scheme with “frozen” coefficients, that is the influence coefficients are updated only once per time step, while four solutions of the boundary value problem are performed.
NUMERICAL RESULTS
Nonlinear Diffraction of Long Waves by a Vertical Cylinder
A number of studies, experimental or numerical, have been recently undertaken in order to gain some understanding of the so-called “ringing” phenomenon. Ringing events observed during model tests or at sea occur in sea states with peak periods equal to 3 to 5 times the structure 's resonance period, suggesting that highly nonlinear effects are involved.
If the phenomenon is to be modelized using a perturbation approach, it means that at least a third order expansion is required. Such a methodology has recently been adopted by Malenica & Molin (1995), who implemented a consistent perturbation scheme for the evaluation of third order-triple frequency loads on vertical bottom mounted cylinders submitted to regular Stokes waves. A third order time domain approach based on the code SWAN has also been undercome by Sclavounos & Kim (1995), but up to our knowledge, no third order numerical results have yet been reported. Following a different approach, Faltinsen, Newman & Vinje (1995) developed a long wave theory in which both the radius of the cylinder and the wave amplitude are assumed to be small compared to the wavelength. The comparison of both methods gave rise to some controversy (see for example discussions at the 10th WWWFB in Oxford), as results from Malenica and Molin seemed to restrict the validity of FNV theory to very low ka (under 0.025). However, in their conclusion, Malenica & Molin insisted on the lack of experimental validation of their results, while they suggested that fully nonlinear simulation codes were not mature enough for the accurate capture of such higher order diffraction effects.
In this section, we aim at partially answer this need for more validation, by reporting on nonlinear simulations of the diffraction of long waves on a vertical bottom-mounted cylinder. Full results including nonlinear time depending forces and runup on the cylinder as well as free surface maps in the vicinity of the cylinder are produced. Frequency domain coefficients for the forces and runups are then obtained by moving window Fourier analysis of the time series, and it is shown that with the adopted mesh density, stable results are obtained up to the fourth harmonics. However, the analysis is focused on triple frequency diffraction loads which tend to confirm M&M results in the long wave regime.
We use the semi-Lagrangian formulation with markers fixed horizontally. The incident nonlinear wave potential and elevation are given by a stream function model (Rienecker & Fenton 1981), and the problem is solved in terms of the perturbation flow, as described in a previous section.
A series of simulations have been undercome with parameters corresponding to cases already treated by Malenica & Molin. The wavelength is set to a constant, λ/H=0.785, i.e. kH=8., where H is the water depth, while the radius a of the bottom-mounted cylinder is varied so that 0.05≤ka≤0.30. The incident wave amplitude is A/H=0.0075, except for the lowest wavenumber, ka=0.05, for which the amplitude has been cut by half, because of stability problems in the simulations. For each different wavenumber (and cylinder radius), an adapted mesh is set up, with the free surface being discretised up to a radius equal to two wavelenths, and with a density of about 100 panels per wavelength in the vicinity of the cylinder, in order to be able to capture diffracted 3ω free waves. The mesh density becomes lower when the distance from the body increases, and the total number of panels on the half-domain is about 4000. Free surface conditions modified by damping terms acting on the perturbation potential and wave elevation are applied for radial distances over one incident wavelength.
Starting with initial conditions corresponding to
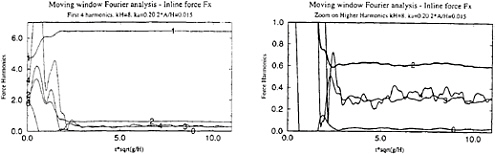
the undisturbed incident wave in the domain, the Neumann condition on the body is progressively introduced during the first wave period. Full time-depending nonlinear quantities such as wave patterns, runups and forces are available. Examples of time series are given here, for ka=0.20 (cylinder radius a/H=0.025). Figure 1 is a plot of the horizontal force Fx on the cylinder. Figures 2 and 3 represent runups upwave and downwave, respectively. On each of these plots, the total wave elevation as well as the difference between the the total wave and the undisturbed wave, i.e. the perturbation, are given. For each of these signals, a periodic behaviour is reached within less than two periods. Nonlinearities are mostly apparent in the runups, especially at the upwave position. For comparison with frequency domain results, moving window Fourier analyses of these signals are then undercome. A window width equal to one wave period is applied. The resulting nondimensional force harmonics obtained for ka=0.20 are given by figure 4, with results for the drift force F0 up to the fourth harmonic F4. A zoomed graph excluding F1 is given by figure 5. F0, F1 and F2 are very stable, some perturbations appearing for F3 and more sensibly for F4, but without any drift, which is quite satisfying. F0 and F2 are scaled by ρgA2a, F1
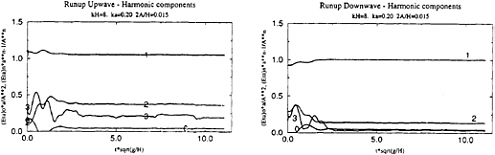
by ρgAa2, F3 by ρgA3 and F4 by ρgA4/a, where A is the wave amplitude and a is the cylinder radius. The same analysis has been applied to runups upwave and downwave, see figures 6 and 7 respectively. Significant perturbations appear for the third harmonic in place of the fourth for the force. One can notice the stronger harmonic content of the runup upwave, which was already apparent on the time series.
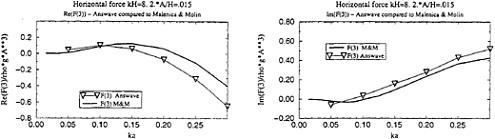
These analyses have been repeated for values of ka ranging from 0.05 to 0.30, that is in the range for which ringing is observed. Figures 8 and 9 compare the real and imaginary parts of the triple frequency force F3 obtained with ANSWAVE, with results from the frequency domain third order analysis of Malenica and Molin. The agreement is believed to be quite satisfactory, especially when one considers the very low absolute level of the 3ω force which is extracted from the force time series. For example, for ka=0.20 and 2*A/H=0.015, there is a scale of about 1 to 200 between F1 and F3.
Globally, a quite satisfactory agreement has been found with previously published frequency domain results of Malenica & Molin on the triple frequency horizontal force. With the levels of time and space discretization adopted, nonlinear simulations using ANSWAVE produce stable results up to the fourth
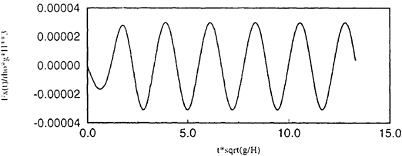
Figure 1: Time series of the inline force Fx, ka=0.20. kH=8.
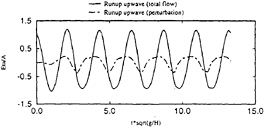
Figure 2: Runup upwave. ka=0.2 kH=8. 2A/H=.015
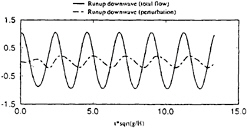
Figure 3: Runup downwave
harmonic for the forces and to the third harmonic for the runups.
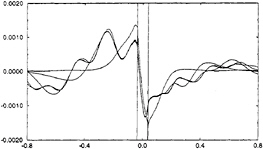
Figure 10: Perturbated wave in the symmetry plane t/T=1.5,…4.5. ka=0.3 kH=0.8 2A/H=0.015
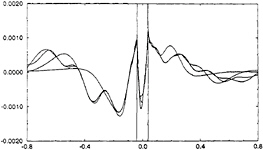
Figure 11: Perturbated wave in the symmetry plane t/T=1.5,…4.5. ka=0.3 kH=0.8 2A/H=0.015
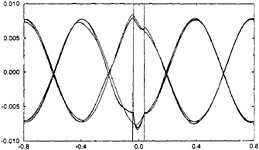
Figure 12: Total wave in the symmetry plane
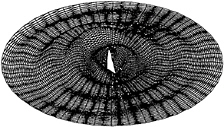
Figure 13: Perturbated wave elevation t=5T ka=0.3
Some further results concerning the free surface deformation are presented in figures 10 to 13. These figures correspond to ka=0.30, kH=8. and 2A/H=0.015. Figures 10 and 11 represent plots of the perturbation elevation in the vertical symmetry plane, respectively for integer values of the number of simulated periods for figure 10 (t/T=1,2,3,4,5) and for intermediate values for figure 11 (t/T=1.5, 2.5, 3.5, 4.5.). Only a part of the computational domain of radius equal to one wavelength is considered. The perturbation wave field is mainly composed of a fundamental part of wavelength λ, plus 2ω waves of wavelength λ/4. One can notice the onset of a periodic steady state perturbation around the cylinder, and also the relatively steep trough on the side of the cylinder, which, if extrapolated to larger incoming waves, would certainly lead to a local breaking as observed in some experiments. Figure 12 represents the total wave in the symmetry plane, plotted every half of a period, while figure 13 is a three dimensional plot of the perturbation free surface in the disk of radius λ, around the cylinder. In figures 10, 11 and 12, the incident waves comes from the left. In figure 13, the incident waves propagates from the upper left of the plot to the opposite corner.
As a conclusion to this section, we first recognize that simulations with larger amplitudes are obviously desirable, in order to illustrate the anticipated divergence between fully nonlinear modelization and perturbation analysis. However we need first to improve the stability of the model. Another necessary comment is on the fact that the estimation of the higher harmonic components of the diffraction force in long waves from fully nonlinear simulations is very difficult, because of contradictory requirements. On one side, we must work with very low incoming wave amplitudes in order to respect the conditions of applicability of perturbation analysis. One the other side, the estimation of higher order harmonics from the time series becomes less and less accurate when their relative contribution to the signal goes to zero. In fact some further computations recently performed with varying amplitudes seem to indicate that the value of the amplitude chosen for comparison with perturbation analysis, 2A/H=0.015, is not enough small to get stabilized values of the force coefficients. This probably explains the remaining small difference between coefficients obtained from
nonlinear simulation and those from perturbation analysis, illustrated by figure 8 and 9.
Cross comparison between, existing three dimensional fully nonlinear simulation programs is also very desirable for quantities for which no reference results are available, such as higher order runups and 4ω forces (and over).
Nonlinear Motion of a Floating Dock in Regular Ambient Waves
In this section we present results of the simulation of the nonlinear motion of a floating body induced by regular incident waves. The formulation used is the same as for the application described in the previous section, except that here we simultaneously solve the dynamic equations of the body motion and the fluid flow problem. The floating body is a truncated vertical cylinder of radius r/H=1/3 and of draft at equilibrium d/H=1/6. Only vertical motions are allowed, the other degrees of freedom being inhibited. We consider a regular incoming wave of wavelength λ/H=6.064, and of amplitude A/H=0.05. The period is T.sqrt(g/H)=7.0, that is twice the natural heaving period of the floating body. The radius of the computational domain is equal to two wavelengths, and the mesh is composed of 3560 panels on the half domain, that is 3160 on the free surface and 400 on the body. Figure 14 gives a plot of the mesh, after truncation at a radial distance of about half a wavelength. We used 50 constant time steps per period, and the simulation was run for 10 periods. The resulting time series of the vertical displacement, velocity and acceleration are given in figure 15. As expected, the motion contains a significant 2ω component, resulting from the resonant excitation of the natural heaving motion of the body by nonlinear terms in the hydrodynamic force. Figure 16 illustrate the
Figure 14: Partial view of the mesh
result of a moving window Fourier analysis of the vertical motion. Only the fondamental and secund harmonics are significant. The amplitude of the fundamental component is close to the wave amplitude, which is consistent with the relatively low wave frequency. The amplitude of the 2ω component of the motion is about 20% of the fundamental one.
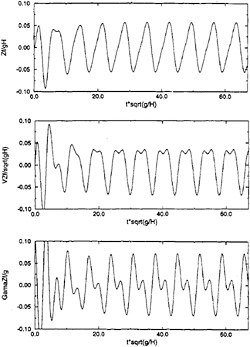
Figure 15: Vertical displacement, velocity and acceleration of a freely floating cylinder in regular incoming waves.
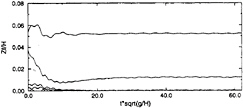
Figure 16: Moving window Fourier analysis of the vertical displacement
Large Amplitude Standing Waves in a Three Dimensional Tank
This last numerical application is dedicated to the demonstration of the behaviour of the fully Lagrangian version of the code. We compute the nonlinear fluid motion inside a three dimensional tank subject to an initial surface elevation. The tank dimensions are (Lx, Ly, H)=(2, 4, 1), and the initial free surface elevation is ηo=Acos(πX/2)cos(πY/2), with A=0.3. The half domain is discretized by a total of 2450 panels. Figure 17 gives a view of the initial shape of the fluid domain. A constant time step Δt.sqrt(g/Ho)=0.025 has been adopted, and the simu-

Figure 17: Initial free surface elevation in the tank.
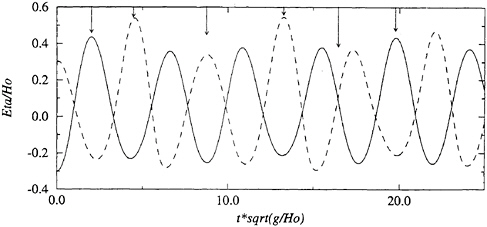
Figure 18: Free surface elevation at (X, Y)=(0., 2.) (solid line) and (X, Y)=(0., 0.) (dashed line)
lationwas run for 1000 time steps. The fully Lagrangian formulation is used here, and we regrid the free surface at each time step with the constraint of keeping a constant difference in arc length between neighbouring nodes. Without regridding, we observed the concentration of nodes in certain regions of the free surface, leading to a necessary reduction of the time step and thus of the computing time. Walls are simply regridded in vertical directions at each time step, starting from the position of nodes on the intersection line with the free surface. The time marching is based here on the full Runge-Kutta scheme, with no “frozen coefficients” approximation. In these conditions, the total computing time was about 30 hours on a HP9000/J200 workstation.
Figure 18 gives the time series of the free surface elevations at two particular points: (X, Y)=(0., 2.) and (X, Y)=(0., 0.). We observe that, due to nonlinearities, there is no periodicity in the time series. Furthermore, large amplifications are observed, especially in the corner (0., 0.), where the elevation is above 0.5 for t=4.5 and t=13.2. We give in figures 19 to 24 plots of the computational domain at instants marked by vertical arrows in figure 18. Equal scales are adopted in horizontal and vertical directions. The free surface never recovers its initial shape, and there is no instant at which it is flat, as would be observed in a linearized computation.
The initial fluid volume is Vo=8.0. After 1000 time steps, the final value is Vf=7.99, so that mass
conservation is satisfied within an relative accuracy of about 10 –3. Similar figures are obtained regarding energy conservation.
CONCLUSION
Significant results of two different version of the three dimensional Rankine panel code ANSWAVE have been presented. Both version solve fully nonlinear free surface problems under the assumptions of potential flow.
The first version is based on a semi Lagrangian representation of free-surface motions, with markers fixed horizontally, and is formulated in terms of a perturbation flow defined as the difference between the incident and the total flow. This splitting is possible here with fully nonlinear free surface conditions because of the characteristics of the incident wave model based on a stream function theory. We first discuss with more details original results on the nonlinear diffraction of long waves by a bottom-mounted vertical cylinder, already presented at the 11th WWWFB in Hamburg (Ferrant 1996). The capacity of the model to capture stable higher order components of the diffracted flow is attested, although it seems to be difficult to find a common range of applicability of fully nonlinear simulation and of higher order perturbation analysis. This point will motivate further reseach in order to improve the accuracy of the model at low amplitudes, as well as its stability for larger ones. This first model has been extended to the problem of the free motions of a floating body in regular incoming waves. The behaviour of the model in such a configuration is illustrated by the stable simulation of the nonlinear vertical motion of a floating cylinder, over 10 wave periods.
The secund version is based on a fully Lagrangian formulation. It is applied here to the computation of large amplitude standing waves in a three dimensional tank. Strongly nonlinear effects are observed, while the accuracy of the simulation is attested by mass and energy conservation. The Lagrangian representation of the free surface is potentially more adapted to the simulation of steep waves interfering with moving boundaries, a problem on which we concentrate our present research efforts.
Acknowledgments
The development of the code ANSWAVE was supported by the French Ministry of Defense, under contract DRET/SIREHNA 94/360. The application to nonlinear diffraction problems was part of a CLAROM project on “ high frequency resonance of offshore structures”, with BUREAU VERITAS, DORIS ENGINEERING, IFP, IFREMER, PRINCIPIA and SIREHNA as partners.
References
[1] Beck R.F., Cao Y. & Lee T.H. ( 1993) ‘Fully nonlinear waterwave computations using the desingularized method '—Proceedings 6th Conference on Numerical Ship Hydrodynamics, University of Iowa.
[2] Beck R.F., Cao Y., Scorpio S.M. ( 1994) ‘Nonlinear ship motion computations using the desingularized method '—Proceedings 20th Symposium on Naval Hydrodynamics, University of California, Santa Barbara.
[3] Boo S.Y., Kim C.H., Kim M.H. ( 1994) ‘A numerical wave tank for nonlinear irregular waves by 3D higher order boundary element method'—Int. Journal of Offshore and Polar Eng., Vol. 4, no 4
[4] Broeze J. ( 1993) ‘Numerical modelling of monlinear free surface waves with a panel method'— Ph. D. Thesis, University of Twente, Netherlands
[5] Chan J.L.K. & Causal S.M. ( 1993) ‘A numerical procedure for time domain nonlinear surface waves calculations '—Ocean Engng., Vol. 20, no 1, 19–32
[6] Clément A., Mas S. ( 1995) ‘Hydrodynamics forces induced by a solitary wave on a submerged circular cylinder'—ISOPE'95 Conference, The Hague, Netherlands
[7] Cointe R., Geyer P. & Molin B. ‘Nonlinear and linear motions of a rectangular barge in a perfect fluid'—Proc. 18th ONR Symp. on Naval Hydrodynamics, Ann Arbor, Michigan
[8] Cooker M.J., Peregrine D.H., Vidal C. & Dold J.W. ( 1990) ‘The interaction between a solitary wave and a submerged semicircular cylinder' — J.F.M., 215, 1–22
[9] Dommermuth D.G., Yue D.K., Lin W.M., Rapp R.J., Chan E.S. & Melville N.K. ( 1988) ‘Deep water plunging breakers: A comparison between potential theory and experiments'—J.F.M., Vol. 189, pp. 423–442
[10] Dold J.W. ( 1992) ‘An efficient surface-integral algorithm applied to unsteady gravity waves'—Journal of Comp. Physics, Vol. 103, PP 90–115
[11] Faltinsen O.M. ( 1977) ‘Numerical solution of transient free-surface motion outside or inside moving bodies'—Proceedings 2nd Conf. on Num. Ship Hydro., U.C. Berkeley
[12] Faltinsen, O.M., Newman, Vinje T. ( 1995), ‘Nonlinear wave loads on a slender vertical cylinder', J.F.M. vol. 289, pp 179–198
[13] Ferrant P. ( 1991) ‘Threedimensional unsteady wave-body interactions in a bounded domain ' —6th International Workshop on Water Waves and Floating Bodies, Woods Hole, Massachusetts
[14] Ferrant P. ( 1993a) ‘Computation of fully nonlinear free surface flows in three dimensions '— 8th International Workshop on Water Waves and Floating Bodies, St John's, Newfoundland
[15] Ferrant P. ( 1993b) Threedimensional unsteady wave-body interactions by a boundary element method'—Ship Technology Research, Vol. 40 no 4, 165–175
[16] Ferrant P. ( 1994) ‘Radiation and diffraction of nonlinear waves in three dimensions'— Proceedings of the BOSS'94 Conference, MIT, Cambridge
[17] Ferrant P. ( 1996) “Computaion of higher order diffraction effects using a fully nonlinear simulation method” 11th International Workshop on Water Waves and Floating bodies, Hamburg
[18] Grilli S.T., Losada M.A., Martin F. ( 1993) ‘Impact of breaking waves over emerged and submerged coastal structures '—8th International Workshop on Water Waves and Floating Bodies, St John's, Newfoundland
[19] Kang C.G. & Gong I.Y. ( 1990) ‘A numerical solution for three dimensional nonlinear free surface problems'—18th ONR Symposium on Naval Hydrodynamics, Ann Arbor, Michigan
[20] Lalli F, Di Mascio, A. & Landrini M. ( 1995) ‘Nonlinear diffraction effects around a surface-piercing structure ', Proceedings of the ISOPE'95 Conference, The Hague
[21] Longuet-Higgins M.S., Cokelet E.D. ( 1976) ‘The deformation of steep water waves on water: I.A. numerical method of computation'— Proc. R. Soc. Lond, A350, pp. 1–26
[22] Malenica S., Molin B. ( 1995) ‘Third harmonic wave diffraction by a vertical cylinder” J.F.M. vol 302, pp203–229.
[23] Nakos D.E. ( 1993) ‘Rankine panel methods for transient free surface flows'—6th International Conference on Numerical Ship Hydrody-namics, Iowa City
[24] Nestegard A. ( 1994) ‘Comparative study of fully nonlinear wave simulation programs'. DNV Research report 94–2041.
[25] Rienecker M.M. & Fenton J.D. ( 1981) ‘A Fourier approximation method for steady water waves'—J.F.M., 104, 119–137
[26] Romate J.E. ( 1989) ‘The numerical simulation of nonlinear gravity waves in three dimensions using a higher order panel method'— Ph.D. Thesis, University of Twente, Netherlands
[27] Saad Y. & Schultz M.H. ( 1983) ‘GMRES : A generalized minimal residual algorithm for solving nonsymmetric linear systems'—Research Report Yale University, RR-254
[28] Sclavounos P.D., Kim, Y. ( 1995) ‘Third-order diffraction of surface waves by a time-domain Rankine panel method', 10th Workshop on Water Waves and Floating Bodies, Oxford
[29] Tanizawa K., Yue D.K.P. ( 1992) “Numerical computation of plunging wave impact loads on a vertical wall. Part2. The air pocket” 7th Workshop on Water Waves and Floating Bodies. Val de Reuil, France.
[30] Wang P., Yao Y., Tulin M.P. ( 1993) ‘Wave group evolution, wave deformation and breaking: Simulations using Longtank, a numerical wavetank'—Third ISOPE Conference, Singapour
[31] Wu G.X., Eatock-Taylor R. ( 1996) “Transient motion of a floating body in steep water waves”, 11th International Workshop on Water Waves and Floating bodies, Hamburg
[32] Xü H. & Yue D. ( 1992) ‘Computations of fully non linear three dimensional water waves'— 19th ONR Symposium on Naval Hydrodynamics, Seoul, Korea
[33] Yang C. & Ertekin R.C. ( 1992) ‘Numerical simulations of nonlinear wave diffraction by a vertical cylinder'—J. Offshore Mech. and Artic Eng., Vol. 114, pp. 36–44
[34] Zhou Z. & Gu M. ( 1990) ‘Numerical research of nonlinear body-wave interactions'—18th ONR Symposium on Naval Hydrodynamics, Ann Arbor, Michigan.
DISCUSSION
A.D.Papanikolaou
National Technical University of Athens, Greece
The author should be congratulated for a very interesting theoretical-numerical paper with various practical applications. The paper describes a fully nonlinear 3-D simulation method for the assessment of strong nonlinear effects in wavebody interaction problems. As an example of application and validation of the developed computer code, the results of Fig.15 hold for an incident wave period equal to twice the natural heaving period of the studied floating body. For this particular case, the amplitude of the 2ω motion component appears to be quite significant, namely about 20% of the fundamental frequency component. Could the author explain how these results change, when the wave excitation period is equal to the simple natural heaving period of the floating cylinder? Do the higher-order motion components become relatively larger?
AUTHOR'S RESPONSE
Thank you for your kind comment. I ran the numerical model in the conditions you were interested in, i.e., for an incident wave period equal to the natural heaving frequency of the floating cylinder. The resulting vertical motion of the body is plotted in Figure A1. Contrary to the simulation presented in the paper, the present signal is almost purely monochromatic, with an amplification factor equal to about 1.7 with respect to the incident wave amplitude. Higher harmonics are negligible, but there is sensible negative vertical drift, as shown by Figure A2 representing the moving window Fourier analysis of the time series. The wave amplitude is A/H=0.025, the wave period is T*sqrt(g/H)=3.5, and the wave length is λ/H=1.956.
In this resonant regime, body and free surface tend to move with opposite phases, and runs with larger wave amplitudes led to numerical breakdown, the bottom of the body getting very close to aerating. This problem could be solved by implementing a more refined remeshing procedure for the body, instead of the simple redistribution of nodes in the vertical direction used for the present simulations.
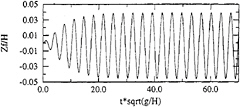
Fig. A1: Vertical motion of the body. A/H=0.025; T*sqrt(g/H)=3.5
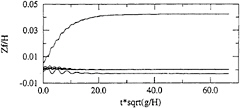
Fig. A2: Harmonic components of the motion