Influence of the Cavitation Nuclei on the Cavitation Bucket when Predicting the Full-Scale Behavior of a Marine Propeller
B.Gindroz (Bassin d'Essais des Carènes, France), G.Bailo (MARISPENAV, Italy), F.Matera, M.Elefante (MARISTAT SPMM, Italy)
ABSTRACT
The important role of nuclei on cavitation inception and cavitation development is now well known. Several recent studies, such as the large one suggested by the 20th ITTC and conducted in 1992 at the Grand Tunnel Hydrodynamique (GTH) of the Bassin d'Essais des Carènes, have allowed a precise correlation between cavitation inception for different types of cavitation on marine propellers and nuclei distributions (20th ITTC report) [33]. In a standard cavitation facility the nuclei distribution will depend on the hydrodynamic operating conditions, and can change during whole cavitation tests. Indeed, the “natural” nuclei spectrum of any cavitation facility depends on the history of the fluid through the different parts that constitute the facility. This means that this spectrum will depend on the hydrodynamic conditions, such as dissolved air content, pressure level and velocity, and the transit time through any part of the circuit, such as the main pump, vanes, resorber, etc. As a consequence, the “natural” spectra will be different in each cavitation facility. To quantify this effect, cavitation tests were conducted in the Italian Navy cavitation tunnel (CEIMM), on a frigate propeller. The inception cavitation characteristics of the model propeller (cavitation bucket) was determined, following the standard procedure of the CEIMM. In parallel, cavitation nuclei were measured for each operating condition. These measurements were conducted by the Bassin d'Essais des Carènes (French navy), using a Centerbody Venturi, similar to the one that equipped in standard the large French cavitation tunnel (GTH). In this paper, we describe the test procedure and the measurements. Then, the results are analyzed, using the procedure suggested by Gindroz and Billet [1, 2, 3], which correlates nuclei distributions characteristics with cavitation inception data. This new approach is very interesting, as taking into account the nuclei characteristics leads to a unique cavitation inception bucket, independent of the hydrodynamic test conditions.
INTRODUCTION
Cavitation is one of the main limiting feature to the increase of hydrodynamic performances. Then, it is impossible to determine the performance of any hydraulic component without taking into account its cavitation behavior. Prediction of the cavitation performance of a propeller or a pump, a turbine, a vane, etc…is generally determined from model tests in cavitation facilities. The transposition from model results to full-scale characteristics is obtained by scaling laws and specific test procedures, established for some time by each organisation involved in hydrodynamic performances assessment. However, various problems remain unsolved, mainly due to the lack of knowledge of the local fluid mechanics and water quality. A significant illustration of this problem was given by Lindgren and Johnsson in 1966 [32], during the “standard” cavitation tests performed for the ITTC at several facilities. Then, many experiments were conducted that demonstrate the role of viscous effects [4, 5] and water quality [6,7,8] on cavitation.
Numerous research has been carried out to attempt to identify, understand, predict and control the physical mechanism leading to cavitation
inception. Rood [9], in his paper entitled “Mechanisms of Cavitation Inception”, makes a precise review of research progress during the last twenty years. He underlines that the scaling laws to predict the full-scale cavitation behavior from the model tests, are based on empirical rules, defined on a correlation between measurements at model scale and observations of full-scale characteristics. The need to better understand the scale phenomena and to develop physical prediction laws has led to focus studies on real fluid characteristics. For an engineer, the purpose of any model scale test is the accurate prediction of the full-scale behavior.
Experimental observations have shown the persistence of microbubbles in a real fluid. These free microbubbles, called nuclei, have been found to be a major parameter in the cavitation inception process. According to the study of Billet [10] and Gindroz [11], natural waters such as rivers and oceans contain free microbubbles.
The influence of the nuclei on the cavitation behavior has been written in numerous publications [12 to 30]. To summarize all these studies, the role of free cavitation nuclei was found to be of major importance in the cavitation inception and developments processes. More particularly, we must be able to measure the nuclei content in a facility, when performing cavitation tests on a model.
Thus, in order to relate nuclei size distributions with inception cavitation in cavitation facilities, a test program was conducted in 1992 at the Grand Tunnel Hydrodynamique (GTH) of the Bassin d 'Essais des Carènes. The GTH, which has a complete air control system including dissolved gas and nuclei (microbubbles) control, offered the opportunity to answer this question.
The tests were conducted on three 34 mm diameter propellers used by Kuiper [6], each of these propellers being characterized by a different cavitation type: bubble, sheet and vortex cavitation.
Four different nuclei distributions were generated (Figure 1): strong degassed water (maximum tension, T4), low injection of medium size nuclei (medium tension-low content, T3), large injection of medium size nuclei (medium tension-high content, T2) and large injection of large nuclei (minimum tension, T1). By injecting medium size nuclei for a low content and a high content, we were able to examine the influence of the number of nuclei on the cavitation inception characteristic. During all the tests, the dissolved air content was kept constant.
The GTH on-line Cavitation Nuclei Counter (Centerbody Venturi) was used to measure both the water nuclei distribution and the liquid tension.
Figure 1 summarizes the influence of the nuclei characteristic distributions on the cavitation inception parameter, σi, referred to its value for the T4 nuclei distribution (maximum tension case). The nuclei measurements are presented as a cumulative nuclei distribution, in Number of nuclei per ccm versus their critical pressure referred to the vapor pressure, Pcr—Pv (Figure 1).
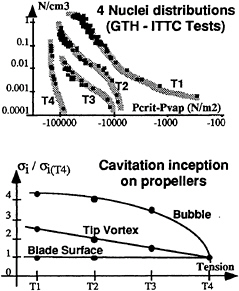
FIGURE 1: NUCLEI INFLUENCE ON THE CAVITATION INCEPTION CHARACTERISTIC FOR SHIP PROPELLER
These tests at the GTH clearly demonstrate the direct influence of water quality on propeller cavitation inception (1, 2, 3). With a large increase in liquid tension, little change in cavitation inception was found for blade surface cavitation (sheet cavitation), but, in the case of both tip vortex cavitation and travelling bubble cavitation, the nuclei measurements from the GTH standard Centerbody Venturi correlated with many observed trends. Moreover, for the case of tip vortex cavitation inception, it appears that the measurement of both nuclei size (liquid tension) and nuclei number distribution (event rate) are necessary to correlate the data. Indeed, for the medium tension case, a strong influence on the inception of tip vortex cavitation can be observed from the two different nuclei concentrations (high and low).
The cavitation inception generally corresponds to an event rate of the order of magnitude of 1 event per second. When analyzing the cavitation inception results from the point of view of event rates Gindroz and Billet [3] show that the so-called “water tension” leading to cavitation inception
must be related to different nuclei concentrations, specific to each type of cavitation, mainly bubble and tip vortex cavitation for propellers. Thus, the tension T*, corresponding to inception must be determined from the nuclei measurements. If S* is the cross section of the cavitating flow, C* is the absolute velocity of the flow through this section and ![]()
![]() is the number of activated nuclei per unit volume, the nuclei content leading to an event rate ξ can be defined as follows:
is the number of activated nuclei per unit volume, the nuclei content leading to an event rate ξ can be defined as follows:
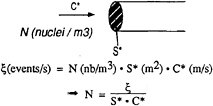
Then, considering that cavitation inception generally corresponds to an event rate of 1 per second, the corresponding number of activated nuclei N* and the corresponding tension, T* will be:
For the characteristic conditions of the GTH-ITTC 1992 tests [33], the nuclei content that must be activated to lead to cavitation inception was of the order of magnitude of 0.0001 N/ccm for the Bubble cavitation (B) and 0.01 N/ccm for the Tip vortex one(TV). Then, the corresponding inception tensions, T*, were determined from each of the 4 nuclei distributions (Figure 2).
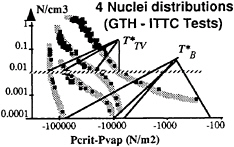
FIGURE 2: NUCLEI DISTRIBUTIONS AND CORRESPONDING CHARACTERISTIC TENSIONS, T*B AND T*TV
Using these characteristic values, it was possible to precisely correlate the tension value T* with the cavitation inception value, σi.
The relation between T* and σi for both bubble and tip vortex cases are linear and the characteristic slope of the curves are equal to:
This means that the cavitation inception value, σi, directly depends on the normalized tension, ![]() based on the event rate analysis:
based on the event rate analysis:
were ![]() =Normalizex "event rate"
=Normalizex "event rate" ![]()
and σio=σi value for zero tension (T*=0 N/m2)
Figure 3 represents this major result and leads to the conclusion that it is no longer possible to conduct meaningful cavitation tests without determining the complete nuclei distributions.
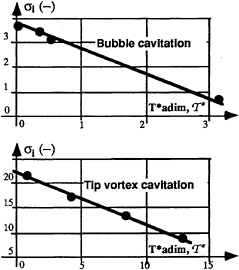
FIGURE 3: INFLUENCE OF T*adim TENSION, ![]() ON CAVITATION INCEPTION
ON CAVITATION INCEPTION
PURPOSE OF THE STUDY
The conclusion of the above study clearly shows the importance of understanding the role of nuclei distribution (liquid tension and nuclei number distribution) in the cavitation inception process. Minimizing the liquid tension and maximizing the number of nuclei (number distribution) is one method to reduce scale effects; however, in many facilities, this is not practical. Also, in some cases, this can alter the bubble dynamics and appearance of the cavitation, especially when the increase of nuclei number distribution is obtained by increasing the dissolved air content in the facility.
Rood in his review [9], underlines the fact that different facilities are characterized by different nuclei distributions, corresponding to the hydrodynamic configuration of each facility. The nuclei spectrum is affected by the whole nuclei time history through the facility. The use of a deaerator to remove air and a resorber to dissolve the small nuclei can change significantly the spectrum. As a consequence, the “natural ” spectra will not only be different in each cavitation facility, but will also strongly depend on the facility operating conditions. This is not acceptable when determining a precise cavitation model bucket, that must be representative of the model characteristics.
Generally, scale effects between model and full-scale equipment are analyzed without taking into account any nuclei influence [38]. As a result, transposition laws established by hydrodynamic laboratories from theoretical analysis and many experimental results on both models and full-scale equipment, omit the major influence of the nuclei. This means that, for different nuclei distributions, the model results will be transposed exactly in the same way, without any water quality transposition parameter. Particularly, the four characteristic cavitation inception values corresponding to the four nuclei distribution generated during the GTH-ITTC tests (Figure 1), will be transposed with the exact same laws, as the transposition laws are mainly a function of the geometric scale, the Reynolds number and the surface roughness, but not of the free nuclei distribution:
The purpose of any model test is to try to predict the full-scale characteristic. It is then necessary to determine a precise cavitation bucket that corresponds to the model behavior, as its own and unique characteristic. It has not to include the own facility and the water quality characteristics.
To quantify this effect, cavitation tests are conducted in the Italian Navy cavitation tunnel (CEIMM), on a frigate propeller. The inception cavitation characteristic of the model propeller (cavitation bucket) is determined visually, by the CEIMM staff, following their standard procedure. In parallel, cavitation nuclei are measured for each tunnel operating condition (each measured point). These nuclei measurements are conducted by the Bassin d'Essais des Carènes (French Navy), using a Centerbody Venturi [31, 34, 35], similar to the one that equipped in standard the large French cavitation tunnel (GTH), and that was used during the GTH-ITTC tests [1, 2, 3, 33].
The tests are carried out for two different dissolved O2 contents, and their influence on the cavitation bucket is analyzed, using a similar approach that the one proposed by Gindroz and Billet [3] to correlate nuclei characteristics with cavitation inception data.
The main purpose of this study is to try to determine a unique characteristic cavitation bucket, which does not depend on the facility and its hydrodynamic operating conditions. The new bucket will correspond to a “zero tension” water quality, determined from the event rate analysis of Gindroz and Billet [3].
TEST FACILITIES AND INSTRUMENTATION
The tests are conducted in the CEIMM Cavitation Tunnel, designed in 1962 by Kempf & Remmers (Figure 4).

FIGURE 4: CEIMM CAVITATION TUNNEL
It has the following technical characteristics:
-
Length: 12 m
-
Height: 8.5 m
-
Stainless steel AISI 316
-
Test section: 600mm×600mm×2.6 m
-
Power: 213 kW, 4-blades axial flow impeller with Ward-Leonard
-
Max. velocity: 12 m/s
-
Max & Min abs pressure: 150–10 kPa
-
Cavitation: σ=0.2 and over
INSTRUMENTATION:
3 sets of propeller dynamometers,
3 & 5 components balances,
pressure transducers,
Laser Doppler,
Wake survey, hydrophones, etc…
PROPELLER SIZE RANGE:
Standard diameter: 250 mm
Maximum diameter: 300 mm
The tests are conducted on a 4-blades propeller, that equipped a LUPO Class frigate, characterized by a maximum velocity of 35 knots. The propeller model has a diameter of 274.1 mm and is installed in the CEIMM Tunnel test section with brackets on the main shaft inclined with 5°30 (Figure 5).
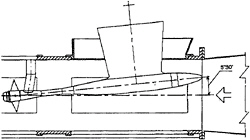
FIGURE 5: PROPELLER TEST CONFIGURATION IN THE CEIMM CAVITATION TUNNEL
The cavitation nuclei distributions are measured by a fully calibrated Centerbody Venturi similar to the one that is used during standard cavitation tests on the GTH. The major advantage of the hydrodynamic technique of the Venturi is that the nuclei are determined using the same phenomenon that governs the cavitation development [11, 35, 36,37]. Thus, only the micro-bubbles (cavitation nuclei) are counted, not the solid particles. This technique is particularly well-adapted to this kind of measurement.
MEASUREMENTS
The main purpose of this study is to determine how the nuclei distributions change with the tunnel operating conditions during model cavitation tests, and how they influence the global result, i.e. the whole cavitation bucket.
A cavitation bucket, σn versus J, is visually determined (Figure 6), within the following range of the advance ratio parameter, J:
0.93 JN≤J≤1,04 JN
where JN is the nominal advance value
|
|
(-) |
|
|
|
(-) |
|
|
V |
: Flow velocity |
(m/s) |
|
n |
: Propeller rotational speed |
(rps) |
|
D |
: Propeller diameter |
(m) |
|
Pts |
: Pressure in the test section |
(N/m2) |
|
Pv |
: Vapor pressure |
(N/m2) |
|
ρ |
: water density |
(kg/m3) |
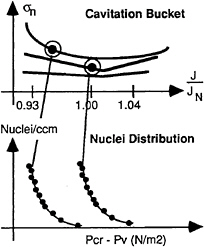
FIGURE 6: CHARACTERISTIC MEASUREMENTS DURING THE CEIMM TESTS
Changing the J value, is obtained for a constant propeller rotational speed, n, by modifying the flow velocity, V. Thus, for the above defined range of J, the flow velocity varies within the following range:
8 m/s≤V≤8.9 m/s
The “natural” nuclei spectrum of any cavitation facility depends on the history of the fluid through the different parts that constitute the facility. This means that this spectrum will depend on the hydrodynamic conditions, such as dissolved air content, pressure level and velocity, and the transit time through any part of the circuit, such as the main pump, vanes, resorber, etc. As a consequence, the “natural” spectra will change with the tunnel operating conditions. Thus, for each point of the bucket, a complete nuclei distribution is measured by the Centerbody Venturi (Figure 6). The results are presented as a cumulative nuclei distribution, in Number of nuclei per ccm versus their critical pressure referred to the vapor pressure, Pcr—Pv (Figure 6).
This complete sequence is measured for 2 different dissolved O2 contents, respectively 3 ppm and 5 ppm, in order to analyze the influence of the dissolved air content on the nuclei “natural” distributions, and their consequence on the cavitation inception characteristics (Bucket). The dissolved O2 content is directly measured with a Beckman equipment. In the CEIMM tunnel, it is possible to maintain constant the dissolved O2 content, in a relatively wide range of values.
RESULTS
During the cavitation measurements, the pressure level in the test section (sigma value) and the dissolved O2 content is found to strongly influence the nuclei distributions. However, due to the very good stability of the CEIMM tunnel and its deep resorber, the nuclei spectra are particularly well repetitive and stable for a given hydrodynamic condition. Figure 7 illustrates the direct influence of both parameters, i.e. pressure level in the test section and O2 content. Within the narrow range of flow velocity (8≤V≤8.9 m/s), no sensible effect of this parameter was found.
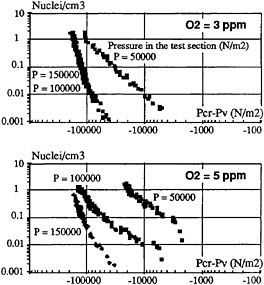
FIGURE 7: INFLUENCE OF THE OPERATING CONDITIONS ON THE CHARACTERISTIC NUCLEI DISTRIBUTIONS, DURING THE CEIMM TESTS
The analysis of the above results shows a large influence of both the pressure value and the dissolved O2 content on the nuclei characteristics. Thus, as the cavitation parameter, σn, is directly related to the absolute pressure level in the test section, this result means that the water tension, leading to cavitation inception, will change during the determination of a complete cavitation inception bucket, even if the dissolved O2 content can be kept constant. To quantify this effect, figure 8 represents the evolution of the minimum normalized water tension, corresponding to the nuclei with the highest critical pressure, i.e. the “weakest nuclei” (the biggest ones), versus the cavitation parameter, σn. The tension is normalized by the same value than the cavitation parameter, σn:
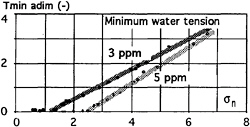
FIGURE 8: INFLUENCE OF THE OPERATING CONDITIONS ON THE CHARACTERISTIC WATER TENSION, CORRESPONDING TO THE “WEAKEST” NUCLEI.
The evolution of the minimum tension versus the σn, can reasonably be represented by a linear curve, for both 3 ppm and 5 ppm dissolved O2 contents. However, for σn value below 2.5, the tension is close to zero for the 5 ppm case, but remains relatively important for the 3 ppm case, for which the zero tension is reached only below σn=1.
Under this modification of the nuclei characteristics, no wonder that the whole cavitation inception bucket will be influenced.
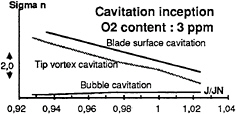
FIGURE 9: CAVITATION INCEPTION BUCKET FOR 3 PPM O2 CONTENT.
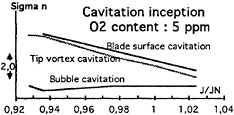
FIGURE 10: CAVITATION INCEPTION BUCKET FOR 5 PPM O2 CONTENT.
Figures 9 and 10 represent the global cavitation inception bucket, for blade surface cavitation, tip vortex and bubble cavitation, corresponding to a dissolved O2 content of respectively 3 ppm and 5 ppm.
To better evaluate how the modification of nuclei characteristics through the change of O2 content, influences the cavitation inception bucket, figure 11 represents both buckets on the same graph. The solid lines correspond to the 3 ppm case, while the dotted line to the 5 ppm case.
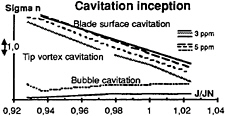
FIGURE 11: CAVITATION INCEPTION BUCKETS FOR 3 AND 5 PPM O2 CONTENTS.
A significant difference is observed between the two water conditions. Then, the practical question remains: which bucket is the correct one, leading to the accurate prediction of the full-scale cavitation behavior? The answer can not be either the 3 ppm one or the other one. Indeed, when determining the “cavitation bucket” of a model propeller, how can we guarantee the model results when the nuclei distribution changes with the operating conditions (pressure, flow rate, dissolved air content) and when the nuclei distribution is not known? Moreover, how can we transpose such a result to full-scale prediction, when the model free nuclei content changes with the operating conditions, which is not the case at sea, as the nuclei distributions will not directly depend on the advance velocity?
Moreover, during a normal procedure, several problems can happen, as, for example, the increase of dissolved air content during the tests. In this case, if the tests are done quickly to ensure the dissolved gas content doesn't change significantly, the characteristic σi—J inception curve will be one of those corresponding to a constant O2 content (Figure 12, TVA or TVB). But, when the dissolved gas content changes during the cavitation bucket tests, results can be altered as shown in Figure 12. Depending where the tests start (either from point C or D, for example), the characteristic curves will be different. Indeed, if the tests start with a low
dissolved air content, the water will generally increase its air content with the time. Then, as the nuclei distributions change with the dissolved air content in the water (Figure 7), the cavitation behavior of the propeller will be influenced, and the characteristic inception curve will evolve along the TVC or TVD curve (Figure 12).
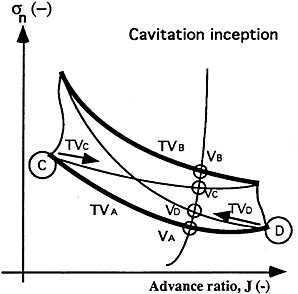
FIGURE 12: INFLUENCE OF THE TESTS PROCEDURE ON THE CHARACTERISTIC CAVITATION INCEPTION CURVES
As a consequence, the prediction of the range of advance velocity free of cavitation depends on the procedure of the model tests. This is not acceptable when determining a precise cavitation model bucket that must be representative of its own cavitation characteristics. Then, as long as scale effects between model and full-scale equipment are analyzed without taking into account any nuclei influence, the four characteristic curves represented in figure 12 will be transposed with the exact same laws, which means that the corresponding uncertainty on the predicted full-scale advance velocity leading to cavitation inception can be as large as several knots.
Fortunately, the problem of O2 content evolution during the tests doesn't appear in the CEIMM tunnel., as it is possible to reasonably maintain constant the dissolved gas content.
ANALYSIS
Following the same analysis than proposed by Gindroz and Billet [ 2, 3], to correlate nuclei distributions with cavitation inception data, there is an attempt to transpose the model cavitation bucket to a model “zero tension” one, using the nuclei distribution characteristics. This means that this new cavitation inception bucket corresponds to a “weak water” with a zero tension, as defined in the introduction, and based on the events rate analysis. Applying this procedure to the CEIMM tests, must lead to the transposition of both 3 ppm and 5 ppm buckets to a single one, as schematically represented in figure 13.
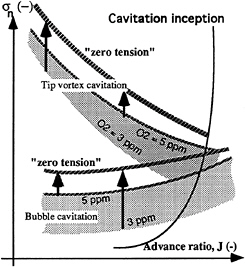
FIGURE 13: “ZERO WATER TENSION” CHARACTERISTIC CAVITATION BUCKET
The transposition of the cavitation inception curves is made by adding the inception normalized tension, ![]() , to the cavitation inception parameter, σni:
, to the cavitation inception parameter, σni:
Where σni“0” is the new transposed inception cavitation value, corresponding to a “zero tension” water.
For the application of the above described procedure, it is necessary to determined the tension, T*, as a function of the nuclei content. Indeed, the tension leading to cavitation inception is based on an events rate analysis, which means that the number of activated nuclei corresponding to cavitation inception, will depend on the hydrodynamic conditions and the type of cavitation, as already
mentioned in the introduction [2, 3]. Thus, the evolution of the tension, T*, with the cavitation parameter, σn, is determined for different nuclei contents, from the nuclei distributions measured during the CEIMM tests for each σn—J point. Figures 14 et 15 represent the evolution of the normalized tension, ![]() , for 4 different nuclei contents, resp. 0,001; 0,003; 0,005 and 0,01 Nucleus/ccm. Figures 14 and 15 correspond respectively to the 3 ppm and 5 ppm dissolved O2 contents.
, for 4 different nuclei contents, resp. 0,001; 0,003; 0,005 and 0,01 Nucleus/ccm. Figures 14 and 15 correspond respectively to the 3 ppm and 5 ppm dissolved O2 contents.
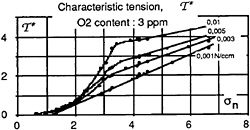
FIGURE 14: EVOLUTION OF THE ![]() NORMALIZED TENSION WITH THE σn PARAMETER, FOR DIFFERENT NUCLEI CONTENTS, AT 3 PPM OF DISSOLVED O 2
NORMALIZED TENSION WITH THE σn PARAMETER, FOR DIFFERENT NUCLEI CONTENTS, AT 3 PPM OF DISSOLVED O 2
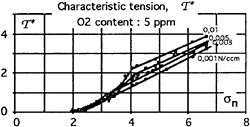
FIGURE 15: EVOLUTION OF THE ![]() NORMALIZED TENSION WITH THE σn PARAMETER, FOR DIFFERENT NUCLEI CONTENTS, AT 5 PPM OF DISSOLVED O 2
NORMALIZED TENSION WITH THE σn PARAMETER, FOR DIFFERENT NUCLEI CONTENTS, AT 5 PPM OF DISSOLVED O 2
Large influence of the dissolved O2 content can be observed. Indeed, within the range of σn values corresponding to cavitation inception, the normalized tension difference, Δ![]() can be larger than 1,0 for the highest nuclei contents (0.005 and 0.01 N/ccm).
can be larger than 1,0 for the highest nuclei contents (0.005 and 0.01 N/ccm).
In order to determined the particular normalized tension, ![]() , leading to cavitation inception, the corresponding number of activated nuclei (nuclei content), must be determined. This amount is specific to each type of cavitation. In this study, we concentrate on tip vortex cavitation and bubble cavitation. Following the same analysis than used by Gindroz and Billet [2], the required nuclei content corresponding to tip vortex cavitation inception based on one event per second is of 0,003 N/ccm. The bubble cavitation only appears at the root of the blades. In this area, the absolute velocity and the cross section (see introduction) are not very important, which means that it is necessary to activate a rather large amount of nuclei. In our case, the corresponding nuclei content leading to bubble cavitation inception corresponds to about 0,05 N/ccm.
, leading to cavitation inception, the corresponding number of activated nuclei (nuclei content), must be determined. This amount is specific to each type of cavitation. In this study, we concentrate on tip vortex cavitation and bubble cavitation. Following the same analysis than used by Gindroz and Billet [2], the required nuclei content corresponding to tip vortex cavitation inception based on one event per second is of 0,003 N/ccm. The bubble cavitation only appears at the root of the blades. In this area, the absolute velocity and the cross section (see introduction) are not very important, which means that it is necessary to activate a rather large amount of nuclei. In our case, the corresponding nuclei content leading to bubble cavitation inception corresponds to about 0,05 N/ccm.
Then, from the above results, it is possible to determine the corresponding normalized tension, ![]() (Figures 14 and 15). By adding the specific tension
(Figures 14 and 15). By adding the specific tension ![]() to the measured cavitation inception parameter, σni, we can reach the desired “zero tension” cavitation inception value, σnio. Figure 16 represents this final result
to the measured cavitation inception parameter, σni, we can reach the desired “zero tension” cavitation inception value, σnio. Figure 16 represents this final result
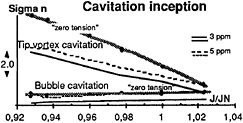
FIGURE 16: “ZERO TENSION” CAVITATION INCEPTION BUCKET, MEASURED AT THE CEIMM TUNNEL
Interesting results are obtained here. Indeed, the two different cavitation inception curves corresponding to two different dissolved gas contents (3 ppm and 5 ppm in Figure 2), collapse on a single curve: the transposed “zero water tension” characteristics deducted from the nuclei measurements. This “new bucket”, corresponding to the “zero water tension”, is unique and does not depend on the hydrodynamic conditions.
SYNTHESIS AND PERSPECTIVE
In order to relate nuclei characteristics with the cavitation inception, a large study was conducted in 1992 at the Grand Tunnel Hydrodynamique (GTH) of the Bassin d'Essais des Carènes in cooperation with the ITTC cavitation committee [33]. The GTH, which has a complete air control system including dissolved gas and free nuclei (microbubbles) control,
offered the opportunity to answer this question. The main result of this study was the direct correlation between the cavitation inception and the water tension based on an events rate analysis. Indeed, as cavitation inception corresponds to a certain amount of events per second (generally of the order of magnitude of 1), it is necessary to activate a certain amount of nuclei in the flow. Thus, the tension T*, corresponding to the minimum nuclei content leading to cavitation inception was defined from the measured nuclei distributions. Due to the GTH design, the nuclei distribution can be controlled and set as desired. This means that during the complete determination of a cavitation inception bucket, the nuclei distribution will stay constant. However, when conducting cavitation inception tests in a classical cavitation tunnel, we must be very careful to not only attribute the results to the propeller itself, but also to consider the influence of the free nuclei distribution that will change with the tunnel operating conditions. It is well known that comparing the results obtained with the same model in different facilities is almost impossible [32]. But we are convinced that a large part of the reason comes from the lack of knowledge about the nuclei characteristics and their evolution with the hydrodynamic conditions. In order to try to quantify this effect, this study was conducted at the CEIMM tunnel, in Roma, on a 4 blades frigate propeller. The results obtained confirm the strong influence of the tunnel hydrodynamic parameters on the nuclei distribution. Then, as the free nuclei mainly govern the whole cavitation inception process, no wonder that the global cavitation inception bucket is influenced.
Following the analysis from Gindroz and Billet [2, 3], who succeed in correlating the nuclei distribution and the cavitation inception characteristics, the results obtained at the CEIMM are transposed to a “zero tension” bucket. This transposition is made for 2 different O2 contents, that lead to a large difference in the nuclei content. To ensure the upstream velocity field (wake field) doesn't change between the two different O2 content conditions, the flow velocity was similar. Thus, if the reason why the cavitation buckets are different between the two conditions is mainly due to the free nuclei, the 2 transposed “zero tension” buckets must be similar. Then, the comparison made in figure 16 confirmed the direct influence of the free nuclei on the cavitation inception characteristics, which is shown in figure 16. This major result means that conducting cavitation inception tests in different facilities and/or for different water qualities, on the same model and ensuring the same upstream velocity field, can lead to the same global bucket only if the nuclei characteristics are taken into account. Then, the unique “zero tension” bucket could be defined as the own cavitation inception characteristic of the model. In order to confirm this major result, similar tests will be conducted at the GTH, in the same configuration, for different nuclei distributions. Due to the specific design of the GTH, the nuclei distributions will be controlled, which means that it is possible to ensure no dependence of the tension with the σn value (Figure 17).
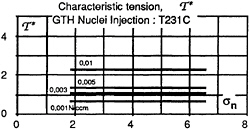
FIGURE 17: EXAMPLE OF NUCLEI CHARACTERISTICS GENERATED AND CONTROLLED IN THE GTH.
From the generated nuclei distributions, the measured cavitation inception bucket will be transposed to its corresponding “zero tension ” one. Cavitation inception buckets will be determined in the GTH on the same Italian frigate propeller for several nuclei characteristics, and transposed to their “zero tension” ones. Then, all these “zero tension” curves will be compared with the ones determined at the CEIMM tunnel. If the wake field is similar between both facilities, all these different characteristic “zero tension” curves must collapse to a unique one: The model cavitation inception characteristics.
Then, the prediction of the full-scale behavior could be made from this new “zero tension” model bucket, using the usual transposition laws, that do not take into account the nuclei characteristics. The so-determined full-scale bucket will then correspond to weak water without any tension. Then, finally, as a further perspective, the accurate evaluation of the full-scale risk of cavitation could be more precisely determined by taking into account the sea nuclei characteristics [39].
CONCLUSION
The present study shows the direct influence of the hydrodynamic operating conditions of a standard cavitation tunnel on the characteristic cavitation inception bucket of a propeller. Careful attention must be taken when conducting cavitation tests, as the final results can include important effects from the evolution of the nuclei with the tunnel
operating conditions and the water quality. However, due to the very good stability and repeatability of the CEIMM tunnel, it was possible to directly relate the nuclei distribution with the cavitation inception characteristics, and to transpose the results to an accurate unique “zero tension” bucket, that defines the own propeller behavior under the actual test configuration. This result is very important, but further studies will be conducted in order to confirm it and to examine its influence on the full-scale characteristic bucket.
Several vain attempts have been made for many years to try to compare similar tests carried out in different facilities, but this new approach looks promising.
ACKNOWLEDGEMENTS
The authors wish to acknowledge first the Italian Navy and the French Navy, who agreed in working together on this subject.
The authors wish to acknowledge all the colleagues from the CEIMM, and specially the staff of the cavitation tunnel, for their enthusiastic participation during the tests campaigns.
This work is supported financially by the Italian Navy and the DRET, that the authors wish to acknowledge more particularly.
REFERENCES
1. Gindroz, B., Billet, M.L., “Influence of the Nuclei on the Cavitation Inception for Different Types of Cavitation on Ship Propellers”, Proceedings of the ASME WAM '93, December 1993, New Orleans, USA.
2. Gindroz, B., Billet, M.L., “Nuclei and Acoustic Cavitation Inception of Ship Propellers”, Proceedings of the Second International Symposium on Cavitation, April 1994, Tokyo, Japan.
3. Gindroz, B., Billet, M.L., “Nuclei and Propellers Cavitation Inception”, Proceedings of the ASME FED Symposium on Cavitation, June 1994, Lake Tahoe, USA.
4. Arakeri, V.H., Acosta A.J., “Viscous Effects in Inception of Cavitation on Axisymmetric Bodies ”, Journal of Fluid Engineering, Trans ASME, 1973, pp. 519–526.
5. Van der Meulen, J.H.J., “A Holographic Study of Cavitation on Axisymmetric Bodies and the Influence of Polymer Additives”, Publication No509, 1976, Netherlands Ship Model Basin, Wageningen , The Netherlands.
6. Kuiper, G., “Cavitation Inception on Ship Propellers Models”, Ph. D. Dissertation, 1981, Wageningen, The Netherlands.
7. Gates, E.M., Billet, M.L., “Cavitation Nuclei and Inception”, Proceedings of IAHR Symposium, 1980, Tokyo, Japan, pp 3–25.
8. Katz, J., “Cavitation Inception in Separated Flows”, California Institute of Technology, 1981, Report No Eng. 183–5.
9. Rood, E.P., “Review-Mechanisms of Cavitation Inception”, Journal of Fluid Engineering, June 1991, vol. 113.
10. Billet, M.L., “Cavitation Nuclei Measurements-A Review”, Proceedings of the Cavitation and Multiphase Flow Forum, 1985, ASME.
11. Gindroz, B., “Lois de similitude dans les essais de cavitation des turbines Francis ”, PhD. dissertation, 1991, Lausanne, Ecole Polytechnique Fédérale.
12. Henry, P., “Influence of the Amount of Bubble Nuclei on Cavitation Tests of a Francis Turbine”, Proceedings of the ASME Symposium, Cavitation and Polyphase Flow Forum , 12–14 June, 1978, Fort Collins, pp. 23–28.
13. Avellan, F., Gindroz, B., Henry, P., Bachmann, P., Vullioud, G., Wegner, M., “Influence de la chute d'essai et de la nucléation sur les performances en cavitation des modèles de turbines Francis”, Proceedings of the 13th I.A.H.R. Symp. on Progress in Technology, September 1986, Montréal, vol. 1, pp. 2–1, 2–15.
14. Billet, M.L., “The Importance and Measurement of Cavitation Nuclei”, Advancements in Aerodynamics, Fluid Mechanics and Hydraulics, 1986, Minneapolis.
15. Billet, M.L., “Cavitation Nuclei Measurements”, Proceedings of the International Symposium on Cavitation Inception, ASME WAM, 1984, New Orleans.
16. Kuiper, G., “Some Experiments With Distinguished Types of Cavitation on Ship Propellers ”, Proceedings of the International Symposium on Cavitation Inception, ASME WAM, 1979, New York.
17. Kuiper, G., “Some Experiments With Distinguished Types of Cavitation on Ship Propellers ”, Journal of Fluid Engineering, 1982, vol. 104.
18. Kuiper, G., “Reflections on Cavitation Inception,” Proceedings of the Cavitation and Multiphase Flow Forum, ASME, 1985.
19. Gindroz, B., Avellan, F., Henry, P., “Similarity rules of cavitation tests: The case of the Francis turbine ”, Proceedings of the 14th I.A.H.R. Symp. on Progress within large and high-specific energy units, June 1988, Trondheim, vol. 2, Session L, pp 755–766.
20. Gindroz, B., Henry, P., Avellan, F., “Similarity of cavitation inception in Francis turbine”, Proceedings of the 15h I.A.H.R. Symp., September, 1990, Belgrade, Yugoslavia.
21. Gindroz, B., Avellan, F., Henry, P., “Guide lines for performing cavitation tests”, Proceedings of the 15h I.A.H.R. Symp., September, 1990, Belgrade, Yugoslavia.
22. Gowing, S., Shen, Y.T., “The Role of Microbubbles on Cavitation Inception on Head Forms”, 1982, David Taylor Research Center Report.
23. Gowing, S., Shen, Y.T., “Cavitation Susceptibilities in Ocean Waters” , 1987, David Taylor Research Center Report DTNSRDC-SHD-1241–01, Aug.
24. Brennen, C.E., Kuhn de Chizelle, Y., “Cavitation Nuclei Concentrations and Event Rates”, Internal Report, CALTEC, Pasadena, CA, July 1992.
25. Shen, Y.T., Gowing, S., Pierce, R., “Cavitation Susceptibility Measurements by a Venturi”, Proceedings of the International Symposium on Cavitation Inception, ASME WAM, 1984, New Orleans.
26. Shen, Y.T., Gowing, S., Eckstein, B., “Cavitation Susceptibility Measurements of Ocean, Lake and Laboratory Water”, 1986, David Taylor Research Center Report No. 86/019.
27. Liu, Z., Brennen, C.E., “Cavitation Nuclei Measurements and Population Dynamics”, Internal Report, California Institute of Technology (CALTEC), Pasadena, California, July 1992.
28. Tanger, H., Strechwall, H., Weitendorf, E.-A., Mills, L., “Recent Investigations of the Free Air Content and its Influence on Cavitation and Propeller-Exited Pressure Fluctuations”, Proceedings of the ISPC, Hamburg, Germany, June 1992.
29. Keller, A.P., “Scale effects at beginning cavitation applied to submerged bodies ” , Proceedings of the ASME Int. Symp. on Cavitation Inception, 1984.
30. Meyer, R.S., Billet, M.L., Holl, J.W., “Free Stream Nuclei and Travelling-Bubble Cavitation”, JFM, Vol. 114, December 1992.
31. Lavigne, S., Noe, Ph., “Venturi à ogive centrale”, Rapport d'essais, R. 21.025, 1988.
32. Lindgren, H., Johnsson, C.A., “Cavitation Inception on Head Forms—ITTC Comparative Experiments”, 1966, Pub. of the Swedish State Shipbuilding Exper. Tank No58.
33. 20 ITTC, “Report of Cavitation Committee”, 19–24 September 1993, San Francisco.
34. Lavigne, S., “Le Venturi analyseur de germes”, Proceedings of the Journées DRET Cavitation, Arcueil 1991.
35. Gindroz, B., Billard, J.-Y., Lavigne, S., “Complete Study of a Well-improved Centerbody Venturi”, Proceedings of the Second International Symposium on Cavitation, April 1994, Tokyo, Japan.
36. Gindroz, B., Briançon-Marjollet, L., “Experimental Comparison Between Different Techniques of cavitation Nuclei Measurements”, Proceedings of the 2ndInternational Symposium on Propeller and Cavitation, September 1992, Hangzhou, China.
37. Gindroz, B., “Qualification of a Centerbody Cavitation Nuclei Counter Using Optical Techniques”, Proceedings of the 16h I.A.H.R. Symp., September 1992, São Paulo, Brazil.
38. Gindroz, B., “Propeller Cavitation Characteristics: The practical Interest of Nuclei Measurements in Test Facilities and at Sea”, Proceedings of the ASME FED Symposium on Cavitation, August 1995, Hilton Head Island, USA.
39. Gindroz, B., Billard, J.-Y., Geistdoerfer, P., “Cavitation Nuclei Measurements at Sea”, Proceedings of the ASME WAM, November 1995, San Francisco CA, USA.
40. 19 ITTC, “Report of Cavitation Committee”, 12–22 September 1990, Madrid, Spain.












