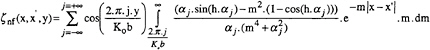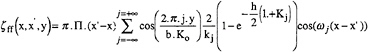Accuracy of Wave Pattern Analysis Methods in Towing Tanks
F.-X.Dumez, S.Cordier (Bassin d'Essais des Carènes, France)
INTRODUCTION
Wave pattern analysis methods enable the estimation of the wave resistance of a body in steady rectilinear motion using measured wave heights. The obvious advantage of applying these techniques in a towing tank is that the value of wave resistance which is extrapolated based on Froude number similarity is obtained directly and not by subtracting an empirical estimate of viscous drag from the total drag. These methods rely on conservation of momentum in a control volume attached to the body. The assumptions of potential flow, linearized free-surface conditions are essential in the development of these methods. Various wave pattern analysis methods have been developed in the sixties and seventies 1, 2 and three of them are considered in this paper:
The longitudinal-cut method (LCM) developed by Newman 3 and Sharma 1 is based on the analysis of wave height measurements along a semi-infinite line parallel to the model's axis assuming infinite depth, far field waves, and no reflection. In practice, the signal is cut before the reflected waves are measured and a correction has to be made for the lost momentum.
The discrete decomposition method (DDM) developed by Eggers 4, Landweber 5, and Hogben 6 is based on the use of one or several longitudinal cuts including reflections. These data are used to identify a wave field based on a decomposition in transverse wave numbers which correspond to the tank's transverse natural frequencies. Its use is not limited by wave reflection or finite depth. The linear system to be solved is usually over-determined which can add robustness to the result.
The singularity distribution identification method (SDIM) developed by Baba 7, Okhusu 8, Bessho 9, 10, and Ikehata 11 uses a distribution of singularities (sources or doublets, continuous or discrete) located in place of the model. The wave height measurements are used to identify a distribution of singularities whose wave field matches that which was measured. This method also yields an over-determined linear system for the singularity densities, which in turn give the wave resistance.
Recent work has been performed at the Bassin d'Essais des Carènes on the decomposition of resistance into different components for a Series 60 model and three geosims of the “Olive” planing hull, 12, 13, 14, 15. The accuracy required to conduct this work have led to a study of the limitations of the first two methods, and possible enhancements of the second method. As a consequence of this work, a third method was developed and implemented based on the SDIM method in order to obtain accurate and robust estimates of wave pattern resistance in a towing tank for wide ranging test conditions. The evaluation of the various methods was performed on the data base obtained during the Series 60 and “Olive” geosim tests.
It is important to note that limitations in computer resources at the time of their development prevented the application of these methods (particularly the last two). The increase in computational power and consequently in the size of linear systems which can be solved justifies the reexamination of these methods.
LONGITUDINAL CUT METHOD (LCM)
Description
The far field wave elevations ηff(x,y), generated by a body travelling at constant speed U with no confinement (walls or bottom) are given by, 1 and 3:
(1)
with ![]()
where ![]() is a degenerated form of the Kochin function. We also have:
is a degenerated form of the Kochin function. We also have:
θ is the angle between Ox and the direction of propagation of a given wave component and Ko is the longitudinal wave number. The wave elevation ηff(x,y) can also be written as a function of u, F(u) and G(u):
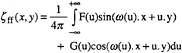
(2)
(3)
The functions F(u) and G(u) are the coefficients of the far field wave amplitude spectrum which, when integrated, yield the wave resistance:
(4)
These coefficients are obtained by a Fourier transform of the wave height measurements along a longitudinal cut which is required to extend to infinity downstream. In practice, the signal is truncated before the reflected waves are present in the signal (figure 1) and the coefficients F(u) and G(u) would tend to 0 for small values of u. The missing part of the signal is treated by introducing a weighted Fourier transform with an analytical asymptotic expression for ηff(x,yc) valid when u → 0:
(5)
However, the coefficients c1, c2, and c3 can only be determined based on a regression on the signal before truncation. Hence, the amplitude coefficients of the transverse waves (θ<35°16') are to a great extent determined by the truncation correction. Since, for moderate Froude numbers, the larger part of the wave resistance is generated by transverse waves, the point where the signal is cut, and the accuracy of the correction, play a large part in the accuracy of the computed wave resistance. For higher speed models the contribution of transverse waves to the resistance diminishes as shown in figure 2.
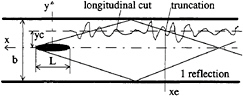
Figure 1: View of model in a towing tank.
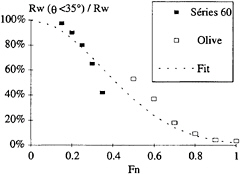
Figure 2: Fraction of the wave resistance generated by transverse waves for Series 60 and Olive model.
Transverse position
Since the transverse position of the cut (yc) influences the length of the signal, it is important to know how close the probe can be to the model axis without introducing the influence of near field waves in the measurements. A value of yc/KoL=0.5 is usually taken as a minimum. A theoretical study by Ikehata (11, figure 5) shows that in order to achieve a 10% accuracy on wave resistance yc should not be less than 40. Tests performed on the analysis of waves numerically generated by a polynomial source distributions show that a 1% accuracy on wave resistance can be achieved with yc not less than 5.
Truncation
Once the minimal distance from the probe to the model axis has been selected, it is possible to study the influence of signal length on the computed resistance. The tests performed on the Series 60 model were used to evaluate this effect. Figure 3 shows the ratio of wave resistance to the average result of the 4 probes (respectively yc/KoL=0.5, 0.53, 0.56, 0.59) for the longest signal, as a function of signal length. The maximum signal length is slightly less than that calculated based on the Kelvin dihedral angle. The results are shown for three values of Fn and for 4 probe positions from position 1 to 4. The effect of Fn on signal length is clearly illustrated. It appears that Rw converges only at the lower Fn and for the closer probes. For the other Froude numbers, the trends for the three probes are very similar but convergence does not appear to be achieved. Hence, despite the rather large ratio of tank width to model length (b/L=2.67), the wave resistance could not be determined accurately using the Longitudinal Cut Method (LCM).
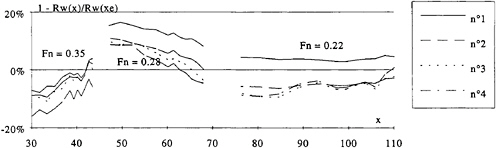
Figure 3: Effect of signal length on calculated wave resistance
Following this study, an analytical estimate of the error as a function of model size, tank width, and towing speed was sought. The relative importance of transverse waves in the wave pattern resistance as presented in figure 2 for the two models (series 60 and Olive) were fitted as follows:
(6)
The difference in the contribution to Rw from the transverse waves between two consecutive truncation points is defined as follows:
(7)
Based on experimental data a fit of ei is proposed:
This error is plotted in figure 4 based on experimental data for the 4 probes. The trend toward a reduction in this difference as the signal length is increased before truncation is clearly shown. Hence, the total error Ei given by the transverse wave components can be expressed as a function of x in the following form:
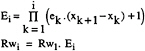
(8)
Based on experimental data a fit of E(x) is proposed (figure 5):
E(x)=e1.02–0.048.x (9)
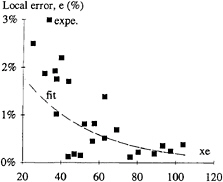
Figure 4: Convergence of wave resistance as a function of signal length
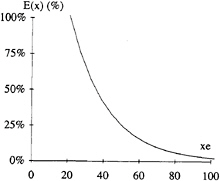
Figure 5: Estimated total error on transverse wave resistance (θ<35°)
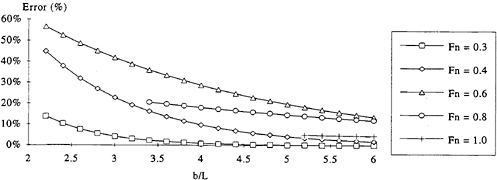
Figure 6: Estimated error inherent in the LCM method as a function of Fn and b/L
By multiplying equations (6) and (9) and assuming that the error on the diverging wave components is negligible, we obtain an estimate of the total error as a function of xe. The useful signal length before truncation for a tank of width b and a gauge located at position yc is given by:
(10)
In order to reduce errors introduced by the near field waves to less than 1% we take y>5. Hence, the theoretical maximum signal length can be written:
(11)
The error is shown to depend only on Fn and b/L and the result is plotted in figure 6. These results show clearly that in order to obtain reasonably accurate (error<5%) wave pattern resistance estimates with the LCM, for displacement vessels with significant wave making component (Fn<0.4), the required b/L is about 5. Hence, for typical large towing tanks (b=15 m) the maximum model length is 3 m, much less than the size typically used in these facilities. Hence, this method is not sufficiently accurate for conventional towing tank use.
The limited accuracy of the LCM method, particularly for large, fast models was the principal reason for the development of a method which could analyse wave height measurements containing the waves reflected by the walls of the tank.
DISCRETE DECOMPOSITION METHOD (DDM)
Description
As opposed to the previous method, the DDM, 4, 5 and 6, assumes the spectrum to be composed of several discrete wave components. We consider the model to be in the middle of a tank of breadth b, the walls being located at y=±b/2. The expression for the far field wave elevation can be written as a discrete summation:
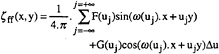
(12)
with ![]() and uj=j.Δu
and uj=j.Δu
For a model symmetric about the oxz plane, and considering the summation to be finite and limited to Jmax components such that the amplitude spectrum coefficients for j>Jmax are negligible, we can write:
(13)
with γj=Gj.cos(uj.y) and σj=Fj.cos(uj.y)
and ![]()
The solution to this problem consists in performing a Fourier decomposition along a segment of a longitudinal cut bounded by xo and xt which includes a certain number of reflections (Nr). The unknowns γj and σj are identified based on the iterative resolution of a linear system where the right hand terms are given by:
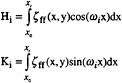
(14)
In order to improve the accuracy of the method and to limit numerical errors, the authors of this method advise selecting transverse positions of the wave probes which correspond to anti-nodes of the transverse natural modes of the tank, and to use several probes such that the system is over determined. This choice leads effectively to a fit of the identified wave field over the measured data. These remarks proved to be well founded when the robustness of this method was tested.
Discussion of results
The results obtained by this method on the Series 60 and Olive models were in relatively good agreement with the results of the LCM method. Nonetheless, significant differences in Rw appeared as a function of the distance from the probe to the model's axis and number of reflections used in the analysis. Hence, a numerical study was performed to evaluate the robustness of this method based on computed longitudinal cuts at different distances yc using near field and far field waves. The test case used for a similar study in 5 was modelled following thin ship theory: an infinitely long, thin strut, 2 m in chord, in a 13 m wide tank, at 1, 2 and 4 m/s. The strut was represented by a distribution of sources located in the plane of symmetry.
The analysis of the results obtained by using the DDM method on several longitudinal cuts, shows that the accuracy of the computed wave resistance depends directly on the number of modes (Jmax) used, and on the length of the signal (xt-xo). The conditioning of the matrix used to solve the linear system is directly dependent on the length of the signal. A poorly conditioned system yields to large amplitudes at specific values of the transverse wave number. As signal length is reduced, this behaviour affects lower and lower frequencies until the solution “blows up”. An alternative method based on the simultaneous resolution of several longitudinal cuts improves this problem but numerical errors in the solution still appear.
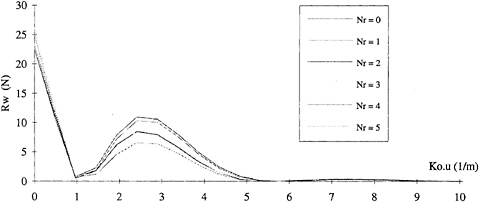
The wave amplitude spectrum calculated by this method for 4 longitudinal cuts measured in the wake of a Series 60 model at Fn=0.35 is shown on figure 7. The ordinate used does not represent the wave amplitude but has been transformed into the wave resistance per unit wave number. Hence, the integral of each curve in figure 7 yields the wave resistance. The longitudinal cuts contain 3 reflections. The 4 longitudinal cuts were also analysed simultaneously to yield an average labelled “fit”.
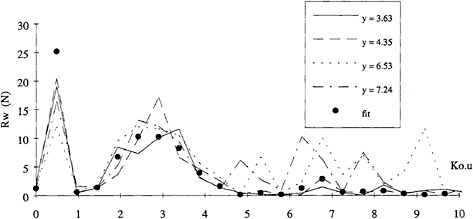
Figure 7: Wave amplitude spectrum for a Series 60 (Fn=0.35) using the DDM method.
It is clear on this graph that each longitudinal cut yields a significantly different spectrum and anomalous amplitudes appear in the high frequency range (Ko.u>5). The advantage of using several cuts (“fit”) is that these amplitudes are filtered through the regression process.
The most stable results and in best agreement with respect to the LCM method, are obtained for a very long signal (Nr=4 or 5) and for a limited number of identified wave number components (Jmax). However there is a systematic difference (10 to 20%) with respect to the LCM results. This discrepancy may be due to imperfection in the reflection and dissipation through the viscous wake.
Compared to the LCM method in which, through the Fourier transform, the wave amplitude components are solved independently, the DDM method solves for all components simultaneously through the resolution of a linear system. Hence, errors in the higher frequency, divergent wave components tend to introduce errors on the lower frequency, transverse wave components.
Also, as Fn is increased, and the energy shifts to the higher frequency components, the limitation in Jmax can introduce significant errors as some of the divergent waves are neglected.
Hence, this method appears limited by the need for an extremely long signal and the relatively few wave numbers identifiable. These conclusions have led us to the study of a third method based on singularity distribution identification.
THE SINGULARITY DISTRIBUTION IDENTIFICATION METHOD (SDIM)
Description
This method is based on the use of an unknown distribution of singularities (sources or doublets, continuous or discrete) located on a line, in the centre plane or otherwise, advancing at the model speed U. The principle of the SDIM method, 7, 8, 9, 10 and 11, is to determine a distribution of singularities such that its far field waves match those measured. Several alternative approaches are then possible. The singularities may be located at the control points of a mesh, or they can be determined analytically based on an analytical expression. In our particular case, the reflections due to the walls of the tank are taken into account so that the whole wave field can be analysed, even where reflected waves are present.
For the sake of simplicity, we first consider a known continuous distribution of sources constant over a depth h and varying with the x direction. We later show that this formulation can be extended to sources which vary as a function of depth as well. Given M(x') a source density distribution in the plane of symmetry located between x'=–1 and x'=1 and constant vertically between z'=0 and z'=–h, translating at speed U, along the centre line of a tank of breadth b, and of infinite depth. The wave elevation can be shown to be given by:
|
near field
far field
|
In (15), Π(x'–x) is the Heaviside function and:
The amplitude coefficients Fi andt Gi are given by:
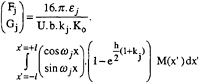
(16)
where ![]() and εj=1 when j≠0
and εj=1 when j≠0
If we assume that the source density distribution is represented by a 3rd degree polynomial, the unknowns of the problem are now the 4 polynomial coefficients of the expression:
(17)
If we consider the measurement of Imax wave heights at abscissa x i along a line of constant y, the far field wave elevation at each position (xi,y) can then be written as follows:
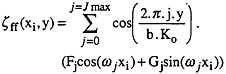
(18)
The amplitude spectrum coefficients corresponding to the Jmax number of wave numbers used in the decomposition can then be expressed as a function of the 4 polynomial coefficients Ak
(19)
where ![]()
can be calculated analytically.
This formulation yields a linear system which is always over-determined since the number of measurement points (Imax) is usually much greater than the number of coefficients in the polynomial expression (4 in this case). Hence, the solution will be equivalent to a least square fit of the identified wave field over the measured wave field.
ζff(xi,y)=Eik.Ak for i=1,Imax and k=0,3 (20)
with ![]()
and ![]()
The first polynomial distribution tested was given by a line of length L=2 m, travelling at 2 m/s with the following polynomial coefficients: A0=A2 =0; A1=–1.622 E-03 m/s; A3=2.411 E-03 m/s. The theoretical resistance of this “model” is 14.729 N. Eleven longitudinal cuts containing 5 reflections
(Nr=5) were computed in a 13 m wide tank at transverse positions: 0.981<yc<7.85. The results obtained in terms of maximum difference compared to theoretical value using both DDM and SDIM methods are tabulated below:
Table 1: Error in % between calculated and theoretical wave resistance using DDM and SDIM methods
|
Method |
DDM |
SDIM |
|
Nr=5 |
0.70% |
0.43% |
|
Nr=0 |
no solution |
1.2% |
These early tests confirmed the potential of the SDIM method to obtain very accurate results, even with a limited signal length.
Near field wave correction
The knowledge of the singularity distribution enables the calculation of near field waves. It is then possible to use this information in the analysis of wave measurements which include a significant contribution from the near field. A method was devised and tested based on this observation.
The previous test case was used but at a speed of 4 m/s (the source distribution is multiplied by 2) and the theoretical resistance is then 32.68 N. The longitudinal cuts computed, with and without the near field (nf) wave contribution, at different transverse positions, were analysed and the results are presented in table 2.
Table 2: Error in % between calculated and theoretical wave resistance for different signal length and transverse positions
|
yc |
Nr=5 |
Nr=0 |
||
|
w/nf |
w/o nf |
w/nf |
w/o nf |
|
|
0.37 |
–0.848 |
0.138 |
–3.862 |
0.159 |
|
0.61 |
–0.315 |
0.135 |
–1.634 |
0.162 |
|
0.86 |
–0.101 |
0.129 |
–0.817 |
0.162 |
Hence, the near field waves, when present in the signal analysed, cause a significant increase in the error, particularly when the longitudinal cuts are close to the “model” and when the signal is short.
In order to take into account the near field waves, an iterative method was devised and programmed. The method is as follows:
![]() Analyse the measured longitudinal cut ζm(xi,yc) to obtain a distribution of sources:
Analyse the measured longitudinal cut ζm(xi,yc) to obtain a distribution of sources:
![]() Compute the near field waves generated by these sources: ζnf(xi,yc)
Compute the near field waves generated by these sources: ζnf(xi,yc)
![]() Compute a corrected far field longitudinal cut: ζ'ff(xi,yc)=ζm(xi,yc)–ζnf(xi,yc)
Compute a corrected far field longitudinal cut: ζ'ff(xi,yc)=ζm(xi,yc)–ζnf(xi,yc)
This procedure is repeated using the corrected longitudinal cut, thereby replacing ζm(xi,yc) by ζ'ff(xi,yc). The differences with the theoretical wave resistance and the computed resistance at steps ![]() and
and ![]() for the same test case and Nr=5 and Nr=0, are tabulated below:
for the same test case and Nr=5 and Nr=0, are tabulated below:
Table 3: Error in % between calculated and theoretical wave resistance using near field correction
|
y |
Nr=5 |
Nr=0 |
||
|
|
|
|
|
|
|
0.37 |
–0.848 |
–0.009 |
–3.862 |
–0.061 |
|
0.61 |
–0.315 |
0.003 |
–1.634 |
0.001 |
|
0.86 |
–0.101 |
0.003 |
–0.817 |
0.018 |
These results show that at the first iteration the accuracy of the method is significantly increased and the results are essentially exact (less than 1/1000) for all transverse positions and signal length. This result can be explained because the source distribution identified is very close to the actual source distribution so that the near field waves are indeed representative of the theoretical near field waves. The rapid convergence of the procedure can also be explained by the relatively small contribution of the near field waves in the analysed wave height data (a few percent on Rw). The fact that this procedure was shown to converge to the theoretical value of wave resistance gives us confidence in the programmed analysis method.
Discrete source distribution
This method was extended to a discrete distribution of sources at the centroid of panels located on the plane of symmetry of the model. A discrete representation was preferred over polynomial distributions because the numerical formulation is simpler and the choice of functions to be used would have required further tests.
The principle of the method is identical to that described above. A discrete distribution of sources is identified such that its wave field matches that measured. Again, the presence of the tank walls is taken into a ccount by choosing a finite number of frequencies which correspond to natural transverse modes of the tank.
A numerical test of this method was performed on the Series 60 form at Fn=0.35 in an infinitely wide tank using the Neumann-Kelvin code POTFLO 16 configured in the slender ship approximation. The ship was discretised by 450 panels and the computed wave resistance based on the slender ship approximation is 596 KN. A signal of length x=75 at a distance yc=4.08 was also calculated by the code.
This signal was analysed using SDIM assuming a 500 m wide tank, and a mesh of 9×3 panels in the centre plane of the ship and a wave resistance of 584 KN was obtained. Hence a 2% error on Rw between POTFLO and SDIM despite the small
number of singularities used. The amplitude spectrum calculated by POTFLO and identified by SDIM are shown in figure 8. The two spectra agree very well which supports the accuracy of the wave resistance result despite the limitations of the method. A further example of the global agreement between the slender ship model and the identified source distribution is the comparison between the wave elevations generated by POTFLO and by the equivalent source distribution (figure 9). The small differences between the two signals are due to the presence of near field waves close to the ship and to the oscillations due to the line integral term in POTFLO.
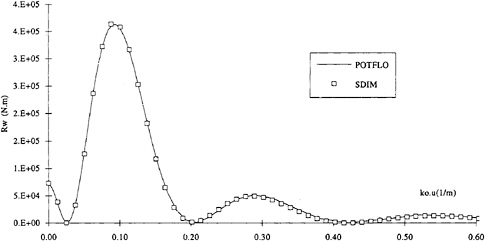
Figure 8: Amplitude spectra calculated by POTFLO and identified by SDIM
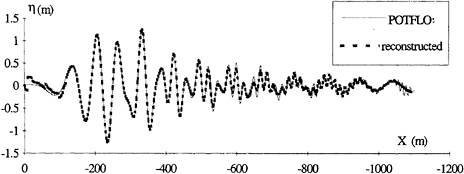
Figure 9: Wave elevations calculated by POTFLO and from the source distribution identified by the SDIM
Application to experimental data
Following the tests performed on the other method, the data used to evaluate the SDIM method are those performed in the Paris model basin (260 m× 13 m×4.5 m). All the results obtained and analysed can not be presented here. The difference between the different methods are illustrated on a representative example: scale 1/25 Series 60 model at Fn=0.35, yc =3.63. The mesh used for the SDIM method is as before: 9×3 panels in the centre plane.
It is important to note that the SDIM method converges as the number of transverse wave numbers (Jmax) is increased, whereas the DDM method tended to diverge. In the present case, the SDIM method was run with Jmax=300 (umax=145) whereas the best compromise with the DDM method limited Jmax to 50 (umax=24.1). The results presented with the DDM method correspond to the average of the results obtained with the 4 gages. The wave resistance results are presented in table 4.
Table 4: Comparison of calculated wave resistance using the three analysis methods
|
Method |
LCM |
DDM |
SDIM |
SDIM |
|
Nr |
Nr=3 |
Nr=0 |
Nr=5 |
|
|
Rw (N) |
24.5 |
24.5 |
21.6 |
19.5 |
These results show significant differences but it is not possible to determine which of these estimates is the closest to the real wave resistance. In order to qualify these results, the amplitude spectra corresponding to each estimate are compared in figure 9. Besides the differences in the resolution in frequency, it is clear that the good agreement between LCM and DDM is fortuitous since there are significant differences in the two spectra. The agreement between SDIM and LCM spectra is good, except as u tends to 0, where the SDIM method shows
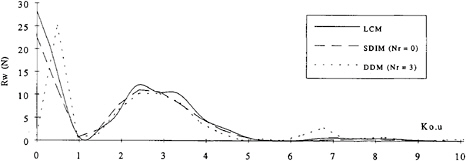
Figure 9: Comparison of the amplitude spectra obtained using the three analysis methods
lower amplitudes, and hence explains the lower wave resistance value.
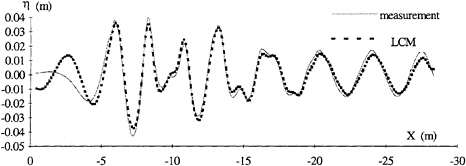
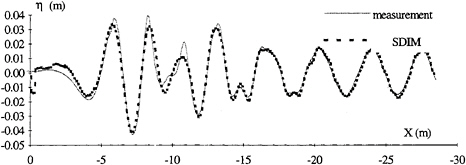
In order to further compare the three methods the experimental wave elevations are compared to the elevations calculated using the spectra obtained from the LCM method (figure 10) and the SDIM method (figure 11). The following comments can be made by the comparing the two figures at different axial positions:
|
x>–5 |
The SDIM method leads to a better agreement close to the model. |
|
–5<x<–15 |
The LCM method is more accurate in the region where the bow and stern waves interact. |
|
x<–15 |
The SDIM method leads to a better identification of the amplitudes of the longitudinal waves. |
Since the main differences between the SDIM and LCM spectra were at low frequencies (transverse waves), the agreement between measured and reconstructed SDIM wave elevations for x<–15, indicates that the wave resistance calculated by SDIM is closer to the real value.
Different tests performed on the parameters of the SDIM method did not succeed in obtaining a perfect agreement between measured and calculated wave elevations. Hence, there seems to be a limit as to the ability of this method to achieve an exact representation of the wave field. One possible explanation lies in the limited number of frequencies used in the analysis, particularly at low frequency.
Influence of signal length
Based on the same experimental data, tests were performed on the length of the signal which is characterized by the number of reflections included in the signal. The wave resistance calculated for 6 values of Nr are presented in table 5. The computed wave resistance decreases significantly as the number of reflections increases. Since previous numerical tests (table 2) showed that the method is independent of this parameter, there must be some physical phenomenon present in the experiment and which is not modelled. The fact that the reduction in computed resistance occurs every other 2 reflections, that is each time the reflected waves cross the viscous wake of the model, is an indication that the interaction of the waves and the wake might be responsible for the reduction in calculated wave resistance.
Table 5: Rw as a function of signal length
|
Nr |
0 |
1 |
2 |
3 |
4 |
5 |
|
Rw (N) |
21.7 |
20.8 |
17.8 |
18.3 |
15.8 |
15.8 |
Further tests were performed on the influence of signal axial position in order to verify these conclusions. The measured wave elevations were split in 3 zones as described in figure 13. The

Figure 13: Measured wave elevations indicating the selected signal segments
signal corresponding to each zone was analysed and the resulting amplitude spectra are shown on figure 14. Again, the reduction in the amplitude spectra as the segment of signal used is taken further and further downstream is clear. These difference, lead to differences in wave resistances similar to those presented in table 5, and represent further evidence of the influence of the viscous wake on the energy present in the reflected waves. These tests further illustrate the robustness of the method which can analyse truncated parts of the wave elevations. This type of analysis is impossible with the LCM or DDM methods.
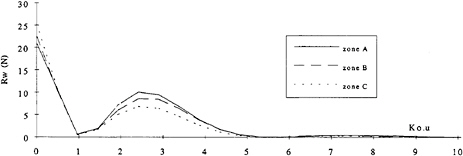
Figure 14: Wave amplitude spectra computed for each of the zone identified in figure 14 using SDIM
Probe transverse position
The influence of probe transverse position was again tested on the Series 60 test data measured at 4 different transverse probe position at Fn=0.35. The results of the SDIM analysis of these longitudinal cuts are presented in figure 15 in the form of amplitude spectra. This graph shows excellent agreement between the 4 cuts and should be compared to figure 7 in order to quantify the improvements gained by using the SDIM method over the DDM method where the scatter is much larger.
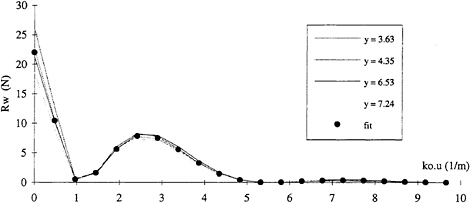
Figure 15: Wave amplitude spectra computed for 4 different longitudinal cuts using SDIM
CONCLUSIONS
The analysis of the two principal methods of wave pattern analysis from longitudinal cut measurements (LCM and DDM) has led to the identification of their respective inherent limitations.
The LCM method is very sensitive to errors in the truncation correction and neglects the influence of near field waves. The estimation of these errors has led to an analytical expression for the relative error on wave resistance as a function of the ratio of tank width to model length and Froude number.
In the DDM method, the presence of the near field is also neglected, and the numerical instabilities limit the length of the signal and the number of frequency components which can be taken into account.
These limitations have led us to develop a third method (SDIM) based on the identification of a singularity distribution in the centerplane of the model which takes into account the tank walls in the boundary conditions. Numerical tests have shown this method capable of taking into account the near field wave components through an iterative process, and of providing very accurate estimates of wave resistance independently of signal length (large number of reflections) and transverse position of the probe.
Tests performed on wave elevation data measured in the wake of a series 60 model have shown that this method is capable of calculating the wave resistance and of reconstituting the signal with an accuracy at least as good as the LCM method. These tests have as shown that the wave resistance could be computed for widely varying signal lengths without numerical problems (convergence, instabilities).
The tests on the experimental data indicate the presence of an interaction between the model wake and the reflected waves leading to a reduction in the wave resistance.
This work is to be continued in the following directions:
-
Implementation of the near field correction in the generalised version of this method.
-
Locate the sources on the hull surface (calculation of the line integral terms)
-
Investigate the possible advantages of extending this approach to an unbounded domain.
ACKNOWLEDGEMENTS
This work has been performed with the support of the Direction des Recherches et Etudes.
NOMENCLATURE
|
LCM |
Longitudinal Cut Method. |
|
DDM |
Discrete Decomposition Method. |
|
SDIM |
Singularity Distribution Identification Method. |
REFERENCES
1 Eggers K.W.H., Sharma S.D. and Ward L.W., “An assessment of some Experimental Methods for Determining the Wavemaking Characteristics of a Ship Form”, Transactions SNAME, Vol 75.
2 Yokoo K. and Tanaka H., “Application of Wave Analysis to Tank Experiments”, Proceedings of the International Seminar on Wave Resistance. Tokyo, February 1976.
3 Newman J.N., “The Determination of Wave Resistance from Wave Measurements along a Parallel Cut”, Proceedings of the International. Seminar on Theoretical Wave Resistance, Univ. of Michigan, 1963.
4 Eggers K.W.H., “Wave Analysis, State of the Art”, Universitat Hambourg, Germany.
5 Tsai C.E. and Landweber L., “Further Development of Procedure for Determination of Wave Resistance from Longitudinal-Cut Surface Profile Measurements”, Journal of Ship Research., vol 19, no 2, June 1975.
6 Hogben N. “Automated recording and analysis of wave patterns behind towed models ”, Transactions of RINA, vol. no 114, 1972.
7 Baba, E. “Study on Separation of Ship Resistance Components”, MITSUBISHI Technical Bulletin No 59, August 1969.
8 Okhusu, “Wave Analysis of Simple Hull Form”, Journal of society Naval Architects of Japan, Vol. 126, 1969.
9 Bessho, “Wave Free Distribution and their Applications”, Proceedings of the International. Seminar on Theorical Wave Resistance. Univ. of Michigan, 1963.
10 Bessho, “A Contribution of Wave Analysis of Ship Waves”, Scientific and Engineering Reports of the Defence Academy, Vol. 7, nº 1, 1969.
11 Ikehata and Nozawa, “Determination of Wave Making Resistance of a Ship by the Method of Wave Analysis”, 1st and 2nd Reports, Journal of the Society Naval Architects of Japan, Vol. 121, 1967 and Vol. 124, 1968.
12 Dumez F.X. and Cordier S., “Scale Effects on the Resistance Components of a High-Speed Semi-Displacement Craft”, FAST 93, Yokohama, December 1993.
13 Dumez F.X. “Décomposition de la Résistance à l'Avancement des Navires”, Proceedings of the Quatrième Journées de l'Hydrodynamique, 1993, Nantes.
14 Cordier S. and Dumez F.X., “Resistance Components of Displacement and Semi-Displacement Hull Forms” Proceedings of the 20th ITTC, Vol. II pp 75,77, 1993, San Francisco.
15 Tanaka H. and Nakatake K., “Cooperative Resistance Tests with Geosim Models of a High-Speed Semi-Displacement Craft” Journal of the society of Naval Architects of Japan, Vol. 169.
16 Hally D. “Implementation of a Free Surface in Calculations of the Flow into the Propeller Plane of a Ship”, Proceedings of CADMO92, Madrid, 1992.