Time-Domain Calculations of First- and Second-Order Forces on a Vessel Sailing in Waves
L.Sierevogel, A.Hermans (Delft University of Technology, The Netherlands), R.Huijsmans (Marine Research Institute, The Netherlands)
Abstract
In this paper we solve the time-dependent linear equations which describe the interaction between a LNG carrier at service speed and the waves. Our numerical algorithm is a time-domain model, solving the linear boundary conditions on the hull and the free surface, and the Laplace equation by using Green's theorem. As absorbing bound ary condition we use a semi-discrete DtN-method. To compute the second-order wave drift forces or added resistance of the LNG carrier, we extend our algorithm to higher speed. Results of our computations are compared with measurements and strip theory results.
Nomenclature
Introduction
In recent years many studies have been carried out solving the unsteady ship motion problem. This problem is very important in predicting the behaviour of a ship in sea-keeping, which includes the interaction between waves and the velocity of a ship. Computing this interaction can be done by using the frequency domain or the physical time domain. The disadvantage of the studies in the frequency domain is their restriction to harmonic waves and their unability to use real time wave elevations for the calculation of the motion response. In the time domain we can also handle non-harmonic waves and it is not necessary to implement the conditions dependent on every frequency explicitly.
Prins [6] has developed a two- and three-dimensional time-domain algorithm to compute the behaviour of a cylinder, a sphere and a com mercial tanker in current and waves. The results
were satisfactory. We have extended this method with, among other things, a frequency independent absorbing boundary condition [8].
In this paper we apply the method to a LNG carrier at service speed. The forward speed of the commercial tanker considered up to now is very low, the maximum Froude number is 0.018, i.e. 2 knots, while the usual speed of a 125,000m3 LNG carrier is about 20 knots (i.e. Froude number is 0.2). This fact causes some problems in our algorithm. We study increasing speed and the effect on our absorbing boundary condition. To remove the instabilities on the free-surface due to increasing forward speed, we introduce upwind discretization. Both cases were done in the two-and tree-dimensional algorithm.
In the first section we give the main idea of the Prins' algorithm and our extension to a frequency independent boundary condition. In the second section we study increasing speed and the the effect on our algorithm. In the third section results are presented for a 125,000m3 LNG carrier, at deep water. We will calculate the drift force or added resistance not only for low forward speed, but also the added resistance for higher forward speed has been studied. In order to check the method, we compare our results with measurements of Wichers [11] and with strip theory results [1, 2]. The last section we give the conclusions and ideas for further research.
1
Time-domain algorithm
The time-domain algorithm given below is based on the one given by Prins [7].
The physical fluid domain is an infinite (or large) domain. The computational domain cannot be infinite, so we have to introduce artificial boundaries and proper boundary conditions. In the literature several methods have been proposed to absorb free surface waves. On the basis of a literature search, Prins decided to use an extension of the Sommerfeld radiation condition for two families of waves. The disadvantage of this Sommerfeld condition is that it is dependent on the wave frequency, so it cannot handle non-harmonic waves, and on the forward velocity.
Keller and Givoli [3] introduce a semi-discrete DtN-method, using an artificial boundary, dividing the original domain into a computational and a residual domain (the interior and exterior). In our method we use a three-dimensional boundary condition independent of the wave frequency, using the idea of the Givoli's method with Prins' algorithm. In the interior domain we use the same mathematical model as Prins [7] use but we do not implement a Sommerfeld radiation condition on the artificial boundary.
1.1
The interior problem
We consider a vessel sailing with an uniform velocity U in the negative x-direction, or an uniform current with velocity U is directed in the positive x-direction. Regular waves are travelling in the water-surface in a direction which makes an angel β with the positive x-direction, see figure 1. The coordinate system is chosen such that the undisturbed free surface coincides with the plane z=0 and the centre of the gravity of the hull is on the z-axis, with z pointing upwards. The hull is free to move in all directions and to rotate around the main axes.
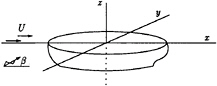
FIGURE 1: The geometry
We assume the following restrictions: there is no viscosity, the fluid is incompressible and homogeneous, and the flow is irrotational. We introduce the velocity potential Φ, which has to satisfy the Laplace equation
(1)
By using the dynamic and kinematic conditions and splitting the potential into a steady and an unsteady part, like
we get the linearized free-surface condition on the undisturbed free surface
(2)
with subscripts denoting the partial derivative. In contrast with the two-dimensional algorithm, we do not include terms of ![]() Including them would cause us to calculate higher derivatives of the unsteady potential at the free surface. This would increase the computation time, because the need of the very fine mesh.
Including them would cause us to calculate higher derivatives of the unsteady potential at the free surface. This would increase the computation time, because the need of the very fine mesh.
On the ship hull we have the linearized version of the body boundary condition
with ![]() the displacement vector of the ship, given by
the displacement vector of the ship, given by
and ![]() the normal pointing out of the fluid domain, see Timman [9]. The bottom is a rigid wall, so we submit the potential on the bottom,
the normal pointing out of the fluid domain, see Timman [9]. The bottom is a rigid wall, so we submit the potential on the bottom, ![]() , to the condition
, to the condition
(3)
The steady potential is represented by the double-body potential.
So far we can only say about the potential on the artificial boundary that it satisfies the Laplace equation and that it remains finite when we take the boundary at infinity.
To solve the interior problem, we introduce a Green's function, G, satisfying equations (1) and (3).
(4)
where ξ′ is the image of ξ with respect to the bottom. By using Green's second theorem it is possible to write the interior problem as
(5)
with D and E matrices built up by the Green's function and its derivative. And with ![]() a vector
a vector ![]() containing the potential on the free surface, on the hull and on the artificial boundary. To solve this integral equation we discretize the boundaries by dividing these into panels. We assume that the potential has a constant value on such a panel. Prins' approach consists of two steps leading to a Fredholm integral equation of the second kind. Firstly, the free-surface condition(2) and the second-order Sommerfeld radiation condition are discretized with respect to t, where an implicit scheme is used for the time derivation. Secondly,
containing the potential on the free surface, on the hull and on the artificial boundary. To solve this integral equation we discretize the boundaries by dividing these into panels. We assume that the potential has a constant value on such a panel. Prins' approach consists of two steps leading to a Fredholm integral equation of the second kind. Firstly, the free-surface condition(2) and the second-order Sommerfeld radiation condition are discretized with respect to t, where an implicit scheme is used for the time derivation. Secondly, ![]() n is expressed in
n is expressed in ![]() and its tangential derivative along the boundaries, while at the object
and its tangential derivative along the boundaries, while at the object ![]() n is supposed to be known. Discretization of the integral equation leads to a matrix equation for the unknown vector
n is supposed to be known. Discretization of the integral equation leads to a matrix equation for the unknown vector ![]()
(6)
with superscripts denoting the time level and ![]() a time- dependent vector. The matrices Di are built up by the Green's function, its derivative and the surface conditions. In our approach we make use of the same algorithm as developed by Prins, except for the boundary
a time- dependent vector. The matrices Di are built up by the Green's function, its derivative and the surface conditions. In our approach we make use of the same algorithm as developed by Prins, except for the boundary ![]() . Experience has taught that the implementation of the Sommerfeld condition on the outer boundary
. Experience has taught that the implementation of the Sommerfeld condition on the outer boundary ![]() is efficient if
is efficient if ![]() is taken at a distance of about three wavelengths, while the coefficients for the two families of waves are dependent on the frequency. Hence, the matrix has to be updated for each frequency. Our purpose is to obtain a genuine time method, where the matrix is independent of the frequency.
is taken at a distance of about three wavelengths, while the coefficients for the two families of waves are dependent on the frequency. Hence, the matrix has to be updated for each frequency. Our purpose is to obtain a genuine time method, where the matrix is independent of the frequency.
1.2
The exterior problem
To solve the exterior problem in the three-dimensional case we developed a special Green's function, the same way as we did for two dimensions, see Sierevogel [8]. The advantage of using our algorithm compared to using the conventional time-domain Green's function in the exterior, is that it will be easier to implement the effects of higher speed, because the boundaries of the exterior are already divided into panels.
In our first two-dimensional set up, we assumed the interior to be moving together with the object, while the exterior was fixed to the earth. To solve the problem in the interior as an overall matrix equation, we applied Green's theorem on the domain between the boundaries, see figure 2.
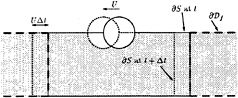
FIGURE 2: The 2-D geometry
In our new set up we assume the exterior also to be moving together with the object, because it is complicated to apply Green's theorem on the domain between the boundaries it the three-dimensional case and an advantage of the new algorithm is that it will be easy to implement the effects of the double-body potential. In the exterior we get the following linearized free surface condition
Where ![]() is the unsteady potential and the steady potential is approximate by the undisturbed flow potential Ux. We use the following discretizations for the time derivatives
is the unsteady potential and the steady potential is approximate by the undisturbed flow potential Ux. We use the following discretizations for the time derivatives
with superscripts denoting the time level. Now we may write equation (7)
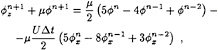
(8)
with ![]() The last term between brackets is new compared to the old set up, the rest is exactly the same. If we also take into account the double-body potential the right-hand side will then also contain terms of that double-body potential. We use an upwind discretization scheme calculate the numerical differentiation of the potential (see section 2.1), and solve our problem by using Green's theorem, the same way we did in our first set up.
The last term between brackets is new compared to the old set up, the rest is exactly the same. If we also take into account the double-body potential the right-hand side will then also contain terms of that double-body potential. We use an upwind discretization scheme calculate the numerical differentiation of the potential (see section 2.1), and solve our problem by using Green's theorem, the same way we did in our first set up.
To use Green's theorem in the exterior problem, we introduce a Green's function, G, which satisfies
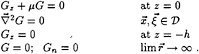
(9)
The last relation is the only physical radiation condition. Now we get for the potential in the exterior
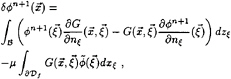
(10)
with
and
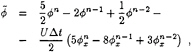
and ![]() the free surface of the exterior. We need to mention that the normal derivative on the boundary in the exterior is the negative of that of the interior. By analogy with Wehausen et al.[10] we derive a Green's function, which satisfies (9), for infinite deep water
the free surface of the exterior. We need to mention that the normal derivative on the boundary in the exterior is the negative of that of the interior. By analogy with Wehausen et al.[10] we derive a Green's function, which satisfies (9), for infinite deep water
and for water with a finite depth
with
with X the horizontal distance and Z=z+ζ. Here J0 denotes the Bessel function of the first kind, order zero. These Green's functions can be rewritten to functions more friendly to computed numerically, the same way Noblesse [5] and Newman [4] rewrite their functions.
By using Green's theorem we have to integrate the Green's function with respect to the artificial boundary or the free surface of the exterior. We write Green's theorem like
(11)
with ![]() a matrix built up by the exterior Green's function and its derivative and with
a matrix built up by the exterior Green's function and its derivative and with ![]() the vector
the vector ![]() and is
and is ![]() the last term of (10).
the last term of (10).
1.3
The total problem
Hence, combining equation(6) and (11), we are able to write the interior problem as an overall matrix equation, like equation(6),
(12)
with ![]() a vector containing
a vector containing ![]()
We now derived an algorithm to compute the potential, knowing the potential due to the diffracted waves, we are able to compute the surface elevation, so we can look at the reflections. Also we are able to compute the hydrodynamic coefficients, like added mass, added damping and the first- and second-order forces.
The developed algorithm is tested on a two- and three dimensional test-problem, i.e. an cylinder of infinite length and a sphere. The results agreed well with known results from literature and the method turned out to be very efficient and accurate. The boundary condition absorbs the outgoing waves. The reflections due
to the artificial boundary are very small, less then ![]() of the total surface elevation, when the boundary is one wavelength away from the object. The method decreases computer time compared to the method using the Sommerfeld radiation condition, when computing the behaviour of an object in harmonic waves. Firstly the boundary will be closer to the object and secondly it is not necessary to implement the conditions dependent on every frequency explicitly. We are also able to use a step-response function to calculate the hydrodynamic coefficients and drift forces.
of the total surface elevation, when the boundary is one wavelength away from the object. The method decreases computer time compared to the method using the Sommerfeld radiation condition, when computing the behaviour of an object in harmonic waves. Firstly the boundary will be closer to the object and secondly it is not necessary to implement the conditions dependent on every frequency explicitly. We are also able to use a step-response function to calculate the hydrodynamic coefficients and drift forces.
Also the calculations of the hydrodynamic coefficients and drift forces of a commercial tanker agreed well with measurements. The forward speed of the commercial tanker is very low, the maximum Froude number is 0.018, i.e. 2 knots. The service speed of the LNG-carrier causes some numerical problems in our algorithm. These are treated in the section 2.
1.4
Movement and forces
To compute the drift forces, we first have to compute the first-order forces and the movement of the ship.
Because the tanker is free to move in all six possible directions, both the force and the moment are needed to calculate the linear movement of the hull. This first-order force is given by
where ![]() is the potential due to the incoming and the diffracted wave, as the motion of the ship is yet unknown. For the moment we have
is the potential due to the incoming and the diffracted wave, as the motion of the ship is yet unknown. For the moment we have
If we do not consider incoming waves but forced oscillation of the ship, we can calculate the added mass and damping coefficients by fitting the force and moment to the acceleration and the velocity:
This expression gives the force in direction i due to a motion in direction j. Note that there is no summation over the index j. For the moment an equivalent formula holds.
The movement of the ship can then be calculated by solving the following set of differential equations:
(13)
with YT=(X1,X2,X3,Ω1,Ω2,Ω3). The mass matrix M is diagonal and consists of the mass and the relevant moments of inertia. ![]() is the force or the moment, whatever is appropriate. The non-zero elements of C are
is the force or the moment, whatever is appropriate. The non-zero elements of C are
with D the deck of the hull.
Now that equation (13) enables us to calculate the movement of the ship, we can solve the equations for the total unsteady potential. Then the averaged second-order force and moment can be calculated by the formulas as derived in [6]:
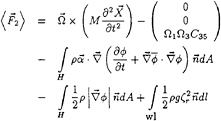
(14)
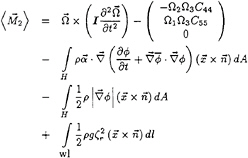
(15)
Here ζr is the linearized relative wave-height, which can be calculated by using Bernoulli's equation and the displacement of the hull. As incoming potential we use
with
–ω2+2kUω+g tanh(kh)=0.
2
Increasing the speed
2.1
Upwind discretization
Increasing the speed, the potential is showing point-to-point oscillations. In this section we are first treating some tests we did with the two-dimensional problem. In figure 3 and 4 is shown that the potential shows local extremes, after one period of forced oscillation in the heave direction, if the Froude number Fn=0.5. These numerical oscillations arise, when we use central discretization.
with subscripts denoting the element number of the clockwise numbered uniform mesh (like figure 2), with mesh size Δx. These oscillations, called wiggles, occur in the stationair convection-diffusion equation, when the Péclet number Pe= UL/k is large and in the instationair convection-diffusion equation, when the Courant-Friedrichs-Lewy number CFL=UΔt/Δx is large. To remove these numerical instabilities upwind discretization is used or artificial viscosity is added.
We noticed that in our case also the CFL-number plays an important role in the determination of stability of the scheme. For increasing values of the CFL-number the scheme becomes unstable. Therefore it seems to be that our problem will also be solvable by using upwind discretization and we replace the central discretization in our algorithm by
This is called upwind discretization, because it is biassed in upstream direction. Now the wiggles disappeared, see figure 5. To act more accurate it is possible to use a higher order three-or four-point scheme, or to use a combination of a two-and a three-point scheme, weighted such as to
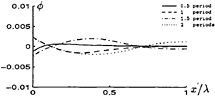
FIGURE 3: The potential, using central discretization, Fn=0.2
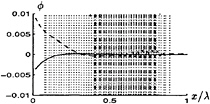
FIGURE 4: The potential, using central discretization, Fn=0.5
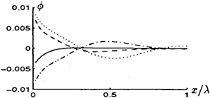
FIGURE 5: The potential, using upwind discretization, Fn=0.5
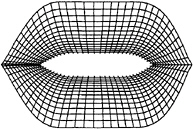
FIGURE 6: The free surface around the LNG carrier
reduce the numerical dispersion and damping to a higher order.
In the three-dimensional problem with the LNG carrier, wiggles also appear when we increase the speed. Implement upwind-discretization is in this case is unfortunately not that easy as in two-dimensions. Firstly the mesh is not equidistant, so it is not possible to use the discretization schemes mentioned above. Secondly the mesh is designed to give a good representation of the waves, but not following the streamlines (See figure 6). By an accurate choice of the neighbour elements in upwind steam direction to give a good representation of the discretization, the wiggles disappear (See figure 7).
FIGURE 7: The free surface around the LNG carrier, upwind discretization is used. The speed is 20 knots and the carrier is forced to heave, the vertical scale is 5:1
3
Results
In this section we test our numerical algorithm, extended to increased forward speed, on a LNG carrier, whose particulars are given in table 1 and whose fine mesh of 1190 panels is given in figure 8. The first calculations were done with the coarse mesh of 384 panels.
TABLE 1: Particulars of the LNG carrier
|
Designation |
Unit |
|
|
Length |
m |
273.90 |
|
Breadth |
m |
42.31 |
|
Draft |
m |
11.50 |
|
Displacement Δ |
m3 |
98,740 |
|
Centre of buoyancy above waterline |
m |
2.16 |
|
Centre of gravity above waterline |
m |
13.70 |
|
Longitudinal radius of gyration |
m |
62.52 |
|
Pitch period |
s |
8.8 |
FIGURE 8: The mesh of the LNG carrier
The free surface was build up out of 14 non equidistantial rings of 84 elements, the number of waterline elements an the hull. The artificial boundary was taken to be one wavelength away from the hull. The exterior was also taken one wavelength. Thus the wave will not be back at the hull during the 4 periods according to the frequency of encounter. On this time interval 200 time steps were taken. The equations of motion were integrated using the implicit method of Crank-Nicholson.
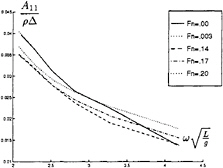
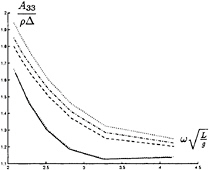
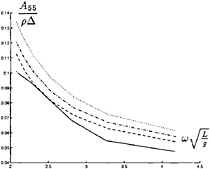
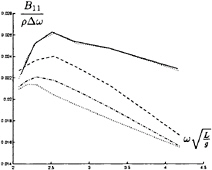
We calculated our results for the same speed, depth and wave frequencies as the measurements in Wichers [11], i.e. Fn=0, Fn=0.14, Fn=0.17, Fn=0.20 and the water depth is 175 m. At the Maritime Research Institute (MARIN) drift force calculations for zero and small forward speed were done, using the frequency domain diffraction program, extended to a small forward speed [12]. Calculations for the other velocities were done using strip theory [1, 2].
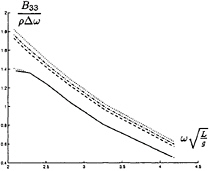
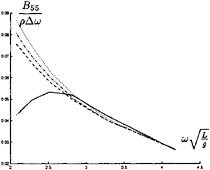
In figure 9 through 26 added mass and damping in surge, heave, and pitch motion are given. For small forward speed the coefficients are fairly independent of the speed, only the coupled coefficients seems depend on small speed. Increasing the speed gives more variation. We have no results to compare with. The reciprocity relations, which are shown by Timman and Newman [9], hold for small forward speed and a35–a53 and b35–b53.
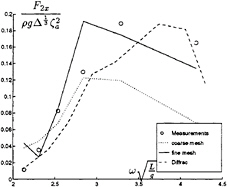
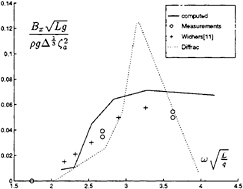
Figure 27 shows the drift forces in head waves for zero speed. We compare our results computed for the fine mesh (1190 elements) and for a coarse mesh (384 elements), the results computed using the frequency domain diffraction program Diffrac, and measurements. It is clear that it is important to use a fine mesh to calculate the
gradients in equation (14). Figure 28 shows the drift forces for small forward speed. In contrast with the Diffrac results, small speed has a small effect on the forces. In figure 29 we show the wave drift damping, which can be written as
Our results agree well with measurements.
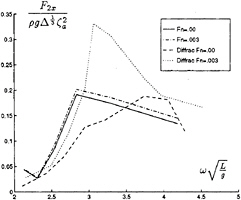
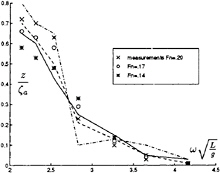
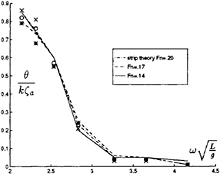
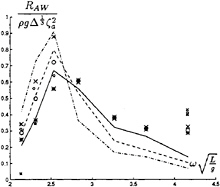
In figures 30 and 31 respectively the heave and pitch response are shown for Fn= .14, .17 and .20. We compare the measurements with the strip theory calculations. In Figure 32 the drift forces or added resistance for higher speed are given. For the higher frequency strip theory doesn't agree very well with the measurements. Our first results, the small markers, look promising. For the lower frequencies the coarse mesh gives good results, but for the higher frequencies we need the finer mesh. At the presentation we will show more results. We have to make more calculation with the finer mesh, so the numerical differentiations on the hull, especially at the bow, will be more accurate.
4
Conclusions and further research
In this paper we show the extension of our method to higher speed. We have made a promising start. Our extended algorithm turns out to be efficient and reliable for low speed up to Fn=.1. Also the hydrodynamic coefficients for higher speed are calculated. Increasing the speed, we need a very accurate numerical differentiation of the gradient of the potential on the hull to compute the added resistance. After the implementation of a finer mesh we are able to tackle this problem as well. In the future we will also carry out the stability analysis.
Acknowledgements
Financial support for this work and the mesh of the ship-hull are given by the Maritime Research Institute Netherlands.
References
[1] C.Flokstra. ”The comparison of ship motion theories with experiments for a container vessel”. Int. Shipbuilding Progress, Vol 21, no 238, 1974.
[2] J.Gerritsma and W.Beukelman. ”Analysis of the resistance increase in waves of a fast cargo ship ”. Int. Shipbuilding Progress, Vol 19, no 217, 1972.
[3] J.B.Keller and D.Givoli. ”Exact nonreflecting boundary conditions”. Journal of computational physics, Vol 82, pp 172–192, 1989.
[4] J.N.Newman. ”Algorithms for the free surface green function”. Journal of Engineering Mathematics, Vol 19, pp 57–67, 1985.
[5] F.Noblesse. ”The green fuction in the theory of radiation and diffraction of regular water waves by a body”. Journal of Engineering Mathematics, Vol 16, pp 137–169, 1982.
[6] H.J.Prins. Time-domain calculations of the drift forces and moments. PhD thesis, Delft University of Technoloy, The Netherlands, 1995.
[7] H.J.Prins and A.J.Hermans. ”Time-domain calculations of the second-order drift force on a tanker in current and waves”. Proceedings of the 20th symposium on naval hydrodynamics, Santa Barbara, USA, 1994.
[8] L.M.Sierevogel and A.J.Hermans. ”Absorbing boundary condition for floating two-dimensional objects in current and waves”. Journal of engineering mathematics (to appear), 1996.
[9] R.Timman and J.N.Newman. ”The coupled damping coefficients of a symmetric ship”. Journal of ship research, Vol 5, pp 1– 7, 1962.
[10] J.V.Wehausen and E.V.Laitone. ”Surface waves”. In Handbuch der physik. Springler-verlag, Berlin, Germany, 1960.
[11] J.E.W.Wichers. Simulation model for a single moored tanker. PhD thesis, Delft University of Technoloy, The Netherlands, 1988.
[12] J.E.W.Wichers and R.H.M.Huijsmans. ”Wave drift current interaction on a tanker in oblique waves”. Hydrodynamics: computations, model tests and reality, (Proceedings of Marin Workshops), Elsevier, Amsterdam, the Netherlands, pp 289–296, 1992.
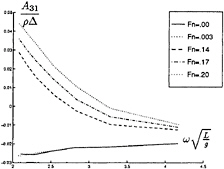
FIGURE 15: Coupled added mass from surge into heave
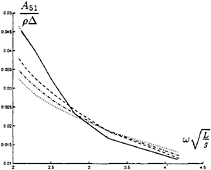
FIGURE 16: Coupled added mass from surge into pitch
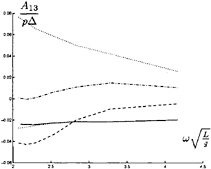
FIGURE 17: Coupled added mass from heave into surge
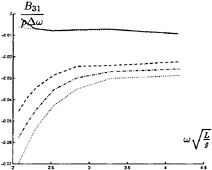
FIGURE 18: Coupled added damping from surge into heave
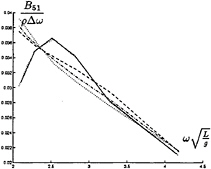
FIGURE 19: Coupled added damping from surge into pitch
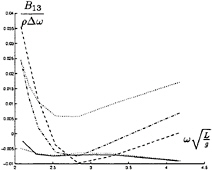
FIGURE 20: Coupled added damping from heave into surge
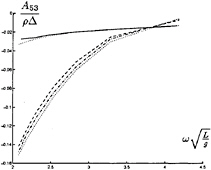
FIGURE 21: Coupled added mass from heave into pitch
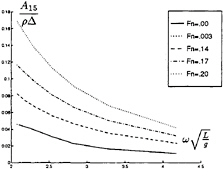
FIGURE 22: Coupled added mass from pitch into surge
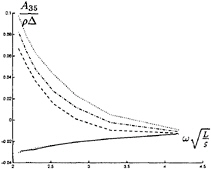
FIGURE 23: Coupled added mass from pitch into heave
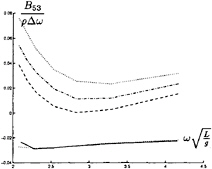
FIGURE 24: Coupled added damping from heave into pitch
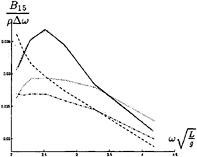
FIGURE 25: Coupled added damping from pitch into surge
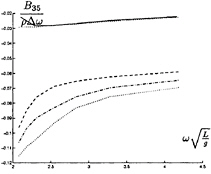
FIGURE 26: Coupled added damping from pitch into heave