Third-Order Volterra Modeling of Ship Responses Based on Regular Wave Results
L.Adegeest (Delft University of Technology, The Netherlands)
Abstract
A third order Volterra modelling was used to calculate the nonlinear vertical hull girder loads in irregular head waves in two slender models with different degrees of bow flare. The first order and the required approximations of the second and third order frequency response functions were derived from systematical experiments in regular waves only. The comparison of time traces, power spectra and probability density functions with experiments in irregular waves showed a good agreement for both models. For the model with bow flare it was not possible to obtain the same degree of correspondence with the experiments using a linear or second order modelling.
1
Introduction
A practical and complete seakeeping theory should involve at least the following elements:
-
A deterministic theory to relate ship's responses to the excitation by well-defined waves.
-
A statistical model of the ship's response in irregular waves.
-
A theory to describe the statistics of response maxima, minima and ranges as a function of the response statistics.
Since many years the validation of deterministic ship motion computer codes is based on the results obtained from towing tank experiments. Most of the experiments are performed in small amplitude waves to provide the necessary validation data for linear codes. Statistical techniques to analyse the linear seakeeping problem are widely available nowadays.
However, it is commonly known that the vertical hull girder loads can show a significant nonlinear behaviour when the relative motions at the bow are large compared with the draft or freeboard of the vessel.
Different solutions can be applied to nonlinear problems. Kac and Siegert [1] presented the mathematical fundamentals to calculate the probability density function of the second order problem. Some years later Wiener [2] introduced a method to analyse nonlinear electric circuits. The proposed method is based on a functional power series model, or a so-called Volterra series expansion. Hasselmann [3] suggested the use of a second order Volterra model to predict the linear and quadratic transfer functions from full scale measurements or model tests. This procedure was applied by many other researchers to analyse phenomena such as the added resistance of a ship in waves (Dalzell [4]), slowly varying drift forces (Pinkster [5]), sum and difference frequency loads on cylinders (Kim and Yue [6]) and vertical hull girder loads (Jensen and Pedersen [7]).
Based on the same principles, Longuet-Higgins [8] and Vinje and Skjørdal [9] both showed that for slightly quadratic processes, the distribution of the extreme values can be derived analytically based on the nonlinear frequency response functions. The expressions are presented in the form of perturbation series expansions, called Edge worth or Charlier series. Jensen and Pedersen [7] applied this method to predict extreme hull girder loads in ships. The fatigue damage inflicted on a construction by non-Gaussian wave-induced stresses was analysed by Jensen [10]. The results of these practical applications were obtained on the assumption of a weakly second order behaviour and a narrow band response spectrum.
The extension to a third order modelling of nonlinear ship motions was already suggested by Dalzell [11,12]. Formulations were derived for the probability density, the statistical moments and the distributions of extremes. Starting point was an assumed set of linear, quadratic and cubic frequency response functions. The results were compared with numerical results obtained for a particular nonlinear differential equation for which the linear, quadratic and cubic frequency response functions could be derived analytically. In principle, the statistics were assumed to be well-defined by the first four statis-
tical moments only (mean, variance, skew and kurtosis).
The similar assumption was made by Winterstein [13]. Using Hermite moment formulations approximate probability density functions, crossing rates and extreme values were derived solely based on the aforementioned statistical moments.
In summary, it was shown by different researchers that the statistics of weakly nonlinear stationary seakeeping problems are reasonably well defined by the first four statistical moments only. This paper shows the applicability of an approximate third-order Volterra modelling to analyze the statistics of the vertical hull girder loads in irregular waves. The numerical results are compared with extensive model tests in irregular waves. The comparisons comprise time traces, power spectra and spectral moments, statistical moments and probability density functions of the samples and of the peak-peak values. The required linear, quadratic and cubic frequency response functions were derived from the first three harmonic components measured in regular waves.
2
Experiments
The first results of systematical experiments, focussed on the nonlinear vertical hull girder loads, were presented by Dalzell [14,15] in 1964. Models of three variants of a Mariner ship, a tanker and a destroyer were subjected to a range of regular waves over a range of wave lengths and heights. The vertical bending moments were presented in hogging and sagging condition separately, not providing information about the harmonic components in the response signals. However, it was proved without a doubt that the sag/hog-ratio was not equal to unity, which should be the case for linear signals. Furthermore the experiments showed that the sag/hog-ratios tended to be larger for the slender destroyer model and the Mariner variants than for the full tanker model. Similar conclusions followed from two other model test series, reported by Murdey [16] and Nethercote [17].
O'Dea et al [18] reported the measurement of nonlinear heave and pitch responses for a S-175 model. The higher harmonic components were only a few percent in magnitude of the first harmonic response. This seems to be a negligible effect. It has to be realised, however, that the accelerations are more strongly nonlinear than the displacements when we compare them with the magnitude of their linear components. This can be illustrated on the assumption of a third order, zero mean periodic displacement, which is written in terms of the first three harmonic components as
(1)
Hence, the displacement, velocity and acceleration are given in matrix notation by
(2)
It can easily be seen that relative to the first harmonic component, the second harmonic acceleration is four times as large as the second harmonic displacement while the third harmonic component is even nine times larger. This much more pronounced nonlinear inertia effect directly influences the hull girder loads behaviour.
After a survey of literature it had to be concluded that the data sets presented were not sufficient to study the nonlinear hull girder loads in very much detail. Many of the experiments were performed in regular waves only. From those test results, too much information was lost due to the presentation of the results in terms of hog/sag-ratios or double amplitudes. No systematical results were presented showing the harmonic components of a response experienced in regular wave conditions in order to investigate the actual order of the process.
Therefore new extensive experiments were performed both in regular and irregular waves. The results were extensively reported and discussed by Adegeest [19,20,21]. The objective of the experiments was to collect motion and load data that can be studied and compared with numerical solutions in much more detail.
The experiments were conducted on a Wigley hull form with and without bow flare. The normalised beam y of the under water ship is described by a polynomial in the x- and z-coordinate according to
y=(1–z2)(1–x2)(1+0.2x2) +z2(1–z8)(1–x2)4 (3)
where x ∈ [–1,1] and z ∈ [–1,0]. Table 1 shows the main characteristics of the Wigley geometries. The bow form variation is clearly illustrated in figure 1.
In regular waves both models were tested at two forward speeds, thirteen frequencies and at least four wave amplitudes. Fourier analyses of the results clearly showed the presence of pronounced higher harmonic components in the hull girder load
Table 1: Main characteristics of the Wigley models
|
Length on waterline (LWL) |
2.500 |
m |
|
Beam (B) |
0.357 |
m |
|
Draught (T) |
0.139 |
m |
|
Displacement volume |
0.0696 |
m3 |
|
L/B |
7.000 |
|
|
L/T |
18.000 |
|
|
Block coefficient (CB) |
0.561 |
|
|
Midship coefficient (CM) |
0.909 |
|
|
Water plane coefficient |
0.693 |
|
|
kyy/L |
0.25 |
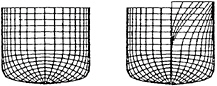
Figure 1: Plans of both Wigley variants
responses while the motion responses were hardly affected by nonlinear contributions, see for example figure 2.
In irregular waves about 50 runs were made for both models at one forward speed Fn=0.3. This resulted in about 5000 wave encounters per model. The applied wave spectrum is shown in figure 3. In the same figure the Gaussiannity of the waves was investigated by comparing the probability density with the theoretical normal distribution. It seems reasonable to assume a Gaussian distributed wave elevation. Figure 4 shows some examples of the measured response probability densities compared with their equivalent theoretical Gaussian probability density. The deviations from the Gaussian probability densities were an order larger than those observed in the excitation waves.
The equivalent first order RAOs were derived according to ![]() and successively compared with the measured first harmonic responses in regular waves (figure 5). For the original hull form in regular waves, only minor spreading was observed between the normalized first harmonics in different wave heights. This implied that third order effects hardly occurred. As expected, the RAOs from the irregular wave tests confirmed
and successively compared with the measured first harmonic responses in regular waves (figure 5). For the original hull form in regular waves, only minor spreading was observed between the normalized first harmonics in different wave heights. This implied that third order effects hardly occurred. As expected, the RAOs from the irregular wave tests confirmed
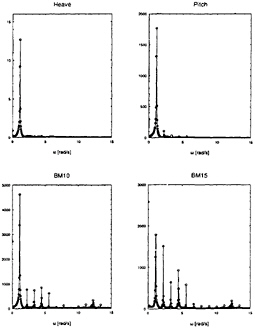
Figure 2: Fast Fourier Transforms of some measured responses of the Wigley with bow flare, Fn=0.3, λ/L=1.36, H/λ ≈ 1/75
this result. For the Wigley with bow flare, significant spreading between the regular wave results was observed. Yet, the RAOs derived from the irregular wave tests approximate the regular wave results in the examined frequency range reasonably well. The result for the bending moment in the forward however immediately shows the presence of severe nonlinear effects.
The problem with the measured responses is the significant contribution to the total hull girder loads of not only second order but also of third order components. The low-frequency third order responses cause the response in the wave-frequency area to deviate from the linear predictions. The high-frequency higher order components cause the response spectra to become wider, which is another complication in extreme statistics.
In the following section a theory is outlined to derive approximations for the linear, quadratic and cubic frequency response functions using which it is possible to derive the response statistics in irregular waves for those nonlinear responses in which the first order term is still dominant.
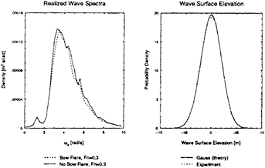
Figure 3: Realised wave spectra during experiments with both Wigley huli variants (left) and the probability density of the samples compared with the equivalent Gaussian probability density function (right)
3
The Third Order Volterra Model
The presented experimental results clearly identified the need for nonlinear computational methods in the statistical analysis of vertical hull girder loads, whether it concerns the prediction of the life time maximum wave-induced loads or a long-term distribution of load cycles for the purpose of fatigue analyses.
The general way to describe the nonlinear relation between an inputand output-signal as a Volterra series model is by means of a power series with memory. This memory effect is represented by a functional series which is, up to the third order, given by
y(t)=y1(t)+y2(t)+y3(t)+n(t) (4)
in which the total nonlinear system's output y(t) is the sum of a linear or first order time-varying output y1(t), a bi-linear or second order time-varying output y2(t), a tri-linear or third order time-varying output y3(t) and, since no analytical model fits perfectly to a physical model, a zero mean term n(t) representing higher order terms and measuring noise. This term is assumed not to be correlated with the other output components. From now on the component n(t) will be assumed to be zero, which does not change the results derived below.
The Volterra functionals as defined in equation (4) are given by
(5)
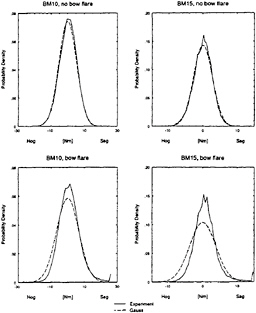
Figure 4: Probability density functions of the recorded bending moments in the original Wigley (upper) and in the Wigley with bow flare (lower) compared with the equivalent Gaussian probability density function
(6)
(7)
The functions h1(t1), h2(t1,t2) and h3(t1,t2,t3) are, respectively, the linear, quadratic and cubic time-domain Volterra kernels or weighting functions. In terms of impulse responses, these functions represent the system's memory effect in the time domain, affecting a linear response at time t due to an impulsive excitation at time t–t1, a quadratic response due to two impulsive excitations at times t–t1 and t–t2 and a cubic response due to impulsive excitations at times t–t1, t–t2 and t–t3. In physically realisable models, t1, t2 and t3 are positive quantities, which implies that only excitations in the past can result in a response. It can be derived that h2(t1,t2) and h3(t1,t2,t3) are unique and symmetric with respect to their variables.
The frequency-domain kernels H1(ω), H2(ω1,ω2) and H3(ω1,ω2,ω3), representing the lin-
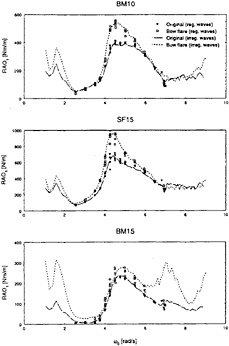
Figure 5: Equivalent RAO's derived from the irregular wave tests compared with the regular wave results
ear, quadratic and cubic frequency response functions respectively are given by the single, double and triple Fourier transform of the time-domain kernels and show the same symmetry relations with respect to the variables as the time-domain kernels.
By expressing the time domain kernels and the time-dependent wave surface elevation ζ(t) in terms of their equivalent frequency domain representation, it follows that
(8)
(9)
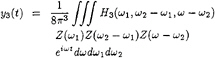
(10)
in which, by means of a particular substitution of frequencies, the exponent occurring in all three equations is equal to iωt. This substitution is advantageous during the actual time history generation process, which can now be performed by a single inverse Fast Fourier Transformation. If the linear and nonlinear frequency response functions are known, the Volterra model offers the opportunity to perform simulations of realistic ship's responses in arbitrary random sea conditions very quickly. Generally this is an impossibility with direct nonlinear boundary value solutions in the time domain.
The general problem encountered when using the Volterra modelling is the determination of the full two- and three-dimensional nonlinear frequency response functions of the underlying system. A direct calculation in the frequency domain would be an enormous task. A second possibility is to derive these functions from existing time histories, provided that these are available. A major practical problem herein is the rapidly increasing amount of data required to make accurate predictions of the second but especially of the third order frequency response functions.
Bendat [22] presented two different types of third order system modellings which made it possible to make an estimation of the nonlinear frequency response functions purely based on regular wave results. For many types of responses it is hardly possible to predict the degree of fitting of their approximate modellings.
O'Dea et al [18] applied one of those modellings to analyse the nonlinear motion behaviour in head waves of a S-175 model. In regular waves, the same third order behaviour of the normalised first harmonic components was observed as discussed in the previous chapter. After substituting the frequency response function H2(ω1,ω2) by an additive frequency response function A2(ω1+ω2) and the third order frequency response function H3(ω1,ω2,ω3) by A3(ω1+ω2+ω3), a polyspectral analysis of motion recordings in irregular waves confirmed the dominant role of third order effects in the wave frequency band.
It was shown by the author [23], however, that in case of the nonlinear hull girder loads, modelling of the nonlinear response as a linear frequency transfer operation followed by a zero-memory quadratic or cubic operation gave very good results. In that modelling, the frequency response functions as introduced in the equations (8)–(10) are redefined as frequency response functions of constant parameter linear systems:
H1(ω)=B1(ω) (11)
H2(ω1,ω2)=B2(ω1)B2(ω2) (12)
H3(ω1,ω2,ω3)=B3(ω1)B3(ω3) (13)
Some typical results of this model are
(14)
(15)
H2(ω,–ω)=B2(ω)B2(–ω)=|B2(ω)|2 (16)
H3(ω,ω,–ω)=B3(ω)|B3(ω)|2 (17)
From these equalities it follows that the required frequency response functions B1(ω), B2(ω) and B3(ω) can be derived from the response in a regular wave train.
Assume that the degree of nonlinearity in the waves is negligible compared with the nonlinearities in the response. A regular monochromatic wave with frequency ω0 is written as
ζ(t)=A cosω0t (18)
or its Fourier transformation
Z(ω)=π[Aδ(ω0–|ω|)] (19)
Substitution of the frequency-domain representation of the wave surface elevation (19) into the equations describing the individual functionals of the complete third order Volterra model, given by equations (8) –(10), and making use of the symmetry of the frequency domain kernels, the following expressions are found for the first, second and third order response:
(20)
(21)
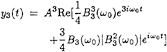
(22)
The response y(t) in regular waves can also be written in the form:
(23)
in which the Rj's are the complex amplitudes of the individual harmonic components. These amplitudes follow from a Fourier analysis of the response in regular waves.
The amplitude and phase of the frequency response function B2(ω) are derived from the measured second harmonic component:
(24)
The degree of fitting of the second order component of the proposed modelling to the underlying physical phenomenon is easily checked by comparing the measured mean value with the equivalent expression in terms of B2(ω) as derived from the second harmonic. It was observed in the analysis of the regular wave results that the modulus of the experienced second harmonic and mean bending moment were generally of the same magnitude, especially for the Wigley with bow flare which shows the severest nonlinear behaviour [21].
The third and first order frequency response functions B3(ω) and B1(ω) are prescribed by
(25)
(26)
Theoretically, the results obtained over a range of frequencies, each at just one wave amplitude, are sufficient to obtain a first estimate of B1(ω0), B2(ω0) and B3(ω0). It should be recognised that the first order frequency response function as predicted using equation (26) depends very much on the accuracy of the measured third harmonic responses, i.e. the high-frequency third order response.
In order to predict the first order results in a less sensitive way, use is made of the availability of regular wave results per frequency over a range of different wave amplitudes. From equation (26) it follows that B1(ω0) and B3(ω0) can be determined by a least square fitting of the results R1,i for i=1…n different wave amplitudes Ai to a polynomial of the type
(27)
where B3(ω) has been replaced by ![]() to indicate that we are dealing with the low-frequency component of the third order response. The equivalent high-frequency third order component
to indicate that we are dealing with the low-frequency component of the third order response. The equivalent high-frequency third order component ![]() is determined from the third harmonic response:
is determined from the third harmonic response:
(28)
The separation of the third order response into a low-frequency and a high-frequency contribution, accounted for by ![]() and
and ![]() respectively, allows the use of the maximum available information enclosed in regular wave results at the cost of a modification of the modelling given by definitions (11)–(13). Generally spoken
respectively, allows the use of the maximum available information enclosed in regular wave results at the cost of a modification of the modelling given by definitions (11)–(13). Generally spoken ![]() and
and ![]() will not have the same value although this
will not have the same value although this
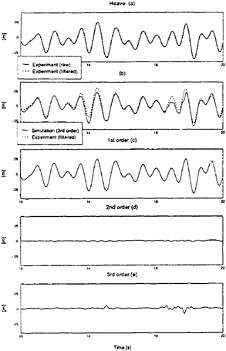
Figure 6: Measured and simulated heave motion of the Wigley with bow flare, Fn=0.3
was implied by the proposed modelling. The virtue of this modification, however, is that the resulting first order results are less sensitive to variations or errors in the triple frequency response which in general is difficult to determine.
4
The Results
In this section, reconstructed time histories resulting from the first, second and third order Volterra modellings are analysed and compared in detail with experiments in irregular waves. The main purpose of these analyses is to investigate whether or not it is possible to make a proper prediction of the probability densities and of the statistics of the maxima, minima and ranges of the hull girder loads.
It should be realised that the presented simulations are purely transformations of a frequency domain formulation to time traces by adopting a specific wave spectrum. The benefit of analysing time traces is the applicability of ready-available techniques for determining response and extreme statistics. After validation of the applicability of the proposed modelling, direct frequency domain analyses are preferred.
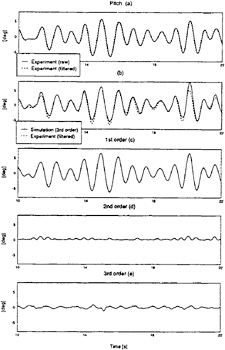
Figure 7: Measured and simulated pitch motion of the Wigley with bow flare, Fn=0.3
4.1
Time Histories
In order to compare the statistical properties of the simulations with the experimental values, simulations were performed in exactly the same wave trains as realised during the experiments. When obtaining the wave surface elevation experienced during the irregular wave tests in the centre of gravity, use was made of the assumed linearity of the waves. This assumption was verified by the degree of fitting of the realised probability density to the theoretical Gaussian probability density function as shown in figure 3.
The amplitudes and phases of the wave components were calculated by Fourier transformation of the recorded wave signal in front of the model after which a phase correction per wave component was applied using the dispersion relation for shallow water.
After substituting the nonlinear frequency responses functions B1(ω), B2(ω) and B3(ω) into the equations 8–10, time traces of the irregular responses were calculated using Fast Fourier Transform (FFT) routines. This method required the interpolation of 2n frequency response function values at equal distances Δω. Use was made of the mea-
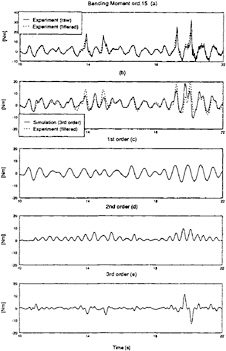
Figure 8: Measured and simulated vertical bending moment in the forward of the Wigley with bow flare, Fn=0.3
sured first three harmonic components in regular waves. These responses were measured at incident wave frequencies in the range from ω0=2.5–7.0 rad/s. Outside this range proper estimates were made based on the known response at low and high frequency limits.
The reconstructed motion responses of the Wigley with bow flare are shown in figure 6 and 7. Figure 8 and 9 show some examples of the measured and numerically reconstructed vertical bending moments in the same Wigley model.
The upper graphs in these figures show the unfiltered signals resulting from the model test. Slamming events are noticed in the load recordings as sharp peaks in sagging condition, followed by a slowly decaying vibration. In order to remove the structure dependent springing loads and slam-induced whipping loads from the experimental results, all time recordings were filtered at 4 Hz. To allow an honest comparison, all simulated results were filtered at 4 Hz too.
It is clear that the motion responses are predicted well just by taking into account the first order contribution. The higher order components did
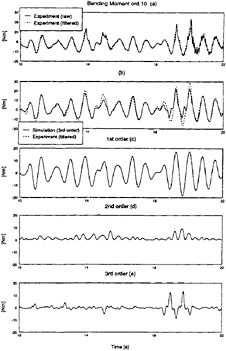
Figure 9: Measured and simulated vertical midship bending moment in the Wigley with bow flare, Fn =0.3
not contribute significantly to the total motion response.
A satisfactory agreement was also found between the experimental load results and the third order simulations as can be seen from figures 8 (b) and 9 (b). Especially when it is realised that the wave had to be transformed to the centre of gravity and that hundreds of frequency response function values were interpolated linearly using only thirteen estimates. The individual first, second and third order contributions are presented in figures 8 and 9 (c), (d) and (e). It can be observed that at the instant of a slam, the second and third order contribution obtain similar magnitudes as the linear component of the simulation, especially in the forward. Furthermore it can be seen that the third order contribution is dominated by the low frequency component.
4.2
Response Spectra
The power spectra of the responses were calculated from the measured and simulated time histories. Each run was analysed separately after which the resulting spectra were averaged. Figure 10 shows
the power spectra of the bending moments amidships and at the bow for both the original Wigley and the Wigley with bow flare.
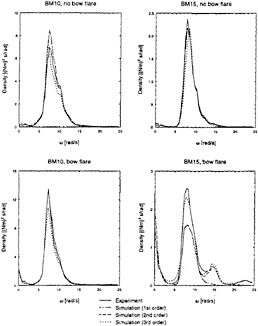
Figure 10: Measured and simulated auto-power spectra of the bending moments at Fn=0.3, averaged over 50 runs of 50 seconds each
For the original Wigley hull form, no distinct higher order peaks can be observed in the power spectra of the experimental results nor in those of the simulated results. Generally a good correspondence with the experiments was obtained for all simulations. The main difference was found for the midship bending moment. For that case, the first and second order simulations overestimate the energy density in the wave frequency range. Using the third order simulations, the energy density is calculated more accurately.
For the Wigley with bow flare, a low frequency second order effect becomes visible in the bending moment response amidships. For this model, the use of the third order simulation model resulted in an energy density in the wave frequency range that was not high enough; i.e. the low frequency third order contribution is overestimated. The most interesting result, however, is found for the bending moment response in the forward. The experiments show a clear low frequency hump in the response spectrum due to the low frequency second order response. Humps are also noticed at twice and three times the main peak frequency. Comparison of this experimental result with first, second and third order simulations respectively tells us that the first and second order simulation underestimate the peak in the wave frequency band of the power spectrum severely. Approximately 40% of the spectral energy is missed by the linear and second order prediction. This is the explanation for the large spreading in the normalised first harmonic responses in regular waves, which showed an increase of the normalised first harmonic response amplitude in the frequency response peak of more than 20 % over the range of tested wave amplitudes, see figure 5. The low frequency and double frequency peak are very well predicted by applying the second order Volterra modelling. But only by using the third order Volterra modelling the triple frequency peak and particularly the energy density in the wave frequency range are predicted well. This illustrates that the high peak in the wave frequency range is the net result of the linear response plus the low-frequency third order response.
The characteristics of the response spectra are determined by the spectral moments. The nth order moment is defined as
(29)
The variance of the response y(t), E[y(t)2], is found for n=0. For linear responses, the mean square velocity E![]() (t)2] is given by m2 and m4 defines the mean square acceleration E[ÿ(t)2]. The spectral moments of the measured and simulated hull girder loads are presented in table 2.
(t)2] is given by m2 and m4 defines the mean square acceleration E[ÿ(t)2]. The spectral moments of the measured and simulated hull girder loads are presented in table 2.
In general, it can be observed that the spectral moments for the original Wigley are not very sensitive to the order of simulation. A good correspondence with the experiments is found for every order of simulation. Therefore, for this particular Wigley model, a first or second order simulation would satisfy to predict the spectral moments.
The spectral moments of the bending moment responses in the Wigley with bow flare, however, are very sensitive to the order of simulation. As expected, this is especially true for the higher order moments since these moments characterise the time derivatives of the responses. In the previous chapter, it was discussed already that the time derivatives of the responses are significantly more sensitive to nonlinearities than the responses themselves. This is confirmed by the higher order spectral moments. It can be concluded that the third order
Table 2: Comparison of the measured and simulated spectral moments of the vertical hull girder loads in both Wigley variants, all simulations filtered at 4 Hz
|
Response: |
No bow flare |
Bow flare |
||||||||
|
Shear Force st.15 [N] |
m0 |
m1 |
m2 |
m3 |
m4 |
m0 |
m1 |
m2 |
m3 |
m4 |
|
Experiment |
78.3 |
790 |
1.72e4 |
9.12e5 |
6.73e7 |
125 |
1.40e3 |
3.99e4 |
2.24e7 |
1.79e8 |
|
Experiment (4Hz) |
75.9 |
632 |
6.04e3 |
6.81e4 |
1.10e6 |
119 |
955 |
8.43e3 |
8.82e4 |
1.52e6 |
|
1st order |
88.4 |
705 |
6.16e3 |
5.97e3 |
8.47e5 |
129 |
1.00e3 |
8.26e3 |
7.59e4 |
1.13e6 |
|
2nd order |
93.6 |
751 |
6.88e3 |
7.21e4 |
1.08e6 |
133 |
1.03e3 |
8.71e3 |
8.39e4 |
1.29e6 |
|
3rd order |
78.1 |
635 |
6.18e3 |
7.26e4 |
1.20e6 |
113 |
883 |
7.64e3 |
7.84e4 |
1.29e6 |
|
Bending Moment st.15 [Nm] |
m0 |
m1 |
m2 |
m3 |
m4 |
m0 |
m1 |
m2 |
m3 |
m4 |
|
Experiment |
7.8 |
87.2 |
2.30e3 |
1.38e5 |
1.06e7 |
14.8 |
250 |
9.64e3 |
5.84e5 |
4.11e7 |
|
Experiment (4Hz) |
7.5 |
65.3 |
631 |
6.88e3 |
1.02e5 |
12.3 |
115 |
1.33e3 |
1.85e4 |
3.36e5 |
|
1st order |
6.7 |
57.3 |
526 |
5.20e3 |
6.98e4 |
6.1 |
54 |
500 |
4.98e3 |
6.62e4 |
|
2nd order |
7.0 |
59.7 |
560 |
5.77e3 |
8.11e4 |
9.1 |
80 |
864 |
1.07e4 |
1.72e5 |
|
3rd order |
6.9 |
59.9 |
588 |
6.54e3 |
9.97e4 |
12.4 |
116 |
1.36e3 |
1.92e4 |
3.52e5 |
|
Shear Force st.10 [N] |
m0 |
m1 |
m2 |
m3 |
m4 |
m0 |
m1 |
m2 |
m3 |
m4 |
|
Experiment |
48.6 |
458 |
5.91e3 |
1.73e5 |
1.17e7 |
35.3 |
337 |
5.73e3 |
1.69e5 |
8.94e6 |
|
Experiment (4Hz) |
48.2 |
437 |
4.43e3 |
5.10e4 |
7.69e5 |
34.2 |
328 |
3.50e3 |
4.21e4 |
6.32e5 |
|
1st order |
46.9 |
417 |
4.07e3 |
4.39e4 |
6.27e5 |
31.2 |
286 |
2.84e3 |
3.09e4 |
4.38e5 |
|
2nd order |
49.5 |
439 |
4.40e3 |
4.95e4 |
7.34e5 |
35.4 |
323 |
3.38e3 |
3.96e4 |
6.13e5 |
|
3rd order |
49.9 |
453 |
4.68e3 |
5.45e4 |
8.28e5 |
41.5 |
385 |
4.06e3 |
4.90e4 |
7.75e5 |
|
Bending Moment st.10 [Nm] |
m0 |
m1 |
m2 |
m3 |
m4 |
m0 |
m1 |
m2 |
m3 |
m4 |
|
Experiment |
28.9 |
330 |
9.53e3 |
6.02e5 |
4.70e7 |
46.2 |
662 |
2.57e4 |
1.70e6 |
1.27e8 |
|
Experiment (4Hz) |
27.8 |
234 |
2.23e3 |
2.43e4 |
3.78e5 |
41.3 |
344 |
3.19e3 |
3.52e4 |
6.62e5 |
|
1st order |
30.5 |
251 |
2.25e3 |
2.21e4 |
3.13e5 |
36.6 |
298 |
2.55e3 |
2.40e4 |
3.47e5 |
|
2nd order |
32.0 |
265 |
2.67e3 |
2.58e4 |
3.81e5 |
38.7 |
316 |
2.81e3 |
2.84e4 |
4.36e5 |
|
3rd order |
27.2 |
224 |
2.17e3 |
2.48e4 |
3.97e5 |
34.4 |
293 |
2.84e3 |
3.35e4 |
5.81e5 |
simulations gave the best results for the higher order spectral moments.
These computations were performed in order to investigate the characteristics of the simulated results with those of the experiments. However, it is also possible to calculate the response spectra including first, second and third order contributions directly in the frequency domain. The suitable formulations were summarized in [21].
4.3
Sample Probability Densities
It was already shown in the qualitative analysis of the irregular wave experiments that the sample probability densities of the bending moments deviated strongly from the equivalent Gaussian probability density function. This was especially noticeable for the Wigley with bow flare.
Deviations from the Gaussian distribution can be expressed by the statistical moments such as there are the mean µ, skew κ3 and kurtosis κ4, which should all be zero in case of Gaussian signals. The statistical moments presented in this section are defined by the following expressions:
(30)
(31)
(32)
(33)
(34)
where N is the number of samples. The analyses and comparisons made in this section were performed by regarding the ensemble of runs as one set of data, in this case 100,000 samples with a total length of 2500 seconds. This was allowed since the input wave spectrum was stationary and ergodic.
Table 3 shows the statistical moments of the recorded loads before and after filtering as well as the statistical moments of the reconstructed signals by applying the first, second and third order
Table 3: Comparison of the measured and simulated statistical moments of the vertical hull girder loads in both Wigley variants, all simulations filtered at 4 Hz
|
Response: |
No bow flare |
Bow flare |
||||||||
|
Shear Force st.15 [N] |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
|
Experiment |
–0.089 |
7.067 |
78.26 |
0.130 |
0.142 |
–0.951 |
8.753 |
125.4 |
–0.271 |
1.439 |
|
Experiment (4Hz) |
–0.089 |
6.999 |
75.91 |
0.075 |
–0.180 |
–0.951 |
8.635 |
118.5 |
–0.197 |
0.172 |
|
1st order |
0.007 |
7.476 |
88.42 |
0.016 |
0.047 |
–0.008 |
9.012 |
129.1 |
0.007 |
0.181 |
|
2nd order |
–0.426 |
7.617 |
93.59 |
–0.217 |
0.402 |
–0.903 |
9.057 |
132.6 |
–0.325 |
0.535 |
|
3rd order |
–0.426 |
7.020 |
78.13 |
–0.135 |
0.179 |
–0.901 |
8.440 |
113.4 |
–0.322 |
0.328 |
|
Bending Moment st.15 [Nm] |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
|
Experiment |
–0.041 |
2.177 |
7.764 |
–0.097 |
1.420 |
0.826 |
2.522 |
14.76 |
2.575 |
28.57 |
|
Experiment (4Hz) |
–0.041 |
2.157 |
7.509 |
–0.159 |
0.415 |
0.826 |
2.563 |
12.30 |
1.511 |
8.013 |
|
1st order |
0.006 |
2.045 |
6.678 |
–0.015 |
0.184 |
–0.001 |
1.958 |
6.113 |
–0.005 |
0.308 |
|
2nd order |
–0.175 |
2.084 |
6.964 |
–0.020 |
0.201 |
0.975 |
2.301 |
9.148 |
0.779 |
2.723 |
|
3rd order |
–0.175 |
2.060 |
6.823 |
–0.024 |
0.268 |
0.975 |
2.465 |
12.39 |
1.391 |
14.35 |
|
Shear Force st.10 [N] |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
|
Experiment |
–0.003 |
5.464 |
48.56 |
0.316 |
0.937 |
0.282 |
4.659 |
35.32 |
0.341 |
1.498 |
|
Experiment (4Hz) |
–0.003 |
5.439 |
48.20 |
0.292 |
0.741 |
0.282 |
4.589 |
34.23 |
0.235 |
0.739 |
|
1st order |
0.015 |
5.432 |
46.90 |
0.022 |
0.118 |
–0.008 |
4.425 |
31.21 |
0.008 |
0.246 |
|
2nd order |
–0.233 |
5.566 |
49.50 |
–0.022 |
0.197 |
0.654 |
4.589 |
35.39 |
0.617 |
1.606 |
|
3rd order |
–0.234 |
5.589 |
49.92 |
–0.041 |
0.251 |
0.655 |
4.756 |
41.51 |
1.008 |
5.207 |
|
Bending Moment st.10 [Nm] |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
µ |
κ1 |
σ2 |
κ3 |
κ4 |
|
Experiment |
0.209 |
4.241 |
28.91 |
–0.072 |
0.905 |
1.161 |
5.049 |
46.25 |
0.949 |
6.322 |
|
Experiment (4Hz) |
0.209 |
4.194 |
27.76 |
–0.060 |
0.034 |
1.162 |
4.927 |
41.34 |
0.685 |
1.821 |
|
1st order |
–0.003 |
4.382 |
30.45 |
–0.016 |
0.089 |
0.004 |
4.792 |
36.59 |
–0.003 |
0.258 |
|
2nd order |
0.202 |
4.449 |
31.97 |
0.240 |
0.419 |
1.133 |
4.840 |
38.71 |
0.677 |
1.225 |
|
3rd order |
0.202 |
4.140 |
27.02 |
0.166 |
0.106 |
1.133 |
4.579 |
34.39 |
0.610 |
1.312 |
Volterra modelling. It was shown that by filtering, the standard deviation, variance, skew and kurtosis were significantly reduced.
The presence of bow flare resulted in a skew and kurtosis for the bending moments which were an order larger than those resulting from the model without bow flare. The skew and kurtosis of the shear force responses were less sensitive to the degree of bow flare. Particularly noticeable in this context is the kurtosis of the bending moment in the forward of the original Wigley and the Wigley with bow flare of 0.4 and 8.0 respectively. The third order simulations predicted 0.3 and 14.3 respectively. In the previous section, an increase as a function of the order of the simulations could already be noticed for the variance of the bending moment in the flared bow. This is also shown in table 3. It was found that the variance resulting from the third order simulation was twice as high as the variance resulting from the first order simulation, 12.4 and 6.1 respectively. The measured variance was 12.3 which is remarkably close to the third order result.
The applied modelling also allowed the computation of the response moments directly in the frequency domain. Formulations for the moments of the responses were derived in [21] by expressing the statistical moments in terms of auto-correlation functions.
For the most interesting response regarding the degree of nonlinearity, i.e. the bending moment in the forward of the Wigley with bow flare, the measured and, with different orders, simulated probability density functions are plotted in figure 11.
Two aspects are important to notice when looking at these curves; the shape of the curves and the predicted positive and negative extreme values. It is interesting to see how well the third order simulation was able to predict the probability density in sagging condition.
Up to the maximum plotted values with a probability of slightly more than 0.001, the experimental results are simulated very well. In the linear simulations, the loads did not even reach these values and the probability of these loads would already be less than 0.00001. A better overall correspondence was found with the second order modelling but the extreme sagging moments were slightly underestimated.
The bending moments in hogging condition seem to be predicted better by the second order simulations than by the third order simulations. Whereas the probability density of the sagging moments
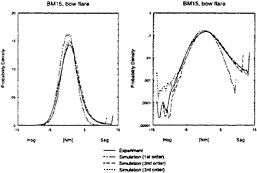
Figure 11: Measured and simulated probability density functions of the bending moment in the forward of the Wigley with bow flare at Fn=0.3 on linear scale (left) and logarithmic scale (right) resulting from 100,000 samples
could not be predicted with a linear theory, it was possible to calculate the shape of the probability density of the bending moment in hogging condition quite well down to the 0.001 probability level. The calculated extreme linear hogging moment, however, was much smaller than observed in the experiments.
4.4
Peak-Peak Probability Densities
The final test for the proposed Volterra modelling was the comparison of the probability density of the peak-peak values. The time histories as well as the power spectra showed a wide band hull girder load response, which was not the result after the linear simulation, and was only partly estimated by the second order simulation. This implied that the number of extremes or cycles in the total simulated period varied for the different types of simulations. Values for the measured and calculated number of maxima are presented in table 4. From this table it can be read that the number of maxima in the motion responses was hardly affected by the order of the simulation. This was not the case for the hull girder loads. A maximum difference between the linear prediction and the third order prediction of 24 % was found, again for the bending moment in the forward of the Wigley with bow flare. For the original hull form, those differences were not as significant.
In order to compare the corresponding distributions of the response ranges properly, not the probability density functions py(y) but the probability rates per unit of time were compared. Here, the
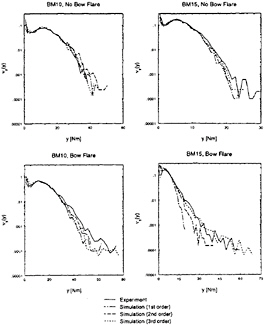
Figure 12: Probability density functions of the peak-peak values of the bending moments as measured and simulated for both Wigley models at Fn =0.3
probability rate is defined as
(35)
where N is the total number of cycles and T is the total length of all records together. Several counting methods, applied to stress records for fatigue damage analyses, were proposed in literature. In this report, the rain flow counting method is applied, which was proved to be superior to other counting methods by Wirsching and Moshen Shehata [24]. Using the rain flow counting method, high and low frequency cycles can be identified.
Figure 12 shows the probability density functions of the bending moments in terms of the probable number of events per second. The area under the curves from zero to the maximum observed value is a measure of the total number of events during a unity period. For the original Wigley, it was found that the different simulated curves and the experimental results were all within a rather narrow band. The predicted maxima were also of the same order.
For the Wigley with bow flare, the differences between the observed bending moment maxima in
Table 4: Number of maxima N observed in the experiments and the first, second and third order simulations for the original Wigley (upper) and Wigley with bow flare (lower). All recordings filtered at 4 Hz, total length 2500 seconds
|
Response (Original) |
Experiment NE (100%) |
1st order N/NE (%) |
2nd order N/NE (%) |
3rd order N/NE (%) |
|
Wave |
5050 |
100 |
100 |
100 |
|
Shear Force st.15 |
4286 |
86 |
94 |
103 |
|
Bending Moment st.15 |
4134 |
92 |
96 |
102 |
|
Shear Force st.10 |
4262 |
99 |
103 |
107 |
|
Bending Moment st.10 |
4075 |
91 |
96 |
104 |
|
Heave |
2724 |
100 |
100 |
100 |
|
Pitch |
2830 |
99 |
100 |
100 |
|
Response (Bow flare) |
Experiment NE (100%) |
1st order N/NE (%) |
2nd order N/NE (%) |
3rd order N/NE (%) |
|
Wave |
4953 |
100 |
100 |
100 |
|
Shear Force st.15 |
3872 |
90 |
93 |
97 |
|
Bending Moment st.15 |
4986 |
78 |
92 |
102 |
|
Shear Force st.10 |
4593 |
93 |
96 |
99 |
|
Bending Moment st 10 |
3952 |
90 |
95 |
103 |
|
Heave |
2664 |
100 |
99 |
100 |
|
Pitch |
2789 |
98 |
99 |
101 |
the forward resulting from the linear simulations and the third order simulations or experiments were about 300%. The second order simulation only obtained values not more than about 60 % of the experimental maxima. It can also be seen that the third order simulated maximum bending moments in the forward were similar to the maximum bending moments amidships. This was confirmed by the experimental results.
5
Discussion and Conclusion
A third order Volterra modelling was developed for the calculation of the hull girder load responses in irregular waves. The fully nonlinear second and third order frequency response functions were estimated using the known nonlinear response in regular waves only. To validate the proposed modelling, the results from regular wave experiments were used as input of the modelling at this stage. This way, no assumptions had to be made concerning the physical origin of the different nonlinear effects in the response. The wave surface elevation itself was assumed to be Gaussian.
Using the proposed modelling, it was possible to make accurate predictions of the power-spectra of the most severe responses recorded. From the comparison of measured and simulated response spectra, it was concluded that including third order responses can be very important for two reasons.
The first reason is that the peak of the low frequency third order response spectrum coincides with the peak of the energy spectrum of the first order response. This implies an additional third order response in the frequency band in which the responses are traditionally assumed to be linear and in which the wave energy density is generally high. The bending moments in the forward of the Wigley with bow flare were heavily affected by this contribution in particular.
The second reason is that due to the higher order contributions, the spectrum becomes wider. This is expressed by the higher order spectral moments, which were predicted better by the higher order simulations. This, in turn, also increases the number of cycles in a fixed period, which has its impact on the fatigue damage. The best prediction of the number of cycles were made using the third order modelling.
The probability density functions of the samples were calculated. For the severest nonlinear responses, it was shown that the first four statistical moments were predicted accurately. This could not be achieved with a lower order modelling.
The distribution functions of the peak-peak values showed that the maximum bending moments in the flared bow reached the same magnitudes as amidships. This could only be calculated using the third order simulation model.
Other researchers showed that the statistical characteristics of nonlinear responses are mainly determined by the first four statistical moments. Using the suggested modelling, these moments can be derived for realistic ship responses under severe non-
linear conditions, either directly in the frequency domain or indirectly by the analysis of long simulated time traces. Only the nonlinear response in regular waves is required to be known. In this paper, this information was deducted from the regular wave experiments but the results of a set of large amplitude ship motion simulations could be used as well.
Acknowledgements
The work reported herein was performed during the author's stay at the Laboratory of Ship Hydromechanics of the Delft University of Technology. The author is grateful to professor J.A.Pinkster and staff for inspiring discussions and for their assistance in model testing in particular. The research was financially supported by the Royal Netherlands Navy.
References
[1] M.Kac and A.J.F.Siegert. On the theory of noise in radio receivers with square law detecters . Journal of Applied Physics, 18:383– 397, 1947.
[2] N.Wiener. Nonlinear problems in random theory. M. I. T. Press, Cambridge, Mass., 1958.
[3] K.Hasselmann. On nonlinear ship motions in irregular waves. Journal of Ship Research, 10:64–68, 1966.
[4] J.F.Dalzell. The applicability of the functional polynomial input-output model to ship resistance in waves. Technical Report SIT-DL-75–1794, Stevens Inst. of Technology, Hoboken, New Jersey, 1975.
[5] J.A.Pinkster. Low frequency second order wave exciting forces on floating structures. PhD thesis, Techn. Univ. of Delft, 1980.
[6] M.H.Kim and D.K.P.Yue. Sum- and difference-frequency wave loads on a body in unidirectional gaussian seas. Journal of Ship Research, 35(2):127–140, 1991.
[7] J.J.Jensen and P.T.Pedersen. Bending moments and shear forces in ships sailing in irregular waves . Journal of Ship Research, 25:243– 251, 1981.
[8] M.S.Longuet-Higgins. The effect of nonlinearities on statistical distributions in the theory of sea waves. Journal of Fluid Mechanics, 17:459– 480, 1963.
[9] T.Vinje and S.O.Skjørdal. On the calculation of the statistical distribution of maxima and minima of slightly non-linear, quadratic, stationary stochastic variables . International Shipbuilding Progress, 22:265–274, 1975.
[10] J.J.Jensen. Fatigue analysis of ship hulls under non-gaussian wave loads. In Marine Structures, Design, Construction and Safety, pages 279–294. Elsevier Applied Science, 1991.
[11] J.F.Dalzell. An investigation of the applicability of the third degree functional polynomial model of nonlinear ship motion problems. Technical Report SIT-DL-82–9-2275, Stevens Inst. of Technology, Hoboken, New Jersey, December 1982.
[12] J.F.Dalzell. Approximations to the probability density of maxima and minima of the response of a nonlinear system. Technical Report EW-22–84, US Naval Academy, Annapolis, Maryland, 1984.
[13] S.R.Winterstein. Nonlinear vibration models for extremes and fatigue. Journal of Eng. Mech., ASCE, 114(10):1772–1790, 1988.
[14] J.F.Dalzell. An investigation of midship bending moments experienced in extreme regular waves by a Mariner-type ship and three variants. Technical Report SSC-155, Ship Structure Committee, 1964.
[15] J.F.Dalzell. An investigation of midship bending moments experienced in extreme regular waves by models of a tanker and a destroyer. Technical Report SSC-156, Ship Structure Committee, 1964.
[16] D.C.Murdey. An analysis of longitudinal bending moments measured on models in head waves. Transactions of Royal Institute of Naval Architects, 114:221–240, 1972.
[17] W.C.E.Nethercote. Motions and bending moments of a warship design. Transactions of Royal Institute of Naval Architects, 123:353– 375, 1981.
[18] J.F.O'Dea, E.Powers, and J.Zselecsky. Experimental determination of nonlinearities in vertical plane ship motions. In Proc. of 19th Symp. on Naval Hydrodynamics, pages 53–70, Seoul, Korea, 1992.
[19] L.J.M.Adegeest. Experimental results of motion, shear force and bending moment measurements in large amplitude regular waves for a wigley model with bowflare . Technical Report 975, Delft University of Technology, Ship Hydromechanics Laboratory, 1993.
[20] L.J.M.Adegeest. Experimental investigation of the influence of bow flare and forward speed on the nonlinear vertical motions, bending moments and shear forces in extreme regular waves. Technical Report 993 MEMT 32, Delft University of Technology, Ship Hydromechanics Laboratory, February 1994.
[21] L.J.M.Adegeest. Nonlinear Hull Girder Loads in Ships. PhD thesis, Delft University of Technology, The Netherlands, 1995.
[22] J.S.Bendat. Nonlinear System Analysis & Identification from Random Data. John Wiley and Sons, 1990.
[23] L.J.M.Adegeest. Third-order volterra modeling of ship responses based on regular wave results. Technical Report 988 MEMT 30, Delft University of Technology, Ship Hydromechanics Laboratory, 1994.
[24] P.H.Wirsching and A.Moshen Shehata. Fatigue under wide band random stresses using the rain-flow method . Journal of Engineering Materials and Technology, 99(3):205–211, 1977.
Nomenclature
DISCUSSION
L.J.Doctors
University of New South Wales, Australia
The computed results seem to show that there is much more nonlinearity in the responses for the forces and moments than for the motions themselves. Is this simply due to the factor that the frequencies associated with the harmonics are higher and that the forces and moments depend on temporal derivatives of the motions?
AUTHOR'S REPLY
As mentioned by the discussor, the measured hull girder loads showed a much more pronounced nonlinear behavior than the motions did. To explain this phenomenon, it is necessary to explain the physical origin of the loads. In general, hull girder loads are defined as the forces and moments in a hull cross-section, i.e., the “internal loads,” which make equilibrium with the net external forces and moments and the inertial reactions of the ship. The external loads are the net result of a pressure integration over the hull surface.
There are two reasons for the observation of much more pronounced nonlinearities in the hull-girder loads than in the motion responses. The first reason is the dominance of inertial effects in the hull girder loads. As illustrated by equation (2), the relative magnitudes of amplitudes of higher order effects in time-varying signals are increased simply by a time-derivation of the signal. It should be understood that the acceleration of the vessel is the net result of the global mass inertia characteristics of the vessel and of the overall excitation forces. The second reason is the sensitivity of hull girder loads to local external forces. Locally, the external forces acting on a part of the vessel can behave much more nonlinearly than the overall forces. This is because the local nonlinear force contributions are smoothed out over the whole surface. The internal loads are directly affected by these local nonlinearities in the bow and aft region of the vessel, especially in the case of bow flare in combination with large relative motions. Even then, it is possible that hardly any nonlinear behavior can be observed in the motion responses.
















