Nonlinearly Interacting Responses of the Two Rotational Modes of Motion—Roll and Pitch Motions
I.-G. Oh (Samsung Heavy Industries, Korea), A.Nayfeh (Virginia Polytechnic Institute and State University, USA)
ABSTRACT
The nonlinear dynamic responses and stability of marine vehicles are investigated when they are excited by regular waves. When the vehicles are under the condition of a two-to-one internal or autoparametric resonance in which the natural frequency of the pitch mode is twice that of the roll mode, they may exhibit large-amplitude responses in an indirectly excited mode by the direct excitation of the other mode. Moreover, it is known that the damping in the roll mode is a highly viscous and thus a strongly nonlinear one while that in the pitch mode a linear one over a relatively wide range of motions.
The problem is modeled mathematically by a dissipative nonlinear two-degree-of-freedom system subject to harmonic external excitations in the presence of a two-to-one internal resonance. Also to take into account the damping effects, a linear-plus-quadratic damping model is introduced in the equation for the roll mode while a linear damping model is kept in the equation for the pitch mode. The method of multiple scales is used to determine the influence of the quadratic nonlinear roll damping on the periodic responses of both modes and their stability.
The cases when the encounter frequency is near the natural frequency of the pitch mode and when the encounter frequency is near the natural frequency of the roll mode are investigated to provide the force-response curves and frequency-response curves.
1.
INTRODUCTION
The extent of the motion that a marine vehicle may experience has important consequences on its safety, operability, and economical aspects. So, one must understand the complicated dynamics of a vessel moving in a general environment to design more comfortable and safe vessels.
Loss of stability due to excessive motions, such as heavy rolling, can happen through the energy transfer between the modes of motion if nonlinearities are present and various resonances of the internal, external, or parametric type occur. The present research is concerned with the dynamic stability and excessive motion of a vessel in the presence of two-to-one internal or autoparametric resonance in which the natural frequency in pitch is twice that in roll.
The significance of internal resonance has been recognized recently in many mechanical and elastic systems. To model the mechanism of nonlinear interactions between modes, one needs to model the system by two or more nonlinearly coupled oscillators. There are a number of references dealing with physical two-degree-of-freedom systems. Among others, Nayfeh and Mook (1) discussed problems involving the forced responses of robots, elastic pendulums, beams and plates under static loadings, composite plates, arches, shells, and the sloshing of liquid gasoline in the fuel container of an airplane. All of these problems can be modeled by coupled, inhomogeneous ordinary-differential equations with quadratic nonlinearities. When these systems possess internal (or autoparametric) resonances, which may occur if the natural frequencies of the system are commensurate, their responses may exhibit extraordinarily complicated behaviors, which cannot be explained by linear formulations.
Interestingly, two-to-one autoparametric or internal resonances may strongly influence the dynamic behavior and stability of vessels (1). A strong coupling of the involved modes of motion produced by internal or autoparametric resonance was first observed by Froude in 1863. He observed that a vessel whose linear undamped natural frequency in
pitch is twice that in roll (2) has undesirable seakeeping characteristics. This observation was a manifestation of the two-to-one internal resonance whose significance cannot be determined using linearized equations (3, 4, 5, 6, 7).
For a century after Froude, however, no further research on this phenomenon was pursued. In 1959, Paulling and Rosenberg (8) studied the coupled heave-roll motion of a vessel using a set of nonlinear ordinary-differential equations. They simplified the equations of motion and obtained a single roll equation having the form of a simple linear Mathieu equation which contains a time-varying coefficient due to a simple harmonic motion of the heave mode. In this model, the heave influences the roll but the roll does not influence the heave. Experimentally, they tested the case of unstable rolling motion excited by the heave mode only. This study has two principal shortcomings. First, due to the lack of consideration for damping and nonlinear coupling terms, the analytical model was not capable of yielding realistic results. Second, in the experimental setup, the heave mode was given a prescribed motion and hence the effect of roll motion and waves generated thereafter on the heave mode are not taken into account.
Kinney (9), Kerwin (10), Blocki (11), and Sanchez and Nayfeh (12) also studied the response of the roll to longitudinal waves. Except for Blocki's study, all other studies are theoretical ones. In his experiment, Blocki considered coupling of the heave and roll modes of a ship that possesses fore and aft symmetry, which is placed in beam waves. As in the study of Paulling and Rosenberg, he studied the case of parametrically excited roll motions in which energy is fed to the roll mode by a prescribed heave or pitch motion, or equivalently, wave motion. His equations reduce essentially to a one-degree-of-freedom model governing only the roll mode.
To explain Froude's observation, Nayfeh, Mook, and Marshall (13) and Mook, Marshall, and Nayfeh (14) modeled the ship motion by two nonlinearly coupled equations involving the pitch and roll modes; they included the dependence of the pitching moment on the roll orientation. Thus, the pitch (heave) motion is not prescribed but is coupled to the roll motion, and consequently, the pitch (heave) and roll orientations are determined simultaneously as functions of a prescribed excitation. They clearly showed the significance of the frequency ratio in causing undesirable roll behaviors, such as the “saturation” phenomenon. They offered an explanation of the observations of Froude.
Nayfeh (15) considered the nonlinearly coupled roll and pitch motions of a ship in regular head waves in which the couplings are primarily in the hydrostatic terms when the pitch frequency is approximately twice the roll frequency and the encounter frequency is near either the pitch or roll natural frequency. He demonstrated the saturation phenomenon when the encounter frequency is near the pitch natural frequency.
In the present paper, we use a linear-plus-quadratic damping model for the roll motion and investigate the cases of primary resonances. The linear-plus-quadratic damping model has long been recognized by investigators to describe closely the dissipation of energy in the roll mode. However, it was not used so far because of some analytical difficulties. We obtain various complicated responses, which are common features of the nonlinear dynamics of many mechanical and elastic systems. These responses include supercritical and subcritical instabilities, periodic motions, and coexistence of multiple solutions and associated jumps. The quadratic damping eliminates the saturation phenomenon. Such phenomena can never be addressed by the linear approach because it is incapable of representing not only the strong nonlinear interaction between the two modes but also the effect of the viscous damping in the roll mode.
2.
EQUATIONS OF MOTION
We consider the response of a ship that is restricted to pitch and roll to a regular wave. We assume that the ship is laterally symmetric. We use the right-handed coordinate systems: a body-fixed coordinate system oxyz such that its origin o is at the center of mass, the x-axis is positive toward the bow, the y-axis is positive toward starboard, and the z-axis is positive downward. The orientation of the ship with respect to an inertial frame OXYZ is defined by the Euler angles ![]() and θ as follows: θ is a pitch rotation about the original y-axis, and
and θ as follows: θ is a pitch rotation about the original y-axis, and ![]() is a roll rotation about the new x-axis. The components p and q of the angular velocity about the x- and y-axes are related to
is a roll rotation about the new x-axis. The components p and q of the angular velocity about the x- and y-axes are related to ![]() ,θ,
,θ, ![]() and
and ![]() by
by
(1)
The equations of motion can be written as
Ixx![]() –Ixzpq=K+Ko cosΩt (2)
–Ixzpq=K+Ko cosΩt (2)
Iyy![]() +Ixzp2=M+M0 cos(Ωt+τ) (3)
+Ixzp2=M+M0 cos(Ωt+τ) (3)
where Ixx,Iyy, and Ixz are the moments and product of inertia, Ω is the encounter frequency, K0 and M0 are the amplitudes of the moments produced by the waves, and τ is a phase; they are assumed constants. We assume that the hydrodynamic moments K and M are analytic functions of ![]() and θ and their derivatives. Following Nayfeh (15) and Nayfeh, Mook, and Marshall (16) and including a quadratic damping term in the roll equation, we obtain
and θ and their derivatives. Following Nayfeh (15) and Nayfeh, Mook, and Marshall (16) and including a quadratic damping term in the roll equation, we obtain
(4)
(5)
where ε is a small dimensionless parameter that is introduced as a bookkeeping device in the perturbation analysis that follows.
3.
ANALYSIS
We use the method of multiple scales (17,18) to determine a first-order approximation to the solutions of equations (4) and (5). We let
(6)
θ(t;ε)=θ0(T0,T1)+εθ1(T0,T1)+… (7)
where T0=t is a fast time scale, characterizing motions on the scales ω1 and Ω; and T1=εt is a slow time scale, characterizing the modulation of the amplitudes and phases of the motion. In terms of T0 and T1, the time derivatives are transformed into
and ![]()
(8)
where Dn=∂/∂Tn.
Substituting equations (6)–(8) into equations (4) and (5) and equating coefficients of like powers of ε, we obtain
O(ε0):
(9)
(10)
O(ε):
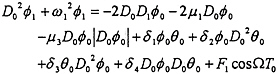
(11)
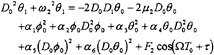
(12)
The solutions of equations (9) and (10) can be expressed as
(13)
(14)
where A1 and A2 are unknown functions at this level of approximation. They are determined by imposing the solvability conditions at the next level of approximation. Alternatively, the solutions of equations (13) and (14) can be expressed as
![]() 0=a1(T1)cos[ω1T0+β1(T1)] (15)
0=a1(T1)cos[ω1T0+β1(T1)] (15)
θ0=a2(T1)cos[ω2T0+β2(T1)] (16)
where the an and βn are the amplitudes and phases of the roll and pitch modes. Comparing equations (13) and (14) with equations (15) and (16), we conclude that
(17)
Substituting equations (13) and (14) into equations (11) and (12) yields
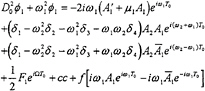
(18)
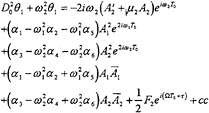
(19)
where the prime indicates the derivative with respect to T1, is ![]() the complex conjugate of An, and the function f accounts for the term –µ3D0
the complex conjugate of An, and the function f accounts for the term –µ3D0![]() 0|D0
0|D0![]() 0|. Depending on the functions An, particular solutions of equations (18) and (19) contain terms proportional to
0|. Depending on the functions An, particular solutions of equations (18) and (19) contain terms proportional to ![]() (i.e., secular terms). They also contain small-divisor terms if Ω ≈ ω1 or Ω ≈ ω2 (i.e., primary resonances of the pitch or roll mode) and/or if ω2 ≈ 2ω1 (the frequency of pitch mode is approximately twice that of roll mode; i.e., two-to-one internal or autoparametric resonance).
(i.e., secular terms). They also contain small-divisor terms if Ω ≈ ω1 or Ω ≈ ω2 (i.e., primary resonances of the pitch or roll mode) and/or if ω2 ≈ 2ω1 (the frequency of pitch mode is approximately twice that of roll mode; i.e., two-to-one internal or autoparametric resonance).
To eliminate the secular and small-divisor terms, we first expand f(D0![]() 0) in a Fourier series as
0) in a Fourier series as
(20)
where
(21)
Consequently, the component of f that produces a secular term is
(22)
We analyze the case of primary resonance of the pitch mode in Section 4 and of primary resonance of the roll mode in Section 5.
4.
PRIMARY RESONANCE OF THE PITCH MODE
4.1
Modulation Equations
To express the nearness of the resonances, we introduce two detuning parameters, σ1 and σ2, defined as
ω2=2ω1+εσ1 and Ω=ω2+εσ2 (23a)
Hence,
ω2T0=2ω1T0+σ1T1 and ΩT0=ω2T0+σ2T1 (23b)
Using equations (23) and (22) and eliminating the terms that produce secular terms from equations (18) and (19), we obtain
(24)
(25)
where
(26)
(27)
(28)
Nayfeh (15) and Nayfeh, Mook, and Marshall (13) concluded that Λ1 and Λ2 have the same sign; otherwise, the unforced ship would be self-oscillating, which is unrealistic due to dissipation.
Substituting equation (17) into equations (24) and (25), rewriting equation (15) as
![]() 0=a1(T1)cosχ1, χ1=ω1T0+β1(T1) (29)
0=a1(T1)cosχ1, χ1=ω1T0+β1(T1) (29)
After seperating real and imaginary parts of equations (24) and (25) and evaluating the terms corresponding to the last term in equation (24) by replacing the function f with –µ3D0![]() 0|D0
0|D0![]() 0|, we obtain
0|, we obtain
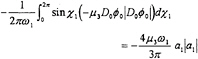
(30)
(31)
Applying the appropriate transformation of variables, we obtain a generic system of equations as follows:
(32)
(33)
(34)
(35)
where
γ1=σ1T1+β2–2β1 and y2=σ2T1–β2+τ (36)
4.2
Fixed Points
We investigate the fixed points of the modulation equations (32)–(35), which correspond to periodic responses of the ship. They correspond to ![]() and
and ![]() It follows from equation (36) that
It follows from equation (36) that
(37)
Hence, the fixed points of equations (32)–(36) are given by
(38)
(39)
(40)
(41)
There are two possible solutions for equations (38)–(41). First,
(42)
and the response is given by
![]() =0 and θ=a2 cos(Ωt+τ–γ2)+… (43)
=0 and θ=a2 cos(Ωt+τ–γ2)+… (43)
which is essentially the linear solution. Second,
(44)
and a1 is given by the algebraic equation
(45)
where ci (i=0,1,2, and 3) are constant coefficients determined from control parameters in use, such as σ1,σ2,µ1,µ2,µ3,f2, and ω1; they are given by
(46)
(47)

(48)
(49)
The response in this case is given by
(50)
θ=a2 cos(Ωt+τ–y2)+… (51)
We note from equations (44) and (45) that if a1=0, then c0=0 and thus this second solution reduces to the first solution (42); that is, the linear solution.
When µ3=0, but a1≠0, equation (44)
becomes
(52)
which is independent of a1 and f2. Moreover, c1=c3=0, then we obtain
(53)
where
(54)
(55)
The solution (52)–(55) is a special case of the second solution given by equations (44) and (45) and indicates the saturation phenomenon.
We note that the second solution (44)–(51) does not exhibit the saturation phenomenon unless µ3=0. Instead, the amplitude a2 of the directly excited pitch mode as well as the amplitude a1 of the roll mode vary as functions of f2. We have developed a computer code to solve equation (45) for a1. Then, a2 is obtained from equation (44) and the corresponding γ1 and γ2 (β1 and β2 also) are obtained from equations (38)–(41).
4.3
Stability of Fixed Points
The stability of the fixed points and hence the stability of the periodic responses are determined in the following manner using the modulation equations (32)–(36).
The stability of a fixed point depends on the real parts of the eigenvalues of the Jacobian matrix A; that is, the roots of
|A–λI|=0 (56)
where
A=∇F(![]() 0) (57)
0) (57)
is the Jacobian matrix evaluated at a given fixed point ![]() 0 and F is a real four-dimensional vector function of the four-dimensional vector
0 and F is a real four-dimensional vector function of the four-dimensional vector ![]() =(a1,a2,γ1,γ2)T. A given fixed point is asymptotically stable if and only if all the λ's lie in the left half of the complex plane and is unstable if at least one eigenvalue lies in the right half of the complex plane. If the real part of a pair of complex-conjugate eigenvalues is positive, the modulation equations possess either periodically or chaotically modulated solutions.
=(a1,a2,γ1,γ2)T. A given fixed point is asymptotically stable if and only if all the λ's lie in the left half of the complex plane and is unstable if at least one eigenvalue lies in the right half of the complex plane. If the real part of a pair of complex-conjugate eigenvalues is positive, the modulation equations possess either periodically or chaotically modulated solutions.
A Hopf bifurcation point is defined as a critical value of a control parameter at which a pair of complex-conjugate eigenvalues of the Jacobian matrix cross the imaginary axis into the right half of the complex plane with nonzero speed. This type of loss of stability fits the Hopf bifurcation theorem, according to which the modulation equations possess limit-cycle solutions near the bifurcation points.
We note again that fixed points of the modulation equations correspond to periodic oscillations of the pitch and roll modes. Moreover, limit-cycle solutions of the modulation equations correspond to two-period quasiperiodic pitch and roll motions. Furthermore, chaotic solutions of the modulation equations correspond to chaotically modulated motions. Consequently, the response is an amplitude- and phase-modulated combined pitch and roll motion, with the energy being continuously exchanged between the two modes.
4.4
Numerical Results and Discussion
We implemented the computer simulations using an IBM 3090 digital supercomputer. The fixed-point solutions are verified by numerically integrating the autonomous amplitude- and phase-modulation equations (32)–(35) using a 5th- and 6th-order Runge-Kutta-Verner algorithm with double precision arithmetics. We examined bifurcations as we vary a bifurcation parameter, such as the detuning parameter σ2, the excitation amplitude f2, or the quadratic damping coefficient µ3 while all the other parameters (i.e., σ1, µ1, µ2) are kept constant.
We point out here that the existence of real solutions for a1 and a2 can be determined by examining equations (44) and (45). From equation (44), we can say that a2 is real if a1 is real, where a1 is determined from equation (45). Because equation (45) is a fourth-order algebraic equation, an analytic solution for a1 is not readily available. To determine the region where a1 is real, we use
analytical continuations starting from µ3=0. Thus, we start by putting µ3 equal to zero and obtain equations (52)–(55).
For simplicity in further discussion, we define the following two critical values of f2:
ζ1=|Γ2| (58)
(59)
It is clear that ζ1≤ζ2. It follows from equation (53), that f2 must be greater than or equal to |Γ2| (i.e., f2≥|Γ2|=ζ1) for a1 to be real. Then, there are two possibilities, depending on whether Γ1 is positive or negative. When Γ1<0, there is only one real root of equation (53) when ![]() When Γ1>0, equation (53) has two real roots when
When Γ1>0, equation (53) has two real roots when ![]() or ζ1≤f2≤ζ2 and one real root when
or ζ1≤f2≤ζ2 and one real root when ![]() or f2≥ζ2.
or f2≥ζ2.

Fig. 1 (a) Force-Response Curves (Supercritical Type): for µ3=0 and 0.6; stable(—), unstable(…)
4.4.1
Breaking of Saturation in Force-Response Curves
Figures 1 show the results for µ3=0 and µ3≠0 when µ1=0.2, µ2=0.5, σ2=0.3, σ1= 0.1, and thus Γ1=–0.04. Figure 1 (a) shows typical force-response curves of the supercritical-type in which a1 and a2 vary with f2 for µ3=0 and
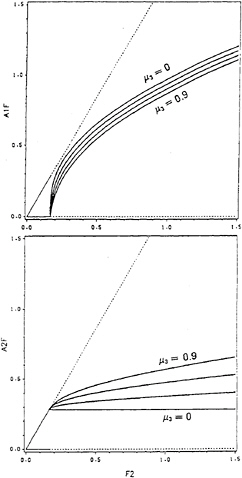
Fig. 1 (b)&(c) Force-Response Curves Supercritical Type): variation of (b) roll amplitude a1 and (c) pitch amplitude a2, for different values of µ3; stable(—), unstable(…)
µ3 = 0.6, a typical value of nonzero µ3. Since Γ1 <0 in this case, equation (53) has one stable real root for f2 ≥ ζ2 (ζ2 ≈ 0.1649), irrespective of whether µ3 = 0 or µ3 ≠ 0. When f2 ≤ ζ2, the responses are given by equation (43); their amplitudes are given by (42), which are independent of µ3. Thus, the response is linear in which the roll motion is not excited while the amplitude of the pitch mode is proportional to f2. When f2 > ζ2, the responses are given by equations (50) and (51); their amplitudes are given by (52) and (53) for µ3 = 0 and by (44) and (45) for µ3 ≠ 0. We note that when µ3 ≠ 0 the amplitude a2 of the pitch mode no longer exhibits the saturation phenomenon which exists for µ3 = 0. Thus, the quadratic damping µ3 breaks the saturation. Instead, the amplitude a2 of the pitch mode grows nonlinearly rather than staying at a constant value ![]() as f2 increases beyond ζ2. We note, however, that the slope of a2 for f2 ≥ ζ2 is still much less than that corresponding to the linear case. With the introduction of the quadratic damping µ3, the rate of increase of the amplitude a1 of the roll mode with f2 is less than that in the case of µ3 = 0. Consequently, as f2 increases beyond the bifurcation point ζ2, not all the extra energy input to the pitch mode is spilled over into the roll mode.
as f2 increases beyond ζ2. We note, however, that the slope of a2 for f2 ≥ ζ2 is still much less than that corresponding to the linear case. With the introduction of the quadratic damping µ3, the rate of increase of the amplitude a1 of the roll mode with f2 is less than that in the case of µ3 = 0. Consequently, as f2 increases beyond the bifurcation point ζ2, not all the extra energy input to the pitch mode is spilled over into the roll mode.
Figure 1 (b) shows variation of the amplitude a1 of the roll mode with f2 for different values of the quadratic roll damping coefficient µ3. We note that, for a given f2, a1 decreases as µ3 increases. While a ship is being operated in the ocean, the surface of the ship hull gets rougher and rougher due to peeling-off of paint or foul bottom. As a result, the magnitude of the quadratic damping coefficient will increase, producing a behavior as discussed here. Figure 1 (c) shows force-response curves for the pitch mode corresponding to Figure 1 (b). It is clear that the saturation phenomenon of the pitch mode no longer exists when µ3 is different from zero. Moreover, for a given f2, the amplitude a2 of the pitch mode increases with increasing quadratic roll damping coefficient µ3.
Figures 2 show typical force-response curves when Γ1 > 0 (Γ1 = 0.2484) when µ1 = µ2 = 0.04 and σ1 = σ2 = 0.5 for µ3 = 0 and µ3 ≠ 0. Figure 2 (a) shows typical force-response curves of the subcritical-instability type for µ3 = 0 and µ3 = 0.6. Since Γ1 > 0 in this case, equation (53) has only one stable real root for f2 ≥ ζ2 (ζ2 ≈ 0.2517) for µ3 = 0 and µ3 ≠ 0; two real roots for ζ1 ≤ f2 ≤ ζ2, where ζ1 ≈ 0.04 when µ3 = 0 and ζ1 ≈ 0.1020 when µ3 = 0.6. In the latter case, the larger root is stable whereas the smaller one is unstable. We note that the larger bifurcation value ζ2 is independent of the value of µ3, whereas the smaller bifurcation value ζ1 increases as µ3 increases. When f2 ≤ ζ1, there exists only one stable response given by equation (43), which is linear and consists of only the pitch mode. When ζ1 ≤ f2 ≤ ζ2, two stable solutions coexist with an unstable solution; one of the stable responses is given by equation (43), and the other stable solution is given by equations (50) and (51). The response of the ship in this region depends on the initial conditions. When f2 ≥ ζ2, there exists only one stable response given again by equations (50) and (51). We note that the response of the roll mode exhibits the coexistence of two stable motions and the associated jump phenomenon for both µ3 = 0 and µ3 = 0.6. The saturation phenomenon of the response of the pitch mode, which exists when µ3 = 0, does not exist
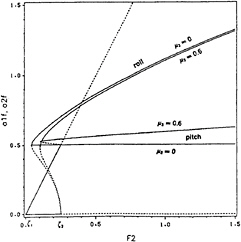
Fig. 2 (a) Force-Response Curves (Subcritical Type): for µ3=0 and 0.6; stable(—), unstable(…)
when µ3 = 0.6. When µ3 = 0.6, the amplitude a2 of the pitch mode grows rather than remains constant as f2 increases beyond ζ2. We refer to this phenomenon as “breaking of saturation”. We note, here again, that for a given f2 ≥ ζ1, a2 increases as µ3 increases. As in Figure 1 (a), for a given f2, a1 decreases as µ3 increases.
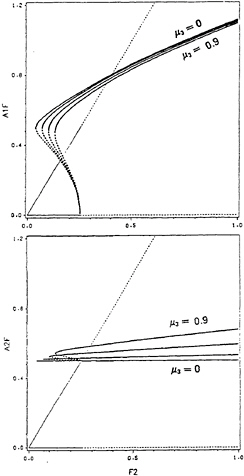
Fig. 2 (b)&(c) Force-Response Curves (Subcritical Type): variation of (b) roll amplitude a1 and (c) pitch amplitude a2, for different values of µ3; stable(—), unstable(…)
Figure 2 (b) shows variation of the amplitude a1 of the roll mode with f2 for different values of the quadratic roll damping coefficient µ3. We note that a1 decreases as µ3 increases, as in Figure 1 (b). As µ3 increases, the bifurcation value ζ1 increases while ζ2 does not change. For example, ζ1 = 0.0715, 0.1020, and 0.1313 when µ3 = 0.3, 0.6, and 0.9, respectively. Hence, the overhang region between ζ1 and ζ2 decreases as µ3 increases. This indicates that the bifurcation values ζ1 and ζ2 can coalesce as µ3 increases, which results in the qualitative change of the responses from the subcritical type into the supercritical type. Then, when this happens, the response of the roll mode would no longer exhibit the coexistence of two stable motions and the subsequent jump phenomenon for large values of the quadratic roll damping coefficient µ3.
Figure 2 (c) shows the force-response curves of the pitch mode corresponding to Figure 2 (b). We note here again that the saturation phenomenon of the pitch mode no longer exists when µ3 is different from zero. Moreover, the pitch amplitude a2 increases as µ3 increases.
We conclude from Figures 1 (a)–(c) and 2 (a)– (c) that the mechanism of energy transfer from the directly excited pitch mode to the indirectly excited roll mode becomes less effective as the quadratic damping coefficient µ3 of the roll mode increases. When µ3 is zero, all the extra energy into the pitch mode after saturation is transferred to the indirectly excited roll mode. When µ3 is different from zero, only part of the energy input into the pitch mode is transferred to the roll mode.
4.4.2
Effect of Quadratic Roll Damping on Frequency-Response Curves
In Figures 3, we show frequency-response curves when µ1=µ2=0.02, σ1=0.12, and f2=0.1 for µ3=0 and µ3≠0. Figure 3 (a) shows typical frequency-response curves when µ3 = 0 and µ3 = 0.6. We note that the reversed pitchfork bifurcation points are independent of the value of µ3, whereas the saddle-node bifurcation points move closer to the reversed pitchfork bifurcation points as µ3 increases. We also note that the jump phenomenon in the response of the roll mode exists for
both µ3 = 0 and µ3 = 0.6. The interval –0.047 ≤ σ2 ≤ –0.0127 between the Hopf bifurcation points when µ3 = 0 disappears or becomes indiscernible when µ3 = 0.6. In this interval, the real part of a pair of complex-conjugate roots of equation (56) is positive, and hence the response is an amplitude- and phase-modulated combined pitch and roll motion. The frequency-response curves are shifted slightly leftward with respect to σ2 = 0 because the detuning σ1 is positive. They would be shifted to the right if σ1 is negative, and they would be symmetric with respect to σ2 = 0 if σ1 = 0; that is, the case of perfect tuning. The qualitative behavior of the solutions in the three cases is the same.
Figure 3 (b) shows variation of the amplitude a1 of the roll mode with σ2 for different values of µ3. We note that, for a given σ2, a1 decreases as µ3 increases, except near σ2 = 0, where a1 is almost independent of µ3. Moreover, the reversed pitchfork bifurcation points are independent of µ3 but the saddle-node bifurcation points move closer to σ2 = 0 as µ3 increases. For example, the left saddle-node bifurcation points are –0.9367, –0.7091,
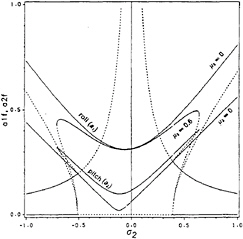
Fig. 3 (a) Frequency-Response Curves: for µ3 = 0 and 0.6; stable(—), unstable(…)
and –0.6066 whereas the right ones are 0.8729, 0.6442, and 0.5388 for µ3 = 0.3, 0.6, and 0.9, respectively. The reversed pitchfork bifurcation values are –0.5050 and 0.3950 for all values of µ3.
In Figure 3 (c), we show the frequency-response curves for the pitch mode corresponding to Figure 3 (b). We note that, for a given σ2, a2 increases as µ3 increases.
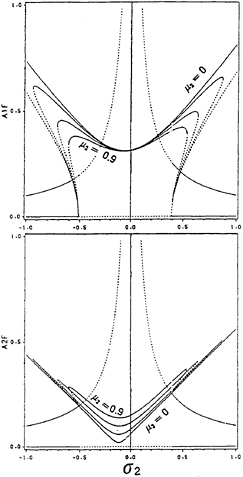
Fig. 3 (b)&(c) Frequency-Response Curves: variation of (b) roll amplitude a1 and (c) pitch amplitude a2, for different values of µ3; stable(—), unstable(…)
4.4.3
Hopf Bifurcation Region
Figure 4 shows the Hopf bifurcation curves in the parameter space σ2 – σ1 for different values of the quadratic roll damping parameter µ3 when µ1 = µ2 = 0.02 and f2 = 0.1. In the outer region, the fixed points of the modulation equations are asymptotically stable and hence correspond to periodic motions. On the transition curves, a complex conjugate pair of eigenvalues of the Jacobian matrix cross the imaginary axis into the right half of the complex plane with nonzero speed. The modulation equations possess limit-cycle solutions near the bifurcation curves. Between the two curves (i.e., in the inner region), oscillatory solutions, which may be either limit cycles or chaotic attractors, may be found.
Figure 4 shows that the Hopf bifurcation curves move upward and approach each other as the quadratic roll damping coefficient µ3 increases. This implies that increasing µ3 causes the disappearance of aperiodic responses.
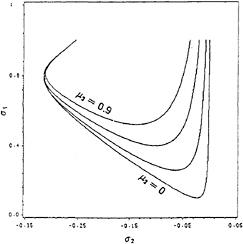
Fig. 4 Hopf Bifurcation Curves: for different values of µ3
5.
PRIMARY RESONANCE OF THE ROLL MODE
5.1
Modulation Equations
To express the nearness of the resonances, we let, Ω = ω1 + εσ2 and ω2 = 2ω1 + εσ1. Then,
ΩT0 = ω1T0 + σ2T1 (60)
and
ω2T0 = 2ω1T0 + σ1T1 (61)
Using equations (60), (61), and (22) to eliminate the terms that produce secular terms from equations (18) and (19), we obtain
(62)
(63)
where Λ1 and Λ2 are defined in equations (26) and (27) and
(64)
Substituting equation (17) into equations (62) and (63), using equation (29), and separating real and imaginary parts of equations (62) and (63), we obtain, after applying the appropriate transformation of variables, a generic system of equations as follows:
(65)
(66)
(67)
(68)
where
γ1 = σ1T1 + β2 – 2β1 and γ2 = σ2T1 – β1 (69)
and the evaluated results given in equations (30) and (31), which are the terms corresponding to the last term of equation (62), have been used.
5.2
Fixed Points
Periodic solutions of (4) and (5) correspond to the fixed points of equations (65)–(69). They are obtained by setting ![]() and
and ![]() It follows from equation (69) that
It follows from equation (69) that
(70)
Hence, the fixed points of equations (65)–(69) are given by the solutions of the following set of coupled nonlinear algebraic equations:
(71)
(72)
a1σ2 =–a1a2 cosγ1 – f1 cosγ2 (73)
(74)
Equations (71)–(74) can be manipulated to yield the following polynomial equation for a1:
(75)
where Di(i=0,1,…,5) are constant coefficients determined from control parameters in use, such as σ1, σ2, µ1, µ2, µ3, f1, and ω1; they are given by
(76)
d1 = 0, (77)
(78)
(79)
(80)
(81)
(82)
v1 = σ2, (83)
and v2 = 2σ2 – σ1. (84)
We note that if µ3 = 0, then d3 = d5 = 0 and d4 = 2µ1µ2 – 2v1v2. It follows from equations (71)– (74) that a2 is given by
(85)
The solutions of the sixth-order algebraic equation (75) are obtained numerically. Then, a2 is calculated from equation (85). Finally, the corresponding phases γ1 and γ2 (β1 and β2 also) are obtained from equations (71)–(74).
5.3
Stability of Fixed Points
The stability of the fixed-point solutions are determined by the same procedure used in Section 4; that is, by investigating the eigenvalues of the Jacobian matrix of equations (65)–(69).
Again, a given fixed point is asymptotically stable if and only if all the λ's lie in the left half of the complex plane and is unstable if at least one eigenvalue lies in the right half of the complex plane. If a pair of complex-conjugate eigenvalues crosses the imaginary axis with nonzero speed, then we have a Hopf bifurcation. Near these bifurcation points, the response is an amplitude- and phase-modulated combined pitch and roll motion, with the energy being continuously exchanged between the two modes.
5.4
Numerical Results and Discussion
In Figures 5, we show the frequency-response curves when µ1 = µ2 = 0.08, σ1 = 0, and f1 = 0.08 for different values of µ3. The unstable solutions are represented by broken lines and the stable solutions are marked by solid lines. Figures 5 (a) and (b) show variations of the roll amplitude a1 and pitch amplitude a2 with σ2 for different values of µ3. As µ3 increases from zero to 0.3, the reversed
pitchfork bifurcation points slightly change, whereas the saddle-node bifurcation points move towards σ2 = 0. As µ3 is increased further to 0.6 and 0.9, the saddle-node bifurcation points disappear and the frequency-response curves become single-valued. Consequently, the jump phenomenon and subcritical instability disappear. Moreover, the Hopf bifurcation points approach each other as µ3 increases. For example, the Hopf bifurcation interval –0.09995 ≤ σ2 ≤ 0.09995 for µ3 = 0 shrinks gradually to –0.055 ≤ σ2 ≤ 0.055 for µ3 = 0.9.
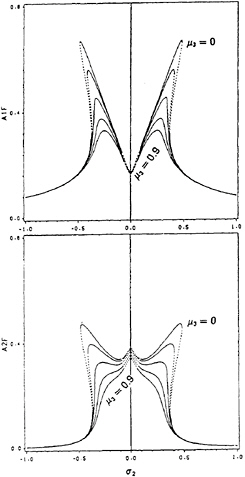
Fig. 5 (a) & (b) Frequency-Response Curves (σ1 = 0): variation of (a) roll amplitude a1 and (b) pitch amplitude a2, for different values of µ3; stable(—), unstable(…)
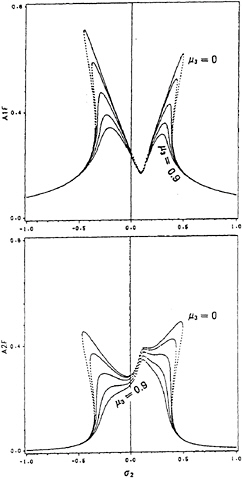
Fig. 6 (a) & (b) Frequency-Response Curves (σ1 = 0.2): variation of (a) roll amplitude a1 and (b) pitch amplitude a2, for different values of µ3; stable(—), unstable(...)
We note that for a fixed value of σ2, a1 and a2 decrease as µ3 increases. The curves of unstable fixed points around the region of perfect tuning, σ2≈0, converge in both modes. The introduction of quadratic roll damping µ3, by say attaching antirolling devices like bilge keels, causes the region between the two Hopf bifurcation frequencies (close to perfect resonance) to shrink. However, it does not eliminate complicated motions completely in this region.
Figures 6 show the frequency-response curves for the case in which the values of all the parameters are the same as those in Figures 5 except that σ1=0.2. In this case, the curves are shifted slightly to the right and the peak amplitudes of the right branches of the roll mode are smaller than those of the left branches. The opposite occurs in the response of the pitch mode. If σ1 is chosen to be negative, the frequency-response curves would be shifted to the left. When σ1=0, the case of perfect tuning, the curves would be symmetric with respect to σ2=0. The qualitative behavior of the solutions in the three cases is the same.
6.
SUMMARY AND CONCLUSIONS
To design more comfortable and safe vessels, one must understand the complicated dynamics of a vessel moving in a general environment. Included among the important dynamic parameters are the ratios of natural frequencies and the nonlinear interactions among the hydrostatic and hydrodynamic forces and moments. One of the objectives of the present work is to investigate the undesirable and potentially dangerous characteristics of the dynamics of a vessel.
It has been believed for a long time that the linear-plus-quadratic model could adequately describe the hydrodynamic damping of the roll motion. However, many investigators avoided using this model because of the difficulties in the analyses. In the present paper, a quadratic nonlinear damping model is introduced into the equation of the roll mode. We investigated the nonlinearly coupled pitch and roll response of a vessel in regular waves when the natural frequency in pitch is twice that of roll (a condition of a two-to-one internal or autoparametric resonance). The method of multiple scales was used to derive four first-order autonomous ordinary-differential equations for the modulation of the amplitudes and phases of the pitch and roll modes when either mode is excited. The modulation equations were used to determine the influence of the quadratic nonlinear damping on the periodic responses and their stability.
When the encounter frequency is near the pitch natural frequency, the jump phenomenon exists for both zero and nonzero quadratic roll damping (µ3 is the coefficient of the quadratic roll damping.). The saturation phenomenon is broken if a quadratic roll damping term is introduced. This implies that there is no critical value of the excitation amplitude beyond which all of the extra energy input to the pitch mode is spilled over into the roll mode. The amplitude of the roll mode decreases while that of the pitch mode increases as the magnitude of the quadratic roll damping µ3 increases. In the subcritical case of force-response and frequency-response curves, the overhang regions narrow down as µ3 increases. The fixed points of the modulation equations undergo a Hopf bifurcation as one of the control parameters is varied. Between the Hopf bifurcation points, the response is an amplitude- and phase-modulated motion consisting of both the pitch and roll modes.
When the encounter frequency is near the roll natural frequency, the amplitudes of both the roll mode and the pitch mode decrease as the magnitude of the quadratic roll damping coefficient µ3 increases. Again, Hopf bifurcations occur as either the encounter frequency or excitation amplitude is varied.
REFERENCES
1. Nayfeh, A.H. and Mook, D.T., Nonlinear Oscillations, Wiley, New York, 1979.
2. Froude, W., “Remarks on Mr. Scott-Russell's Paper on Rolling,” The papers of William Froude, published by the Institution of Naval Architects, 1995.
3. Evan-Iwanowski, R.M., Resonance Oscillations in Mechanical Systems, Elsevier Scientific Publishing Co., New York, 1976.
4. Haddow, A.G., Barr, A.D.S., and Mook, D.T., “Theoretical and Experimental Study of Modal Interaction in a Two-Degree-of-Freedom Structure,” Journal of Sound and Vibration, Vol. 97, 1984, pp. 451.
5. Hatwal, H., Mallik, A.K., and Ghosh, A., “Nonlinear Vibrations of a Harmonically Excited Autoparametric System, ” Journal of Sound and Vibration, Vol. 81, 1982, pp. 153.
6. Nayfeh, A.H. and Zavodney, L.D., “The Response of Two-Degree-of-Freedom Systems with Quadratic Nonlinearities to a Combination
Parameteric Resonance,” Journal of Sound and Vibration, Vol. 107, 1986, pp. 329.
7. Schmidt, G. and Tondl, A., Nonlinear Vibrations, Akademie-Verlag, Berlin, 1986.
8. Paulling, J.R. and Rosenberg, R.M., “On Unstable Ship Motions Resulting from Nonlinear Coupling,” Journal of Ship Research, Vol. 3, 1959, pp. 36.
9. Kinney, W.D., “On the Unstable Rolling Motions of Ships Resulting from Nonlinear Coupling with Pitch Including the Effect of Damping in Roll,” Series No. 173, Issue No. 3, 1961, Institute of Engineering Research, University of California, Berkeley.
10. Kerwin, J.E., “Notes on Rolling in Longitudinal Waves,” International Shipbuilding Progress, Vol. 2, 1955, pp. 597.
11. Blocki, W., “Ship Safety in Connection with Parametric Resonance of the Roll,” International Shipbuilding Progress, Vol. 27, 1980, pp. 36.
12. Sanchez, N.E. and Nayfeh, A.H., “Nonlinear Rolling Motions of Ships in Longitudinal Waves,” International Shipbuilding Progress, Vol. 37, 1990, pp. 247.
13. Nayfeh, A.H. and Mook, D.T., and Marshall, L. R., “Nonlinear Coupling of Pitch and Roll Modes in Ship Motion,” Journal of Hydronautics, Vol. 7, Oct. 1973, pp. 145.
14. Mook, D.T., Marshall, L.R., and Nayfeh, A.H., “Subharmonic and Superharmonic Resonances in the Pitch and Roll Modes of Ship Motions,” Journal of Hydronautics, Vol. 8, 1974, pp. 32.
15. Nayfeh, A.H., “On the Undesirable Roll Characteristics of Ships in Regular Seas, ” Journal of Ship Research, Vol. 32, 1988, pp. 92.
16. Nayfeh, A.H., Mook, D.T., and Marshall, L.R., “Perturbation-Energy Approach for the Development of the Nonlinear Equations of Ship Motion,” Journal of Hydronautics, Vol. 8, 1974, p. 130.
17. Nayfeh, A.H., Perturbation Methods, Wiley, New York, 1973.
18. Nayfeh, A.H., Introduction to Perturbation Techniques, Wiley, New York, 1981.
19. Oh, I.G., Theoretical and Experimental Nonlinear Dynamics of Floating Oscillatory System, Ph. D. Dissertation, Department of Engineering Science and Mechanics, Virginia Polytechnic Institute and State University , Blacksburg, Virginia, 1992.















